A Transfer Learning Remote Sensing Landslide Image Segmentation Method Based on Nonlinear Modeling and Large Kernel Attention
Abstract
1. Introduction
2. Materials and Methods
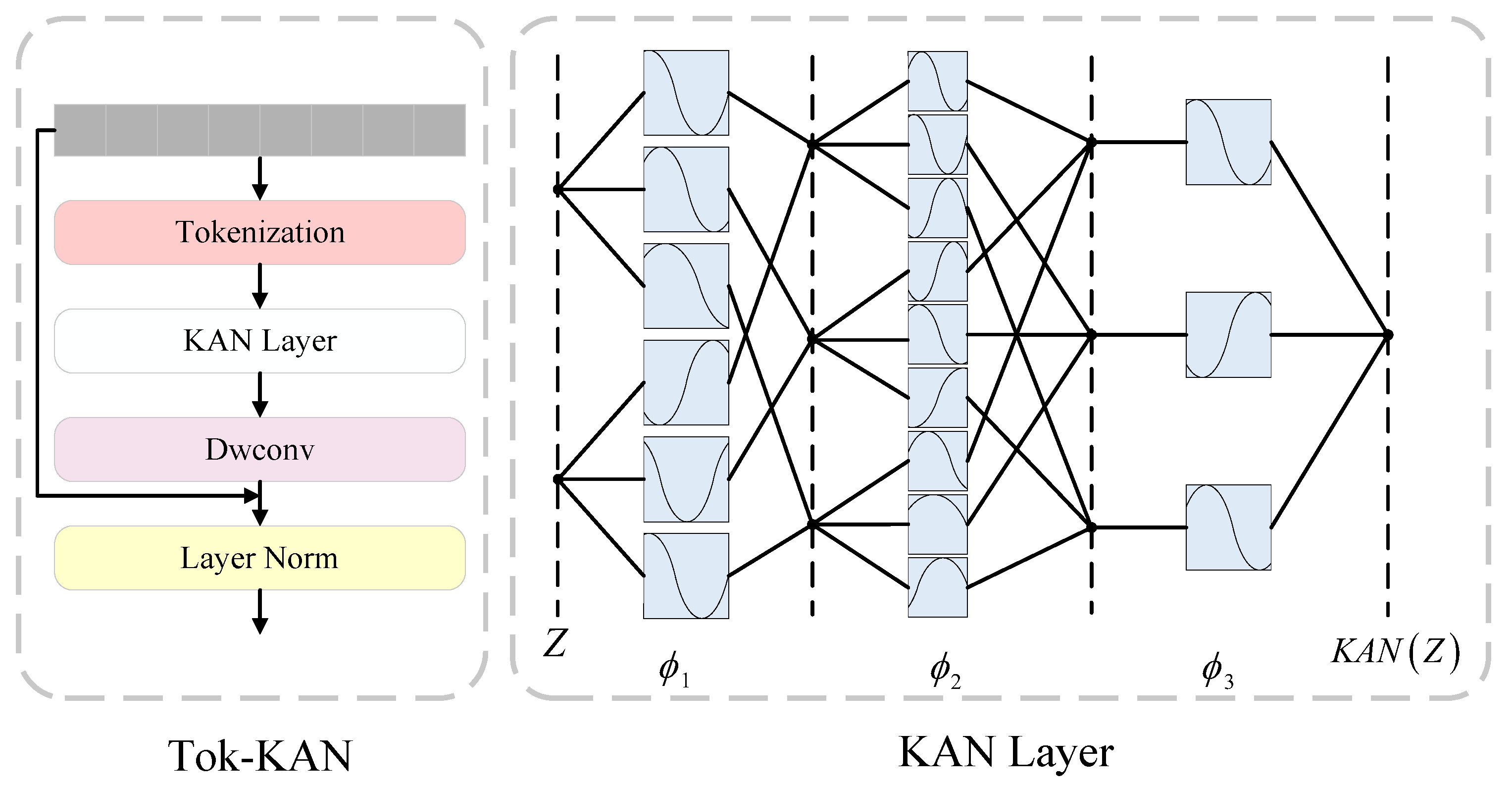
2.1. Tokenized KAN Block (Tok-KAN)
2.2. Dual Large Feature Fusion Selective Kernel Attention (DLFFSKA)
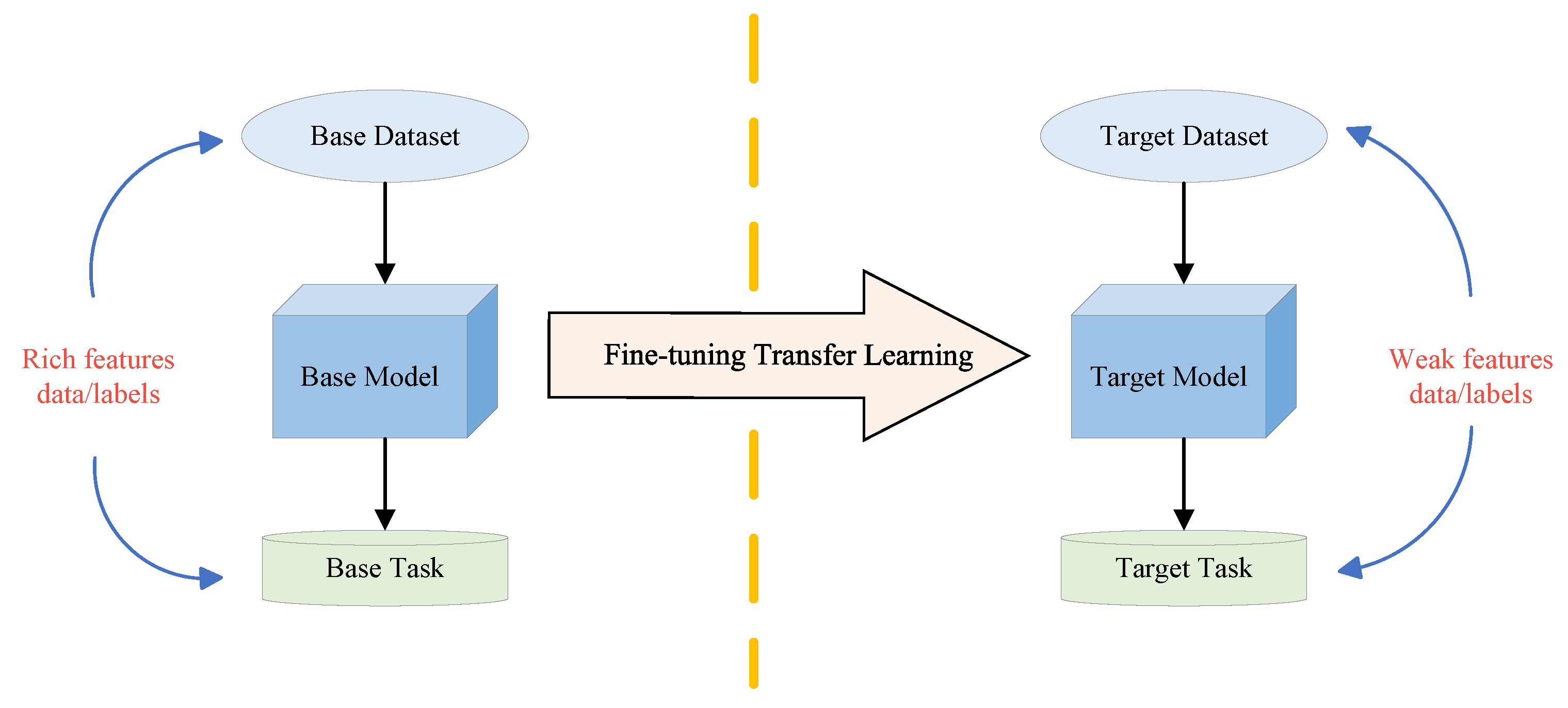
2.3. Fine-Tuning Transfer Learning (FTTL)
2.4. Dataset
2.4.1. Base Model Dataset
2.4.2. Target Model Dataset
2.5. Model Performance Evaluation Indicators
2.6. Experimental Set-Up
3. Results and Discussion
3.1. Ablation Experiment Results and Discussion
3.1.1. Tokenized KAN Block Ablation Experiment
3.1.2. Dual Large Feature Fusion Selective Kernel Attention Ablation Experiment
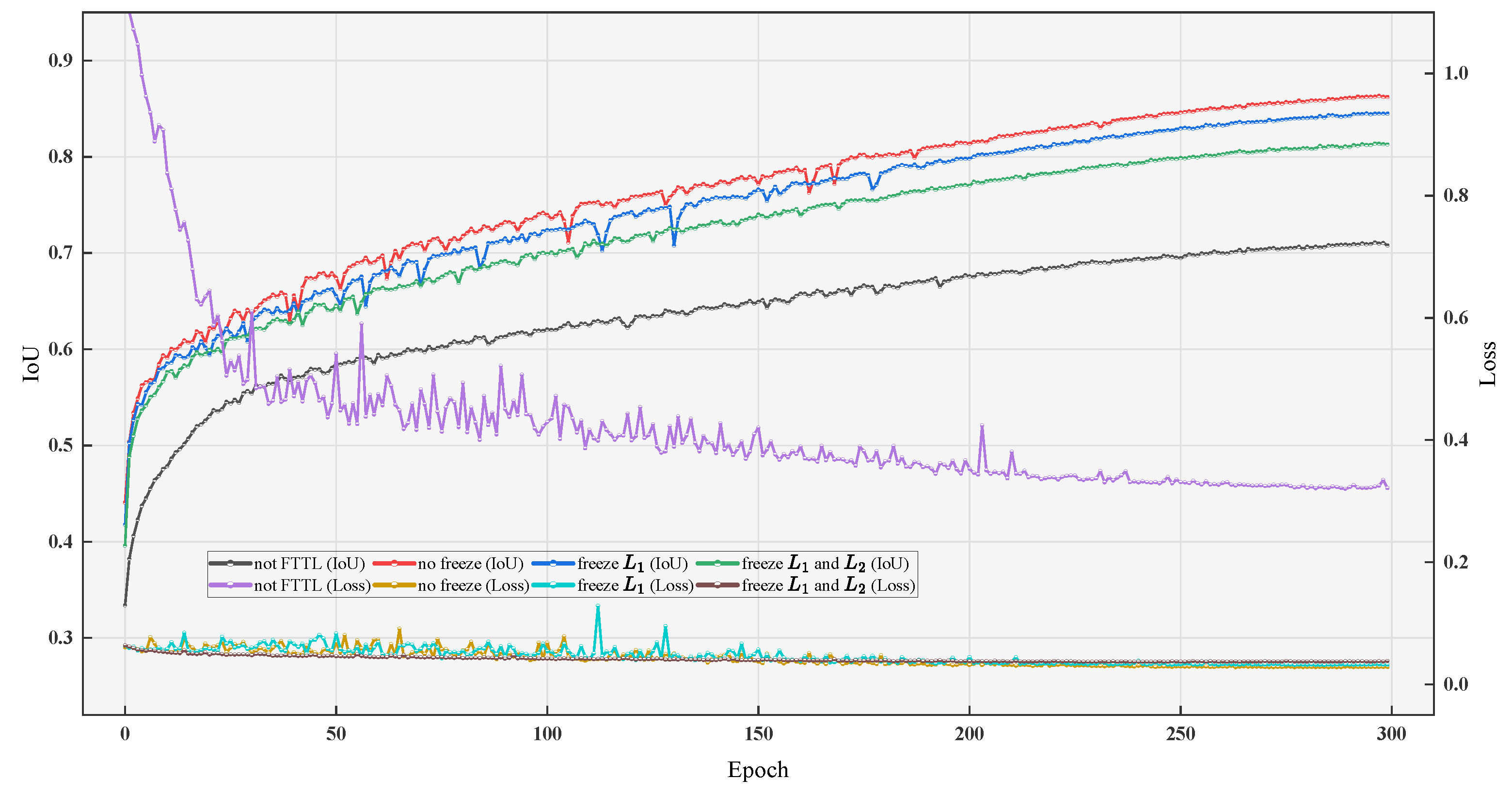
3.1.3. Fine-Tuning Transfer Learning Ablation Experiment
3.1.4. Ablation Experiment Between Different Methods
3.2. Comparative Experiments Results and Discussion
4. Conclusions and Outlook
4.1. Conclusions
4.2. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LKN-UKAN | Large Kernel Nested UKAN |
| KANs | Kolmogorov–Arnold networks |
| DLFFSKA | Dual Large Fusion Selective Kernel Attention |
| LiDAR | Light detection and ranging |
| SVM | Support vector machine |
| CNNs | Convolutional neural networks |
| FTTL | Fine-tuning transfer learning |
| Tok-KAN | Tokenized KAN block |
| MLP | Multilayer perceptron |
| LSK | Large selective kernel |
| GT | Ground truth |
| BCE | Binary cross-entropy |
| BN | Batch normalization |
| LN | Layer normalization |
References
- Thanh-Nhan-Duc Tran; Tapas, M.R.; Do, S.K.; Etheridge, R.; Lakshmi, V. Investigating the impacts of climate change on hydroclimatic extremes in the Tar-Pamlico River basin, North Carolina. J. Environ. Manag. 2024, 363, 121375. [Google Scholar] [CrossRef]
- Lakshmi, V. Enhancing human resilience against climate change: Assessment of hydroclimatic extremes and sea level rise impacts on the Eastern Shore of Virginia, United States. Sci. Total Environ. 2024, 947, 174289. [Google Scholar] [CrossRef]
- Marín-Rodríguez, N.J.; Vega, J.; Zanabria, O.B.; González-Ruiz, J.D.; Botero, S. Towards an understanding of landslide risk assessment and its economic losses: A scientometric analysis. Landslides 2024, 1865–1881. [Google Scholar] [CrossRef]
- Van Westen, C.J. Remote sensing for natural disaster management. Int. Arch. Photogramm. Remote Sens. 2000, 33, 1609–1617. [Google Scholar]
- Han, W.; Zhang, X.; Wang, Y.; Wang, L.; Huang, X.; Li, J.; Wang, S.; Chen, W.; Li, X.; Feng, R.; et al. A survey of machine learning and deep learning in Remote Sens. of geological environment: Challenges, advances, and opportunities. ISPRS J. Photogramm. Remote Sens. 2023, 202, 87–113. [Google Scholar] [CrossRef]
- Liu, X.; Peng, Y.; Lu, Z.; Li, W.; Yu, J.; Ge, D.; Xiang, W. Feature-Fusion Segmentation Network for Landslide Detection Using High-Resolution Remote Sens. Images and Digital Elevation Model Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4020405. [Google Scholar] [CrossRef]
- Casagli, N.; Intrieri, E.; Tofani, V.; Gigli, G.; Raspini, F. Landslide detection, monitoring and prediction with remote-sensing techniques. Nat. Rev. Earth Environ. 2023, 4, 51–64. [Google Scholar] [CrossRef]
- Su, H.; Ma, J.; Zhou, R.; Wen, Z. Detect and identify earth rock embankment leakage based on UAV visible and infrared images. Infrared Phys. Technol. 2022, 122, 104105. [Google Scholar] [CrossRef]
- Nava, L.; Monserrat, O.; Catani, F. Improving Landslide Detection on SAR Data Through Deep Learning. IEEE Geosci. Remote Sens. Lett. 2021, 19, 4020405. [Google Scholar] [CrossRef]
- Crutchley, S. Light detection and ranging (lidar) in the Witham Valley, Lincolnshire: An assessment of new Remote Sens. techniques. Archaeol. Prospect. 2006, 13, 251–257. [Google Scholar] [CrossRef]
- Fang, C.; Fan, X.; Zhong, H.; Lombardo, L.; Tanyas, H.; Wang, X. A Novel Historical Landslide Detection Approach Based on LiDAR and Lightweight Attention U-Net. Remote Sens. 2022, 14, 4357. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J. A survey on object detection in optical Remote Sens. images. ISPRS J. Photogramm. Remote Sens. 2016, 117, 11–28. [Google Scholar] [CrossRef]
- Medwedeff, W.G.; Clark, M.K.; Zekkos, D.; West, A.J. Characteristic landslide distributions: An investigation of landscape controls on landslide size. Earth Planet. Sci. Lett. 2020, 539, 116203. [Google Scholar] [CrossRef]
- Varol, N.; Cengiz, L.D. An Overview of Landslide Management: Scope, Difficulties, Limitations with Future Directions and Opportunities. Afet Risk Derg. 2023, 6, 609–621. [Google Scholar] [CrossRef]
- Al-Amri, S.S.; Kalyankar, N.V.; Khamitkar, S.D. Image segmentation by using threshold techniques. arXiv 2010, arXiv:1005.4020. [Google Scholar]
- Martha, T.R.; Kerle, N.; Van Westen, C.J.; Jetten, V.; Kumar, K.V. Segment Optimization and Data-Driven Thresholding for Knowledge-Based Landslide Detection by Object-Based Image Analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4928–4943. [Google Scholar] [CrossRef]
- Ziou, D.; Tabbone, S. Edge Detection Techniques-An Overview. Pattern Recognit. Image Anal. Adv. Math. Theory Appl. 1998, 8, 537–559. [Google Scholar]
- Wang, F.; Wu, E.; Chen, S.; Wu, H. Texture Feature Extraction and Morphological Analysis of Landslide Based on Image Edge Detection. Math. Probl. Eng. 2022, 2022, 2302271. [Google Scholar] [CrossRef]
- Mehnert, A.; Jackway, P. An improved seeded region growing algorithm. Pattern Recognit. Lett. 1997, 18, 1065–1071. [Google Scholar]
- Beheshtifar, S. Identification of landslide-prone zones using a GIS-based multi-criteria decision analysis and region-growing algorithm in uncertain conditions. Nat. Hazards 2023, 115, 1475–1497. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. Automatica 1975, 11, 23–27. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 6, 679–698. [Google Scholar] [CrossRef]
- Adams, R.; Bischof, L. Seeded region growing. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 641–647. [Google Scholar]
- Zhong, C.; Liu, Y.; Gao, P.; Chen, W.; Li, H.; Hou, Y.; Nuremanguli, T.; Ma, H. Landslide mapping with remote sensing: Challenges and opportunities. Int. J. Remote Sens. 2020, 41, 1555–1581. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Bui, D.T.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 2017, 151, 147–160. [Google Scholar] [CrossRef]
- Plank, S.; Twele, A.; Martinis, S. Landslide Mapping in Vegetated Areas Using Change Detection Based on Optical and Polarimetric SAR Data. Remote Sens. 2016, 8, 307. [Google Scholar] [CrossRef]
- Dai, F.C.; Lee, C.F. Terrain-based mapping of landslide susceptibility using a geographical information system: A case study. Can. Geotech. J. 2001, 38, 911–923. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, T. Deep Learning for Exploring Landslides with Remote Sens. and Geo-Environmental Data: Frameworks, Progress, Challenges, and Opportunities. Remote Sens. 2024, 16, 1344. [Google Scholar] [CrossRef]
- Shi, W.; Zhang, M.; Ke, H.; Fang, X.; Zhan, Z.; Chen, S. Landslide Recognition by Deep Convolutional Neural Network and Change Detection. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4654–4672. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the 18th International Conference Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. In Proceedings of the Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, Granada, Spain, 20 September 2018; pp. 3–11. [Google Scholar]
- Du, G.; Cao, X.; Liang, J.; Chen, X.; Zhan, Y. Medical Image Segmentation based on U-Net: A Review. J. Imaging Sci. Technol. 2020, 64, 2. [Google Scholar]
- Gy, X.; Li, S.; Ren, S.; Zheng, H.; Fan, C.; Xu, H. Adaptive enhanced swin transformer with U-net for remote sensing image segmentation. Comput. Electr. Eng. 2022, 102, 108223. [Google Scholar] [CrossRef]
- Chen, H.; He, Y.; Zhang, L.; Yao, S.; Yang, W.; Fang, Y.; Liu, Y.; Gao, B. A landslide extraction method of channel attention mechanism U-Net network based on Sentinel-2A Remote Sens. images. Int. J. Digit. Earth 2023, 16, 552–577. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Q.; Xie, H.; Chen, Y.; Sun, R. Enhanced Dual-Channel Model-Based with Improved Unet++ Network for Landslide Monitoring and Region Extraction in Remote Sens. Images. Remote Sens. 2024, 16, 2990. [Google Scholar] [CrossRef]
- Dong, Z.; An, S.; Zhang, J.; Yu, J.; Li, J.; Xu, D. L-Unet: A Landslide Extraction Model Using Multi-Scale Feature Fusion and Attention Mechanism. Remote Sens. 2022, 14, 2552. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar] [CrossRef]
- Li, Z.; Guo, Y. Semantic segmentation of landslide images in Nyingchi region based on PSPNet network. In Proceedings of the 2020 7th International Conference on Information Science and Control Engineering (ICISCE), Changsha, China, 18–20 December 2020; pp. 1269–1273. [Google Scholar] [CrossRef]
- Gao, O.; Niu, C.; Liu, W.; Li, T.; Zhang, H.; Hu, Q. E-DeepLabV3+: A Landslide Detection Method for Remote Sensing Images. In Proceedings of the 2022 IEEE 10th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 17–19 June 2022; pp. 573–577. [Google Scholar] [CrossRef]
- Ghobadi, F.; Yaseen, Z.M.; Kang, D. Long-term streamflow forecasting in data-scarce regions: Insightful investigation for leveraging satellite-derived data, Informer architecture, and concurrent fine-tuning transfer learning. J. Hydrol. 2024, 631, 130772. [Google Scholar] [CrossRef]
- Huang, S.; Li, Q.; Li, J.; Lu, J. 4RATFNet: Four-Dimensional Residual-Attention Improved-Transfer Few-Shot Semantic Segmentation Network for Landslide Detection. In Proceedings of the Computer Graphics International Conference, Shanghai, China, 28 August–1 September 2023; pp. 65–77. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. KAN: Kolmogorov-Arnold Networks. arXiv 2024, arXiv:2404.19756. [Google Scholar]
- Li, C.; Liu, X.; Li, W.; Wang, C.; Liu, H.; Liu, Y.; Chen, Z.; Yuan, Y. U-KAN Makes Strong Backbone for Medical Image Segmentation and Generation. arXiv 2024, arXiv:2406.02918. [Google Scholar]
- Zhou, N.; Hong, J.; Cui, W.; Wu, S.; Zhang, Z. A Multiscale Attention Segment Network-Based Semantic Segmentation Model for Landslide Remote Sens. Images. Remote Sens. 2024, 16, 1712. [Google Scholar] [CrossRef]
- Hou, C.; Yu, J.; Ge, D.; Yang, L.; Xi, L.; Pang, Y.; Wen, Y. TransLandSeg: A Transfer Learning Approach for Landslide Semantic Segmentation Based on Vision Foundation Model. arXiv 2024, arXiv:2403.10127. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, H.; Liu, X.; Shi, T.; Zhang, R.; Liu, D.; Xiong, Z.; Wu, F. TokenUnify: Scalable Autoregressive Visual Pre-training with Mixture Token Prediction. arXiv 2024, arXiv:2405.16847. [Google Scholar]
- Cao, J.; Li, Y.; Sun, M.; Chen, Y.; Lischinski, D.; Cohen-Or, D.; Chen, B.; Tu, C. DO-Conv: Depthwise Over-Parameterized Convolutional Layer. IEEE Trans. Image Process. 2022, 31, 3726–3736. [Google Scholar] [CrossRef] [PubMed]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer Normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Li, Y.; Hou, Q.; Zheng, Z.; Cheng, M.-M.; Yang, J.; Li, X. Large Selective Kernel Network for Remote Sensing Object Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 16794–16805. [Google Scholar] [CrossRef]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks? Adv. Neural Inf. Process. Syst. 2014, 27, 964. [Google Scholar]
- Pires, L.; Marfurt, K. Convolutional neural network for remote-sensing scene classification: Transfer learning analysis. Remote Sens. 2019, 12, 86. [Google Scholar] [CrossRef]
- Shao, Z.; Yang, K.; Zhou, W. Performance Evaluation of Single-Label and Multi-Label Remote Sens. Image Retrieval Using a Dense Labeling Dataset. Remote Sens. 2018, 10, 964. [Google Scholar] [CrossRef]
- Chaudhuri, B.; Demir, B.; Chaudhuri, S.; Bruzzone, L. Multilabel Remote Sens. Image Retrieval Using a Semisupervised Graph-Theoretic Method. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1144–1158. [Google Scholar] [CrossRef]
- Landslide Segmentation. Available online: https://www.kaggle.com/datasets/niyarrbarman/landslide-divided (accessed on 3 October 2024).








| Method | Configuration |
|---|---|
| Brightness | 2 |
| Rotate | −135 |
| Transpose | FLIP_TOP_BOTTOM |
| Positive Sample | Negative Sample | |
|---|---|---|
| Forecast positive | TP | FP |
| Forecast negative | TN | FN |
| Platform | Configuration |
|---|---|
| Operating System | Ubuntu 20.04 |
| IDE | Pycharm |
| Scripting Language | Python 3.10.11 |
| Framework | torch-2.0.0+cu118 |
| CPU | Intel Xeon silver 4210R |
| GPU | NVIDIA RTX 4500 (20 G) |
| RAM | 128 G |
| Super Parameter | Configuration |
|---|---|
| Optimizer | SGD |
| Momentum | 0.9 |
| Learning rate | 0.001 |
| Weight decay | 0.0001 |
| Dataset | Epoch |
|---|---|
| DLRSD-Expand | 1000 |
| Landslide-Expand | 300 |
| Dataset | Method | IoU (%) ↑ | R (%) ↑ | P (%) ↑ | F1 (%) ↑ | Loss ↓ | Params (M) ↓ |
|---|---|---|---|---|---|---|---|
| DLRSD- Expand | U-KAN | 70.33 | 81.60 | 80.78 | 81.19 | 0.3282 | 2.36 |
| U-Net++ | 71.37 | 82.80 | 81.55 | 82.17 | 0.3146 | 7.07 | |
| U-Net++ add Tok-KAN | 72.55 | 82.78 | 83.13 | 82.94 | 0.2995 | 6.28 | |
| Landslide- Expand | U-KAN | 57.78 | 72.63 | 71.78 | 72.20 | 0.3402 | 2.36 |
| U-Net++ | 57.88 | 72.02 | 72.26 | 72.14 | 0.3388 | 7.07 | |
| U-Net++ add Tok-KAN | 57.92 | 72.63 | 72.03 | 72.32 | 0.3402 | 6.28 |
| Dataset | Method | IoU (%) ↑ | R (%) ↑ | P (%) ↑ | F1 (%) ↑ | Loss ↓ | Params (M) ↓ |
|---|---|---|---|---|---|---|---|
| DLRSD- Expand | Tok-KAN | 72.55 | 82.78 | 83.13 | 82.94 | 0.2995 | 6.28 |
| Tok-KAN and LSK | 72.77 | 83.26 | 82.93 | 83.10 | 0.2956 | 6.35 | |
| Tok-KAN and DLFFSKA | 76.58 | 85.61 | 85.90 | 85.76 | 0.2498 | 6.38 | |
| Landslide- Expand | Tok-KAN | 57.92 | 72.63 | 72.03 | 72.32 | 0.3402 | 6.28 |
| Tok-KAN and LSK | 58.01 | 71.91 | 72.28 | 72.09 | 0.3395 | 6.35 | |
| Tok-KAN and DLFFSKA | 59.62 | 73.18 | 74.09 | 73.63 | 0.3212 | 6.38 |
| Dataset | Method | IoU (%) ↑ | F1 (%) ↑ | Loss ↓ |
|---|---|---|---|---|
| DLRSD- Expand | add LSK | 72.77 | 83.10 | 0.2956 |
| add DLFFSKA ( = 0.25, = 0.75) | 72.69 | 83.11 | 0.2972 | |
| add DLFFSKA ( = 0.5, = 0.5) | 76.58 | 85.76 | 0.2498 | |
| add DLFFSKA ( = 0.75, = 0.25) | 73.99 | 83.94 | 0.2797 | |
| Landslide- Expand | add LSK | 58.01 | 72.09 | 0.3395 |
| add DLFFSKA ( = 0.25, = 0.75) | 58.09 | 72.33 | 0.3406 | |
| add DLFFSKA ( = 0.5, = 0.5) | 59.62 | 73.63 | 0.3212 | |
| add DLFFSKA ( = 0.75, = 0.25) | 59.47 | 73.43 | 0.3233 |
| Method | IoU (%) ↑ | R (%) ↑ | P (%) ↑ | F1 (%) ↑ | Loss ↓ | Params (M) ↓ | BatchTime (S) ↓ |
|---|---|---|---|---|---|---|---|
| not FTTL | 59.62 | 73.18 | 74.09 | 73.63 | 0.3212 | 6.38 | 123 |
| not frozen | 70.00 | 78.03 | 83.25 | 80.56 | 0.0283 | 6.38 | 114 |
| freeze the | 67.58 | 77.06 | 80.51 | 78.74 | 0.0324 | 6.38 | 105 |
| freeze the and | 62.49 | 73.15 | 77.05 | 75.05 | 0.0382 | 6.38 | 100 |
| Method | IoU (%) ↑ | R (%) ↑ | P (%) ↑ | F1 (%) ↑ | Loss ↓ | Params (M) ↓ |
|---|---|---|---|---|---|---|
| U-Net++ | 57.88 | 72.02 | 72.26 | 72.14 | 0.3388 | 7.07 |
| U-Net++ add Tok-KAN | 57.92 | 72.63 | 72.03 | 72.32 | 0.3402 | 6.28 |
| U-Net++ add DLFFSKA | 58.19 | 73.49 | 71.36 | 72.41 | 0.3407 | 7.17 |
| U-Net++ add Tok-KAN and DLFFSKA | 59.62 | 73.18 | 74.09 | 73.63 | 0.3212 | 6.38 |
| U-Net++ with FTTL | 64.86 | 76.29 | 77.36 | 76.82 | 0.0343 | 7.07 |
| Ours | 70.00 | 78.03 | 83.25 | 80.56 | 0.0283 | 6.38 |
| Method | IoU (%) ↑ | R (%) ↑ | P (%) ↑ | F1 (%) ↑ | Loss ↓ | Params (M) ↓ |
|---|---|---|---|---|---|---|
| PSPNet | 30.78 | 34.82 | 69.13 | 46.31 | 0.0608 | 16.67 |
| Deeplabv3+ | 47.47 | 63.87 | 66.36 | 65.09 | 0.2415 | 13.47 |
| U-Net | 46.35 | 62.76 | 62.37 | 62.56 | 0.4825 | 3.12 |
| U-KAN | 57.78 | 72.63 | 71.78 | 72.20 | 0.3402 | 2.36 |
| U-Net++ | 57.88 | 72.02 | 72.26 | 72.14 | 0.3388 | 7.07 |
| TransLandSeg | 62.97 | 73.96 | 77.27 | 75.58 | 0.3107 | 4.18 |
| U-Net++ with FTTL | 64.86 | 76.29 | 77.36 | 76.82 | 0.0343 | 7.07 |
| Ours | 70.00 | 78.03 | 83.25 | 80.56 | 0.0283 | 6.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Li, Q.; Lu, J.; Zheng, K.; Wei, L.; Xiang, Q. A Transfer Learning Remote Sensing Landslide Image Segmentation Method Based on Nonlinear Modeling and Large Kernel Attention. Appl. Sci. 2025, 15, 3855. https://doi.org/10.3390/app15073855
Li J, Li Q, Lu J, Zheng K, Wei L, Xiang Q. A Transfer Learning Remote Sensing Landslide Image Segmentation Method Based on Nonlinear Modeling and Large Kernel Attention. Applied Sciences. 2025; 15(7):3855. https://doi.org/10.3390/app15073855
Chicago/Turabian StyleLi, Jiajun, Qiang Li, Jinzheng Lu, Kui Zheng, Lijuan Wei, and Qiang Xiang. 2025. "A Transfer Learning Remote Sensing Landslide Image Segmentation Method Based on Nonlinear Modeling and Large Kernel Attention" Applied Sciences 15, no. 7: 3855. https://doi.org/10.3390/app15073855
APA StyleLi, J., Li, Q., Lu, J., Zheng, K., Wei, L., & Xiang, Q. (2025). A Transfer Learning Remote Sensing Landslide Image Segmentation Method Based on Nonlinear Modeling and Large Kernel Attention. Applied Sciences, 15(7), 3855. https://doi.org/10.3390/app15073855






