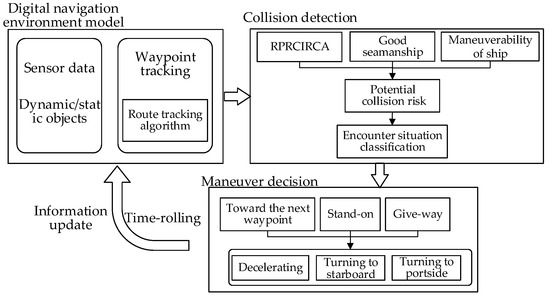
Abstract
The inherent complexity of traffic patterns in inland river tributary waterways presents significant challenges in predicting ship behavior, resulting in elevated accident risks compared to general waterways. With the intelligent development of inland navigation, conducting research on autonomous navigation decision-making for tributary waterway ships is crucial to improving navigation safety and efficiency. Based on the characteristics of the navigation environment, a digital traffic environment model for inland waterways with tributaries is constructed to meet the information requirements of autonomous navigation decision-making. The ship encounter process is analyzed, and a collision risk identification model based on trajectory derivation is proposed, which accounts for the uncertainty of ship maneuvering in tributary waterways. Under the premise of compliance with the “Rules of the People’s Republic of China for Inland River Collision Avoidance” (RPRCIRCA) and adherence to good seamanship, an autonomous navigation decision-making method is developed by integrating an improved Line-of-Sight tracking model with a collision avoidance strategy based on exhaustive course-speed maneuver combinations. The system’s performance is validated through simulation experiments, with trajectory tracking deviations demonstrated to remain below 49 m under wind-current disturbances while minimum encounter distances with target ships are maintained above 48 m. Adaptive response capabilities to maneuvering variations of target ships are confirmed, along with the preservation of navigation precision in complex tributary environments.
1. Introduction
China’s inland waterway transportation is developing rapidly. By 2025, the navigable mileage of the nation’s inland waterways is projected to reach approximately 133,000 km, of which about 18,600 km will be high-grade waterways, thereby increasing the proportion of high-grade waterways to 14%. With the growth of transportation volume [1], an inevitable rise in ship collision accidents is anticipated, with the majority caused by human error [2]. In particular, at the confluence areas of inland waterways, environmental complexity and uncertainty in ship maneuvering make crews more prone to misjudging collision avoidance actions [3]. The development of autonomous ship navigation technology offers novel solutions and technical support for enhancing inland navigation safety. By advancing ship autonomy, it can assist crews in identifying potential collision risks as early as possible and determining the optimal timing for collision avoidance actions as well as feasible maneuvering schemes, thereby reducing the impact of human factors in inland waterway collisions [4].
Therefore, the primary objective of this research is to develop an autonomous navigation system tailored to typical confluence areas of inland river main channels and tributaries. This system aims to alert crews to collision risks and support them in promptly implementing effective collision avoidance measures, thereby preventing ships from entering hazardous situations or suffering collisions due to vigilance lapses or situational misjudgments. The significance of this research lies in its potential to enhance the safety and efficiency of inland waterway navigation, particularly in challenging tributary environments. By leveraging intelligent technologies, the proposed methods seek to reduce reliance on human intervention, mitigate collision risks, and optimize ship operations. This study not only advances autonomous navigation systems but also provides practical solutions for the sustainable development of inland waterway transportation.
1.1. Literature Review
The advancement of autonomous and unmanned ship technologies represents a critical frontier in maritime research, with breakthroughs in autonomous navigation systems significantly enhancing marine operational efficiency. As these technologies mature, numerous navigation frameworks and computational models [5] have been developed, enabling novel solutions to complex navigational challenges, particularly in collision risk mitigation and collision avoidance strategies.
Research on ship collision avoidance decision-making began in the 1950s and has transitioned from qualitative to quantitative analysis. Quantifying collision risk is the first step toward autonomous collision avoidance. Current studies primarily utilize the Collision Risk Index (CRI) [6] to identify collision risk, which can be categorized into macro and micro perspectives [7]. Early quantitative research on microscopic ship collision risk focused on the Distance to the Closest Point of Approach (DCPA) and the Time to the Closest Point of Approach (TCPA) [8,9,10]. Kearon [11] later introduced a method to quantify collision risk using a weighted sum of the DCPA and TCPA. The curvature of inland waterways necessitates frequent vessel course adjustments, causing erratic DCPA fluctuations that deviate substantially from actual closest encounter distances. Conventional DCPA and TCPA calculations fail to reliably identify collision risks in such scenarios due to constrained waterways’ dynamic navigation patterns [12]. Subsequently, artificial intelligence has been progressively integrated into collision risk calculations [13,14,15]. Zheng [16] developed an SVM-based algorithm integrating ship domain interactions for risk quantification, while Li, B. [17] proposed evidence theory to overcome neural networks’ accuracy limitations and computational inefficiencies in such assessments. For specific waterways, researchers utilize AIS data to calculate collision risks. For instance, Nieh [18] leveraged AIS data combined with environmental, vessel, and meteorological parameters to evaluate navigation safety during port entry/exit maneuvers.
Ship encounter dynamics identification forms the basis for collision avoidance decisions following risk quantification. Defined by vessels’ relative positions, velocities, and courses [19], encounter situations determine navigation right-of-way allocation [20]. Most researchers assess encounter situations using parameters such as inter-ship distance and relative angles [21,22,23], with Sun et al. [24,25] employing fuzzy statistical methods for classification through relative angle membership functions. Ni [26] established an identification model via collision rule analysis; conventional spatial parameter analyses often neglect spatiotemporal evolutionary patterns. Ma [27] resolved this limitation through spatiotemporal feature integration and SVM-based classification systems. However, current research predominantly assumes stable inter-vessel relative motion in open-water scenarios, thereby disregarding the constraining effects of navigational environments on the dynamic evolution of ship encounter situations.
Autonomous collision avoidance technology is a core component of autonomous ship navigation, requiring consideration of navigation rules, encounter situations, ship maneuverability, and environmental constraints to generate collision-free maneuvering schemes [28,29,30,31]. Geometric approaches derive collision parameters (e.g., DCPA/TCPA) from encounter geometry for navigational guidance. While Wilson’s [32] two-ship collision avoidance decision framework prioritizes evasive maneuvers over tracking, it risks rule violations in complex scenarios. The Velocity Obstacle (VO) method, introduced by Fiorini [33] in 1998, is widely applied to mobile robot obstacle avoidance. B Kufoalor [34] developed a dynamic Reciprocal Velocity Obstacle (RVO) method by incorporating COLREGs-based responsibility allocation. Chen et al. [35,36] further enhanced VO applicability by incorporating maneuverability constraints via trajectory prediction and VO boundary analysis. However, conventional VO algorithms and their enhanced variants demonstrate predominant applicability in open waters or linear channels, while remaining constrained in curved inland waterways due to complex hydrodynamic interactions and restricted maneuverability space. Advancements in artificial intelligence have accelerated the intelligentization of the maritime industry. Tomasz [37] designed a neural evolution-based collision avoidance system for bionic underwater robots, while Cheng [38] fused artificial neural networks (ANNs) with sparse polynomial chaos expansion to process high-dimensional sensor data. Subsequently, Zeng [39] advanced genetic algorithm encoding by incorporating environmental parameters (wind/waves/currents) and rule-based fitness functions. Subsequent developments include Tsou’s [40] ECDIS-integrated multi-objective algorithm for dynamic obstacle navigation, Xie’s [41] ship dynamics-constrained Tennyson-Whisker search enabling safety–cost tradeoffs, and Ni’s [42,43] co-evolutionary multi-swarm genetic algorithms for autonomous optimal path generation. However, despite their potential, intelligent algorithms face critical limitations: their design complexity often offsets computational efficiency gains, suboptimal solutions are prone to emerge during optimization, and the reliability and stability of results remain challenging to guarantee. These shortcomings are particularly unacceptable in safety-critical navigational decision-making systems.
In summary, while substantial scholarly attention has been devoted to autonomous navigation decision-making systems for maritime ships, the domain of inland tributary waterways navigation has remained relatively under-explored. This research gap stems from the unique challenges posed by the distinct navigational characteristics and environmental complexities of these waterways. The operational environment in tributary systems presents three primary challenges: unpredictable target ship maneuverability, intricate navigational conditions, and significant constraints on ship mobility. Therefore, an autonomous navigation decision-making method for ships in tributary waterways accounting for the constraints of the inland river environment is proposed, which fully integrates the “Rules of the People’s Republic of China for Inland River Collision Avoidance” (RPRCIRCA), good seamanship, and ship maneuverability.
1.2. Motivation and Contribution
Currently, significant progress has been made in autonomous navigation research. However, most studies have predominantly focused on open-sea navigation under favorable weather conditions, which—while nearing practical maturity—reveal a critical gap in addressing inland tributary waterways. To address this gap, this article systematically identifies core challenges in autonomous navigation decision-making for inland ships through three key research deficiencies:
- A methodology integrating RPRCIRCA compliance and good seamanship for collision risk identification in inland tributaries remains absent. The complexity and variability of inland navigation environments (e.g., channel dynamics, hydrographic conditions, and traffic patterns) render conventional indicator-based risk identification methods inadequate.
- Adaptive optimization frameworks for autonomous navigation decisions are underdeveloped. In dynamic inland river environments, incomplete or inaccurate information may lead to prediction errors in ship maneuvering processes and target vessel trajectories. Furthermore, existing methods lack mechanisms to adaptively adjust decision-making based on real-time error feedback.
- Current autonomous navigation decision-making methods insufficiently address the interplay between ship maneuvering dynamics and environmental constraints. Specifically, the nonlinear maneuvering characteristics of underactuated ships and time-varying traffic environments—critical factors influencing collision avoidance decisions—are not yet fully quantified.
In response to the challenges posed by inland tributary waterways, an advanced autonomous navigation decision-making method is proposed. This method is designed to detect potential collision risks and provide ships with actionable guidance on when and whether to execute evasive maneuvers. Adhering to the requirements of the RPRCIRCA and good seamanship, a position projection method integrated with a ship domain model is developed to accurately assess collision risks in inland tributary waterways. By considering the avoidance intentions of the target ship, the collision avoidance principles and optimal timing of actions are determined for the current encounter scenario. Furthermore, based on the predicted behavior of the target ship, a collision avoidance decision-making model is proposed. This model combines a ship maneuvering motion model and course control method with an inland waterway route tracking technique to derive the optimal autonomous navigation decision-making strategy for the given situation. The proposed autonomous navigation decision-making scheme is dynamically adjusted in response to changes in ship position, demonstrating enhanced robustness in handling complex and variable inland tributary waterway encounters. Additionally, the method incorporates considerations of ship maneuverability, compliance with the RPRCIRCA, and adherence to good seamanship, making it well suited for autonomous navigation decision-making in complex inland tributary waterways.
3. Methodology
3.1. Digitalization of Transportation Environment
The perception and extraction of aquatic environmental data, coupled with the construction of a digital navigation environment, form the foundation of the autonomous decision-making method. Environmental information is classified and reconstructed based on the characteristics of the generalized navigation environment components, enabling the mathematical expression of static traffic environment information. Key information in navigational channels, including channel boundaries, recommended routes, channel separation lines/zones, and anchorages, is abstracted into computer-recognizable formulas composed of points, lines, and surfaces. According to traffic element information, a long waterway can be decomposed into multiple short straight waterways, each of which is typically a rectangular one-way navigation area defined by four points. As shown in Figure 6, a curved waterway is deconstructed into three straight segments, each of which includes four vertex coordinates.
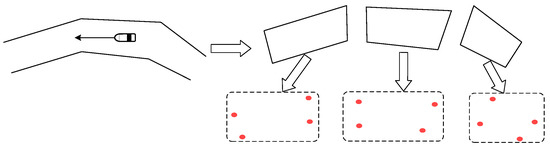
Figure 6.
Deconstruction of inland waterway data.
Thus, the ith segment in inland waterways can be mathematically represented as follows, where p denotes the coordinate information of the four vertices. The recommended route is defined as the polyline connecting midpoints of channel entry/exit boundaries.
A digitized instream tributary scenario is shown in Figure 7. The area “A” surrounded by green lines represents the upstream waterway, the area “B” surrounded by red lines represents the downstream waterway, and the interval area “D” between the upstream and downstream channels represents the channel divider. The area “C” surrounded by black lines represents the tributary waterway.
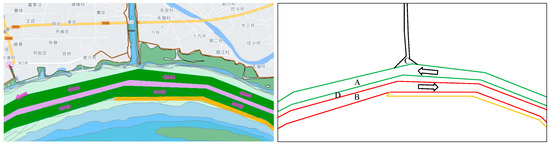
Figure 7.
Digitization of inland tributary waterway environments.
3.2. Collision Risk Model Based on Ship Trajectory Projection
In inland navigation scenarios where a ship’s course aligns with the designated channel traffic flow, the ship is typically classified as a channel-following ship. Such vessels maintain their course along the channel axis until reaching predefined turning points, where directional adjustments are executed to align with subsequent channel segments. Conversely, TSs exhibiting substantial angular deviation from the channel direction or sailing outside channel boundaries may be categorized as non-channel-following vessels. For these special cases, TS position estimation can be performed through velocity vector projection analysis based on real-time kinematic data. According to the captain’s experience, the maximum angle difference between the navigating ship and the channel in the inland waterway is about 5°. This study accordingly adopts a threshold angular deviation of θ = 5° as the criterion for channel-following status determination. The methodology employs continuous monitoring of the angular differential between a ship’s course and the channel direction to classify TS navigation patterns, as formalized in Equation (12).
where CTS = the course of TS; Cchannel = the direction of the channel where the TS is located. As shown in Figure 8, TS1 is the ship sailing along the channel when TS2 and TS3 are both not. The corresponding trajectory projection method for the TS is shown in Equations (13) and (14).
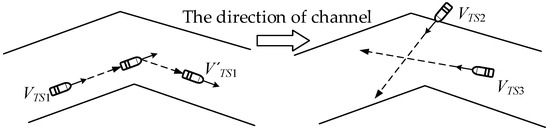
Figure 8.
Schematic diagram of the ship’s navigation posture.
Current methodologies for modeling tributary egress maneuvers typically oversimplify TS kinematics through constant-velocity linear motion assumptions, as exemplified by the dead reckoning formulation in Equation (13). This conventional approach calculates projected position PTS(t2|t1) at time t2 using initial parameters PTS(t1), CTS, vTS, but fundamentally misrepresents the curvilinear trajectory characteristics inherent to channel transition maneuvers. Such linear extrapolation proves particularly inadequate when modeling vessels transitioning from tributary to mainstream channels, where hydrodynamic constraints and navigational protocols necessitate deliberate course alterations. A paradigm shift emerges through the anticipatory integration of TS’s channel transition intent, enabled by rate of turn (ROT) analysis. By monitoring angular displacement between sequential course measurements CTS(t) and CTS(t + ∆t), this ROT-driven predictive framework reconstructs nonlinear motion patterns during tributary egress. The methodology not only enhances trajectory forecasting precision but also enables strategic differentiation between essential collision avoidance actions and superfluous maneuvers.
To prevent overestimation of vessel steering angles (as exemplified by the projected position P′TS(t3) at time t3 in Figure 9), this study establishes a transitional zone at the confluence of tributary and mainstream channels. Within this demarcated area, tributary vessels are presumed to complete steering maneuvers before mainstream entry, maintaining a constant ROT throughout the transitional phase. The navigational status of the TS upon mainstream ingress is determined by its kinematic state at the transitional boundary, as shown in Figure 10.
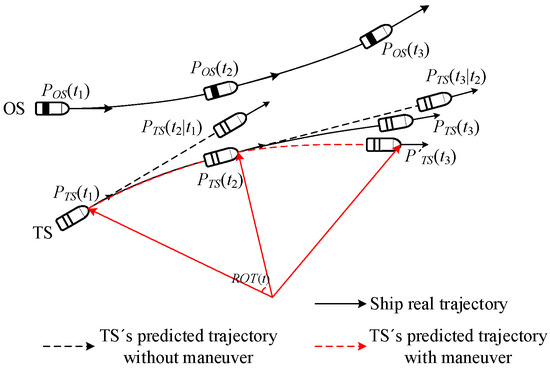
Figure 9.
Trajectory of a ship pair involved in a conflict.
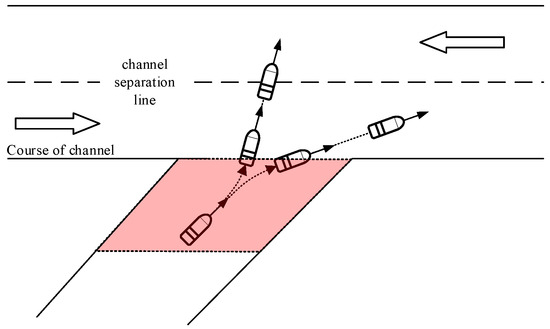
Figure 10.
Derivation of trajectories in inland tributary waterways.
The collision avoidance model for the TS within the transitional zone (shaded in Figure 10) operates under dual constraints: (1) conflict resolution is achieved solely through course alteration, and (2) steering maneuvers occur at a fixed ROT. The ROT is derived computationally through analysis of course variations between successive time intervals CTS(t) and CTS(t + ∆t), as formalized in Equation (15). Subsequent trajectory prediction integrates angular displacement calculations to determine the TS’s velocity vector and positional coordinates at future timestamps via Equations (16) and (17). This methodology ensures kinematic continuity between transitional steering maneuvers and post-entry navigation states, enabling accurate collision risk identification while adhering to inland vessel navigation practices.
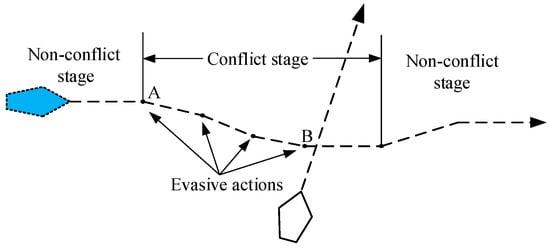
A conflict is characterized as a scenario with a high likelihood of collision, representing a near-collision situation. This conflict can be quantified by assessing whether the projected trajectory of one ship intrudes upon a predefined restricted area surrounding another ship. An elliptical ship domain is employed to delineate this restricted area based on the Fujii model. The major axis of the elliptical domain is defined as four times the ship’s length, while the minor axis is 1.6 times the ship’s length. Consequently, a conflict is identified by evaluating whether a ship, maintaining its current course and speed, is projected to encroach upon the elliptical domain of another ship. The risk of collision is assessed by analyzing the projected trajectories of the OS and TSs. The presence of potential collision risks is indicated if the TSs are predicted to intrude into the OS’s ship domain within a future timeframe T.
First of all, judge the navigation situation of the OS: when the OS is located outside the channel, such as the OS3 in Figure 11, the position of OS can be projected according to the MMG model of the OS and the current movement state. If the OS is sailing within the channel, the ship’s navigation is constrained by the channel and cannot sail out of the channel, which usually includes two cases. If the OS is sailing along the channel, i.e., when |COS − Cchannel| ≤ 5°, such as OS1, under this premise, it can be assumed that the OS will change course to continue along the direction of the next section of the channel after reaching the channel turning point. If the OS’s course is at a certain angle to the channel, such as OS2, it is estimated that the OS will sail out of the channel boundary according to the current course. Therefore, when the projected ship’s trajectory is close to the channel boundary, the OS should steer in the same direction as the channel boundary Cchannel, to ensure that the OS continues to sail along the channel boundary and will not sail out of the channel.
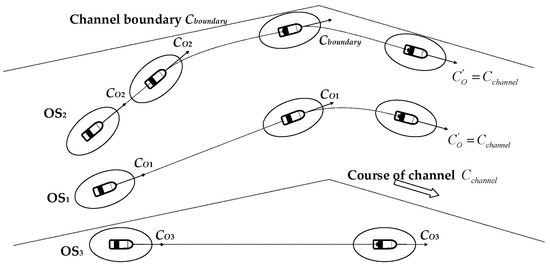
Figure 11.
Nonlinear motion processes of ships under environmental constraints.
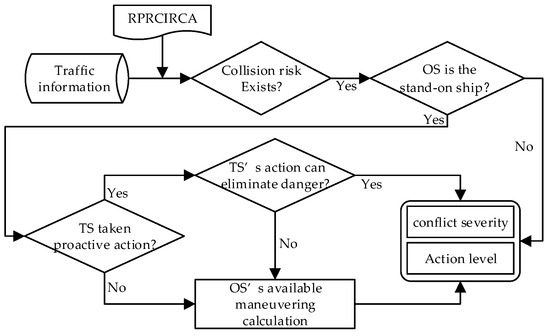
Based on navigation practices, a 3-nautical-mile radius surrounding the OS is established as the alert zone. This designated area serves as the operational boundary for monitoring both static and dynamic objects, with the collision risk model framework visually represented in Figure 12.
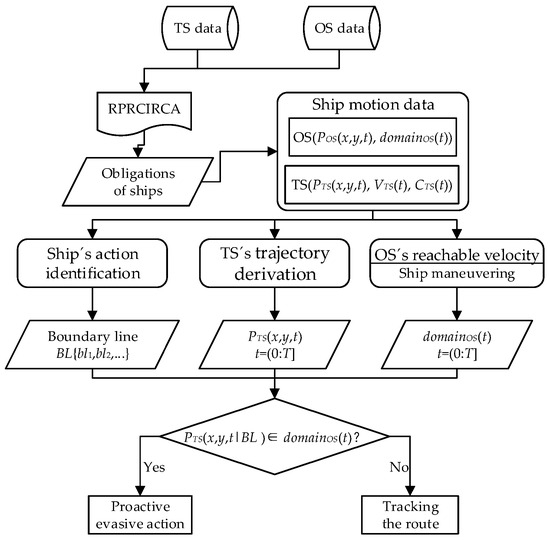
Figure 12.
Methodological framework for collision risk identification.
Based on the initial motion state of the OS and TSs in the alert zone, combined with the digitized traffic environment, the trajectories of ships are projected for a certain period T in the future, and then the time series of the ship positions of the OS and TSs are compared to determine the danger of a collision based on whether or not the TS will intrude into the ship domain of the OS. Empirical studies with inland waterway captains have established T = 900 s as the standard prediction window. The shorter the inferred time for the intruding ship to enter the ship domain of the OS, the more imminent the collision risk is.
3.3. Encounter Situation Identification Model
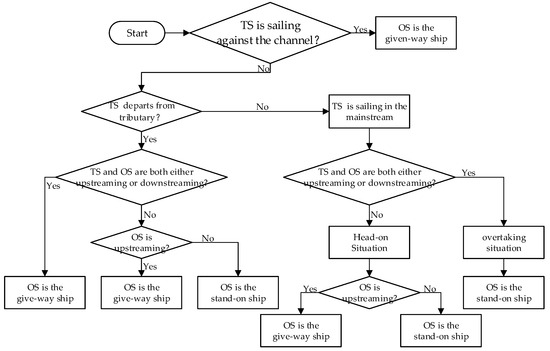
In tributary waterway navigation scenarios where both the OS and the TS sail as mainstream channel vessels, encounter situation classification aligns with conventional channel navigation protocols. This classification framework, as tabulated in Table 1, employs angular parameters to quantify the course-channel alignment of the OS and TS, respectively, where θO denotes the angular deviation between the OS’s course and the channel axis, and θT represents the equivalent deviation for the TS.

Table 1.
Encounter situation identification modeling in tributary waterways.
For a TS departing from tributary to mainstream channels, a specialized encounter recognition model has been developed in compliance with inland waterway regulations. This model synthesizes vessel–channel spatial relationships and inter-vessel dynamics to characterize tributary convergence scenarios, as systematically categorized in Figure 13 and Table 2. The framework accounts for right-of-way priorities inherent to tributary egress maneuvers, enabling precise identification of collision risks during the exiting tributary phase.
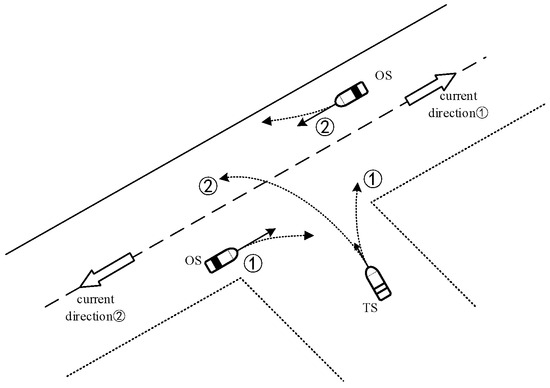
Figure 13.
Classification of encounter situations in tributary waterways.

Table 2.
Avoidance relationships in tributary waterways.
3.4. Collision Avoidance Decision-Making Model
In open waters, collision avoidance typically relies on steering maneuvers, and conventional VO methods calculate collision-inducing velocity vectors through relative motion analysis under stable course assumptions. This approach becomes inadequate in confined inland waterways due to the mandatory dynamic heading adjustments required by channel curvature, as the VO framework inherently neglects nonlinear maneuvering dynamics and time-dependent steering processes. To resolve this limitation, a ship motion model integrating a control methodology is developed to simulate inland navigation-compliant collision avoidance strategies. By analytically deriving motion vector evolution under different maneuvering protocols and coupling these with ship domain constraints, the proposed framework enables the quantitative assessment of target vessel intrusion into navigational safety boundaries. This establishes a functional mapping between the maneuvering decision protocols and collision avoidance effectiveness in the inland waterway environment.
In Figure 14, the TS is the ship crossing the channel, and the initial course and position of the OS are VOS and POS. Considering the nonlinear maneuvering process of the OS, the TS will arrive at when the OS turns to starboard to and arrives at , and the TS will arrive at when the OS turns to portside to and arrives at . The TS is just outside the ship domain of the OS for safety under the two maneuvering scenarios. Therefore, the maneuvering range [, ] is the motion vector that indicates that the OS cannot avoid the TS safely, and the OS can avoid the TS safely when the maneuvering angle θ > − VOS or θ < − VOS.
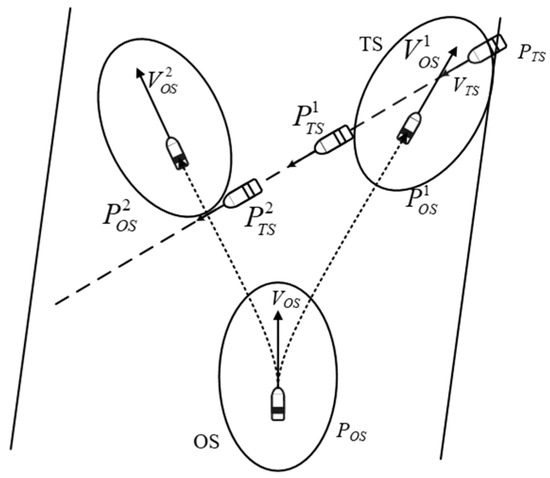
Figure 14.
Relationship between motion vectors and safe collision avoidance.
In restricted inland waterways, collision avoidance may not be reliably achieved through heading adjustments alone due to operational constraints in narrow channels necessitating coordinated maneuvers that integrate course alterations with deceleration. Define f(V) to denote the ship motion vector, including course and speed changes. The position POS(t) and PTS(t) of the OS and TS at the moment t are [XOS(t), YOS(t)] and [XTS(t), YTS(t)], respectively. When the OS’s motion vector changes, the OS’s position after the moment t can be projected based on the ship motion model, which is expressed as
domain(POS(t)) denotes the ship domain space centered on the OS, and the safety space constituted during the OS’s movement is expressed by the following equation:
The trajectory of the TS is represented as
Therefore, the motion vector of the OS that can safely avoid the TS can be expressed as
In multi-ship encounter scenarios, the collision avoidance obligations of the OS become inherently complex due to the necessity of coordinating interactions and decision-making among multiple vessels. To address this complexity, a decomposition approach is proposed, wherein multi-ship encounters are reduced to multiple two-ship encounter subproblems. This analytical simplification facilitates focused investigation of pairwise collision avoidance strategies while streamlining the resolution of collision avoidance challenges. The prioritization of avoidance targets is achieved through comparative collision risk identification between the OS and TS. The operational framework mandates that evasive actions must either prioritize avoidance of the highest-risk vessel without inducing secondary collision risks or eliminate collision risks with all TSs through a single coordinated maneuver.
Notably, the RPRCIRCA do not necessitate maximum evasive actions but emphasize constrained optimization under navigational limitations. Given the spatial constraints of inland waterways, excessive steering maneuvers are prohibited to ensure navigational safety and efficiency. Empirical evidence from inland navigation practices supports the imposition of a maximum permissible steering angle range of θ = [−45°, 45°]. This angular restriction maintains ship stability during collision avoidance maneuvers while preventing emergent risks with external obstacles or adjacent ships. The two-dimensional solution space ζ = {θ, T} integrates course alteration (θ) and engine telegraph adjustments (T), where T represents engine speed reductions relative to current operational levels. Through ship motion modeling and control systems, theoretical solutions are translated into executable commands m(W, T).
Different telegraphing corresponds to different propeller RPM (Revolutions Per Minute), and the RPM of the propeller is controlled to realize the variable speed control of the ship. According to the general ship speed change performance, the change rate of propeller RPM is generally 0.2 r/s, that is, 1 RPM is increased or decreased every 5 s. According to the current ship propeller RPM TO and the target propeller RPM T, the propeller RPM Tt after time t can be obtained. If the current RPM Tt has reached the maximum or minimum RPM, it will not increase or decrease.
The decision-making protocol incorporates navigational rule constraints through situational filtering. For instance, in starboard crossing scenarios, course alteration is restricted to θ = [0°, 45°]. Computational simulations based on ship motion models project spatiotemporal trajectories under various m(W, T) combinations. Then, based on the mathematical model of ship motion, the change process of the ship’s motion vector under different maneuvering combination schemes is calculated, and the position of TSs at the same time can be obtained based on each TS’s motion situation. Through the spatiotemporal evolution relationship between the OS and the TSs, combined with the ship domain model, the maneuvering scheme that can enable TSs to pass from the outside of the OS’s ship domain is judged, which is the safe collision avoidance decision-making scheme under the current multi-objective encounter situation.
4. Case Study
4.1. The Verification of the Route Tracking Model
To better validate the effectiveness of the improved LOS algorithm, ship trajectory tracking experiments are conducted. The experimental scenario is configured as a winding course with a wind direction of 035°, wind speed of 5 m/s, current direction of 180°, and current speed of 0.5 m/s. The ship trajectories of the route tracking model (red line) and the planned route (black line) are shown in Figure 15a. Figure 15b illustrates the deviation between the planned route and the actual trajectory, demonstrating that the error remains below 200 m despite wind and current interference.
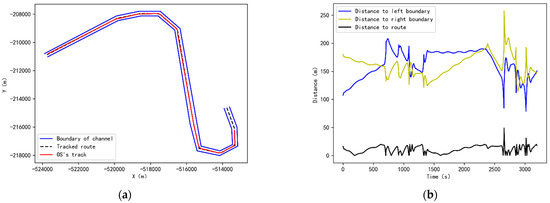
Figure 15.
Simulation validation of route tracking model.
The straight-line tracking results exhibit superior performance compared to waypoint tracking, which shows higher maximum deviation errors. From the route tracking results, it can be observed that the downstream ship’s trajectory remains largely consistent with the recommended curved route, maintaining minimal deviation in straight sections. To prevent the ship from drifting out of the channel before reaching a turning point, the OS performs preemptive steering maneuvers. At sharp-angle channel turns, the ship’s maneuverability may induce trajectory drift, leading to abrupt changes in deviation from the planned route. However, the maximum trajectory error throughout the entire process is 49 m.
These simulation results indicate that the inland waterway tracking method effectively controls ship navigation trajectories in curved waterways under environmental disturbances. The trajectory tracking error is significantly smaller than the waterway width, generally satisfying the requirements for autonomous navigation decision-making for inland ships.
4.2. The Verification of the Autonomous Navigation Decision-Making
This section presents three case studies to verify the capabilities and effectiveness of the proposed autonomous navigation decision-making model in various encounter scenarios, with the same environmental conditions set as in Section 4.1. Scenario 1 analyzes the response of the OS to a TS’s maneuver in a single-ship encounter. Scenarios 2 and 3 involve more complex multi-ship encounters, where the OS navigates inland tributary waterways using the proposed autonomous decision-making method. In this study, the ship’s velocity is defined by its speed over ground (SOG) and course over ground (COG), reflecting its motion relative to the true ground coordinate system.
4.2.1. Single-Ship Encounter Scenario 1
Two target ships (TS1 and TS2) are designed with identical initial states. TS1 maintains a constant course and speed, while TS2 initiates a starboard turn (75° steering angle) after 100 s. The ships’ states are summarized in Table 3. The autonomous navigation decision-making process and results for this scenario are illustrated in Figure 16.

Table 3.
The initial information of scenario 1.
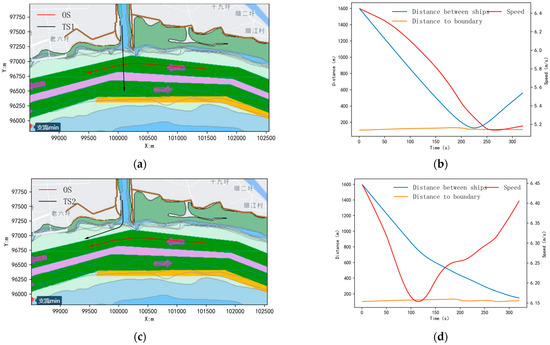
Figure 16.
Autonomous navigation trajectories and encounter data of scenario 1. (a) Collision avoidance trajectories with TS1 without maneuvering (b) encounter data with TS1 without maneuvering (c) Collision avoidance trajectories with TS1 under maneuvering condition (d) encounter data with TS1 under maneuvering condition.
Based on the initial motion analysis, TS1 is about to sail out of the tributary and into the mainstream. If TS1 exits the tributary and turns to starboard to follow the upstream channel (same direction as the OS), the OS is a give-way ship. Similarly, if TS1 turns to portside to enter the downstream channel (opposite direction to the OS), the OS remains the give-way ship, necessitating proactive collision avoidance measures. TS2 follows the same logic as TS1.
Since TS1 approaches from the OS’s starboard side, the OS reduces speed to avoid collision, achieving a minimum distance of 123 m from TS1 at 221 s—outside the OS’s ship domain. After passing and clearing TS1, the OS resumes the recommended route, stabilizes its course, and increases its propeller RPM to restore its original speed.
For TS2, which executes a starboard steering, the OS initially decelerates to avoid conflict. After 100 s, TS2 turns to starboard to exit the tributary and merge into the upstream channel. Given TS2’s steering maneuver and trajectory, the conflict resolves itself if TS2 maintains its current turn rate. Consequently, the OS resumes its rated speed early and continues along the recommended route.
4.2.2. Multi-Ship Encounter Scenario 2
A multi-ship encounter scenario involving the OS and seven target ships (TS1~TS7) in a tributary channel was designed. The initial states of the ships are provided in Table 4.

Table 4.
The initial information of scenario 2.
Based on the analysis of the ships’ initial data and navigation statuses, TS6 is a retrograde ship, requiring the OS to act as the give-way ship. The OS and TS4 form an overtaking situation, with the OS designated as the give-way ship; TS1 and TS7 are exiting the tributary channel, and OS is a stand-on ship; TS3 is entering the tributary channel, again making the OS the give-way ship. The autonomous navigation decision-making process and results for this scenario are illustrated in Figure 17.
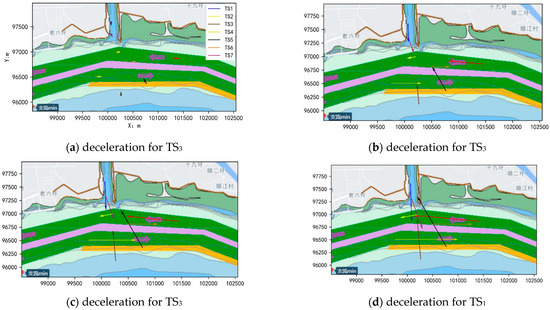
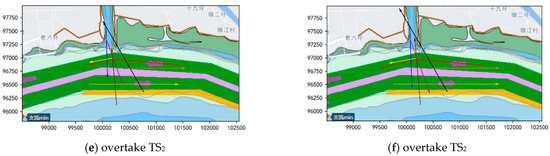
Figure 17.
Autonomous navigation trajectories of scenario 2.
Using the collision risk identification model, the OS prioritizes avoiding TS3 (entering the tributary) as the most urgent threat. To mitigate this risk, the OS implements a deceleration maneuver, passing astern of TS6 at 96 s. To safely avoid TS1 and TS7, the OS evaluates feasible maneuvering combinations, maintains deceleration, and adheres to the recommended route. This strategy ensures safe distances of 93 m from TS1 at 217 s and 149 m from TS7 at 293 s. Finally, the OS executes a portside turn and completes overtaking TS4 at 447 s.
As shown in the results of Figure 18, the minimum distances between the OS and TSs during autonomous navigation are as follows: 93 m to TS1, 48 m to TS2, 83 m to TS3, 437 m to TS4, 152 m to TS5, 110 m to TS6, and 149 m to TS7.
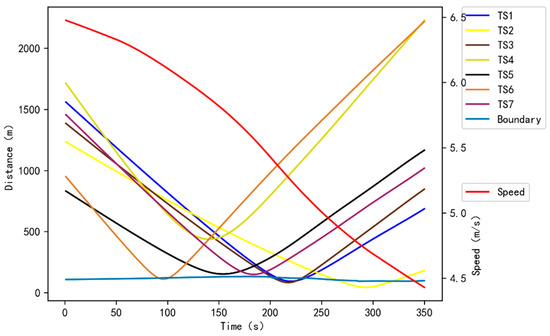
Figure 18.
Multi-ship encounter data of scenario 2.
4.2.3. Multi-Ship Encounter Scenario 3
The initial states and steering parameters of the ships in the multi-ship encounter scenario within the tributary channel under the TSs’ maneuvering conditions are provided in Table 5.

Table 5.
The initial information of scenario 3.
The initial encounter situation mirrors the multi-ship scenario described in the previous section, with the exception that TS7 initiates a 30° portside turn at 50 s, TS3 starts to turn 55° to starboard at 60 s, and TS1 starts to turn 55° to starboard at 115 s. The autonomous navigation decision-making process and results for this modified scenario are illustrated in Figure 19.
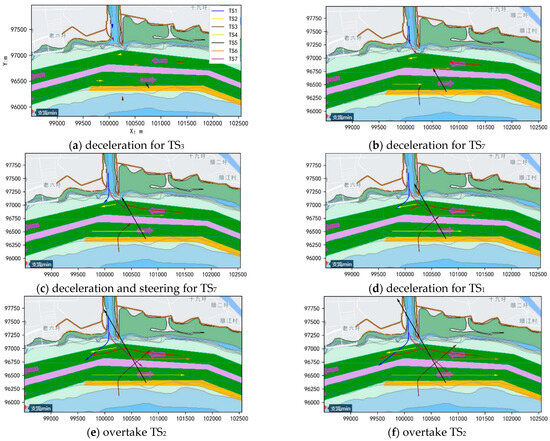
Figure 19.
Autonomous navigation trajectories of scenario 3.
Initially, to avoid TS3, the OS proactively implements a deceleration maneuver. At 60 s, TS3 alters its course from 355° to 30°, taking collision avoidance action that eliminates the risk with the OS. Concurrently, TS7 begins adjusting its course from 160° to 130° at 50 s, inadvertently escalating collision risks with the OS. At this point, deceleration alone proves insufficient for the OS to avoid TS7. Consequently, the OS combines deceleration with turning to starboard, safely passing astern of TS7 at 173 s. When no initial collision risk exists between TS1 and the OS, TS1 initiates a starboard turn at 115 s. Based on turn rate calculations, it is projected that TS1 will exit the tributary channel and cross the OS’s starboard side, creating a collision risk. To mitigate this, the OS maintains its deceleration strategy, completed overtaking TS4 at 304 s, and ultimately clears TS1 at 337 s.
As shown in the results of Figure 20, the minimum distances between the OS and TSs during autonomous navigation are as follows: 131 m to TS1, 54 m to TS2, 353 m to TS3, 455 m to TS4, 145 m to TS5, 111 m to TS6, and 61 m to TS7.
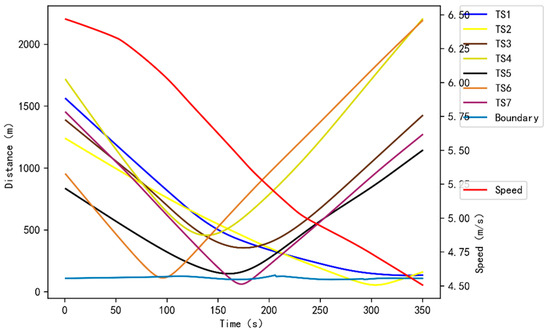
Figure 20.
Multi-ship encounter data of scenario 3.
5. Discussion
5.1. Result and Discussion
The core autonomous navigation decision-making algorithm combines the MMG model-based ship collision avoidance motion process derivation and the exhaustive course-speed maneuver method, and successfully identifies the navigation intention of TSs and realizes autonomous collision avoidance and navigation tracking under the multi-ship encounter scenarios under the premise of conforming to the ships’ motion characteristics and the navigation rules. The feasibility and effectiveness of the autonomous navigation decision-making algorithm in inland tributary waterway scenarios are proved through several simulation experiments. The results and discussions are as follows.
The trajectory tracking methodology demonstrates consistent navigational performance in both linear and curvilinear channel segments, as evidenced by the simulation results shown in Figure 15. The ship’s path-following errors relative to prescribed recommended routes remain constrained within acceptable operational thresholds throughout all navigation phases. In single-ship encounter scenario 1, the OS successfully anticipates the TS’s navigational intent through real-time analysis of its maneuvering patterns, thereby optimizing the collision avoidance strategy. This adaptive approach enables the simultaneous execution of coordinated avoidance maneuvers and precise route tracking while maintaining operational efficiency. In multi-ship encounter scenario 2, the collision risk between the OS and TS3 reaches maximum intensity. Collision avoidance can be achieved through portside maneuvers or speed reduction, though the methodology requires dual considerations: eliminating immediate collision threats while preventing new navigational conflicts with TS1 and TS7. Comparative analysis reveals that speed reduction minimizes heading alterations, proving optimal for narrow channel operations. Consequently, the OS maintains the original heading while decelerating to follow recommended routes, resuming speed to overtake TS2. Scenario 3 necessitates combined maneuvers when TS7 completes its turn, as speed reduction alone proves insufficient. The implemented strategy integrates continuous deceleration with turning 9° to starboard (276°→285°), balancing safety margins and channel constraints. Navigational safety is confirmed through relative distance metrics in Figure 18 and Figure 20, demonstrating sustained separation exceeding minimum safety thresholds between the OS and all TSs, while channel boundary compliance remains intact throughout the maneuvers.
The proposed collision avoidance scheme employs an exhaustive search method with iterative computational validation. However, by pre-filtering solutions that violate environmental constraints, ship maneuverability limits, navigation rules, or good seamanship, we significantly narrow the search space before optimization. This strategy not only reduces computational complexity but also mitigates the risk of local optima, which is a common pitfall in metaheuristic approaches like genetic algorithms or particle swarm optimization [42]. In contrast, our method ensures globally optimal solutions through constrained brute-force verification. Coupled with an optimized algorithmic architecture, this framework achieves real-time performance (~0.1 s per decision cycle) while maintaining superior stability compared to stochastic intelligent algorithms, which often exhibit inconsistent outputs under similar multi-constraint scenarios.
5.2. Comparison Analysis
This study develops an autonomous navigation model for inland tributary waterways through the integration of a ship collision avoidance model utilizing exhaustive course-speed maneuver combinations and a ship trajectory tracking model. Although maritime collision avoidance has been extensively investigated [43], the existing research predominantly examines open-water scenarios and single-vessel encounters, often overlooking the critical influence of environmental factors on navigational decision-making [45,46]. Conversely, the development of autonomous navigation systems for inland tributary environments remains significantly understudied, particularly regarding the unique challenges posed by narrow, dynamic waterways with complex hydrological characteristics. Multi-vessel collision avoidance demonstrates significantly greater complexity compared to single-ship scenarios. While prior studies on multi-vessel collision avoidance often oversimplify ship dynamics [34], our MMG-integrated trajectory predictor accounts for inertial drift and propulsion latency, enabling evasion paths that align with real-world vessel maneuverability. The failure to account for the dynamic maneuvering behaviors of TSs may render collision avoidance strategies vulnerable to abrupt course alterations or speed adjustments [20], ultimately compromising the reliability of evasive actions. While collision avoidance strategies leveraging propeller speed modulation remain underexplored—particularly the hydrodynamic coupling between variable-speed dynamics and evasion trajectories [12]—our hybrid control framework ensures safer clearance margins through synchronized propeller RPM adjustments, enabled by high-fidelity prediction of the OS’s transient states during maneuvers.
To address the existing disconnect between theoretical collision avoidance algorithms and real-world maritime operational requirements, this study develops an improved MMG framework for simulating high-fidelity ship dynamics. The proposed integrated autonomous navigation method incorporates comprehensive considerations of inland waterway environmental factors and navigation rule constraints, enabling robust multi-vessel collision avoidance and coordinated path following in complex inland river scenarios.
6. Conclusions
In this study, an autonomous navigation model is developed by combining a ship collision avoidance model and a ship trajectory tracking model based on ship motion dynamics. The principal contributions of this research are twofold. First, the proposed methodology enables effective collision risk identification and generates actionable avoidance recommendations tailored to the vessel’s maneuverability characteristics. Second, it incorporates dynamic detection of TS course-speed variations, intention interpretation, and adaptive decision recalibration mechanisms. Furthermore, all course-speed adjustments are executed through a holistic framework that systematically integrates inland waterway environmental constraints, good seamanship, regulatory compliance, and vessel maneuvering performance limitations, ensuring reliable performance in multi-vessel collision avoidance scenarios within complex inland waterway environments.
While simulation results demonstrate the effectiveness of the proposed method, several limitations warrant further investigation. Firstly, the current model oversimplifies target ship behavior by exclusively considering course alterations as collision avoidance maneuvers, overlooking the complexity of real-world navigation scenarios. Furthermore, the ship motion model incorporates only wind and current environmental influences, whereas practical navigation environments involve multiple factors—including bank effects, ship-to-ship interactions, and shallow-water effects—that significantly impact vessel maneuverability and induce nonlinear steering responses, which remain insufficiently captured in the current framework. Additionally, the model’s treatment of target vessel dynamics remains constrained, with motion characteristics simplified into a uniform nonlinear pattern, contrasting with the more sophisticated kinematic modeling applied to the OS. This discrepancy in motion representation may compromise the accuracy of collision risk identification and avoidance strategy formulation.
To enhance the applicability of the proposed method in practical inland tributary navigation environments, future work will incorporate vessel motion models considering shallow-water effects, bank effects, and ship-to-ship interaction effects. Autonomous navigation simulations will be conducted using real-world AIS data. Additionally, addressing highly complex encounter scenarios through sequential course and speed adjustments to achieve autonomous collision avoidance remains a critical research direction. In addition, we will also consider a hybrid approach combining the methodological framework of this paper with machine learning to achieve faster iterative decision updating in more complex encounter scenarios.
Author Contributions
Conceptualization, J.C.; methodology, J.C.; software, J.C.; validation, J.C.; formal analysis, J.C.; investigation, J.C.; resources, J.C.; data curation, J.C.; writing—original draft preparation, J.C.; writing—review and editing, J.C., L.H., L.X., H.L., G.H. and Y.H.; visualization, J.C.; supervision, L.H. and Y.H.; project administration, L.H. and Y.H.; funding acquisition, L.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partially supported by the Research Program of Hubei Key Laboratory of Inland Shipping Technology, grant number NHHY2023004, and Hubei Provincial Natural Science Foundation of China, grant number 2023AFB148.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RPRCIRCA | Rules of the People’s Republic of China for Inland River Collision Avoidance |
| CRI | Collision Risk Index |
| DCPA | Distance to the Closest Point of Approach |
| TCPA | Time to the Closest Point of Approach |
| MMG | Maneuvering Modeling Group |
| SVM | Support Vector Machine |
| VO | Velocity Obstacle |
| RVO | Reciprocal Velocity Obstacle |
| UAVs | unmanned aerial vehicles |
| MMG | mathematical model group |
| LOS | Line-of-Sight guidance algorithm |
| SOG | speed over ground |
| COG | course over ground |
| Nomenclature | |
| Symbols | Definition |
| m | the total mass of the vessel |
| mx | additional vertical mass |
| my | additional horizontal mass |
| u | lateral velocity |
| v | longitudinal velocity |
| r | yaw angular velocity |
| lateral acceleration | |
| longitudinal acceleration | |
| angular acceleration | |
| T | propeller thrust |
| the thrust deduction coefficient | |
| βR | the drift angle |
| B | beam |
| d | ship draft |
| L | ship length |
| xc | longitudinal coordinate of the center of flotation |
| kt | thrust correction factor |
| γA | hull wake correction factor |
| Cb | square coefficient |
| lcb | longitudinal center of buoyancy |
| lR | rudder drift angle coefficient |
| γp | the course of the recommended route |
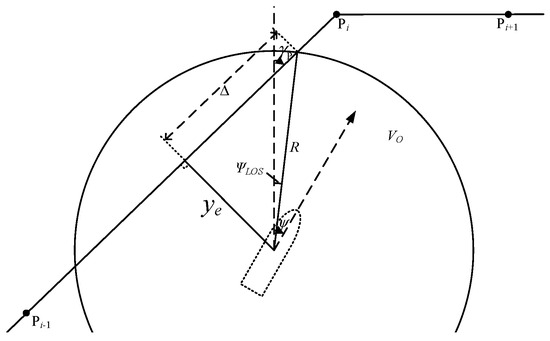
| ye(t) | transverse distance error |
| Δ | the longitudinal tracking error |
| CTS | course of target ship |
| Cchannel | the direction of the channel |
| vTS | speed of target ship |
| θO | the angle between the course of the OS and the channel |
| θT | the angle between the course of the TS and the channel |
| Dp | propeller diameter |
References
- Chen, P.; Huang, Y.; Mou, J.; van Gelder, P.H.A.J.M. Ship Collision Candidate Detection Method: A Velocity Obstacle Approach. Ocean Eng. 2018, 170, 186–198. [Google Scholar]
- Eleftheria, E.; Apostolos, P.; Markos, V. Statistical Analysis of Ship Accidents and Review of Safety Level. Saf. Sci. 2016, 85, 282–292. [Google Scholar]
- Teixeira, P.; Yan, X.; Jiang, J. An Inland Waterway Traffic Complexity Evaluation Method Using Radar Sequential Images. Ocean. Eng. 2025, 315, 119842. [Google Scholar] [CrossRef]
- Chen, J.; Huang, L.; Zhang, K.; Hao, G.; Zhao, X.; He, Y. Research of Methods of Collision Warning and Avoidance Assistant Decision Making for the Ship in Typical Inland TSS Waters. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2024, 10, 04024023. [Google Scholar]
- Liu, C.; Chu, X.; Wu, W.; Li, S.; He, Z.; Zheng, M.; Zhou, H.; Li, Z. Human–Machine Cooperation Research for Navigation of Maritime Autonomous Surface Ships: A Review and Consideration. Ocean Eng. 2022, 246, 110555. [Google Scholar]
- He, Y.; Jin, Y.; Huang, L.; Xiong, Y.; Chen, P.; Mou, J. Quantitative Analysis of COLREG Rules and Seamanship for Autonomous Collision Avoidance at Open Sea. Ocean Eng. 2017, 140, 281–291. [Google Scholar] [CrossRef]
- Karahalios, H. The Contribution of Risk Management in Ship Management: The Case of Ship Collision. Saf. Sci. 2014, 63, 104–114. [Google Scholar] [CrossRef]
- Bukhari, A.C.; Tusseyeva, I.; Lee, B.G.; Kim, Y.G. An Intelligent Real-Time Multi-Vessel Collision Risk Assessment System from VTS View Point Based on Fuzzy Inference System. Expert Syst. Appl. 2013, 40, 1220–1230. [Google Scholar] [CrossRef]
- Park, G.K.; Kim, D.Y. Building an Intelligent Supporting System for Safe Navigation Using Fuzzy Theory. In Proceedings of the 2012 International Conference on Fuzzy Theory and Its Applications (iFUZZY2012), Taichung, Taiwan, 16–18 November 2012. [Google Scholar] [CrossRef]
- Chin, H.C.; Debnath, A.K. Modeling Perceived Collision Risk in Port Water Navigation. Saf. Sci. 2009, 47, 1410–1416. [Google Scholar] [CrossRef]
- Kearon, J. Computer Programs for Collision Avoidance and Traffic Keeping; Academic Press: London, UK, 1977; pp. 229–242. [Google Scholar]
- Yu, D.; He, Y.; Zhao, X.; Chen, J.; Liu, J.; Huang, L. Dynamic Adaptive Autonomous Navigation Decision-Making Method in Traffic Separation Scheme Waters: A Case Study for Chengshanjiao Waters. Ocean Eng. 2023, 285, 115448. [Google Scholar]
- Li, W.; Yang, J.; Gao, X.; Yu, J. Modelling and Simulation of Intelligent Collision Avoidance Based on Ship Domain. Int. J. Simul. Process Model. 2020, 15, 64–75. [Google Scholar] [CrossRef]
- Shaobo, W.; Yingjun, Z.; Lianbo, L. A Collision Avoidance Decision-Making System for Autonomous Ship Based on Modified Velocity Obstacle Method. Ocean Eng. 2020, 215, 107910. [Google Scholar]
- Fiskin, R.; Nasiboglu, E.; Yardimci, M.O. A Knowledge-Based Framework for Two-Dimensional (2D) Asymmetrical Polygonal Ship Domain. Ocean Eng. 2020, 202, 107187. [Google Scholar]
- Zheng, K.; Chen, Y.; Jiang, Y.; Qiao, S. A SVM Based Ship Collision Risk Assessment Algorithm. Ocean Eng. 2020, 202, 107062. [Google Scholar]
- Li, B. Navigation Risk Assessment Scheme Based on Fuzzy Dempster–Shafer Evidence Theory. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418799572. [Google Scholar]
- Nieh, C.Y.; Lee, M.C.; Huang, J.C.; Kuo, H.C. Risk Assessment and Traffic Behaviour Evaluation of Inbound Ships in Keelung Harbour Based on Ais Data. J. Mar. Sci. Technol. 2019, 27, 311–325. [Google Scholar]
- Fang, Z.; Yu, H.; Ke, R.; Shaw, S.L.; Peng, G. Automatic Identification System-Based Approach for Assessing the Near-Miss Collision Risk Dynamics of Ships in Ports. IEEE Trans. Intell. Transp. Syst. 2018, 20, 534–543. [Google Scholar] [CrossRef]
- Huang, Y.; van Gelder, P.H.A.J.M. Time-Varying Risk Measurement for Ship Collision Prevention. Risk Anal. 2020, 40, 24–42. [Google Scholar]
- Ma, Y.; Zhao, Y.; Incecik, A.; Yan, X.; Wang, Y.; Li, Z. A Collision Avoidance Approach via Negotiation Protocol for a Swarm of USVs. Ocean Eng. 2021, 224, 108713. [Google Scholar]
- Zheng, J.; Liu, B.; Li, Y.; Huang, C. Unmanned Ship Collision Avoidance Action Plan Deduction Method under Man–Machine Interactive Negotiation in Collision Avoidance Scenarios. J. Mar. Sci. Eng. 2024, 12, 1842. [Google Scholar] [CrossRef]
- Coenen, F.P.; Smeaton, G.P.; Bole, A.G. Knowledge-Based Collision Avoidance. J. Navig. 1989, 42, 107–116. [Google Scholar]
- Sun, M.; Zheng, Z. Uncertainty Analysis Method Based on Fuzzy Random Variables and Time Window Selection. IOP Conf. Ser. Mater. Sci. Eng. 2018, 382, 052015. [Google Scholar]
- Zhou, D.; Zheng, Z. Dynamic Fuzzy Ship Domain Considering the Factors of Own Ship and Other Ships. J. Navig. 2019, 72, 467–482. [Google Scholar]
- Ni, S.; Liu, Z.; Cai, Y.; Wang, X. Modelling of Ship’s Trajectory Planning in Collision Situations by Hybrid Genetic Algorithm. Pol. Marit. Res. 2018, 25, 14–25. [Google Scholar]
- Ma, J.; Jia, C.; Shu, Y.; Liu, K.; Zhang, Y.; Hu, Y. Intent Prediction of Vessels in Intersection Waterway Based on Learning Vessel Motion Patterns with Early Observations. Ocean Eng. 2021, 232, 109154. [Google Scholar]
- Szlapczynski, R.; Szlapczynska, J. A Method of Determining and Visualizing Safe Motion Parameters of a Ship Navigating in Restricted Waters. Ocean Eng. 2017, 129, 363–373. [Google Scholar]
- Candeloro, M.; Lekkas, A.M.; Sørensen, A.J. A Voronoi-Diagram-Based Dynamic Path-Planning System for Underactuated Marine Vessels. Control Eng. Pract. 2017, 61, 41–54. [Google Scholar]
- Sun, X.; Wang, G.; Fan, Y.; Mu, D.; Qiu, B. Collision Avoidance Using Finite Control Set Model Predictive Control for Unmanned Surface Vehicle. Appl. Sci. 2018, 8, 926. [Google Scholar] [CrossRef]
- Degre, T.; Lefevre, X. A Collision Avoidance System. J. Navig. 1981, 34, 294–302. [Google Scholar]
- Wilson, P.A.; Harris, C.J.; Hong, X. A Line of Sight Counteraction Navigation Algorithm for Ship Encounter Collision Avoidance. J. Navig. 2003, 56, 111–121. [Google Scholar]
- Fiorini, P.; Shiller, Z. Motion Planning in Dynamic Environments Using Velocity Obstacles. Int. J. Rob. Res. 1998, 17, 760–772. [Google Scholar]
- Kufoalor, D.K.M.; Brekke, E.F.; Johansen, T.A. Proactive Collision Avoidance for ASVs Using A Dynamic Reciprocal Velocity Obstacles Method. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2402–2409. [Google Scholar]
- Chen, P.; Huang, Y.; Papadimitriou, E.; Mou, J.; van Gelder, P. Global Path Planning for Autonomous Ship: A Hybrid Approach of Fast Marching Square and Velocity Obstacles Methods. Ocean Eng. 2020, 214, 107793. [Google Scholar]
- Huang, Y.; van Gelder, P.H.A.J.M.; Wen, Y. Velocity Obstacle Algorithms for Collision Prevention at Sea. Ocean Eng. 2018, 151, 308–321. [Google Scholar]
- Praczyk, T. Neural Collision Avoidance System for Biomimetic Autonomous Underwater Vehicle. Soft Comput. 2020, 24, 1315–1333. [Google Scholar]
- Cheng, X.; Li, G.; Skulstad, R.; Chen, S.; Hildre, H.P.; Zhang, H. A Neural-Network-Based Sensitivity Analysis Approach for Data-Driven Modeling of Ship Motion. IEEE J. Ocean. Eng. 2019, 45, 451–461. [Google Scholar]
- Zeng, X.M.; Ito, M. Planning a Collision Avoidance Model for Ship Using Genetic Algorithm. In Proceedings of the 2001 IEEE International Conference on Systems, Man and Cybernetics. e-Systems and e-Man for Cybernetics in Cyberspace (Cat.No.01CH37236), Tucson, AZ, USA, 7–10 October 2001; Volume 4, pp. 2355–2360. [Google Scholar]
- Tsou, M.C. Multi-Target Collision Avoidance Route Planning under an ECDIS Framework. Ocean Eng. 2016, 121, 268–278. [Google Scholar]
- Xie, S.; Chu, X.; Zheng, M.; Liu, C. Ship Predictive Collision Avoidance Method Based on an Improved Beetle Antennae Search Algorithm. Ocean Eng. 2019, 192, 106542. [Google Scholar] [CrossRef]
- Ni, S.; Liu, Z.; Cai, Y.; Gao, S. Coordinated Anti-Collision Path Planning Algorithm for Marine Surface Vessels. IEEE Access 2020, 8, 160825–160839. [Google Scholar] [CrossRef]
- Ni, S.; Liu, Z.; Cai, Y. Ship Manoeuvrability-Based Simulation for Ship Navigation in Collision Situations. J. Mar. Sci. Eng. 2019, 7, 90. [Google Scholar] [CrossRef]
- Zhao, X.; He, Y.; Huang, L.; Mou, J.; Zhang, K.; Liu, X. Intelligent Collision Avoidance Method for Ships Based on COLRGEs and Improved Velocity Obstacle Algorithm. Appl. Sci. 2022, 12, 8926. [Google Scholar] [CrossRef]
- He, Y.; Liu, X.; Zhang, K.; Mou, J.; Liang, Y.; Zhao, X.; Wang, B.; Huang, L. Dynamic Adaptive Intelligent Navigation Decision Making Method for Multi-Object Situation in Open Water. Ocean Eng. 2022, 253, 111238. [Google Scholar] [CrossRef]
- Zhang, K.; Huang, L.; Liu, X.; Chen, J.; Zhao, X.; Huang, W.; He, Y. A Novel Decision Support Methodology for Autonomous Collision Avoidance Based on Deduction of Manoeuvring Process. J. Mar. Sci. Eng. 2022, 10, 765. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).