Research on Offshore Vessel Trajectory Prediction Based on PSO-CNN-RGRU-Attention
Abstract
1. Introduction
2. Related Works
2.1. CNN Residual Module
2.2. GRU Model
2.3. Attention Layer
2.4. PSO-CNN-RGRU-Attention Trajectory Prediction Model
3. Methods
3.1. Data Selection and Preprocessing
3.2. Evaluation Criteria
3.3. Model Hyperparameter Optimization
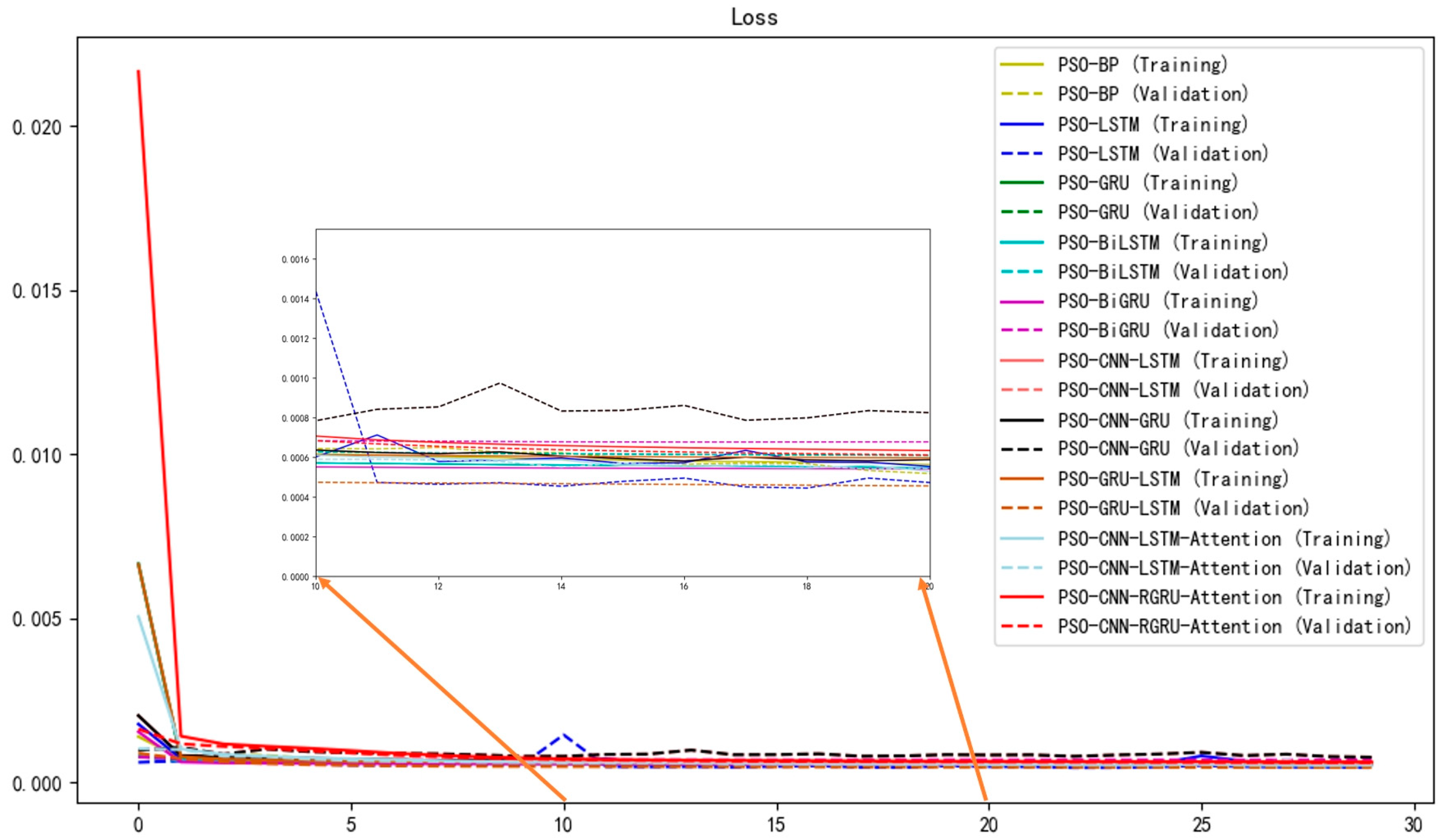
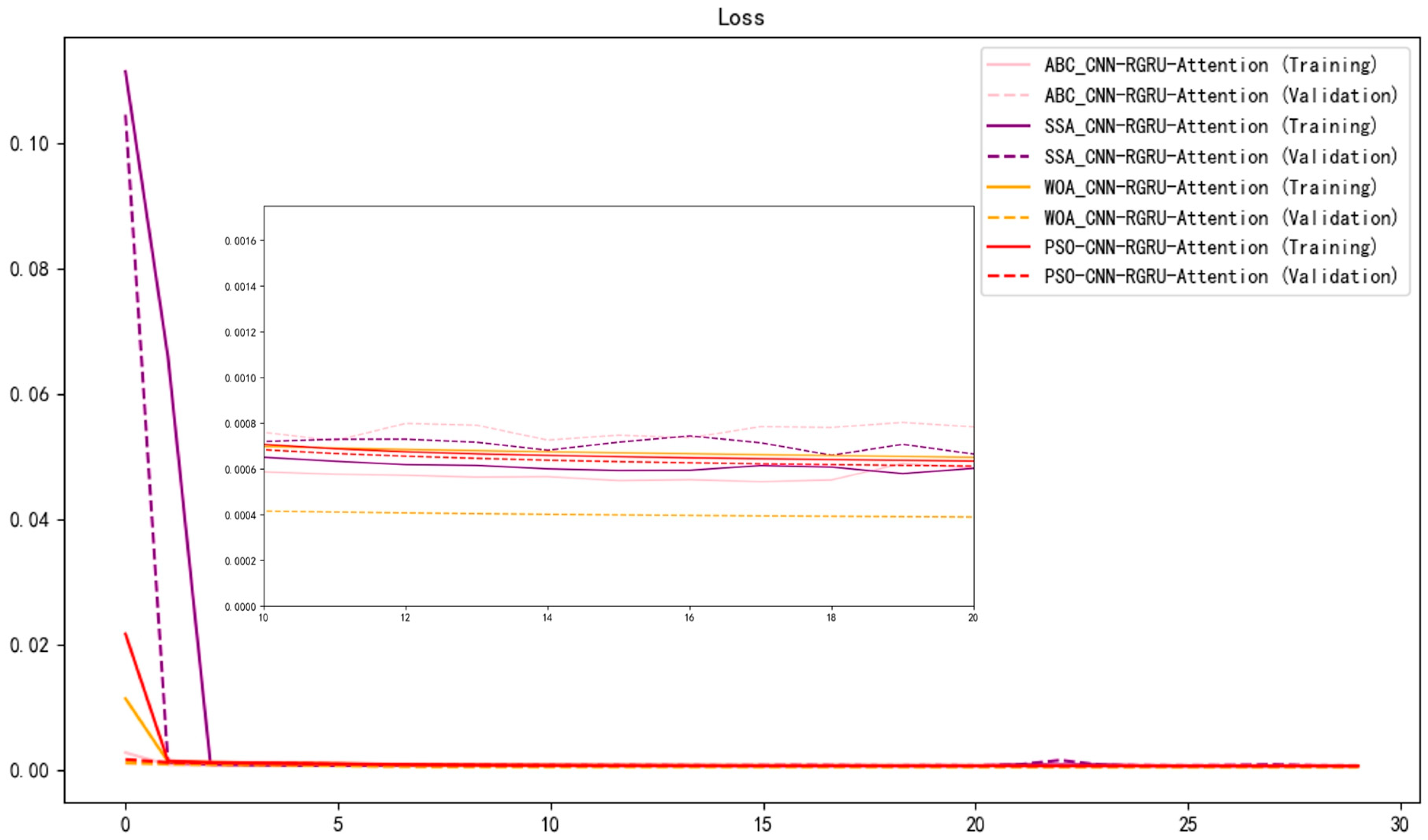
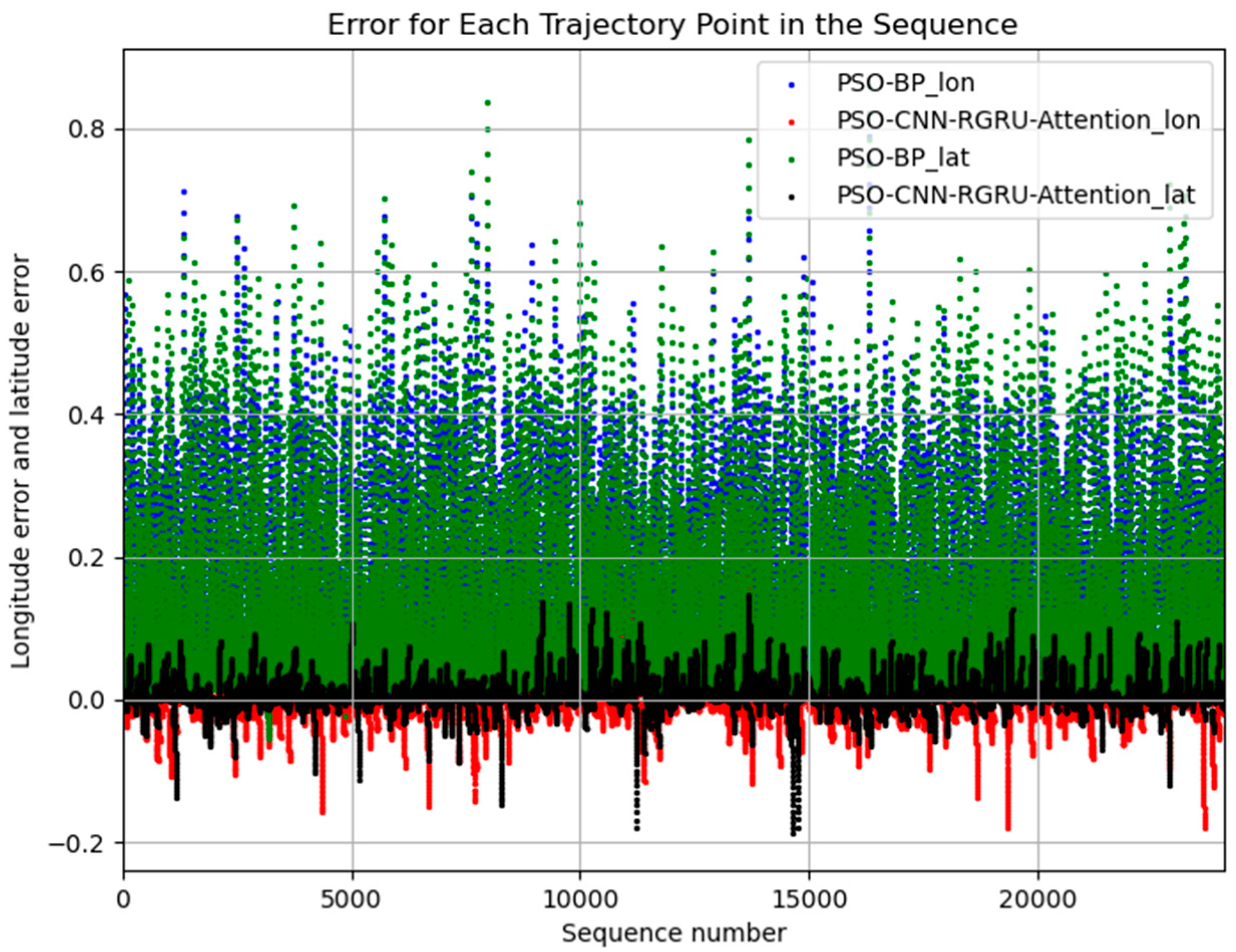
4. Results
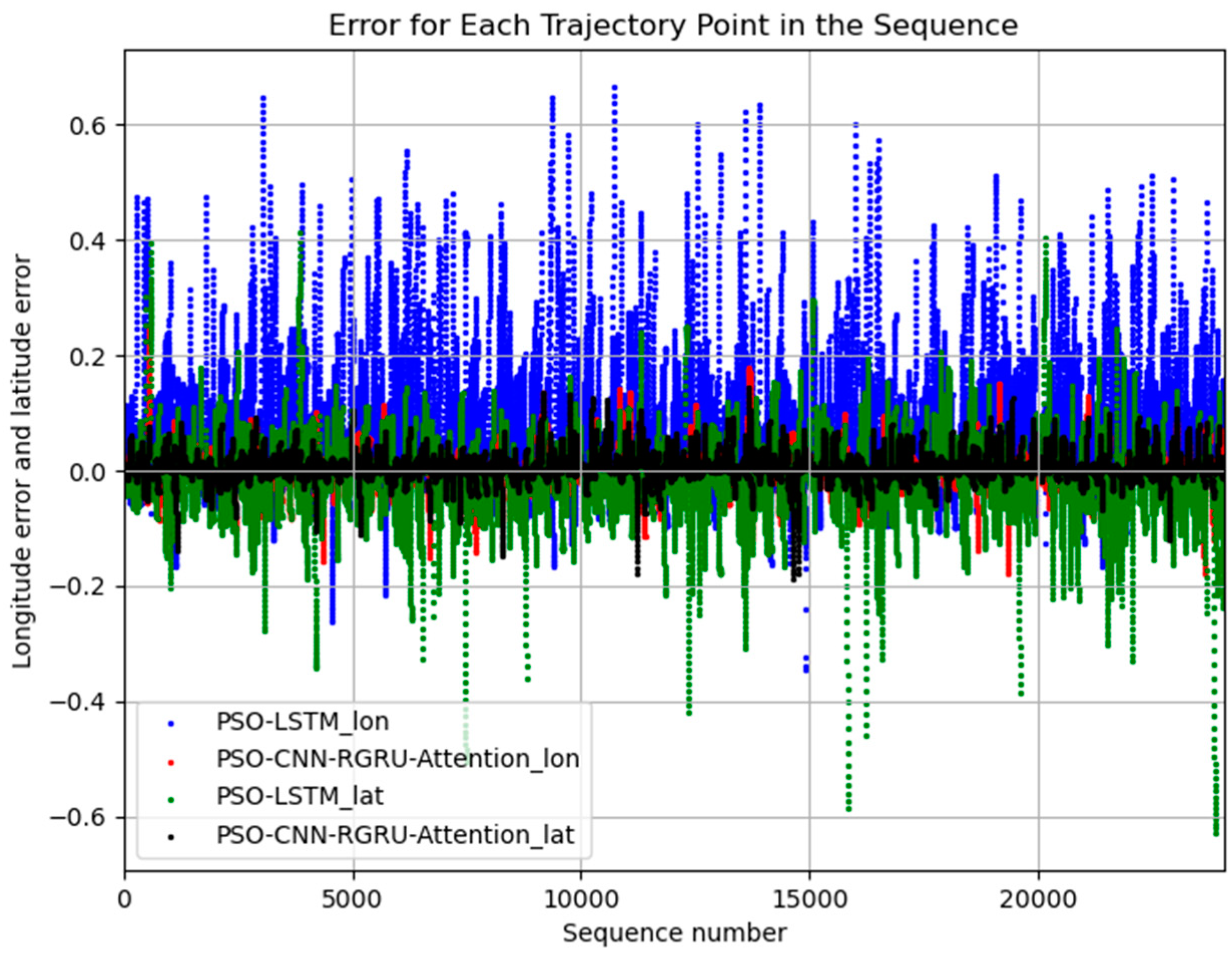
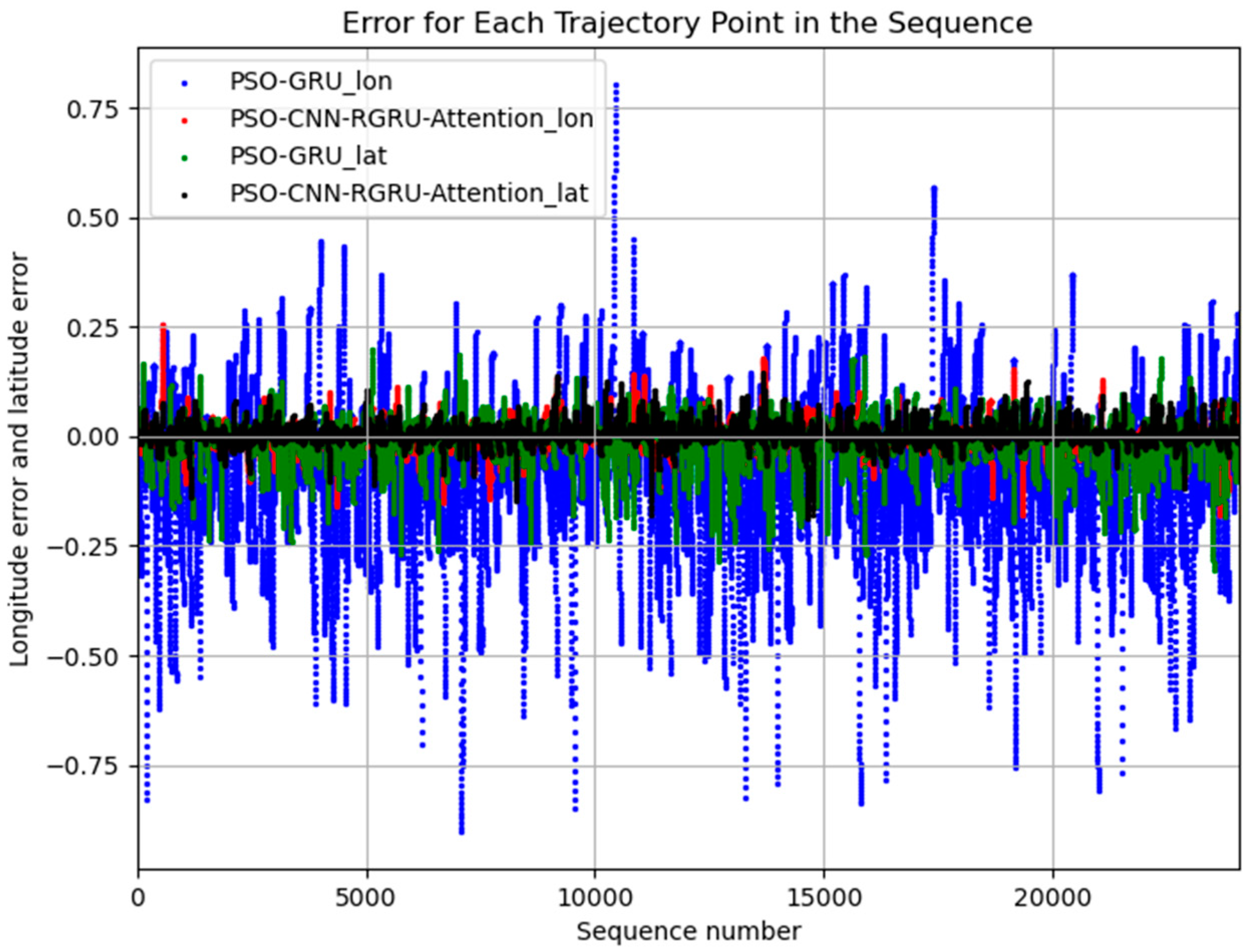
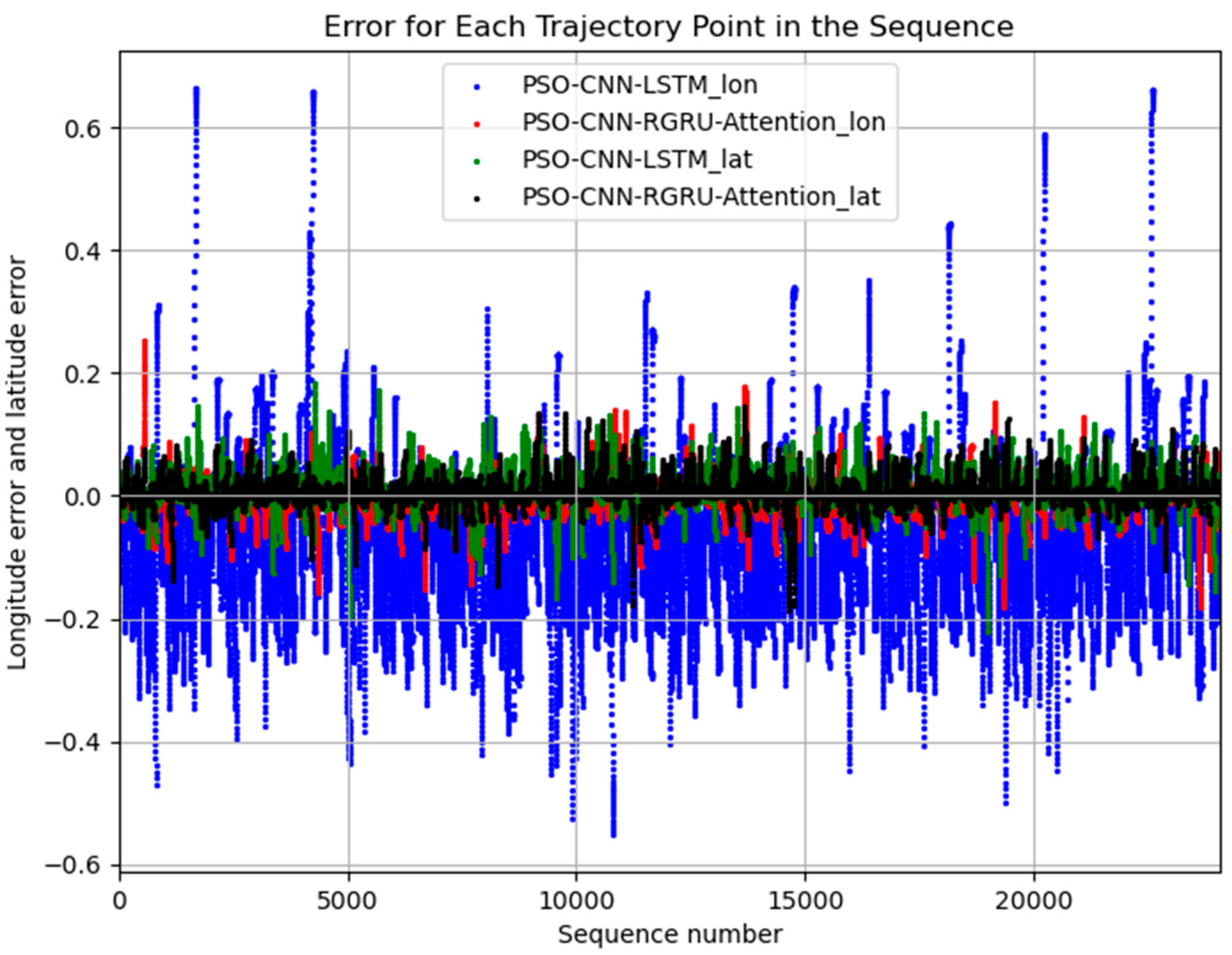
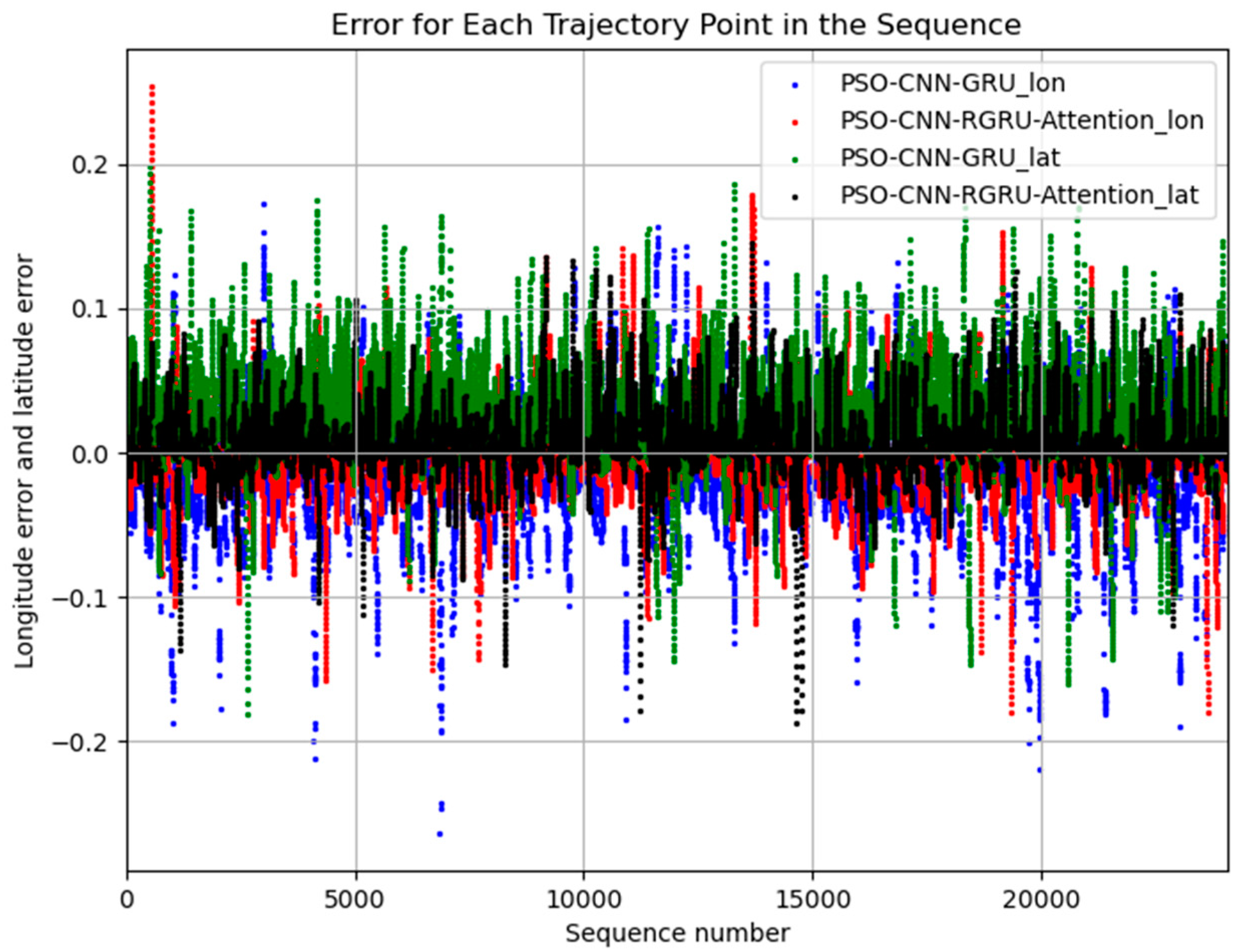
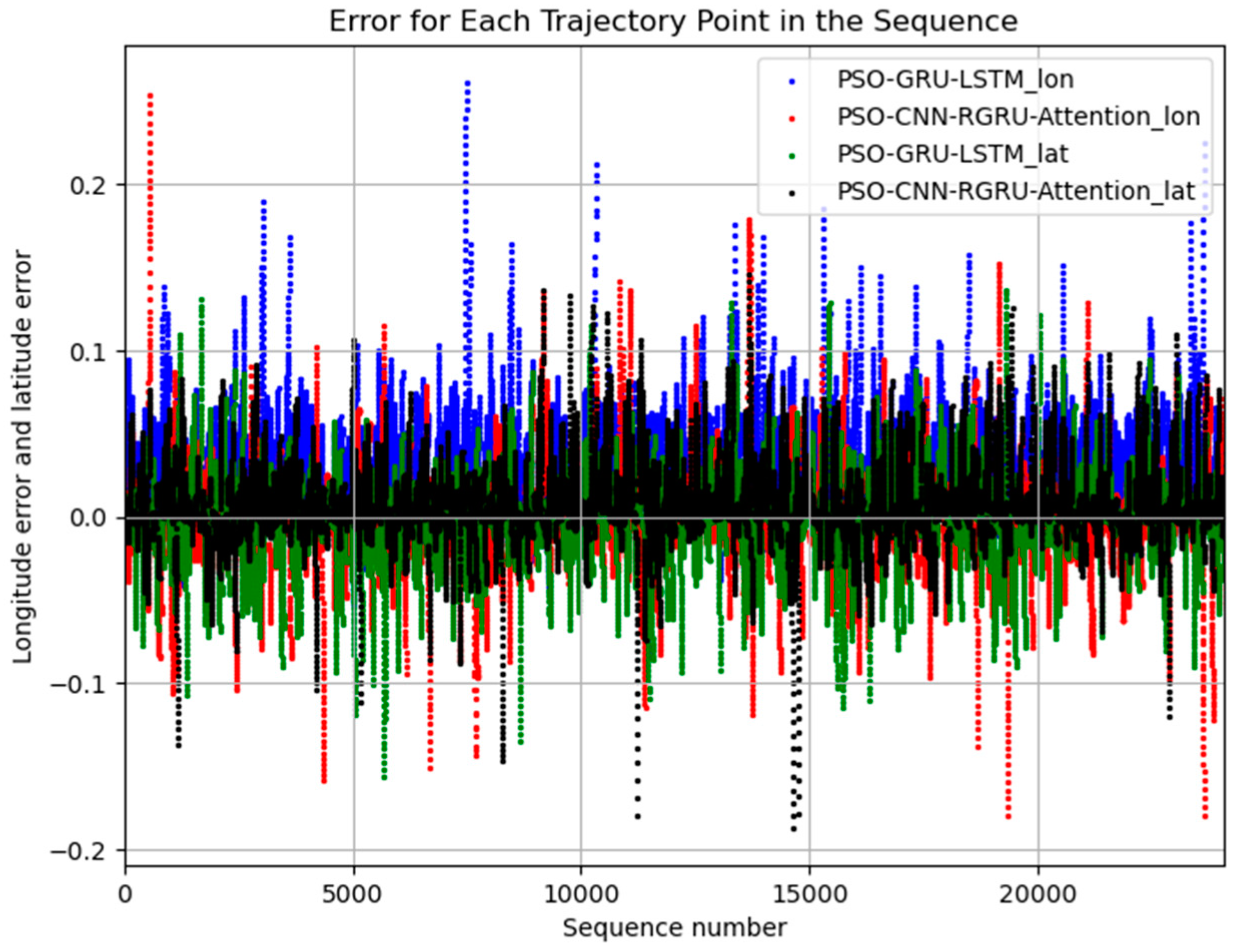
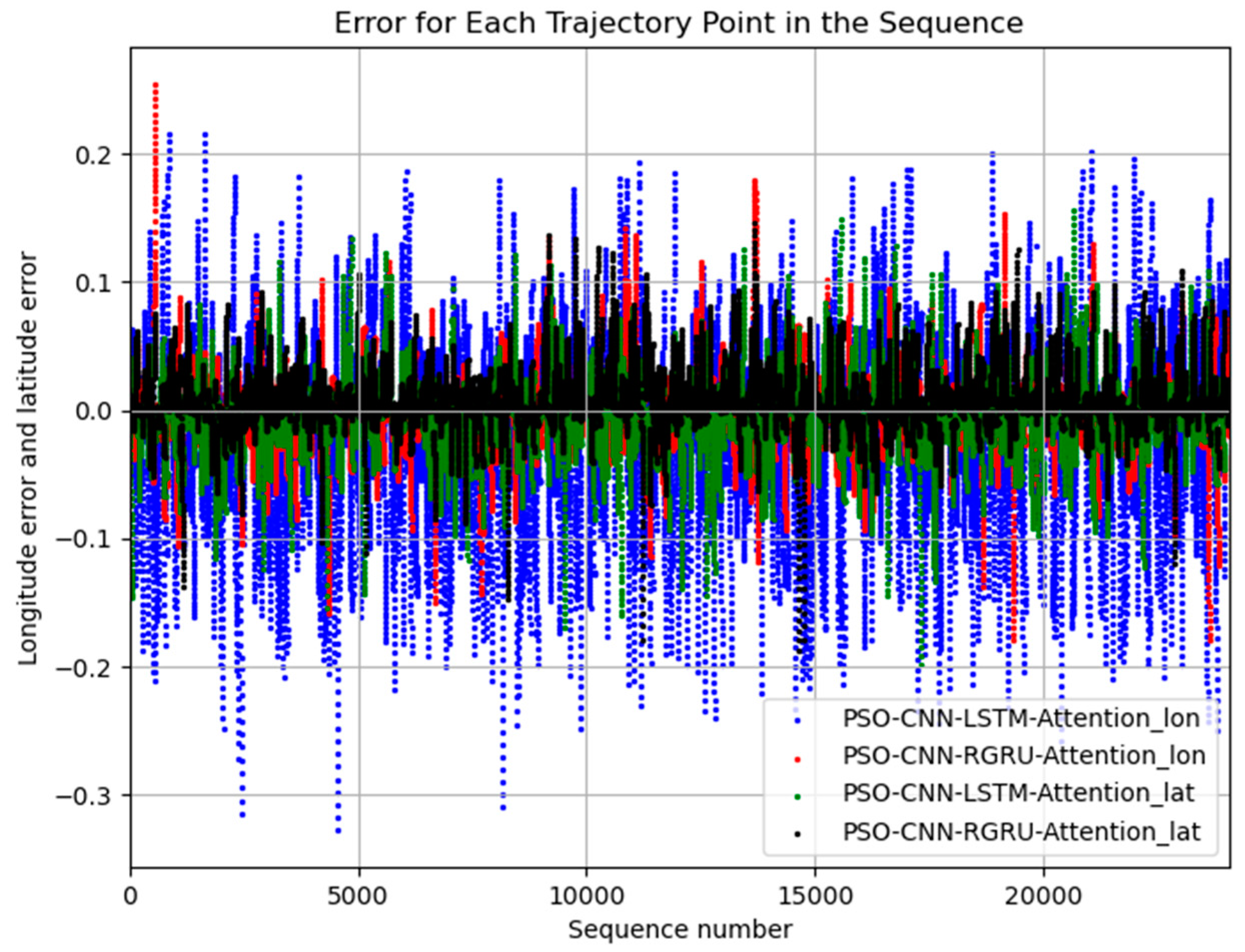
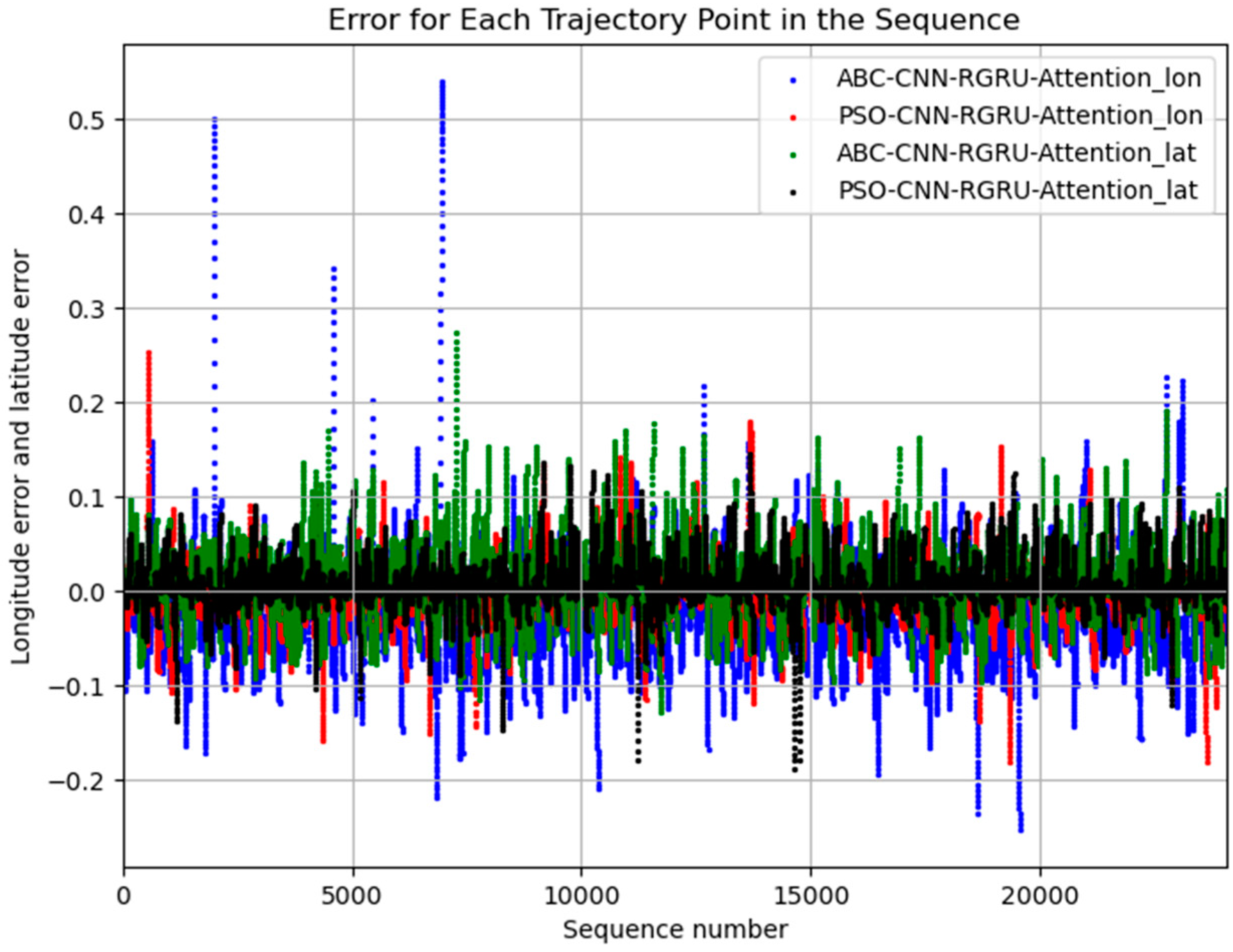
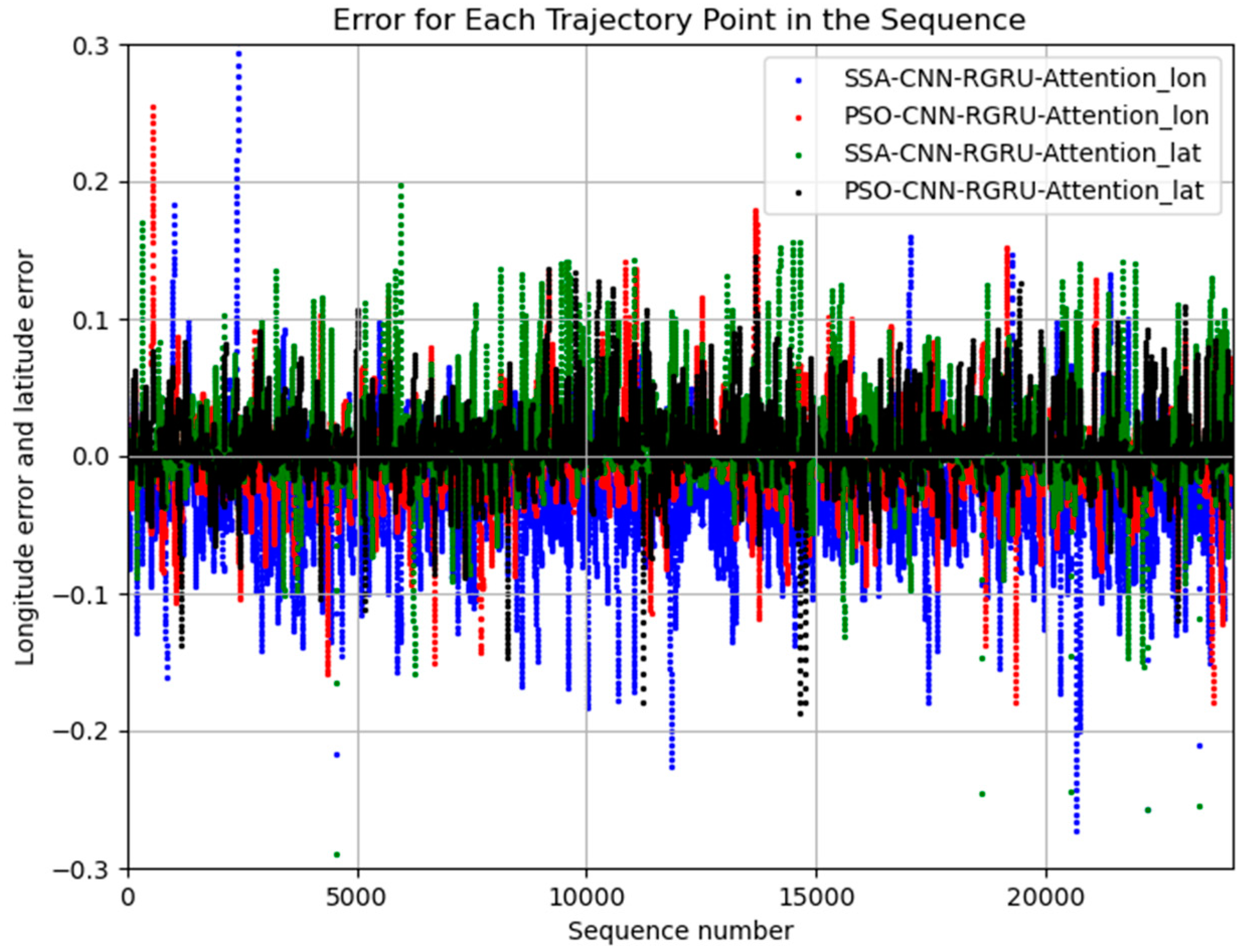
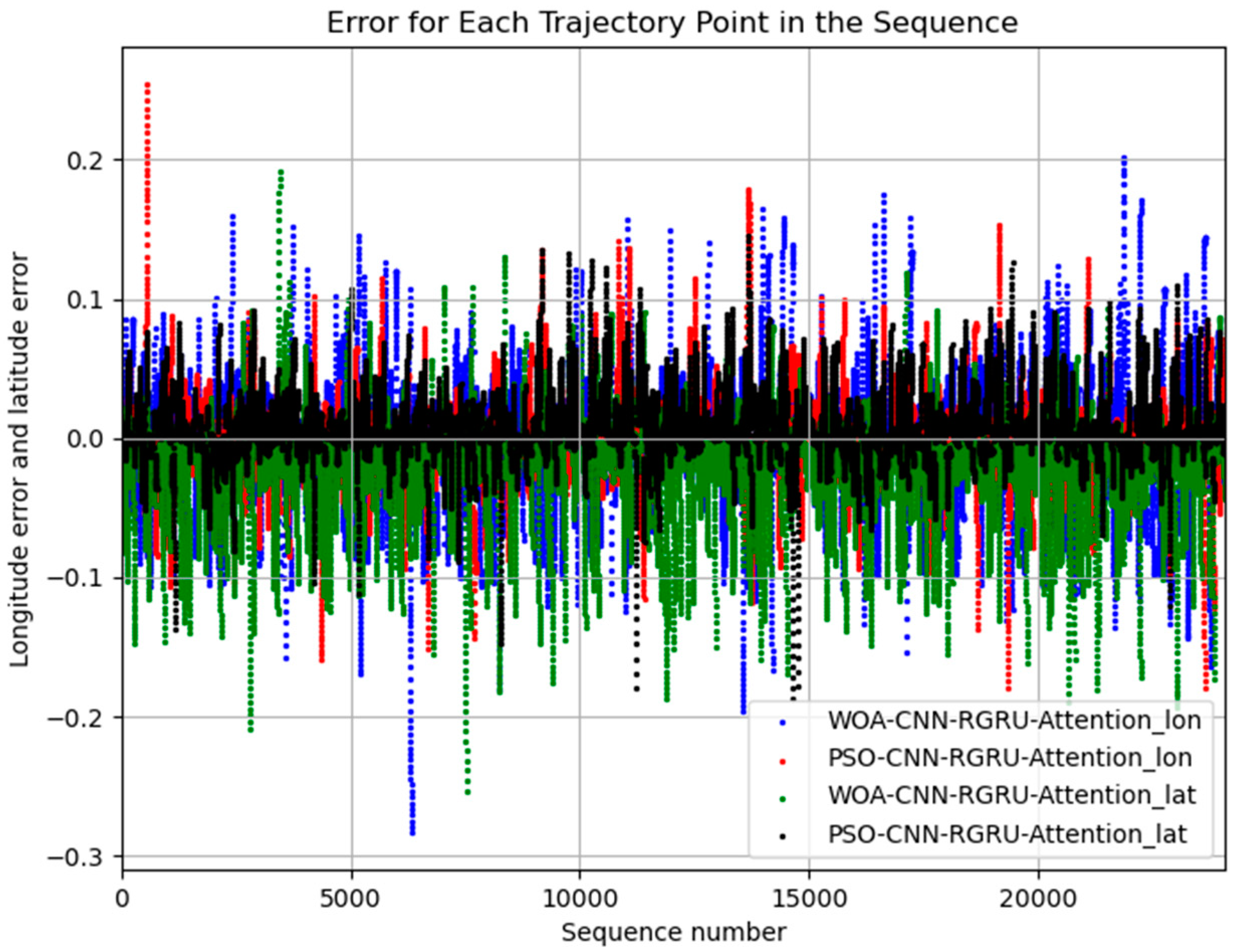
Experiment Results Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tu, E.; Zhang, G.; Rachmawati, L.; Rajabally, E.; Huang, G.-B. Exploiting AIS data for intelligent maritime navigation: A comprehensive survey from data to methodology. IEEE Trans. Intell. Transp. Syst. 2017, 19, 1559–1582. [Google Scholar]
- Qiao, S.; Shen, D.; Wang, X.; Han, N.; Zhu, W. A self-adaptive parameter selection trajectory prediction approach via hidden Markov models. IEEE Trans. Intell. Transp. Syst. 2014, 16, 284–296. [Google Scholar]
- Mazzarella, F.; Arguedas, V.F.; Vespe, M. Knowledge-based vessel position prediction using historical AIS data. In Proceedings of the 2015 Sensor Data Fusion: Trends, Solutions, Applications (SDF), Bonn, Germany, 6–8 October 2015; pp. 1–6. [Google Scholar]
- Ma, X.; Tao, Z.; Wang, Y.; Yu, H.; Wang, Y. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data. Transp. Res. Part C Emerg. Technol. 2015, 54, 187–197. [Google Scholar]
- Zhang, Z.; Ni, G.; Xu, Y. Ship trajectory prediction based on LSTM neural network. In Proceedings of the 2020 IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 12–14 June 2020; pp. 1356–1364. [Google Scholar]
- Tang, H.; Yin, Y.; Shen, H. A model for vessel trajectory prediction based on long short-term memory neural network. J. Mar. Eng. Technol. 2022, 21, 136–145. [Google Scholar]
- Zhang, J.; Wang, H.; Cui, F.; Liu, Y.; Liu, Z.; Dong, J. Research into ship trajectory prediction based on an improved LSTM network. J. Mar. Sci. Eng. 2023, 11, 1268. [Google Scholar] [CrossRef]
- Han, P.; Wang, W.; Shi, Q.; Yang, J. Real-time short-term trajectory prediction based on GRU neural network. In Proceedings of the 2019 IEEE/AIAA 38th Digital Avionics Systems Conference (DASC), San Diego, CA, USA, 8–12 September 2019; pp. 1–8. [Google Scholar]
- Yang, C.-H.; Wu, C.-H.; Shao, J.-C.; Wang, Y.-C.; Hsieh, C.-M. AIS-Based Intelligent Vessel Trajectory Prediction Using Bi-LSTM. IEEE Access 2022, 10, 24302–24315. [Google Scholar] [CrossRef]
- Wang, C.; Ren, H.; Li, H. Vessel trajectory prediction based on AIS data and bidirectional GRU. In Proceedings of the 2020 International Conference on Computer Vision, Image and Deep Learning (CVIDL), Chongqing, China, 10–12 July 2020; pp. 260–264. [Google Scholar]
- Cen, J.; Li, J.; Liu, X.; Chen, J.; Li, H.; Huang, W.; Zeng, L.; Kang, J.; Ke, S. A hybrid prediction model of vessel trajectory based on attention mechanism and CNN-GRU. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2024, 238, 809–823. [Google Scholar] [CrossRef]
- Gao, D.; Zhu, Y.; Zhang, J.; He, Y.-K.; Yan, K.; Yan, B.-R. A novel MP-LSTM method for ship trajectory prediction based on AIS data. Ocean. Eng. 2021, 228, 108956. [Google Scholar] [CrossRef]
- Pang, S.; Zou, L.; Zhang, L.; Wang, H.; Wang, Y.; Liu, X.; Jiang, J. A hybrid TCN-BiLSTM short-term load forecasting model for ship electric propulsion systems combined with multi-step feature processing. Ocean. Eng. 2025, 316, 119808. [Google Scholar]
- Zhao, C.D.; Zhuang, J.H.; Cheng, X.M.; Li, Y.H.; Guo, D.P. Ship trajectory prediction of RNN-Bi-LSTM based on characteristic attention mechanism. J. Guandong Ocean. Univ. 2022, 42, 102–109. [Google Scholar]
- Gundu, V.; Simon, S.P. PSO–LSTM for short term forecast of heterogeneous time series electricity price signals. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 2375–2385. [Google Scholar]
- Li, C.; Guo, Q.; Shao, L.; Li, J.; Wu, H. Research on short-term load forecasting based on optimized gru neural network. Electronics 2022, 11, 3834. [Google Scholar] [CrossRef]
- Mittal, S.; Sangwan, O.P. ABC LSTM optimizing parameters of deep LSTM using ABC algorithm for big datasets. Int. J. Eng. Adv. Technol. 2020, 9, 221–226. [Google Scholar] [CrossRef]
- Luo, J.; Gong, Y. Air pollutant prediction based on ARIMA-WOA-LSTM model. Atmos. Pollut. Res. 2023, 14, 101761. [Google Scholar]
- Liu, W.; Cao, Y.; Guan, M.; Liu, L. Research on Ship Trajectory Prediction Method Based on CNN-RGRU-Attention Fusion Model. IEEE Access 2024, 12, 63950–63957. [Google Scholar] [CrossRef]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Shen, G.; Tan, Q.; Zhang, H.; Zeng, P.; Xu, J. Deep learning with gated recurrent unit networks for financial sequence predictions. Procedia Comput. Sci. 2018, 131, 895–903. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30, pp. 6000–6010. [Google Scholar]
- Koshevyy, V.; Konovets, V.; Shishkin, A. SMART digital selective calling user interface on the base of Integration maritime navigation and radiocommunication equipment. Int. J. Mar. Navig. Saf. Sea Transp. 2021, 15, 291–297. [Google Scholar]
- Liu, Y.; Zhao, Y.; Cheng, H. Processing and Stationarity Analyzing of Accelerometer Parameter Based on Cubic Spline Interpolation. In Advances in Electronic Commerce, Web Application and Communication; Jin, D., Lin, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 2, pp. 589–595. [Google Scholar]







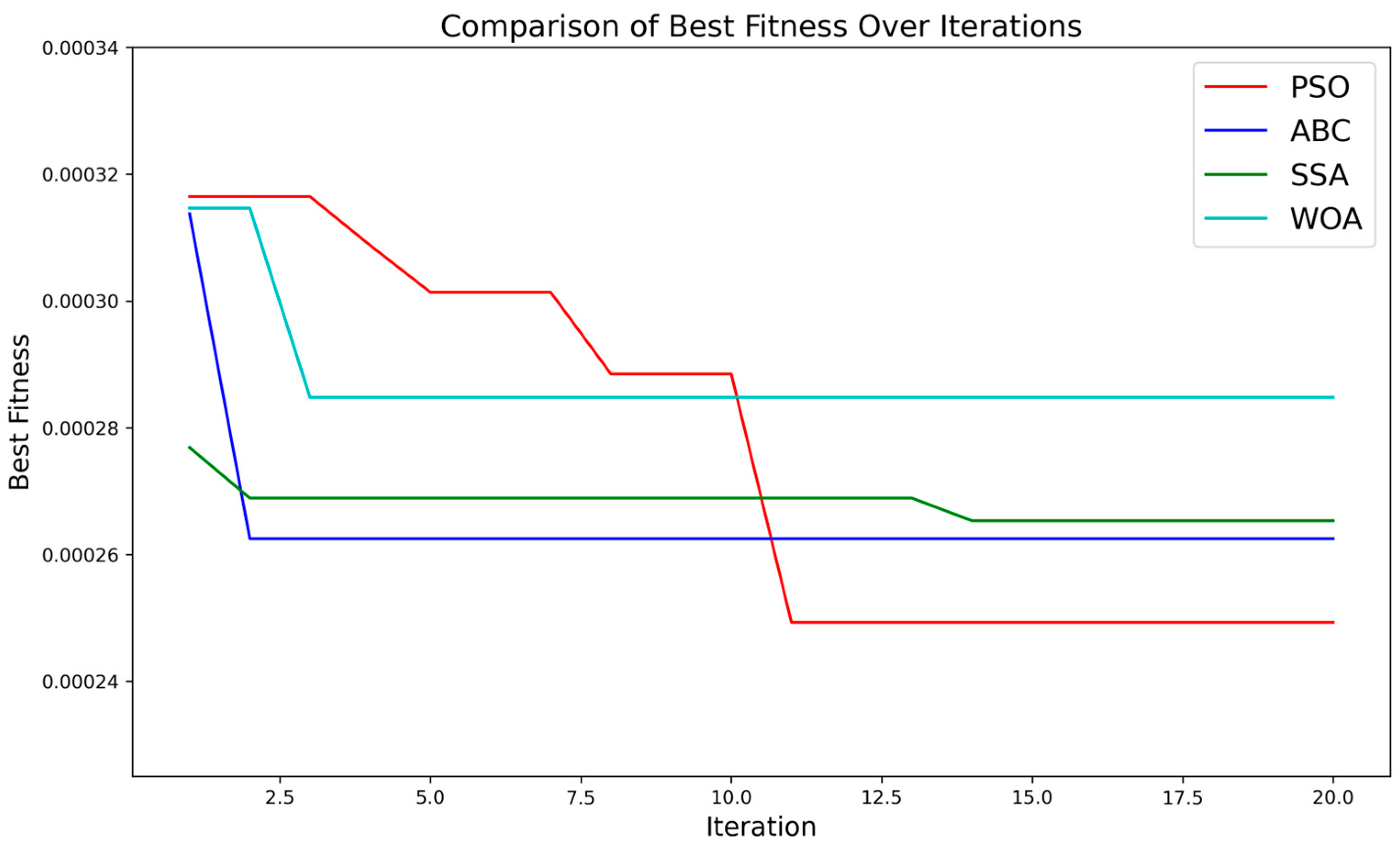


| Inertia Weight w | Number of Particles | Individual Learning Factor C1 | Global Learning Factor C2 | Number of Iterations |
|---|---|---|---|---|
| 0.8 | 5 | 2 | 2 | 20 |
| Model | MAE | MSE | RMSE |
|---|---|---|---|
| PSO-BP | 0.05107755 | 0.00473161 | 0.06878676 |
| PSO-LSTM | 0.09581701 | 0.01831781 | 0.12556596 |
| PSO-GRU | 0.12906489 | 0.03170017 | 0.17804541 |
| PSO-BiLSTM | 0.02661157 | 0.00138471 | 0.03721178 |
| PSO-BiGRU | 0.05415891 | 0.00504971 | 0.07106135 |
| PSO-CNN-LSTM | 0.10783649 | 0.01916146 | 0.13842495 |
| PSO-CNN-GRU | 0.02387195 | 0.00121191 | 0.03481251 |
| PSO-GRU-LSTM | 0.02641866 | 0.00131173 | 0.03621787 |
| PSO-CNN-LSTM-Attention | 0.04683651 | 0.00427090 | 0.06535212 |
| ABC-CNN-RGRU-Attention | 0.03751446 | 0.00261446 | 0.05113182 |
| SSA-CNN-RGRU-Attention | 0.03133182 | 0.00292325 | 0.05406715 |
| WOA-CNN-RGRU-Attention | 0.03794286 | 0.00382171 | 0.06182004 |
| PSO-CNN-RGRU-Attention | 0.02201033 | 0.00117039 | 0.03421106 |
| Model | MAE | MSE | RMSE |
|---|---|---|---|
| PSO-BP | 0.03319885 | 0.00192588 | 0.04388492 |
| PSO-LSTM | 0.04516268 | 0.00475778 | 0.06897666 |
| PSO-GRU | 0.03420336 | 0.00276886 | 0.05261996 |
| PSO-BiLSTM | 0.01900496 | 0.00070055 | 0.02646798 |
| PSO-BiGRU | 0.03123733 | 0.00200800 | 0.04481072 |
| PSO-CNN-LSTM | 0.02013612 | 0.00087166 | 0.02952389 |
| PSO-CNN-GRU | 0.02916388 | 0.00147378 | 0.03838990 |
| PSO-GRU-LSTM | 0.01653731 | 0.00060200 | 0.02453578 |
| PSO-CNN-LSTM-Attention | 0.01806733 | 0.00075004 | 0.02738693 |
| ABC-CNN-RGRU-Attention | 0.02459865 | 0.00118986 | 0.03449439 |
| SSA-CNN-RGRU-Attention | 0.01623029 | 0.00096784 | 0.03111023 |
| WOA-CNN-RGRU-Attention | 0.02685349 | 0.00185097 | 0.04302294 |
| PSO-CNN-RGRU-Attention | 0.01508747 | 0.00054552 | 0.02335655 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Cao, Y. Research on Offshore Vessel Trajectory Prediction Based on PSO-CNN-RGRU-Attention. Appl. Sci. 2025, 15, 3625. https://doi.org/10.3390/app15073625
Liu W, Cao Y. Research on Offshore Vessel Trajectory Prediction Based on PSO-CNN-RGRU-Attention. Applied Sciences. 2025; 15(7):3625. https://doi.org/10.3390/app15073625
Chicago/Turabian StyleLiu, Wei, and Yu Cao. 2025. "Research on Offshore Vessel Trajectory Prediction Based on PSO-CNN-RGRU-Attention" Applied Sciences 15, no. 7: 3625. https://doi.org/10.3390/app15073625
APA StyleLiu, W., & Cao, Y. (2025). Research on Offshore Vessel Trajectory Prediction Based on PSO-CNN-RGRU-Attention. Applied Sciences, 15(7), 3625. https://doi.org/10.3390/app15073625






