Research on the Coupled Bending–Torsional Flutter Mechanism for Ideal Plate

Abstract

In order to explore the inducing mechanism of negative damping of bending–torsional coupling flutter, an ideal plate with a width of 0.45 m was taken as the research object. The changes in frequency, critical wind speed, aerodynamic stiffness, and aerodynamic damping were systematically analyzed by using the “incentive-feedback” mechanism theory. The source of modal damping and the inducing mechanism of bending–torsional coupling flutter were identified. The research results show that the torsional modal damping of the ideal plate mainly comes from the aerodynamic positive damping of the torsional velocity self-excitation ($A_2^{*}$) and the aerodynamic negative damping of the torsional displacement incentive feedback ($A_1^{*}{H}_3^{*}$). Among them, the aerodynamic negative damping of the item ($A_1^{*}{H}_3^{*}$) causes the torsional mode damping to be negative, and the ideal plate undergoes bending–torsion-coupled flutter under the drive of the torsional mode aerodynamic negative damping. The reason why the aerodynamic damping of the item ($A_1^{*}{H}_3^{*}$) is negative depends on two aspects: one is that the flutter derivatives $A_1^{*}$ and $H_3^{*}$ have opposite signs; the second is that the torsional displacement self-excited lift excites the vertical vibration to produce negative stiffness $-m_h{\omega }_{s\alpha }^2$. This results in the phase difference between the torsional displacement self-excited lift and the vertical displacement response in the range of (90–180°).

1. Introduction

Large-span suspension bridges typically exhibit low structural damping and stiffness, making them highly sensitive to both static and dynamic wind loads. Large-span bridge structures can face static wind instability when subjected to static wind loads, which may compromise their load-bearing capacity. Additionally, under dynamic loads, bridges with blunt bodies as the main beam section are susceptible to vortex-induced vibrations, flutter, galloping, and buffeting. These phenomena can adversely affect the structure’s fatigue life and overall safety. In 1940, the Tacoma Narrows Suspension Bridge collapsed as a result of wind-induced vibration, thereby initiating a period of research into the wind resistance of modern long-span bridges and leading to the establishment of the discipline of bridge wind engineering. In recent years, with the in-depth development of the research on the flutter performance of bridges, scholars in the field of bridge wind resistance have carried out extensive research on the flutter performance of super-large-span suspension bridges [1], flutter critical wind speed prediction [2,3], box girder aerodynamic shape optimization [4], post-flutter characteristics [5,6,7], nonlinear flutter [8], and bridge flutter performance in complex wind environments [9,10]. Compared with the previous research results on flutter, the accuracy and method of flutter critical wind speed identification, flutter morphology analysis, and actual complex wind environments are considered in more detail and comprehensively. However, in order to analyze and solve the flutter problem of long-span bridges in essence, it is necessary to carry out a mechanism analysis of flutter.

Since the inception of bridge wind engineering, two dominant theories have emerged to explain the vibration mechanism of large-span suspension bridges: the “stiffness-driven” and the “torsional negative damping drive” theories. Xiang Haifan proposed the “stiffness-driven” mechanism theory for flutter in streamlined and non-streamlined box girder sections, as well as the “torsional negative damping-driven” mechanism theory. The “stiffness-driven” mechanism theory suggests that the streamlined box beam section may experience classical aeroelastic flutter similar to that of an aircraft wing. In other words, the stiffness effects caused by high-speed airflow will alter the vertical bending and torsional vibration frequencies of the structure, ultimately coupling them into a unified flutter frequency, thereby driving vibration divergence. The theory of “negative damping driven by torsional flutter” suggests that non-streamlined cross-sections are more prone to experiencing torsional flutter. In other words, flowing air creates a negative damping effect on the cross-section’s torsional motion. When the critical wind speed for flutter is reached, the air’s negative damping overcomes the structure’s inherent positive damping, leading to vibration divergence. In the “torsional negative damping drive” mechanism, the decoupling of bending–torsion-coupled vibration modes and the source of torsional mode aerodynamic negative damping become the primary issues to be addressed in this theory. For this purpose, various solution methods and theories have been proposed, such as the “step-by-step solution” method, the “incentive feedback” mechanism theory, and the “coupled flutter closure solution” theory. Matsumoto [11,12,13,14,15,16,17], a Japanese scholar, employs a “step-by-step” approach to investigate the mechanism of vibration-induced instability. His research specifically centers on modal decoupling in relation to torsional vibrations. Matsumoto [12] conducted wind tunnel experiments to investigate flutter. He subjected both rectangular and H-shaped cross-sections to forced twisting and measured their surface-unsteady pressures. Using a step-by-step approach, he identified the torsional modal aerodynamic damping. His research revealed that the mechanism behind torsional flutter is fundamentally similar to coupled flutter. Both types of flutter are self-excited oscillations caused by torsional aerodynamic damping, specifically, a mechanism known as the “torsional negative damping drive”, which induces flutter in bluff body sections. Xu [18] used the “step-by-step solution” method to analyze the torsional coupling flutter of the Akashi Kaikyo Bridge and the torsional flutter of the Suramadu Bridge.

Yang Yongxin [19,20,21] utilized the “incentive feedback” mechanism to separate the modal analysis of bending–torsion-coupled vibration. They identified the aerodynamic damping associated with both vertical and torsional modes. The research findings on the “incentive feedback” mechanism reveal how the self-excited, lift-induced vertical bending system responds to torsional displacement. The self-excited moments caused by vertical vibrations act as aerodynamic negative damping in the torsional vibration system. This interaction can lead to the divergence of the torsional vibrations in the bridge structure. The vertically vibrating system, influenced by coupled self-excited lift, enters a divergent state that causes torsional coupling flutter in the bridge structure. This phenomenon, known as the “torsional negative damping drive” mechanism, is responsible for the torsional coupling flutter of the bridge. Chen [22,23,24] conducted research on the mechanisms of coupled flutter and torsional flutter, using the theory known as “coupled flutter closure solution”. He transformed the time-domain vibration equations into complex-domain vibration equations through Laplace transformation, considering the characteristics of very small structural damping ratios. He simplified the terms related to complex frequencies, and then decoupled them using the bending–torsion amplitude ratio function. Finally, based on the real and imaginary parts of the vibration equations, he identified the vertical and torsional modal damping ratios and modal frequencies. His research revealed that torsional negative damping results in torsional–axial coupling flutter, which aligns with the analysis conclusion regarding the “incentive feedback” mechanism. However, the existing “incentive feedback” theory fails to strictly adhere to the vibration equation when performing modal decoupling of the coupled vibration system through the “incentive feedback” mechanism. Moreover, the process of flutter aerodynamic damping identification necessitates a cyclic search for the vibration frequency, leading to low identification efficiency.

In this paper, we explore the influence of direct aerodynamic damping and direct aerodynamic stiffness on the intrinsic damping and stiffness of the structure, building on the “incentive feedback” mechanism of flutter and previous research findings [19,20,21]. A flutter equation system is developed, and we perform modal decoupling of the coupled vibration system using the “incentive feedback” mechanism to identify the modal damping and modal stiffness. Compared to the previous analysis theory of the “incentive feedback” mechanism for flutter, this paper, while adhering to the flutter vibration equation, omits the cyclic search process for identifying flutter aerodynamic damping, thereby improving computational efficiency.

2. Flutter “Incentive-Feedback” Mechanism Theory

This text discusses the modal decoupling of a bending–torsion-coupled vibration system using an “incentive-feedback” mechanism, with the identification of aerodynamic damping for flutter vertical modes and torsional modes. The bending–torsional coupling of flutter [25] is shown in Equations (1) and (2):

$$m_h\ddot{h}+\left(C_{h0}-H_1\right)\dot{h}+\left(K_{h0}-H_4\right)h=H_2\dot{\alpha }+H_3\alpha$$

(1)

$$I\ddot{\alpha }+\left(C_{\alpha 0}-A_2\right)\dot{\alpha }+\left(K_{\alpha 0}-A_3\right)\alpha =A_1\dot{h}+A_{4}h$$

(2)

where $m_h$ and $I$ represent the unit mass per length in the vertical direction and the mass moment of inertia, respectively; $C_{h0}$ and $C_{\alpha 0}$ represent the inherent damping in the vertical and torsional directions, respectively; $C_{h0}=2m_h{\xi }_{h0}{\omega }_{h0}$, ${\omega }_{h0}=2\pi f_{h0}$, ${\xi }_{h0}$, and ${\omega }_{h0}$ are the vertical natural damping ratio and circular frequency, respectively; $C_{\alpha 0}=2I{\xi }_{\alpha 0}{\omega }_{\alpha 0}$, ${\omega }_{\alpha 0}=2\pi f_{\alpha 0}$, ${\xi }_{\alpha 0}$, and ${\omega }_{\alpha 0}$ are the torsional natural damping ratio and circular frequency, respectively; $K_{h0}$ and $K_{\alpha 0}$ are the inherent stiffness in the vertical and torsional directions, respectively, $K_{h0}=m_h{\omega }_{h0}^2$, $K_{\alpha 0}=I{\omega }_{h0}^2$; $\ddot{h}$, $\dot{h}$, and $h$, respectively, represent vertical acceleration, velocity, and displacement; $\ddot{\alpha }$, $\dot{\alpha }$, and $\alpha$ are torsional acceleration, velocity, and displacement, respectively; $H_i\left(i=1,2,3,4\right)$ are the aerodynamic derivatives of the lift; $A_i\left(i=1,2,3,4\right)$ are the aerodynamic derivatives of the lifting moment; $H_1\dot{h}+H_{4}h$ and $H_2\dot{\alpha }+H_3\alpha$ are the vertical self-excited lift and the coupled torsional self-excited lift, respectively; and $A_2\dot{\alpha }+A_3\alpha$ and $A_1\dot{h}+A_{4}h$ are the torsional self-excited lift moment and the coupled vertical self-excited lift moment, respectively. Among them, the torsional self-excited lift force $H_2\dot{\alpha }+H_3\alpha$ and the vertical self-excited lift moment $A_1\dot{h}+A_{4}h$ cause the vertical vibration system and the torsional vibration system to couple with each other, forming a bending–torsion-coupled vibration system.

The relationship between aerodynamic derivatives and dimensionless flutter derivatives of aerodynamic forces is presented in Equations (3) and (4):

$$\left\{\begin{array}{c}\begin{array}{cc}{H}_1=\rho B^2\omega H_1^{*}& H_2=\rho B^3\omega H_2^{*}\end{array}\\ \begin{array}{cc}{H}_3=\rho B^3{\omega }^2{H}_3^{*}& H_4=\rho B^2{\omega }^2{H}_4^{*}\end{array}\end{array}\right.$$

(3)

$$\left\{\begin{array}{c}\begin{array}{cc}{A}_1=\rho B^3\omega A_1^{*}& A_2=\rho B^4\omega A_2^{*}\end{array}\\ \begin{array}{cc}{A}_3=\rho B^4{\omega }^2{A}_3^{*}& A_4=\rho B^3{\omega }^2{A}_4^{*}\end{array}\end{array}\right.$$

(4)

where $\rho$ is air density, $U$ is incoming average flow velocity, and $B$ is structural cross-sectional width; $H_i^{*}\left(i=1,2,3,4\right)$ are the dimensionless flutter derivatives of lift; and $A_i^{*}\left(i=1,2,3,4\right)$ are dimensionless flutter derivatives of lift moments.

2.1. Torsional Modal Damping and Stiffness

Set the torsional displacement to $\alpha ={\alpha }_0{e}^{-{\epsilon }_{s\alpha }t}\cos {\omega }_{s\alpha }t$; then, the torsional velocity is:

$$\dot{\alpha }=-{\epsilon }_{s\alpha }\alpha -{\alpha }_0{e}^{-{\epsilon }_{s\alpha }t}{\omega }_{s\alpha }\sin {\omega }_{s\alpha }t$$

(5)

where ${\epsilon }_{s\alpha }$ is the torsional mode attenuation rate, ${\epsilon }_{s\alpha }={\xi }_{s\alpha }{\omega }_{s\alpha }$; ${\xi }_{s\alpha }$ is the torsional mode damping ratio; and ${\omega }_{s\alpha }$ is the torsional mode circle frequency.

The vertical vibration system response under the torsional displacement self-excited lift $H_3\alpha$ is:

$$m_h\ddot{h}+\left(C_{h0}-H_1\right)\dot{h}+\left(K_{h0}-H_4\right)h=H_3\alpha$$

(6)

Substituting the torsional displacement $\alpha ={\alpha }_0{e}^{-{\epsilon }_{s\alpha }t}\cos {\omega }_{s\alpha }t$ into the right side of the vertical vibration Equation (6), the vertical vibration displacement and velocity response are solved, as shown in Equation (7) and Equation (8), respectively:

$$h_1(t)={\displaystyle \frac{H_3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(\cos {\theta }_1-{\xi }_{s\alpha }\sin {\theta }_1\right)\alpha -{\displaystyle \frac{H_3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}{\displaystyle \frac{1}{{\omega }_{s\alpha }}}\sin {\theta }_1\dot{\alpha }$$

(7)

$${\dot{h}}_1(t)={\displaystyle \frac{H_3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(\cos {\theta }_1+{\xi }_{s\alpha }\sin {\theta }_1\right)\dot{\alpha }+{\displaystyle \frac{H_3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(1+{\xi }_{s\alpha }^2\right){\omega }_{s\alpha }^2\sin {\theta }_1\alpha$$

(8)

where ${\gamma }_{h\alpha }$ and ${\Gamma }_{h\alpha }$ are stiffness parameters of the vertical vibration system, which are as follows: ${\gamma }_{h\alpha }=\left(K_{h0}-H_4\right)+m_h\left({\xi }_{s\alpha }^2-1\right){\omega }_{s\alpha }^2-\left(C_{h0}-H_1\right){\xi }_{s\alpha }{\omega }_{s\alpha }$, ${\Gamma }_{h\alpha }=-2m_h{\xi }_{s\alpha }{\omega }_{s\alpha }^2+\left(C_{h0}-H_1\right){\omega }_{s\alpha }$. ${\theta }_1$ is the phase difference between the torsional displacement self-excited lift force and the vertical vibration displacement response, ${\theta }_1=\arctan \left({\Gamma }_{h\alpha }/{\gamma }_{h\alpha }\right)$. The sine function value and cosine function value of phase difference ${\theta }_1$ are:

$$\sin {\theta }_1={\displaystyle \frac{{\Gamma }_{h\alpha }}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}$$

(9)

$$\cos {\theta }_1={\displaystyle \frac{{\gamma }_{h\alpha }}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}$$

(10)

The vertical vibration system response under the excitation of torsional speed-induced lift $H_2\dot{\alpha }$ is:

$$m_h\ddot{h}+\left(C_{h0}-H_1\right)\dot{h}+\left(K_{h0}-H_4\right)h=H_2\dot{\alpha }$$

(11)

Substituting the torsional velocity $\dot{\alpha }=-{\epsilon }_{s\alpha }\alpha -{\alpha }_0{e}^{-{\epsilon }_{s\alpha }t}{\omega }_{s\alpha }\sin {\omega }_{s\alpha }t$ into the right side of the vertical vibration in Equation (11), the vertical vibration displacement and velocity response are solved, as shown in Equation (12) and Equation (13), respectively:

$$h_2\left(t\right)={\displaystyle \frac{H_2}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(1+{\xi }_{s\alpha }^2\right){\omega }_{s\alpha }\sin {\theta }_1\alpha +{\displaystyle \frac{H_2}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(\cos {\theta }_1+{\xi }_{s\alpha }\sin {\theta }_1\right)\dot{\alpha }$$

(12)

$${\dot{h}}_2\left(t\right)={\displaystyle \frac{H_2}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(\begin{array}{l}\sin {\theta }_1-2{\xi }_{s\alpha }\cos {\theta }_1\\ -{\xi }_{s\alpha }^2\sin {\theta }_1\end{array}\right){\omega }_{s\alpha }\dot{\alpha }-{\displaystyle \frac{H_2}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(\begin{array}{l}\left(\cos {\theta }_1+{\xi }_{s\alpha }\sin {\theta }_1\right)\\ \left(1+{\xi }_{s\alpha }^2\right){\omega }_{s\alpha }^2\alpha \end{array}\right)$$

(13)

Substituting the vertical vibration displacement response expression (7) and the corresponding velocity response expression (8) into the vertical self-excited lifting moment on the right side of the torsional vibration Equation (2), the vertical vibration response feedback self-lifting moment is:

$$\begin{array}{l}\hspace{1em}\hspace{1em}{M}_1\left({\dot{h}}_1,h_1\right)=A_1{\dot{h}}_1\left(t\right)+A_4{h}_1\left(t\right)\\ =\left[\begin{array}{l}{\displaystyle \frac{A_1{H}_3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(\cos {\theta }_1+{\xi }_{s\alpha }\sin {\theta }_1\right)\\ -{\displaystyle \frac{A_4{H}_3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}{\displaystyle \frac{1}{{\omega }_{s\alpha }}}\sin {\theta }_1\end{array}\right]\dot{\alpha }+\left[\begin{array}{l}{\displaystyle \frac{A_1{H}_3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(1+{\xi }_{s\alpha }^2\right){\omega }_{s\alpha }^2\sin {\theta }_1\\ +{\displaystyle \frac{A_4{H}_3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(\cos {\theta }_1-{\xi }_{s\alpha }\sin {\theta }_1\right)\end{array}\right]\alpha \end{array}$$

(14)

Substituting the vertical vibration displacement response expression (12) and the corresponding velocity response expression (13) into the right side of the torsional vibration Equation (2), the vertical vibration response feedback self-lifting moment is:

$$\begin{array}{l}{M}_2\left({\dot{\mathrm{h}}}_2,h_2\right)=A_1{\dot{h}}_2\left(t\right)+A_4{h}_2\left(t\right)\\ =\left[\begin{array}{l}{\displaystyle \frac{A_1{H}_2}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(\begin{array}{l}{\omega }_{s\alpha }\sin {\theta }_1-2{\xi }_{s\alpha }{\omega }_{s\alpha }\cos {\theta }_1\\ -{\xi }_{s\alpha }^2{\omega }_{s\alpha }\sin {\theta }_1\end{array}\right)\\ +{\displaystyle \frac{A_4{H}_2}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(\cos {\theta }_1+{\xi }_{s\alpha }\sin {\theta }_1\right)\end{array}\right]\dot{\alpha }+\left[\begin{array}{l}-{\displaystyle \frac{A_1{H}_2}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(\cos {\theta }_1+{\xi }_{s\alpha }\sin {\theta }_1\right)\left(1+{\xi }_{s\alpha }^2\right){\omega }_{s\alpha }^2\\ +{\displaystyle \frac{A_4{H}_2}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(1+{\xi }_{s\alpha }^2\right){\omega }_{s\alpha }\sin {\theta }_1\end{array}\right]\alpha \end{array}$$

(15)

Moving the vertical vibration response feedback expression (14) and expression (15) from the right-hand side of the torsional vibration equation to the left-hand side yields the damping and stiffness of the torsional vibration system, respectively, as shown in Equations (16) and (17):

$$\begin{array}{l}{C}_{\alpha h}=C_{\alpha 0}-A_2-{\displaystyle \frac{A_1{H}_2}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(\sin {\theta }_1-2{\xi }_{\alpha }\cos {\theta }_1-{\xi }_{\alpha }^2\sin {\theta }_1\right){\omega }_{s\alpha }-{\displaystyle \frac{A_4{H}_2}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(\cos {\theta }_1+{\xi }_{\alpha }\sin {\theta }_1\right)\\ \hspace{1em}\hspace{1em}-{\displaystyle \frac{A_1{H}_3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(\cos {\theta }_1+{\xi }_{\alpha }\sin {\theta }_1\right)+{\displaystyle \frac{A_4{H}_3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}{\displaystyle \frac{1}{{\omega }_{s\alpha }}}\sin {\theta }_1\end{array}$$

(16)

$$\begin{array}{l}{K}_{\alpha h}=K_{\alpha 0}-A_3+{\displaystyle \frac{A_1{H}_2}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(\cos {\theta }_1+{\xi }_{\alpha }\sin {\theta }_1\right)\left({\xi }_{s\alpha }^2+1\right){\omega }_{s\alpha }^2-{\displaystyle \frac{A_4{H}_2}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left({\xi }_{s\alpha }^2+1\right){\omega }_{s\alpha }\sin {\theta }_1\\ \hspace{1em}\hspace{1em}-{\displaystyle \frac{A_1{H}_3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left({\xi }_{s\alpha }^2+1\right){\omega }_{s\alpha }\sin {\theta }_1-{\displaystyle \frac{A_4{H}_3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}\left(\cos {\theta }_1-{\xi }_{s\alpha }\sin {\theta }_1\right)\end{array}$$

(17)

The torsional modal damping ratio and the modal frequency can be obtained by Equation (18) and Equation (19), respectively:

$${\xi }_{s\alpha }={\displaystyle \frac{C_{\alpha h}}{2I{\omega }_{\alpha h}}}$$

(18)

$${\omega }_{s\alpha }={\omega }_{\alpha h}\sqrt{1-{\xi }_{s\alpha }^2}$$

(19)

where ${\omega }_{\alpha h}$ is the frequency of the torsional vibration system, ${\omega }_{\alpha h}=\sqrt{{\displaystyle \frac{K_{\alpha h}}{I}}}$.

The aerodynamic derivatives $H_i$ and $A_i$ in the damping of the torsional vibration system are expressed by the dimensionless flutter derivatives $H_i^{*}$ and $A_i^{*}$, respectively, and the damping of the torsional vibration system is as follows:

$$C_{\alpha h,1}=C_{\alpha 0}$$

(20)

$$C_{\alpha h,2}=-\rho B^4{\omega }_{s\alpha }{A}_2^{*}={\rho }^2{B}^6{\displaystyle \frac{{\omega }_{s\alpha }^3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}{A}_2^{*}\left(-{\displaystyle \frac{1}{\rho B^2}}{\displaystyle \frac{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}{{\omega }_{s\alpha }^2}}\right)$$

(21)

$$C_{\alpha h,3}={\rho }^2{B}^6{\displaystyle \frac{{\omega }_{s\alpha }^3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}{A}_1^{*}{H}_2^{*}\left(\begin{array}{l}-\sin {\theta }_1+{\xi }_{s\alpha }^2\sin {\theta }_1\\ +2{\xi }_{s\alpha }\cos {\theta }_1\end{array}\right)$$

(22)

$$C_{\alpha h,4}={\rho }^2{B}^6{\displaystyle \frac{{\omega }_{s\alpha }^3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}{A}_4^{*}{H}_2^{*}\left(-\cos {\theta }_1-{\xi }_{s\alpha }\sin {\theta }_1\right)$$

(23)

$$C_{\alpha h,5}={\rho }^2{B}^6{\displaystyle \frac{{\omega }_{s\alpha }^3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}{A}_1^{*}{H}_3^{*}\left(-\cos {\theta }_1-{\xi }_{s\alpha }\sin {\theta }_1\right)$$

(24)

$$C_{\alpha h,6}={\rho }^2{B}^6{\displaystyle \frac{{\omega }_{s\alpha }^3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}{A}_4^{*}{H}_3^{*}\sin {\theta }_1$$

(25)

The aerodynamic damping of the torsional vibration system is written in the following form:

$$\begin{array}{l}{C}_{\alpha h,i}={\rho }^2{B}^6{\displaystyle \frac{{\omega }_{s\alpha }^3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}{\psi }_{\alpha h}\left(A_j^{*},H_k^{*}\right){\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)\\ \begin{array}{ccc}\left(i=2,\cdots ,6\right)& \begin{array}{c}\begin{array}{c}\left(\mathrm{j}=1,2,4\right)\end{array}\end{array}& \left(k=2,3\right)\end{array}\end{array}$$

(26)

where the function ${\psi }_{\alpha h}\left(A_j^{*},H_k^{*}\right)$ is the flutter derivative relation. Function ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ is a function of the phase difference angle ${\theta }_1$ and the torsional modal damping ratio ${\xi }_{s\alpha }$ where $C_{\alpha h,2}$ represents aerodynamic damping $-{\displaystyle \frac{1}{\rho B^2}}{\displaystyle \frac{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}{{\omega }_{s\alpha }^2}}$. In order to show the relationship between the aerodynamic damping and the flutter derivative, the flutter derivative contained in the aerodynamic damping is named; for example, $C_{\alpha h,5}$ is called “$A_1^{*}{H}_3^{*}$ term aerodynamic damping”, and the naming of each aerodynamic damping in this article is named according to this principle.

The aerodynamic derivatives $H_i$ and $A_i$ in the stiffness of the torsional vibration system are expressed by the dimensionless flutter derivatives $H_i^{*}$ and $A_i^{*}$, respectively, and the stiffness of the torsional vibration system is as follows:

$$K_{\alpha h,1}=K_{\alpha 0}$$

(27)

$$K_{\alpha h,2}=-\rho B^4{\omega }_{s\alpha }^2{A}_3^{*}$$

(28)

$$K_{\alpha h,3}={\rho }^2{B}^6{\displaystyle \frac{{\omega }_{s\alpha }^4}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}{A}_1^{*}{H}_2^{*}\left(\cos {\theta }_1+{\xi }_{s\alpha }\sin {\theta }_1\right)\left({\xi }_{s\alpha }^2+1\right)$$

(29)

$$K_{\alpha h,4}=-{\rho }^2{B}^6{\displaystyle \frac{{\omega }_{s\alpha }^4}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}{A}_4^{*}{H}_2^{*}\left({\xi }_{s\alpha }^2+1\right)\sin {\theta }_1$$

(30)

$$K_{\alpha h,5}=-{\rho }^2{B}^6{\displaystyle \frac{{\omega }_{s\alpha }^4}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}{A}_1^{*}{H}_3^{*}\left({\xi }_{s\alpha }^2+1\right){\omega }_{s\alpha }\sin {\theta }_1$$

(31)

$$K_{\alpha h,6}=-{\rho }^2{B}^6{\displaystyle \frac{{\omega }_{s\alpha }^4}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}{A}_4^{*}{H}_3^{*}\left(\cos {\theta }_1-{\xi }_{s\alpha }\sin {\theta }_1\right)$$

(32)

2.2. Vertical Modal Damping and Stiffness

If the vertical displacement is $h=h_0{e}^{-{\epsilon }_{sh}t}\cos {\omega }_{sh}t$, then the vertical velocity is

$$\dot{h}=-{\epsilon }_{sh}h-h_0{e}^{-{\epsilon }_{sh}t}{\omega }_{sh}\sin {\omega }_{sh}t$$

(33)

where ${\epsilon }_{sh}$ is the vertical mode attenuation rate, ${\epsilon }_{sh}={\xi }_{sh}{\omega }_{sh}$; ${\xi }_{sh}$ is the vertical modal damping ratio; and ${\omega }_{sh}$ is the vertical mode circular frequency.

Under the excitation of vertical displacement self-excited lifting moment $A_{4}h$, the torsional vibration system response is

$$I\ddot{\alpha }+\left(C_{\alpha 0}-A_2\right)\dot{\alpha }+\left(K_{\alpha 0}-A_3\right)\alpha =A_{4}h$$

(34)

The vertical displacement $h=h_0{e}^{-{\epsilon }_{sh}t}\cos {\omega }_{sh}t$ is substituted into the right side of the torsional vibration Equation (34), and the torsional vibration displacement and velocity response are solved, as shown in Equation (35) and Equation (36), respectively:

$${\alpha }_1(t)=-{\displaystyle \frac{A_4}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}{\displaystyle \frac{1}{{\omega }_{sh}}}\sin {\theta }_2\dot{h}+{\displaystyle \frac{A_4}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(\cos {\theta }_2-{\xi }_{sh}\sin {\theta }_2\right)h$$

(35)

$${\dot{\alpha }}_1(t)={\displaystyle \frac{A_4}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(\cos {\theta }_2+{\xi }_{sh}\sin {\theta }_2\right)\dot{h}+{\displaystyle \frac{A_4}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(1+{\xi }_{sh}^2\right){\omega }_{sh}\sin {\theta }_{2}h$$

(36)

where ${\gamma }_{\alpha h}$ and ${\Gamma }_{\alpha h}$ are the stiffness parameters of the torsional vibration system, respectively: ${\gamma }_{\alpha h}=\left(K_{\alpha 0}-A_3\right)+I\left({\xi }_{\mathrm{sh}}^2-1\right){\omega }_{sh}^2-\left(C_{\alpha 0}-A_2\right){\xi }_{sh}{\omega }_{sh}$; ${\Gamma }_{\alpha h}=-2I{\xi }_{sh}{\omega }_{sh}^2+\left(C_{\alpha 0}-A_2\right){\omega }_{sh}$.

${\theta }_2$ is the phase difference between the vertical displacement self-excited moment and the torsional vibration displacement response, ${\theta }_2=\arctan \left({\Gamma }_{\alpha h}/{\gamma }_{\alpha h}\right)$. The sine function value $\sin {\theta }_2$ and cosine function value $\cos {\theta }_2$ of the phase difference ${\theta }_2$ are as follows:

$$\sin {\theta }_2={\displaystyle \frac{{\Gamma }_{\alpha h}}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}$$

(37)

$$\cos {\theta }_2={\displaystyle \frac{{\gamma }_{\alpha h}}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}$$

(38)

Under the excitation of vertical velocity self-excited moment $A_1\dot{h}$, the response of the torsional vibration system can be expressed by Equation (39):

$$I\ddot{\alpha }+\left(C_{\alpha 0}-A_2\right)\dot{\alpha }+\left(K_{\alpha 0}-A_3\right)\alpha =A_1\dot{h}$$

(39)

Substituting the vertical velocity $\dot{h}=-{\epsilon }_{sh}h-h_0{e}^{-{\epsilon }_{sh}t}{\omega }_{sh}\sin {\omega }_{sh}t$ into the right side of the torsion Equation (39), the torsional vibration displacement and velocity response are solved, as shown in Equation (40) and Equation (41), respectively:

$${\alpha }_2(t)={\displaystyle \frac{A_1}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(\cos {\theta }_2+{\xi }_{sh}\sin {\theta }_2\right)\dot{h}+{\displaystyle \frac{A_1}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(1+{\xi }_{sh}^2\right){\omega }_{sh}\sin {\theta }_{2}h$$

(40)

$${\dot{\alpha }}_2(t)={\displaystyle \frac{A_1}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(\begin{array}{l}\sin {\theta }_2-2{\xi }_{sh}\cos {\theta }_2\\ -{\xi }_{sh}^2\sin {\theta }_2\end{array}\right){\omega }_{sh}\dot{h}-{\displaystyle \frac{A_1}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(\begin{array}{l}\left(\cos {\theta }_2+{\xi }_{sh}\sin {\theta }_2\right)\\ \left(1+{\xi }_{sh}^2\right)\end{array}\right){\omega }_{sh}^{2}h$$

(41)

Substituting the torsional vibration displacement response expression (35) and the corresponding velocity response expression (36) into the right side of Equation (1), the torsional vibration response feedback self-excited lift force is

$$\begin{array}{l}\hspace{1em}\hspace{1em}{F}_{L1}\left({\dot{\alpha }}_1,{\alpha }_1\right)=H_2{\dot{\alpha }}_1\left(t\right)+H_3{\alpha }_1\left(t\right)\\ =\left[\begin{array}{l}{\displaystyle \frac{H_2{A}_4}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(\cos {\theta }_2+{\xi }_{sh}\sin {\theta }_2\right)-{\displaystyle \frac{H_3{A}_4}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}·\\ {\displaystyle \frac{1}{{\omega }_{sh}}}\sin {\theta }_2\end{array}\right]\dot{h}+\left[\begin{array}{l}{\displaystyle \frac{H_2{A}_4}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(1+{\xi }_{sh}^2\right){\omega }_{sh}\sin {\theta }_2+{\displaystyle \frac{H_3{A}_4}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}·\\ \left(\cos {\theta }_2-{\xi }_{sh}\sin {\theta }_2\right)\end{array}\right]h\end{array}$$

(42)

Substituting the torsional vibration displacement response expression (40) and the corresponding velocity response expression (41) into the right side of Equation (1), the torsional vibration response feedback self-excited lift is

$$\begin{array}{l}{F}_{L2}\left({\dot{\alpha }}_2,{\alpha }_2\right)=H_2{\dot{\alpha }}_2\left(t\right)+H_3{\alpha }_2\left(t\right)\\ \hspace{1em}\hspace{1em}=\left[\begin{array}{l}{\displaystyle \frac{H_2{A}_1}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(\begin{array}{l}\sin {\theta }_2-2{\xi }_{sh}\cos {\theta }_2\\ -{\xi }_{sh}^2\sin {\theta }_2\end{array}\right){\omega }_{sh}\\ +{\displaystyle \frac{H_3{A}_1}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(\cos {\theta }_2+{\xi }_{sh}\sin {\theta }_2\right)\end{array}\right]\dot{h}+\left[\begin{array}{l}-{\displaystyle \frac{H_2{A}_1}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(\cos {\theta }_2+{\xi }_{sh}\sin {\theta }_2\right)(1+{\xi }_{sh}^2){\omega }_{sh}^2\\ +{\displaystyle \frac{H_3{A}_1}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(1+{\xi }_{sh}^2\right){\omega }_{sh}\sin {\theta }_2\end{array}\right]h\end{array}$$

(43)

The damping and stiffness of the vertical vibration system can be obtained by moving expression (42) and expression (43) of the torsional vibration response self-excited lift force on the right side of the vertical vibration equation to the left side of the vertical vibration equation, as shown in the following Equations (44) and (45), respectively:

$$\begin{array}{l}{C}_{h\alpha }=C_{h0}-H_1-{\displaystyle \frac{H_2{A}_1}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(\sin {\theta }_2-{\xi }_{sh}^2\sin {\theta }_2\right.\left.-2{\xi }_{sh}\cos {\theta }_2\right){\omega }_{sh}-{\displaystyle \frac{H_3{A}_1}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(\cos {\theta }_2+{\xi }_{sh}\sin {\theta }_2\right)\\ \hspace{1em}\hspace{1em}-{\displaystyle \frac{H_2{A}_4}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(\cos {\theta }_2+{\xi }_{sh}\sin {\theta }_2\right)+{\displaystyle \frac{H_3{A}_4}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}{\displaystyle \frac{1}{{\omega }_{sh}}}\sin {\theta }_2\end{array}$$

(44)

$$\begin{array}{l}{K}_{h\alpha }=K_{h0}-H_4+{\displaystyle \frac{H_2{A}_1}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(\cos {\theta }_2+{\xi }_{sh}^2\sin {\theta }_2\right)\left(1+{\xi }_{sh}^2\right){\omega }_{sh}^2-{\displaystyle \frac{H_3{A}_1}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(1+{\xi }_{sh}^2\right){\omega }_{sh}\sin {\theta }_2\\ \hspace{1em}\hspace{1em}-{\displaystyle \frac{H_2{A}_4}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(1+{\xi }_{sh}^2\right){\omega }_{sh}\sin {\theta }_2-{\displaystyle \frac{H_3{A}_4}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}\left(\cos {\theta }_2-{\xi }_{sh}\sin {\theta }_2\right)\end{array}$$

(45)

The vertical modal damping ratio and modal frequency can be obtained by Equations (46) and (47), respectively:

$${\xi }_{sh}={\displaystyle \frac{C_{h\alpha }}{2m_h{\omega }_{h\alpha }}}$$

(46)

$${\omega }_{sh}={\omega }_{h\alpha }\sqrt{1-{\xi }_{sh}^2}$$

(47)

where ${\omega }_{h\alpha }$ is the frequency of the vertical vibration system, ${\omega }_{h\alpha }=\sqrt{{\displaystyle \frac{K_{h\alpha }}{m_h}}}$.

The aerodynamic derivatives $H_i$ and $A_i$ in the damping of the vertical vibration system are expressed by the dimensionless flutter derivatives $H_i^{*}$ and $A_i^{*}$, and the damping of the vertical vibration system is as follows:

$$C_{h\alpha ,1}=C_{h0}$$

(48)

$$C_{h\alpha ,2}=-\rho B^2{\omega }_{sh}{H}_1^{*}={\rho }^2{B}^6{\displaystyle \frac{{\omega }_{sh}^3}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}{H}_1^{*}\left(-{\displaystyle \frac{1}{\rho B^4}}{\displaystyle \frac{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}{{\omega }_{sh}^2}}\right)$$

(49)

$$C_{h\alpha ,3}={\rho }^2{B}^6{\displaystyle \frac{{\omega }_{sh}^3}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}{H}_2^{*}{A}_1^{*}\left(-\sin {\theta }_2+2{\xi }_{sh}\cos {\theta }_2+{\xi }_{sh}^2\sin {\theta }_2\right)$$

(50)

$$C_{h\alpha ,4}={\rho }^2{B}^6{\displaystyle \frac{{\omega }_{sh}^3}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}{H}_3^{*}{A}_1^{*}\left(-\cos {\theta }_2-{\xi }_{sh}\sin {\theta }_2\right)$$

(51)

$$C_{h\alpha ,5}={\rho }^2{B}^6{\displaystyle \frac{{\omega }_{sh}^3}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}{H}_2^{*}{A}_4^{*}\left(-\cos {\theta }_2-{\xi }_{sh}\sin {\theta }_2\right)$$

(52)

$$C_{h\alpha ,6}={\rho }^2{B}^6{\displaystyle \frac{{\omega }_{sh}^3}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}{H}_3^{*}{A}_4^{*}\sin {\theta }_2$$

(53)

The aerodynamic damping of the vertical vibration system is uniformly written in the following form:

$$\begin{array}{l}{C}_{h\alpha ,i}={\rho }^2{B}^6{\displaystyle \frac{{\omega }_{sh}^3}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}{\psi }_{h\alpha }\left(H_j^{*},A_k^{*}\right){\varphi }_{h\alpha }\left({\theta }_2,{\xi }_{sh}\right)\\ \begin{array}{ccc}\left(i=2,\cdots ,6\right)& \begin{array}{c}\begin{array}{c}\left(\mathrm{j}=1,2,3\right)\end{array}\end{array}& \left(k=1,4\right)\end{array}\end{array}$$

(54)

where the function ${\psi }_{h\alpha }\left(H_j^{*},A_k^{*}\right)$ is the flutter derivative correlation term; and ${\varphi }_{h\alpha }\left({\theta }_2,{\xi }_{sh}\right)$ is a function of the phase difference ${\theta }_2$ and the vertical modal damping ratio ${\xi }_{sh}$, where the aerodynamic damping of $C_{h\alpha ,2}$ is $-{\displaystyle \frac{1}{\rho B^4}}{\displaystyle \frac{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}{{\omega }_{sh}^2}}$.

The aerodynamic derivatives $H_i$ and $A_i$ in the stiffness of the vertical vibration system are expressed by the dimensionless flutter derivatives $H_i^{*}$ and $A_i^{*}$, and the stiffness of the torsional vibration system is as follows:

$$K_{h\alpha ,1}=K_{h0}$$

(55)

$$K_{h\alpha ,2}=-\rho B^2{\omega }_{sh}^2{H}_4^{*}$$

(56)

$$K_{h\alpha ,3}={\rho }^2{B}^6{\displaystyle \frac{{\omega }_{sh}^4}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}{H}_2^{*}{A}_1^{*}\left(\cos {\theta }_2+{\xi }_{sh}^2\sin {\theta }_2\right)\left(1+{\xi }_{sh}^2\right)$$

(57)

$$K_{h\alpha ,4}=-{\rho }^2{B}^6{\displaystyle \frac{{\omega }_{sh}^4}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}{H}_3^{*}{A}_1^{*}\left(1+{\xi }_{sh}^2\right)\sin {\theta }_2$$

(58)

$$K_{h\alpha ,5}=-{\rho }^2{B}^6{\displaystyle \frac{{\omega }_{sh}^4}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}{H}_2^{*}{A}_4^{*}\left(1+{\xi }_{sh}^2\right)\sin {\theta }_2$$

(59)

$$K_{h\alpha ,6}=-{\rho }^2{B}^6{\displaystyle \frac{{\omega }_{sh}^4}{\sqrt{{\gamma }_{\alpha h}^2+{\Gamma }_{\alpha h}^2}}}{H}_3^{*}{A}_4^{*}\left(\cos {\theta }_2-{\xi }_{sh}\sin {\theta }_2\right)$$

(60)

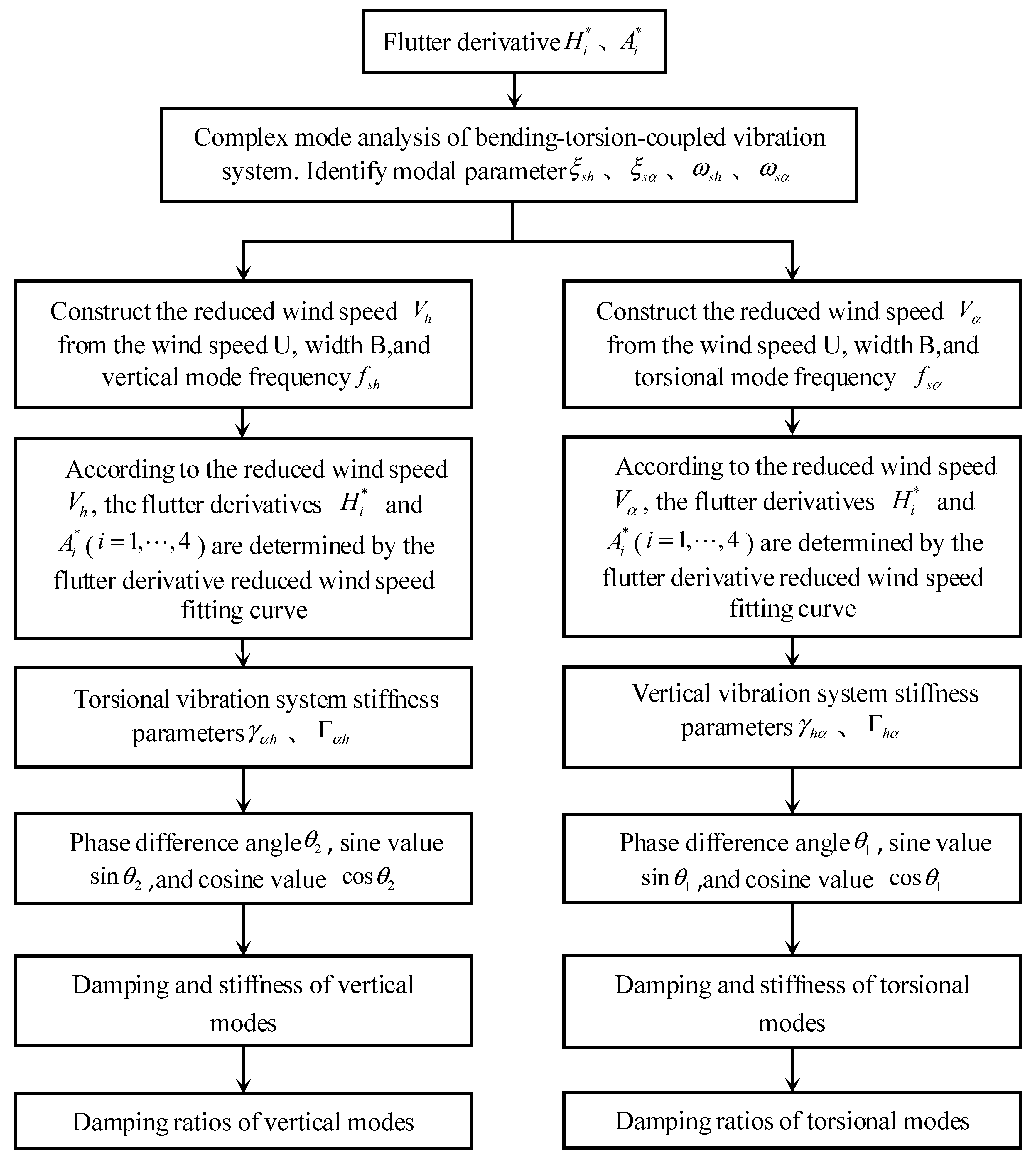
3. Identification Steps for Aerodynamic Damping Based on the “Incentive-Feedback” Mechanism

For the bending–torsion-coupled vibration system, the “incentive-feedback” mechanism identifies the aerodynamic damping of the vertical and torsional vibration of the bridge structure for chirp vibration according to the flowchart in Figure 1. In the process of identifying the aerodynamic damping of the vertical and torsional flutter vibrations of the bridge structure, curve fitting is performed on each flutter derivative with respect to the reduced wind speed $U/\left(fB\right)$, and the corresponding flutter derivatives of the bridge structure at various wind speeds are determined according to the reduced wind speed.

4. Ideal Flat Plate Flutter Analysis

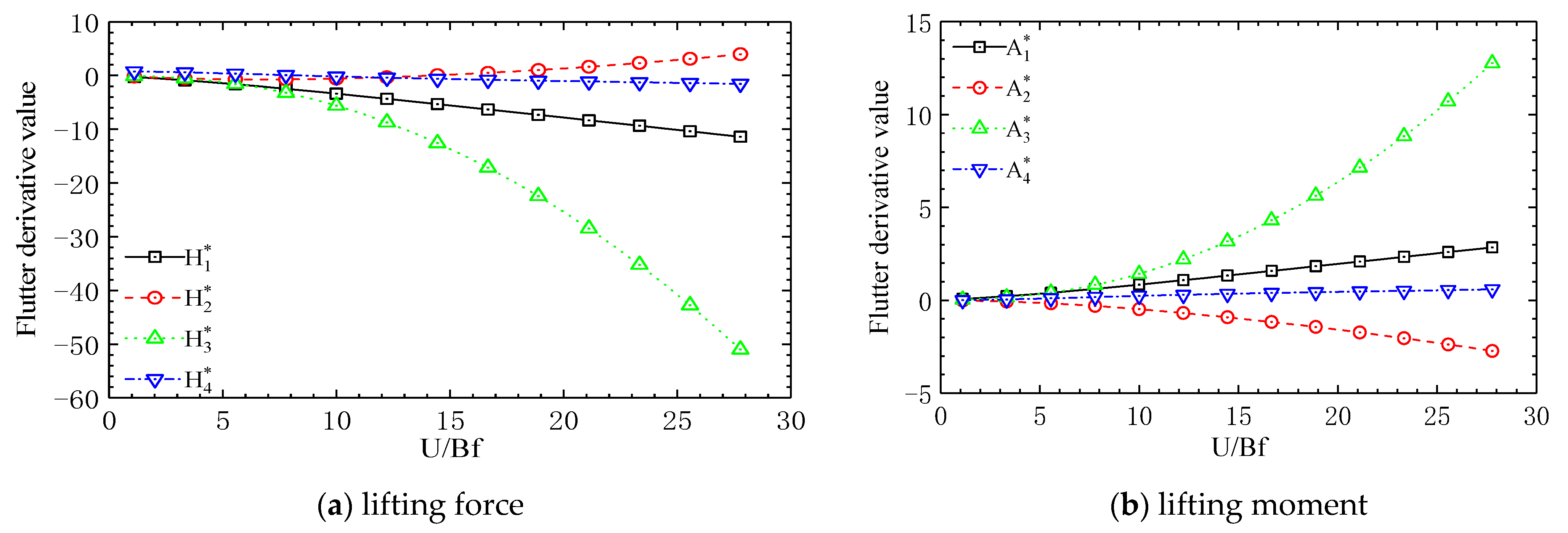
4.1. Ideal Flat Plate Flutter Derivative

To verify the accuracy of the “incentive-feedback” mechanism vibration analysis theory in this article, we conducted an analysis of the bending–torsion-coupled vibration mechanism of an ideal flat plate with a width of 0.45 m as the research object. The inherent vibration parameters [26] of the ideal flat plate are shown in

Table 1. Natural vibration parameters of an ideal plate.

Unit length Mass mh (Kg/m)	Vertical Inherent Damping Ratio ξh0	Vertical Natural Frequency fh0 (Hz)	Equivalent Mass Moment of Inertia per Unit Length I (Kg·m2/m)	Torsional Inherent Damping Ratio ξα0	Torsional Inherent Frequency fα0 (Hz)
7.100	0.005	1.927	0.283	0.005	3.024

.

The flutter derivative of an ideal plate is calculated by Theodorsen’s theoretical solution formula [27], and the lift-related flutter derivative and moment-dependent flutter derivative with reduced wind speed are shown in Figure 2.

4.2. Flutter Critical Wind Speed

Based on the ideal flat plate flutter derivatives, the critical flutter wind speed and critical flutter frequency are identified through complex modal analysis, the “torsional negative damping drive” mechanism, and the “stiffness drive” mechanism, as shown in

Table 2. Flutter critical wind speed and frequency of an ideal flat plate.

Parameter	Flutter Critical Wind Speed (m/s)	Flutter Critical Frequency (Hz)
Complex modal analysis	14–15	2.59–2.53
Torsional negative damping drive Mechanism (incentive feedback)	14–15	2.59–2.53
Stiffness drive mechanism	14.22	2.58
Van der Put formula [27]	16.78	-
Selberg formula [27]	16.78	-
Xiang Haifan formula [27]	19.35	-

. From the table, it can be seen that the ideal flutter critical wind speed and critical flutter frequency identified by the complex modal analysis, the “torsional negative damping drive” mechanism, and the “stiffness drive” mechanism are similar. However, their critical flutter wind speed is 14% lower than the calculated value (JTG/T3360-01—2018) in the literature [27] by Van der Put and Selberg, and 25% lower than the calculated value by Xiang Haifan’s flutter critical wind speed formula.

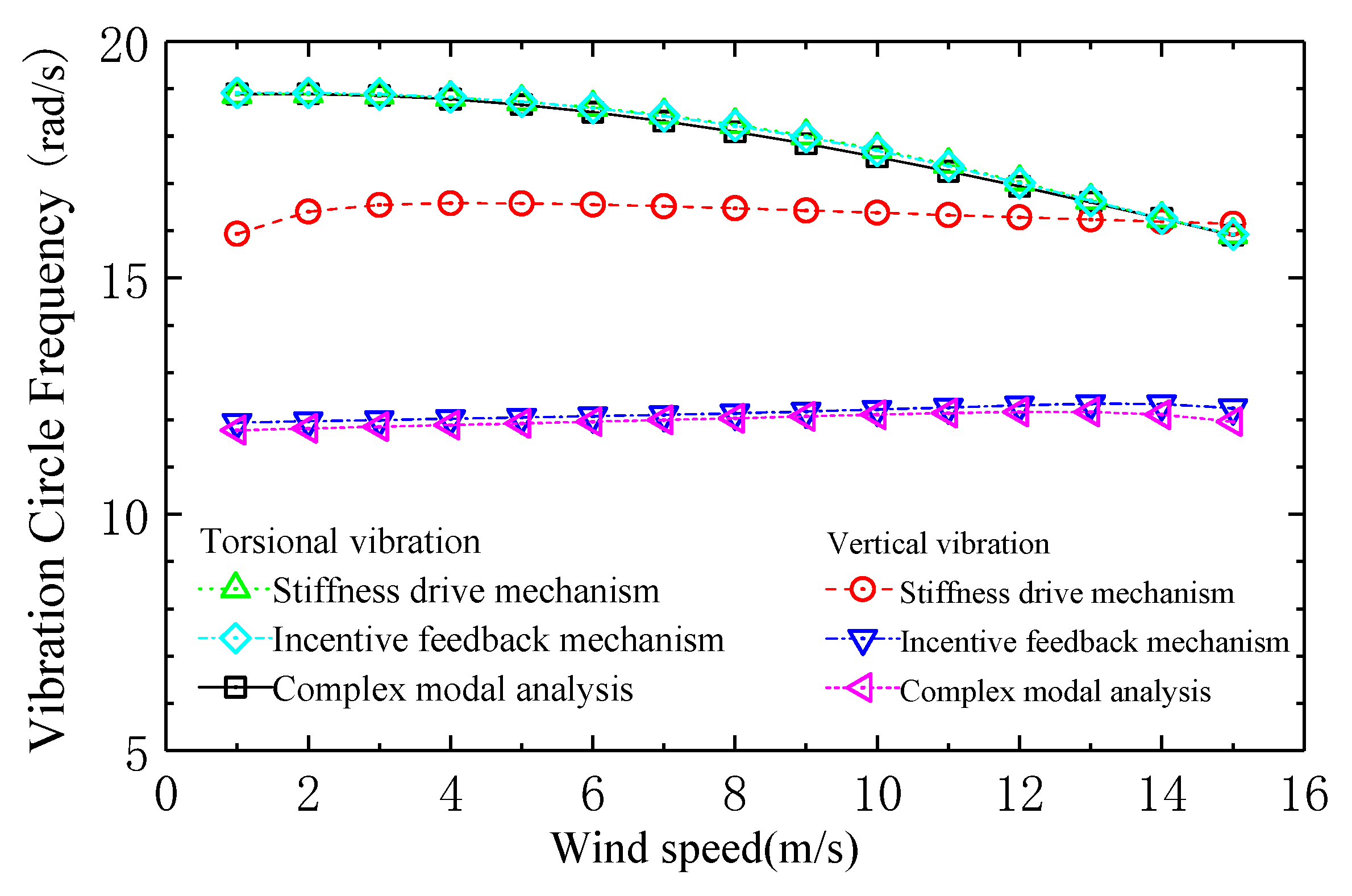
4.3. Flutter Frequency

Figure 3 shows the variation curves of the vertical and torsional modes of the ideal plate with wind speed obtained by the methods of “complex mode analysis”, “stiffness drive” mechanism, and “incentive feedback” mechanism. From the diagram, it can be concluded that:

(1)

The vertical and torsional mode frequencies identified by the two theories of “complex mode analysis” and “incentive feedback” mechanism are consistent with each other. The torsional mode frequencies identified by the “stiffness-driven” mechanism theory are consistent with the “complex mode analysis” and “incentive feedback” mechanisms, and the vertical vibration frequency is equal to the torsional vibration frequency in the flutter critical state.

(2)

The torsional vibration damping ratio is close to zero at all levels of wind speed, while the vertical vibration damping ratio gradually increases with the increase of wind speed, and is obviously greater than zero. Therefore, the variation curve of the torsional mode frequency with wind speed identified by the “stiffness-driven” mechanism is consistent with the torsional vibration frequency identified by the complex mode analysis and the incentive feedback mechanism, while the vertical mode frequency identified by the “stiffness-driven” mechanism is deviated from the modal frequency identified by the complex mode analysis and the “incentive-feedback” mechanism. However, in the flutter critical state, the damping ratios of vertical and torsional vibrations are zero, which is consistent with the assumption of the “stiffness drive” mechanism, where the vertical and torsional vibration frequencies are the same, and the flutter critical frequency is located on the torsional vibration frequency change curve, indicating that the ideal plate flutter is a bending–torsion-coupled vibration driven by its torsional mode. When the wind speed is greater than the flutter critical wind speed, the torsional mode damping is identified as negative damping and the vertical mode damping is positive by the “complex mode analysis” and “incentive feedback” mechanisms. Therefore, when the wind speed exceeds the flutter critical wind speed, the flutter morphology of the ideal plate is due to the negative damping of the torsional mode.

Based on the above analysis, the results of the “stiffness-driven” mechanism analysis show that flutter is a bending–torsional-coupled vibration generated by torsional mode drive, while the results of “complex mode analysis” and “incentive feedback” mechanism analysis show that the reason why flutter is divergent is that the torsional mode damping is negative. It can be seen that there is no contradiction between the two theories of the “stiffness-driven” mechanism and “torsional negative damping driven” mechanism in flutter analysis, and they expound the characteristics of flutter bending–torsional-coupled vibration and self-excitation divergence from the aspects of “flutter frequency” and “flutter damping”, respectively.

4.4. Ideal Flat Plate Aerodynamic Damping

Based on the formulation of the “incentive feedback” mechanism derived in Section 3, the damping ratios of the vertical and torsional vibrations of an ideal flat plate are identified, as shown in Figure 4. The following can be seen from the figure:

(1)

The torsional modal damping is mainly derived from terms $A_2^{*}$ and $A_1^{*}{H}_3^{*}$, that is, the feedback aerodynamic damping of torsional velocity self-excited aerodynamic damping in the torsional vibration system and the vertical vibration induced by the torsional displacement self-excited lift force in the torsional vibration system, in which the aerodynamic damping of item $A_2^{*}$ is positive damping and the aerodynamic damping of item $A_1^{*}{H}_3^{*}$ is negative damping, while the intrinsic damping of the torsional vibration system and the aerodynamic damping of other items are significantly smaller than the aerodynamic damping of items $A_2^{*}$ and $A_1^{*}{H}_3^{*}$, and their contribution to the total damping of the torsional vibration system is very small.

(2)

The vertical modal damping is mainly derived from terms $H_1^{*}$ and $H_3^{*}{A}_1^{*}$, that is, the vertical velocity self-excited aerodynamic damping in the vertical vibration system and the pneumatic damping fed back by the torsional vibration induced by the vertical velocity self-excited moment in the vertical vibration system, among which the $H_1^{*}$ and $H_3^{*}{A}_1^{*}$ terms are both positive damping. However, the intrinsic damping and other aerodynamic damping of the vertical vibration system are significantly smaller than those of $H_1^{*}$ and $H_3^{*}{A}_1^{*}$ aerodynamic damping, and their contribution to the total damping of the vertical vibration system is small.

(3)

When the wind speed exceeds the flutter critical wind speed, the negative aerodynamic damping of the “incentive feedback” torsional displacement of the ideal flat plate leads to the dispersion of its torsional vibration, and its vertical vibration system is forced to disperse due the torsional self-excited lifting force, which leads to the occurrence of the bending–torsional-coupled flutter.

4.5. Function ${\psi }_{\alpha h}\left(A_j^{*},H_k^{*}\right)$ and Function ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$

The expression for general aerodynamic damping in the torsional vibration system reveals that its positive or negative value is not related to ${\rho }^2{B}^6{\displaystyle \frac{{\omega }_{s\alpha }^3}{\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}}}$ but entirely depends on whether the values of functions ${\psi }_{\alpha h}\left(A_j^{*},H_k^{*}\right)$ and ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ have the same sign. In other words, the sign of each aerodynamic damping term in the torsional vibration system is determined solely by the sign of the product of the aforementioned two functions, ${\psi }_{\alpha h}\left(A_j^{*},H_k^{*}\right)\varphi \left({\theta }_1,{\xi }_{s\alpha }\right)$.

Figure 5 shows the curves of functions ${\psi }_{\alpha h}\left(A_j^{*},H_k^{*}\right)$ and ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ and the product function ${\psi }_{\alpha h}\left(A_j^{*},H_k^{*}\right)\varphi \left({\theta }_1,{\xi }_{s\alpha }\right)$ of aerodynamic damping in an ideal flat torsional vibration system as wind speed varies. From the graph, the following can be observed:

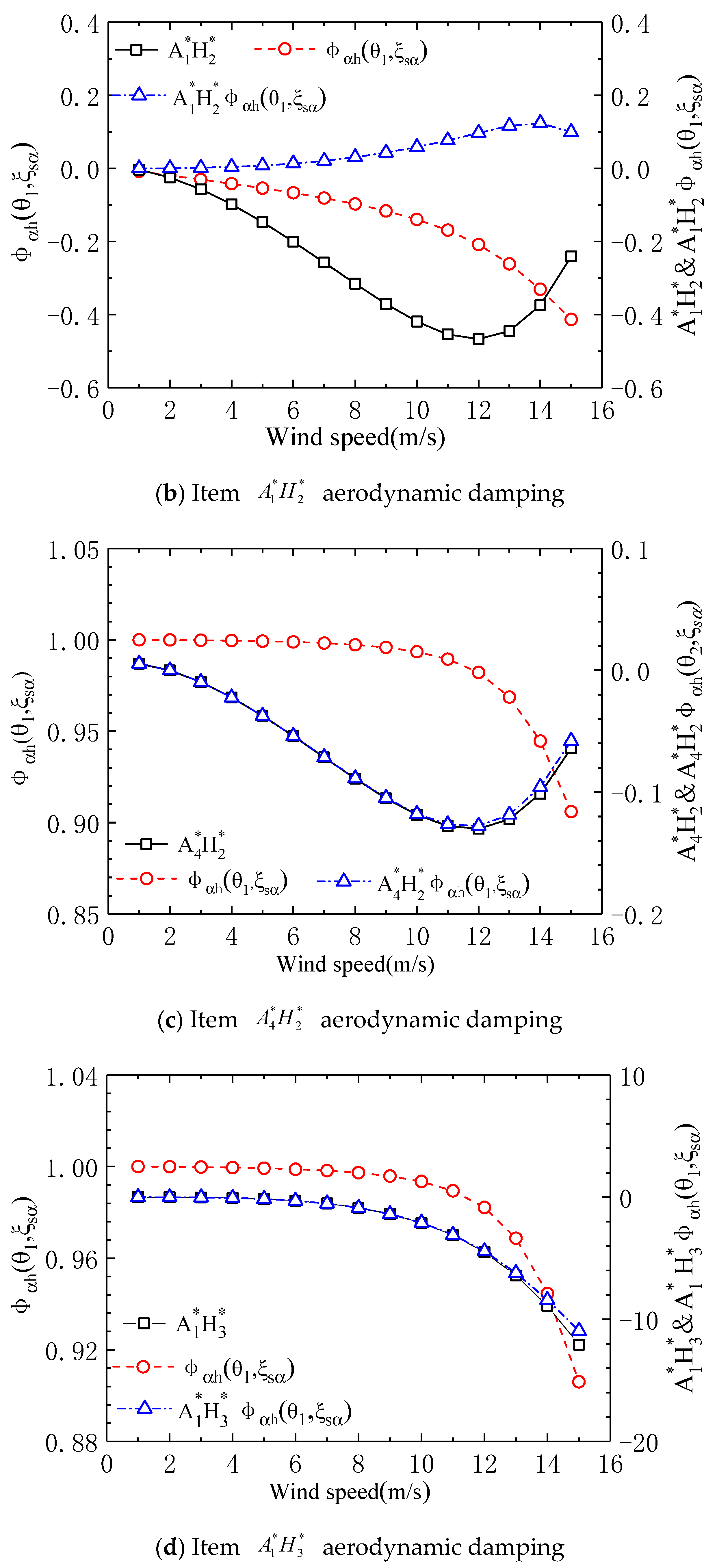
(1)

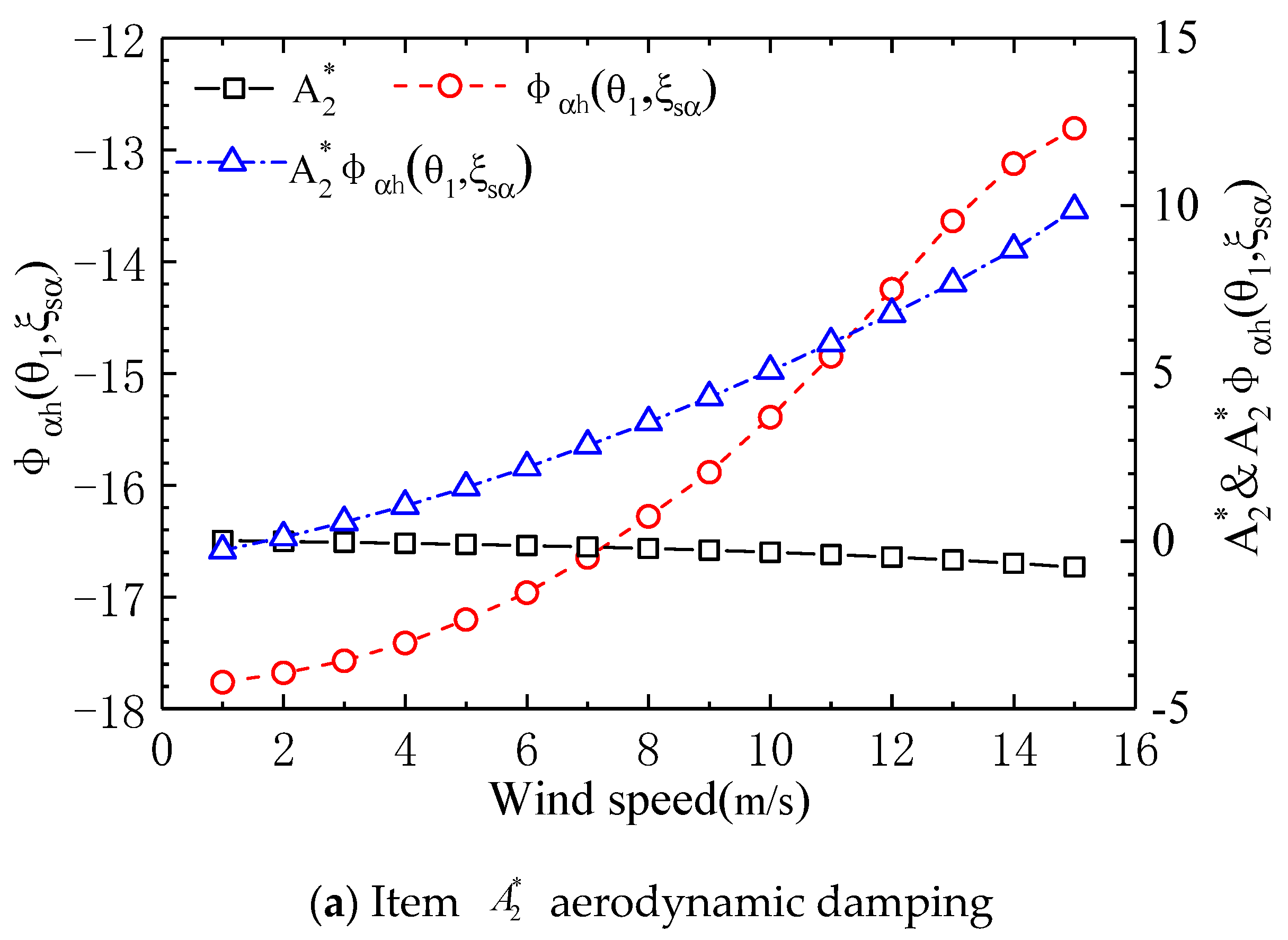
The function ${\psi }_{\alpha h}\left(A_j^{*},H_k^{*}\right)$ is the aerodynamic damping function of the flutter derivative $A_2^{*}$, and the flutter derivative $A_2^{*}$ is positive at the wind speed of 1 m/s, while the wind speed at all other levels is negative, and its value gradually decreases with the increase of wind speed. The function ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ is always negative, and its value gradually increases with increasing wind speed. Therefore, at a wind speed of 1 m/s, $A_2^{*}{\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ is negative, while at all other wind speeds, it is positive, and its value gradually increases with increasing wind speed. It can be seen from this that the trend of $A_2^{*}{\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ depends on the derivative of vibration $A_2^{*}$. Although function ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ has a small impact on the value of $A_2^{*}{\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$, its value is negative, determining that the aerodynamic damping of term $A_2^{*}$ is positive damping.

(2)

Function ${\psi }_{\alpha h}\left(A_j^{*},H_k^{*}\right)$ is the aerodynamic damping function of the product $A_1^{*}{H}_2^{*}$, which is always negative in value. Its absolute value gradually increases with increasing wind speed and then rapidly decreases. The value of ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ is always negative, and its absolute value gradually increases with increasing wind speed. Therefore, the aerodynamic damping of $A_1^{*}{H}_2^{*}$ is positive damping, and when the wind speed exceeds 12 m/s, the absolute value of function ${\psi }_{\alpha h}\left(A_j^{*},H_k^{*}\right)$ decreases, resulting in a significant decrease in $A_1^{*}{H}_2^{*}{\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ with increasing wind speed.

(3)

Function ${\psi }_{\alpha h}\left(A_j^{*},H_k^{*}\right)$ is the aerodynamic damping function of the product $A_4^{*}{H}_2^{*}$, which is always negative in value. Its absolute value increases initially with wind speed and then decreases. As the wind speed increases, ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ decreases. Its value lies between 0.9 and 1.0. Its impact on $A_4^{*}{H}_2^{*}{\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ is minimal, while its value aligns closely with the product of $A_4^{*}{H}_2^{*}{\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ and the flutter derivative $A_4^{*}{H}_2^{*}$.

(4)

Function ${\psi }_{\alpha h}\left(A_j^{*},H_k^{*}\right)$ is the aerodynamic damping function of the product $A_1^{*}{H}_3^{*}$, which is always negative in value and gradually decreases with increasing wind speed. ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ decreases with the increase of wind speed, and its value is between 0.9 and 1.0, which has little effect on $A_1^{*}{H}_3^{*}{\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$, and the value of $A_1^{*}{H}_3^{*}{\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ is basically consistent with the value of flutter derivative $A_1^{*}{H}_3^{*}$. The reason why the aerodynamic damping of item $A_1^{*}{H}_3^{*}$ appears as negative damping is because the vibration derivatives $A_1^{*}$ and $H_3^{*}$ have opposite signs, and function ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ is positive.

(5)

Function ${\psi }_{\alpha h}\left(A_j^{*},H_k^{*}\right)$ is the aerodynamic damping function of the product $A_4^{*}{H}_3^{*}$, which always maintains a negative value and gradually decreases with increasing wind speed. The value of ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ always remains positive, ranging between 0.0 and 0.44, and gradually increases with wind speed. Therefore, the aerodynamic damping of $A_4^{*}{H}_3^{*}$ is negative, and function ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ leads to a significant decrease in the value of $A_4^{*}{H}_3^{*}{\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ relative to the flutter derivative $A_4^{*}{H}_3^{*}$.

(6)

It can be seen from (f) in Figure 5 that among the aerodynamic damping of torsional modes, $A_1^{*}{H}_3^{*}{\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ in the aerodynamic damping of $A_2^{*}{\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ and $A_1^{*}{H}_3^{*}$ in the aerodynamic damping of term $A_2^{*}$ are significantly greater than that of aerodynamic damping ${\psi }_{\alpha h}\left(A_j^{*},H_k^{*}\right)\varphi \left({\theta }_1,{\xi }_{s\alpha }\right)$, which shows that the aerodynamic damping of flutter torsional mode mainly comes from two aspects: one is the self-excited aerodynamic damping of torsional velocity in the torsional vibration system; the second is the vertical vibration velocity response induced by the torsional displacement lift in the vertical vibration system, and the pneumatic damping in the torsional vibration system is fed back to the torsional vibration system through the vertical velocity self-excited torque.

4.6. Analysis of Function ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ in Torsional Pneumatic Damping

For an ideal flat plate, the main sources of modal damping reversal are aerodynamic damping from factors $A_2^{*}$ and $A_1^{*}{H}_3^{*}$, with the sign of aerodynamic damping closely related to the sign of function ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$. Therefore, further analysis should be conducted regarding function ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$.

Figure 6 shows the function term ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$, the phase difference ${\theta }_1$, and the stiffness parameters of the vertical vibration system in the torsional vibration system with wind speed in the pneumatic damping of term $A_1^{*}{H}_3^{*}$ and term $A_2^{*}$. From the graph, the following can be observed:

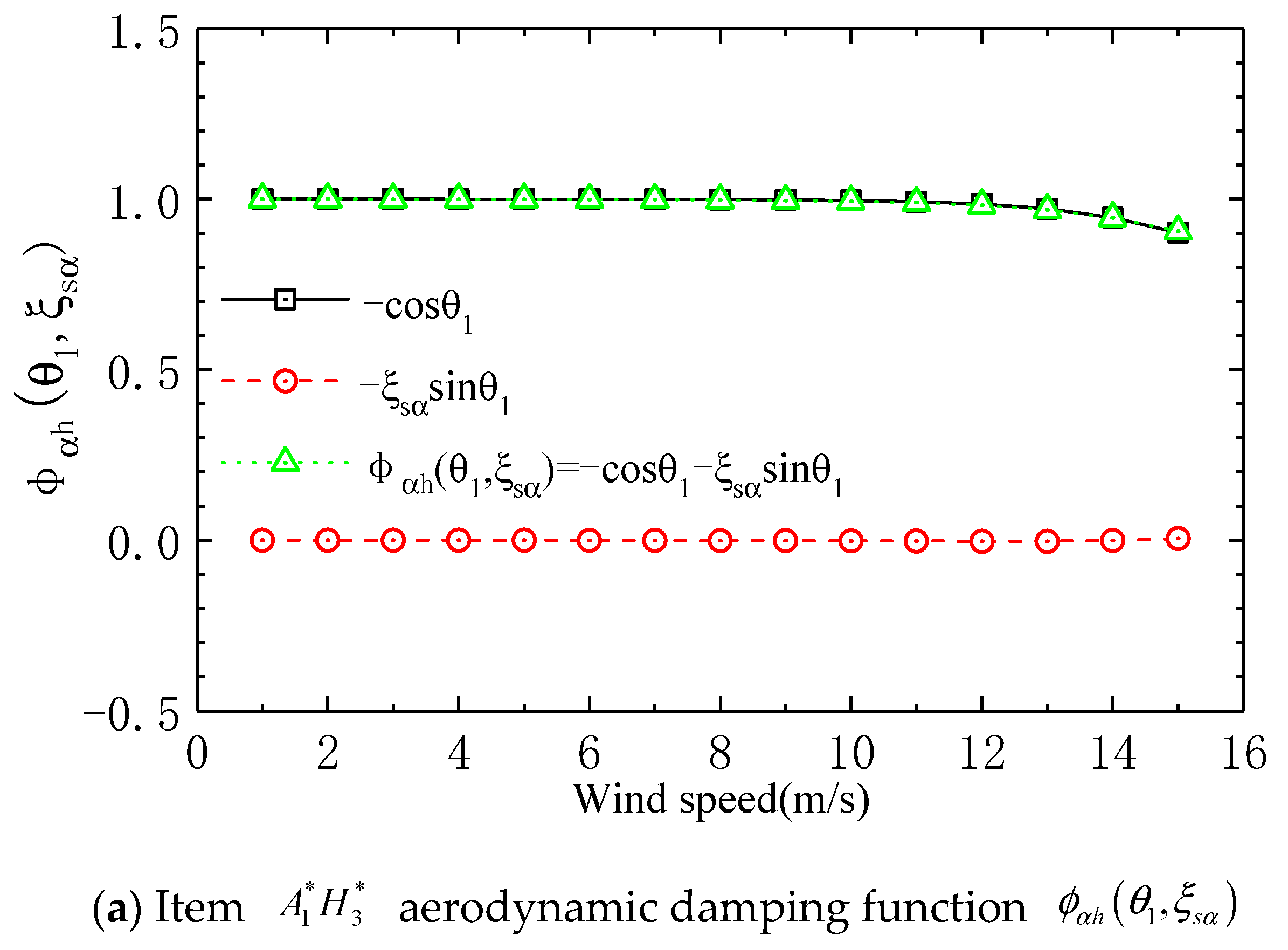
(1)

In the torsional vibration system, the value of $-{\xi }_{s\alpha }\sin {\theta }_1$ in the aerodynamic damping function ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ of term $A_1^{*}{H}_3^{*}$ is close to 0, and its contribution to ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ is very small. The value of function ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ is basically equal to $-\cos {\theta }_1$, while $-{\xi }_{s\alpha }\sin {\theta }_1$ does not affect the positive or negative value of function ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$.

(2)

In the torsional vibration system, the aerodynamic damping function term ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ of term $A_2^{*}$ is only related to the stiffness parameter and the torsional mode circle frequency ${\omega }_{s\alpha }$, where $\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}$ and ${\omega }_{s\alpha }^2$ are both positive values, so that ${\varphi }_{\alpha h}\left({\theta }_1,{\xi }_{s\alpha }\right)$ is a negative value; then, the aerodynamic damping of term $A_2^{*}$ is a positive value.

(3)

The phase difference ${\theta }_1$ between the lift force reversal and vertical displacement gradually decreases as wind speed increases but it always remains within the range of (90° to 180°), meaning that the cosine function $\cos {\theta }_1$ is negative, resulting in a positive value for $-\cos {\theta }_1$. Therefore, under the condition that the flutter derivative product $A_1^{*}{H}_3^{*}$ is negative, the aerodynamic damping of the torsional vibration system $A_1^{*}{H}_3^{*}$ exhibits negative damping.

(4)

The value of phase difference ${\theta }_1$ being in the interval (90–180°) depends entirely on the parameters of the vertical vibration system ${\gamma }_{h\alpha }$ and ${\Gamma }_{h\alpha }$. From the graph, it can be observed that ${\gamma }_{h\alpha }$ is always negative, while ${\Gamma }_{h\alpha }$ is always positive, so $\sin {\theta }_1={\Gamma }_{h\alpha }/\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}$ is positive and $\cos {\theta }_1={\gamma }_{h\alpha }/\sqrt{{\gamma }_{h\alpha }^2+{\Gamma }_{h\alpha }^2}$ is negative. Therefore, the phase difference ${\theta }_1$ angle must be in the 90° to 180° interval.

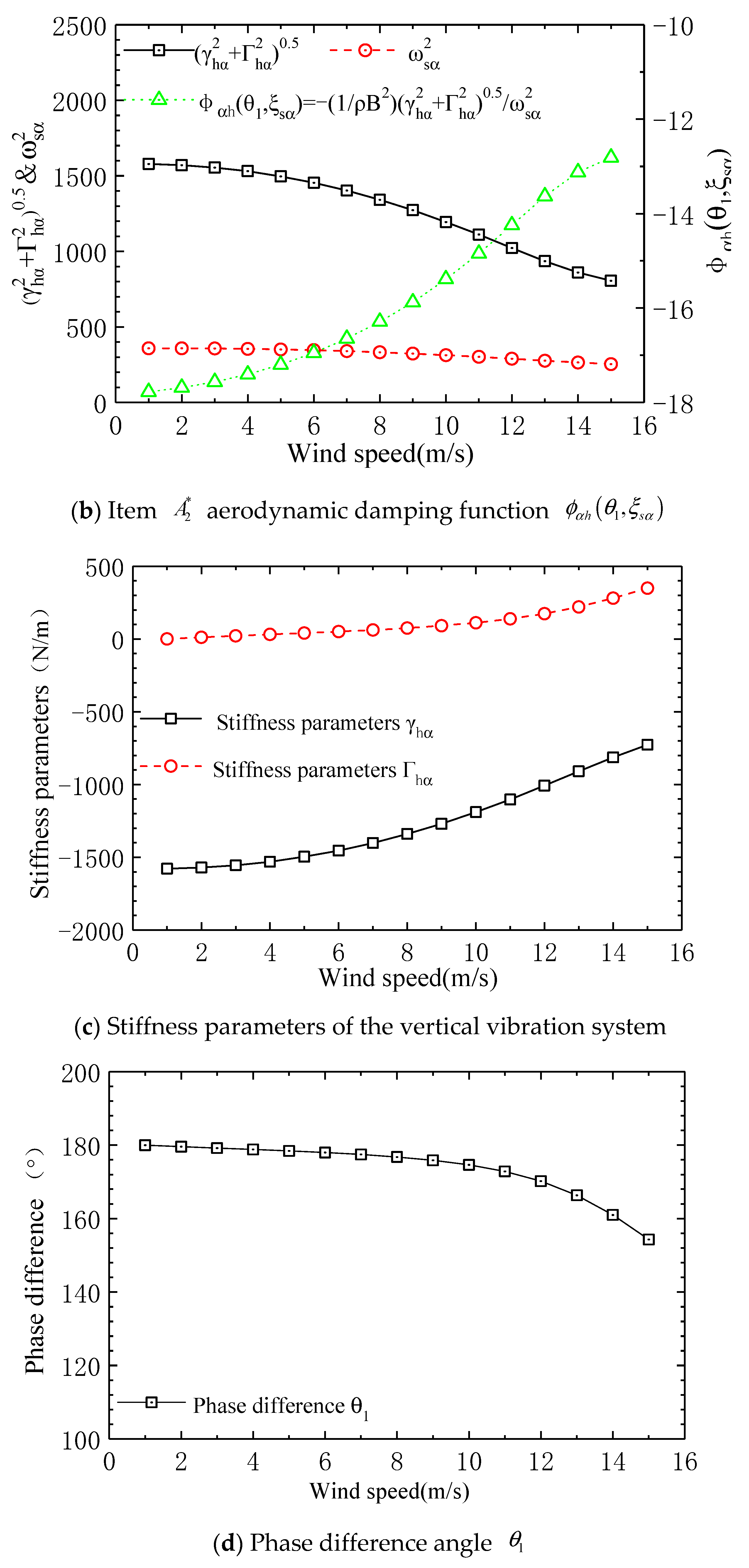
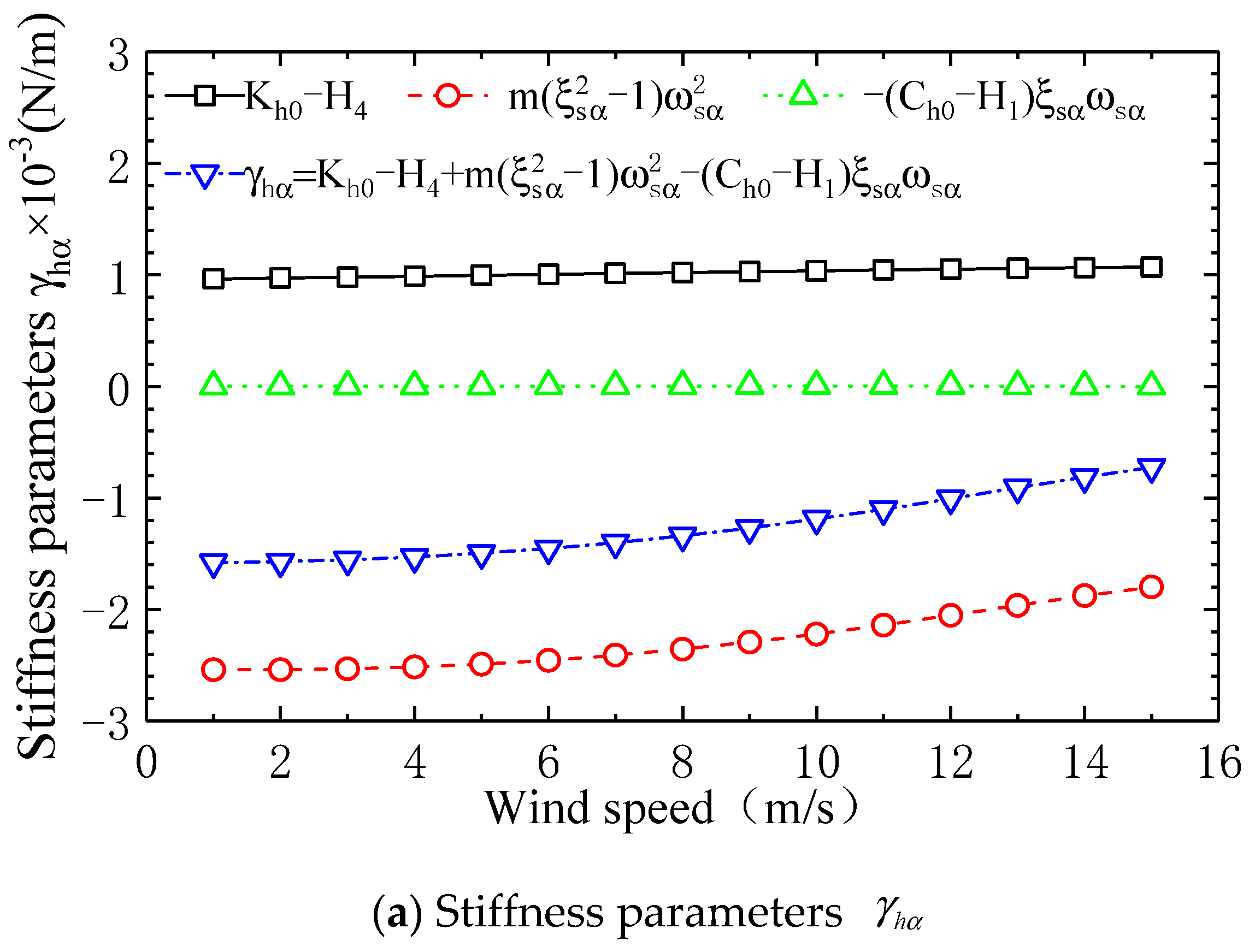
4.7. Stiffness Parameter Analysis

The phase difference ${\theta }_1$ of torsional displacement self-excitation force and vertical vibration displacement is closely related to the stiffness parameters ${\gamma }_{h\alpha }$ and ${\Gamma }_{h\alpha }$ of the vertical vibration system, so it is necessary to further analyze the stiffness parameters ${\gamma }_{h\alpha }$ and ${\Gamma }_{h\alpha }$ of the vertical vibration system.

Figure 7 shows the stiffness parameters of the vertical vibration system and the curve with wind speed. From the graph, the following can be observed:

(1)

In the stiffness parameter expression ${\gamma }_{h\alpha }$, the value of $-\left(C_{h0}-H_1\right){\xi }_{s\alpha }{\omega }_{s\alpha }$ is close to zero relative to the other two stiffness parameters in ${\gamma }_{h\alpha }$. Therefore, the numerical value of stiffness parameter ${\gamma }_{h\alpha }$ depends on the sum of $K_{h0}-H_4$ and $m_h\left({\xi }_{s\alpha }^2-1\right){\omega }_{s\alpha }^2$. Among them, because the torsional mode damping ratio of square ${\xi }_{s\alpha }^2$ in term $m_h\left({\xi }_{s\alpha }^2-1\right){\omega }_{s\alpha }^2$ is significantly less than 1, the value of this term is approximately equal to $-m_h{\omega }_{s\alpha }^2$, and $-m_h{\omega }_{s\alpha }^2$ is the negative stiffness generated by the torsional displacement self-excited force during the excitation of vertical vibration. The stiffness parameter ${\gamma }_{h\alpha }$ has a negative value because the negative stiffness $-m_h{\omega }_{s\alpha }^2$ is significantly greater than the vertical vibration system’s positive stiffness $K_{h0}-H_4$.

(2)

In the stiffness parameter expression ${\Gamma }_{h\alpha }$, $-2m_h{\xi }_{s\alpha }{\omega }_{s\alpha }^2$ is always negative before flutter, and it changes from negative to positive as it approaches the critical flutter wind speed; whereas $\left(C_{h0}-H_1\right){\omega }_{s\alpha }$ is always positive, with its value increasing linearly with wind speed $-2m_h{\xi }_{s\alpha }{\omega }_{s\alpha }^2$, being significantly greater than at all wind speeds, resulting in a positive value for stiffness parameter ${\Gamma }_{h\alpha }$.

(3)

Negative stiffness $-m_h{\omega }_{s\alpha }^2$ results in a negative value for stiffness parameter ${\gamma }_{h\alpha }$, while positive stiffness $\left(C_{h0}-H_1\right){\omega }_{s\alpha }$ leads to a negative value for stiffness parameter ${\Gamma }_{h\alpha }$. Therefore, the cosine function $\cos {\theta }_1$ is negative, causing the phase angle between torsional displacement self-excited lift and vertical displacement response to be in the (90° 180°) interval.

5. Conclusions

In this paper, the modal decoupling of bending–torsional-coupled flutter is carried out through the theory of the “incentive-feedback” mechanism, and the flutter mechanism of the ideal plate is analyzed. From the above analysis, the following conclusions are drawn:

(1)

The main sources of vertical modal damping in an ideal plate are twofold: firstly, the aerodynamic positive damping induced by vertical velocity self-excitation in the vertical vibration system; secondly, the torsional vibration system, where vertical velocity self-excites a twisting moment, and the twisting displacement self-excites aerodynamic positive damping that feeds back to the vertical vibration system.

(2)

The main sources of damping for the ideal flat plate’s torsional mode come from two aspects: firstly, the self-excited aerodynamic positive damping due to torsional velocity in the torsional vibration system; secondly, the vertical displacement self-excites the vertical vibration velocity through lift-induced vertical excitation in the vertical vibration system, and the vertical velocity self-excites the aerodynamic negative damping feedback to the torsional vibration system.

(3)

The torsional displacement of the ideal plate produces the aerodynamic negative damping through “incentive-feedback”, which is greater than its torsional velocity and self-excited positive damping, resulting in the divergence of its torsional vibration. Because the self-excited aerodynamic forces are coupled with each other, and the vertical vibration system diverges at the same time under the excitation of torsional self-excited lift, bending–torsional-coupled flutter occurs.

(4)

The “incentive feedback mechanism” indicates that in the process of exciting vertical vibrations, the torsional displacement of an ideal flat plate is caused by self-excited lift. The vertical vibration system produces a negative stiffness $-m_h{\omega }_{s\alpha }^2$, significantly greater than the stiffness $K_{h0}-H_4$ of the vertical vibration system, resulting in a cosine value of the phase difference between the torsional displacement due to self-excited lift and the vertical vibration displacement response being less than zero. In other words, the phase difference angle between the torsional displacement due to self-excited lift and the vertical vibration displacement response lies in the interval of 90° to 180°. As a result, when the product of flutter derivatives $A_1^{*}{H}_3^{*}$ is negative, the torsional displacement generates torsional aerodynamic negative damping through incentive feedback.

(5)

This paper further improves the existing theory in the process of modal decoupling through the “excitation-feedback” mechanism. The process of cyclic search frequency is omitted and improves the calculation efficiency.