Abstract
Multiple criteria decision-making (MCDM) is a significant area of decision-making theory that certainly warrants attention. It might be difficult to accurately convey the necessary decision facts when navigating decision-making problems since we frequently run into complicated issues and unpredictable situations. To address this, introducing the novel idea of the bipolar pqr-spherical fuzzy set (SFS), a hybrid structure of the bipolar fuzzy set (BFS) and the pqr-spherical fuzzy set (pqr-SFS), is the main goal of this work. The fundamental (set-theoretic and algebraic) operations on SFSs are explained as well as their relations to several known models. A distance measure, such as Euclidean distance, among SFNs, is provided. Afterward, we expand the fundamental aggregation operators to the pqr-spherical fuzzy (SF) environment by developing bipolar pqr-spherical fuzzy-weighted averaging and bipolar pqr-spherical fuzzy-weighted geometric operators for aggregating SFNs. According to the aforementioned distance measure and operators, an MCDM approach is established consisting of two algorithms, namely, the TOPSIS method and the method using the proposed operators in the SF context. Moreover, a numerical example is provided in order to ensure that the presented model is applicable. By using the two algorithms, a comparative analysis of the proposed method with other existing ones is given in order to verify the feasibility of the suggested decision-making procedure.
1. Introduction
This part provides a literature overview of relevant concepts that will be employed in this study.
Extensions of Fuzzy Set Theory: Review
Numerous real-world problems involve fuzziness, such as MCDM, pattern recognition, data mining, etc. The knowledge in these areas is often subject to intrinsic ambiguity or uncertainty and is incomplete. Dealing with this massive information is essential for making informed decisions, gaining meaningful insights, and revealing valuable insights.
To resolve such issues, Zadeh [1] introduced the idea of fuzzy sets (FSs), where each element receives a membership degree (MD) that indicates how closely the element is related to the other elements. These fractions are generally encapsulated as real numbers in the closed interval, where 0 means not a part of this group, 1 means completely a member of the group, and everything in between represents some level of participation.
After the concept of FSs, Atanassov [2] proposed the concept of intuitionistic fuzzy sets (IFSs). IFSs provided a more descriptive presentation by accounting for membership degrees (MDs) along with non-membership degrees (¬MDs), representing the intrinsic uncertainty and confusion presented in practical situations. IFS is extensively used for MCDM processing, particularly when MD and ¬MD sums range from zero to one. But in real situations, the sum of MD and ¬MD is sometimes .
Yager [3] established an innovative notion known as the Pythagorean fuzzy set (PyFS) that generalized IFS. In this regard, the MCDM domain has been extended due to the excellent features of PyFS to describe and control undecided. As we know, PyFS is limited to having the sum of the squares of MD and ¬MD be ≤1.
Yager [4] introduced the q-rung orthopair FS (q-ROFS) as a subsequent evolution of both PyFS and IFS, removing the restrictions mentioned above. Dounis and Stefopoulos [5] used q-ROFS for intelligent medical diagnosis. By extending the latter models, decision-makers have more freedom in selecting values as they wish; on the other hand, it forces them to pick one parameter for all selected values.
Seikh and Mandal [6] introduced p,q-quasirung orthopair fuzzy sets (p,q-QOFSs), which give decision-makers the flexibility to choose different powers for MD and ¬MD, i.e., (, such that p and q could be the same or different). A similar approach appeared in [7] under the name of n,m-rung orthopair fuzzy sets (nm-ROFSs), where are in . This change allows for a more flexible encoding of information that accommodates diverse preferences and needs in decision-making contexts. All the aforementioned studies focus on the application of MD and ¬MD while overlooking the impact of the neutral degree, which is a significant factor during the DM process as well.
Cuong and Kreinovich [8] solved the above challenge by introducing the notion of picture fuzzy sets (PFSs). PFSs define the degree of membership as positive (+ve), negative (−ve), and neutral degrees, which correspond to MD, a neutral membership degree (NMD), and ¬MD, respectively, under three distinct functions, inferring the following constraint: . But in some real-life scenarios, the requirement might not be met.
Mahmood et al. [9] proposed a spherical fuzzy set (SFS), which imposes the new restriction , making uncertainty management more flexible. It was also introduced by Gündoğdu and Kahraman [10]. So, let us try specific values for MD = , NMD , and ¬MD ; squaring these numbers does not work, as .
Mahmood et al. [9] extended SFSs to T-spherical FSs (T-SFSs), where , for some integer . Such an arrangement affords the decision-makers flexibility in assigning any MD, NMD, or ¬MD value inside . For instance, if we take , and MD , NMD , and ¬MD , we obtain . Ullah et al. [11] introduced and defined the term ’correlation coefficients of T-SFS’, where levels of membership degrees of the terms should meet the constraints, i.e., . This assumes homogeneity in the levels of MD, NMD, and ¬MD. In actual scenarios, these levels might differ. So, if a decision-maker sets MD , NMD , and ¬MD , for instance, we see that implies this violate linearly aggregation rule. So, a more nuanced approach is needed. Enabling different term levels for MD, NMD, and ¬MD makes it possible to reflect the multi-factorial reality.
Ali and Naeem [12] proposed a new extension of T-SFS, called r,s,t-spherical fuzzy sets (srt-SFSs), which lift all restrictions inflicted by classical sets. Equivalently, Rahim et al. [13] introduced the concept of pqr-spherical fuzzy sets (pqr-SFSs) with little restriction. We follow the latter notation in this work. In pqr-SFSs, the triplet (MD, NMD, and ¬MD) is constrained according to , where are +ve integers with . The pqr-SFSs have been studied in several manners by several researchers; see [14,15]. Karaaslan and Karamaz [16] also extended this concept to interval-valued pqr-spherical fuzzy sets.
Bipolarity is the existence of two opposing or contrasting components, powers, or circumstances. In many areas, it refers to the state of balance between two opposing or complementary poles, commonly considered as good/bad or beneficial/non-beneficial angles. Thus, bipolarity has practical and theoretical applications in everything from psychology and political science to physics and decision-making. Bipolar fuzzy sets are a generalization of conventional fuzzy sets, which are very useful in complex real-life situations where both, +ve, and negative, −ve, feelings need to be considered. These methods can accommodate dual uncertainties, making them applicable in a variety of fields like decision-making, pattern identification, medical diagnosis, sentiment analysis, risk assessment, and AI. As the demand for higher-level models in ambiguous and uncertain situations develops, extended bipolar fuzzy sets are anticipated to play an increasingly important role in enhancing computer intelligence.
The first extension in this form was the bipolar intuitionistic fuzzy set (BIFS) [17] introduced by Ezhilmaran and Sankar. By the same scenario stated in the first paragraph, the bipolar Pythagorean fuzzy set (BPyFS) [18], Fermatean bipolar fuzzy set (FBFS) [19], bipolar q-rung orthopair fuzzy set (Bq-ROFS) [20], bipolar m,n-rung orthopair fuzzy set (Bmn-ROFS) [21], and spherical bipolar fuzzy set (SBFS) [22] are introduced.
Lastly, the bipolar T-spherical fuzzy set (BT-FS) [23], is a model that includes both +ve and −ve values of MD, NMD, and ¬MD. Specifically, , NMD+, ¬MD+ , and MD−, , , satisfy the conditions and , for some +ve integer, . This requirement forces decision-makers to give an equal n to MD, NMD, and ¬MD. In some cases, decision-makers may have to assign different levels of authority to the MD, NMD, or ¬MD. Such requirements cannot be catered to by BT-SFSs. Therefore, in order to overcome these limitations, we introduce the bipolar pqr-spherical fuzzy set (SFS), which allows decision-makers to choose any +ve integers , without violating condition , and . By permitting decision-makers to allocate different parameters, , and r to , , and , , , respectively, SFSs create a relatively open stage for DM processes. More specifically, if a decision-maker sets , , and ; , , and for example. In that case, for , one can see that and violate the restricted conditions for the BT-F model. However, for , , and , both restrictions hold true, showing the power of choosing different parameters and, consequently, the robustness of the proposed model. Figure 1 illustrates its position and demonstrates how the most well-known extended fuzzy sets are derived from the conventional fuzzy set.
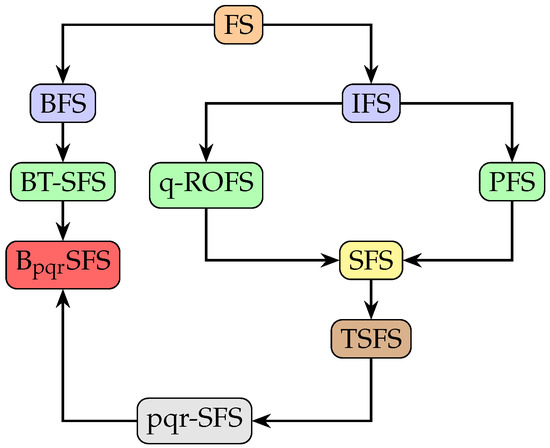
Figure 1.
Using main variant structures to obtain SFSs from fuzzy sets.
A T-spherical fuzzy set, which satisfies the restriction for some integer , is a verbal generalization of various types of extended fuzzy sets (discussed above). However, it is not free from limitations. Then, the concept of pqr-spherical fuzzy sets lifts approximately all restrictions imposed by earlier sets. In a pqr-spherical fuzzy set, the triplet (MD, NMD, and ¬MD) is constrained to , where such that . This approach does not allow DM to evaluate MD, NMD, and ¬MD in a +ve as well as −ve manner. The bipolar T-spherical fuzzy set [23] appeared in the literature, which contains both +ve and −ve values of MD, NMD, and ¬MD. However, this approach fails to provide an additional flexible atmosphere for DM procedures by permitting decision-makers to set multiple values for for +ve and −ve values of MD, NMD, and ¬MD, respectively. This encourages us to put forward the bipolar pqr-spherical fuzzy set, a model that overcomes the preceding restrictions. Furthermore, bipolar pqr-spherical fuzzy sets generalize various fuzzy models in the literature and many MCDM techniques can be extended based on them.
This article offers a new notion of bipolar pqr-spherical fuzzy sets along with its principal operations, which expand on the existing bipolar T-spherical fuzzy sets and pqr-spherical fuzzy sets. Both averaging and geometric aggregation operators are put forward to aggregate bipolar pqr-spherical fuzzy information in the MCDM issues based on the prescribed operations. An extension of the TOPSIS technique for bipolar pqr-spherical fuzzy sets is proposed, which generalizes other methods.
The structure of this paper is outlined as follows: Section 2 presents some fundamental definitions and associated concepts succinctly. In Section 3, we present the operational laws and aggregation operators pertaining to pqr-spherical fuzzy numbers. Section 4 introduces the MCDM and TOPSIS methods, along with a numerical example to illustrate the suggested approach. Section 5 conducts an intensive comparative evaluation of the suggested methods in relation to previously established models. The conclusion of this paper is found in Section 6.
2. Background Concepts
The development of the intended model will be aided by keeping in mind the following basic definitions and properties:
Definition 1
([22]). Let U denote a non-empty finite set. A T-spherical fuzzy set (T-SFS) is defined as follows:
where represents a +ve membership, represents neutral membership, and represents a −ve membership with
and
where can be adjusted to a range of values based on the situation or requirements, the triplet is named a T-spherical fuzzy number (abbreviated as T-SFN), such that .
Definition 2
([22]). Let , , and be three T-SFNs. Then, we have the following:
- 1.
- 2.
- 3.
- 4.
Definition 3
([23]). Let U be an initial universe. A bipolar T-spherical fuzzy set (BT-SFS) over U is defined as follows:
where refer to the +ve degree membership, neutral, and non-membership functions, respectively, and refer to the −ve degree membership, neutral, and non-membership functions, respectively, such that
and
for each and some . The 6-tuple is conveniently called a bipolar T-spherical fuzzy number (BT-SFN).
Definition 4
([23]). Let and denote two BT-SFNs. Then, we have the following:
- 1.
- 2.
- 3.
- 4.
Definition 5
([12,13]). Let U denote a non-empty finite set. A pqr-spherical fuzzy set (pqr-SFS) is defined as follows:
such that represents a +ve membership, represents neutral membership, and represents a −ve membership, where
and
for any +ve integers . The triplet such that is called a pqr-spherical fuzzy number (pqr-SFN).
Definition 6
([13]). Let , , and denote three pqr-SFNs. Then, we have the following:
- 1.
- 2.
- 3.
- 4.
3. Bipolar pqr-Spherical Fuzzy Sets
In this section, a bipolar pqr-spherical fuzzy set, which is a hybrid model that incorporates both BFS and pqr-SFS, is defined, and we provide its fundamental operations:
Definition 7.
Let U be an initial universe. A bipolar pqr-spherical fuzzy set (SFS) over U is defined as follows:
where refer to the +ve degree membership, neutral, and non-membership functions, respectively, and refer to the −ve degree membership, neutral, and non-membership functions, respectively, such that
and
for each and some . For convenience, we call a bipolar pqr-spherical fuzzy number (SFN).
This model can be effectively applied to various real-world situations, including electoral voting systems, business strategies, finance, agricultural optimization, and medical treatments. More precisely, profit and loss statements are commonly used in the business and finance fields. BpqrSFS allows us to link business decision-making activities. When people invest their money in certain firms, their primary goal is to maximize profits within a set time frame. BpqrSFS has the ability to deal with such situations and issues by BpqrSFN, which is represented by , where is the degree of satisfaction that produces profit, is the degree of abstinence that produces profit, and is the degree of dissatisfaction that produces profit, where is the degree of satisfaction that causes a loss, is the degree of abstinence that causes a loss, and is the degree of dissatisfaction that causes a loss.
In accordance with existing literature, we shall refer to the proposed set as a bipolar (p,q,r)-spherical (or bipolar (r,s,t)-spherical) fuzzy set. However, we prefer to stick with the way mentioned above.
Remark 1.
Definition 7 yields the following definitions in certain cases:
- 1.
- bipolar T-spherical fuzzy set (BT-SFS) [23] if .
- 2.
- spherical bipolar fuzzy set (SBFS) [22] if .
- 3.
- bipolar picture fuzzy set (BPFS) [24] if .
- 4.
- bipolar mn-rung orthopair fuzzy set (Bmn-ROFS) [21] if .
- 5.
- Fermatean bipolar fuzzy set (FBFS) [19] if and .
- 6.
- bipolar Pythagorean fuzzy set (BPyFS) [18] if and .
- 7.
- bipolar intuitionistic fuzzy set (BIFS) [17] if and .
- 8.
- pqr-spherical fuzzy set (pqr-SFS) [12,13] if .
- 9.
- T-spherical fuzzy set (T-SFS) [9] if and .
- 10.
- spherical fuzzy set (SFS) [9,25] if and .
- 11.
- picture fuzzy set (PFS) [8] if and .
- 12.
- p,q-quasirung orthopair fuzzy set (pq-QROFS) [6] if .
- 13.
- q-rung orthopair fuzzy set (q-ROFS) [4] if and .
- 14.
- Fermatean fuzzy set (FFS) [26] if and .
- 15.
- Pythagorean fuzzy set (PyFS) [3] if and .
- 16.
- intuitionistic fuzzy set (IFS) [2] if and .
- 17.
- fuzzy set (FS) [1] if and .
Next, Table 1 highlights the exceptional performance of our novel model compared to existing models, excelling in membership degree (MD), neutral degree (NMD), non-membership degree (¬MD), offering greater flexibility in parameter selection, and effectively capturing bipolarity.

Table 1.
Superiority of the proposed model compared to existing ones.
Now, we present the fundamental operations on SFNs.
Definition 8.
Let and be two SFNs. Then, we have the following:
- 1.
- , if , , , , , and .
- 2.
- if and .
- 3.
- , where means the complement of .
- 4.
- .
- 5.
- .
Proposition 1.
Let , , and denote SFNs. Then, we have the following:
- 1.
- and .
- 2.
- .
- 3.
- .
- 4.
- .
- 5.
- .
- 6.
- .
- 7.
- .
- 8.
- .
- 9.
- .
Proof.
See Appendix A (1). □
Proposition 2.
Let and denote SFNs. Then, we have the following:
- 1.
- .
- 2.
- .
- 3.
- .
Proof.
See Appendix A (2). □
Remark 2.
Given any SFNs and , then , , are also SFNs.
Example 1.
Consider the initial universe , and let , be SFNs. Then, we have the following:
- 1.
- Neither nor , since and .
- 2.
- .
- 3.
- .
- 4.
- .
Next, we present the sum, product, scalar product, and exponent operations on the SFSs.
Definition 9.
Let and denote SFNs (SFNs) and let . Then, we have the following:
- 1.
- 2.
- 3.
- 4.
Example 2.
Recall the SFNs and considered in Example 1 such that and let . Then, we have the following:
- 1.
- .
- 2.
- .
- 3.
- .
- 4.
- .
Theorem 1.
Let , , and denote SFSs. Then, we have the following:
- 1.
- .
- 2.
- .
- 3.
- .
- 4.
- .
Proof.
Straightforward. □
Theorem 2.
Let , , and denote three SFSs and . Then, we have the following:
- 1.
- .
- 2.
- .
- 3.
- .
- 4.
- .
Proof.
See Appendix A (3). □
One of the most important tools in the fuzzy set analysis is the distance measure. It is commonly used when making decisions. The most commonly used distance measurement is the Euclidean distance. This distance measure between SFNs, which will be utilized later in the TOPSIS method, is provided in this section.
Definition 10.
Let and be two SFNs on a set . A distance measure between and is , if the following conditions are satisfied:
- 1.
- ;
- 2.
- ;
- 3.
- if and only if .
Definition 11.
Let and be two SFNs on a set . We define the distance measure between and as follows:
Notice that characteristics of Definition 10 are clearly met by the distance measure mentioned in Equation (1).
Example 3.
Recalling again the SFNs and given in Example 1 such that . Then, we have the following:
4. Bipolar pqr-Spherical Fuzzy Aggregation Operators
This section extends the basic aggregation operators into the SFS environment by creating bipolar pqr-spherical fuzzy-weighted averaging and bipolar pqr-spherical fuzzy-weighted geometric operators for aggregating the SFNs.
4.1. Bipolar pqr-Spherical Fuzzy-Weighted Average Operators
In this subsection, the weighted average operator for aggregating SFNs is introduced, and its key characteristics are examined.
Definition 12.
Let , for , be a collection of SFNs, then the formulation of the bipolar pqr-spherical fuzzy-weighted average (SFWA) operator is expressed as follows:
whereas is meant to the weight of for such that and each .
The following theorems are derived from the SFNs operating rules.
Theorem 3.
The SFWA operator is defined as follows:
Proof.
See Appendix A (4). □
Theorem 4
(Idempotency). Let denote a family of SFNs, for . If for all j, then
Proof.
See Appendix A (5). □
Theorem 5
(Monotonicity). If and are two families of SFNs indexed by , and if for all j, then
Proof.
See Appendix A (6). □
Theorem 6
(Boundedness). Let denote a collection of SFNs. Then, we have the following:
Proof.
See Appendix A (7). □
4.2. Bipolar pqr-Spherical Fuzzy-Weighted Geometric Operators
The novel concept of the weighted geometric operator for aggregating SFNs is presented in this subsection, along with an examination of its key characteristics.
Definition 13.
Let , for , be a collection of SFNs. Then the formulation of the bipolar pqr-spherical fuzzy-weighted geometric (SFWG) operator is expressed as follows:
where denotes the weight of for such that and .
Theorem 7.
The SFWG operator is defined as follows:
Proof.
The same steps as those outlined in the proof of Theorem 3. □
Theorem 8
(Idempotency). Let denote a family of SFNs indexed by . If for all j, then
Proof.
The proof is similar to the proof of Theorem 4. □
Theorem 9
(Monotonicity). If and are two families of SFNs indexed by , and if for all j, then
Proof.
The proof is similar to the proof of Theorem 5. □
Theorem 10
(Boundedness). Let denote a collection of SFNs. Then,
Proof.
The proof is similar to the proof of Theorem 6. □
Definition 14.
Let denote a SFN. Then, the score function of SFN is defined as follows:
Definition 15.
Let denote a SFN. Then, the accuracy function of SFN is defined as follows:
Definition 16.
Let and be SFNs. Then, from Definitions 14 and 15, we have the following:
- 1.
- If , then ( is inferior to );
- 2.
- If , then ( is superior to );
- 3.
- If , thenif , then ( is "inferior” to );if , then ( is “superior” to );if , then ( is “equivalent” to ).
5. MCDM Algorithms
In this part, two fundamental methods (algorithms) are applied to MCDM. The first one is the TOPSIS technique, and the second one involves using the proposed operators in the SF context, which introduces an approach for handling MCDM problems in a bipolar pqr-spherical environment using the two aforementioned aggregation operators. Let denote a family of alternatives and denote a set of criteria. Using the SFNs, the decision-maker assesses the n options in light of the l criteria.
5.1. Extension of the TOPSIS Method with Bipolar pqr-Spherical Fuzzy Sets
TOPSIS is a multi-criteria evaluation approach, established in 1981 by Hwang and Yoon [27], with subsequent improvements by Yoon in [28] and by Hwang et al. in [29]. TOPSIS was founded on the premise that the preferred option should have the lowest geometrical distance from the +ve ideal solution (PIS) and the greatest geometrical distance from the −ve ideal solution (NIS). In 2021, a booklet on TOPSIS in the fuzzy setting was released [30]. The TOPSIS approach comprises several essential metrics. A few researchers introduced the TOPSIS approach based on similarity measures (Hamming, Euclidean, and Dice similarity measures); others discovered the presence of various clustering operators and addressed several real-world issues. As a result, effective and suitable actions will be implemented. However, many strategic decision-making problems inside businesses will be mutually exclusive. Maldonado-Macías et al. [31] analyzed intuitionistic fuzzy TOPSIS. Junior et al. [32] compared the AHP technique with the TOPSIS technique in their application to specific supplier selections. Yilmaz et al. [33] developed the interval-valued type-2 fuzzy TOPSIS method to help international law practitioners and engineers make better decisions while dealing with unpredictable and dynamic systems. Jin et al. [34] introduced the picture fuzzy TOPSIS method to apply it to risk management problems. In 2019, Gündoğdu [10] formulated the fuzzy TOPSIS technique based on spherical fuzzy sets. Akram and Arshad [35] identified bipolar fuzzy TOPSIS methodologies and applications. Recently, Karaaslan and Karamaz [16] proposed the interval-valued pqr-spherical fuzzy TOPSIS method with some applications. This work developed the fuzzy TOPSIS method with SFs, named the SF TOPSIS method. The method’s stepwise procedure is explained as follows:
- 1.
- The alternatives are evaluated using l criteria. The final values of the alternatives in relation to each criterion create a SF decision matrix, which is formed as follows:where and represent the +ve and −ve satisfaction degrees of alternative under criterion ; and represent the +ve and −ve neutrality degrees; and and represent the +ve and −ve dissatisfaction degrees.
- 2.
- If the criteria are not on the same scale, normalizing is needed, which is the normalizing of the decision matrix according to each criterion’s nature as follows:
- 3.
- The decision-makers give each criterion a weight value in order to accomplish the normalcy condition, regarding the weight vector with
- 4.
- The SF-weighted normalized decision matrix is calculated using the attribute weight vector in the manner described below:where each is calculated via Equation (3), for each and .
- 5.
- The bipolar pqr-spherical fuzzy +ve ideal solution (SFPIS) and the bipolar pqr-spherical fuzzy −ve ideal solution (SFNIS) are calculated as follows:where for ;andwhere
- 6.
- The normalized Euclidean distance of alternatives, for , from bipolar pqr-spherical fuzzy +ve and −ve ideal solutions, is calculated as follows:and
- 7.
- The relative closeness degree of the corresponding alternative to the bipolar pqr-spherical fuzzy +ve ideal solution, denoted by for , is computed by the following formula:
- 8.
- The alternative that has the highest closeness degree value is selected as the best alternative.
5.2. Bipolar pqr-Spherical Fuzzy Aggregation Operator Method
Aggregation tools are essential in MCDM issues that utilize this method, as aggregation involves merging multiple numerical values into a single value; thus, we can refer to this method as an aggregator [36,37,38]. Numerous researchers have focused on the aggregation operators associated with different types of fuzzy numbers. After exploring certain operations concerning intuitionistic fuzzy numbers (IFNs), both geometric and averaging aggregation operators based on IFNs were developed, as described by Xu and Yager [39] and Xu [40]. Subsequently, picture fuzzy geometric and averaging aggregation operators were studied in [41]. Then, spherical aggregation operators were discussed in [25] in the context of MCDM problems. The latter operators were extended to the so-called T-spherical aggregation operators [42]. The concepts of pqr-spherical weighted (geometric and averaging) aggregation operators were proposed in [12,13], generalizing all earlier operators. The T-spherical aggregation operators were further extended to the bipolar T-spherical aggregation operators that appeared in [23], aggregating the given +ve and −ve values. In this study, we build upon the previous ideas by extending bipolar T-spherical aggregation operators to SF aggregation operators, which are the basis of the new method in MCDM. The stepwise procedure of the proposed method is explained as follows:
- 1.
- The alternatives are evaluated using the l criterion. The final values of the alternatives with regard to each criterion are used to generate a SF decision matrix similar to Equation (5).
- 2.
- If the criteria are not on the same scale, normalizing is needed, which is the normalizing of the decision matrix according to each criterion’s nature, as in Equation (6).
- 3.
- The decision-makers give each criterion a weight value in order to accomplish the normalcy condition, regarding the weight vector with
- 4.
- 5.
- Score function of , denoted by , is calculated using Definition 14.
- 6.
- We sort the alternatives in decreasing order using the score values we obtained in step 5.
6. A Numerical Example Example of the Supplier Assessment Process
The supplier assessment process is critical for any business that wants to ensure its entire supply chain will be both efficient and reliable while also being cost-effective. The supplier assessment process involves evaluating potential and existing suppliers to determine their ability to meet the firm’s requirements in terms of quality, price, delivery time, and other defining criteria.
Supplier assessment data were collected in order to create long-term relationships with suppliers who can always provide products or services that meet company standards. This process also allows businesses to mitigate risks, like supply chain disruptions or compromised quality, and can lead to cost savings by making supplier partnerships more effective.
In this part, three criteria are used by a firm to assess four suppliers (, , , ) for a long-term contract. The criteria are as follows: cost (minimization), where lower costs are preferred; quality (maximization): superior quality is appreciated; delivery time (minimization): It is preferable to have faster delivery times, where the weight vector for the criteria is defined as To apply the first algorithm:
- 1.
- We obtain the SF evaluation matrix in Table 2.
 Table 2. SF evaluation matrix.
Table 2. SF evaluation matrix. - 2.
- The weight vector for the criteria above is .
- 3.
- In this step, normalizing is needed as criteria are not on the same scale; in order to normalize them, we use step (3) in Definition 8. Criteria and need to be normalized by using Equation (6), as shown in Table 3.
 Table 3. Normalized SF evaluation matrix.
Table 3. Normalized SF evaluation matrix. - 4.
- We calculate the weighted normalized SF decision matrix values by using Equation (7), where , , and , as obtained in Table 4.
 Table 4. Weighted normalized SF evaluation matrix.
Table 4. Weighted normalized SF evaluation matrix. - 5.
- The SFPIS and SFNIS are computed in Table 5:
 Table 5. BpqrSFPIS and BpqrSFNIS.
Table 5. BpqrSFPIS and BpqrSFNIS. - 6.
- The Euclidean distances of alternatives for from the bipolar pqr-spherical fuzzy +ve and −ve ideal solutions are calculated from Equations (8) and (9), respectively, in Table 6.
 Table 6. The Euclidean distances of all alternatives with SFPIS and SFNIS, with the weighted normalized SF evaluation matrix.
Table 6. The Euclidean distances of all alternatives with SFPIS and SFNIS, with the weighted normalized SF evaluation matrix. - 7.
- The relative closeness degree of the corresponding alternative to the bipolar pqr-spherical fuzzy +ve ideal solution, denoted by for , is computed by Formula (10), which is shown in Table 7 and Figure 2.
 Table 7. The relative closeness degrees.
Table 7. The relative closeness degrees.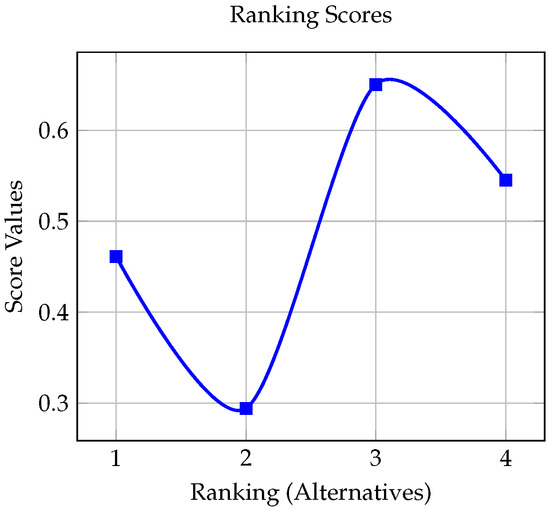 Figure 2. Ranking scores.
Figure 2. Ranking scores. - 8.
- The alternatives are ranked based on their final scores (relative closeness values) as follows:Therefore, is the best supply to be selected.
To apply the second algorithm to the same numerical example used for the first algorithm:
- 1.
- We obtain the SF evaluation matrix , as in Table 2.
- 2.
- The weight vector for criteria is .
- 3.
- 4.
- In order to aggregate the information presented in Table 3, we calculate the SFWA operator or the SFG operator, computed via as shown below:
- 5.
- Score values; the aggregated data are provided in Table 8.
 Table 8. The score values.
Table 8. The score values. - 6.
- Based on the score values in Table 8, the ranking of alternative suppliers, as depicted in Figure 3, is as follows:
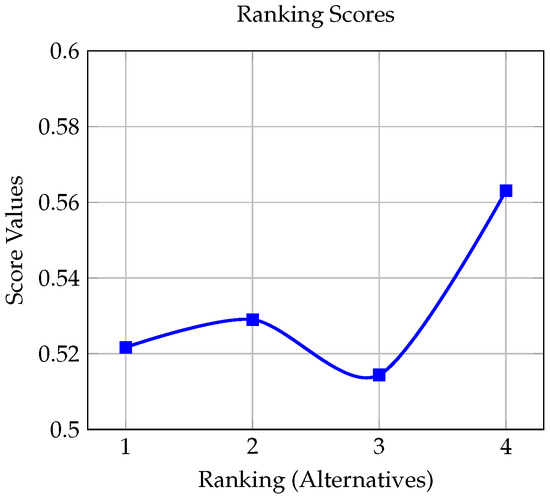 Figure 3. Ranking scores.
Figure 3. Ranking scores.
7. Sensitivity Analysis
In this section, we performed a sensitivity analysis of the suggested approaches by varying the parameters , and r. As a result, the SF TOPSIS procedure was divided into three situations. First, we set values to the parameters , , and . Second, we swapped the values of p and r while keeping the value of q. Finally, we assigned a similar value to each parameter to analyze the performance of the proposed operators. Data from the preceding DM problem were gathered again using the processes outlined in the pqr-TOPSIS technique. Later, the relative closeness degrees for the alternatives were determined, and in all situations, was found to be the best option and to be the worst; see Table 9 and Figure 4.

Table 9.
SF TOPSIS ranking results.
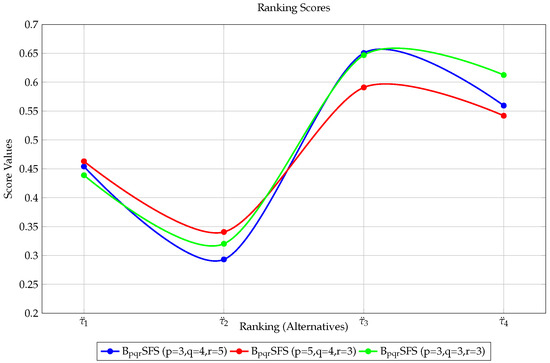
Figure 4.
SF TOPSIS ranking results for different values of p,q,r.
In the second part of the analysis, we altered the parameters , and r. As a consequence, the operation started with the parameters , , and , in order to investigate the performance of the proposed operator. Data from the aforementioned DM problem were aggregated once more with the SFWA operator. The score function was then used to calculate the score values for the alternatives, which were ranked by . Fixing and switching p and r values yielded alternatives ranked as (the rank of the final two options flips). This adjustment occurred when the value of . Table 10 and Figure 5 display the scores for different values of , and r and show that is always the best.

Table 10.
SFWA ranking results.
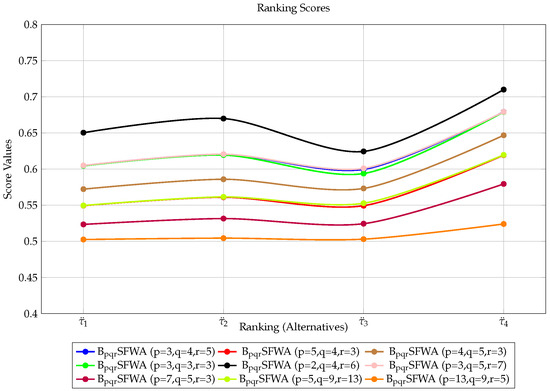
Figure 5.
Ranking results of SFWA operators for different values of p,q,r.
8. Comparative Analysis
This section of the paper provides a comparative analysis to ensure the stability of the suggested work. Before proceeding, it is recommended that you review Remark 1 in Section 3 and Table 1 to comprehend the superiority of the provided work. For example, if we set , we can derive the BT-SF TOPSIS technique. In addition, if we remove the neutrality degree membership and set , the q-ROF TOPSIS technique can be achieved. For additional study, we consider the numerical data in Table 9, Table 11, Table 12. We used our proposed approaches along with existing ones to the data supplied by the decision expert. The relative closeness of the alternatives suggests that is the optimum alternative for all the previously described techniques, except in q-ROF TOPSIS, where , is optimal, whereas either or is ranked last; see Figure 4, Figure 6, Figure 7.

Table 11.
q-ROF TOPSIS ranking results.

Table 12.
BT-SF TOPSIS ranking results.
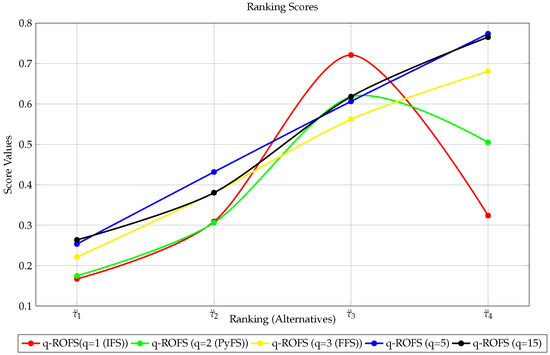
Figure 6.
q-ROFS TOPSIS ranking results, for q = 1,2,3,5,15.
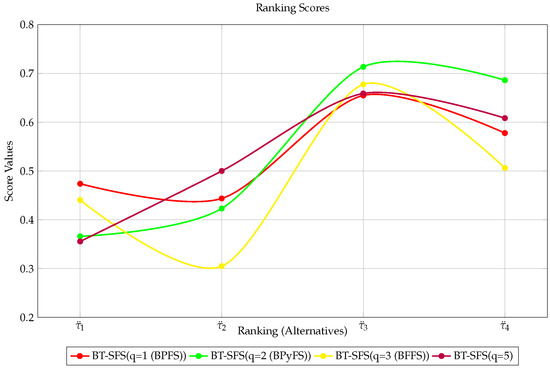
Figure 7.
BT-SFS TOPSIS ranking results, for q = 1,2,3,5.
For the second method, Remark 1 in Section 3 justifies that different existing aggregation operators (in the contexts of IFSs, PyFSs, FFSs, q-ROFSs, mn-ROFSs, PFSs, SFSs, T-SFSs, pqr-FSs, BIFSs, BPyFSs, FBFSs, Bq-ROFSs, Bmn-ROFSs, BPFSs, SBFSs, and BT-SFSs) can be deduced from the Bpqr-SFWA operator. The aggregated results presented in Table 10, Table 13, Table 14, Table 15, Table 16, Table 17 and Table 18 suggest that is the best alternative to be selected in almost all the operators except in the T-SF-weighted average (T-SFWA) and BTSF-weighted average (BTSFWA) operators for , where is the best. The good news is that the score values generated by the proposed operators for various values of , and r demonstrate that the results almost match their findings, implying the proposed work’s stability. Figure 5, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 show how the prospective operators’ score values compare to those of existing operators. This demonstrates that the proposed operator yields stable mathematical conclusions and can be utilized in place of existing operators in the context of Bpqr-SFSNs, and any extensions that may be derived from them. For some additional details, see the comparison in Table 19.

Table 13.
pqr-SFWA Ranking Results.

Table 14.
Ranking results of q-ROFWA operators for different values of q.

Table 15.
Ranking results of -ROFWA operators.

Table 16.
Ranking results of ROFWA operators for different values of m,n.

Table 17.
Ranking results of T-SFWA operators for different values of q.

Table 18.
Ranking results of BT-SFWA for different values of q.
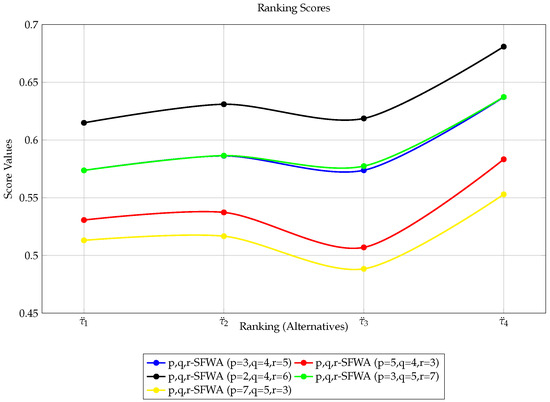
Figure 8.
Ranking results of pqr-SFWA operators for different values of p,q,r.
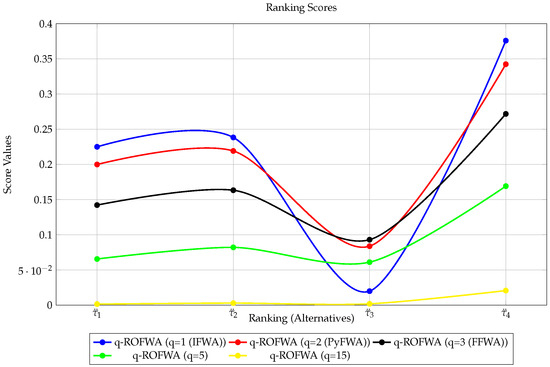
Figure 9.
Ranking results of q-ROFWA operators for different values of p,q,r.
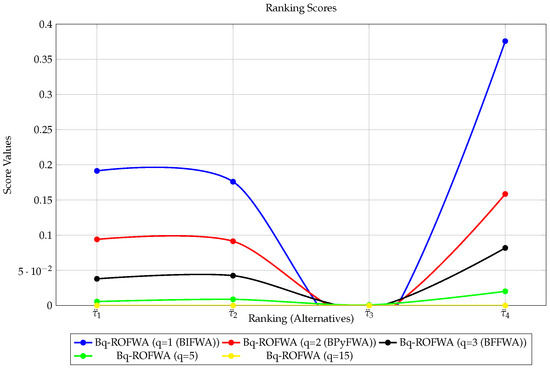
Figure 10.
Ranking results of Bq-ROFWA operators for different values of p,q,r.
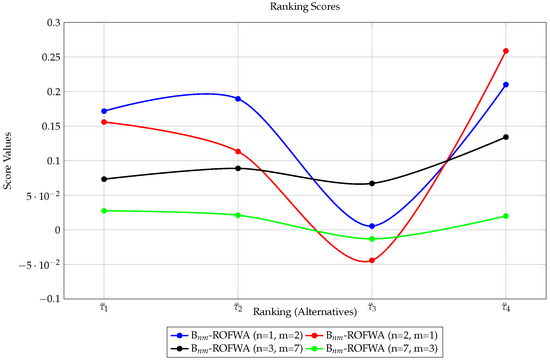
Figure 11.
Ranking results of -ROFWA operators for different values of m,n.
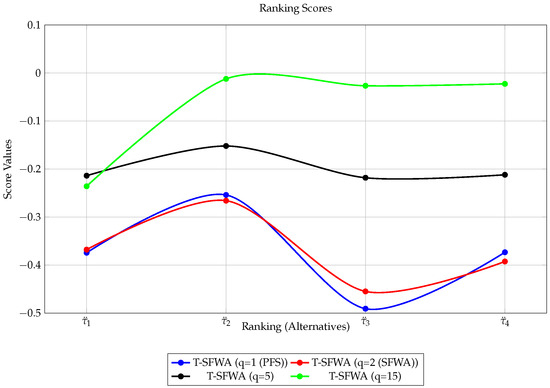
Figure 12.
Ranking results of T-SFWA operators for different values of q.
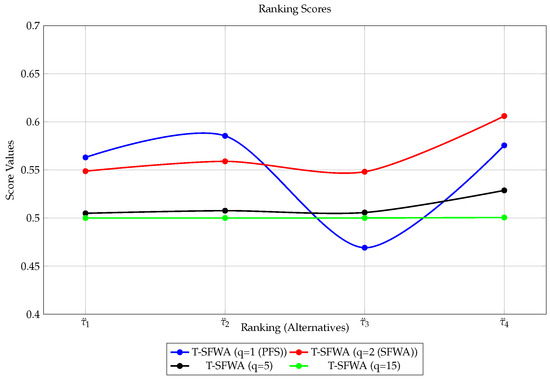
Figure 13.
Ranking results of T-SFWA operators for different values of q.

Table 19.
A comparison between the proposed method and existing methods.
9. Conclusions
In this work, we define a new notion, named bipolar pqr-spherical fuzzy sets (SFS), which is a combination of bipolar fuzzy sets and pqr-spherical fuzzy sets. Then, we investigate some basic properties of FSs, including the basic operational laws, complement operation, union operation, and intersection operation. This new framework allows for a more nuanced representation of uncertainty by accounting for different degrees of membership, non-membership, and neutrality, in addition to bipolarity. This adaptability of bipolar pqr-SFS has proven to be immensely valuable in intricate decision-making processes that involve evaluating both affirmative and adverse perceptions. Its utility in multi-criteria group decision-making problems has been demonstrated, and it has been shown that this framework is well-suited for capturing the complexities of bipolar judgmental reasoning during the decision-making process. This has been conducted by using two algorithms—the first one is referred to as the `technique for order of preference by similarity to ideal solution’ (TOPSIS) and the second one involves using the proposed operators themselves in the SF context, as well as providing a numerical example, which demonstrates the usefulness of the proposed set. Targeted applications were developed in the multi-criteria decision-making field to address problems in the SF environment using the two aforementioned aggregation operators. Additionally, a comparative study was used to show the applicability and viability of the proposed approach.
Future works will be applied with more decision-making methods, like VIKOR. In addition, a few other aggregation operators can be introduced to enhance the existing approaches owing to the generation of a more precise ranking outcome.
Author Contributions
Conceptualization, Z.A.A. and H.F.M.S.; methodology, Z.A.A., H.F.M.S. and B.A.A.; formal analysis, Z.A.A., H.F.M.S., A.I.A. and R.A.M.; investigation, H.F.M.S., A.I.A., R.A.M. and B.A.A.; writing—original draft preparation, Z.A.A. and H.F.M.S.; writing—review and editing, Z.A.A., H.F.M.S., A.I.A. and R.A.M.; funding acquisition, A.I.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Acknowledgments
The researchers would like to thank the Deanship of Graduate Studies and Scientific Research at Qassim University for the financial support (QU-APC-2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Proof
Proof of proposition 1.
We shall only prove the first statement; the others are straightforward to conclude.
(1) Suppose and . Therefore, , , , , , , and , , , , , and . Now, we have the following:
Summing up all of the implications above yields . □
Proof of proposition 2.
(1) Starting from LHS, we have the following:
The other parts are similar. □
Proof of Theorem 2.
We prove that 1 and 3, and the proofs of 2 and 4 are similar, respectively. To prove 1, consider two SFSs, and and ,
To prove 3, for and ,
□
Proof of Theorem 3.
Equation (2) is verified by using the principle of mathematical induction. For , we have the following:
Hence, for , the conclusion is true.
Now, it is assumed that the result is true for ,
We now show that the result is true for :
Therefore, for , the statement is true. Thus, (2) is guaranteed to hold true for all natural numbers through the process of mathematical induction. □
Proof of Theorem 4.
By assumption, for each j, , so we have the following:
Since , we have the following:
□
Proof of Theorem 5.
Let and be two SFNs. Since , then ,
This fulfills the inequality for the initial components of and . We use the same method for every other component.
Since ,
Since ,
Since , then ,
Since , we have the following:
Since , we have the following:
Based on the analysis above, we have the following:
□
Proof of Theorem 6.
For the first component for , if and , and notice that , we have the following:
which satisfies the inequality for the first component of SFWA.
We now apply this process to the remaining components. If and , then we have the following:
If and , then we have the following:
If and , then we have the following:
If and , we have the following:
If and , we have the following:
From the above investigation, by satisfying inequality 3 for all components of for , we obtain the following:
□
References
- Zadeh, L. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar]
- Yager, R.R. Pythagorean fuzzy subsets. In Proceedings of the 2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 24–28 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 57–61. [Google Scholar]
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2016, 25, 1222–1230. [Google Scholar] [CrossRef]
- Dounis, A.; Stefopoulos, A. Intelligent Medical Diagnosis Reasoning Using Composite Fuzzy Relation, Aggregation Operators and Similarity Measure of q-Rung Orthopair Fuzzy Sets. Appl. Sci. 2023, 13, 12553. [Google Scholar] [CrossRef]
- Seikh, M.R.; Mandal, U. Multiple attribute group decision making based on quasirung orthopair fuzzy sets: Application to electric vehicle charging station site selection problem. Eng. Appl. Artif. Intell. 2022, 115, 105299. [Google Scholar] [CrossRef]
- Ibrahim, H.Z.; Alshammari, I. n,m-Rung orthopair fuzzy sets with applications to multicriteria decision making. IEEE Access 2022, 10, 99562–99572. [Google Scholar]
- Cuong, B.C.; Kreinovich, V. Picture fuzzy sets. J. Comput. Sci. Cybern. 2014, 30, 409–420. [Google Scholar]
- Mahmood, T.; Ullah, K.; Khan, Q.; Jan, N. An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 2019, 31, 7041–7053. [Google Scholar]
- Kutlu Gündoğdu, F.; Kahraman, C. Spherical fuzzy sets and spherical fuzzy TOPSIS method. J. Intell. Fuzzy Syst. 2019, 36, 337–352. [Google Scholar]
- Ullah, K.; Garg, H.; Mahmood, T.; Jan, N.; Ali, Z. Correlation coefficients for T-spherical fuzzy sets and their applications in clustering and multi-attribute decision making. Soft Comput. 2020, 24, 1647–1659. [Google Scholar]
- Ali, J.; Naeem, M. r,s,t-spherical fuzzy VIKOR method and its application in multiple criteria group decision making. IEEE Access 2023, 11, 46454–46475. [Google Scholar] [CrossRef]
- Rahim, M.; Amin, F.; Tag Eldin, E.M.; Khalifa, A.E.W.; Ahmad, S. p,q-Spherical fuzzy sets and their aggregation operators with application to third-party logistic provider selection. J. Intell. Fuzzy Syst. 2024, 46, 505–528. [Google Scholar] [CrossRef]
- Rahim, M.; Ahmad, S.; Bajri, S.A.; Alharbi, R.; Khalifa, H.A.E.W. Confidence Levels-Based p,q,r–Spherical Fuzzy Aggregation Operators and Their Application in Selection of Solar Panels. IEEE Access 2024, 12, 57863–57878. [Google Scholar] [CrossRef]
- Kang, L.; Khan, S.; Rahim, M.; Shah, K.; Abdeljawad, T. Development p,q,r–Spherical Fuzzy Einstein Aggregation Operators: Application in Decision-Making in Logo Design. IEEE Access 2024, 12, 68393–68409. [Google Scholar] [CrossRef]
- Karaaslan, F.; Karamaz, F. Interval-valued (p,q,r)-spherical fuzzy sets and their applications in MCGDM and MCDM based on TOPSIS method and aggregation operators. Expert Syst. Appl. 2024, 255, 124575. [Google Scholar] [CrossRef]
- Ezhilmaran, D.; Sankar, K. Morphism of bipolar intuitionistic fuzzy graphs. J. Discret. Math. Sci. Cryptogr. 2015, 18, 605–621. [Google Scholar] [CrossRef]
- Mohana, K.; Jansi, R. Bipolar Pythagorean fuzzy sets and their application based on multi-criteria decision-making problems. Int. J. Res. Advent Technol. 2018, 6, 3754–3764. [Google Scholar]
- Palanikumar, M.; Iampan, A. Novel approach to decision making based on type-II generalized fermatean bipolar fuzzy soft sets. Int. J. Innov. Comput. Inf. Control 2022, 18, 769–781. [Google Scholar]
- Li, J.; Yüksel, S.; Dınçer, H.; Mikhaylov, A.; Barykin, S.E. Bipolar q-ROF hybrid decision making model with golden cut for analyzing the levelized cost of renewable energy alternatives. IEEE Access 2022, 10, 42507–42517. [Google Scholar] [CrossRef]
- Ibrahim, H.Z. Multi-attribute group decision-making based on bipolar n,m-rung orthopair fuzzy sets. Granul. Comput. 2023, 8, 1819–1836. [Google Scholar] [CrossRef]
- Princy, R.; Mohana, K. Spherical bipolar fuzzy sets and its application in multi criteria decision making problem. J. New Theory 2019, 32, 58–70. [Google Scholar]
- Wang, H.; Saad, M.; Karamti, H.; Garg, H.; Rafiq, A. An Approach Toward Pattern Recognition and Decision-Making Using the Concept of Bipolar T-Spherical Fuzzy Sets. Int. J. Fuzzy Syst. 2023, 25, 2649–2664. [Google Scholar] [CrossRef]
- Riaz, M.; Garg, H.; Athar Farid, H.M.; Chinram, R. Multi-criteria decision making based on bipolar picture fuzzy operators and new distance measures. Comput. Model. Eng. Sci. 2021, 127, 771–800. [Google Scholar]
- Ashraf, S.; Abdullah, S.; Mahmood, T.; Ghani, F.; Mahmood, T. Spherical fuzzy sets and their applications in multi-attribute decision making problems. J. Intell. Fuzzy Syst. 2019, 36, 2829–2844. [Google Scholar]
- Senapati, T.; Yager, R.R. Fermatean fuzzy sets. J. Ambient Intell. Humaniz. Comput. 2020, 11, 663–674. [Google Scholar]
- Hwang, C.L.; Yoon, K. Methods for multiple attribute decision making. In Multiple Attribute Decision Making: Methods and Applications A State-of-the-Art Survey; Springer: Berlin/Heidelberg, Germany, 1981; Volume 186, pp. 58–191. [Google Scholar]
- Yoon, K. A reconciliation among discrete compromise solutions. J. Oper. Res. Soc. 1987, 38, 277–286. [Google Scholar]
- Hwang, C.L.; Lai, Y.J.; Liu, T.Y. A new approach for multiple objective decision making. Comput. Oper. Res. 1993, 20, 889–899. [Google Scholar]
- El Alaoui, M. Fuzzy TOPSIS: Logic, Approaches, and Case Studies; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Maldonado-Macías, A.; Alvarado, A.; García, J.L.; Balderrama, C.O. Intuitionistic fuzzy TOPSIS for ergonomic compatibility evaluation of advanced manufacturing technology. Int. J. Adv. Manuf. Technol. 2014, 70, 2283–2292. [Google Scholar]
- Junior, F.R.L.; Osiro, L.; Carpinetti, L.C.R. A comparison between Fuzzy AHP and Fuzzy TOPSIS methods to supplier selection. Appl. Soft Comput. 2014, 21, 194–209. [Google Scholar]
- Yilmaz, I.; Ecemis Yilmaz, H.K. A consensus framework for evaluating dispute resolution alternatives in international law using an interval-valued type-2 fuzzy TOPSIS approach. Appl. Sci. 2024, 14, 11046. [Google Scholar] [CrossRef]
- Jin, J.; Zhao, P.; You, T. Picture fuzzy TOPSIS method based on CPFRS model: An application to risk management problems. Sci. Program. 2021, 2021, 6628745. [Google Scholar] [CrossRef]
- Akram, M.; Shumaiza; Arshad, M. Bipolar fuzzy TOPSIS and bipolar fuzzy ELECTRE-I methods to diagnosis. Comput. Appl. Math. 2020, 39, 1–21. [Google Scholar] [CrossRef]
- Calvo, T.; Mayor, G.; Mesiar, R. Aggregation operators, Studies Fuzziness Soft Computing 97. Phys. Heidelb. 2002. [Google Scholar]
- Grabisch, M.; Marichal, J.L.; Mesiar, R.; Pap, E. Aggregation Functions, Cambridge University Press. In Proceedings of the 2008 6th International Symposium on Intelligent Systems and Informatics, Subotica, Serbia, 26–27 September 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–7. [Google Scholar]
- Yager, R.R.; Kacprzyk, J. The Ordered Weighted Averaging Operators: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Xu, Z.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Xu, Z. Intuitionistic fuzzy aggregation operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar]
- Wei, G. Picture fuzzy aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2017, 33, 713–724. [Google Scholar] [CrossRef]
- Garg, H.; Ullah, K.; Mahmood, T.; Hassan, N.; Jan, N. T-spherical fuzzy power aggregation operators and their applications in multi-attribute decision making. J. Ambient Intell. Humaniz. Comput. 2021, 12, 9067–9080. [Google Scholar] [CrossRef]
- Akram, M.; Dudek, W.A.; Ilyas, M.F. Group decision making based on Pythagorean fuzzy TOPSIS method. Int. J. Intell. Syst. 2019, 34, 1455–1475. [Google Scholar] [CrossRef]
- Gul, M.; Lo, H.W.; Yucesan, M. Fermatean fuzzy TOPSIS-based approach for occupational risk assessment in manufacturing. Complex Intell. Syst. 2021, 7, 2635–2653. [Google Scholar] [CrossRef]
- Pınar, A.; Rouyendegh, B.D.; Özdemir, Y.S. q-Rung orthopair fuzzy TOPSIS method for green supplier selection problem. Sustainability 2021, 13, 985. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).