Mechanical Properties of Marble Under Triaxial and Cyclic Loading Based on Discrete Elements
Abstract
1. Introduction
2. Laboratory Tests on Marble
2.1. Test Materials and Equipment
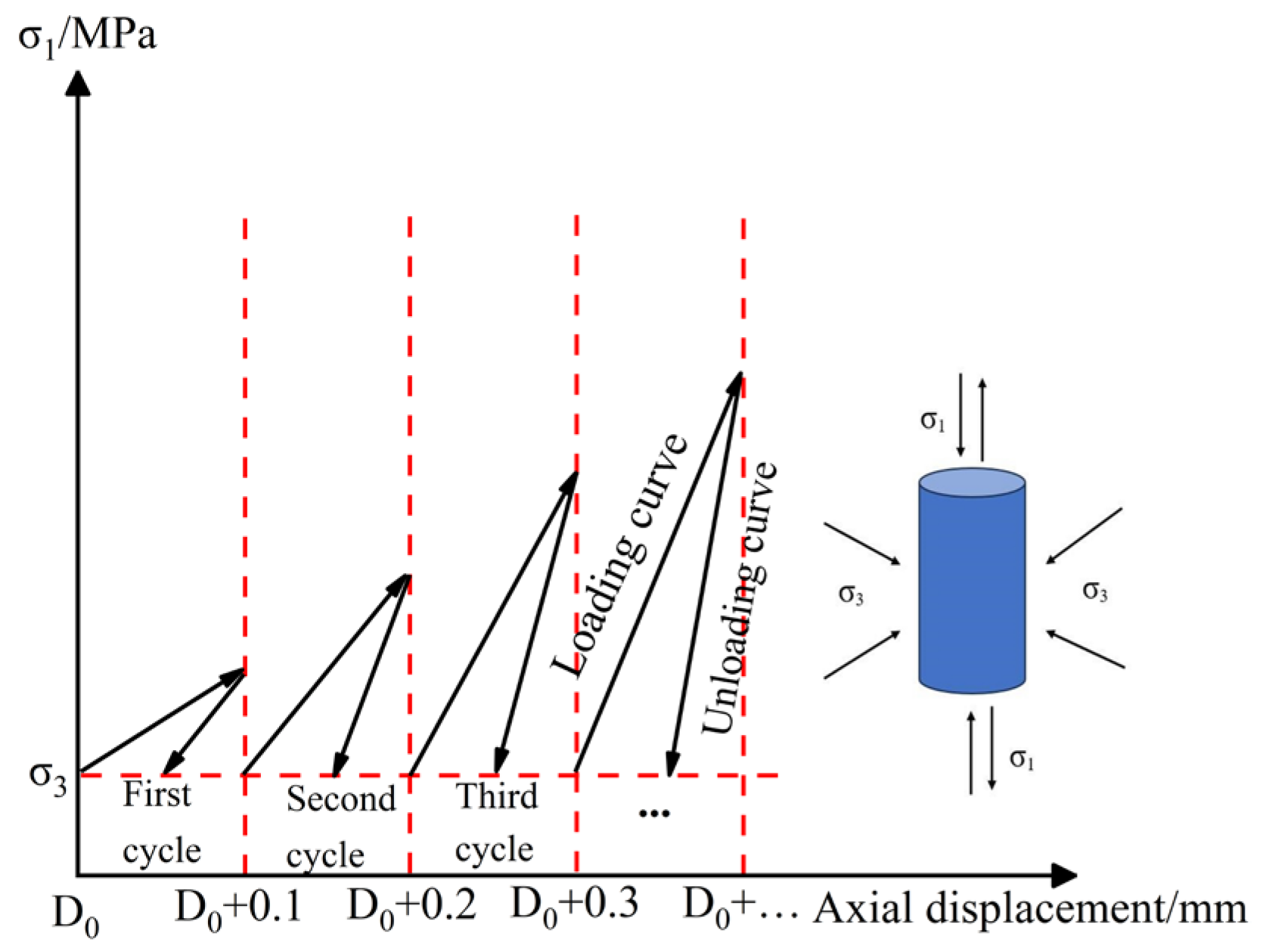
2.2. Test Scheme
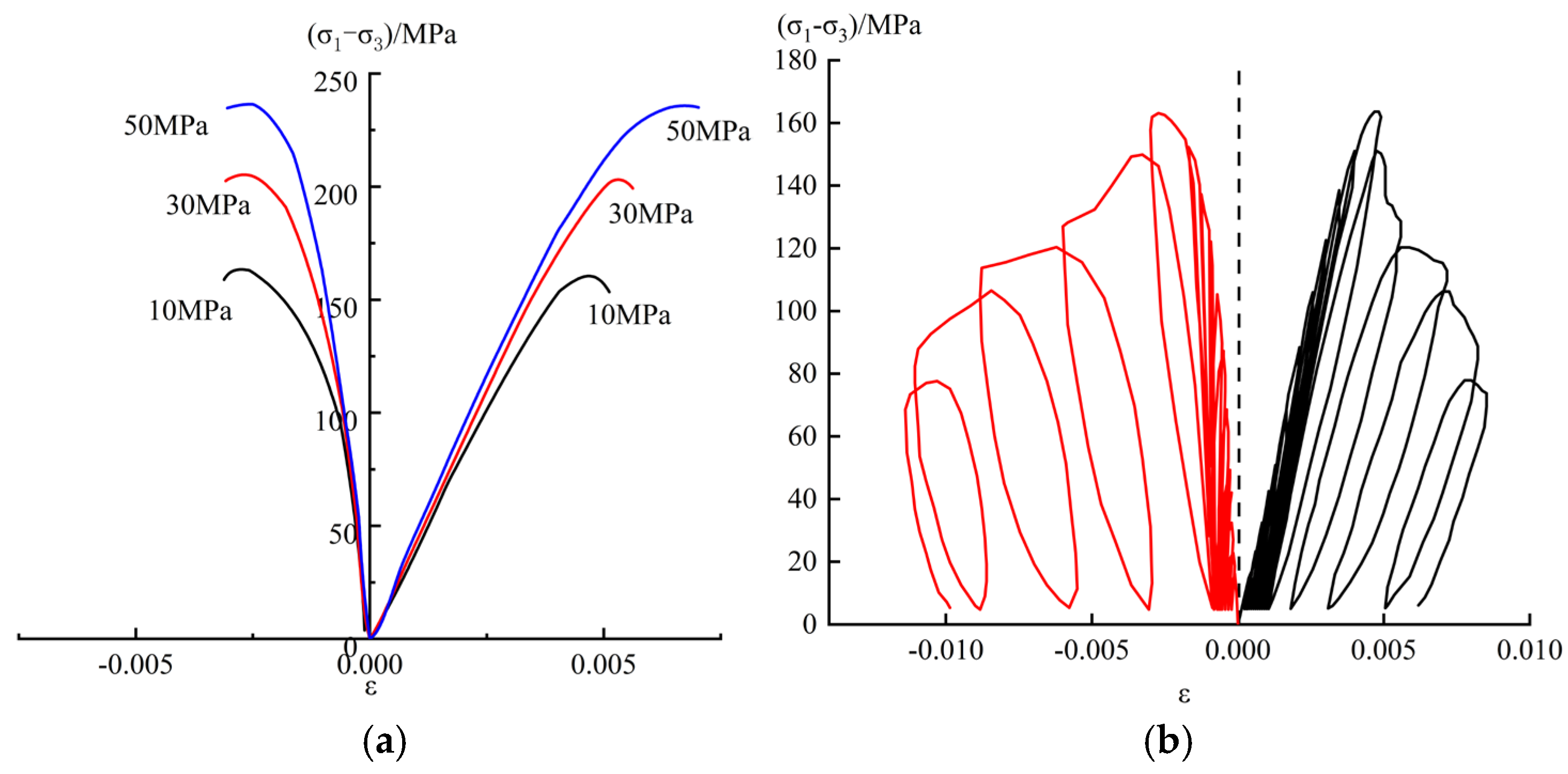
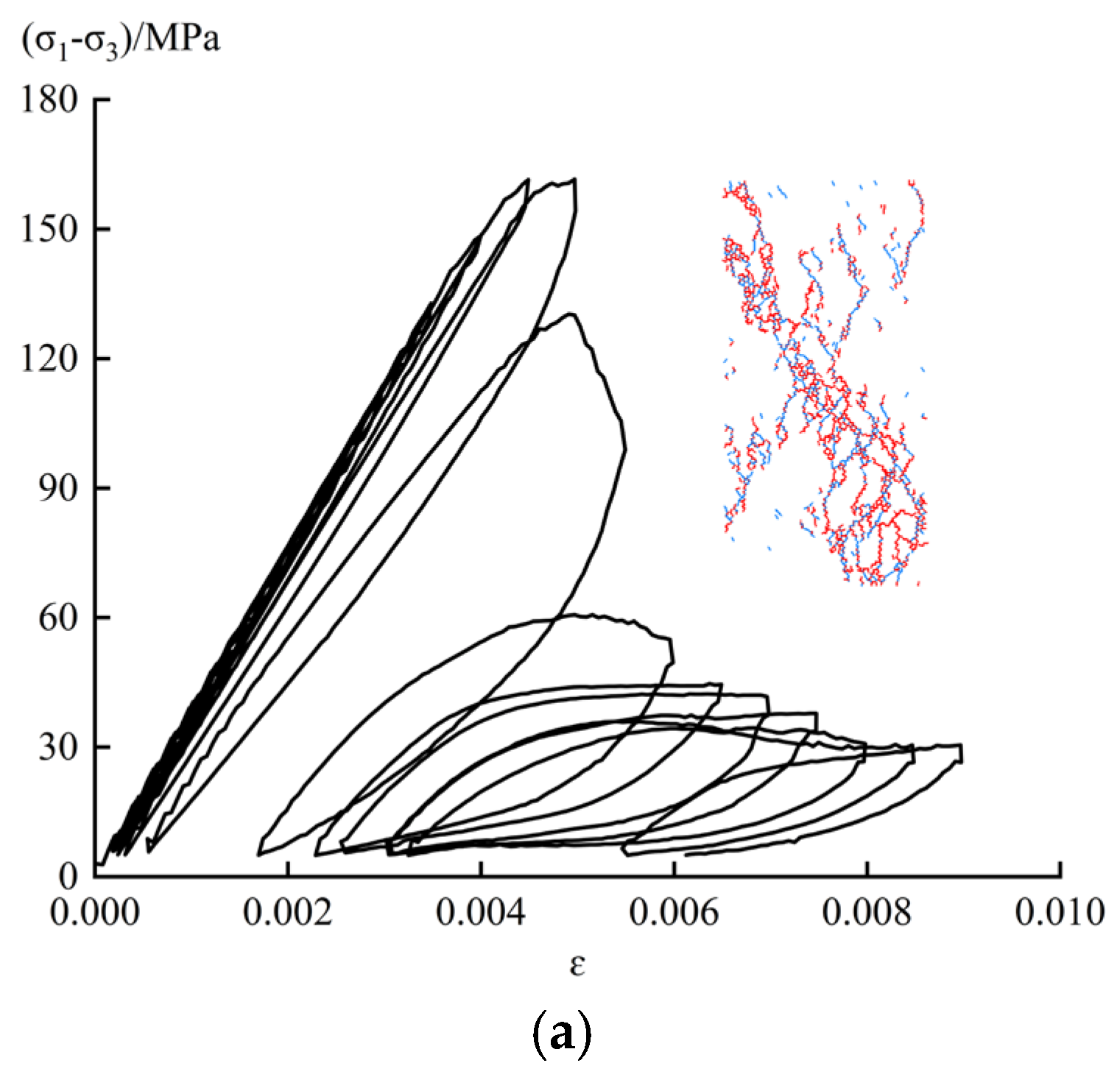
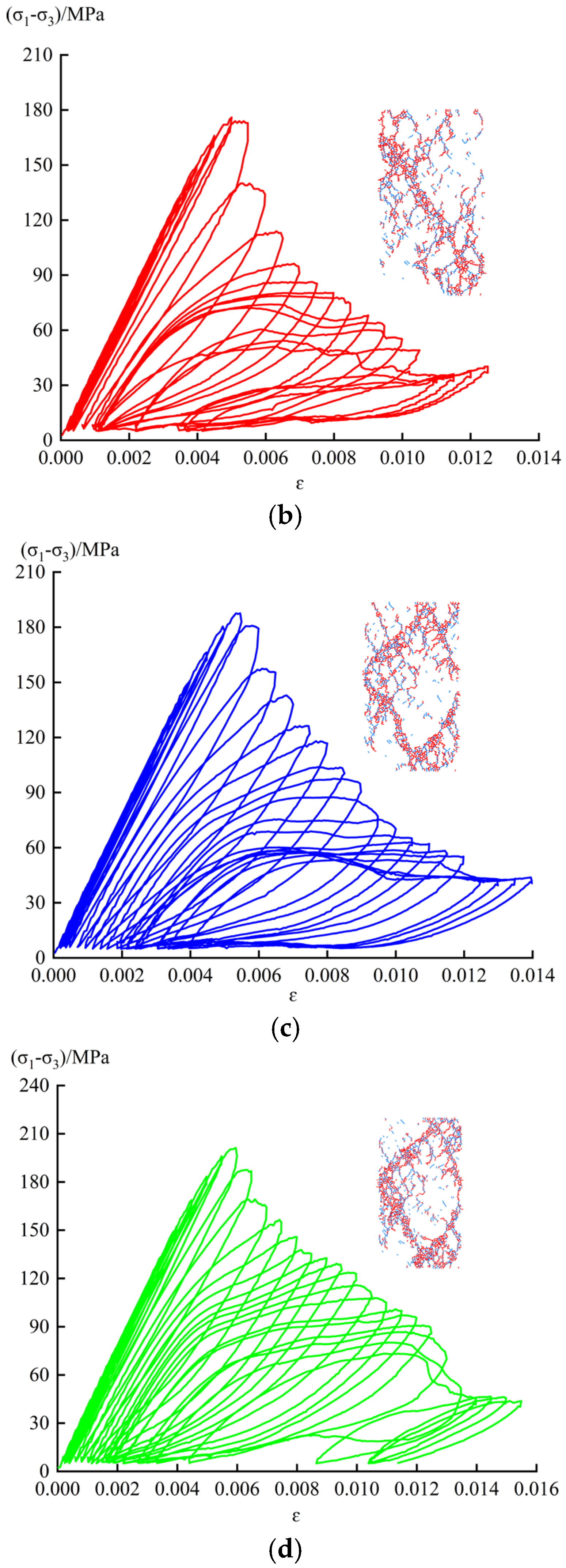
2.3. Experimental Results
3. Model Building and Parameter Verification
3.1. Numerical Modeling
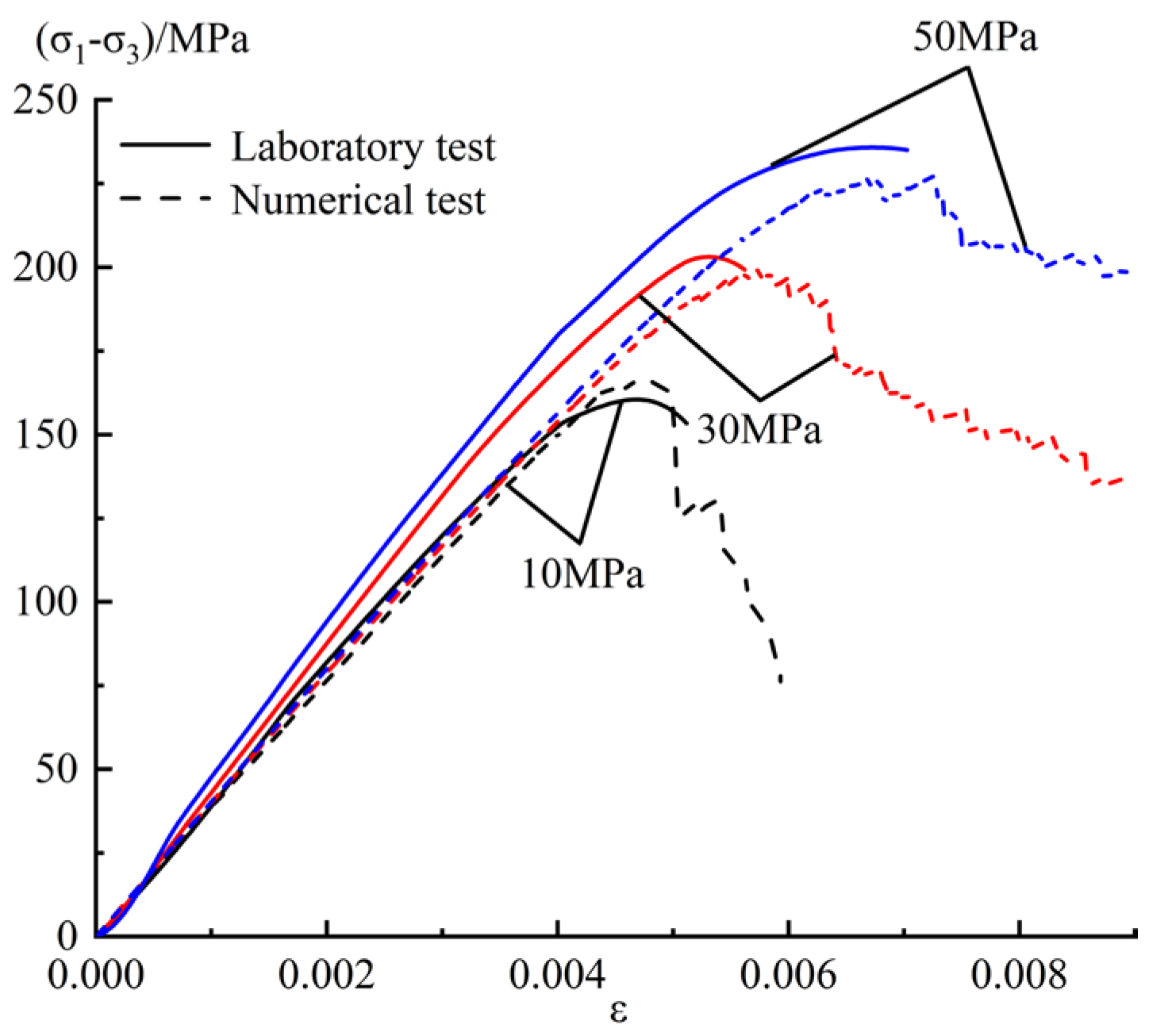
3.2. Parameter Verification
4. Numerical Simulation
4.1. Numerical Test Loading Scheme
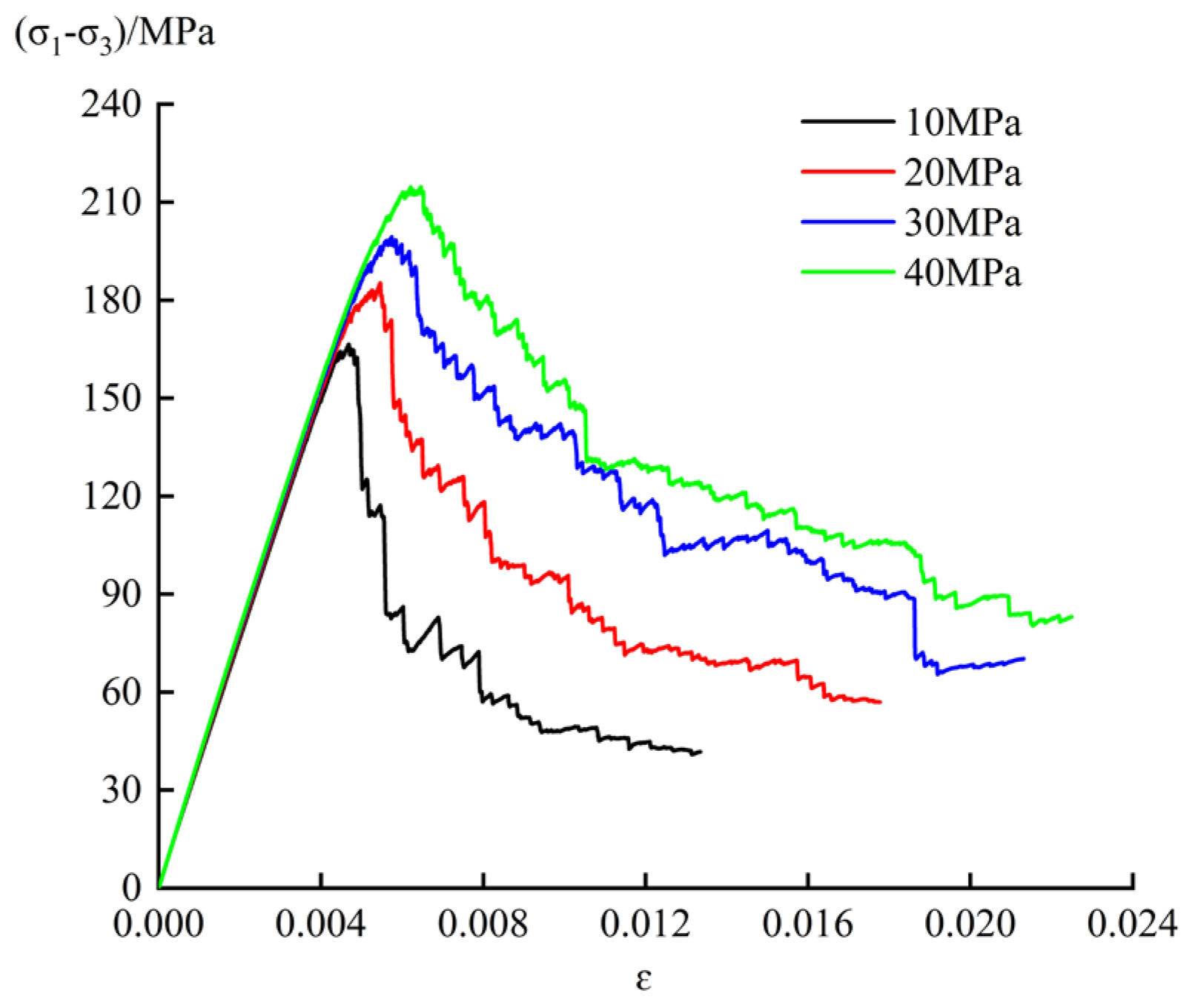
4.2. Strength and Deformation Characteristics
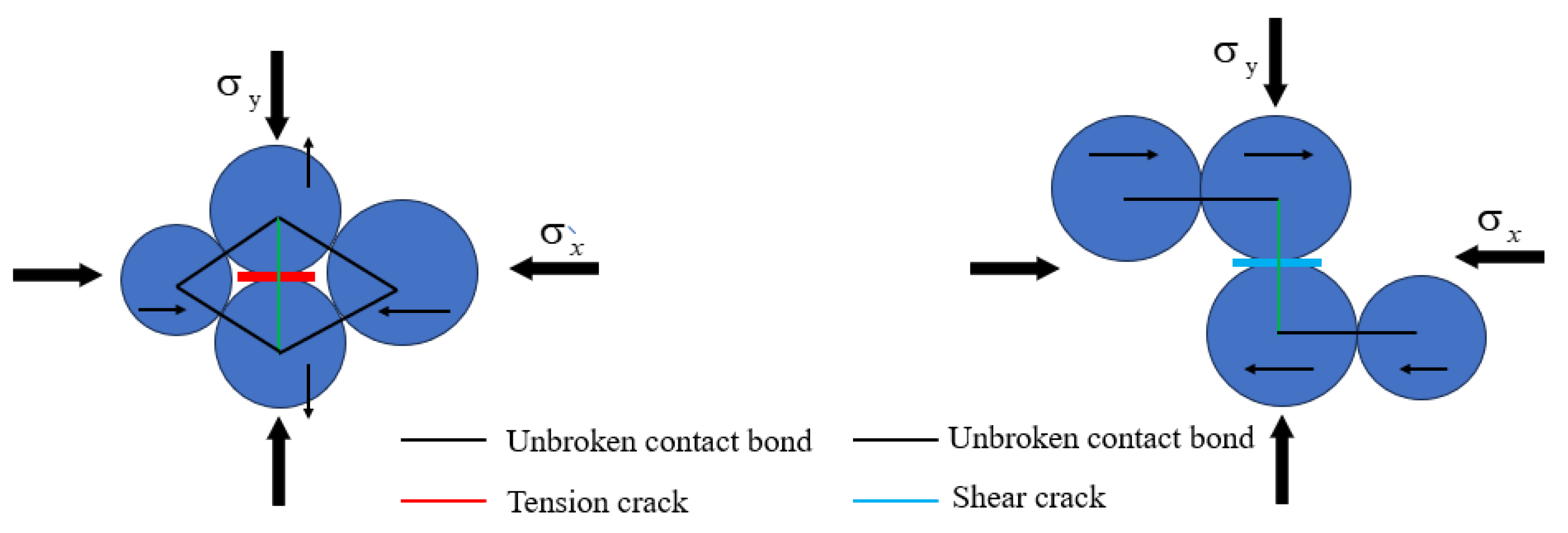
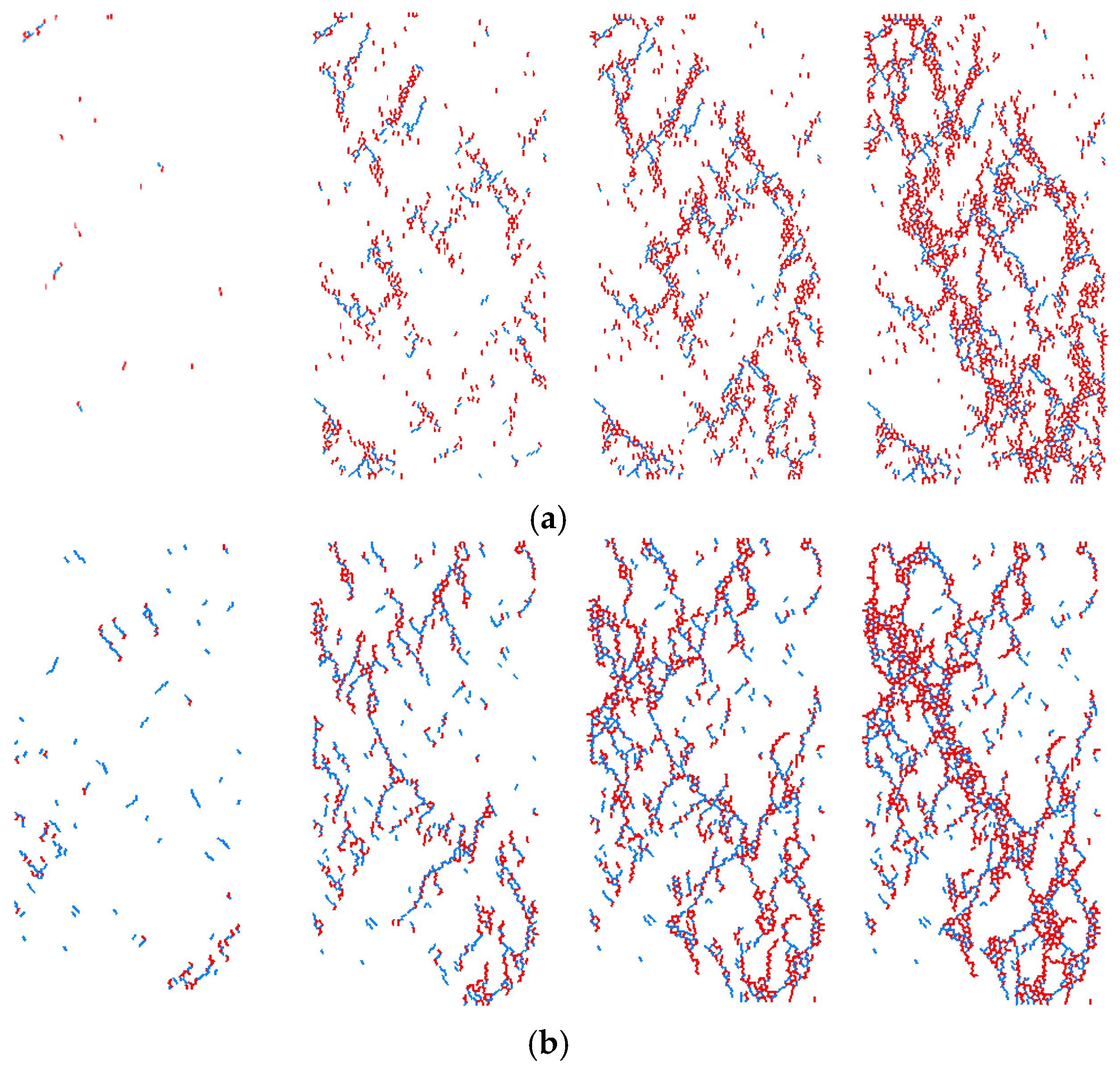
5. Micromechanical Response and Analysis
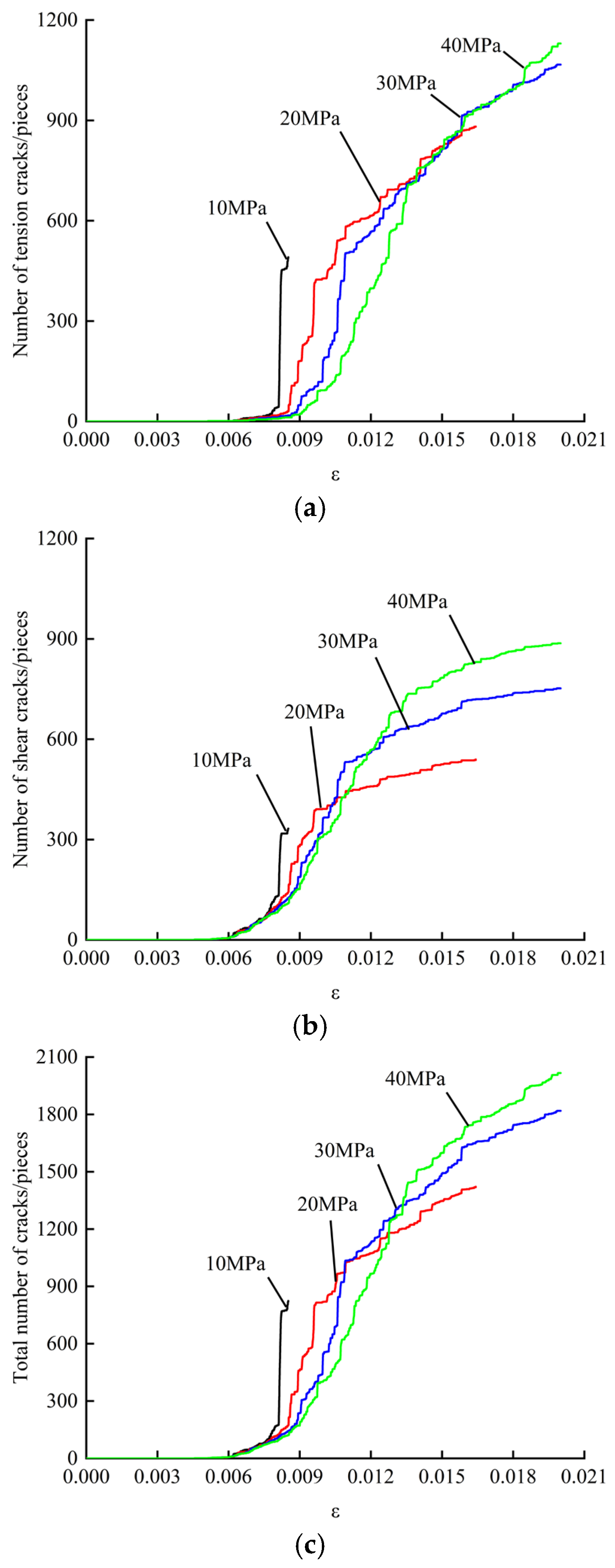
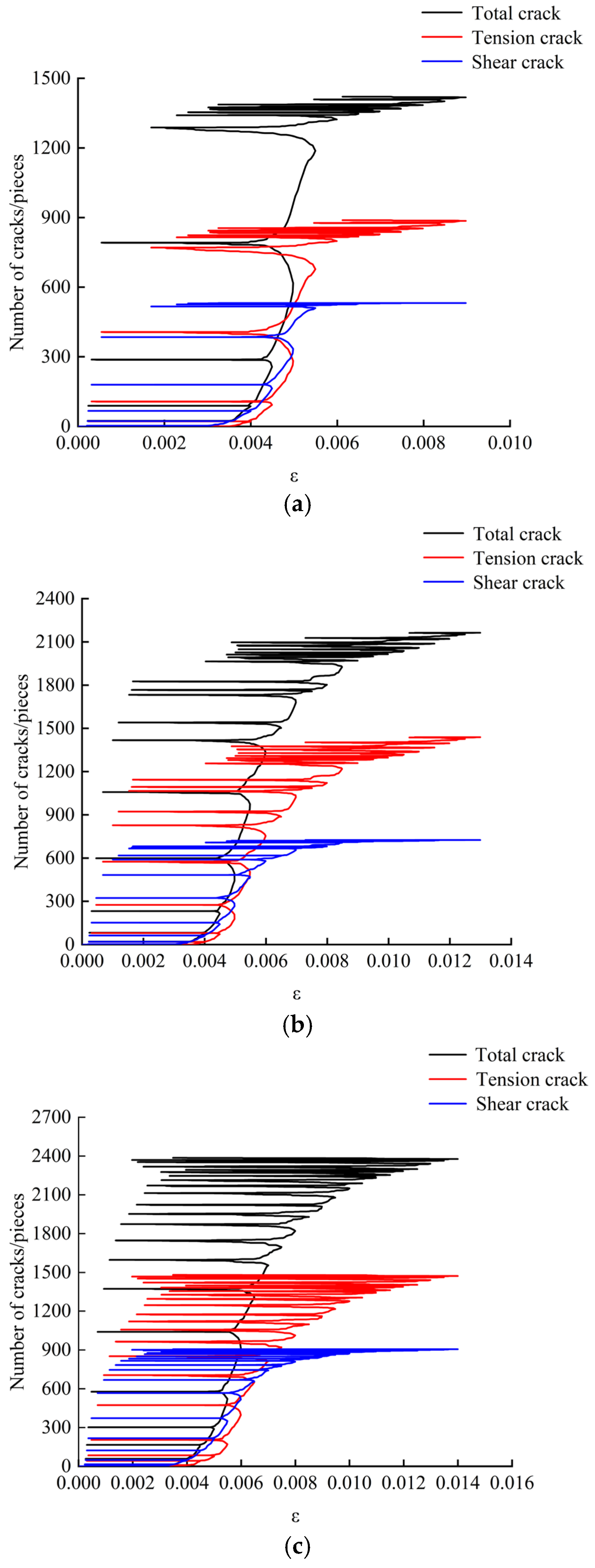
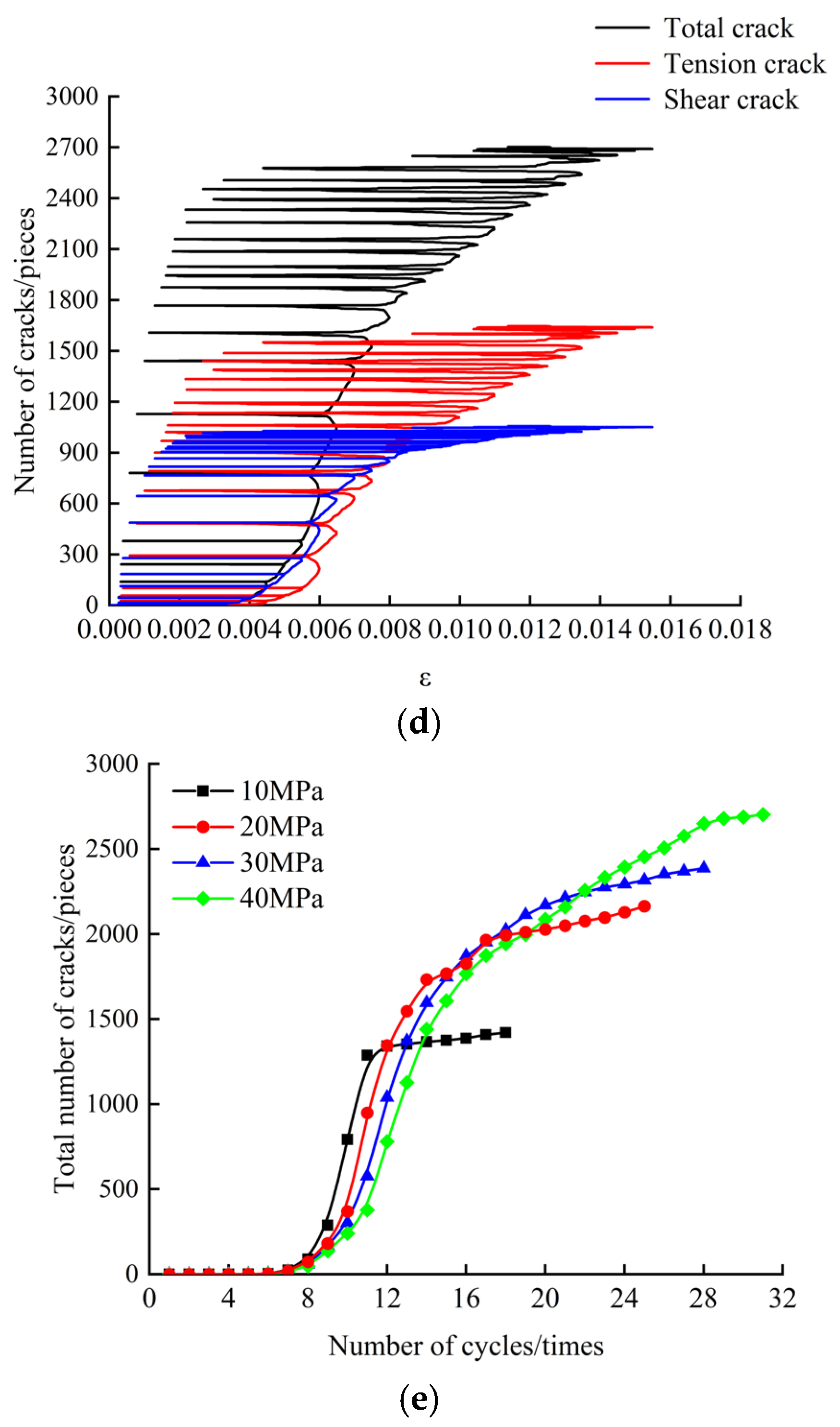
5.1. Microcrack Number Evolution
5.2. Microcrack Angle Distribution
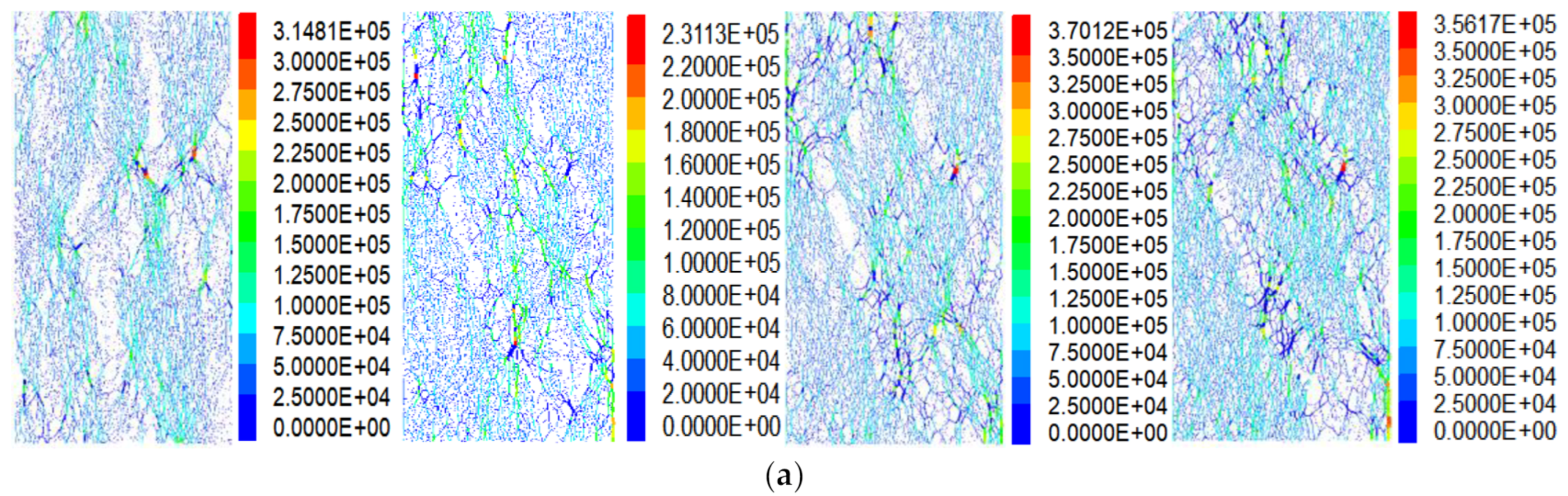
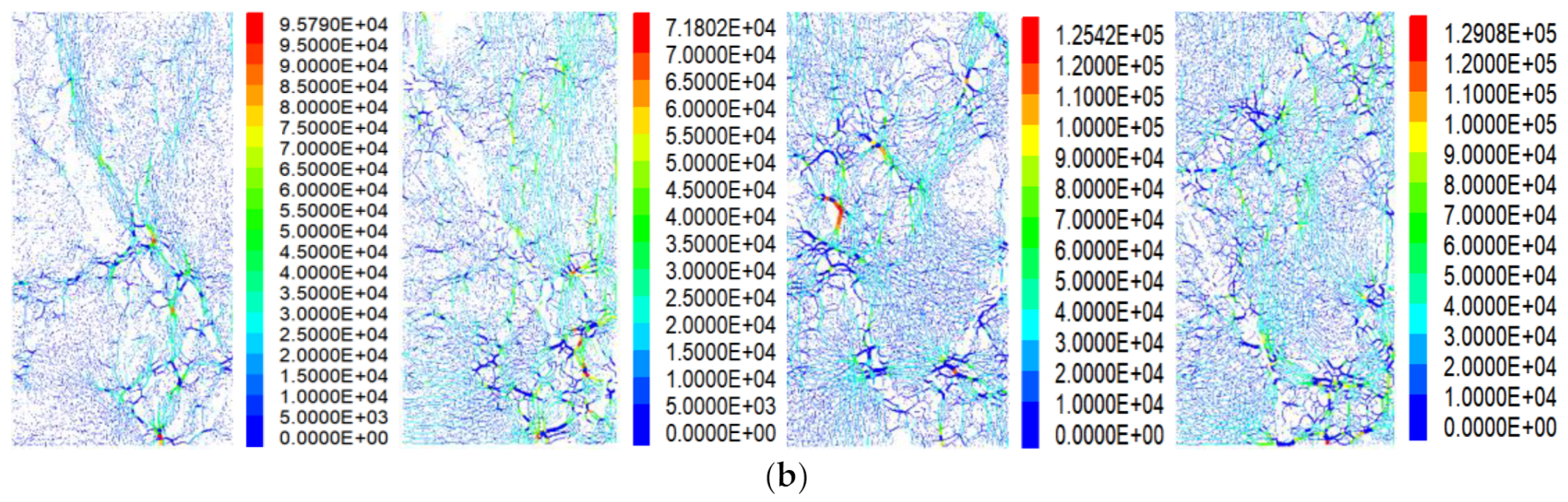
5.3. Microscopic Force Field Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lou, C.D.; Zhang, Z.P.; Wu, S.Y.; Zhou, J.F.; Peng, Y.; Ai, T.; Liu, Y.; Zhang, R.; Ren, L. Study on mechanical properties and energy evolution of Jinping deep buried marble. Hydro-Sci. Eng. 2022, 87–96. [Google Scholar]
- Wang, Q.; Wang, Z.Q.; Cheng, Y.Q.; Li, C.H. Experimental study on deep marble deformation characteristics and energy evolution under high circumferential pressures. Prot. Eng. 2023, 45, 7–15. [Google Scholar]
- Jiang, Q.; Fei, X.T.; Li, S.J.; Su, G.S.; Xiao, Y.X. Cracking-restraint design method for large underground caverns with hard rock under high geostress condition and its practical application. Chin. J. Rock Mech. Eng. 2019, 38, 1081–1101. [Google Scholar]
- Xie, H.P. Research Framework and Anticipated Results of Deep Rock Mechanics and Mining Theory. Adv. Eng. Sci. 2017, 49, 1–16. [Google Scholar]
- Zhu, L.; Pei, X.J.; Cui, S.H.; Liang, Y.F.; Luo, L.G. Experimental study on cycle loading and unloading damage and strength characteristics of rocks with vein defects. Chin. J. Rock Mech. Eng. 2019, 38, 900–911. [Google Scholar]
- Li, J.T.; Xiao, F.; Ma, Y.P. Deformation Damage and Energy Evolution of Red Sandstone under Uniaxial Cyclic loading. J. Hunan Univ. (Nat. Sci.) 2020, 47, 139–146. [Google Scholar]
- Liu, Z.Y.; Dong, X.; Zhang, X.Y. Experimental study on mechanical properties of bedding coal and rock under graded cyclic loading. Chin. J. Rock Mech. Eng. 2021, 40 (Suppl. S1), 2593–2602. [Google Scholar]
- Wang, W.; Wang, T.; Xiong, D.F.; Cheng, L.; Zhang, H.Y.; Zhu, Q.Z. Experiment of Fractal Characteristics of Acoustic Emission of Sandstone Under Triaxial Cyclic loading. Adv. Eng. Sci. 2022, 54, 90–100. [Google Scholar]
- Chen, X.; Xiao, Y.; Tang, M.G.; Jiao, T.; Zhang, F. Experimental study on deformation permeability and AE characteristics of sandstone under multi-stage cyclic loading with a constant amplitude. Chin. J. Rock Mech. Eng. 2024, 43, 1923–1935. [Google Scholar]
- Meng, Q.B.; Liu, J.F.; Li, R.; Hai, P.; Chen, Y.L. Experimental Study on Rock Strength and Deformation Characteristics Under Triaxial Cyclic loading Conditions. Rock Mech. Rock Eng. 2021, 54, 777–797. [Google Scholar] [CrossRef]
- Shirani Faradonbeh, R.; Taheri, A.; Karakus, M. Failure Behavior of a Sandstone Subjected to the Systematic Cyclic Loading: Insights from the Double-Criteria Damage-Controlled Test Method. Rock Mech. Rock Eng. 2021, 54, 5555–5575. [Google Scholar] [CrossRef]
- Geranmayeh Vaneghi, R.; Ferdosi, B.; Okoth, A.D.; Kuek, B. Strength degradation of sandstone and granodiorite under uniaxial cyclic loading. J. Rock Mech. Geotech. Eng. 2018, 10, 117–126. [Google Scholar] [CrossRef]
- Naderloo, M.; Kumar, K.R.; Hernandez, E.; Hajibeygi, H.; Barnhoorn, A. Experimental and numerical investigation of sandstone deformation under cycling loading relevant for underground energy storage. J. Energy Storage 2023, 64, 107198. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, Z.Q.; Fang, C.; Cong, B.T. Three-dimensional Particle Flow Simulation on Macro-micro Mechanical Properties of Granite under Triaxial Cyclic loading. Min. Res. Dev. 2019, 39, 52–58. [Google Scholar]
- Zhou, X.; Li, J.T. Crack propagation law of brittle rock mass under cyclic loading. J. Cent. South Univ. (Sci. Technol.) 2020, 51, 724–731. [Google Scholar]
- Zhao, B.; Xu, T.; Yang, S.Q.; Fu, T.F. Experimental and numerical study of fatigue damage of highly stressed rocks under cyclic loading. J. Cent. South Univ. (Sci. Technol.) 2021, 52, 2725–2735. [Google Scholar]
- Lee, H.; Jeon, S. An experimental and numerical study of fracture coalescence in pre-cracked specimens under uniaxial compression. J. Solids Struct. 2011, 48, 979–999. [Google Scholar] [CrossRef]
- Zhou, Y.Q.; Sheng, Q.; Li, N.N.; Fu, X.D. Numerical investigation of the deformation properties of rock materials subjected to cyclic compression by the finite element method. Soil Dyn. Earthq. Eng. 2019, 126, 105795. [Google Scholar] [CrossRef]
- Wang, Z.C.; Li, S.C.; Qiao, L.P.; Zhang, Q.S. Finite element analysis of the hydro-mechanical behavior of an underground crude oil storage facility in granite subject to cyclic loading during operation. Int. J. Rock Mech. Min. Sci. 2015, 73, 70–81. [Google Scholar] [CrossRef]
- Cerfontaine, B.; Charlier, R.; Collin, F.; Taiebat, M. Validation of a New Elastoplastic Constitutive Model Dedicated to the Cyclic Behavior of Brittle Rock Materials. Rock Mech. Rock Eng. 2017, 50, 2677–2694. [Google Scholar] [CrossRef]
- Zhu, J.B. The ‘Rock Testing Regulations for Water Conservancy and Hydropower Engineering’ (SL/T 264-2020), revised under the auspices of the Yangtze Academy of Sciences, was promulgated and implemented. J. Yangtze River Sci. Res. Inst. 2020, 37, 2. [Google Scholar]
- Zhang, K.; Zhou, H.; Feng, X.T.; Shao, J.F.; Yang, Y.S.; Zhang, Y.G. Experimental research on elastoplastic coupling character of marble. Rock Soil Mech. 2010, 8, 2425–2434. [Google Scholar]
- Zhang, X.W.; Xu, J.H.; Sui, L.; Zhang, H.W.; Wang, Q. Mechanical properties evolution of thermally damaged limestone under triaxial cyclic loading and unloading. J. Min. Strat. Control Eng. 2022, 4, 87–98. [Google Scholar]
- Liu, X.P.; Jiang, Q.; Li, S.J.; Xin, J.; Chen, P.F. Energy characteristics of progressive damage of Jinping marble under cyclic loading and unloading. Rock Soil Mech. 2024, 45, 2373–2386. [Google Scholar]
- Zhang, L.; Li, B.; Zhu, B.L.; Luo, B. Loading and Unloading Mechanical Properties and Energy Evolution Mechanism of Red-Bed Mudstone. J. Southwest Jiaotong Univ. 2023, 58, 592–602+612. [Google Scholar]
- Tomac, I.; Gutierrez, M. Coupled hydro-thermo-mechanical modeling of hydraulic fracturing in quasi-brittle rocks using BPM-DEM. J. Rock Mech. Geotech. Eng. 2017, 9, 92–104. [Google Scholar]
- Wang, H.B.; Ma, Z.; Wu, L.T.Y.; Fan, Z.P.; Wang, C.G. Calibration method of mesoscopic parameters using BP neural network and Burgers model. Trans. Chin. Soc. Agric. Eng. 2024, 38, 152–161. [Google Scholar]
- Tian, W.L.; Yang, S.Q.; Fang, G. Particle flow simulation on mechanical behavior of coal specimen under triaxial cyclic loading. J. China Coal Soc. 2016, 41, 603–610. [Google Scholar]
- Zhen, Z.G.; Yang, S.Q.; Chen, C.P.; Tian, W.L.; Qian, J.H.; Li, X. Simulation Study on Mechanical Behavior of Bedding Yellow Sandstone Under Triaxial Cycling Loading-unloading. J. Basic Sci. Eng. 2023, 31, 731–740. [Google Scholar]
- Cho, N.; Martin, C.D.; Sego, D.C.; Venturi, N. A clumped particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Liu, J.; Li, J.T. Analysis on meso-damage characteristics of marble under triaxial cyclic loading based on particle flow simulation. J. Cent. South Univ. (Sci. Technol.) 2018, 49, 2797–2803. [Google Scholar]
- Zhen, Z.G.; Sui, B.W.; Chen, C.P.; Yang, S.Q.; Xu, J. Experimental and 3D DEM Simulation on the Triaxial Compression Mechanical Behavior of Limestone. Chin. J. Undergr. Space Eng. 2023, 19 (Suppl. S2), 610–616. [Google Scholar]
- Peng, J.; Rong, G.; Cai, M.; Peng, K. Determination of residual strength of rocks by a brittle index. Rock Soil Mech. 2015, 36, 403–408. [Google Scholar]
- Zhao, J.; Guo, G.T.; Xu, D.P.; Huang, X.; Hu, S.; Xia, Y.L.; Zhang, D. Experimental study of deformation and failure characteristics of deeply-buried hard rock under triaxial and cyclic loading stress paths. Rock Soil Mech. 2020, 41, 1521–1530. [Google Scholar]
- Yang, S.Q.; Ranjith, P.G.; Huang, Y.H.; Yin, P.F.; Jing, H.W.; Gui, Y.L.; Yu, Q.L. Experimental investigation on mechanical damage characteristics of sandstone under triaxial cyclic loading. Geophys. J. Int. 2015, 201, 662–682. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Zhao, Y.; Jiang, Y.H.; Zou, Y.; Cai, X.; Li, D.Y. Dynamic behavior of rock during its post failure stage in SHPB tests. Trans. Nonferrous Met. Soc. China 2017, 27, 184–196. [Google Scholar] [CrossRef]
- Yang, S.Q.; Dong, J.P.; Yang, J.; Yang, Z.; Huang, Y.H. An experimental investigation of failure mechanical behavior in cylindrical granite specimens containing two non-coplanar open fissures under different confining pressures. J. Cent. South Univ. 2022, 29, 1578–1596. [Google Scholar]
- Chen, B.R.; Feng, X.T.; Ming, H.J.; Zhou, H.; Zeng, X.H.; Feng, G.L.; Xiao, Y.X. Laws and Mechanisms of Rockburst Generation in Deeply Buried Tunnels: Time Lag Rockbursts. Chin. J. Rock Mech. Eng. 2012, 31, 561–569. [Google Scholar]
- Wang, Y.; Liu, X.H.; Hu, A.K.; Li, H.Y.; Qu, X. Crack Propagation Characteristics of Deep Marble Under Triaxial Compression. Adv. Eng. Sci. 2024, 56, 21–31. [Google Scholar]







| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Particle density/(kg·m−3) | 2700.00 | Porosity | 0.36 |
| Particle size ratio | 1.66 | Parallel bond radius factor | 1.00 |
| Minimum particle size/mm | 0.40 | Parallel bond modulus/GPa | 27.40 |
| Particle contact modulus/GPa | 27.40 | Parallel bond stiffness ratio | 3.20 |
| Particle contact stiffness ratio | 3.20 | Parallel bond normal strength/MPa | 78.00 |
| Friction coefficient | 0.30 | Parallel bond shear strength/MPa | 62.00 |
| Circumferential Pressures/MPa | Peak Strength/MPa | Peak Strain/% | Elasticity Modulus/GPa | |||
|---|---|---|---|---|---|---|
| Laboratory Test | Simulation Test | Laboratory Test | Simulation Test | Laboratory Test | Simulation Test | |
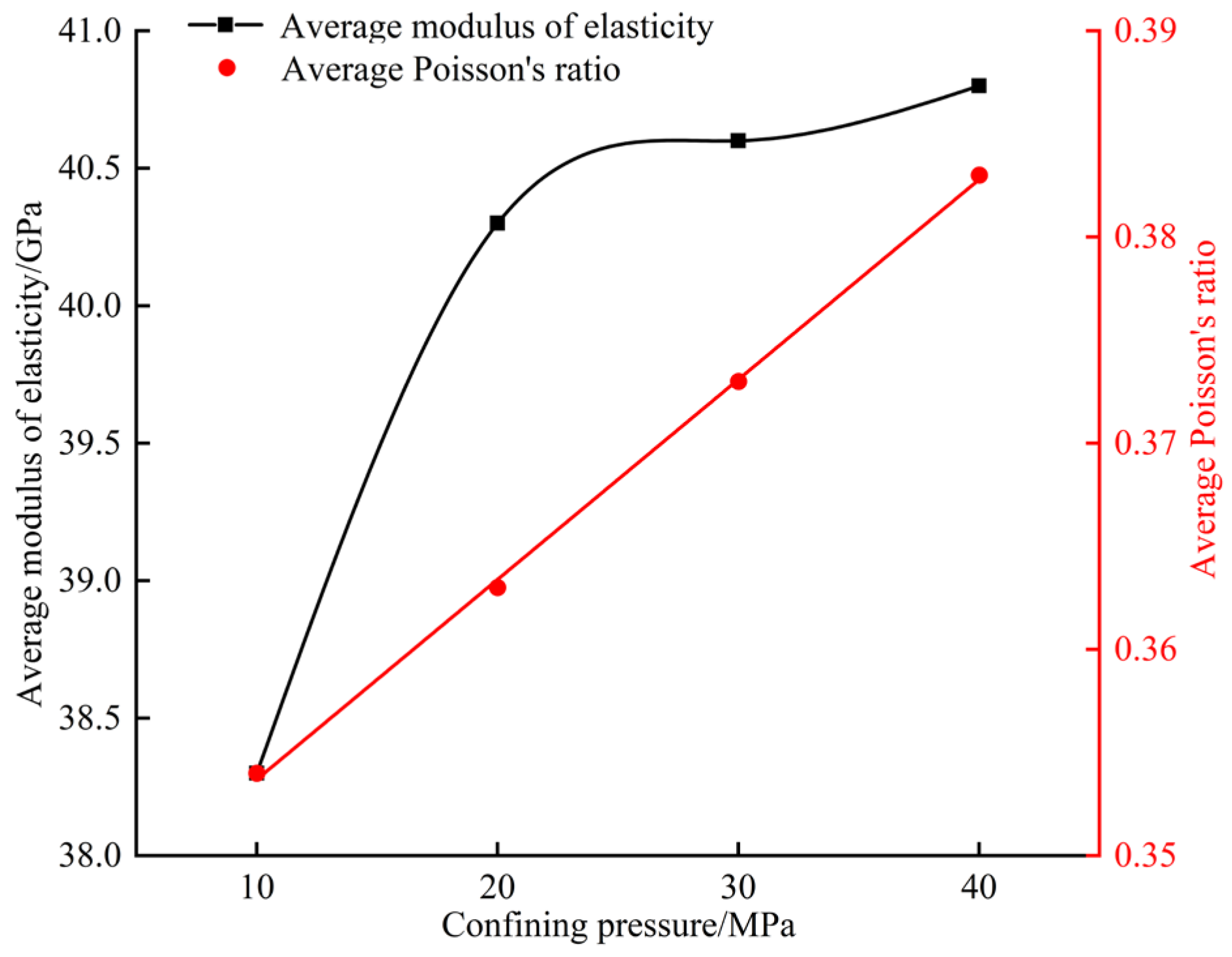
| 10 | 163.43 | 166.27 | 0.484 | 0.467 | 41.24 | 38.92 |
| 30 | 204.25 | 199.41 | 0.531 | 0.574 | 44.23 | 40.55 |
| 50 | 236.29 | 227.68 | 0.667 | 0.727 | 44.47 | 41.12 |
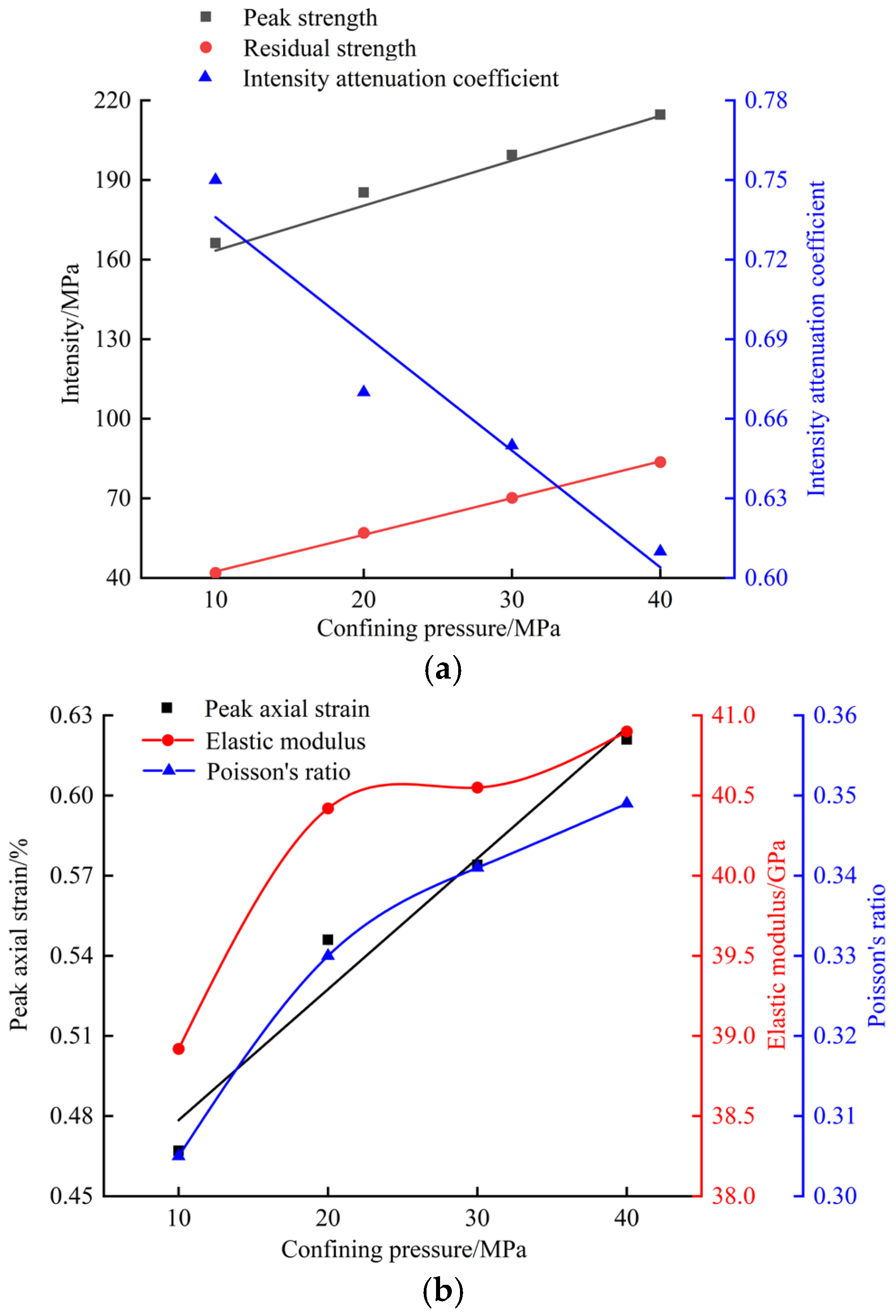
| Circumferential Pressures/MPa | Peak Strength/MPa | Residual Strength/MPa | Peak Axial Strain/% | Elastic Modulus/GPa | Poisson’s Ratio |
|---|---|---|---|---|---|
| 10 | 166.27 | 41.93 | 0.467 | 38.92 | 0.305 |
| 20 | 185.28 | 57.03 | 0.546 | 40.42 | 0.330 |
| 30 | 199.42 | 70.21 | 0.574 | 40.55 | 0.341 |
| 40 | 214.64 | 83.70 | 0.621 | 40.90 | 0.349 |
| Circumferential Pressures/MPa | Peak Strength/MPa | Residual Strength/MPa | Peak Axial Strain/% |
|---|---|---|---|
| 10 | 161.57 | 30.55 | 0.449 |
| 20 | 176.35 | 36.25 | 0.499 |
| 30 | 187.62 | 42.81 | 0.545 |
| 40 | 201.26 | 46.22 | 0.595 |
| Circumferential Pressures/MPa | Total Number of Cracks/Pieces | Number of Tension Cracks/Pieces | Proportions/% | Number of Shear Cracks/Pieces | Proportions/% |
|---|---|---|---|---|---|
| 10 | 824 | 539 | 65.41 | 285 | 34.59 |
| 20 | 1412 | 895 | 63.39 | 517 | 36.61 |
| 30 | 1819 | 1142 | 62.78 | 677 | 37.22 |
| 40 | 2017 | 1196 | 59.30 | 821 | 40.70 |
| Circumferential Pressures/MPa | Total Number of Cracks/Pieces | Number of Tension Cracks/Pieces | Proportions/% | Number of Shear Cracks/Pieces | Proportions/% |
|---|---|---|---|---|---|
| 10 | 1421 | 896 | 63.05 | 525 | 36.95 |
| 20 | 2232 | 1399 | 62.67 | 833 | 37.32 |
| 30 | 2386 | 1471 | 61.65 | 915 | 38.34 |
| 40 | 2702 | 1595 | 59.03 | 1107 | 40.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Peng, J.; Cui, Z.; Yan, L.; Kang, Z. Mechanical Properties of Marble Under Triaxial and Cyclic Loading Based on Discrete Elements. Appl. Sci. 2025, 15, 3576. https://doi.org/10.3390/app15073576
Yang Y, Peng J, Cui Z, Yan L, Kang Z. Mechanical Properties of Marble Under Triaxial and Cyclic Loading Based on Discrete Elements. Applied Sciences. 2025; 15(7):3576. https://doi.org/10.3390/app15073576
Chicago/Turabian StyleYang, Yanshuang, Jiancheng Peng, Zhen Cui, Lei Yan, and Zhaopeng Kang. 2025. "Mechanical Properties of Marble Under Triaxial and Cyclic Loading Based on Discrete Elements" Applied Sciences 15, no. 7: 3576. https://doi.org/10.3390/app15073576
APA StyleYang, Y., Peng, J., Cui, Z., Yan, L., & Kang, Z. (2025). Mechanical Properties of Marble Under Triaxial and Cyclic Loading Based on Discrete Elements. Applied Sciences, 15(7), 3576. https://doi.org/10.3390/app15073576






