Abstract
Aiming at the problems of complex calculation processes, insufficient risk data, and reliance on experts’ subjective judgments that exist in traditional probability analysis methods, this paper proposes a probability analysis method for hazardous chemical storage tank leakage accidents based on neural networks and fuzzy dynamic fault trees (Fuzzy DFT). This method combines fuzzy set theory (FST) and Bootstrap technology to accurately quantify the failure probabilities of basic events (BEs) and reduce the dependence on experts’ subjective judgments. Furthermore, an artificial neural network (ANN) model for tank failures is constructed. This model can accurately calculate the probability of tank leakage accidents by taking into account the dependency relationships among basic events. Finally, a long short-term memory (LSTM) network is utilized to analyze the dynamic evolution trend of the probability of storage tank accidents over time. In this paper, this method is applied to the case of the “11.28” Shenghua vinyl chloride leakage accident. The results show that the calculation results of this method are highly consistent with the actual situation of the accident, indicating that it is a scientific and effective method for analyzing the probability of hazardous chemical storage tank leakage accidents.
1. Introduction
As important industrial equipment, storage tanks are widely used in the petrochemical, chemical, energy, and other fields [1]. According to a survey, in 2021, Huizhou, Qingdao, Shanghai, Zhoushan, Tianjin, Yantai, and other large ports had about 31,000 oil, gas, and chemical storage tanks of various types, with a total tank capacity of more than 300 million cubic meters; 320,000 mobile transport tanks and other various types of transit tanks, raw material tanks, media tanks, inter-plant tanks are numerous [2]. However, most of the storage tanks store large amounts of dangerous explosive and volatile chemicals, and their operation involves a number of potential risks such as leakage, explosion, and fire, which may pose a serious threat to the industry’s reputation, assets, and the environment, as well as a serious hazard to the safety of personnel and the environment [3]. Historical data show that leakage accidents are one of the most common accidents in the process industry, accounting for approximately 17.98% of the total number of accidents [4]. For example, accidents such as the storage tank fire at the ITC tank farm in Houston on 18 March 2019 and the toluene storage tank fire at Sinopec Dalian Petrochemical Company on 2 June 2013 demonstrated the serious consequences and property losses of such accidents. Therefore, conducting effective quantitative analyses of dynamic accident probabilities is crucial for the safe management of storage tanks [5].
Fault tree analysis (FTA) is a deductive analysis method widely used in probabilistic analysis to qualitatively identify the critical and root causes of unexpected events in system failures and quantitatively assess the likelihood of accidents [6]. In the traditional FTA approach, the failure probabilities of basic events are exact values. However, because of insufficient data, performing an exact calculation of the BEs’ failure probabilities in quantitative accident probability analyses is difficult to achieve [7,8]. In the absence of a precise value for the probability of failure, it is common to approximate the probability and justify using ‘likelihood’ rather than ‘probability’ [9]. In order to solve this limitation, scholars combine FTA with other technologies. For example, Lin and Wang [10] combined FST with expert judgment to evaluate the failure probability of BEs in a robotic drilling system. Liang and Wang [7] proposed a fuzzy fault tree analysis method based on failure possibility. They combined fuzzy set theory with FTA to better deal with the inaccuracy in fault probability assessment.
In view of the dynamic nature of the causes of hazardous chemical tank leakage accidents with temporal correlation, it is difficult to provide reliable results using traditional static probabilistic analysis methods. To cope with the time-series correlation in accident risk analysis, dynamic probabilistic analysis methods have been widely used in risk assessment [11,12,13]. In 2002, Čepin and Mavko [14] proposed the dynamic fault tree (DFT) method, which is a modified classical FT that takes into account the time dependence of system failure. To address the dynamics of accident probability, Badreddine and Amor [15] proposed the Bayesian network (BN) method. The method is a probabilistic inference technique for uncertainty reasoning and has been shown to be a practical approach for modeling and probability calculating of dynamic risk with uncertainty [16].
In view of the lack of risk data, the traditional expert evaluation method relies too much on the subjective evaluation of experts, which has great uncertainty. BN-based models assume that the state of each node (variable) is independent of each other [17]. Determining conditional probability tables may face difficulties when BN is applied to variables with unknown or nonlinear dependencies. When dealing with noisy or large-scale data, BN may face computational complexity or even incompatibility. Compared to the traditional BN method, Fuzzy DFT can better handle the uncertainty dependencies and fuzzy information present in the system [18], which makes it more robust in practical applications, especially in the context of storage tank accidents [19]. Additionally, although Markov Chains (MC) and Monte Carlo simulation perform well in simulating system state transitions, they require significant computational resources and are often unable to meet real-time risk assessment needs, particularly when dealing with high-dimensional data [20,21].
In contrast, ANNs, with their powerful nonlinear modeling capabilities, can effectively capture complex system behaviors and long-range dependencies, thus demonstrating higher accuracy in risk assessment tasks [22,23,24]. Compared to BN, neural networks do not need to assume that the variables are independent of each other when building the model. The neural network model has a data-driven feature that enables it to deal with unknown nonlinear dependencies more easily. In addition, neural networks can learn and optimize the model automatically and perform particularly well when dealing with large-scale or imprecise data, leading to reliable results. Currently, other subject areas have begun to apply neural networks for accident risk research. For example, Qiao et al. [25] developed a comprehensive accident analysis model that organically integrated the Human Factors Analysis and Classification System (HFACS) and ANN to accurately quantify the failure probabilities caused by human factors in maritime accidents, providing a new perspective and method for maritime accident risk assessment. Sarbayev et al. [17] innovatively adopted the technical approach of mapping fault tree (FT) to ANN and successfully applied it to the probability analysis of process systems. This method effectively overcame the shortcomings of traditional fault trees in dealing with system complexity and complex calculation processes, significantly improving the accuracy and efficiency of probability analysis for process systems. Lin et al. [26] proposed a probability analysis method for mining systems based on FST and machine learning, skillfully solving the key problem of data uncertainty in probabilistic risk analysis and providing more reliable technical support for risk assessment in the mining industry. However, the current research status of dynamic probability analysis still has certain limitations. Most research methods often only focus on local factors and fail to comprehensively consider and properly address all aspects involved in accident probability analysis from a global perspective. Especially in the important field of probability analysis of storage tank leakage accidents, research on probability analysis using neural networks is relatively scarce.
This study proposes a probability analysis method for accident risk based on Fuzzy DFT and neural network technologies. Unlike traditional methods, which often face the issue of data scarcity, the proposed method calculates the failure probabilities of BEs using FST and introduces the Bootstrap algorithm to augment risk data, creating a more comprehensive dataset for probabilistic risk analysis. This not only alleviates the problem of insufficient data in the quantitative analysis of storage tank accidents but also reduces reliance on experts’ subjective judgments through a data-driven approach. In terms of accident scenario analysis, traditional FT methods may overlook the dynamic nature of accident development. However, the method proposed in this paper utilizes DFT to comprehensively capture these dynamic features, enabling a more accurate reflection of risk state changes. In terms of model construction, the ANN model for storage tank risk analysis, based on the structure and principles of Fuzzy DFT, can better account for dependencies between events compared to traditional models, thereby simplifying the calculation process and significantly improving computational efficiency and accuracy. Additionally, the development of an LSTM model for tank accidents is another key advantage. Unlike traditional static models, this LSTM model can quickly predict the dynamic changes in the failure probability of the top event (TE) over time, providing a real-time analytical tool for storage tank safety management.
In terms of implementation, the method uses widely available software tools. Data processing and model construction are primarily carried out in the Python 3.7 programming environment. Libraries such as pandas and numpy are used for data processing, scikit-learn for data preprocessing, including normalization and data splitting, while deep learning frameworks like PyTorch 1.13 or Keras 2.11 are employed to construct and train the ANN and LSTM models. These tools have user-friendly interfaces and powerful functionalities, ensuring the smooth implementation of the proposed method and making it easy to use and apply in practical scenarios. Overall, this new method represents a significant advancement in storage tank accident probability analysis, providing the industry with a more reliable and efficient solution.
In this study, Section 2 systematically introduces the method for constructing a quantitative probability calculation model based on Fuzzy DFT and neural networks, including the construction of the DFT, fuzzy calculation of failure probabilities for storage tank accident factors, data acquisition preprocessing, and the development of a hazardous chemical storage tank leakage accident model based on neural networks. Section 3 conducts a case analysis using a storage tank leakage accident as an example, covering the introduction of the accident case, specific application of the proposed method, including the construction of the dynamic fault tree for the tank leakage accident, determination of fuzzy failure probabilities for basic events, risk data augmentation, hyperparameter tuning, and data processing and parameter setting for the ANN and LSTM models. Section 4 presents a discussion of the results, which not only verifies the proposed quantitative probability calculation method based on Fuzzy DFT and neural networks for storage tanks but also provides an in-depth analysis of the impact of different parameters on the performance of the ANN model, model performance evaluation based on data updates, independence of basic events, input variable sensitivity, and the temporal development of the failure probability of hazardous chemical storage tank leakage accidents. Section 5 summarizes the research conclusions and synthesizes the overall work.
2. Model Construction for Quantitative Probability Calculation Based on Fuzzy DFT and Neural Networks
The process of the proposed quantitative probability calculation method for hazardous chemical storage tank accidents based on Fuzzy DFT and neural networks is shown in Figure 1. First, the causal factors of the accident are determined through analysis of accident reports and other sources, and a Fuzzy DFT model for hazardous chemical storage tank leakage accidents is constructed. Corresponding ANN and LSTM models are then built for the DFT model to calculate the failure probability of the top event and the temporal changes in this probability. For the basic events in the DFT model, the failure probabilities are calculated using fuzzy set theory, and the obtained failure probability data are augmented using the Bootstrap method to create a dataset for the storage tank neural network model. This data-driven approach reduces the influence of expert subjective judgment. Additionally, risk data for each accident factor, changing over time, is collected to construct a time-series dataset. Finally, the dataset is input into the constructed ANN model and time-series LSTM model to compute and quantitatively analyze the failure probability of the storage tank accident.
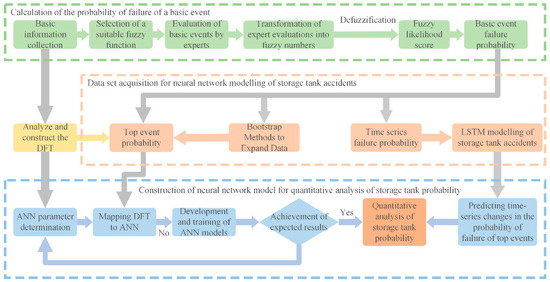
Figure 1.
Constructing a probabilistic quantitative calculation model based on Fuzzy DFT and neural networks.
2.1. Construction of Dynamic Fault Tree
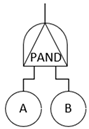
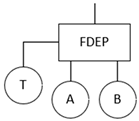
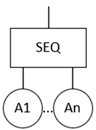
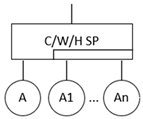
To address the limitation of traditional fault tree analysis (FTA) methods that cannot model temporal sequences [26], this study introduces the dynamic fault tree (DFT) analysis method, which uses a series of dynamic logic gates to consider the temporal rules and dynamic failure behaviors of the system [27,28]. The dynamic fault tree mainly includes four typical dynamic logic gates: Priority-AND Gate (PAND), Functional Dependency Gate (FDEP), Sequence Enforcing Gate (SEQ), and Spare Gate (SP). The Spare Gate is further divided into Cold Spare Gate (CSP), Warm Spare Gate (WSP), and Hot Spare Gate (HSP), and the basic introduction is shown in Table 1. The logic gates mainly used in this paper are AND Gate, OR Gate, Priority-AND Gate, Sequence Enforcing Gate, and Functional Dependency Gate.

Table 1.
Introduction to Fault Tree Dynamic Logic Gates.
2.2. Fuzzy Calculation of Storage Tank Accident Factors Failure Probability
In the quantitative calculation of storage tank probability, it is crucial to accurately assess the failure probability of basic events. Fuzzy set theory (FST) was proposed by Zadeh in 1965 [10] to handle problems of imprecision and fuzziness in phenomena. Since the data and information provided in accident analysis and risk assessment often contain considerable uncertainty, FST has been applied in many fields. Well-known risk analysis techniques, such as FTA [29], FMEA [30], and HAZOP [31,32], have all been modified and enhanced using FST. This study combines fuzzy set theory (FST) and expert evaluation to calculate the basic events’ failure probability to improve the accuracy and reliability of failure probability assessment [33]. Fuzzy numbers can be represented in various forms to express linguistic values. Common forms include triangular membership functions, trapezoidal membership functions, and Gaussian membership functions. The triangular membership function and the trapezoidal membership function are adopted as fuzzy set affiliation functions in this research. The steps for calculating the failure data of basic events using expert evaluation and fuzzy set theory are as follows:
Step 1: Define the linguistic variables based on expert opinions and determine the corresponding membership functions
Let (real numbers). Suppose a fuzzy number A in R is a triangular fuzzy number, then its membership function is given by Equation (1):
where . A triangular fuzzy number is denoted as A = (a, b, c). The parameter ‘b’ represents the maximum value of fA(x), that is, fA(b) = 1, which is the most likely value of the evaluation data. ‘a’ and ‘c’ are the lower and upper limits of the available evaluation range.
Similarly, assume that a fuzzy number A in R is a trapezoidal fuzzy number, then its membership function is given by Equation (2):
where . A trapezoidal fuzzy number can be represented as . The interval [b, c] is the most likely value of fA(x), ‘a’ and ‘d’ are the lower and upper limits of the available area for evaluating data.
These two types of fuzzy numbers are used because, under some weak assumptions, these specific membership functions meet relevant optimization criteria and are also easy to evaluate intuitively evaluation [10,34].
The fuzzy number is calculated based on the linguistic variables used by the experts to evaluate the risk factors, where each linguistic variable corresponds to a fuzzy set containing the affiliation function of that variable. The linguistic variables are {Very low (VL), Low (L), Mildly low (ML), Medium (M), Mildly high (MH), High (H), and Very high (VH)} [35] and their corresponding fuzzy numbers are shown in Figure 2. The triangular fuzzy numbers are converted into trapezoidal fuzzy numbers for ease of computation.
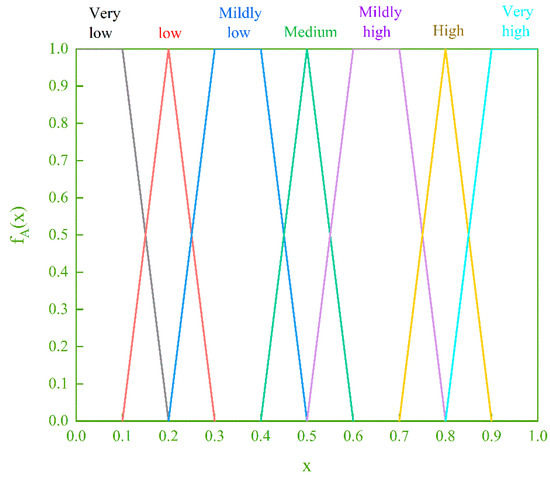
Figure 2.
Fuzzy membership functions.
Step 2: Aggregation of expert opinions
In order to obtain accurate and objective results, the ratings of multiple experts are aggregated and processed using the following Equation [5]:
where n is the number of basic events, m is the number of experts, wj is the weight coefficient of each expert, Aij is the value of the horizontal coordinates (a, b, c, d), and Mi is the number of aggregated fuzzy numbers of basic events.
Step 3: Defuzzification to obtain failure probabilities
The resulting fuzzy numbers are defuzzied by the left-right fuzzy ranking method [36] to obtain the fuzzy possibility score (FPS).
Finally, the fuzzy possibility scores are converted into failure probabilities of basic events using Equations (6) and (7):
where p(x) is the failure probability of the x-th basic event.
2.3. Data Acquisition and Preprocessing
Based on the analysis of accident reports or previous research papers, the basic events that may lead to an accident in the DFT model are determined. Experts from various industries are hired to assess the risk of basic events and provide linguistic variables for the accident risk, which are then used in FST to estimate the specific failure probabilities. However, the failure probabilities obtained from this method have some uncertainty due to subjective evaluation. To reduce the uncertainty of subjective evaluation, the Bootstrap algorithm is introduced to perform 1000 Bootstrap sampling of the original data, generating an expanded dataset (where each dataset is centered around the mean and the standard deviation is set to 10% of the mean). This method helps reduce the uncertainty caused by data scarcity, making the results of the proposed method more accurate.
Additionally, for the time-series variation of failure probabilities, it is necessary to monitor the state changes of each basic event in real-time and obtain the changes in probabilities, which is difficult to obtain in real scenarios. Therefore, for the time-series dynamic characteristics of failure probabilities, a device degradation model based on the principles of Hidden Markov Chains (HMM) is constructed [37], assuming that the state at the next time point is determined solely by the current state, and calculating the failure probability changes of each basic event for the subsequent model dataset.
2.4. Neural Network-Based Leakage Accident Model for Hazardous Chemical Storage Tanks
To achieve a faster and more accurate analysis of the probability of hazardous chemical storage tank leakage accidents, this study constructs a storage tank ANN model and LSTM model based on the storage tank DFT. By means of nonlinear activation functions, this model can effectively process the input data and deeply learn the relationship between the input data and the probability of a tank leakage accident.
2.4.1. ANN Model Construction for Hazardous Chemical Storage Tank Accidents
The ANN-based model for quantitatively calculating the probability of hazardous chemical storage tank accidents was conducted by mapping a Fuzzy DFT to an ANN. The mapping rule from Fuzzy DFT to ANN is shown in Figure 3, which demonstrates how the BEs and logic gates of the DFT are transformed into the input, hidden, and output layers of the ANN.
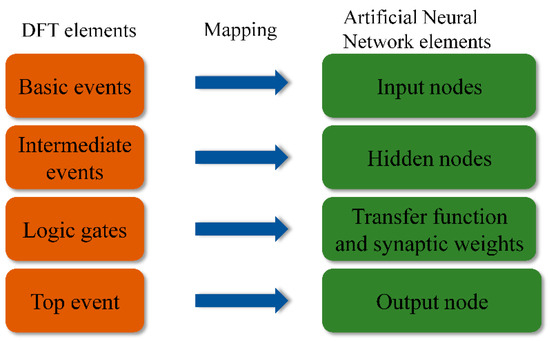
Figure 3.
Mapping rules from fuzzy DFT to ANN.
The backpropagation algorithm and Levenberg–Marquardt optimization technique were used to improve the generalization ability of the model while training the ANN model. The above process is repeated over and over again to optimize the performance of the network until the training is stopped when the stopping condition is reached (i.e., the computed error meets the preset target requirements) [38]. The article uses mean squared error (MSE) for measuring the overall error, which is functionally represented in Equation (8) [39,40]:
where n represents the number of samples, Y0,i is the true value (or target value) of the i-th sample, and Ypre,i is the predicted value of the i-th sample, i.e., the output value computed by the neural network model.
The number of input nodes in the ANN model is chosen based on the number of basic events in the DFT, while the number of hidden layers and the number of nodes in each hidden layer are determined according to the hierarchical structure and the number of intermediate nodes in the DFT. Meanwhile, in order to prevent overfitting and underfitting problems from occurring in network training, this paper proposes a rule for selecting the hidden layers by combining the methods proposed by Panchal and Panchal [41] and combining the characteristics of the DFT in this paper, which is demonstrated in Appendix A, verifying the validity of the rule in Section 4.2.
2.4.2. Constructing the LSTM Model for Storage Tank Accidents
In order to deeply explore the changing law of storage tank accident probability over time, the LSTM model is used for time-series prediction to capture and analyze the dynamic change in the time dimension of accident probability [42,43]. The LSTM model can alleviate problems such as gradient explosion, which is common in traditional recurrent neural networks (RNNs) in time-series prediction tasks [44]. Special gating devices (input gates, output gates, and forgetting gates) are added to the LSTM model to deal with the large time span in time-series prediction. The model consists of multiple units; each unit only stores the information at the current time, as shown in Figure 4. The three gating devices in the unit control the flow of the information passed between the units, which gives the LSTM model excellent memory capability in dealing with sequential data, and the model is trained using the Adam algorithm.
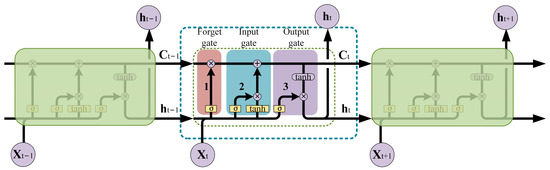
Figure 4.
Schematic diagram of LSTM structure.
3. Case Analysis of Storage Tank Leakage Accidents
3.1. Case Introduction: Shenghua Chemical Company “11.28” Accident
At the China National Chemical Corporation Shenghua Chemical Company, located in Zhangjiakou City, Hebei Province, China, at 00:40:55 on 28 November 2018, vinyl chloride leakage from the Shenghua Chemical Company Limited spread to an area outside the plant and burst into flames when it met with an ignition source, resulting in the deaths of 24 people (including 1 person who died in the late stage of medical treatment); 21 people were injured (4 people who recovered from minor injuries were discharged from the hospital), and the damages to 38 large lorries and 12 small cars resulted in direct economic losses of CNY 41.48 million as of 24 December 2018.
3.2. Application of the Proposed Method
3.2.1. Constructing a Dynamic Fault Tree for Tank Leakage Accidents
The proposed method is used to evaluate the above-mentioned tank leakage accident cases. Based on the investigation report of the above accident [45] and the tank design code [46], the DFT of the accident is constructed as in Figure 5. According to the development process of the accident, the tank leakage is set as a DFT top event, and it is assumed that each event has two states, Normal and Fault.
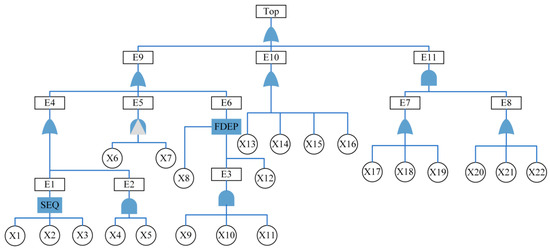
Figure 5.
Construction of dynamic fault trees.
The names and descriptions of their corresponding events are illustrated in Table 2, where X1–X22 are the basic events, E1–E9 are the intermediate events, and Top is the top event. The specific events that each of them represents are listed in the following table.

Table 2.
Introduction to Dynamic Fault Tree Events.
3.2.2. Determination of Fuzzy Failure Probability of Basic Events
Ten experts were recruited to evaluate the failure probability of BEs based on their experience and knowledge of tank leaks, considering four aspects: title, years of experience, education, and continuing education and professional development. As shown in Table 3, weights ranging from 1 to 5 were assigned to attributes such as title, years of experience, education, continuing education, and professional development. The weighting coefficients for each expert were calculated by Equation (9), and Table 4 shows the personal information, weighting scores, and weighting coefficients of the 10 experts consulted about the accident.

Table 3.
Expert weight distribution mode.

Table 4.
Expert information and weight scores.
All basic events are evaluated by experts, and the linguistic variables used are the seven linguistic expressions previously defined, represented by triangular fuzzy numbers and trapezoidal fuzzy numbers, respectively. For ease of calculation, triangular fuzzy numbers are converted into trapezoidal fuzzy numbers, with each trapezoidal fuzzy number represented by four range values (a, b, c, d) corresponding to the linguistic variable. Table 5 summarizes the linguistic evaluations of the BEs by ten experts.

Table 5.
Expert’s linguistic evaluation of BEs.
The linguistic evaluations of each expert on the BEs are aggregated to obtain the fuzzy aggregation number (M), the fuzzy possibility score (FPS) is calculated, and finally, calculating the failure probability P(Xi) of each basic event according to Equations (2) and (3), the results are obtained as in Table 6, and the last column is the ranking of the failure probability of each basic event.

Table 6.
Parameters for each BEs.
3.2.3. Risk Data Augmentation
According to the accident investigation report, the top event was the leakage of vinyl chloride stored in the tank. Based on the calculated failure probabilities of the basic events and the DFT calculation code, the failure probability of the top event is calculated to be 0.04255. The failure probabilities of the basic events are taken as the mean, with a standard deviation assumed to be 10%. Then, 1000 sets of data are generated based on a normal distribution using the Bootstrap algorithm. The failure probability of the top event is calculated from the failure probabilities of the basic events and the dynamic fault tree calculation code. Table 7 lists the data samples used for ANN training and testing in the case study [18]. Additionally, based on the failure probabilities of the basic events, a Hidden Markov Model (HMM) is used to calculate 14,460 time slices of data, as shown in Table 8.

Table 7.
Failure probability extension of basic events in DFT.

Table 8.
Time-series variation of failure probability of basic events.
3.2.4. Hyperparameter Tuning
In order to improve the model’s performance and avoid overfitting, this study uses a combination of grid search and cross-validation methods to tune the key hyperparameters of the ANN. The tuning process mainly focuses on the following hyperparameters: learning rate, batch size, and L2 regularization weight (weight decay).
During the hyperparameter tuning process, we first defined a grid containing multiple possible values. Specifically, the following hyperparameter ranges were set: learning rate: 0.001, 0.01, 0.1; batch size: 32, 64, 128; L2 regularization weight: 0, 0.001. Through grid search, we systematically explored these hyperparameter combinations and trained and evaluated the model for each hyperparameter configuration.
To further validate the generalization ability of each hyperparameter combination, we used 5-fold cross-validation. In cross-validation, the dataset was divided into 5 subsets, with 4 subsets used for training and 1 subset used for validation, repeating 5 times. By using cross-validation, we were able to assess the performance of each hyperparameter combination under different data splits, ensuring the stability and robustness of the model.
After grid search and cross-validation, the best hyperparameter combination was determined: learning rate (lr) = 0.1, batch size (batch_size) = 64, L2 regularization weight (weight_decay) = 0.001. For this combination, the average mean squared error (MSE) in cross-validation was 2.381 × 10−6, demonstrating strong performance and generalization ability.
Through hyperparameter tuning, the model’s performance was significantly improved. The best hyperparameter combination outperformed other combinations on both the training and testing datasets and avoided overfitting. This result demonstrates that through systematic hyperparameter optimization, we can effectively improve the model’s accuracy and generalization ability.
Similarly, to improve the performance of the LSTM model and avoid overfitting, this study tuned the key hyperparameters of the LSTM model. The tuning process mainly focused on the following hyperparameters: learning rate, batch size, LSTM hidden layer size (hidden size), number of LSTM layers (num layers), and dropout rate (dropout).
During the hyperparameter tuning process, a grid containing multiple possible values was defined. The following hyperparameter ranges were specifically set: learning rate: 0.001, 0.01, 0.1; batch size: 32, 64, 128; L2 regularization weight: 0, 0.1, 0.001, 0.0005; number of LSTM layers (num layers): 2, 3, 4, 5; dropout rate: 0.1, 0.2, 0.3. Through grid search, we systematically explored these hyperparameter combinations and trained and evaluated the model for each hyperparameter configuration.
To further validate the generalization ability of each hyperparameter combination, we used 5-fold cross-validation. In cross-validation, the dataset was divided into 5 subsets, with 4 subsets used for training and 1 subset used for validation, repeating 5 times. By using cross-validation, we were able to assess the performance of each hyperparameter combination under different data splits, ensuring the stability and robustness of the model.
After grid search and cross-validation, the best hyperparameter combination was determined: learning rate (lr) = 0.1, batch size (batch_size) = 64, L2 regularization weight (weight_decay) = 0.001, number of LSTM layers (num_layers) = 3, and dropout rate (dropout) = 0.1.
For this combination, the average mean squared error (MSE) in cross-validation was 5.0337 × 10−5, demonstrating strong performance and generalization ability.
Through hyperparameter tuning, the model’s performance was significantly improved. The best hyperparameter combination outperformed other combinations on both the training and testing datasets and avoided overfitting. The LSTM model, by better controlling the hidden layer size, the number of layers, and regularization methods, achieved more stable prediction results. This result demonstrates that through systematic hyperparameter optimization, we can effectively improve the accuracy and generalization ability of the LSTM model.
3.2.5. Data Processing and Parameter Settings for the ANN Model
According to the mapping rules proposed in Section 2.4.1, 800 sets of data are selected as the training set, 170 sets as the validation set, and 30 sets as the test set. The first 22 columns are extracted as input variables X, corresponding to the 22 basic events, and the 23rd column, the top event data, is used as the output variable y. Next, the data are standardized using the StandardScaler from the sklearn library for X, and the train_test_split function is used to divide the data into training and testing sets with a test set size of 30 samples and a random seed set of 42. The data are then converted into torch.float32-type tensors and a mini-batch data loader is created with a batch size of 64, where the data are shuffled.
In terms of parameter settings, the constructed feedforward backpropagation ANN model contains two hidden layers (with 8 and 3 neurons, respectively) and one output layer, as shown in Figure 6. The activation function used is nn.Sigmoid(). Based on the hyperparameter tuning results from Section 3.2.4, the learning rate (lr) is set to 0.1, the batch size is 64, the L2 regularization weight is 0.001, and the loss function is the mean squared error loss function nn.MSELoss(). The optimizer used is the Adam optimizer with regularization, and training stops if the test set’s mean squared error does not improve for 10 consecutive iterations.
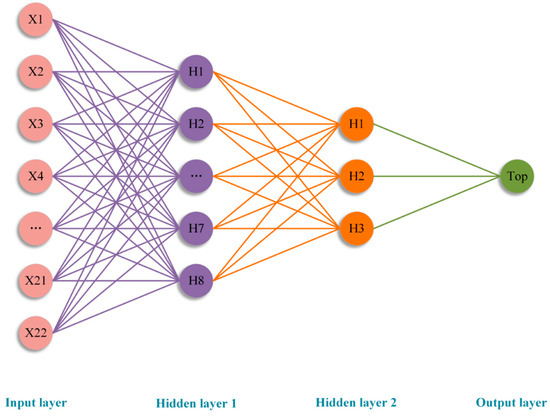
Figure 6.
Constructed ANN Network.
3.2.6. Data Processing and Parameter Settings for the LSTM Model
The constructed model includes two LSTM hidden layers, containing 150 and 200 neurons, respectively, and uses a Dropout regularization layer to reduce the risk of overfitting. The input data for the model are a 3D tensor with the shape (batch_size, time steps, features), where batch_size is 64, time steps are 50, and features are 23. The model is trained using the Adam optimizer and mean squared error loss function to achieve accurate predictions of time-series data.
To analyze the characteristics of the failure probability of storage tank leakage accidents over time, this paper develops an LSTM model for the storage tank accident DFT, which processes time-series data from the DFT to predict the risk of storage tank leakage accidents. In terms of data processing, the random seed is first set to ensure reproducibility, and the random seed for NumPy and PyTorch random number generation is fixed at 42. The pd.read_csv function is used to read the data, and the “Date” column is parsed into a date format and set as the index. Then, the data are split into a training set and a test set by allocating 20% of the dataset length to the test set. To eliminate the impact of scale differences in data features on the model, the StandardScaler is used to standardize both the training and test datasets. Using a custom create_XY function, the previous 50 time steps of data are used as the input sequence, and the first feature of the current time step’s data is used as the target value, generating the training set trainX, trainY, and test set testX, testY, which are then converted into PyTorch tensors.
In terms of parameter settings, based on the results from Section 3.2.4, the model is constructed using a custom MyModel class, which includes two LSTM layers and one fully connected layer. The input feature dimension is 23, with 120 hidden units in the first LSTM layer and 150 hidden units in the second LSTM layer. Dropout layers with a dropout rate of 0.1 are added between layers to prevent overfitting, and the fully connected layer has an output dimension of 1. The activation function used is ReLU to enhance the model’s nonlinear expressiveness. The loss function is the mean squared error loss function, nn.MSELoss(), which measures the difference between the model’s predicted values and the true values. The optimizer used is the Adam optimizer, with the learning rate set to 0.01. During training, the training data are packaged into TensorDataset and DataLoader, with a batch size of 64, and the data are shuffled to introduce randomness into the training process. An EarlyStopping callback function is used to monitor the validation loss (val_loss), and training stops if the validation loss does not decrease for 5 consecutive epochs, thus preventing overfitting.
4. Results and Discussion
4.1. Validating the Quantitative Calculation Method for Storage Tank Probability Based on Fuzzy DFT and Neural Network
In order to validate the feasibility of the developed ANN model, a series of model tests were conducted on the trained ANN model using 30 sets of BEs failure rate data from different scenarios as a test dataset, aiming to simulate the computational process of DFT. The results of the proposed method in this paper were compared with those of the traditional Monte Carlo simulation method, and the results are shown in Figure 7. The green curve in the figure represents the failure probability of the top DFT events obtained from the Monte Carlo simulation, while the orange curve represents the prediction results of the constructed ANN model. The prediction results between the two methods exhibit significant consistency, and the results obtained by the proposed method align with the findings of Sarbayev et al. [17] and Yan et al. [18]. This provides strong evidence to demonstrate the effectiveness and accuracy of the proposed method. In addition, through an estimation of the computation time, we found that using the ANN model significantly improves computational efficiency when handling large amounts of failure data. For example, in this study, when 1000 sets of data were used for computation, the ANN model completed the calculation in just 2 min, while the Monte Carlo model took approximately 2 h. This demonstrates that the ANN model significantly enhances computational efficiency when processing large-scale data, greatly saving computation time.
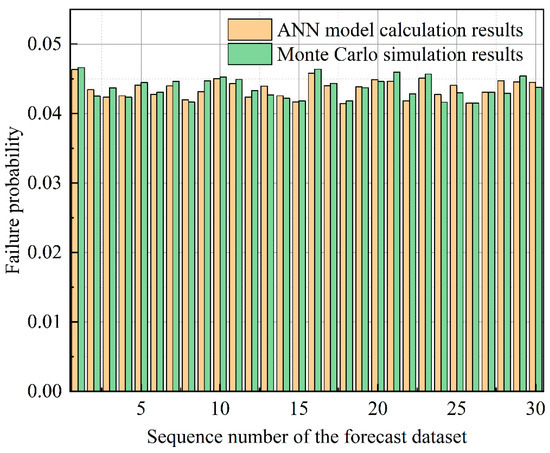
Figure 7.
Comparison of Fault Probability in Prediction Sets using ANN and Monte Carlo Simulation Methods.
In order to assess the performance of the ANN model more comprehensively, the average difference value and the maximum difference value between the predicted results of the two models were calculated. The results show that the average difference value between the results calculated by the two methods is 6.61 × 10−4 and the maximum difference value is 1.82 × 10−3. These small difference values further confirm the high accuracy of the ANN model in predicting the probability of failure of the top event.
4.2. Analysis of the Effect of Different Parameters on the Performance of ANN Models
In order to comprehensively assess the role of different numbers of hidden neurons on the accuracy of model prediction, this study conducted a comprehensive comparative analysis of a series of training datasets of different sizes. Figure 8 indicates that as the size of the training dataset expands, the failure probability predicted by the ANN model gradually approximates the actual observed value, and the model prediction is more reliable. This phenomenon verifies that sufficient data can increase the ability to improve the generalization of the ANN model.
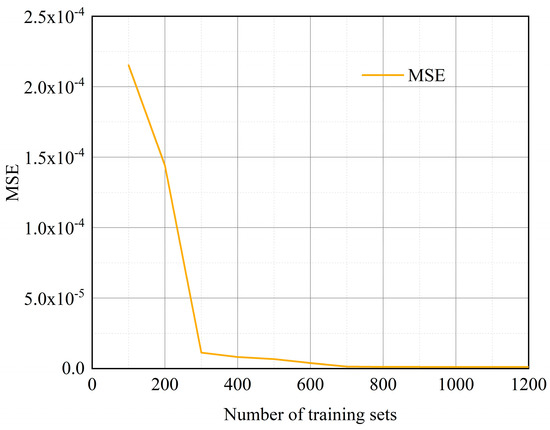
Figure 8.
Comparison of MSE (mean squared error) for different training datasets.
The increase in dataset size also inevitably leads to an increase in computational resources and time, so the balance between computational cost and model performance needs to be considered in model design. Weighing the model performance and practical requirements, the training dataset containing 800 samples is selected for this study. With this dataset size, the MSE of the test set is reduced to 1.23 × 10−6, a result that not only proves the high accuracy of the model prediction but also shows the reasonableness of the model prediction results.
For training datasets of different sizes, choosing the right number of hidden layer neurons is crucial to obtain the best fitting effect. As shown in Figure 9, by comparing the model performance under different configurations, it is found that the appropriate number of hidden neurons can significantly improve the predictive ability of the model and effectively avoid the overfitting problem. In particular, when the number of first hidden layer neurons is set to 8 and the number of second hidden layer neurons is set to 3, the model exhibits the best fitting effect, which is consistent with the rule of thumb presented in Section 2.4.1.
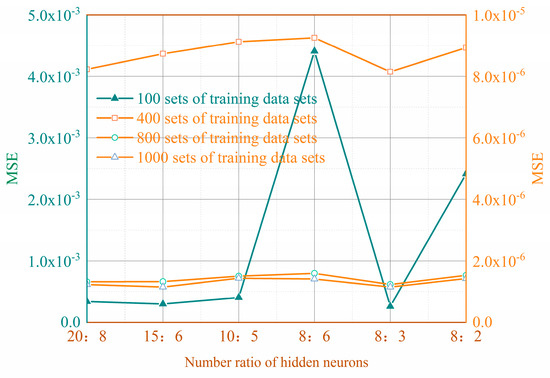
Figure 9.
The comparison of different numbers of hidden layer neurons in different training sets. Note: The MSE curve for 100 training sets is referenced on the left-side y-axis with the same color, while the MSE curves for 400, 800, and 1000 training sets are referenced on the right-side y-axis with the same color.
4.3. Evaluating the Performance of the Model Based on Data Updates
In practical quantitative analyses of storage tank accident probabilities, the emergence of new data may lead to changes in the structure of the DFT, such as the addition of new BEs. In this case, traditional computational methods face a complex recalculation process. In contrast, the ANN-based method proposed in this paper demonstrates remarkable adaptability and efficiency, which can quickly respond to the structural changes in the DFT and provide fast prediction results.
By deeply analyzing the data in Table 6, the ranking of the 22 BEs in terms of their degree of influence on TE occurrence was obtained, and the results are displayed in Table 9. Assuming that only 21 events were included in the initial incident analysis (removing the least influential event X13), in this case, the MSE of the prediction set obtained by applying the Fuzzy DFT-ANN model proposed in this paper is 1.96 × 10−6. However, the MSE of the prediction set is significantly reduced to 1.23 × 10−6 when the model is extended to include all 22 BEs. The result not only highlights that the new data play a key role in improving the model prediction accuracy, which can enhance the accuracy of the calculation, but it also confirms the high efficiency and adaptability of the proposed ANN model for storage tank accidents in the quantitative calculation of accident probability.

Table 9.
Ranking of contributions by BEs to TE.
The findings in this section show that ANN models can be optimized continuously to provide more accurate probability predictions as new data are continuously integrated. This data-driven approach to model optimization provides an effective tool for dynamic risk management, especially in scenarios that require rapid response to system changes and timely updating of risk assessment results.
4.4. Analysis of Independence Between BEs
In this section, the effect of independence between basic events on the quantitative analysis of storage tank probability is analyzed, and the prediction results of the constructed ANN model are compared with the TE failure probability derived from the traditional DFT calculation method. The comparison results show that the average error of the failure probability of the top event predicted by the ANN model is 2.14%. Compared with the 3.44% of the traditional DFT method, the performance of the ANN model is improved by 38%. This performance enhancement may be attributed to the unknown dependencies between BEs in DFT, which are often ignored in traditional methods. The advantage of the ANN model is its ability to capture and account for these interdependencies between input variables, thus outperforming the traditional fault tree computation methods in terms of prediction accuracy. Furthermore, this property of ANN models is particularly important when performing probabilistic calculations for complex systems. Since real-world systems often involve multiple interdependent variables, ANN models can model these complex interactions more accurately, providing a more accurate tool for probabilistic failure calculations.
This section analyzes the impact of the independence between basic events on the quantitative probability analysis of storage tanks and compares the predicted results of the constructed artificial neural network (ANN) model with the failure probabilities obtained using the traditional DFT calculation method. The results of the output set of the test dataset, as shown in Figure 7, are used to calculate the average error of the top event for both models using the following formula and to make a comparison [17].
where T is the calculated average error, is the sum of the top event results for the two models’ test datasets, consisting of 30 datasets, with the denominator being the failure probability of the top event, 0.04255.
By substituting both datasets into the formula and comparing the results, it was found that the average error of the top event failure probability predicted by the ANN model is 2.14%. Compared to 3.44% for the traditional DFT method, the ANN model’s performance improved by 38%. This improvement in performance may be due to the unknown dependencies between basic events in the model design, which are often overlooked in traditional methods. The advantage of the ANN model is that it can capture and explain the interdependencies between input variables, making it superior to traditional fault tree calculation methods in terms of prediction accuracy. Additionally, this characteristic of the ANN model is especially important when performing probabilistic calculations for complex systems. Since real-world systems typically involve multiple interdependent variables, the ANN model can more accurately simulate these complex interactions, providing a more accurate tool for probabilistic failure calculations.
4.5. Sensitivity Analysis of Input Variables
Sensitivity analyses were used to assess the impact of different incident factors on the probability of failure in a leaking vinyl chloride storage tank incident. The extent to which different factors influence system risk is revealed by quantifying how minor changes in input variables can lead to significant changes in output results. In order to perform this analysis, a method based on changes in model input variables is proposed. Using Equation (11), the corresponding degree of change in the output values with minor changes in the model input values is calculated. As shown in Figure 10, the results of the sensitivity analysis clearly demonstrate the extent to which each factor influences the risk of storage tank leakage.
where CRITi is the critical importance of input variable i, i.e., the extent to which input variable i affects the final output, P(TOP) is the probability of system failure, and P(i) is the probability of component i failure.
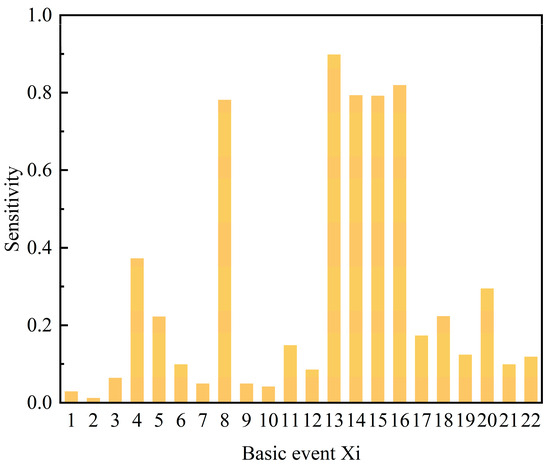
Figure 10.
Sensitivity analysis of BEs.
The results of the sensitivity analysis highlighted the key factors affecting the risk of leakage from vinyl chloride storage tanks, with X4, X8, X13, X14, X15, and X16 identified as having a significant impact on the risk. These findings are essential for the development of targeted safety management measures. In particular, enhanced inspection and maintenance of gas storage tanks, management and maintenance of gas transmission equipment, and consideration of natural conditions were shown to be effective strategies for improving the safety performance of storage tanks.
It is noteworthy that these results are consistent with the risk factors identified in the accident investigation report, thus providing empirical support for the model proposed in this paper and further confirming the validity of the adopted methodology. The sensitivity analysis not only reveals the specific impact of each factor on the risk of storage tank leakage but also provides a scientific basis for risk management and decision-making.
In addition, the study performed SHAP analysis on the model’s inputs to further demonstrate its interpretability. The results are shown in Figure 11, where the X-axis represents the average SHAP values corresponding to each basic event, and the Y-axis lists the different basic event numbers. This bar chart illustrates the contribution of each basic event to the model’s prediction results. From the chart, it can be observed that basic events 13, 16, 14, and 15 have relatively high SHAP values, indicating that these basic events significantly influence the model’s predictions. These basic events may play a crucial role in the occurrence of accidents, and therefore, higher weights were assigned to these features during the model training process. This is consistent with the results of the sensitivity analysis, which shows that these features have a considerable impact on the model’s output, further validating their importance in the prediction process. Based on the results of the SHAP analysis, it is now clearer how the model makes predictions, especially how it relies on these key features. This interpretability enhances our trust in the model’s behavior and provides valuable insights for future optimization and adjustments. For example, features with greater contributions could be further optimized in terms of data preprocessing and feature selection, which would improve the model’s prediction accuracy.
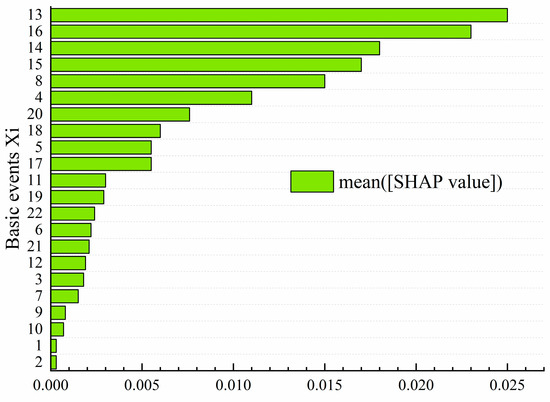
Figure 11.
SHAP analysis of BEs.
4.6. Analysis of the Time-Efficient Development of the Failure Probability in Hazardous Chemical Storage Tank Leakage Accidents
In order to effectively assess the dynamic evolution of the failure probability of hazardous chemical storage tank leakage accidents, an LSTM network model of storage tank DFT is constructed to further model and predict the DFT. When constructing the LSTM model, in the face of the incompleteness of historical data, the equipment degradation model is introduced to estimate the time-series variation of the failure probability of the BEs, and the failure probability of the TE is calculated by the corresponding calculation method of the DFT. To construct the LSTM model dataset, a total of 14,400 datasets are computed and counted, of which 80% is used to construct the training set, and the remaining 20% is used for the test set. In order to verify the applicability and superiority of the proposed model, the corresponding DFT time-series solution model is developed based on the traditional recurrent neural network (RNN) method. The time-series failure probabilities obtained from the Hidden Markov Chain are processed according to the data preprocessing method proposed earlier. The processed time-series dataset is then input into the previously constructed LSTM and RNN models to observe the differences between the output values of the two models and the true values. As shown in Figure 12, it can be seen that the LSTM model has a better performance in capturing the time-series variation.
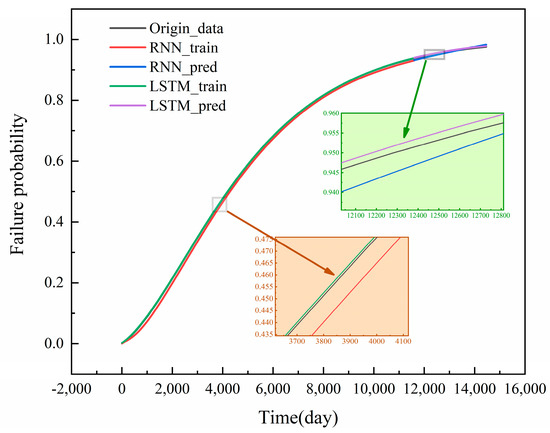
Figure 12.
Comparison of RNN and LSTM prediction results.
The model training results show that the traditional RNN model has a training loss of 2.1473 × 10−4, whereas the training loss of the constructed LSTM model for storage tank accidents is only 5.0337 × 10−5, as shown in Figure 13. This significant improvement confirms the superiority of the LSTM model in dealing with DFT time-series prediction. The lower training loss achieved by the LSTM model is attributed to its unique gating mechanism, which allows the model to capture the long-term dependencies in the time series more efficiently while avoiding the gradient vanishing or explosion problems that are commonly found in the traditional RNN models. In addition, the LSTM model for storage tank accidents not only performs well during the training process but also shows great accuracy and reliability in predicting the future trend of risk probability evolution and is able to more accurately predict the change in the probability of failure of storage tank leakage accidents. Considering the model training loss, prediction accuracy, and model complexity together, this LSTM model proves its potential as an effective probabilistic analysis tool. It provides a new analytical approach to hazardous chemical storage tank safety management and can play an important role in risk assessment and preventive measure development.
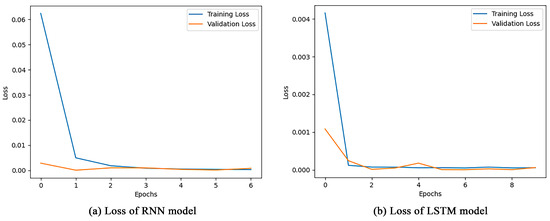
Figure 13.
RNN and LSTM predict the loss of the DFT model.
5. Conclusions
In this study, a modeling approach based on Fuzzy DFT with neural networks is proposed with the aim of improving the accuracy and efficiency of the probability analysis of hazardous chemical storage tank probabilities. The following are the main conclusions of the article.
- (1)
- Combining FST with Bootstrap technology, the data-driven approach effectively solves the problem of quantifying the failure probability of basic events, reduces the dependence on the subjective judgment of experts, and improves the accuracy and reliability of failure probability assessment.
- (2)
- The model was applied to the case of the vinyl chloride leakage accident that occurred at the Shenghua Chemical Company on 11.28. The research results show that the mean square error of the constructed ANN model is only 1.23 × 10−6, indicating that the accident probability calculation method proposed in this study can effectively solve the problem of calculating the probability of hazardous chemical storage tank leakage accidents. According to the sensitivity analysis, the main risk factors calculated by the model are consistent with the accident report. In addition, the model proposed in the research can take into account the coupling relationship between basic events. The average error of the failure probability of the top-level event predicted by the model is 2.14%, representing a 38% performance improvement compared with the traditional DFT method. This research not only addresses the issue of not considering the dependency relationship between basic events in the calculation of the probability of hazardous chemical storage tank leakage accidents but also provides a fast and effective technique for the quantitative calculation of the probability of such accidents.
- (3)
- This study combines the nature of the Markov Chain to obtain the dataset and constructs the correspondence accordingly. The LSTM model based on the DFT of hazardous chemical storage tank leakage accidents is constructed, which implements the calculation of the time-series variation of the failure probability of the basic event and analyzes the dynamic evolution trend of the occurrence probability of storage tank leakage accidents over time. The results of the study demonstrate that the LSTM model performs well in handling time-series-related model predictions, and the loss value from the true value is reduced to 5.0337 × 10−5, which is 1.64393 × 10−4 compared with the traditional RNN method, thus validating the effectiveness of the present method. This study provides a new analytical tool for hazardous chemical tank safety management, making risk prediction more dynamic and forward-looking.
It is worth emphasizing that the method proposed in this study has broad applicability and is not limited to the field of hazardous chemical storage tank risk analysis. It can also be applied in other related fields, such as risk data calculation in the chemical industry and failure probability calculation in the mechanical field. Specifically, it only requires replacing the dataset needed for the model with one that is tailored to the characteristics of different fields and adjusting the model parameters appropriately based on the actual situation. In this way, the method can operate effectively. Despite the positive results of this study, some challenges and limitations remain. Future research needs to explore the effectiveness and robustness of the present method in a wider range of scenarios and further optimize the parameter settings and structural design of the model to fully exploit the performance advantages of the ANN model.
Author Contributions
X.L. and N.Z.: supervisor, reviewing and editing. W.L.: writing—original draft preparation. X.Y.: validation. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the National Key R&D Plan “Internet of Things and Smart City Key Technologies and Demonstration” Key Special Project (No. 2020YFB2103504) funded by the Ministry of Science and Technology of China; the National Key R&D Program of China (No. 2017YFC0805100) funded by the Ministry of Science and Technology of China; the Natural Science Research Project of Higher Education Institutions of Jiangsu Province (No. 20KJB620004) funded by Jiangsu Provincial Department of Education; the Open Project of Jiangsu Key Laboratory of Oil and Gas Storage and Transportation Technology (No. CDYQCY202104) funded by Changzhou University; the Jiangsu Graduate Research and Practice Innovation Project (No. SJCX23_1566; No. SJCX22_1399; SJCX22_1400; SJCX22_1402; SJCX22_1403; KYCX22_3102) funded by Jiangsu Provincial Department of Education.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We would like to express our gratitude to Chen Bing and Liu Xuanya for their invaluable supervision and academic guidance throughout this study. Their insightful suggestions on the research framework and critical reviews of the manuscript significantly contributed to the quality and depth of this work.
Conflicts of Interest
The authors declare that there are no conflicts of interest involved in this study.
Appendix A
Rules for selecting hidden layers:
- The total number of hidden neurons should be between the number of input layer neurons and output layer neurons.
- The number of hidden neurons should be the sum of 2/3 of the number of input layer neurons and output layer neurons.
- If the above two rules are satisfied, the number of neurons in the first hidden layer shall be equal to the number of IEs (intermediate events) in the DFT that are directly connected to the BEs. If the second rule is not satisfied, the maximum number of neurons in the first hidden layer shall be the maximum permissible total number of hidden neurons minus the number of IEs directly connected to TEs (top-level events).
- The number of neurons in the second hidden layer shall be the same as the number of IEs directly connected to the TE in the FT.
References
- Shi, L.; Shuai, J.; Xu, K. Fuzzy fault tree assessment based on improved AHP for fire and explosion accidents for steel oil storage tanks. J. Hazard. Mater. 2014, 278, 529–538. [Google Scholar] [PubMed]
- People’s Network. The “Safety Lock” of Petroleum and Petrochemical Storage and Transportation Tank Farm Needs to Be Upgraded. Available online: http://paper.people.com.cn/zgnyb/html/2023-03/27/content_25973619.htm (accessed on 14 May 2024).
- Bhandari, J.; Abbassi, R.; Garaniya, V.; Khan, F. Risk analysis of deepwater drilling operations using Bayesian network. J. Loss Prev. Process Ind. 2015, 38, 11–23. [Google Scholar]
- Tong, Q.; Gernay, T. Resilience assessment of process industry facilities using dynamic Bayesian networks. Process Saf. Environ. Protect. 2023, 169, 547–563. [Google Scholar]
- Zhou, Q.; Li, B.; Lu, Y.; Chen, J.; Shu, C.; Bi, M. Dynamic risk analysis of oil depot storage tank failure using a fuzzy Bayesian network model. Process Saf. Environ. Protect. 2023, 173, 800–811. [Google Scholar]
- Ejlali, A.; Ghassem Miremadi, S. FPGA-based Monte Carlo simulation for fault tree analysis. Microelectron. Reliab. 2004, 44, 1017–1028. [Google Scholar]
- Liang, G.; Wang, M.J. Fuzzy fault-tree analysis using failure possibility. Microelectron. Reliab. 1993, 33, 583–597. [Google Scholar]
- Ayyub, B.M. Risk Analysis in Engineering and Economics; Chapman and Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Misra, K.B.; Weber, G.G. Use of fuzzy set theory for level-I studies in probabilistic risk assessment. Fuzzy Sets Syst. 1990, 37, 139–160. [Google Scholar] [CrossRef]
- Lin, C.; Wang, M.J. Hybrid fault tree analysis using fuzzy sets. Reliab. Eng. Syst. Saf. 1997, 58, 205–213. [Google Scholar]
- Wang, C.; Liu, Y.; Lian, X.; Luo, J.; Liang, C.; Ma, H. Dynamic risk assessment of plugging and abandonment operation process of offshore wells based on Dynamic Bayesian Network. Ocean Eng. 2023, 270, 113625. [Google Scholar]
- Liu, A.; Chen, K.; Huang, X.; Li, D.; Zhang, X. Dynamic risk assessment model of buried gas pipelines based on system dynamics. Reliab. Eng. Syst. Saf. 2021, 208, 107326. [Google Scholar]
- Sarvestani, K.; Ahmadi, O.; Mortazavi, S.B.; Mahabadi, H.A. Development of a predictive accident model for dynamic risk assessment of propane storage tanks. Process Saf. Environ. Protect. 2021, 148, 1217–1232. [Google Scholar] [CrossRef]
- Čepin, M.; Mavko, B. A dynamic fault tree. Reliab. Eng. Syst. Saf. 2002, 75, 83–91. [Google Scholar]
- Badreddine, A.; Amor, N.B. A Bayesian approach to construct bow tie diagrams for risk evaluation. Process Saf. Environ. Protect. 2013, 91, 159–171. [Google Scholar] [CrossRef]
- Jianxing, Y.; Shibo, W.; Yang, Y.; Haicheng, C.; Haizhao, F.; Jiahao, L.; Shenwei, G. Process system failure evaluation method based on a Noisy-OR gate intuitionistic fuzzy Bayesian network in an uncertain environment. Process Saf. Environ. Protect. 2021, 150, 281–297. [Google Scholar]
- Sarbayev, M.; Yang, M.; Wang, H. Risk assessment of process systems by mapping fault tree into artificial neural network. J. Loss Prev. Process Ind. 2019, 60, 203–212. [Google Scholar]
- Yan, X.; Lv, M.; Wang, H.; Zhao, J. Safety risk analysis of aero-engine based on FTA-ANN. Ship Electron. Eng. 2021, 41, 122–127. [Google Scholar]
- Adabavazeh, N.; Nikbakht, M.; Amindoust, A.; Hassanzadeh-Tabrizi, S.A. Assessing the reliability of natural gas pipeline system in the presence of corrosion using fuzzy fault tree. Ocean Eng. 2024, 311, 118943. [Google Scholar] [CrossRef]
- Robert, C.P.; Casella, G.; Casella, G. Monte Carlo Statistical Methods; Springer: New York, NY, USA, 1999. [Google Scholar]
- Meyn, S.P.; Tweedie, R.L. Markov Chains and Stochastic Stability; Springer Science & Business Media: London, UK, 2012. [Google Scholar]
- Al-Duhaidahawi, H.M.K.; Abdulreza, J.; Sebai, M.; Harjan, S.A. An efficient model for financial risks assessment based on artificial neural networks. J. Southwest Jiaotong Univ. 2020, 55, 1–11. [Google Scholar]
- Islam, R.; Sinha, A.; Hussain, A.; Usama, M.; Ali, S.; Ahmed, S.; Gani, A.; Hassan, N.E.; Mohammadi, A.A.; Deshmukh, K. Application of Monte Carlo simulation and artificial neural network model to probabilistic health risk assessment in fluoride-endemic areas. Heliyon 2024, 10, e40887. [Google Scholar] [CrossRef]
- Rachedi, M.; Matallah, M.; Kotronis, P. Seismic behavior & risk assessment of an existing bridge considering soil-structure interaction using artificial neural networks. Eng. Struct. 2021, 232, 111800. [Google Scholar]
- Qiao, W.; Liu, Y.; Ma, X.; Liu, Y. A methodology to evaluate human factors contributed to maritime accident by mapping fuzzy FT into ANN based on HFACS. Ocean Eng. 2020, 197, 106892. [Google Scholar] [CrossRef]
- Lin, S.; Shen, S.; Zhou, A.; Xu, Y. Risk assessment and management of excavation system based on fuzzy set theory and machine learning methods. Autom. Constr. 2021, 122, 103490. [Google Scholar] [CrossRef]
- Dugan, J.B.; Bavuso, S.J.; Boyd, M.A. Dynamic fault-tree models for fault-tolerant computer systems. IEEE Trans. Reliab. 1992, 41, 363–377. [Google Scholar] [CrossRef]
- Dugan, J.B.; Sullivan, K.J.; Coppit, D. Developing a low-cost high-quality software tool for dynamic fault-tree analysis. IEEE Trans. Reliab. 2000, 49, 49–59. [Google Scholar] [CrossRef]
- Qin, G.; Li, R.; Yang, M.; Wang, B.; Ni, P.; Wang, Y. Failure probability estimation of natural gas pipelines due to hydrogen embrittlement using an improved fuzzy fault tree approach. J. Clean Prod. 2024, 448, 141601. [Google Scholar] [CrossRef]
- Karanović, V.; Ceylan, B.O.; Jocanović, M. Reliable ships: A fuzzy FMEA based risk analysis on four-ram type hydraulic steering system. Ocean Eng. 2024, 314, 119758. [Google Scholar] [CrossRef]
- Cheraghi, M.; Eslami Baladeh, A.; Khakzad, N. A fuzzy multi-attribute HAZOP technique (FMA-HAZOP): Application to gas wellhead facilities. Saf. Sci. 2019, 114, 12–22. [Google Scholar] [CrossRef]
- Solukloei, H.R.J.; Nematifard, S.; Hesami, A.; Mohammadi, H.; Kamalinia, M. A fuzzy-HAZOP/ant colony system methodology to identify combined fire, explosion, and toxic release risk in the process industries. Expert Syst. Appl. 2022, 192, 116418. [Google Scholar] [CrossRef]
- Ding, S.; Pan, X.; Zuo, D.; Zhang, W.; Sun, L. Uncertainty analysis of accident causality model using Credal Network with IDM method: A case study of hazardous material road transportation accidents. Process Saf. Environ. Protect. 2022, 158, 461–473. [Google Scholar] [CrossRef]
- Page, L.B.; Perry, J.E. Standard deviation as an alternative to fuzziness in fault tree models. IEEE Trans. Reliab. 1994, 43, 402–407. [Google Scholar] [CrossRef]
- Mirzaei Aliabadi, M.; Pourhasan, A.; Mohammadfam, I. Risk modelling of a hydrogen gasholder using Fuzzy Bayesian Network (FBN). Int. J. Hydrogen Energy 2020, 45, 1177–1186. [Google Scholar] [CrossRef]
- Cheng, S.J.; Hwang, C.L. Fuzzy Multiple Attribute Decision Making Methods and Applications; Springer-Verlag: New York, NY, USA, 1992. [Google Scholar]
- Abdelhafidh, M.; Fourati, M.; Chaari, L. Dynamic Bayesian network-based operational risk assessment for industrial water pipeline leakage. Comput. Ind. Eng. 2023, 183, 109466. [Google Scholar] [CrossRef]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Bhambu, A.; Bera, K.; Natarajan, S.; Suganthan, P.N. High frequency volatility forecasting and risk assessment using neural networks-based heteroscedasticity model. Eng. Appl. Artif. Intell. 2025, 149, 110397. [Google Scholar] [CrossRef]
- Jena, R.; Pradhan, B. Integrated ANN-cross-validation and AHP-TOPSIS model to improve earthquake risk assessment. Int. J. Disaster Risk Reduct. 2020, 50, 101723. [Google Scholar] [CrossRef]
- Panchal, F.S.; Panchal, M. Review on methods of selecting number of hidden nodes in artificial neural network. Int. J. Comput. Sci. Mob. Comput. 2014, 3, 455–464. [Google Scholar]
- Xiao, R.; Zayed, T.; Meguid, M.A.; Sushama, L. Dynamic risk assessment of natural gas transmission pipelines with LSTM networks and historical failure data. Int. J. Disaster Risk Reduct. 2024, 112, 104771. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, C.; Xu, N.; Peng, S.; Liu, C. Early warning of exchange rate risk based on structural shocks in international oil prices using the LSTM neural network model. Energy Econ. 2023, 126, 106921. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Investigation, Evaluation and Statistics Department of Emergency Management Department of Hebei Province. Investigation Report on the “11.28” Major Deflagration Accident of Shenghua Chemical Company of China National Chemical Corporation in Zhangjiakou, Hebei Province, 2019. Available online: https://www.jiangmen.gov.cn/bmpd/jmsyjglj/zwgk/zdlyxxgk/scaqsgdcbgxx/content/post_1487627.html (accessed on 20 May 2024).
- Ministry of Industry and Information Technology of the People’s Republic of China. Code for Design of Tank Farm of Petrochemical Storage and Transportation System; Ministry of Industry and Information Technology of the People’s Republic of China: Beijing, China, 2014.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).