Research on Investment Estimation of Prefabricated Buildings Based on Genetic Algorithm Optimization Neural Network
Abstract
1. Introduction
2. Improved BP Neural Network Model Based on GA
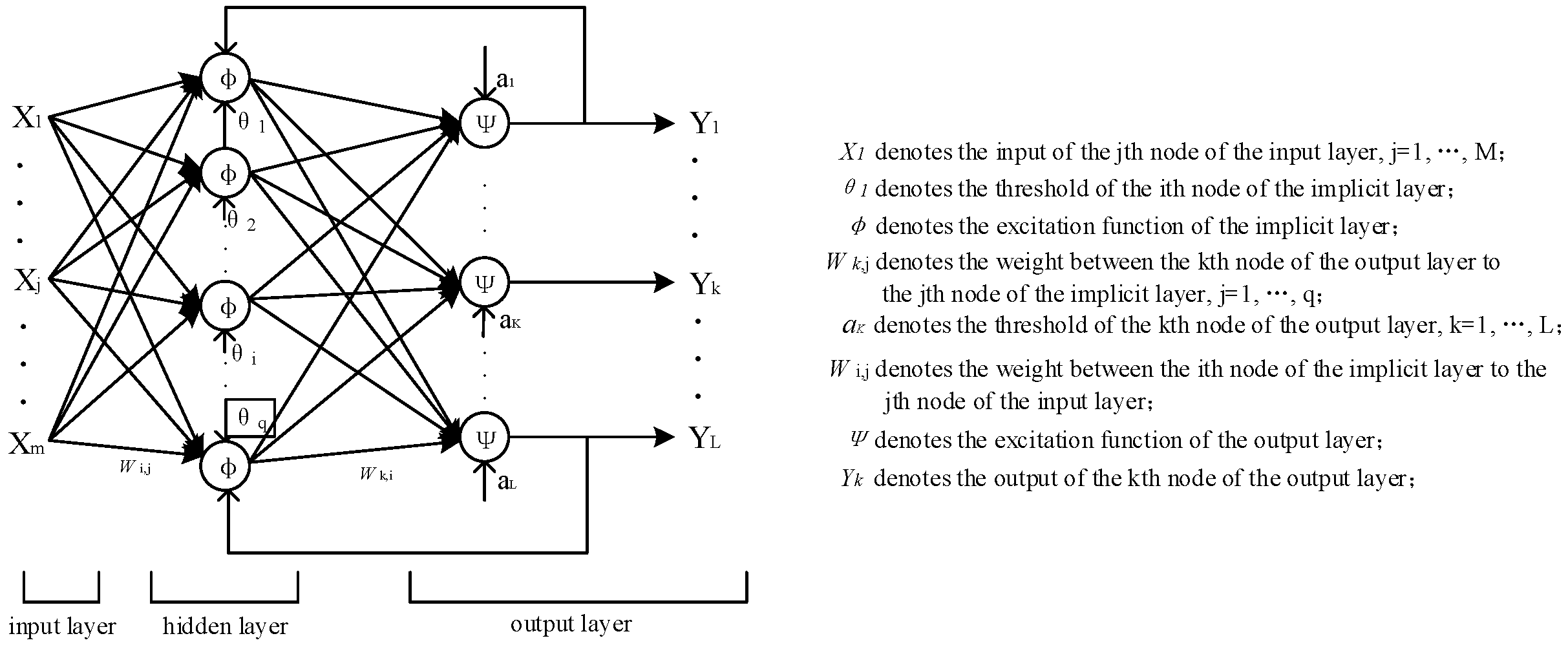
2.1. BP Neural Network Principle
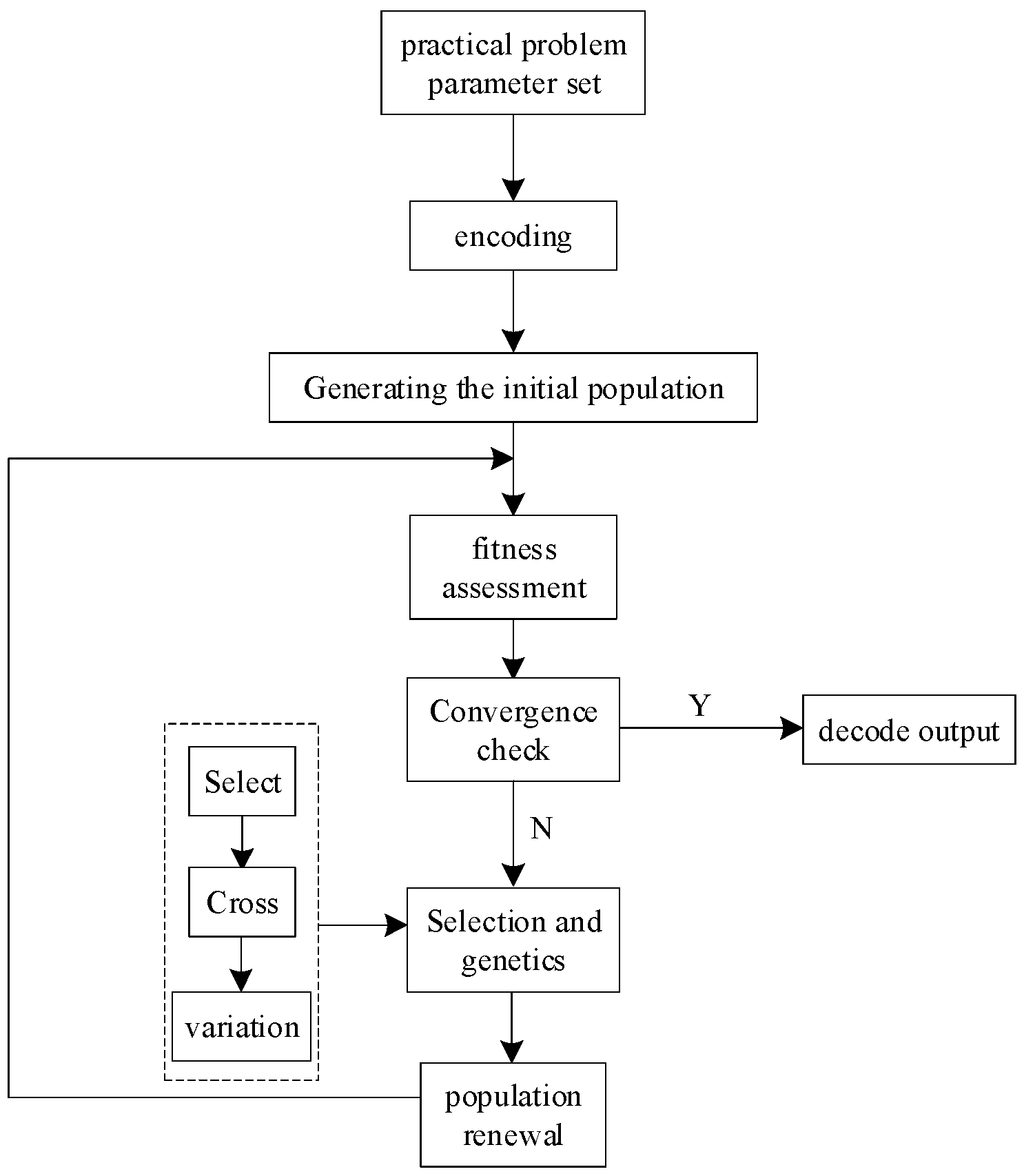
2.2. Principles of Genetic Algorithm
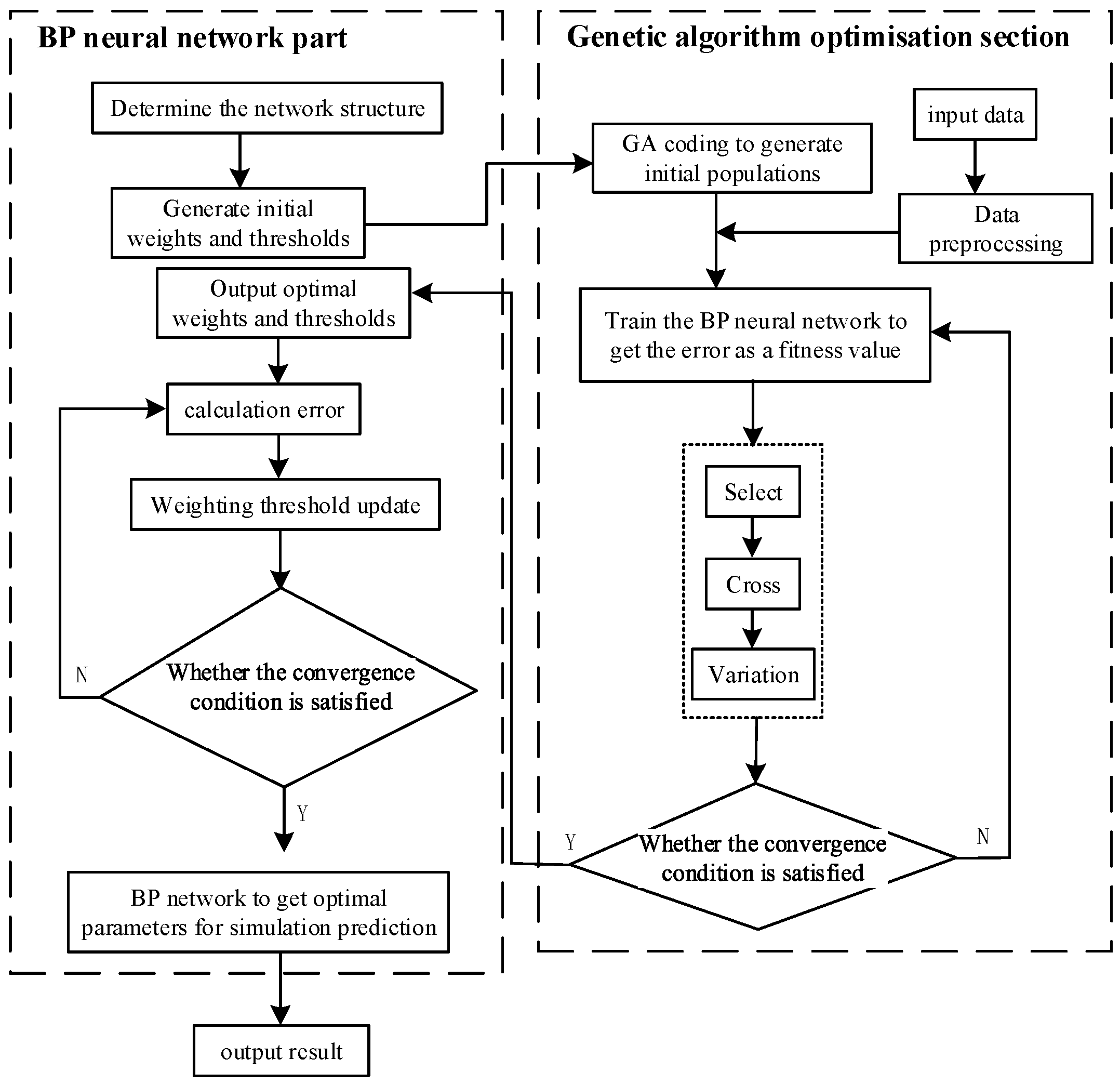
2.3. Construction of the GA–BP Neural Network Model
3. Determination of Engineering Eigenvectors
4. Case Studies
4.1. Neural Network Data Preprocessing
4.2. Model Simulation and Comparative Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, M.; Liang, J. Investment Estimation Method of Construction Project in Decision Stage. Pet. Plan. Eng. 2005, 53–55. [Google Scholar]
- Yan, H.; He, Z.; Gao, C.; Xie, M.; Sheng, H.; Chen, H. Investment estimation of prefabricated concrete buildings based on XGBoost machine learning algorithm. Adv. Eng. Inform. 2022, 54, 101789. [Google Scholar]
- Liu, M.; Luo, M. Cost estimation model of prefabricated construction for general contractors based on system dynamics. Eng. Constr. Archit. Manag. 2025, 32, 621–638. [Google Scholar]
- Choi, Y.; Park, C.Y.; Lee, C.; Yun, S.; Han, S.H. Conceptual cost estimation framework for modular projects: A case study on petrochemical plant construction. J. Civ. Eng. Manag. 2022, 28, 150–165. [Google Scholar]
- Sievers, S.; Seifert, T.; Franzen, M.; Schembecker, G.; Bramsiepe, C. Fixed capital investment estimation for modular production plants. Chem. Eng. Sci. 2017, 158, 395–410. [Google Scholar]
- Zhang, P.; Dong, Y. Strategy transformation of big data green supply chain by using improved genetic optimization algorithm. Soft Comput. 2023, 1–10. [Google Scholar] [CrossRef]
- Yunlong, W.; Hao, W.; Guan, G.; Li, K.; Lin, Y.; Chai, S. Intelligent Layout Design of Ship Pipeline Using a Particle Swarm Optimisation Integrated Genetic Algorithm. Int. J. Marit. Eng. 2021, 163. [Google Scholar] [CrossRef]
- Wang, B.; Yang, C.; Ding, Y. Non-Dominated Sorted Genetic Algorithm-II Algorithm-based Multi-Objective Layout Optimization of Solid Wood Panels. BioResources 2022, 17, 94–108. [Google Scholar]
- Duan, B.; Guo, C.; Liu, H. A hybrid genetic-particle swarm optimization algorithm for multi-constraint optimization problems. Soft Comput. 2022, 26, 11695–11711. [Google Scholar]
- Langazane, S.N.; Saha, A.K. Effects of Particle Swarm Optimization and Genetic Algorithm Control Parameters on Overcurrent Relay Selectivity and Speed. IEEE Access 2022, 10, 4550–4567. [Google Scholar]
- Deep, K.; Thakur, M. Development of a Mutation Operator in a Real- Coded Genetic Algorithm for Bridge Model Optimization. Appl. Math. Comput. 2007, 193, 211–230. [Google Scholar]
- Kim, G.H.; Yoon, J.E.; An, S.H.; Cho, H.H.; Kang, K.I. Neural network model incorporating a Genetic Algorithm in estimating construction costs. Build. Environ. 2004, 39, 1333–1340. [Google Scholar]
- Zhou, C. Discussion of Project Investment Estimation Method based on BP Neural Network. Railw. Eng. Cost Manag. 2015, 30, 6–9+13. [Google Scholar]
- Pan, Y.H.; Zhang, Y.L.; Cai, Y.J.; Wu, H.H.; Sui, H.Y. Research on Highway Engineering Cost Estimation Based on the GA-BP Algorithm. J. Chongqing Jiaotong Univ. (Nat. Sci.) 2016, 35, 141–145. [Google Scholar]
- Zhang, F.; Liang, X. Research on investment estimation method of urban rail transit project based on GA-ELM. J. Railw. Sci. Eng. 2019, 16, 1842–1848. [Google Scholar]
- Wang, F.; Zhang, S.; Li, Y. Application of Neural Network Model of BAS-BP in Investment Estimation of Prefabricated Building. J. Anhui Univ. Technol. (Nat. Sci.) 2019, 36, 382–387. [Google Scholar]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar]
- MATLAB Technology Alliance; Liu, B.; Guo, H. MATLAB Neural Network Super Learning Manual; Posts & Telecom Press: Beijing, China, 2014; pp. 159–161. [Google Scholar]
- Scrucca, L. GA: A package for Genetic Algorithms in R. J. Stat. Softw. 2013, 53, 1–37. [Google Scholar]
- Xiao, Y.; Yang, J.; Zhou, S. Engineering Optimization—Theory, Model and Algorithm; Beihang University Press: Beijing, China, 2021; Volume 1, p. 317. [Google Scholar]
- Hu, Q.; Cai, B.; He, Z.; Dai, Z. Investment estimation of prefabricated building based on BP neural network. J. Chang. Univ. Sci. Technol. (Nat. Sci.) 2018, 15, 66–72+86. [Google Scholar]
- Han, Z.; Zhang, Q.; Wen, F. Rough sets: Theory and application. Inf. Control 1998, 38–46. [Google Scholar]
- Hu, Q.; Tian, X.; He, Z. Green building investment estimation method based on genetic algorithm optimized extreme learning machine. Build. Econ. 2020, 41, 125–130. [Google Scholar]
- Xia, F.; Fang, S.; Chen, P. Typical Project Case About Prefabricated Building. Hous. Sci. 2015, 35, 18–23. [Google Scholar]
- Zhao, W.; Wang, S. Research on the Investment Estimation of Prefabricated Building Based on BAS—BP Model. J. Anhui Univ. Sci. Technol. (Nat. Sci.) 2020, 40, 73–79. [Google Scholar]
- Xu, W.; Shen, J.; Chen, X.; Wan, S. Construction cost prediction model based on RS-RBFNN. J. Qingdao Univ. Technol. 2021, 42, 96–102. [Google Scholar]
| Engineering Features | Quantify the Value | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Foundation type | Independent foundation | Raft foundation | Strip foundations | Pile foundations | |
| Structure type | Shear wall structure | Frame structure | Frame shear wall structure | Tube structure | Prefabricated containerized structure |
| Area | Enter based on actual data, unit: m2 | ||||
| Number of floors of the building | Enter based on actual data | ||||
| The Type of prefabricated component | Prefabricated laminated floor slabs | Prefabricated sandwich insulated exterior wall panels | Prefabricated interior wall panels | Prefabricated stairs | Prefabricated air conditioning panels |
| Prefabricated component connections | Grouting rebar sleeve connection | Reinforcement slurry anchor lap connection | |||
| Roofing and waterproofing | Flat roof Class 1 waterproof | Flat roof Class 2 waterproof | Flat roof Class 3 waterproof | Pitched roof Class 1 waterproof | Curved roofs Class 1 waterproof |
| Decoration works | Simple decoration | Standard finish | Mid-range finish | High-end decoration | |
| Installation, Electrical and Water Supply and Drainage Engineering/(Yuan·m−2). | Enter based on actual data | ||||
| Assembly rate/%. | Enter based on actual data | ||||
| Project cost index | Enter based on actual data | ||||
| Sample No. | Conditional Attributes | Decision Attributes | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Foun-dation Type | Struc-ture Type | Area | Number of Floors of the Building | The Type of Prefabric-ated Component | Prefabricated Component Connections | Roofing and Waterproofing | Decoration Works | Installation, Electrical and Water Supply and Drainage Works (RMB/m2). | Asse-mbly rate (%) | Project Cost Index | Cost per Square Meter (RMB/m2) | |
| 1 | 4 | 1 | 1 | 2 | 1 + 4 + 5 | 1 | 1 | 1 | 3 | 1 | 2 | 3 |
| 2 | 1 | 1 | 3 | 4 | 1 + 3 | 1 | 1 | 2 | 1 | 4 | 3 | 1 |
| 3 | 2 | 1 | 3 | 1 | 1 + 2 + 3 + 4 | 1 | 1 | 2 | 3 | 2 | 3 | 5 |
| 4 | 2 | 1 | 1 | 2 | 1 + 2 + 3 + 4 | 2 | 1 | 2 | 1 | 1 | 2 | 4 |
| 5 | 2 | 4 | 3 | 1 | 1 + 2 + 3 | 1 | 1 | 1 | 3 | 1 | 3 | 2 |
| 6 | 1 | 1 | 3 | 4 | 1 + 3 | 2 | 1 | 2 | 1 | 4 | 2 | 1 |
| 7 | 2 | 1 | 1 | 2 | 1 + 2 + 3 | 1 | 1 | 2 | 1 | 1 | 2 | 3 |
| 8 | 2 | 3 | 5 | 3 | 1 + 4 | 1 | 2 | 1 | 5 | 1 | 2 | 3 |
| 9 | 2 | 3 | 3 | 2 | 1 + 4 | 1 | 2 | 1 | 5 | 4 | 2 | 5 |
| 10 | 4 | 1 | 2 | 1 | 1 + 4 + 5 | 1 | 1 | 1 | 1 | 1 | 2 | 2 |
| 11 | 2 | 4 | 4 | 2 | 1 + 2 + 3 | 1 | 1 | 2 | 1 | 1 | 3 | 1 |
| 12 | 2 | 1 | 1 | 1 | 1 + 2 + 3 | 1 | 4 | 2 | 1 | 1 | 3 | 2 |
| 13 | 1 | 1 | 5 | 4 | 1 + 2 + 3 | 2 | 4 | 2 | 1 | 1 | 3 | 2 |
| 14 | 2 | 1 | 2 | 1 | 1 + 2 + 3 | 1 | 1 | 2 | 1 | 1 | 3 | 1 |
| 15 | 2 | 1 | 4 | 2 | 1 + 3 | 1 | 1 | 2 | 3 | 4 | 3 | 2 |
| 16 | 2 | 1 | 3 | 2 | 1 + 3 | 1 | 1 | 1 | 1 | 2 | 3 | 2 |
| Initial Features | Frequency | Initial Features | Frequency |
|---|---|---|---|
| Base type | 8 | Structure type | 9 |
| Area | 21 | Number of floors of the building | 16 |
| The Type of prefabricated component | 16 | Prefabricated component connections | 21 |
| Roofing and waterproofing | 17 | Decoration works | 14 |
| Installation, electrical and plumbing works | 12 | Assembly rate | 14 |
| Project cost index | 17 |
| Sample Number | Area | Number of Floors of the Building | The Type of Prefabricated Component | Prefabricated Component Connections | Roofing and Waterproofing | Decoration Works | Assembly Rate (%) | Project Cost Index | Cost per Square Meter (RMB/m2) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 21,749 | 25 | 1 + 4 + 5 | 1 | 1 | 1 | 51 | 100 | 2033.03 |
| 2 | 13,841 | 18 | 1 + 3 | 1 | 1 | 2 | 50 | 105 | 2079.71 |
| 3 | 22,164 | 33 | 1 + 2 + 3 + 4 | 1 | 1 | 2 | 65 | 109 | 2286.57 |
| 4 | 20,020 | 30 | 1 + 2 + 3 + 4 | 2 | 1 | 2 | 68 | 113 | 2265.35 |
| 5 | 23,860 | 33 | 1 + 2 + 3 | 1 | 1 | 1 | 63 | 105 | 2104.47 |
| 6 | 14,638 | 18 | 1 + 3 | 2 | 1 | 2 | 50 | 113 | 1997.14 |
| 7 | 19,908 | 30 | 1 + 2 + 3 | 1 | 1 | 2 | 62 | 113 | 2195.35 |
| 8 | 3167 | 6 | 1 + 4 | 1 | 2 | 1 | 30 | 100 | 2805 |
| 9 | 15,733 | 27 | 1 + 4 | 1 | 2 | 1 | 32 | 100 | 2743 |
| 10 | 20,453 | 34 | 1 + 4 + 5 | 1 | 1 | 1 | 51 | 100 | 2192.68 |
| 11 | 16,451 | 27 | 1 + 2 + 3 | 1 | 1 | 2 | 60 | 105 | 2094.53 |
| 12 | 20,246 | 33 | 1 + 2 + 3 | 1 | 4 | 2 | 60 | 109 | 2153.62 |
| 13 | 12,881 | 18 | 1 + 2 + 3 | 2 | 4 | 2 | 60 | 105 | 2135.28 |
| 14 | 21,468 | 33 | 1 + 2 + 3 | 1 | 1 | 2 | 58 | 109 | 2076.81 |
| 15 | 18,200 | 27 | 1 + 3 | 1 | 1 | 2 | 50 | 105 | 2006.45 |
| 16 | 19,309 | 30 | 1 + 3 | 1 | 1 | 1 | 55 | 109 | 2073.73 |
| Sample Number | Area | Number of Floors of the Building | The Type of Prefabricated Component | Prefabricated Component Connections | Roofing and Waterproofing | Decoration Works | Assembly Rate (%) | Project Cost Index | Cost per Square Meter (RMB/m2) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.796 | 0.357 | 1.000 | −1.000 | −1.000 | −1.000 | 0.105 | −1.000 | −0.911 |
| 2 | 0.032 | −0.143 | −1.000 | −1.000 | −1.000 | 1.000 | 0.053 | −0.231 | −0.796 |
| 3 | 0.836 | 0.929 | 1.000 | −1.000 | −1.000 | 1.000 | 0.842 | 0.385 | −0.283 |
| 4 | 0.629 | 0.714 | 1.000 | 1.000 | −1.000 | 1.000 | 1.000 | 1.000 | −0.336 |
| 5 | 1.000 | 0.929 | −0.333 | −1.000 | −1.000 | −1.000 | 0.737 | −0.231 | −0.734 |
| 6 | 0.109 | −0.143 | −1.000 | 1.000 | −1.000 | 1.000 | 0.053 | 1.000 | −1.000 |
| 7 | 0.618 | 0.714 | −0.333 | −1.000 | −1.000 | 1.000 | 0.684 | 1.000 | −0.509 |
| 8 | −1.000 | −1.000 | −0.667 | −1.000 | −0.333 | −1.000 | −1.000 | −1.000 | 1.000 |
| 9 | 0.215 | 0.500 | −0.667 | −1.000 | −0.333 | −1.000 | −0.895 | −1.000 | 0.847 |
| 10 | 0.560 | 0.714 | −1.000 | −1.000 | −1.000 | −1.000 | 0.316 | 0.385 | −0.810 |
| 11 | 0.284 | 0.500 | −0.333 | −1.000 | −1.000 | 1.000 | 0.579 | −0.231 | −0.759 |
| 12 | 0.651 | 0.929 | −0.333 | −1.000 | 1.000 | 1.000 | 0.579 | 0.385 | −0.613 |
| 13 | −0.061 | −0.143 | −0.333 | 1.000 | 1.000 | 1.000 | 0.579 | −0.231 | −0.658 |
| 14 | 0.769 | 0.929 | −0.333 | −1.000 | −1.000 | 1.000 | 0.474 | 0.385 | −0.803 |
| 15 | 0.453 | 0.500 | −1.000 | −1.000 | −1.000 | 1.000 | 0.053 | −0.231 | −0.977 |
| 16 | 0.671 | 1.000 | 1.000 | −1.000 | −1.000 | −1.000 | 0.105 | −1.000 | −0.516 |
| Number | Real Value | Predicted Value | Number | Real Value | Predicted Value |
|---|---|---|---|---|---|
| 1 | 2033.03 | 2092.03 | 9 | 2743 | 2624.79 |
| 2 | 2079.71 | 2052.06 | 10 | 2192.68 | 2137.67 |
| 3 | 2286.57 | 2280.84 | 11 | 2094.53 | 2031.71 |
| 4 | 2265.35 | 2212.65 | 12 | 2153.62 | 2130.39 |
| 5 | 2104.47 | 1997.63 | 13 | 2135.28 | 2138.09 |
| 6 | 1997.14 | 2196.37 | 14 | 2076.81 | 2149.30 |
| 7 | 2195.35 | 2162.74 | 15 | 2006.45 | 2034.42 |
| 8 | 2805 | 2637.37 | Test set | 2073.73 | 2053.40 |
| Name | MSE | MAE | MAPE (%) |
|---|---|---|---|
| Training set | 7657.27 | 67.60 | 3.02 |
| Test set | 413.49 | 20.33 | 0.98 |
| Number | Real Value | Predicted Value | Number | Real Value | Predicted Value |
|---|---|---|---|---|---|
| 1 | 2033.03 | 2453.59 | 9 | 2743 | 1947.21 |
| 2 | 2079.71 | 3923.95 | 10 | 2192.68 | 1092.39 |
| 3 | 2286.57 | 3552.40 | 11 | 2094.53 | 3542.95 |
| 4 | 2265.35 | 8047.56 | 12 | 2153.62 | 6431.30 |
| 5 | 2104.47 | 3538.07 | 13 | 2135.28 | 3401.63 |
| 6 | 1997.14 | 1471.92 | 14 | 2076.81 | 3542.92 |
| 7 | 2195.35 | 3269.72 | 15 | 2006.45 | 3544.70 |
| 8 | 2805 | 770.62 | Test set | 2073.73 | 2010.36 |
| Name | MSE | MAE | MAPE (%) |
|---|---|---|---|
| Training set | 4,973,203.32 | 1751.55 | 79.29 |
| Test set | 4015.43 | 63.37 | 3.06 |
| Optimization Algorithm | MSE | MAE | MAPE |
|---|---|---|---|
| genetic algorithm | 9528.55 ± 8926.31 | 73.35 ± 44.56 | 3.3 ± 2.0% |
| PSO algorithm | 1,406,319.31 ± 626,556.23 | 1123.71 ± 245.06 | 51.1 ± 9.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Zhao, W. Research on Investment Estimation of Prefabricated Buildings Based on Genetic Algorithm Optimization Neural Network. Appl. Sci. 2025, 15, 3474. https://doi.org/10.3390/app15073474
Gao J, Zhao W. Research on Investment Estimation of Prefabricated Buildings Based on Genetic Algorithm Optimization Neural Network. Applied Sciences. 2025; 15(7):3474. https://doi.org/10.3390/app15073474
Chicago/Turabian StyleGao, Jin, and Wanhua Zhao. 2025. "Research on Investment Estimation of Prefabricated Buildings Based on Genetic Algorithm Optimization Neural Network" Applied Sciences 15, no. 7: 3474. https://doi.org/10.3390/app15073474
APA StyleGao, J., & Zhao, W. (2025). Research on Investment Estimation of Prefabricated Buildings Based on Genetic Algorithm Optimization Neural Network. Applied Sciences, 15(7), 3474. https://doi.org/10.3390/app15073474






