Seismic Random Noise Attenuation via Low-Rank Tensor Network
Abstract
1. Introduction
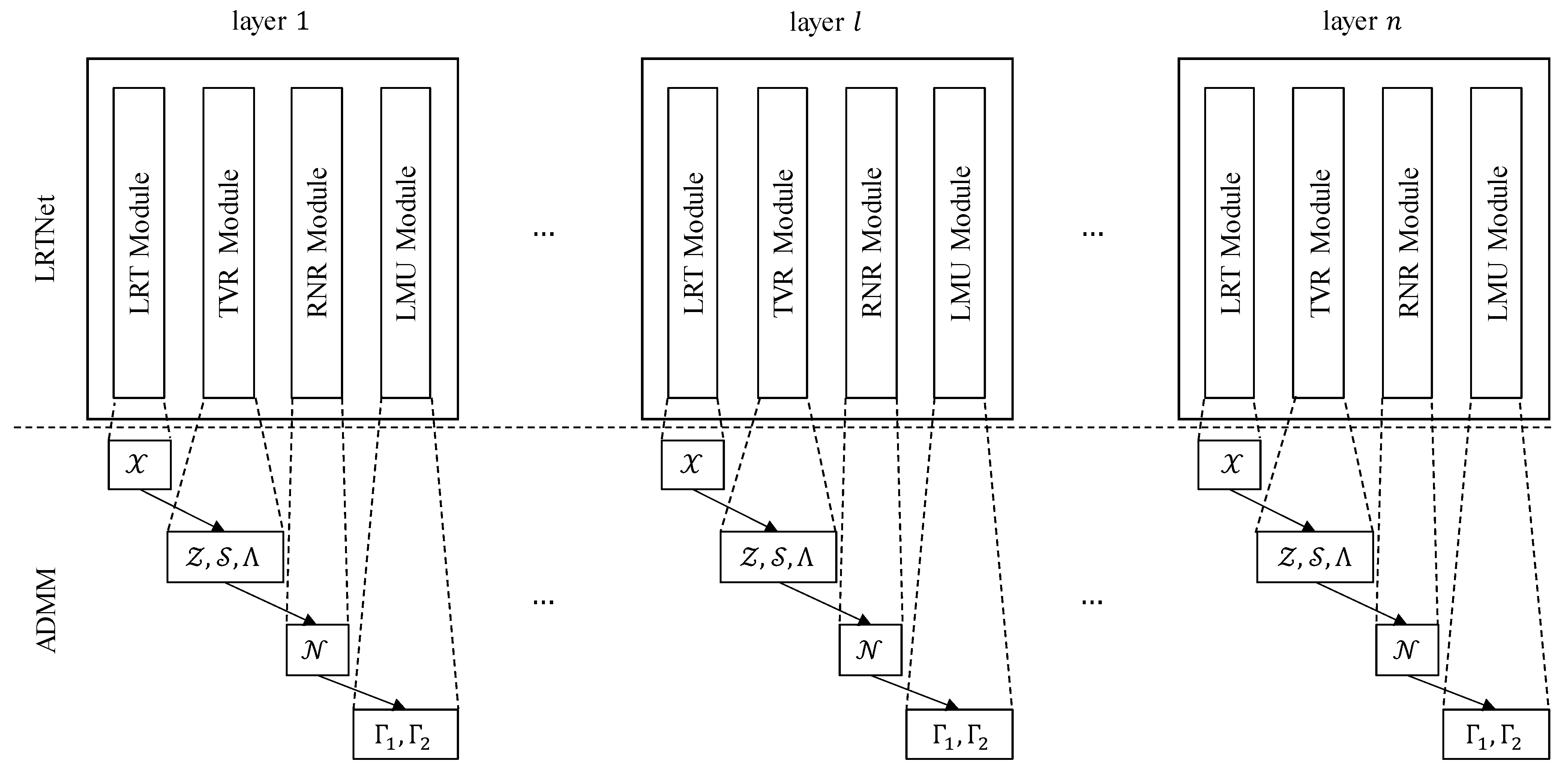
2. Materials and Methods
2.1. Preliminaries
2.2. Problem Statement and Modeling
2.3. Optimization Procedure
2.4. Automatic Parameter Optimization with DNN
| Algorithm 1 Low-Rank Tensor Network |
| Require: |
| Ensure: |
Set and to zero tensor. ▹Initial // layer 1 . ▹update with LRT Module . ▹update with TVR Module . ▹update with RNR Module . ▹update and with LMU Module // layer 2 to layer // layer n . . . . . |
2.5. Data and Data Processing
- We select the first 20 volumes from the training set to train our LRTNet. This decision is based on preliminary experiments where we observed that using the full 200-volume training set required a similar number of epochs to converge, with only a marginal improvement in average SNR (less than 0.5 dB). Given the significant computational cost and time required for training on the full dataset (the limitation of efficiency is discussed in Section 4), we opted for the smaller subset to balance performance and computational efficiency. For each volume, we generate a corresponding noisy volume by adding Gaussian noise at 0 dB SNR, while retaining the original noise-free volume as the ground truth label. The choice of 0 dB SNR is motivated by the observation that all methods perform well at lower noise levels, while performance degrades at higher noise levels. At 0 dB SNR, our method demonstrates a clear advantage over baseline approaches, making it a balanced and representative noise level for evaluation.
- Validation Data: We use all 20 validation volumes. We apply identical noise injection (0 dB Gaussian) to create noisy volumes, with denoised outputs compared against the pristine volumes for metric calculation.
- F3-2020: This is a marine 3D survey of the offshore Netherlands (original size: ). To avoid redundant processing, we extract a random sub-volume () containing representative geological features. No artificial noise is added, as the raw data inherently contain field-acquisition noise.
- Penobscot: This is a publicly available North Atlantic survey with complex subsurface structures. Following the same rationale, we select a sub-volume from the “1-PSTM stack agc” data. Denoising is applied directly to the native noisy volume without preprocessing.
3. Results
3.1. Experimental Setup
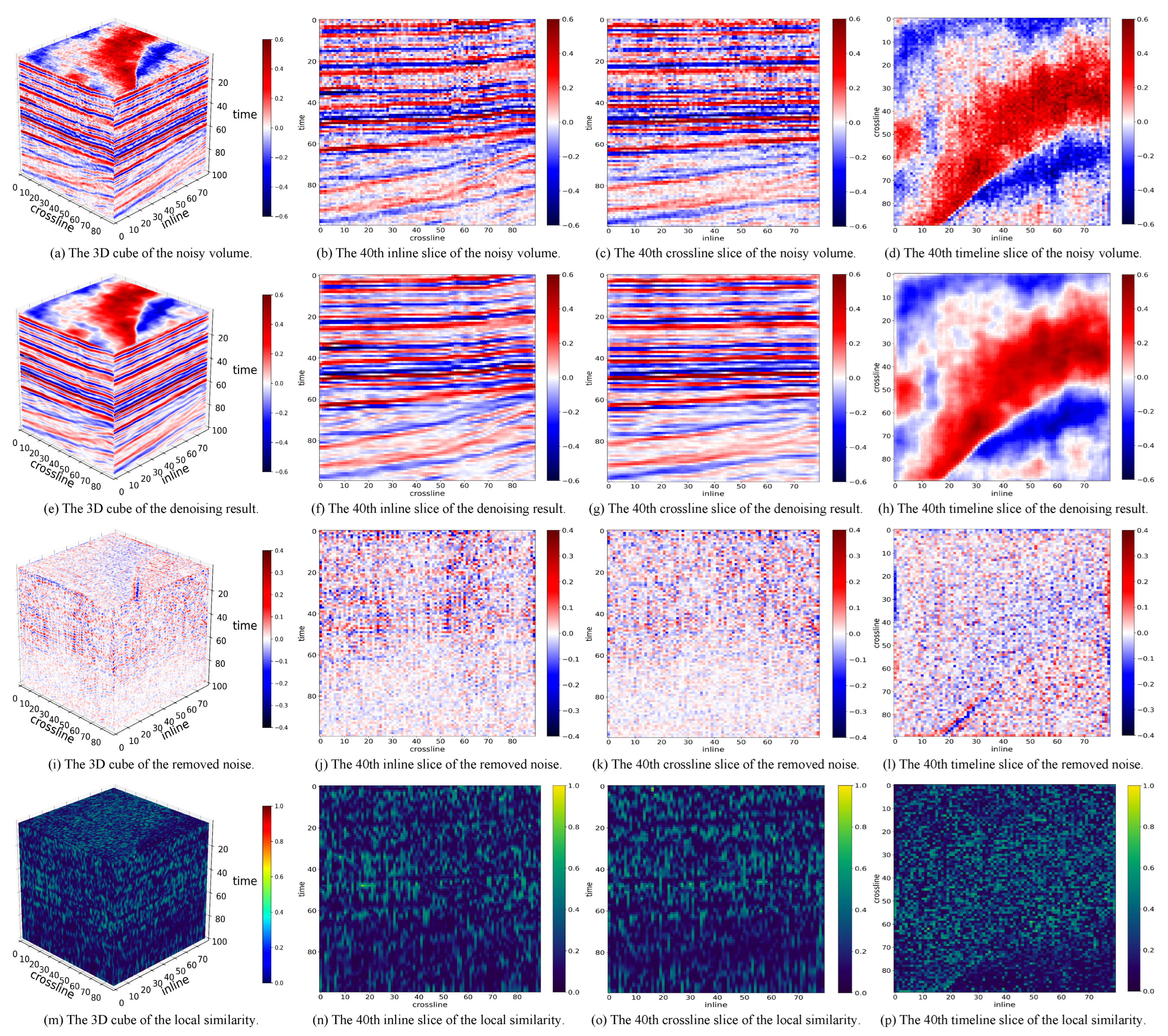
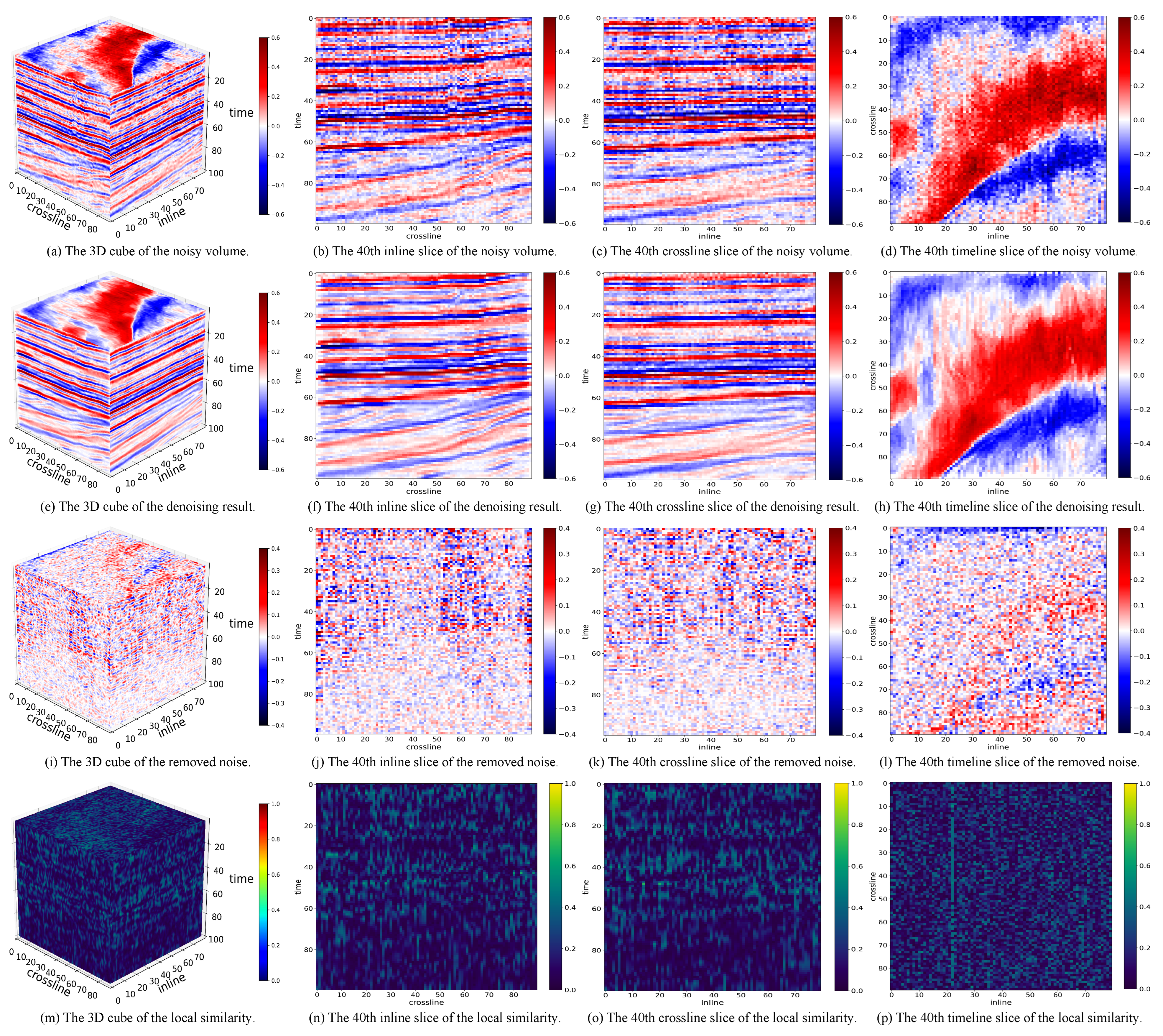
3.2. Experimental Results on Synthetic Data
3.3. Experimental Results on F3-2020
3.4. Experimental Results on Penobscot
4. Discussion
- As presented and analyzed in Section 3, LRTNet exhibits more severe signal leakage compared to Pyseistr and TNN-SSTV. While the severity is not significant in either qualitative or quantitative comparisons, this remains a notable limitation. Additionally, the local similarity metric, which is a tensor of the same size as the input signal, provides only a coarse quantitative comparison through its mean and variance. Future work could explore more refined metrics or visualization techniques to better capture the spatial and temporal characteristics of signal leakage, enabling a more nuanced evaluation of denoising performance.
- LRTNet leverages DL to tune its inner parameters for LRA. Although DL is not the core of LRTNet, it introduces a common challenge: the gap between synthetic and real field data. Deploying LRTNet, which is trained on synthetic data, directly to real data may result in performance degradation due to domain differences. Training LRTNet on real data could mitigate this issue, but it presents its own challenges. For instance, the lack of ground truth for real data complicates the calibration and validation of the model. Furthermore, geographical variations between training and validation datasets may still lead to performance gaps. Potential solutions to this include domain adaptation techniques, transfer learning, and the development of semi-supervised approaches that leverage both synthetic and real data.
- Compared to purely DL-based methods, LRTNet has a significant efficiency drawback. DL methods are inherently well-suited for parallelization, enabling the batch processing of multiple data samples. In contrast, LRTNet follows the ADMM framework, which processes data sequentially, one sample at a time. This limitation restricts the scalability of LRTNet, particularly for large-scale datasets. Future improvements could focus on optimizing the ADMM framework for parallel processing to enhance the computational efficiency of LRTNet.
- While LRTNet demonstrates strong performance under controlled noise conditions, its robustness to varying noise levels and types in real-world scenarios remains to be fully explored. Real filed data often contain complex noise patterns that may differ significantly from the synthetic noise used during training. Investigating LRTNet’s performance under diverse noise conditions and developing adaptive mechanisms to handle noise variability could further enhance LRTNet’s practical applicability.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LRA | Low-rank approximation |
| LRMA | Low-rank matrix approximation |
| LRTA | Low-rank tensor approximation |
| DL | Deep learning |
| TV | Total variation |
| WTNNM | Weighted tensor nuclear norm minimization |
| ADMM | Alternating direction method of multipliers |
| LRTNet | Low-rank tensor network |
References
- Qu, Z.; Gao, Y.; Li, S.; Zhang, X. A Hybrid Deep Learning Approach for Integrating Transient Electromagnetic and Magnetic Data to Enhance Subsurface Anomaly Detection. Appl. Sci. 2025, 15, 3125. [Google Scholar] [CrossRef]
- Wang, Y.; Ge, Q.; Lu, W.; Yan, X. Well-logging constrained seismic inversion based on closed-loop convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5564–5574. [Google Scholar]
- Wu, X.; Shi, Y.; Fomel, S.; Liang, L.; Zhang, Q.; Yusifov, A.Z. FaultNet3D: Predicting fault probabilities, strikes, and dips with a single convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9138–9155. [Google Scholar] [CrossRef]
- Wen, Y.; Qian, F.; Guo, W.; Zong, J.; Peng, D.; Chen, K.; Hu, G. VSP Upgoing and Downgoing Wavefield Separation: A Hybrid Model-Data Driven Approach. IEEE Trans. Geosci. Remote. Sens. 2025, 1. [Google Scholar] [CrossRef]
- Li, S.; Geng, X.; Zhu, L.; Ji, L.; Zhao, Y. Hyperspectral Image Denoising Based on Principal-Third-Order-Moment Analysis. Remote Sens. 2024, 16, 276. [Google Scholar] [CrossRef]
- Henneberger, K.; Qin, J. Hyperspectral Band Selection via Tensor Low Rankness and Generalized 3DTV. Remote Sens. 2025, 17, 567. [Google Scholar] [CrossRef]
- Wu, Y.; Xu, W.; Zheng, L. Hyperspectral Image Mixed Noise Removal via Double Factor Total Variation Nonlocal Low-Rank Tensor Regularization. Remote Sens. 2024, 16, 1686. [Google Scholar] [CrossRef]
- Liu, S.; Feng, J.; Tian, Z. Variational Low-Rank Matrix Factorization with Multi-Patch Collaborative Learning for Hyperspectral Imagery Mixed Denoising. Remote Sens. 2021, 13, 1101. [Google Scholar] [CrossRef]
- Liu, H.; Li, H.; Wu, Z.; Wei, Z. Hyperspectral Image Recovery Using Non-Convex Low-Rank Tensor Approximation. Remote Sens. 2020, 12, 2264. [Google Scholar] [CrossRef]
- Qian, F.; Pan, S.; Zhang, G. Tensor Computation for Seismic Data Processing: Linking Theory and Practice; Earth Systems Data and Models Series; Springer: Cham, Switzerland, 2025. [Google Scholar]
- Shao, O.; Wang, L.; Hu, X.; Long, Z. Seismic denoising via truncated nuclear norm minimization. Geophysics 2021, 86, V153–V169. [Google Scholar]
- Li, J.; Wang, D.; Ji, S.; Li, Y.; Qian, Z. Seismic noise suppression using weighted nuclear norm minimization method. J. Appl. Geophys. 2017, 146, 214–220. [Google Scholar] [CrossRef]
- Liu, X.; Chen, X.; Li, J.; Chen, Y. Nonlocal weighted robust principal component analysis for seismic noise attenuation. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1745–1756. [Google Scholar] [CrossRef]
- Li, J.; Fan, W.; Li, Y.; Qian, Z. Low-frequency noise suppression in desert seismic data based on an improved weighted nuclear norm minimization algorithm. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1993–1997. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, Z.; Gu, H.; Wu, X.; Liu, S. Hankel low-rank approximation for seismic noise attenuation. IEEE Trans. Geosci. Remote Sens. 2018, 57, 561–573. [Google Scholar] [CrossRef]
- Oropeza, V.; Sacchi, M. Simultaneous seismic data denoising and reconstruction via multichannel singular spectrum analysis. Geophysics 2011, 76, V25–V32. [Google Scholar] [CrossRef]
- Huang, W.; Wang, R.; Chen, Y.; Li, H.; Gan, S. Damped multichannel singular spectrum analysis for 3D random noise attenuation. Geophysics 2016, 81, V261–V270. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, W.; Zhang, D.; Chen, W. An open-source Matlab code package for improved rank-reduction 3D seismic data denoising and reconstruction. Comput. Geosci. 2016, 95, 59–66. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, Y.; Chen, W.; Zu, S.; Huang, W.; Zhang, D. Empirical low-rank approximation for seismic noise attenuation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4696–4711. [Google Scholar] [CrossRef]
- Adamo, A.; Mazzucchelli, P.; Bienati, N. Irregular interpolation of seismic data through low-rank tensor approximation. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4292–4295. [Google Scholar]
- Qian, F.; Hua, H.; Wen, Y.; Zong, J.; Zhang, G.; Hu, G. Unsupervised Intense VSP Coupling Noise Suppression with Iterative Robust Deep Learning. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5901817. [Google Scholar] [CrossRef]
- Anvari, R.; Kahoo, A.R.; Mohammadi, M.; Pouyan, A.A. Random noise attenuation in 3D seismic data by iterative block tensor singular value thresholding. In Proceedings of the 2017 3rd Iranian Conference on Intelligent Systems and Signal Processing (ICSPIS), Shahrood, Iran, 20–21 December 2017; pp. 164–168. [Google Scholar]
- Anvari, R.; Mohammadi, M.; Kahoo, A.R. Enhancing 3-D seismic data using the t-SVD and optimal shrinkage of singular value. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 382–388. [Google Scholar] [CrossRef]
- Qian, F.; Yue, Y.; He, Y.; Yu, H.; Zhou, Y.; Tang, J.; Hu, G. Unsupervised seismic footprint removal with physical prior augmented deep autoencoder. IEEE Trans. Geosci. Remote. Sens. 2023, 61, 5910920. [Google Scholar] [CrossRef]
- Qian, F.; Liu, Z.; Wang, Y.; Zhou, Y.; Hu, G. Ground Truth-Free 3-D Seismic Random Noise Attenuation via Deep Tensor Convolutional Neural Networks in the Time-Frequency Domain. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5911317. [Google Scholar] [CrossRef]
- Feng, J.; Liu, X.; Li, X.; Xu, W.; Liu, B. Low-rank tensor minimization method for seismic denoising based on variational mode decomposition. IEEE Geosci. Remote Sens. Lett. 2021, 19, 7504805. [Google Scholar]
- Feng, J.; Li, X.; Liu, X.; Chen, C.; Chen, H. Seismic data denoising based on tensor decomposition with total variation. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1303–1307. [Google Scholar] [CrossRef]
- Gu, X.; Collet, O.; Tertyshnikov, K.; Pevzner, R. Removing Instrumental Noise in Distributed Acoustic Sensing Data: A Comparison Between Two Deep Learning Approaches. Remote Sens. 2024, 16, 4150. [Google Scholar] [CrossRef]
- Banjade, T.P.; Zhou, C.; Chen, H.; Li, H.; Deng, J.; Zhou, F.; Adhikari, R. Seismic Random Noise Attenuation Using DARE U-Net. Remote Sens. 2024, 16, 4051. [Google Scholar] [CrossRef]
- Ding, M.; Zhou, Y.; Chi, Y. Self-Attention Generative Adversarial Network Interpolating and Denoising Seismic Signals Simultaneously. Remote Sens. 2024, 16, 305. [Google Scholar] [CrossRef]
- Zhao, H.; Zhou, Y.; Bai, T.; Chen, Y. A U-Net Based Multi-Scale Deformable Convolution Network for Seismic Random Noise Suppression. Remote Sens. 2023, 15, 4569. [Google Scholar] [CrossRef]
- Wang, W.; Yang, J.; Huang, J.; Li, Z.; Sun, M. Outlier Denoising Using a Novel Statistics-Based Mask Strategy for Compressive Sensing. Remote Sens. 2023, 15, 447. [Google Scholar] [CrossRef]
- Yang, L.; Chen, W.; Wang, H.; Chen, Y. Deep Learning Seismic Random Noise Attenuation via Improved Residual Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7968–7981. [Google Scholar] [CrossRef]
- Liu, D.; Wang, W.; Wang, X.; Wang, C.; Pei, J.; Chen, W. Poststack Seismic Data Denoising Based on 3-D Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1598–1629. [Google Scholar] [CrossRef]
- Yuan, Y.; Si, X.; Zheng, Y. Ground-roll attenuation using generative adversarial networks. Geophysics 2020, 85, WA255–WA267. [Google Scholar] [CrossRef]
- Sun, J.; Slang, S.; Elboth, T.; Greiner, T.L.; McDonald, S.; Gelius, L. Attenuation of marine seismic interference noise employing a customized U-Net. Geophys. Prospect. 2020, 68, 845–871. [Google Scholar]
- Saad, O.M.; Chen, Y. Deep denoising autoencoder for seismic random noise attenuation. Geophysics 2020, 85, V367–V376. [Google Scholar] [CrossRef]
- Qian, F.; Hua, H.; Wen, Y.; Pan, S.; Zhang, G.; Hu, G. Unsupervised 3-D Seismic Erratic Noise Attenuation With Robust Tensor Deep Learning. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5908616. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, S.; Zhou, Y. Tensor nuclear norm-based low-rank approximation with total variation regularization. IEEE J. Sel. Top. Signal Process. 2018, 12, 1364–1377. [Google Scholar] [CrossRef]
- Mu, Y.; Wang, P.; Lu, L.; Zhang, X.; Qi, L. Weighted tensor nuclear norm minimization for tensor completion using tensor-SVD. Pattern Recognit. Lett. 2020, 130, 4–11. [Google Scholar]
- Kilmer, M.E.; Braman, K.; Hao, N.; Hoover, R.C. Third-order tensors as operators on matrices: A theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. Appl. 2013, 34, 148–172. [Google Scholar]
- Kilmer, M.E.; Martin, C.D. Factorization strategies for third-order tensors. Linear Algebra Its Appl. 2011, 435, 641–658. [Google Scholar]
- Zhang, Z.; Ely, G.; Aeron, S.; Hao, N.; Kilmer, M. Novel methods for multilinear data completion and de-noising based on tensor-SVD. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3842–3849. [Google Scholar]
- Qian, F.; Zhang, C.; Feng, L.; Lu, C.; Zhang, G.; Hu, G. Tubal-sampling: Bridging tensor and matrix completion in 3-D seismic data reconstruction. IEEE Trans. Geosci. Remote Sens. 2020, 59, 854–870. [Google Scholar]
- Chen, Y.; Zhang, D.; Jin, Z.; Chen, X.; Zu, S.; Huang, W.; Gan, S. Simultaneous denoising and reconstruction of 5-D seismic data via damped rank-reduction method. Geophys. J. Int. 2016, 206, 1695–1717. [Google Scholar] [CrossRef]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor robust principal component analysis: Exact recovery of corrupted low-rank tensors via convex optimization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5249–5257. [Google Scholar]
- Qian, F.; He, Y.; Yue, Y.; Zhou, Y.; Wu, B.; Hu, G. Improved Low-Rank Tensor Approximation for Seismic Random Plus Footprint Noise Suppression. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5903519. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, J.; Zhao, Q.; Leung, Y.; Zhao, X.L.; Meng, D. Hyperspectral image restoration via total variation regularized low-rank tensor decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 11, 1227–1243. [Google Scholar] [CrossRef]
- An, H.; Jiang, R.; Wu, J.; Teh, K.C.; Sun, Z.; Li, Z.; Yang, J. LRSR-ADMM-Net: A joint low-rank and sparse recovery network for SAR imaging. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5232514. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, J.; Li, H.; Xu, Z. ADMM-CSNet: A deep learning approach for image compressive sensing. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 521–538. [Google Scholar] [CrossRef]
- Chen, Y.; Savvaidis, A.; Fomel, S.; Chen, Y.; Saad, O.M.; Oboué, Y.A.S.I.; Zhang, Q.; Chen, W. Pyseistr: A python package for structural denoising and interpolation of multi-channel seismic data. Seismol. Res. Lett. 2023, 94, 1703–1714. [Google Scholar]
- Wu, X.; Liang, L.; Shi, Y.; Fomel, S. FaultSeg3D: Using synthetic datasets to train an end-to-end convolutional neural network for 3D seismic fault segmentation. Geophysics 2019, 84, IM35–IM45. [Google Scholar] [CrossRef]




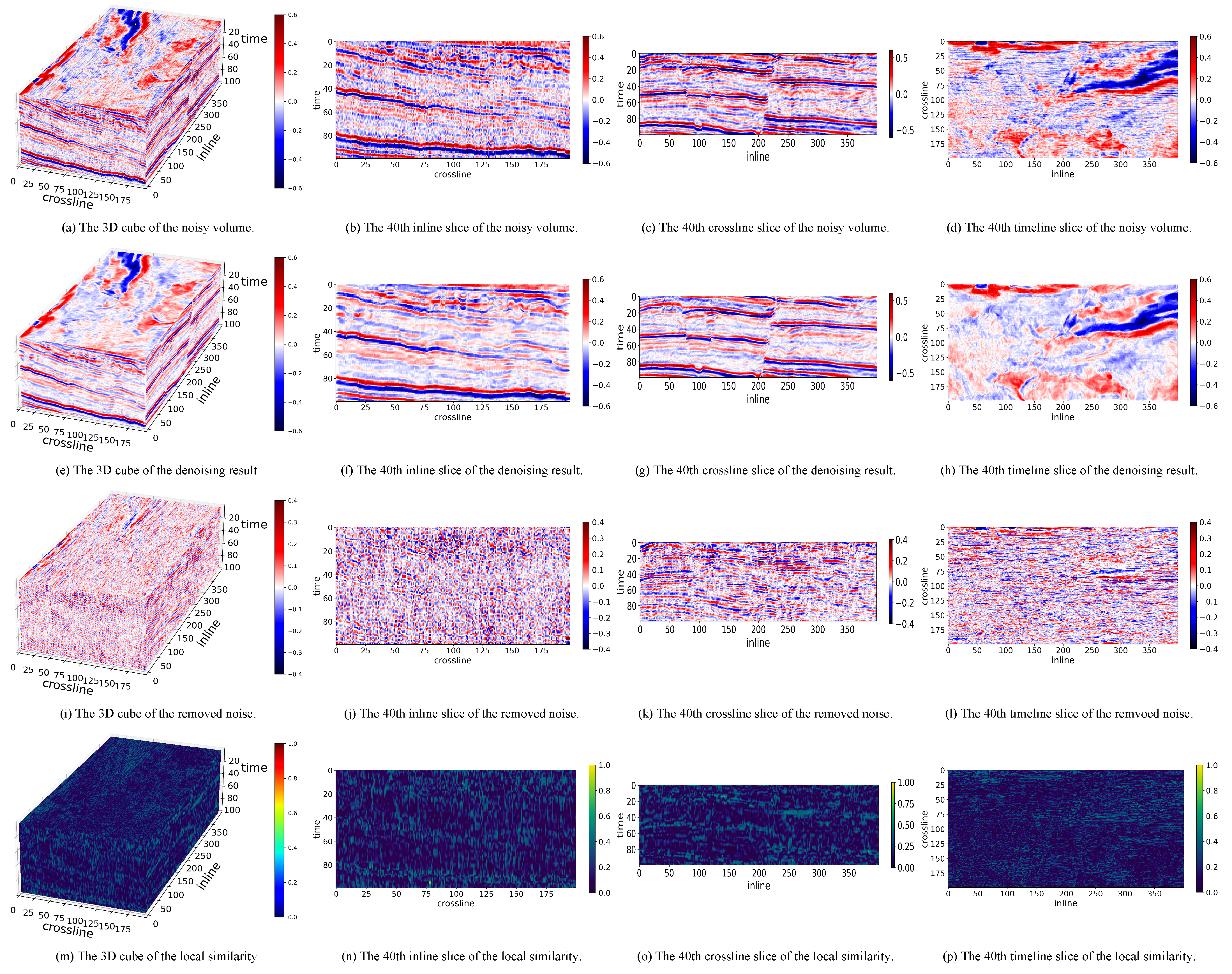
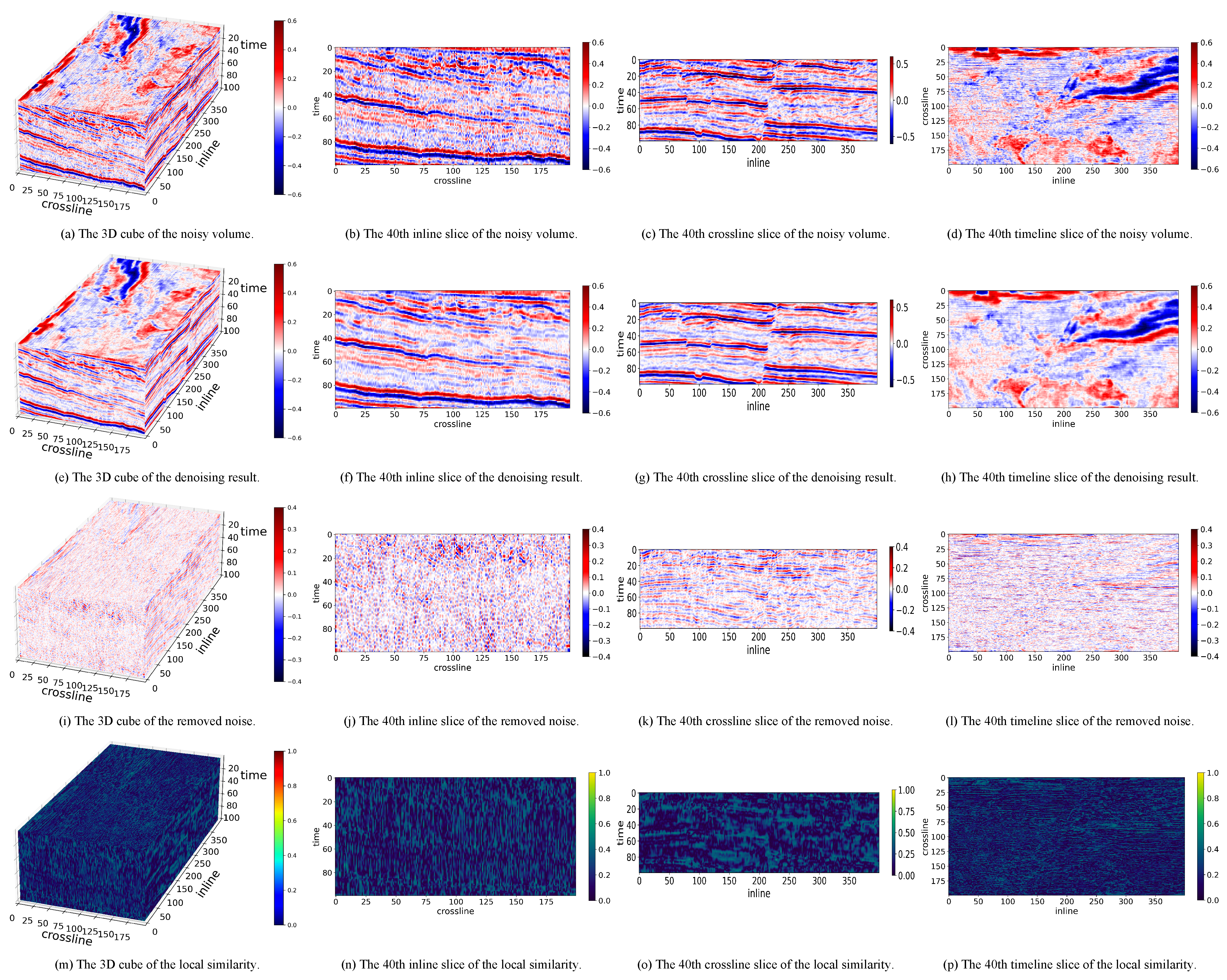
| Data | LRTNet | Pyseistr | TNN-SSTV |
|---|---|---|---|
| No. 0 | 8.6201 | 5.6587 | 5.9185 |
| No. 1 | 10.3855 | 6.9493 | 6.3235 |
| No. 2 | 11.1391 | 7.0777 | 6.4930 |
| No. 3 | 11.1522 | 7.0693 | 6.4857 |
| No. 4 | 9.7105 | 6.0413 | 6.2382 |
| No. 5 | 10.2263 | 6.9657 | 6.3368 |
| No. 6 | 8.6164 | 4.9738 | 5.9795 |
| No. 7 | 7.5633 | 5.0045 | 5.6821 |
| No. 8 | 11.7466 | 7.7944 | 6.5649 |
| No. 9 | 7.2844 | 6.9456 | 5.4583 |
| No. 10 | 8.7218 | 7.9158 | 6.0051 |
| No. 11 | 10.1633 | 6.4033 | 6.3126 |
| No. 12 | 8.5287 | 5.9217 | 5.9668 |
| No. 13 | 8.8158 | 5.0526 | 6.0086 |
| No. 14 | 11.1012 | 5.6594 | 6.3363 |
| No. 15 | 8.9373 | 5.9079 | 6.0704 |
| No. 16 | 8.0733 | 6.0608 | 5.7786 |
| No. 17 | 9.4177 | 8.8425 | 6.1196 |
| No. 18 | 8.3415 | 6.7276 | 5.9270 |
| No. 19 | 8.8629 | 6.1807 | 6.0410 |
| Average | 9.3704 | 6.4576 | 6.1023 |
| Data | LRTNet | Pyseistr | TNN-SSTV |
|---|---|---|---|
| No. 0 | 0.1458, 0.1388 | 0.1692, 0.0166 | 0.1496, 0.0126 |
| No. 1 | 0.1084, 0.0082 | 0.0873, 0.0045 | 0.1065, 0.0065 |
| No. 2 | 0.1091, 0.0086 | 0.1269, 0.0097 | 0.1125, 0.0075 |
| No. 3 | 0.1541, 0.0160 | 0.1591, 0.0144 | 0.1612, 0.0146 |
| No. 4 | 0.1437, 0.0140 | 0.1384, 0.0110 | 0.1487, 0.0126 |
| No. 5 | 0.1448, 0.0140 | 0.1559, 0.0141 | 0.1374, 0.0109 |
| No. 6 | 0.1041, 0.0072 | 0.1485, 0.0125 | 0.1166, 0.0077 |
| No. 7 | 0.1595, 0.0155 | 0.1332, 0.0101 | 0.1584, 0.0141 |
| No. 8 | 0.1484, 0.0160 | 0.1391, 0.0113 | 0.1523, 0.0134 |
| No. 9 | 0.1547, 0.0143 | 0.1146, 0.0079 | 0.1394, 0.0112 |
| No. 10 | 0.1432, 0.0141 | 0.1102, 0.0075 | 0.1470, 0.0133 |
| No. 11 | 0.1052, 0.0079 | 0.0995, 0.0061 | 0.0905, 0.0050 |
| No. 12 | 0.1611, 0.0169 | 0.1416, 0.0116 | 0.1522, 0.0132 |
| No. 13 | 0.1561, 0.0167 | 0.1596, 0.0145 | 0.1565, 0.0140 |
| No. 14 | 0.1416, 0.0141 | 0.1517, 0.0145 | 0.1454, 0.0132 |
| No. 15 | 0.1245, 0.0097 | 0.1216, 0.0087 | 0.1210, 0.0085 |
| No. 16 | 0.1296, 0.0111 | 0.1028, 0.0062 | 0.1246, 0.0087 |
| No. 17 | 0.1435, 0.0139 | 0.0933, 0.0053 | 0.1286, 0.0101 |
| No. 18 | 0.1519, 0.0147 | 0.1345, 0.0106 | 0.1426, 0.0116 |
| No. 19 | 0.1708, 0.0189 | 0.1415, 0.0116 | 0.1677, 0.0160 |
| Average | 0.1400, 0.0133 | 0.1315, 0.0104 | 0.1379, 0.0112 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, T.; Ouyang, L.; Chen, T. Seismic Random Noise Attenuation via Low-Rank Tensor Network. Appl. Sci. 2025, 15, 3453. https://doi.org/10.3390/app15073453
Zhao T, Ouyang L, Chen T. Seismic Random Noise Attenuation via Low-Rank Tensor Network. Applied Sciences. 2025; 15(7):3453. https://doi.org/10.3390/app15073453
Chicago/Turabian StyleZhao, Taiyin, Luoxiao Ouyang, and Tian Chen. 2025. "Seismic Random Noise Attenuation via Low-Rank Tensor Network" Applied Sciences 15, no. 7: 3453. https://doi.org/10.3390/app15073453
APA StyleZhao, T., Ouyang, L., & Chen, T. (2025). Seismic Random Noise Attenuation via Low-Rank Tensor Network. Applied Sciences, 15(7), 3453. https://doi.org/10.3390/app15073453






