Abstract
Seismic data are easily contaminated by random noise, impairing subsequent geological interpretation tasks. Existing denoising methods like low-rank approximation (LRA) and deep learning (DL) show promising denoising capabilities but still have limitations; for instance, LRA performance is parameter-sensitive, and DL networks lack interpretation. As an alternative, this paper introduces the low-rank tensor network (LRTNet), an innovative approach that integrates low-rank tensor approximation (LRTA) with DL. Our method involves constructing a noise attenuation model that leverages LRTA, total variation (TV) regularization, and weighted tensor nuclear norm minimization (WTNNM). By applying the alternating direction method of multipliers (ADMM), we solve the model and transform the iterative schemes into a DL framework, where each iteration corresponds to a network layer. The key learnable parameters, including weights and thresholds, are optimized using labeled data to enhance performance. Quantitative evaluations on synthetic data reveal that LRTNet achieves an average signal-to-noise ratio (SNR) of 9.37 dB on the validation set, outperforming Pyseistr (6.46 dB) and TNN-SSTV (6.10 dB) by 45.0% and 53.6%, respectively. Furthermore, tests on real field datasets demonstrate consistent enhancements in noise suppression while preserving critical stratigraphic structures and fault discontinuities. The embedded LRTA mechanism not only improves network interpretability, but also reduces parameter sensitivity compared to conventional LRA methods. These findings position LRTNet as a robust, physics-aware solution for seismic data restoration.
1. Introduction
Seismic exploration is a critical tool for subsurface imaging, widely used not only in oil and gas exploration, but also in applications such as geothermal energy assessment, carbon capture and storage monitoring, and earthquake hazard analysis [1]. The data collected during seismic surveys, however, are often contaminated by random noise, which arises from limitations in acquisition techniques, geological conditions, and environmental factors. This noise impairs subsequent interpretation tasks, such as seismic inversion, seismic facies analysis, and attribute analysis [2,3,4]. In this study, we focus on Gaussian random noise, which is statistically characterized by a normal distribution and is distinct from structured noise types such as footprint noise. Gaussian noise is frequency-independent and can significantly degrade the quality of seismic data across all frequency ranges. Therefore, the attenuation of random noise (and the enhancement of effective information) in seismic reflection remains a fundamental and enduring research topic.
Over recent decades, numerous methods have been proposed to suppress random noise. Among these, the low-rank approximation (LRA) has received significant attention due to its superior performance [5,6,7,8,9,10]. LRA operates on the hypothesis that seismic signals are inherently low-rank, and seeks to reduce the rank affected by random noise in the physical or transformed domain. LRA can be further categorized as low-rank matrix approximation (LRMA) and low-rank tensor approximation (LRTA). LRMA views seismic data as images or matrixes and then applies image denoising techniques. Due to the presence of similar geologic structures in the subsurface, clean seismic profiles exhibit a high degree of structural similarity, which can be effectively represented using LRMA [11]. References [12,13,14] stack blocks together with a similar seismic structures in a seismic profile to establish a matrix, and then perform LRA to suppress random noise. The Hankel matrix formulated from the useful seismic signal is low-rank [15], so references [16,17,18,19] map the seismic data to a Hankel matrix or a block Hankel matrix and recover the clean seismic data with LRMA. Despite the promising results, LRMA simply treats the seismic data as matrixes and neglects the spatial similarity, i.e., associations along the inline and crossline dimensions, and frequency association in the high-dimensional space.
In contrast, LRTA considers seismic data to be tensors satisfying the low-rank property in high-dimensional space, effectively utilizing their highly structured three-dimensional features [20]. References [21,22,23,24,25] perform tensor singular value decomposition (t-SVD) on seismic data to mitigate random noise. In [26,27], the CANDECOMP/PARAFAC (CP) decomposition is applied to the stacked tensor to achieve the optimal approximation. Although both LRMA and LRTA demonstrate great power, they all share the common limitation that their parameters must be manually selected and meticulously tuned based on prior knowledge.
Deep learning (DL) also shows great potential in eliminating random noise [28,29,30,31,32]. Most DL methods use a supervised learning strategy to train an end-to-end model. Typical models include convolutional neural networks (CNNs) [33], the 3D denoising CNN (3D-DnCNN) [34], generative adversarial networks (GANs) [35], and U-Net [36]. Besides supervised learning, there also exists unsupervised learning, for example, autoencoders [37], the robust tensor DL (RTDL) [38], etc. Compared with LRA, DL has the advantage of not relying on prior knowledge. However, the end-to-end model and purely data-driven attribution make it hard to interpret why the features are learned by DL.
In light of the aforementioned aspects, we introduce the low-rank tensor network (LRTNet), a novel approach that combines LRTA and DL to address the challenge of seismic random noise attenuation. Our method begins with the development of a noise attenuation model based on LRTA, with the total variation (TV) regularization [39] as a constraint and the weighted tensor nuclear norm minimization (WTNNM) [40]. We then apply the alternating direction method of multipliers (ADMM) to solve the model and further unfold the iterative schemes into layers, with one iteration being one layer, as a DL network. Unlike traditional LRTA methods, which require manual parameter tuning, LRTNet leverages DL to automatically optimize critical parameters such as weights and thresholds with a labeled dataset. Furthermore, LRTNet retains the underlying LRTA modeling framework, ensuring high interpretability and alignment with the physical principles of seismic data. Experimental results on both synthetic and real datasets demonstrate that LRTNet can effectively suppress random noise while preserving valuable seismic information.
The remainder of this paper is organized as follows. Section 2 introduces the theoretical background and methodology of the proposed LRTNet. Section 3 presents the experimental setup and demonstrates the results on both synthetic and real-field datasets. Section 4 discusses the limitations of the proposed method and suggests potential directions for future research. Finally, Section 5 concludes this paper by summarizing the key contributions and findings.
2. Materials and Methods
2.1. Preliminaries
We first provide the theoretical foundation required to build LRTNet. We start with the definition of a t-product, and then develop the concepts of t-SVD and the tensor nuclear norm (TNN) with the t-product.
Definition 1
(t-product [41,42]). The t-product between tensor and tensor is defined as
where and are determined as
and is defined as an matrix
It is clear that t-product returns a tensor of size and can be interpreted as a convolution-like operator between two tensors [42]. Leveraging the convolution theorem, the t-product can be computed through matrix multiplications involving two frequency slices in the Fourier domain [41,43]:
It is worth noting that a significant advantage of the Fourier transform is its capability to improve the low-rank properties of the seismic data tensor [44,45]. Building on the definition and the convolutional properties of the t-product, a framework for t-SVD can be developed as
Definition 2
(t-SVD [42]). Given an tensor , can be factored as
where and are orthogonal and , respectively, and is an tensor with each front slice being a diagonal matrix.
It is evident that t-SVD closely resembles that of matrix SVD. In fact, it is simple to interpret that each front slice of t-SVD is equivalent to each frontal slice of matrix SVD in the Fourier domain [42]. With the definition of t-SVD, the tensor tubal rank and the TNN can be defined as:
Definition 3
(Tensor Tubal Rank [41,43]). Given tensor , we can deconstruct as . The tensor tubal rank of , denoted as , is defined by the number of non-zero tubes of , as
Definition 4
(Tensor Nuclear Norm [46]). The TNN of is defined as
where is the identity tensor, the whole initial frontal slice is an identity matrix and the remaining frontal slices are zeros, and .
2.2. Problem Statement and Modeling
For the 3D seismic image denoising problem, we represent recorded images as the superposition of clear 3D seismic images and some additive random noise , and the random noise attenuation model can be expressed as follows:
The goal of seismic image denoising is to recover the clean seismic image from the noisy seismic image in the presence of random noise . As proven in [19,26,47], performing LRA operation on a noisy data matrix or tensor can effectively suppress random noise, and LRTA methods based on WTNNM have achieved excellent results in image denoising [40]. Meanwhile, in order to deal with the boundary roughnesscaused by LRTA, the TV regularization is introduced as a constraint on the denoised result of LRTA methods [26,48]. Thus, the seismic image denoising problem can be formulated as minimizing an objective function that incorporates the data fidelity and the regularization terms, as follows:
where , , and are trade-off parameters to balance all three terms, denotes the weighted tensor nuclear norm (WTNN) of with the weight vector parameters , and denotes the TV regularization defined as follows:
where , , and are the finite-difference operators along the three dimensions, and are weights that control regularization strength for three directions, respectively.
2.3. Optimization Procedure
We introduce two auxiliary variables, and , where is the concatenated difference operation, and , which is able to utilize the alternating direction method of multipliers (ADMM) framework to resolve the above problem (9). Then, the constrained minimization problem can be expressed as follows:
Subsequently, the above problem (11) can be further transformed to find a saddle point of the following disputedLagrangian function:
where , , and are the Lagrangian multipliers, and is a positive penalty parameter. Therefore, we can obtain a solution to the original problem (11) after a finite number of iterations according to the ADMM framework. The iteration scheme can be expressed as follows:
where denotes the tensor singular value decomposition of [47] and , the weight vector in WTNNM is defined as with a constant c and a small positive constant according to [14], and indicate the 3D Fourier transform and its inverse transform, , and it is the same for all iterations, and is the soft-thresholding operator. For the Lagrange multipliers, we have
2.4. Automatic Parameter Optimization with DNN
Denoising performance is closely related to the parameters. Likewise, these parameters are hard to determine due to the lack of prior information, and in the process of iterations, these parameters should also be adjusted as the variables update. Therefore, we unfold the above iterations into a DL network, which is named as LRTNet [49,50], and the flowchart of LRTNet is shown in Figure 1. As a denoising model, LRTNet takes noisy 3D seismic data as the input and produces denoised seismic data as the output. This design aligns with the goal of seismic noise attenuation, where the model learns to recover clean seismic signals from their noisy counterparts. LRTNet is composed of L layers, and each layer has the same structure and layer-varied learnable parameters , where the superscript l denotes the l-th layer of LRTNet and the subscript denotes the corresponding parameter in the iteration scheme (13), so LRTNet can be expressed as follows:
where and are the output and input of LRTNet, respectively, H and h denote the whole net and each layer, respectively, and denotes the set of , which is determined through training by minimizing the associated loss function as follows:
where are the N pairs of the training data. The l-th layer is composed of four modules, and the details of these modules are described as follows:
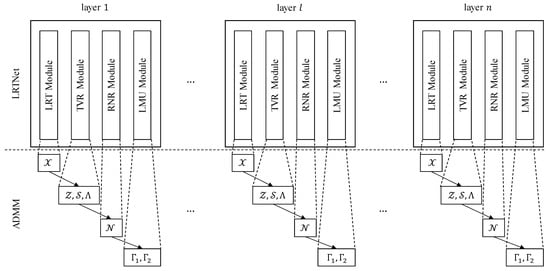
Figure 1.
The flowchart of LRTNet.
(1) Low-Rank Approximation () Module: This module recovers the seismic data by LRTA operation based on WTNNM, and the soft-thresholding operator is replaced by the ReLU function. Then, variable is updated as follows:
where denotes the tensor singular value decomposition of , , and .
(2) TV Regularization () Module: This module introduces the TV regularization to the new denoised seismic data of the previous module and replaces the soft-thresholding operator by the ReLU function. Then, the output of this module, the updated smooth denoised seismic data , can be expressed as follows:
where and .
(3) Random Noise Removal () Module: This module updates the removed random noise according to the new denoised result . This sub-problem is a standard least square regression problem with a closed-form solution, and the output of this module, the new removed random noise , can be expressed as follows:
(4) Lagrange Multiplier Updating () Module: This module updates the Lagrange multipliers and based on the new denoised result , the new removed random noise , and the new smooth denoised seismic data according to the ADMM framework. Then, the outputs of this module, the new Lagrange multipliers and , can be expressed as follows:
The pseudocode of LRTNet is given in Algorithm 1.
| Algorithm 1 Low-Rank Tensor Network |
| Require: |
| Ensure: |
Set and to zero tensor. ▹Initial // layer 1 . ▹update with LRT Module . ▹update with TVR Module . ▹update with RNR Module . ▹update and with LMU Module // layer 2 to layer // layer n . . . . . |
2.5. Data and Data Processing
We compare the attenuation performance of our proposed LRTNet with a recent Python package, Pyseistr 0.0.4.4.0 [51], and an LRA method, TNN-SSTV, on an open synthetic dataset and two real field datasets (F3-2020 and Penobscot).
Synthetic Dataset: The synthetic dataset, released by Wu et al. in FaultSeg [52], contains 200 training and 20 validation pairs of 3D seismic volumes ( per volume) with corresponding faults. To standardize the denoising evaluation, we implement the following preprocessing method:
- We select the first 20 volumes from the training set to train our LRTNet. This decision is based on preliminary experiments where we observed that using the full 200-volume training set required a similar number of epochs to converge, with only a marginal improvement in average SNR (less than 0.5 dB). Given the significant computational cost and time required for training on the full dataset (the limitation of efficiency is discussed in Section 4), we opted for the smaller subset to balance performance and computational efficiency. For each volume, we generate a corresponding noisy volume by adding Gaussian noise at 0 dB SNR, while retaining the original noise-free volume as the ground truth label. The choice of 0 dB SNR is motivated by the observation that all methods perform well at lower noise levels, while performance degrades at higher noise levels. At 0 dB SNR, our method demonstrates a clear advantage over baseline approaches, making it a balanced and representative noise level for evaluation.
- Validation Data: We use all 20 validation volumes. We apply identical noise injection (0 dB Gaussian) to create noisy volumes, with denoised outputs compared against the pristine volumes for metric calculation.
Real Field Datasets:
- F3-2020: This is a marine 3D survey of the offshore Netherlands (original size: ). To avoid redundant processing, we extract a random sub-volume () containing representative geological features. No artificial noise is added, as the raw data inherently contain field-acquisition noise.
- Penobscot: This is a publicly available North Atlantic survey with complex subsurface structures. Following the same rationale, we select a sub-volume from the “1-PSTM stack agc” data. Denoising is applied directly to the native noisy volume without preprocessing.
3. Results
3.1. Experimental Setup
For the sake of testing the ability to suppress random noise, we calculate the signal-to-noise-ratio (SNR) and local similarity. In general, the higher the SNR, the better the performance of the algorithm. The SNR formula is defined as follows:
where are the original noise-free seismic data, and are the denoised seismic data. Local similarity measures how locally similar two data samples are and is often used to indicate signal leakage. It is a cube with the same size as the samples and can be easily computed via Madagascar 4.0. In our experiment on synthetic data, we compute the local similarity between the original noise-free volume and the removed noise and normalize it to range of 0 to 1. Therefore, smaller values of this metric indicate better attenuating performance. In the experiments on F3-2020 and Penobscot, because there exist no ground truth data, we compute the local similarity between the denoised results and the corresponding removed noise.
Regarding the training configuration of LRTNet, we set the number of layers to four. Our experiments indicate that using only two layers does not yield sufficient performance, while increasing the number to six leads to excessive computational cost without any significant performance gains. The remaining hyperparameters are chosen based on standard DL practices: we use the Adam optimizer to train the model for 100 epochs in total, start with a learning rate of 0.05, and reduce the learning rate by a factor of 0.8 every 20 epochs. For the experiments on F3-2020 and Penobscot, we use the LRTNet model tuned on the synthetic data without any additional fine-tuning, ensuring a fair comparison.
3.2. Experimental Results on Synthetic Data
On the synthetic dataset, the average SNR on the validation set computed by our proposed LRTNet, Pyseistr, and TNN-SSTV are 9.37 dB, 6.46 dB, and 6.10 dB, respectively. The SNRs computed for each data sample are given in Table 1. From the quantitative comparison, it can be observed that after tuning with deep learning, LRTNet outperforms Pyseistr and TNN-SSTV in seismic denosing tasks.

Table 1.
The SNR calculated by each method on validation volumes.
In addition, we present the denoising results of each method on validation volume No. 8 in Figure 2, Figure 3 and Figure 4 for qualitative analysis. As shown in the fourth row (subfigures m–p), LRTNet achieves the best denoising performance, as it produces smoother results with sharper fault details compared to baseline methods. This demonstrates its superior ability to preserve structural information while effectively removing noise. In the fifth row (subfigures q–t), the noise removed by LRTNet retains more noticeable signal patterns than Pyseistr, similar to TNN-SSTV. This indicates that LRTNet performs slightly less optimally than Pyseistr, which exhibits the least signal leakage. To further validate these observations, we provide statistical information on the local similarity tensor in Table 2. The local similarity results in the last row (subfigures u–x) align with the conclusions drawn from the removed noise, showing consistency across both qualitative and quantitative evaluations. While Pyseistr yields the best local similarity, LRTNet does not show a significant disadvantage in this regard. Overall, the combined quantitative and qualitative analyses highlight the exceptional performance of our proposed LRTNet on the synthetic dataset.
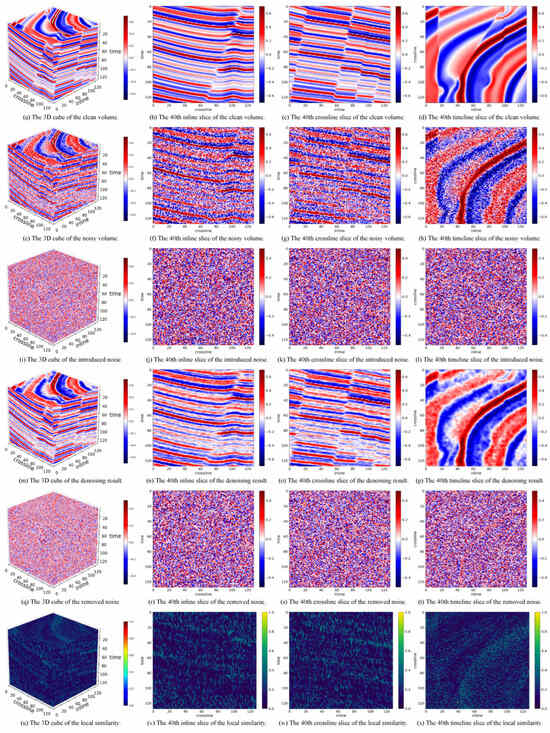
Figure 2.
The denoising results of LRTNet on sample No. 8 of the synthetic dataset.
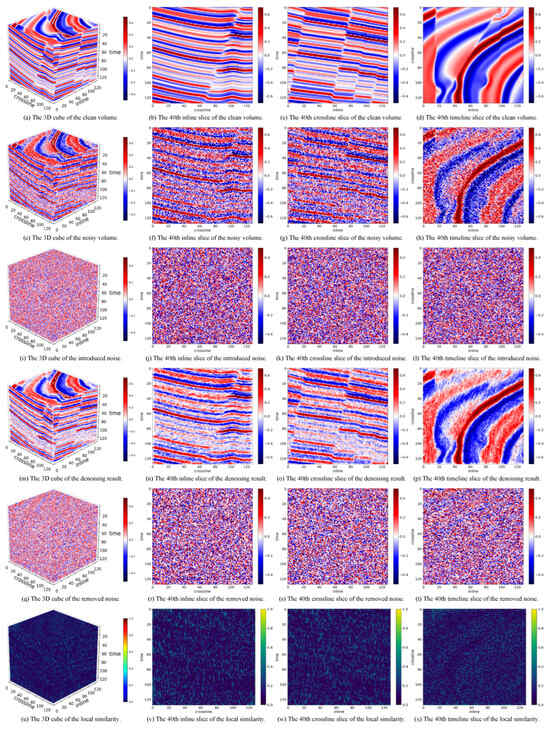
Figure 3.
The denoising results of Pyseistr on sample No. 8 sample of the synthetic dataset.
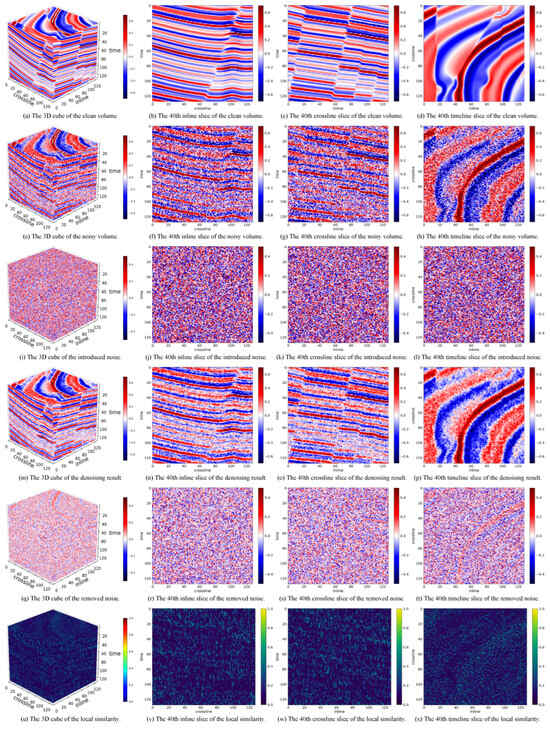
Figure 4.
The denoising results of TNN-SSTV on sample No. 8 of the synthetic dataset.

Table 2.
The mean and variance values of local similarity obtained by each method on validation volumes (in order), with the tensor normalized to 0∼1.
3.3. Experimental Results on F3-2020
Figure 5, Figure 6 and Figure 7 illustrate the denoising results of each method on a F3-2020 volume. It is clear from these figures that all three methods can effectively extract useful information from the noisy seismic volume and suppress random noise. In particular, LRTNet produces the smoothest denoising results, while local similarity corresponding to Pyseistr is visually the worst, which is consistent with the analysis on the experiments on the synthetic data. Although the LRTNet parameters are tuned with the synthetic data, the denoising results on F3-2020 are still competitive, indicating that LRTNet has excellent generalizability. It is worth noting that we do not quantitatively compare three methods on F3-2020, because real field data are naturally contaminated by noise and there exist no ground truth data for quantitative comparison.
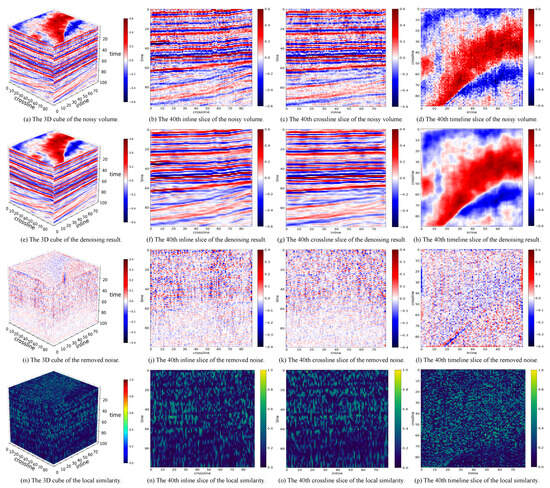
Figure 5.
The denoising results of LRTNet on a F3-2020 volume.
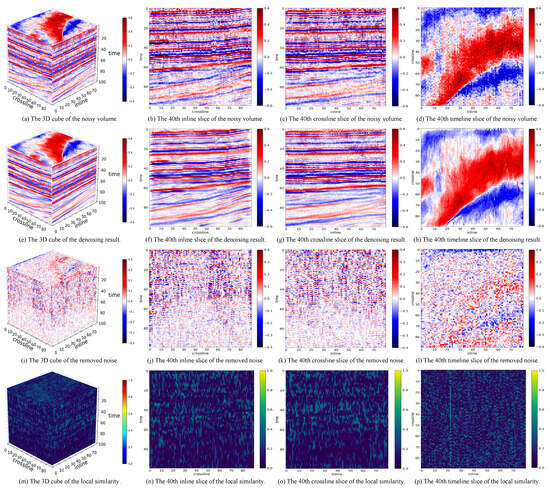
Figure 6.
The denoising results of Pyseistr on a F3-2020 volume.
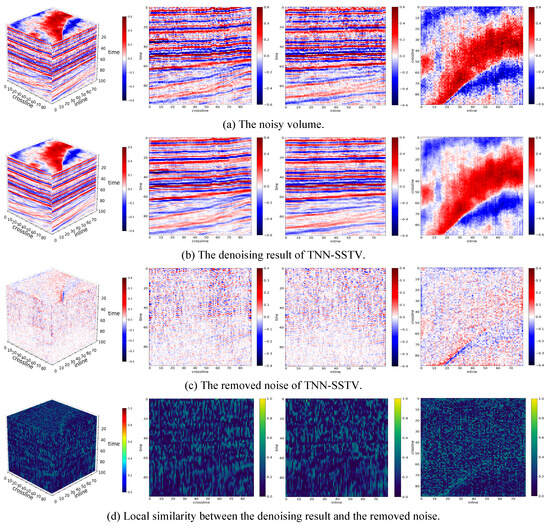
Figure 7.
The denoising results of TNN-SSTV on a F3-2020 volume.
3.4. Experimental Results on Penobscot
Figure 8, Figure 9 and Figure 10 illustrate the denoising results of each method on the randomly selected Penobscot volume. Comparing these results, all methods achieve satisfying denoising results, with faults clearly visible. However, clear footprint noise can be observed in the removed noise by all three methods, indicating that Penobscot contains not only random noise, but also footprint noise. Furthermore, noticeable signal-like features can be seen in the removed noise, suggesting that the noise is not sufficiently random. This phenomenon is more pronounced in the results of Penobscot compared to the synthetic data and F3-2020, which means that all three methods experience significant signal leakage on Penobscot.
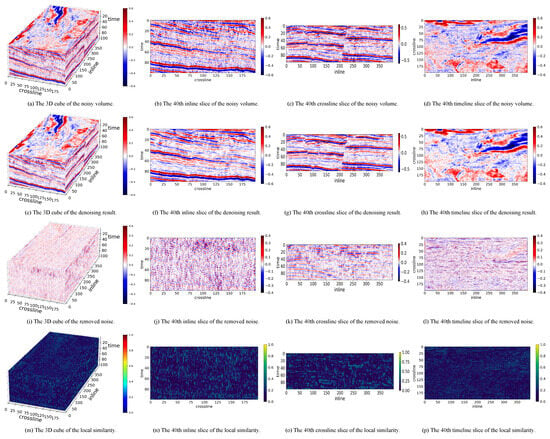
Figure 8.
The denoising results of LRTNet on a Penobscot volume.
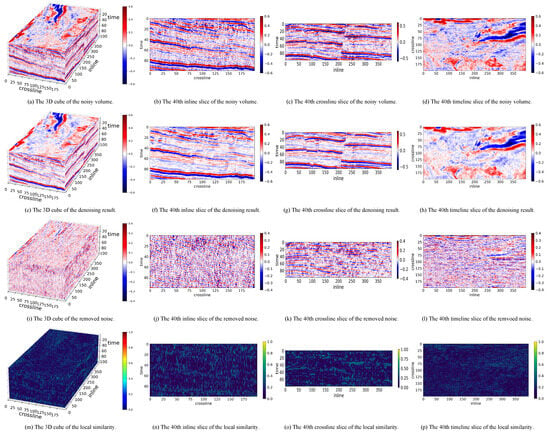
Figure 9.
The denoising results of Pyseistr on a Penobscot volume.
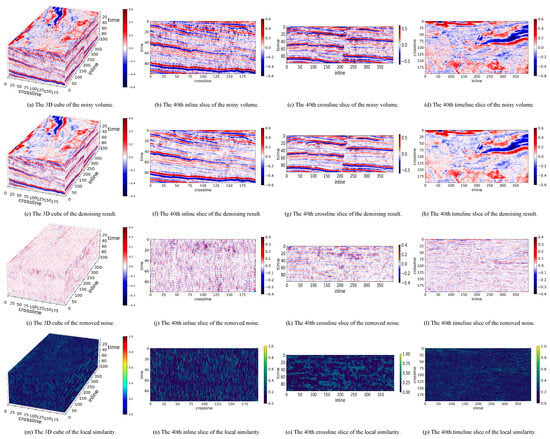
Figure 10.
The denoising results of TNN-SSTV on a Penobscot volume.
4. Discussion
Despite the extraordinary denoising performance of LRTNet, there are still several limitations and areas for improvement that warrant further discussion:
- As presented and analyzed in Section 3, LRTNet exhibits more severe signal leakage compared to Pyseistr and TNN-SSTV. While the severity is not significant in either qualitative or quantitative comparisons, this remains a notable limitation. Additionally, the local similarity metric, which is a tensor of the same size as the input signal, provides only a coarse quantitative comparison through its mean and variance. Future work could explore more refined metrics or visualization techniques to better capture the spatial and temporal characteristics of signal leakage, enabling a more nuanced evaluation of denoising performance.
- LRTNet leverages DL to tune its inner parameters for LRA. Although DL is not the core of LRTNet, it introduces a common challenge: the gap between synthetic and real field data. Deploying LRTNet, which is trained on synthetic data, directly to real data may result in performance degradation due to domain differences. Training LRTNet on real data could mitigate this issue, but it presents its own challenges. For instance, the lack of ground truth for real data complicates the calibration and validation of the model. Furthermore, geographical variations between training and validation datasets may still lead to performance gaps. Potential solutions to this include domain adaptation techniques, transfer learning, and the development of semi-supervised approaches that leverage both synthetic and real data.
- Compared to purely DL-based methods, LRTNet has a significant efficiency drawback. DL methods are inherently well-suited for parallelization, enabling the batch processing of multiple data samples. In contrast, LRTNet follows the ADMM framework, which processes data sequentially, one sample at a time. This limitation restricts the scalability of LRTNet, particularly for large-scale datasets. Future improvements could focus on optimizing the ADMM framework for parallel processing to enhance the computational efficiency of LRTNet.
- While LRTNet demonstrates strong performance under controlled noise conditions, its robustness to varying noise levels and types in real-world scenarios remains to be fully explored. Real filed data often contain complex noise patterns that may differ significantly from the synthetic noise used during training. Investigating LRTNet’s performance under diverse noise conditions and developing adaptive mechanisms to handle noise variability could further enhance LRTNet’s practical applicability.
5. Conclusions
This paper introduces a novel approach for seismic denoising by integrating low-rank tensor approximation (LRTA) with deep learning (DL). By transforming the manually selected parameters of conventional LRTA into learnable parameters of a DL network, our proposed low-rank tensor network (LRTNet) enables the automatic acquisition of optimal values from training data, significantly reducing the parameter sensitivity of traditional LRTA methods. The embedded LRTA mechanism not only enhances the interpretability of the network, but also ensures that the method remains grounded in physical principles, bridging the gap between data-driven and model-driven approaches.
Experimental evaluations on both synthetic and real field datasets demonstrate that LRTNet outperforms traditional methods, such as Pyseistr and TNN-SSTV, in suppressing random noise while preserving critical stratigraphic structures and fault discontinuities. On synthetic data, LRTNet achieves an average signal-to-noise ratio (SNR) improvement of 45.0% and 53.6% over Pyseistr and TNN-SSTV, respectively. Real data tests further confirm its practical applicability, showing consistent enhancements in noise suppression without compromising geological features.
Despite its promising performance, LRTNet has limitations that warrant further investigation. These include signal leakage, computational efficiency challenges due to the sequential nature of the ADMM framework, and the gap between synthetic and real data domains. Future work will focus on addressing these limitations through techniques such as domain adaptation, parallelization of the ADMM framework, and the development of more refined evaluation metrics. Additionally, exploring the integration of LRTNet with other physics-aware DL architectures could further enhance its performance and applicability.
In summary, LRTNet represents a significant advancement in seismic data processing, offering a robust, physics-aware solution for noise attenuation. Its ability to combine the interpretability of LRTA with the adaptive learning capabilities of DL positions it as a valuable tool for both academic research and industrial applications.
Author Contributions
Conceptualization, T.Z.; methodology, T.Z.; software, L.O. and T.C.; validation, T.Z. and L.O.; formal analysis, L.O.; investigation, L.O. and T.C.; resources, T.Z.; data curation, T.C.; writing—original draft preparation, T.Z. and L.O.; writing—review and editing, T.Z.; visualization, T.C.; supervision, T.Z.; project administration, T.Z.; funding acquisition, T.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Chengdu Key Research and Development Support Program “Jie Bang Gua Shuai” Project under grant number 2023-JB00-00012-GX.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data presented in the study are all openly available. The synthetic 3D dataset for fault detection can be found in FaultSeg: https://github.com/xinwucwp/faultSeg (accessed on 15 January 2024). F3-2020 is available on Seg Wiki: https://wiki.seg.org/wiki/F3_Netherlands (accessed on 3 March 2024). Penobscot is available on Seg Wiki: https://wiki.seg.org/wiki/Penobscot_3D (accessed on 18 March 2024).
Acknowledgments
We appreciate all the contributors of FaultSeg for releasing the synthetic 3D fault dataset. We also want to thank all the contributors who collected and released the two real field datasets we used.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LRA | Low-rank approximation |
| LRMA | Low-rank matrix approximation |
| LRTA | Low-rank tensor approximation |
| DL | Deep learning |
| TV | Total variation |
| WTNNM | Weighted tensor nuclear norm minimization |
| ADMM | Alternating direction method of multipliers |
| LRTNet | Low-rank tensor network |
References
- Qu, Z.; Gao, Y.; Li, S.; Zhang, X. A Hybrid Deep Learning Approach for Integrating Transient Electromagnetic and Magnetic Data to Enhance Subsurface Anomaly Detection. Appl. Sci. 2025, 15, 3125. [Google Scholar] [CrossRef]
- Wang, Y.; Ge, Q.; Lu, W.; Yan, X. Well-logging constrained seismic inversion based on closed-loop convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5564–5574. [Google Scholar]
- Wu, X.; Shi, Y.; Fomel, S.; Liang, L.; Zhang, Q.; Yusifov, A.Z. FaultNet3D: Predicting fault probabilities, strikes, and dips with a single convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9138–9155. [Google Scholar] [CrossRef]
- Wen, Y.; Qian, F.; Guo, W.; Zong, J.; Peng, D.; Chen, K.; Hu, G. VSP Upgoing and Downgoing Wavefield Separation: A Hybrid Model-Data Driven Approach. IEEE Trans. Geosci. Remote. Sens. 2025, 1. [Google Scholar] [CrossRef]
- Li, S.; Geng, X.; Zhu, L.; Ji, L.; Zhao, Y. Hyperspectral Image Denoising Based on Principal-Third-Order-Moment Analysis. Remote Sens. 2024, 16, 276. [Google Scholar] [CrossRef]
- Henneberger, K.; Qin, J. Hyperspectral Band Selection via Tensor Low Rankness and Generalized 3DTV. Remote Sens. 2025, 17, 567. [Google Scholar] [CrossRef]
- Wu, Y.; Xu, W.; Zheng, L. Hyperspectral Image Mixed Noise Removal via Double Factor Total Variation Nonlocal Low-Rank Tensor Regularization. Remote Sens. 2024, 16, 1686. [Google Scholar] [CrossRef]
- Liu, S.; Feng, J.; Tian, Z. Variational Low-Rank Matrix Factorization with Multi-Patch Collaborative Learning for Hyperspectral Imagery Mixed Denoising. Remote Sens. 2021, 13, 1101. [Google Scholar] [CrossRef]
- Liu, H.; Li, H.; Wu, Z.; Wei, Z. Hyperspectral Image Recovery Using Non-Convex Low-Rank Tensor Approximation. Remote Sens. 2020, 12, 2264. [Google Scholar] [CrossRef]
- Qian, F.; Pan, S.; Zhang, G. Tensor Computation for Seismic Data Processing: Linking Theory and Practice; Earth Systems Data and Models Series; Springer: Cham, Switzerland, 2025. [Google Scholar]
- Shao, O.; Wang, L.; Hu, X.; Long, Z. Seismic denoising via truncated nuclear norm minimization. Geophysics 2021, 86, V153–V169. [Google Scholar]
- Li, J.; Wang, D.; Ji, S.; Li, Y.; Qian, Z. Seismic noise suppression using weighted nuclear norm minimization method. J. Appl. Geophys. 2017, 146, 214–220. [Google Scholar] [CrossRef]
- Liu, X.; Chen, X.; Li, J.; Chen, Y. Nonlocal weighted robust principal component analysis for seismic noise attenuation. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1745–1756. [Google Scholar] [CrossRef]
- Li, J.; Fan, W.; Li, Y.; Qian, Z. Low-frequency noise suppression in desert seismic data based on an improved weighted nuclear norm minimization algorithm. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1993–1997. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, Z.; Gu, H.; Wu, X.; Liu, S. Hankel low-rank approximation for seismic noise attenuation. IEEE Trans. Geosci. Remote Sens. 2018, 57, 561–573. [Google Scholar] [CrossRef]
- Oropeza, V.; Sacchi, M. Simultaneous seismic data denoising and reconstruction via multichannel singular spectrum analysis. Geophysics 2011, 76, V25–V32. [Google Scholar] [CrossRef]
- Huang, W.; Wang, R.; Chen, Y.; Li, H.; Gan, S. Damped multichannel singular spectrum analysis for 3D random noise attenuation. Geophysics 2016, 81, V261–V270. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, W.; Zhang, D.; Chen, W. An open-source Matlab code package for improved rank-reduction 3D seismic data denoising and reconstruction. Comput. Geosci. 2016, 95, 59–66. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, Y.; Chen, W.; Zu, S.; Huang, W.; Zhang, D. Empirical low-rank approximation for seismic noise attenuation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4696–4711. [Google Scholar] [CrossRef]
- Adamo, A.; Mazzucchelli, P.; Bienati, N. Irregular interpolation of seismic data through low-rank tensor approximation. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4292–4295. [Google Scholar]
- Qian, F.; Hua, H.; Wen, Y.; Zong, J.; Zhang, G.; Hu, G. Unsupervised Intense VSP Coupling Noise Suppression with Iterative Robust Deep Learning. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5901817. [Google Scholar] [CrossRef]
- Anvari, R.; Kahoo, A.R.; Mohammadi, M.; Pouyan, A.A. Random noise attenuation in 3D seismic data by iterative block tensor singular value thresholding. In Proceedings of the 2017 3rd Iranian Conference on Intelligent Systems and Signal Processing (ICSPIS), Shahrood, Iran, 20–21 December 2017; pp. 164–168. [Google Scholar]
- Anvari, R.; Mohammadi, M.; Kahoo, A.R. Enhancing 3-D seismic data using the t-SVD and optimal shrinkage of singular value. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 382–388. [Google Scholar] [CrossRef]
- Qian, F.; Yue, Y.; He, Y.; Yu, H.; Zhou, Y.; Tang, J.; Hu, G. Unsupervised seismic footprint removal with physical prior augmented deep autoencoder. IEEE Trans. Geosci. Remote. Sens. 2023, 61, 5910920. [Google Scholar] [CrossRef]
- Qian, F.; Liu, Z.; Wang, Y.; Zhou, Y.; Hu, G. Ground Truth-Free 3-D Seismic Random Noise Attenuation via Deep Tensor Convolutional Neural Networks in the Time-Frequency Domain. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5911317. [Google Scholar] [CrossRef]
- Feng, J.; Liu, X.; Li, X.; Xu, W.; Liu, B. Low-rank tensor minimization method for seismic denoising based on variational mode decomposition. IEEE Geosci. Remote Sens. Lett. 2021, 19, 7504805. [Google Scholar]
- Feng, J.; Li, X.; Liu, X.; Chen, C.; Chen, H. Seismic data denoising based on tensor decomposition with total variation. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1303–1307. [Google Scholar] [CrossRef]
- Gu, X.; Collet, O.; Tertyshnikov, K.; Pevzner, R. Removing Instrumental Noise in Distributed Acoustic Sensing Data: A Comparison Between Two Deep Learning Approaches. Remote Sens. 2024, 16, 4150. [Google Scholar] [CrossRef]
- Banjade, T.P.; Zhou, C.; Chen, H.; Li, H.; Deng, J.; Zhou, F.; Adhikari, R. Seismic Random Noise Attenuation Using DARE U-Net. Remote Sens. 2024, 16, 4051. [Google Scholar] [CrossRef]
- Ding, M.; Zhou, Y.; Chi, Y. Self-Attention Generative Adversarial Network Interpolating and Denoising Seismic Signals Simultaneously. Remote Sens. 2024, 16, 305. [Google Scholar] [CrossRef]
- Zhao, H.; Zhou, Y.; Bai, T.; Chen, Y. A U-Net Based Multi-Scale Deformable Convolution Network for Seismic Random Noise Suppression. Remote Sens. 2023, 15, 4569. [Google Scholar] [CrossRef]
- Wang, W.; Yang, J.; Huang, J.; Li, Z.; Sun, M. Outlier Denoising Using a Novel Statistics-Based Mask Strategy for Compressive Sensing. Remote Sens. 2023, 15, 447. [Google Scholar] [CrossRef]
- Yang, L.; Chen, W.; Wang, H.; Chen, Y. Deep Learning Seismic Random Noise Attenuation via Improved Residual Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7968–7981. [Google Scholar] [CrossRef]
- Liu, D.; Wang, W.; Wang, X.; Wang, C.; Pei, J.; Chen, W. Poststack Seismic Data Denoising Based on 3-D Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1598–1629. [Google Scholar] [CrossRef]
- Yuan, Y.; Si, X.; Zheng, Y. Ground-roll attenuation using generative adversarial networks. Geophysics 2020, 85, WA255–WA267. [Google Scholar] [CrossRef]
- Sun, J.; Slang, S.; Elboth, T.; Greiner, T.L.; McDonald, S.; Gelius, L. Attenuation of marine seismic interference noise employing a customized U-Net. Geophys. Prospect. 2020, 68, 845–871. [Google Scholar]
- Saad, O.M.; Chen, Y. Deep denoising autoencoder for seismic random noise attenuation. Geophysics 2020, 85, V367–V376. [Google Scholar] [CrossRef]
- Qian, F.; Hua, H.; Wen, Y.; Pan, S.; Zhang, G.; Hu, G. Unsupervised 3-D Seismic Erratic Noise Attenuation With Robust Tensor Deep Learning. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5908616. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, S.; Zhou, Y. Tensor nuclear norm-based low-rank approximation with total variation regularization. IEEE J. Sel. Top. Signal Process. 2018, 12, 1364–1377. [Google Scholar] [CrossRef]
- Mu, Y.; Wang, P.; Lu, L.; Zhang, X.; Qi, L. Weighted tensor nuclear norm minimization for tensor completion using tensor-SVD. Pattern Recognit. Lett. 2020, 130, 4–11. [Google Scholar]
- Kilmer, M.E.; Braman, K.; Hao, N.; Hoover, R.C. Third-order tensors as operators on matrices: A theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. Appl. 2013, 34, 148–172. [Google Scholar]
- Kilmer, M.E.; Martin, C.D. Factorization strategies for third-order tensors. Linear Algebra Its Appl. 2011, 435, 641–658. [Google Scholar]
- Zhang, Z.; Ely, G.; Aeron, S.; Hao, N.; Kilmer, M. Novel methods for multilinear data completion and de-noising based on tensor-SVD. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3842–3849. [Google Scholar]
- Qian, F.; Zhang, C.; Feng, L.; Lu, C.; Zhang, G.; Hu, G. Tubal-sampling: Bridging tensor and matrix completion in 3-D seismic data reconstruction. IEEE Trans. Geosci. Remote Sens. 2020, 59, 854–870. [Google Scholar]
- Chen, Y.; Zhang, D.; Jin, Z.; Chen, X.; Zu, S.; Huang, W.; Gan, S. Simultaneous denoising and reconstruction of 5-D seismic data via damped rank-reduction method. Geophys. J. Int. 2016, 206, 1695–1717. [Google Scholar] [CrossRef]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor robust principal component analysis: Exact recovery of corrupted low-rank tensors via convex optimization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5249–5257. [Google Scholar]
- Qian, F.; He, Y.; Yue, Y.; Zhou, Y.; Wu, B.; Hu, G. Improved Low-Rank Tensor Approximation for Seismic Random Plus Footprint Noise Suppression. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5903519. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, J.; Zhao, Q.; Leung, Y.; Zhao, X.L.; Meng, D. Hyperspectral image restoration via total variation regularized low-rank tensor decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 11, 1227–1243. [Google Scholar] [CrossRef]
- An, H.; Jiang, R.; Wu, J.; Teh, K.C.; Sun, Z.; Li, Z.; Yang, J. LRSR-ADMM-Net: A joint low-rank and sparse recovery network for SAR imaging. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5232514. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, J.; Li, H.; Xu, Z. ADMM-CSNet: A deep learning approach for image compressive sensing. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 521–538. [Google Scholar] [CrossRef]
- Chen, Y.; Savvaidis, A.; Fomel, S.; Chen, Y.; Saad, O.M.; Oboué, Y.A.S.I.; Zhang, Q.; Chen, W. Pyseistr: A python package for structural denoising and interpolation of multi-channel seismic data. Seismol. Res. Lett. 2023, 94, 1703–1714. [Google Scholar]
- Wu, X.; Liang, L.; Shi, Y.; Fomel, S. FaultSeg3D: Using synthetic datasets to train an end-to-end convolutional neural network for 3D seismic fault segmentation. Geophysics 2019, 84, IM35–IM45. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).