Text Alignment in the Service of Text Reuse Detection

Abstract

This study introduces a novel approach to text alignment tailored for ancient languages, with a focus on Hebrew and Aramaic, aimed at enhancing text reuse detection. Unlike previous methods, our approach integrates multiple NLP components into a specialized comparison pipeline, which is then incorporated into the Smith–Waterman algorithm. This integration enables improved alignment accuracy, particularly for historical texts characterized by fluctuations, orthographic changes, transcription variations, and word transpositions. Our key contributions include (1) a refined distance function that integrates fastText embeddings, allowing robust handling of out-of-vocabulary words; (2) a typological correction mechanism that can be integrated into automatic transcription pipelines to enhance text normalization; and (3) an evaluation of historical Hebrew texts, demonstrating an 11% improvement in the F1 score over existing approaches. These findings underscore the importance of computational methodologies in digital humanities and lay the groundwork for future multilingual extensions.

1. Introduction

Text reuse detection may be pivotal in studying the transmission and evolution of ancient texts and examining their intertextual relations. The nature of the affinity between intertextually related texts differs from case to case. It may be a short quotation of exact phrases (as in citations of biblical texts), an extended reproduction of a text with minor changes (as in the transmission of works in manuscripts), or a loose rephrasing of content (as in two different performances of a folk story, two synoptic gospels, or parallel rabbinic traditions).

Computational solutions for text reuse detection have attracted significant recent research interest [1], as they address the challenges of a labor-intensive manual process. Automating this process involves three steps: first, implementing information retrieval methods to select pairs of documents with a high probability of local text reuse; second, applying a text alignment method to each pair, where each word in the first text is matched with its equivalent in the second; and third, using statistical methods on the aligned pairs to infer the strength, directionality, and nature of their affinity [2].

The second step, text alignment, presents unique challenges. Reused texts may appear significantly different, as words may be replaced with synonyms or abbreviations. Sometimes, multiple words are condensed into a single term, as seen with acronyms or gematria.

Additionally, practical challenges arise from the linguistic characteristics of our corpus (Hebrew/Aramaic). Semitic languages are orthographically and morphologically complex [3]. For instance, during the medieval and late antiquity periods, there was no standardized orthography [4], as reflected in the varied usage of Matres Lectionis.

Adding to the complexity is the nature of Semitic morphology, which allows multi-word expressions to be compressed into a single word. For example, the English phrase ‘I taught him’ can appear in Hebrew as a three-word sequence: ănî limmadtî ōtô. However, due to Hebrew’s morphological structure, the same meaning can be conveyed using a single word: limmadtîhû. A practical text alignment method must account for this morphological richness and variability, ensuring that alignments accurately capture both word-to-word correspondences and multi-word-to-single-word mappings.

One might consider the case illustrated in Figure 1, which highlights the intricacy of text collation. The medieval manuscripts Bodleian Opp. Add. fol. 3 (hereafter referred to as Ox3) and British Library Add. 27,169 (denoted as Lon) serve as two textual witnesses of Leviticus Rabba, a rabbinic homiletic work from late antiquity. The illustration presents a color-coordinated alignment, delineating various categories of textual divergences found in these manuscripts: acronyms (highlighted in green), abbreviations (indicated in cyan), gematria (depicted in brown), and word transpositions (evidenced by the interchange of words bearing identical coloration).

Brill et al. [5] introduce a state-of-the-art Hebrew/Aramaic textual alignment methodology. Their approach employs the Needleman–Wunsch global alignment algorithm (hereafter NW) [6], complemented by a novel distance metric designed to quantify word disparity. This metric is derived from a linear combination of word2vec embeddings [7] and the traditional edit distance [8]. However, due to its strict adherence to linearity, the algorithm occasionally fails to align transposed words. Additionally, the proposed distance metric has limited effectiveness in handling abbreviations and acronyms.

In this study, we propose refining the approach introduced by Brill et al. [5] through three key modifications. First, we replaced the Needleman–Wunsch (NW) algorithm with the Smith–Waterman (SW) algorithm [9] to facilitate local alignment, thereby improving the matching of full compositions with their constituent fragments.

Second, to address the challenge of word embeddings for out-of-vocabulary terms, we substituted the word2vec model with fastText [10], which provides better morphological representation. Additionally, we enhanced the distance metric to capture both single-word and multi-word alignments. Finally, we integrated a post-alignment process to ensure the proper alignment of transposed words. Comparative analyses with state-of-the-art methodologies demonstrated that our approach improves the $F_1$ score by 11%.

2. Related Work

2.1. Text Alignment

Local text alignment analyzes a pair of documents to identify segments that exhibit the highest likelihood of correspondence [11]. Many text alignment algorithms are based on one of the seminal techniques for sequence alignment from the bio-informatics research field: (1) The Needleman–Wunsch algorithm (NW) [6], designated for global alignment. (2) The Smith–Waterman algorithm (SW) [9], tailored for local alignment.

While the NW algorithm endeavors to comprehensively align entire texts under the presupposition of their complete reuse, the SW algorithm, contrarily, aims to discern the maximally congruent string segment, operating under the notion that strings may have been interspersed or partially reused.

Both techniques employ a two-step approach. In the initial step, a scoring matrix is generated, with each token from one string serving as columns and each token from the second string serving as rows. The value in each matrix cell is determined by two factors: (1) a function that assesses the distance between the two tokens, and (2) a cost function based on predefined parameters for match, mismatch, and gaps. In bio-informatics, it is customary to employ a straightforward distance function, assigning a value of one if the tokens are identical and zero if they differ. The typically used parameter values are 2 for matching tokens, −1 for mismatching tokens, and −5 for gaps [12]. A traceback function is implemented in the subsequent step to identify the most congruent sequence span among the paired sequences.

A plethora of text alignment algorithms have been predicated either on the foundational principles of NW, as evidenced by works such as [5,13], or on SW, as illustrated by [12,14]. These works differ in the distance metrics and cost functions applied to the algorithm.

Brill et al. [5] utilized the NW approach to present a state-of-the-art algorithm to tackle the linguistic intricacies inherent to our corpus. Notably, while the NW algorithm demonstrates commendable efficacy for aligning entire sequences of texts, the SW—which is designed for local alignment—appears to be better poised for the alignment of disparate text fragments, as needed in text reuse detection.

2.2. Distance Matrices

SW and NW algorithms require the incorporation of a distance metric that measures the degree of similarity between tokens, followed by applying a predetermined threshold to determine their semantic alignment. The simplest comparative method employed by Colavizza et al. [12] and Smith et al. [14] assigns a score of 1 to identical tokens and 0 to tokens that do not match. However, applying such a metric to our corpus may not match tokens exhibiting orthographic variations.

Clough et al. [15] employed stemming processes before comparing tokens. Stemming involves heuristic methods to derive a word’s root or stem form. However, stemming for morphologically rich languages is infeasible [16]. Extracting the lexeme form from each word requires a lemmatization process, which is performed using the part-of-speech (POS) tagging method [16]. More et al. [17] designed a transition-based framework for morphosyntactic dependency parsing (termed YAP). This framework is a POS tagging model trained on modern Hebrew. We tested [17] on ancient Hebrew texts. The results detected the proper base form in 77% of the test cases. The relatively low accuracy is attributed to language changes over the centuries. Retraining YAP on ancient languages like Hebrew is very limited due to the low availability of data [18].

We tested a more recent large language model published by Shmidman et al. [19]. They fine-tuned a BERT model for the lemmatization task of Hebrew words, training it on modern Hebrew. As reported by [19], the model rarely predicts semantically related synonyms instead of the word’s lexeme. We tested this model on rabbinic literature (Ancient Hebrew texts) and found that in 5% of the cases, the model predicted a synonym instead of the actual word’s lexeme. The results detected the proper base form in 75% of the test cases.

An alternative approach involves employing a distance metric based on the edit distance measure [8] to capture orthographic differences, as used by Haentjens [20]. However, this method may also fail to match the conceptual distance between words that have undergone significant morphological alterations [5].

Brill et al. [5] crafted a distance metric specifically tailored to Hebrew/Aramaic languages. They postulated a distance metric as a linear combination of two renowned distance metrics to encapsulate orthographic and semantic discrepancies. Initially, they employed a normalized version of the Levenshtein distance [8], quantifying the requisite character alterations to transmute one token into another. Subsequently, they utilized the cosine similarity between token vectors within a dense, low-dimensional word embedding space. For this purpose, ref. [5] harnessed the word2vec neural network model [7] (termed W2V) trained on an extensive Hebrew corpus. An intrinsic limitation of the W2V model is its inability to proffer embeddings for out-of-vocabulary words [10]. This means that tokens absent during the training phase lack vector representations. To circumvent this limitation, ref. [5] modified their distance function to impose a gap penalty when a token lacks a vector representation.

‘fastText’ [10] is a word embedding methodology engineered to encapsulate word morphologies within a closely aligned vector space. As demonstrated by [21], fastText adeptly captures the intricacies of Hebrew morphology, reflecting the nuanced and multifaceted semantics inherent to the language. A distinguishing feature of fastText is its capability to vectorize entire terms and their respective n-grams during the model training phase. This capability empowers fastText to furnish vector representations even for out-of-vocabulary words [10]. Additionally, the mechanism of n-gram vectorization ensures that inflections of words are proximate within the vector space [10]. Sprugnoli et al. [22] compared fastText with Word2vec word embedding for Latin. fastText exceeded word2vec by 6.9% to fetch similar lemmas. Given these attributes, fastText emerges as a particularly fitting choice for languages with rich morphological structures, such as Hebrew, and is adept at handling texts rife with noise.

3. Methodology

Ref. [5] presents an advanced Hebrew/Aramaic alignment method in their research. They employed the Needleman–Wunsch (NW) global alignment algorithm [6] and established a distance metric for word comparison.

Several modifications are necessary to adapt this method for the text reuse detection framework. First, it is assumed that only a limited portion of one text has been reused in the other. Consequently, the NW global alignment algorithm replaces the Smith–Waterman (SW) local alignment algorithm.

It should be noted that the expectation is not verbatim reuse; instead, the alignment process should accommodate the substitution of words with similar ones, the replacement of words with their abbreviations, and the compression of multiple words into acronyms. Additionally, it should account for typographical errors between the two texts. Finally, while the word order may vary, the algorithm should be able to detect and align word transpositions.

In the subsequent sections, we outline the modifications proposed to address the text reuse criteria established in [5] work. Section 3.1 elaborates on the design of the distance function, which quantifies word distances for all necessary alterations. Section 3.2 explains the cost function, which generates our unique score matrix. Section 3.3 details the adjustments made to the SW traceback function, specifically tailored to accommodate word transpositions and multi-token alignments.

3.1. Distance Function

We designed a custom distance function that measures the closeness of terms within the [0, 1] range, where 0 indicates no similarity, and 1 denotes identical terms. Different methods are combined to assess term alterations, each addressing a specific type of change. Algorithms that measure the distance between terms with typographic variations are discussed in Section 3.1.1. Morphological similarity measurement is detailed in Section 3.1.2. Specific replaceable elements, such as gematria, acronyms, and abbreviations, are handled separately and explained in Section 3.1.3.

3.1.1. Typographic Change Alignment

Machine-readable text can be generated through manual typing or Optical Character Recognition (OCR) technology. Both methods are prone to errors: inexperienced typists introduce character errors at a rate of 3.2% [23], while OCR systems can exhibit error rates of up to 4.1% [24]. These errors include word boundary and spelling mistakes, which we aim to detect and align.

As described by [23], word boundary errors occur in two ways: either a single word is incorrectly split into two (15% of typos), or two valid words are merged into one. To measure the distance between tokens affected by such errors, our algorithm examines surrounding tokens, comparing the first token to the combination of the adjacent token and its neighbor. If similarities are detected, the algorithm suggests that the error results from missing or extra word separators.

Spelling errors, another category highlighted by Kukich [23], often involve substituting similar characters. For example, ‘B’ is frequently replaced by ‘N’ in manual typing due to their proximity on the keyboard, while OCR systems may confuse ‘D’ and ‘O’ due to their visual similarity. Our method allows researchers to define replaceable character pairs, such as ($D,O$), which are then standardized across tokens. The algorithm systematically replaces all instances of ‘D’ with ‘O’ and evaluates token similarity, assuming that the difference results from spelling errors.

While we also developed methods for phonetic and cognitive errors, these were not evaluated in this study.

3.1.2. Rich Morphological Language Alignment

Brill et al. [5] introduced a distance metric formulated as a linear combination of two distinct distance matrices: one measuring the edit distance between words, which accounts for misspellings and orthographic variations, and the other assessing word similarity in an embedding vector space, capturing their contextual usage similarity.

We adopted this compound metric in our approach, substituting the word embedding method with fastText for two main reasons. First, fastText can vectorize words that may not have been encountered in the training dataset. Second, its training methodology allows for the creation of a new model that effectively maps variations of the same word stem to proximate positions within the vector space.

Regarding edit distance, we employ a normalization technique for the Levenshtein distance, denoted as $L_n$, using the formula below. Let $L(t_1,t_2)$ represent the Levenshtein distance between token $t_1$ and token $t_2$, and let S denote the length of the longer of the two tokens. The normalized edit distance is then defined as follows:

$$D_L(t_1,t_2)={\displaystyle \frac{L(t_1,t_2)}{S}}$$

(1)

We utilize cosine similarity to evaluate the semantic similarity between two words in the vector space model, a widely used technique in NLP and information retrieval [25]. Let $V_{t_1}$ and $V_{t_2}$ be the vector representations of $t_1$ and $t_2$, respectively. The cosine similarity between these two vectors is defined as follows:

$$D_C(t_1,t_2)={\displaystyle \frac{V_{t_1}\ast V_{t_2}}{\parallel V_{t_1}\parallel \ast \parallel V_{t_2}\parallel }}$$

(2)

We can now straightforwardly establish the distance measure between $t_1$ and $t_2$ for all scenarios as a weighted mean of the two, incorporating a coefficient denoted as $\alpha$ that falls within the range of $[0,1]$:

$$D(t_1,t_2)=\alpha \ast D_L+(1-\alpha )\ast D_C$$

(3)

3.1.3. Acronyms, Abbreviations, and Gematria

Our focus corpus consists of compositions in Hebrew and Aramaic from late antiquity, which frequently incorporate gematria, a system that represents numbers using alphabetic characters. To address this, we have developed a function capable of determining whether one or both tokens in a pair fall into one of three possible categories:

• A numeric representation, such as 18.
• An alphabetic representation, such as eighteen, or in Hebrew, šĕmōne eśrê.
• A gematria representation, such as KH, or in Hebrew, yôd"ḥêt (yôd is the tenth letter of the Hebrew alphabet, and ḥêt is the eighth letter).

Upon recognizing a token that indicates the beginning of a numeric representation, our algorithm scans the remainder of the input string until it identifies a consecutive sequence of tokens representing the entire numerical value. The algorithm then compares the semantics of the two representations. If they denote the same number, only the first token of each sequence is returned as a match from the distance function.

However, we extended the alignment process in the traceback function. For instance, suppose the algorithm encounters the number 18 token in one text and a sequence of tokens—šĕmōne and eśrê—in the other. Initially, our distance function aligns 18 with šĕmōne, leaving eśrê unmatched. Then, in the traceback function, eśrê is also aligned with 18.

Abbreviations and acronyms were prevalent in medieval manuscripts, providing a concise means of expression, which was particularly valuable given the high cost of writing materials during that era. These abbreviated forms often incorporated special punctuation marks, namely quotation marks (") and apostrophes (').

To facilitate the alignment of such elements, we developed a dedicated distance measurement technique to identify these distinctive markers. When an abbreviation indicator is detected within a token, our algorithm prunes the corresponding token to match the length of the abbreviated form before performing the comparison. Conversely, when an acronym indicator is identified, the algorithm splits it into its components, attempting to align each part as an abbreviation within two adjacent tokens.

For instance, when evaluating the similarity between dābār ’aḥēr (‘Different thing’) and the acronym ‘D”A’, the algorithm aligns ‘D’ as an abbreviation of dābār and ‘A’ as an abbreviation of ’aḥēr.

3.2. Cost Function

The Smith–Waterman algorithm begins by generating a score matrix using a distance function and dynamic programming. Each cell, $c(i,j)$, is filled by selecting the maximum value from three directions: up, left, or diagonal. The up and left values are calculated by adding a gap penalty g, while the diagonal value is computed by adding either a match score m or a mismatch score n, depending on whether the ith and jth tokens match. Since our distance metric measures token similarity, we incorporate this into the diagonal calculation.

The dynamic programming function follows these rules:

$$u=c(i-1,j)+g$$

(4)

$$l=c(i,j-1)+g$$

(5)

$$d=D(x,y)$$

(6)

$$c(i,j)=\left\{\begin{array}{cc}max(0,u,l,c[i-1,j-1]+d\ast n)\hfill & i=j\hfill \\ max(0,u,l,c[i-1,j-1]-m)\hfill & i\ne j\hfill \end{array}\right.$$

(7)

We used match, mismatch, and gap parameters from [12], with $n=2$ for matches, $m=-1$ for mismatches, and $g=-2$ for gaps. This setting is more lenient than the standard gap penalty of $-5$, which helps mitigate proximity mismatches due to text noise.

Each cell in the score matrix depends on the distance function, which incorporates multiple methods. We expanded the Smith–Waterman matrix to indicate which method was used for each match, enabling the alignment of multiple tokens from one string with a single token from another during traceback.

3.3. Traceback Function

The final step of the Smith–Waterman (SW) algorithm is the traceback process, where the algorithm identifies the highest-scoring cell in the matrix and extracts the longest matching sequence between the two texts. However, the standard SW algorithm is unable to detect word transpositions. To address this limitation, we enhanced the traceback procedure by applying a distance function to the gaps between strings.

In some instances, multiple tokens collectively convey a single meaning, as is often the case with numerical values or acronyms. The original SW algorithm does not account for such cases; therefore, we extended its functionality to enable the alignment of multiple tokens from one string with a single token in another.

Our enhanced traceback function incorporates a token-matching method to suggest corrections. For instance, when a ‘missing word separator’ is detected, the algorithm proposes splitting the token into two distinct sub-tokens, which are then aligned separately.

Additionally, our algorithm supports the alignment of a single token with multiple tokens, particularly in cases involving gematria or acronyms. This capability may also aid in correcting input errors, such as typographical mistakes, by ensuring proper alignment.

4. Evaluation

4.1. Alignment Measurement

Our goal is to evaluate the alignment results using precision, recall, and the $F_1$ score by comparing them to a ground truth (GT). The GT and the algorithm results are represented as lists of tuples $(x,y)$, where x and y indicate the positions of aligned tokens in the first and second texts. For example, in the alignment shown in Figure 1, the tuple $(3,6)$ appears in the GT because the third token in the first text (‘lesorek’) should align with the sixth token in the second text.

In cases where two tokens in one text align with a single token in another, this is represented by two tuples. For instance, in Figure 1, the second token in the first text (‘yôd"ḥêt’) aligns with both the third and fourth tokens of the second text, creating two GT tuples: $(2,3)$ and $(2,4)$. This structure is effective in handling transpositions and multi-token alignments.

To assess the computer’s alignment, we calculate a confusion matrix:

• True Positive (TP): A tuple exists in both the computer’s results and the GT.
• False Positive (FP): A tuple exists in the computer’s results but not in the GT.
• False Negative (FN): A tuple exists in the GT but not in the computer’s results.
• True Negative (TN): A tuple is absent in both the computer’s results and the GT.

Using the confusion matrix, we calculate precision, recall, and $F_1$ score as follows:

$$Precision={\displaystyle \frac{TP}{TP+FP}}$$

(8)

$$recall={\displaystyle \frac{TP}{TP+FN}}$$

(9)

$$f_1=2\ast {\displaystyle \frac{Precision\ast Recall}{Precision+Recall}}$$

(10)

To measure these, we need a ground truth dataset with expert-aligned text pairs. In our study on rabbinic literature from the Middle Ages, synoptic editions are common. These editions visually display correspondences between different versions but are limited in handling word transpositions or multi-word alignments.

For example, Figure 1 from Milikovsky’s Vayikra Rabbah synoptic edition [26] shows that misalignments can occur due to the linear structure, as seen with the cyan and yellow tokens.

We built our ground truth dataset using two sources: Vayikra Rabbah [26] and a subset from the Friedberg Project for Talmud Bavli Variants [27], consisting of 234 texts with 69,700 words.

4.2. Word Embedding Models

In our approach, we trained a fastText model. The dataset for training fastText consists of textual corpora sourced from Sefaria [28], a comprehensive digital library of Jewish texts. This corpus spans many historical periods, literary styles, and textual genres, including biblical texts, Talmudic discussions, and rabbinic commentaries. To ensure data quality, we undertook the following preprocessing steps:

• Removal of extraneous formatting artifacts, footnotes, and annotations.
• Standardization of Hebrew orthographic variations, including the normalization of diacritics.
• Excluding metadata and non-linguistic content that could introduce noise into embeddings.

The fastText model was configured with a dimensionality of 300, while subword representations were constructed from character sequences ranging from two to five characters. Additionally, the initial learning rate was set to ${\gamma }_0=0.05$ (for further details, see [10]).

5. Experiments

We conducted a comparative analysis of our method against the baseline method [5], which we refer to as NW-W2V. Given that we introduced several modifications to the baseline, our goal was to systematically evaluate the impact of each individual change.

Initially, we focused on assessing the enhancements to the distance function, which resulted in three distinct configurations:

• NW-Fast: This configuration maintains the same settings as [5] but replaces the Word2Vec (W2V) model with fastText for word embeddings.
• NW-W2V-Hebrew: This configuration retains the original settings of [5] while incorporating Hebrew- and Aramaic-specific enhancements.
• NW-Fast-Hebrew: Building upon the NW-Fast configuration, this version integrates all enhancements tailored for Hebrew and Aramaic.

To further assess the impact of the alignment method, we conducted an additional set of tests, replacing the Needleman–Wunsch global alignment algorithm with the Smith–Waterman local alignment algorithm. These tests resulted in four additional configurations:

• SW-W2V: Employs the Smith–Waterman local alignment algorithm while retaining the same distance function as in [5].
• SW-Fast: Builds upon SW-W2V, incorporating the fastText embedding model.
• SW-W2V-Hebrew: Extends SW-W2V by integrating Hebrew- and Aramaic-specific enhancements for the distance function.
• SW-Fast-Hebrew: Implements our proposed method, combining all introduced enhancements, referred to as SW-Fast-Hebrew.

To adjust the distance function parameter $\alpha$, we evaluated its effect on alignment performance, specifically precision, recall, and $F_1$ score, as shown in Figure 2. The $F_1$ score ranged from 0.86 to 0.88, reaching its peak value of 0.88 at $\alpha =0.2$. The precision varied between 0.86 and 0.87, peaking at $\alpha =0.7$. The recall ranged from 0.87 to 0.90, achieving its highest value of 0.90 at $\alpha =0.1$. Based on these results, we set $\alpha =0.2$ in all configurations to optimize the balance between precision and recall.

6. Results

Table 1. A summary of the alignment results for the different methods.

Methods	${\mathit{F}}_1$	Recall	Precision
NW-W2V	0.83	0.73	0.97
NW-W2V-Hebrew	0.89	0.83	0.97
NW-Fast	0.92	0.90	0.95
NW-Fast-Hebrew	0.90	0.83	0.97
SW-W2V	0.83	0.73	0.96
SW-W2V-Hebrew	0.90	0.84	0.96
SW-Fast	0.93	0.92	0.95
SW-Fast-Hebrew	0.94	0.93	0.95

shows the alignment results for different configurations, including precision, recall, and the $F_1$ score. The Smith–Waterman (SW) algorithm achieves significantly higher recall, outperforming the Needleman–Wunsch (NW) algorithm by up to 10% and increasing the SW algorithm’s $F_1$ score by up to 4%. However, NW demonstrates slightly better precision, improving about 1–2%.

In scenarios where modifications were made to the distance function, SW consistently outperformed NW. For example, with all changes applied (Fast-Hebrew configuration), SW’s recall was 10% higher than NW’s. In most cases, SW yields better overall results; however, without modifications to the distance function, it performs slightly worse than NW.

Among the enhancements, replacing the word embedding model had the greatest impact, increasing the $F_1$ score by 9% for NW and 10% for SW. Hebrew-specific enhancements further improved alignment, particularly with the Word2Vec (W2V) embedding. However, when using fastText with SW, the $F_1$ score improved by only 1%, whereas in the NW-Fast configuration, it decreased by 2%.

Overall, these changes resulted in an 11% increase in the $F_1$ score, primarily driven by adopting a more suitable word embedding model for languages with complex morphology.

6.1. Variant Sizes of Text Reuses

The Needleman–Wunsch algorithm is primarily designed for global alignment. In contrast, the Smith–Waterman algorithm is optimized for scenarios in which a minor segment of one text is incorporated into another. We aim to evaluate the impact of text size disparities on alignment quality. First, we quantified the size differentials across 234 instances within our ground truth dataset, ranging from 0% (denoting identical text sizes) to a maximum variance of 93%.

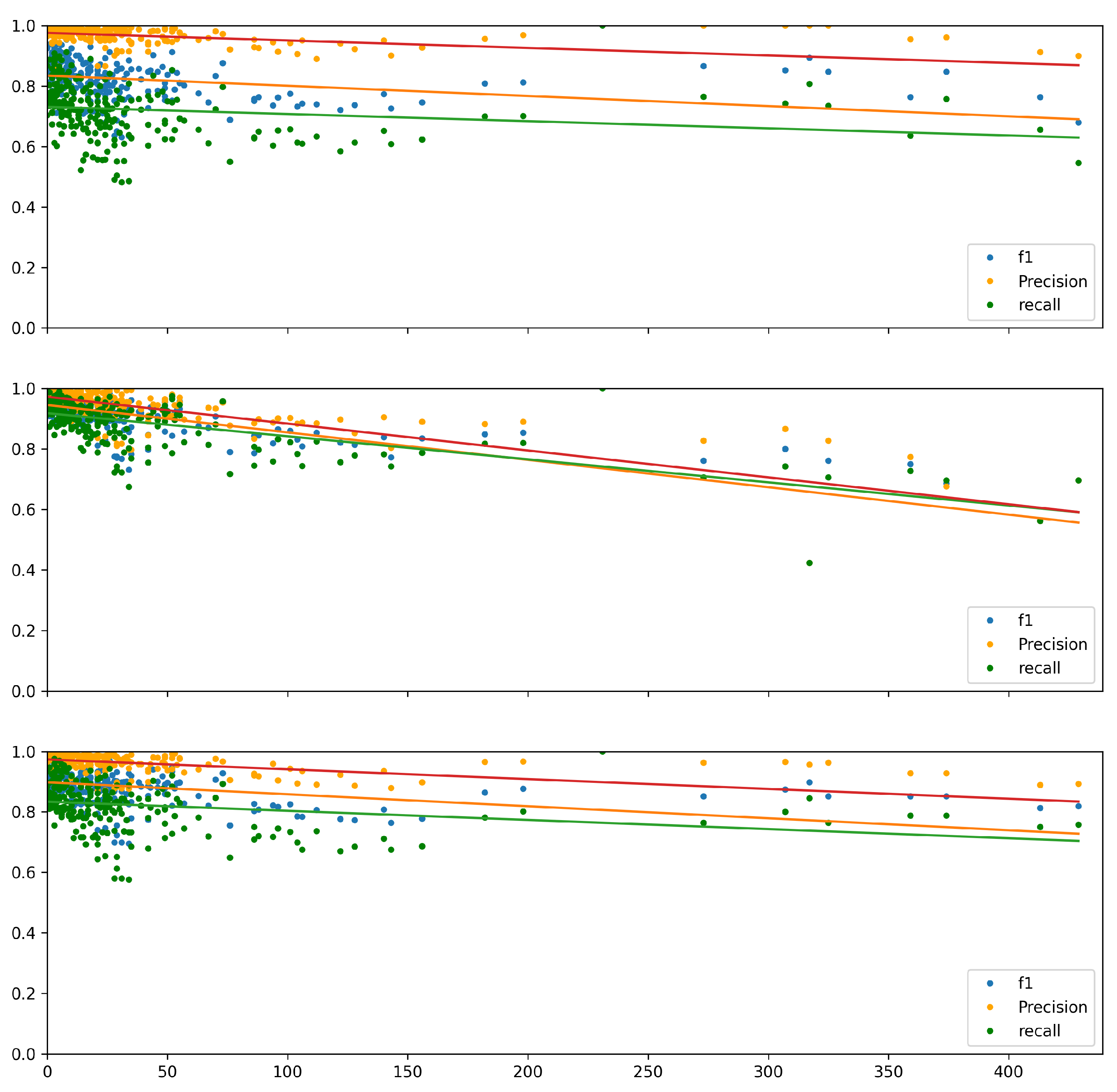
A graphical representation illustrating the alignment quality as a function of text size disparity is shown in Figure 3 and Figure 4 for the Needleman–Wunsch and Smith–Waterman algorithms, respectively. Each figure includes three distinct distance functions: W2V, fastText, and fastText-Hebrew. Linear regression lines are incorporated in each figure to clarify the correlation.

Upon examining the NW-Fast configuration, we observe a decline in alignment quality as the difference in text length increases. This trend is reflected in the negative slope of the linear regression line, indicating that more significant disparities in text length result in lower $F_1$ scores. This suggests that the NW-Fast method struggles with aligning texts of significantly different sizes, highlighting a limitation of this approach.

Conversely, the linear regression line for SW-Fast-Hebrew exhibits an almost negligible slope, indicating a significantly attenuated correlation between text size disparities and alignment quality. To quantify the relationship between text size differences and alignment quality, we employed metrics such as F1 score, precision, and recall, computing the Spearman correlation coefficient. The results for various combinations of alignment methodologies and distance metrics are presented in

Table 2. The Spearman correlation between text size differences and F1 score, precision, and recall for the entire dataset reveals distinct patterns across alignment methods. The Needleman–Wunsch algorithm exhibits a moderate to strong negative correlation with text size variations, whereas the Smith–Waterman algorithm demonstrates a weaker to moderate negative correlation.

Methods	${\mathit{F}}_1$	Recall	Precision
NW-W2V	−0.51	−0.48	−0.35
NW-Fast	−0.66	−0.59	−0.62
NW-Fast-Hebrew	−0.56	−0.51	−0.52
SW-W2V	−0.49	−0.49	−0.36
SW-Fast	−0.45	−0.44	−0.38
SW-Fast-Hebrew	−0.45	−0.44	−0.38

. Different classification schemes exist for interpreting the strength of Spearman’s correlation, as outlined by [29]. In this study, we adopt the psychological approach.

The Needleman–Wunsch algorithm, as configured by [5] (NW-W2V), exhibits a weak to moderate negative correlation between the $F_1$ score and text size differentials ($r_s=-0.51$).

Replacing the word embedding model within the distance metric from W2V to fastText (NW-Fast) significantly amplified the negative correlation to $r_s=-0.66$. This increase is primarily attributed to an enhancement in the recall, which rose from 0.73 to 0.90, particularly impacting the ‘head’ region, where text size disparities are minimal. This effect is clearly illustrated in the linear regression lines in Figure 3, where the contrast between the top sub-figure (NW-W2V) and the middle sub-figure (NW-Fast) highlights an increase in recall, particularly in the upper-left quadrant, while the remainder of the spectrum remains relatively unchanged. This improvement is reflected in the more significant negative correlations.

Implementing subsequent refinements, specifically the Hebrew enhancements, tempered the recall improvement to 83%, slightly reducing the negative correlation. When analyzing the optimal performance of the Needleman–Wunsch algorithm, it is evident that alignment quality declines more sharply as size disparities increase.

Conversely, the Smith–Waterman algorithm exhibits a weak to moderate negative correlation across all distance function combinations. Moreover, the impact of substituting the word embedding model closely mirrored that observed in the NW algorithm, significantly increasing recall from 73% to 92%.

However, unlike the NW algorithm, this effect was distributed across the entire spectrum in the SW algorithm, resulting in no change to the correlation, which remained weakly to moderately negative. In contrast to the NW algorithm, the Hebrew enhancements further increased recall and outperformed all other configurations.

Text Witnesses vs. Text Reusers

Owing to the composition of our ground truth dataset, the instances are not uniformly distributed across the spectrum of size differentials. The cases within our dataset can be divided into two distinct groups. The first group comprises 86% of the dataset and is characterized by negligible size disparities within the range of [0–80]. This cluster can be perceived as two copies of the exact text, with minor modifications interspersed. We designate this cluster as ‘text witnesses’.

Conversely, the secondary group comprises only 14% of the dataset and is characterized by substantial size differences between the aligned texts, ranging from 81 to 500. This suggests this cluster primarily consists of minor text reuse between the paired texts. We refer to this second cluster as ‘text reuses’.

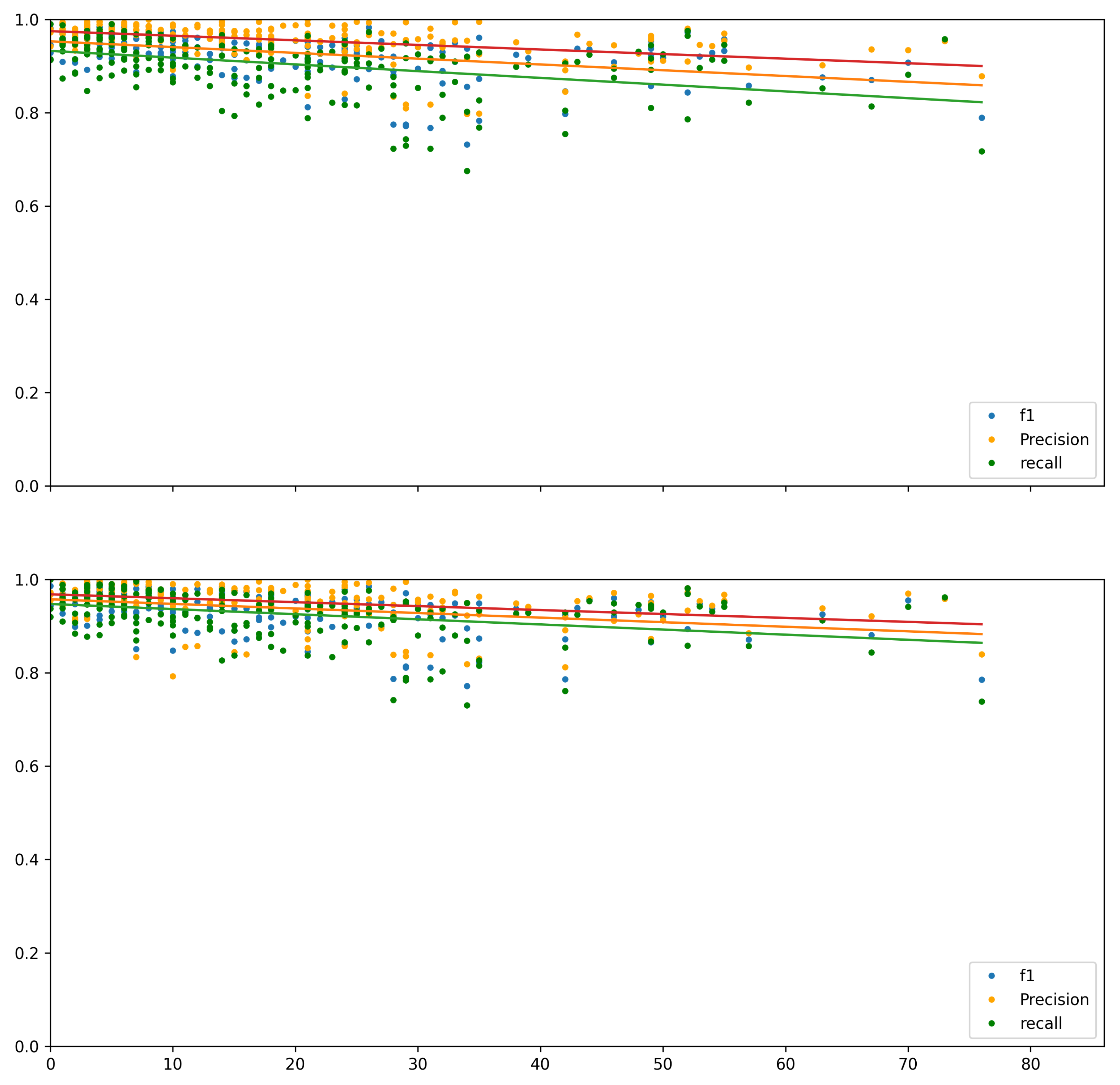
Due to the substantial disparity in the number of cases between the two groups in our dataset and their distinct characteristics, we evaluated alignment quality separately for the best distance function in each group.

The Spearman correlation for the ‘text witnesses’ group is presented in

Table 3. Spearman correlation between text size differences and F1 score, precision, and recall for the ‘text witnesses’ group.

Methods	${\mathit{F}}_1$	Recall	Precision
NW-Fast	−0.53	−0.48	−0.48
SW-Fast-Hebrew	−0.45	−0.41	−0.42

. The results indicate a slight difference in correlation between the two alignment methods, exhibiting moderate negative correlations. This suggests that the quality of all alignment methods slightly declines as size differences increase, maintaining the same proportion. This effect is more pronounced in the NW algorithm and is visually depicted in Figure 5.

The ‘text reuse’ group exhibits a significant disparity between the NW and SW algorithms, as shown in

Table 4. Spearman correlation between text size differences and F1 score, precision, and recall for the ‘text reuses’ group.

Methods	${\mathit{F}}_1$	Recall	Precision
NW-Fast	−0.69	−0.61	−0.68
SW-Fast-Hebrew	+0.72	+0.59	+0.69

. The NW-Fast combination demonstrates a strong negative correlation, indicating that alignment quality deteriorates as the length of text reuse decreases.

Conversely, the SW-Fast-Hebrew combination exhibits a strong positive correlation, suggesting that shorter text reuse leads to improved alignment. This inverse relationship is visually represented in Figure 6.

7. Conclusions

In this study, we developed and evaluated a new text alignment approach to improve text reuse detection in Hebrew and Aramaic texts. By integrating the Smith–Waterman algorithm with a novel distance metric and utilizing fastText embeddings, we addressed key challenges, including word transpositions, orthographic variations, and multi-word alignments. Our approach demonstrated an 11% increase in the F1 score, highlighting substantial improvements over existing methods.

Our findings emphasize the importance of adapting text alignment strategies to accommodate the linguistic and morphological complexities of ancient texts. This enhanced alignment capability deepens our understanding of text reuse and intertextual relationships in historical documents, contributing a valuable tool to digital humanities, particularly for languages with rich morphological structures.

Beyond text reuse detection, our approach proposes a typological correction mechanism, which could be integrated into automatic transcription pipelines to enhance text normalization and improve the accuracy of machine-generated transcriptions. This is particularly relevant given the anticipated transcription of millions of ancient Hebrew manuscripts, reinforcing the necessity of digital humanities methodologies for large-scale textual analysis.

However, our study has some limitations. The size of the ground truth dataset was limited, which may affect the generalizability of our findings. Additionally, varying size differences between aligned texts present challenges in consistently applying and evaluating the method’s effectiveness. Further research using larger and more diverse datasets is needed to assess the scalability and broader applicability of our approach.

Future work should focus on expanding this alignment method to other languages and text corpora, refining distance metrics to further improve accuracy, and integrating the method into digital manuscript transcription projects. By extending our approach beyond Hebrew and Aramaic, we aim to contribute to the next generation of computational tools for historical text analysis, bridging the gap between traditional philological methods and modern NLP techniques.