Application of Simulation Methods and Image Processing Techniques in Rock Blasting and Fragmentation Optimization
Abstract
1. Introduction
2. Problem Description
3. Methodology
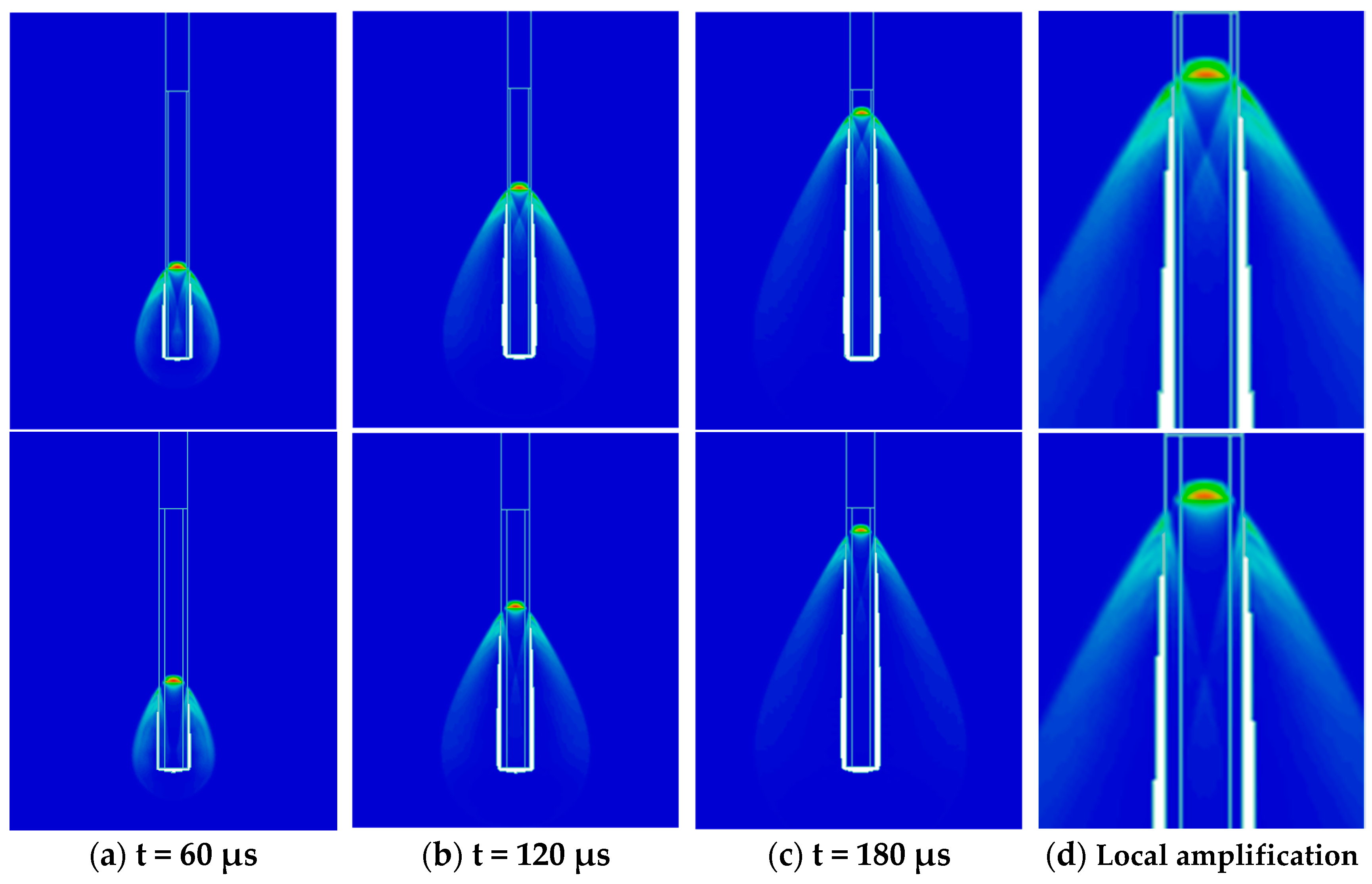
3.1. Simulation of Explosive Detonation
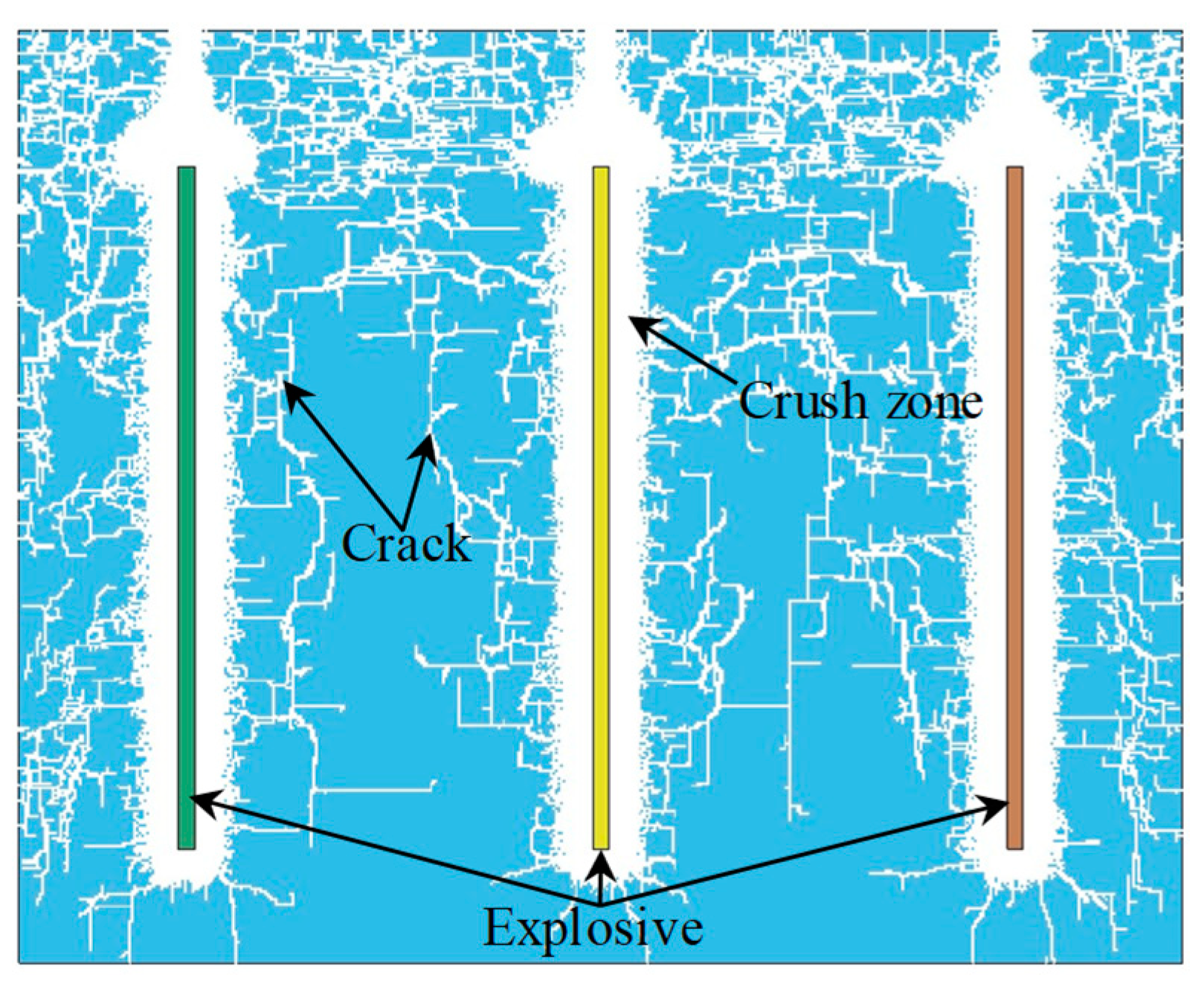
3.2. Simulation of Rock Blasting Fragmentation
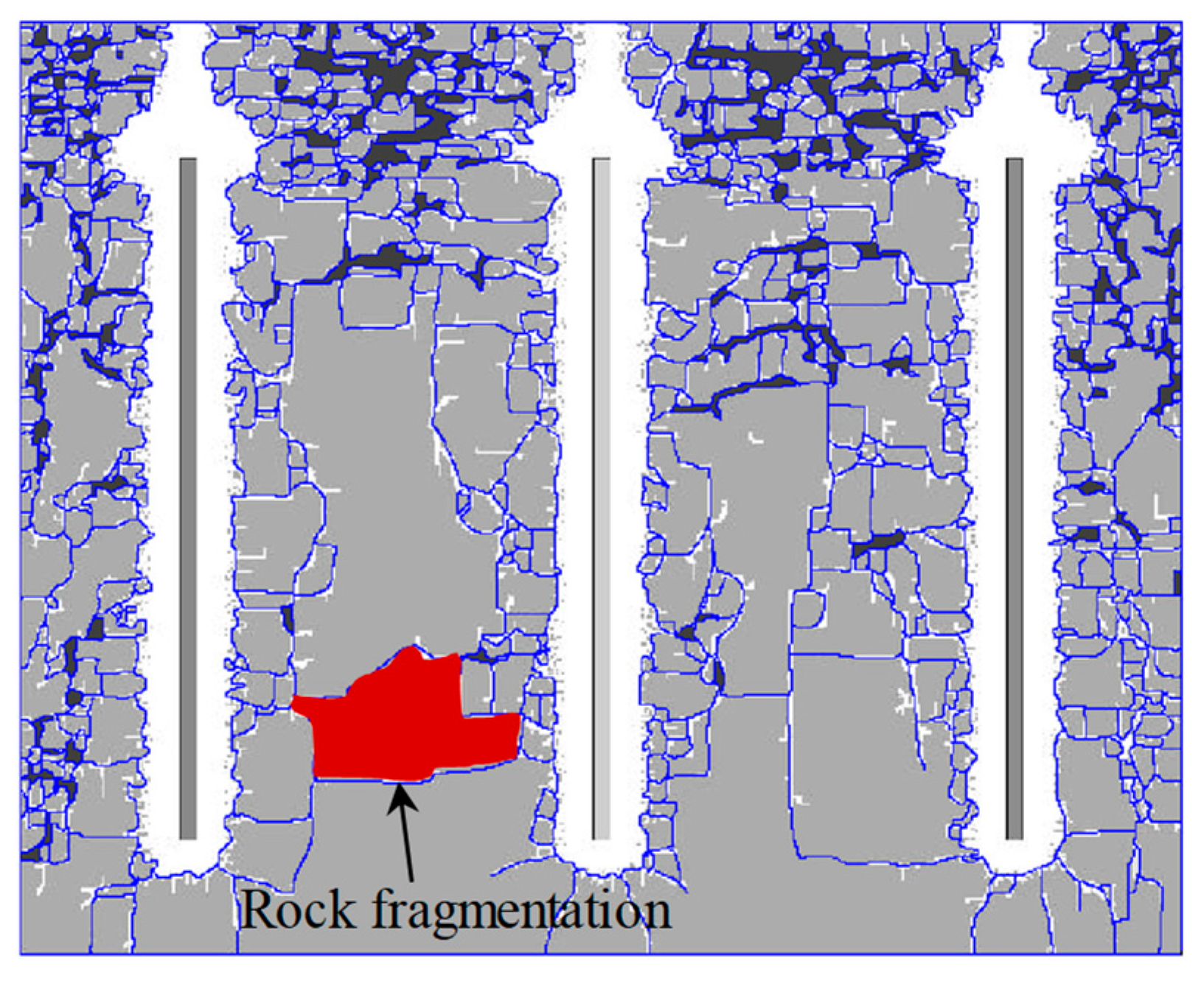
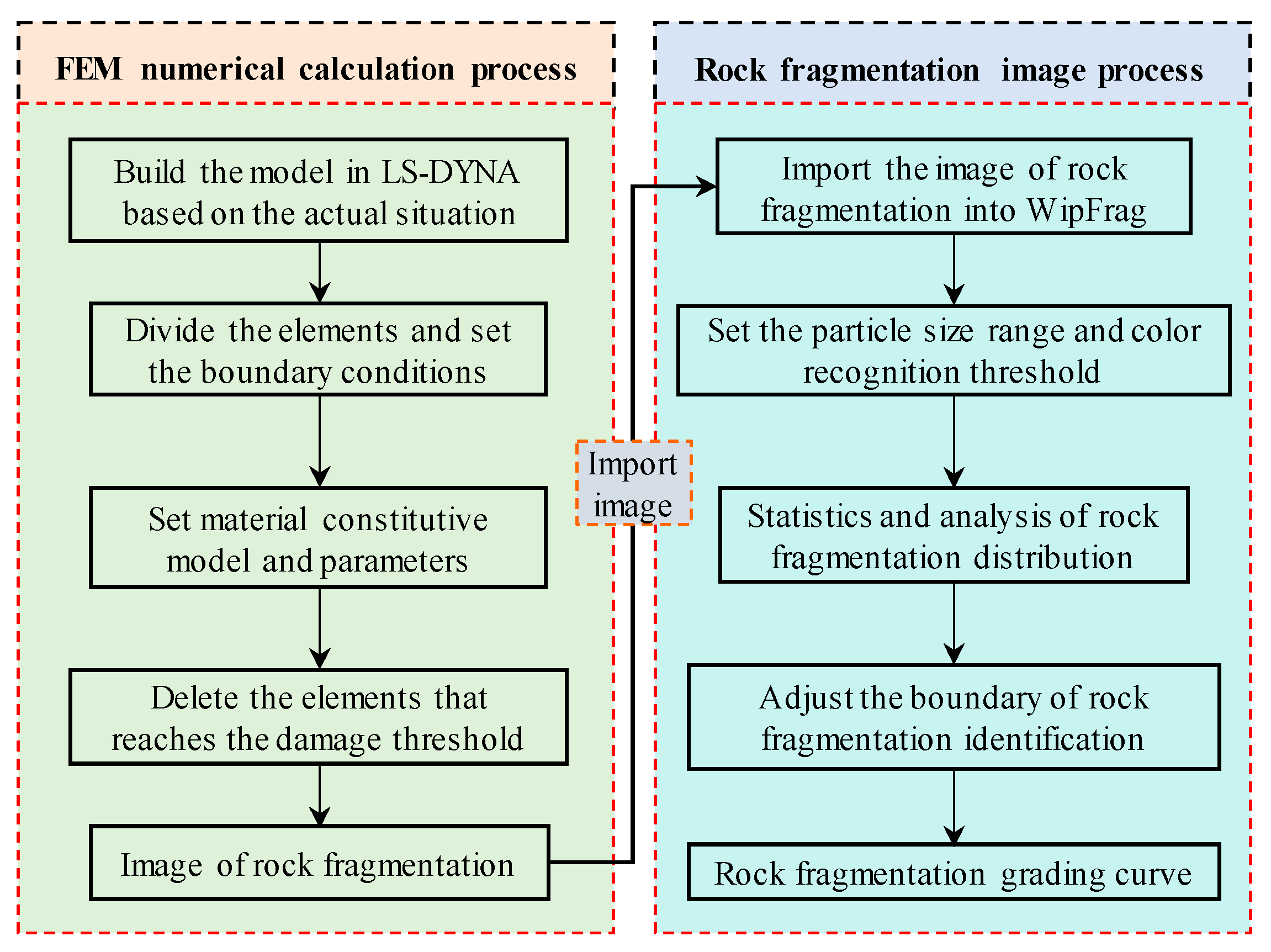
3.3. Flow of Fragmentation Effect Simulation and Analysis Method
4. Onsite Blasting Experiments
4.1. Engineering Background
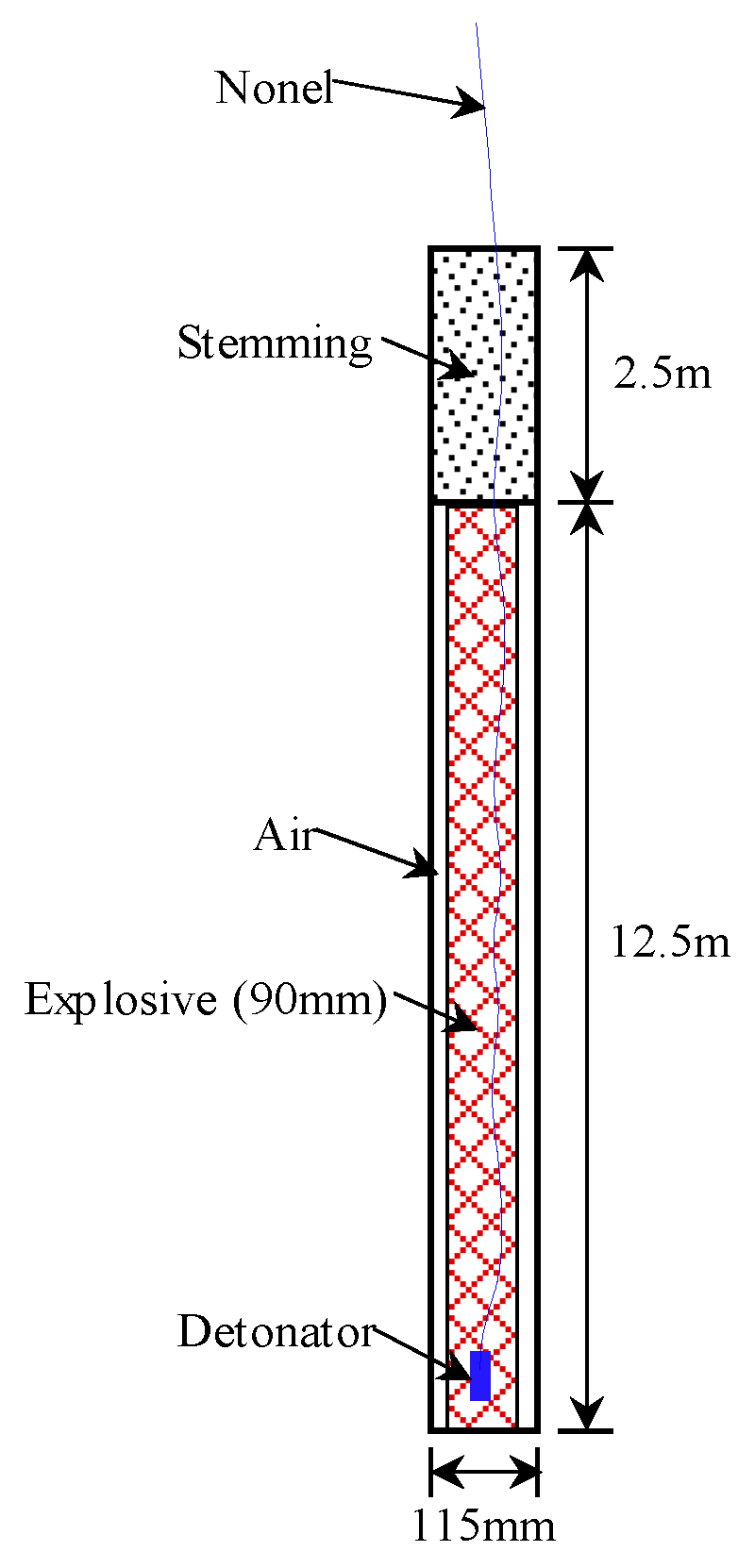
4.2. Blasting Design
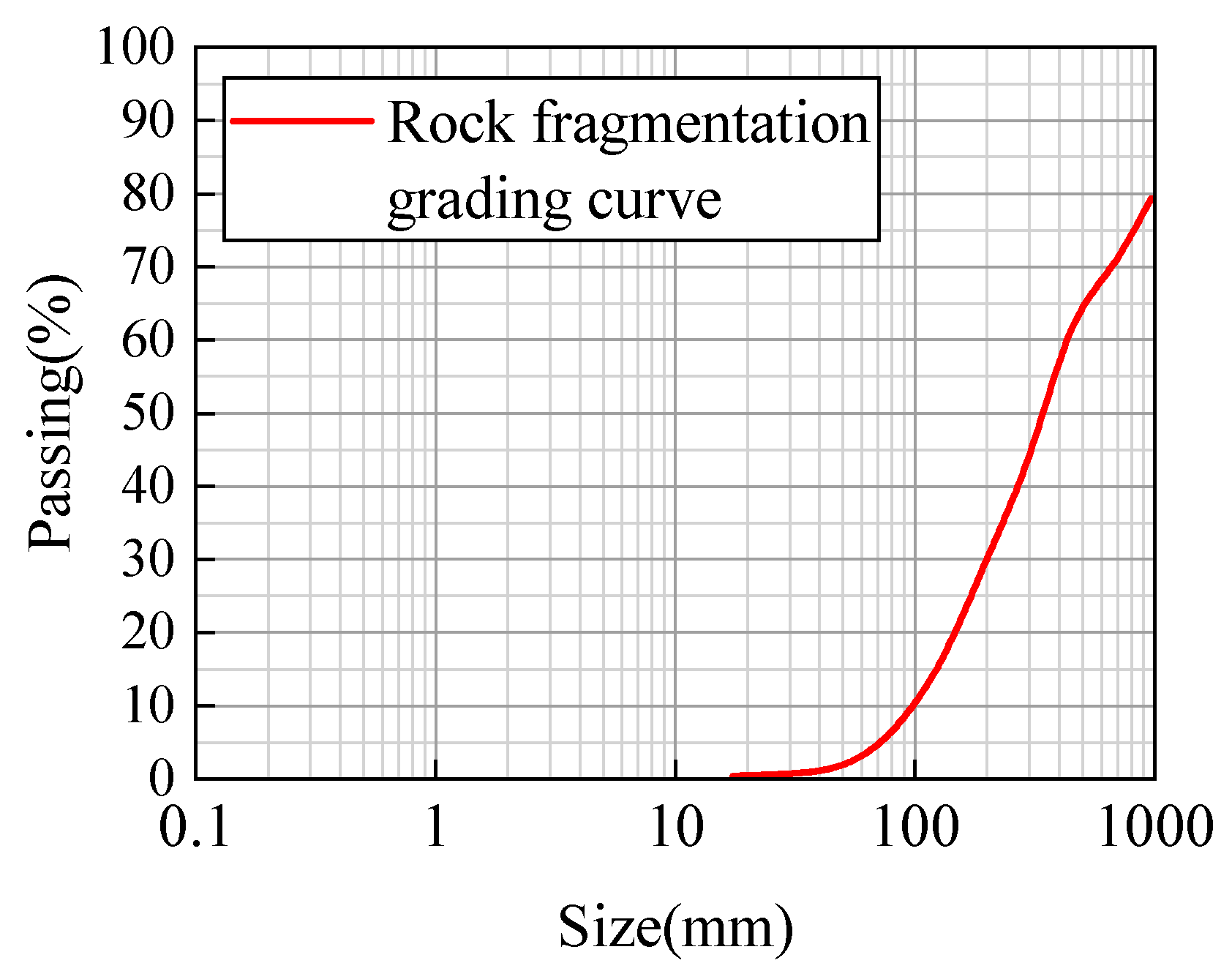
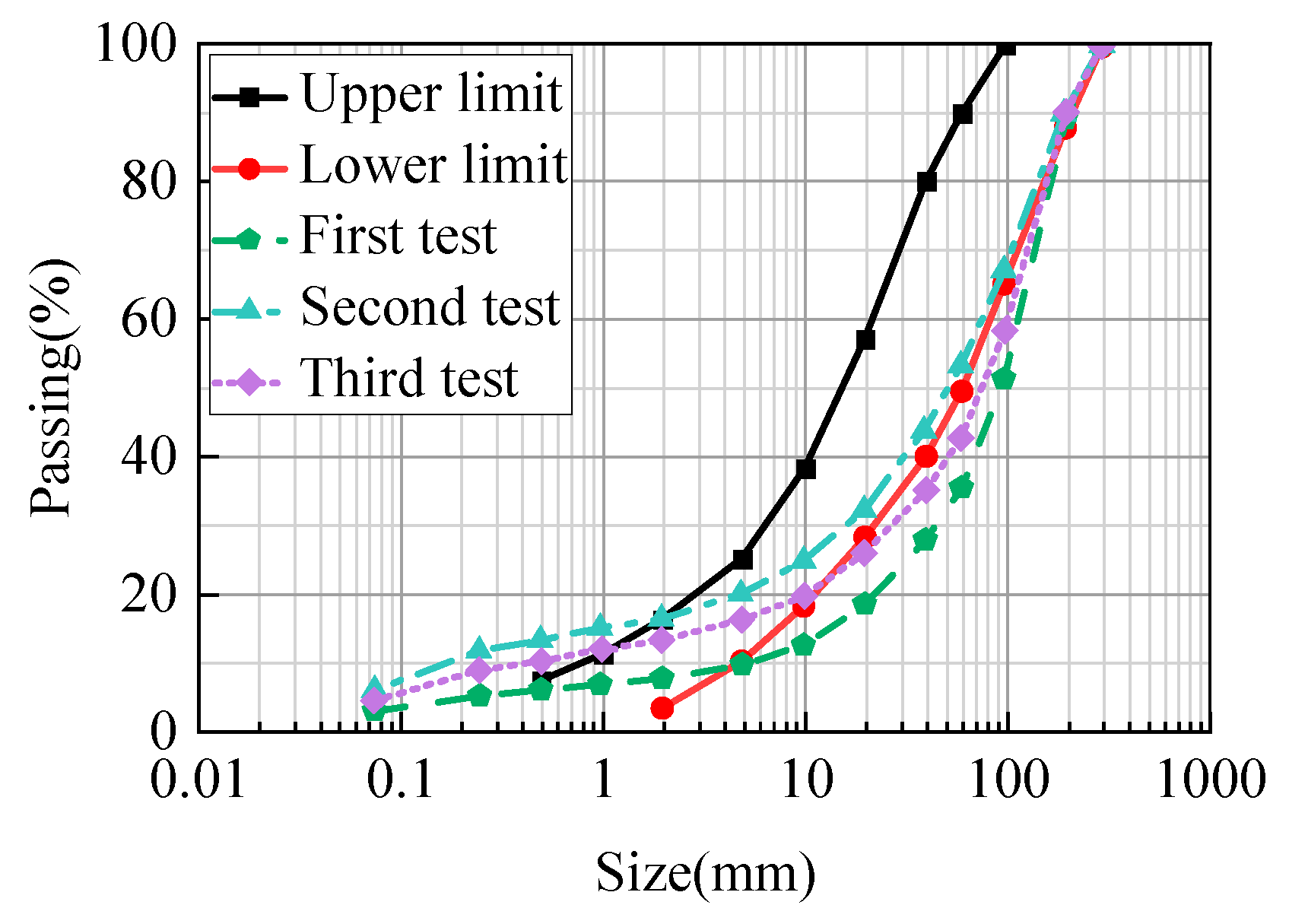
4.3. Results Analysis
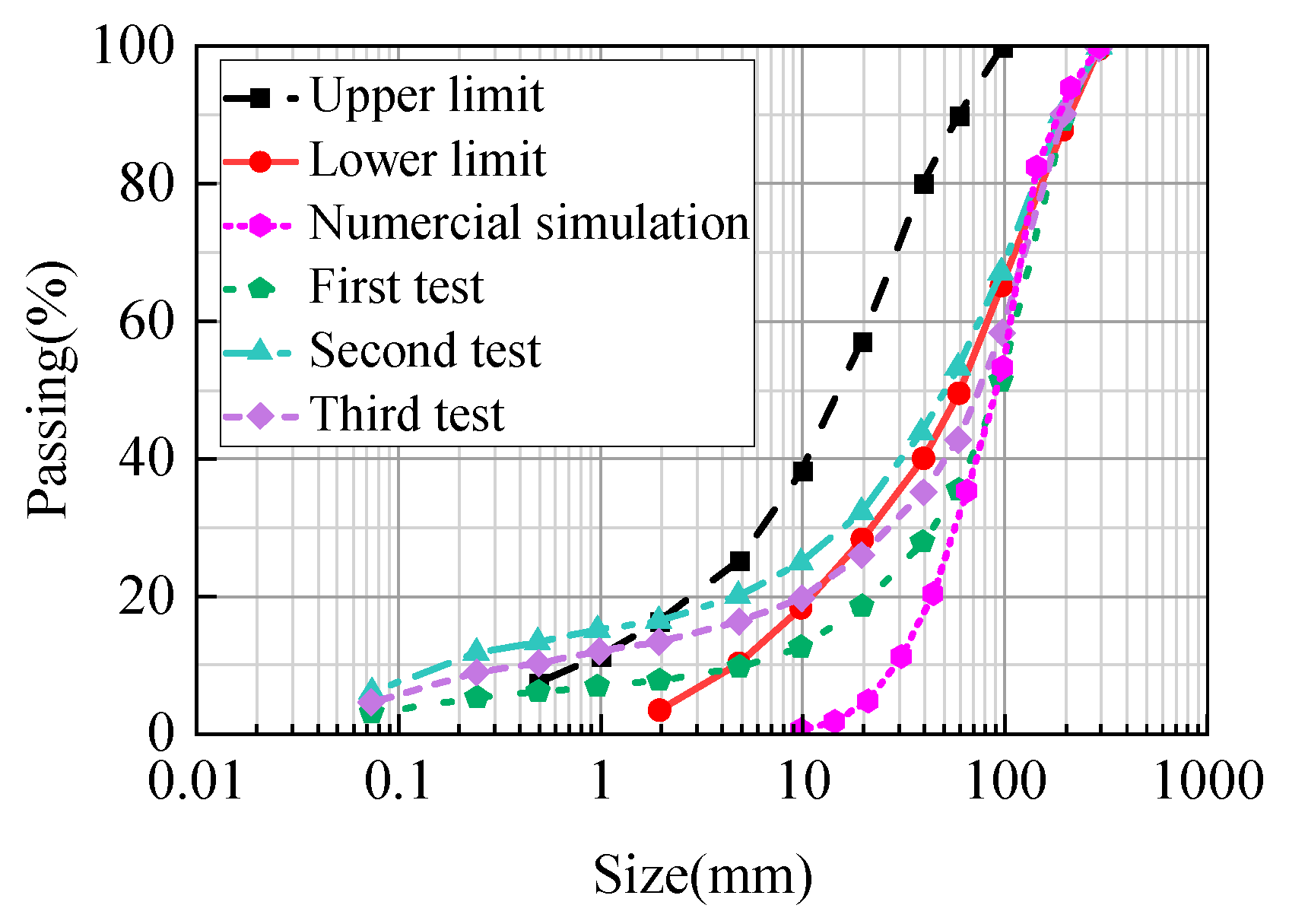
5. Method Verification
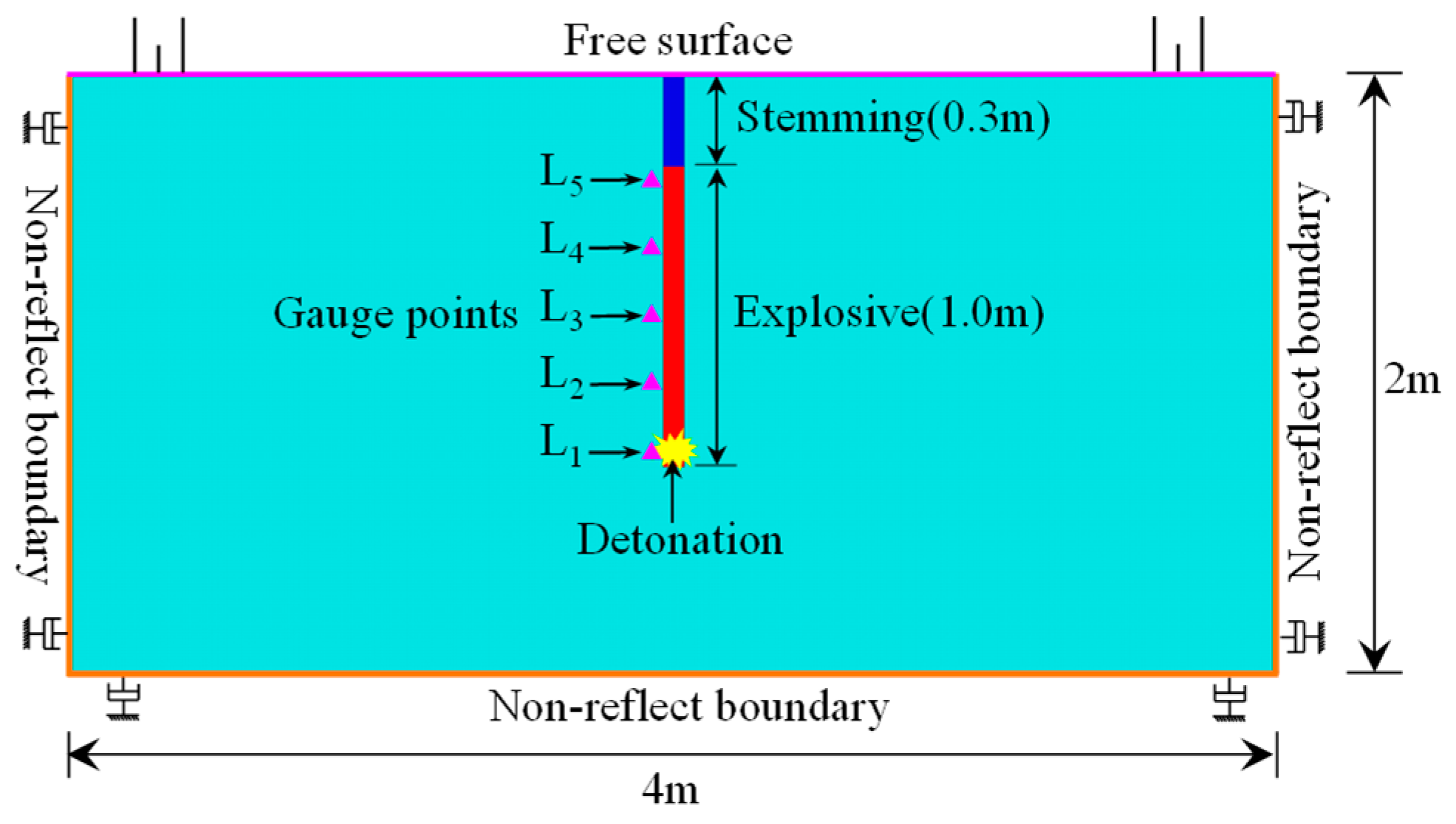
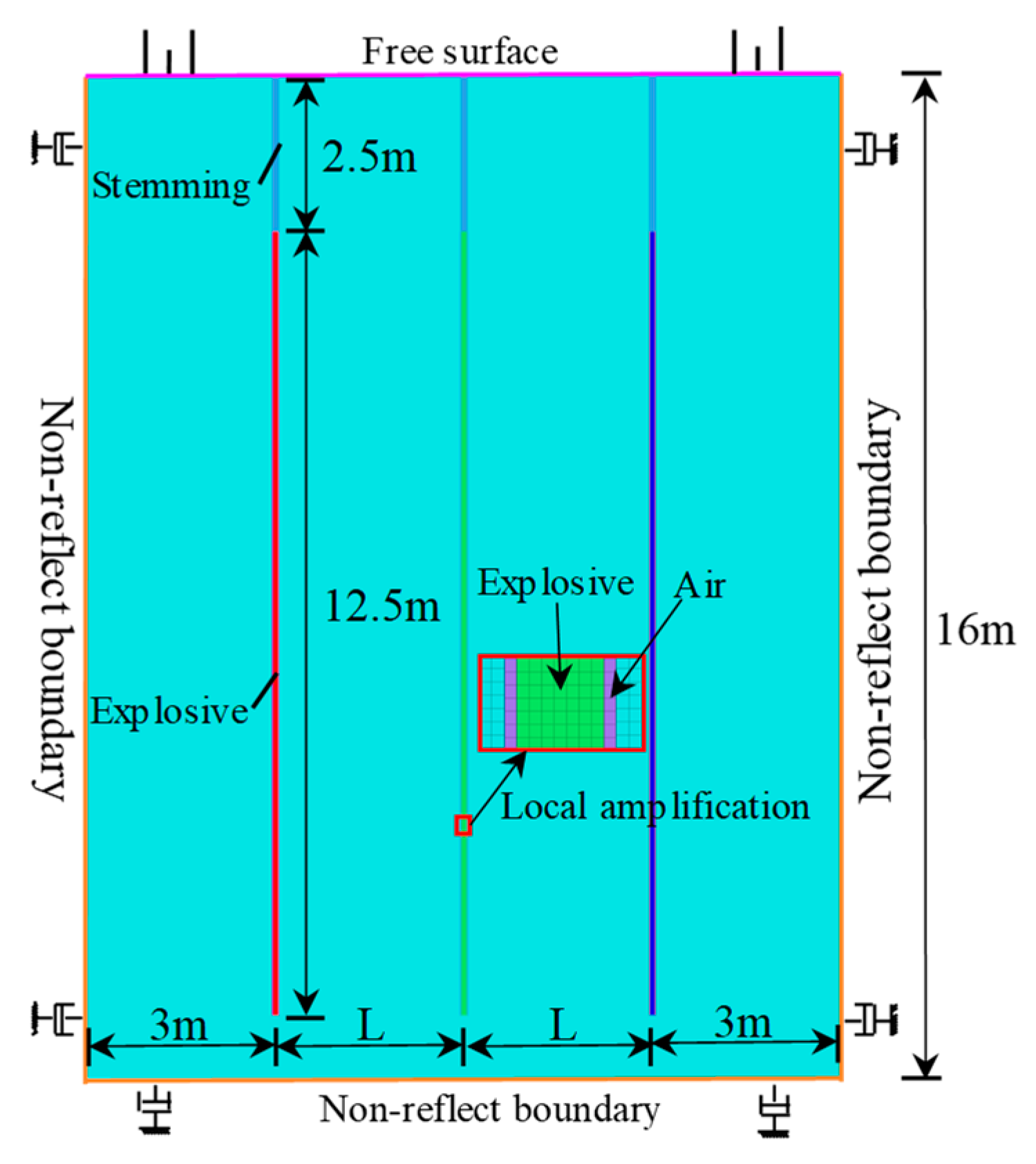
5.1. Model and Parameters
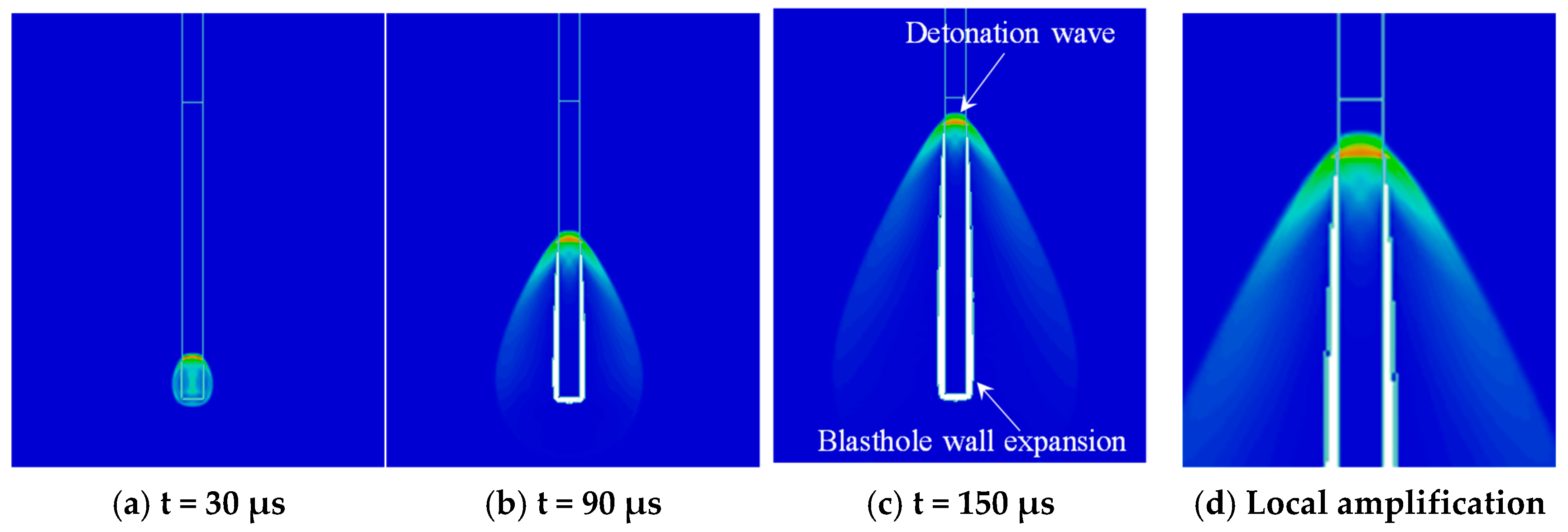
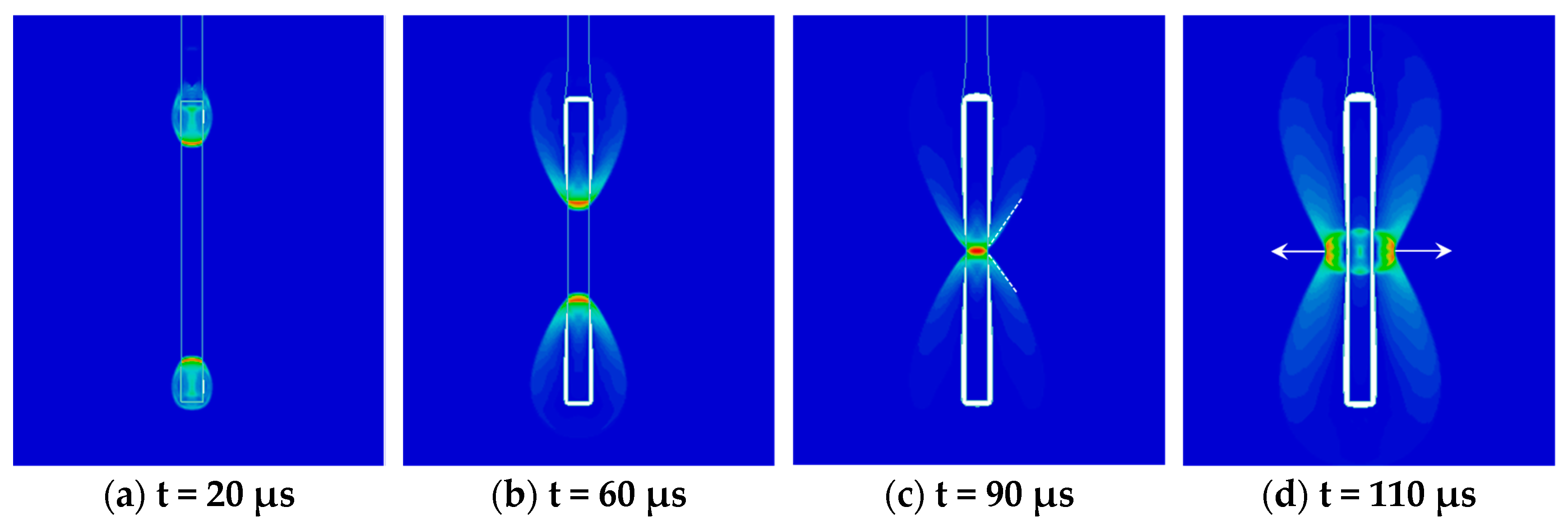
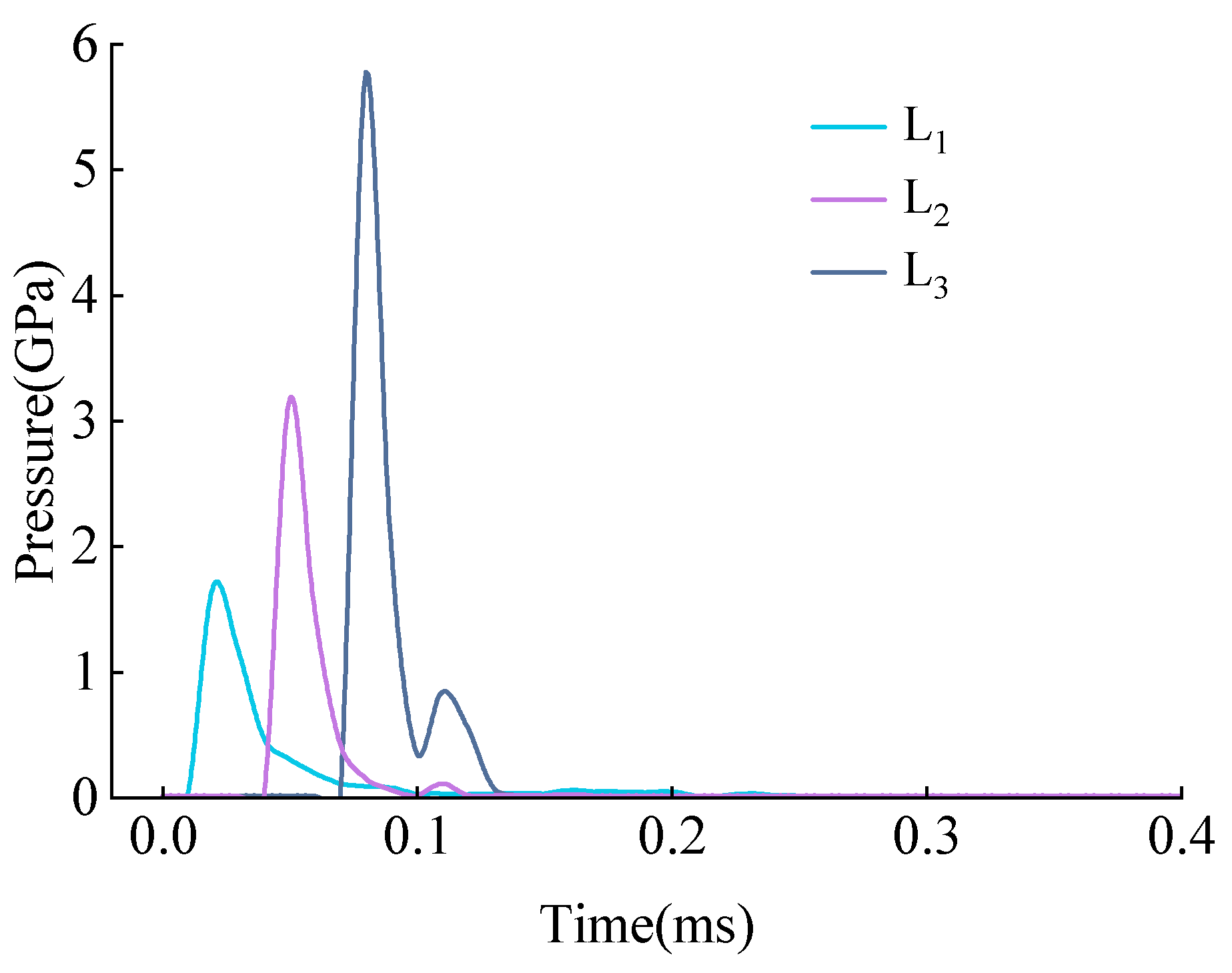
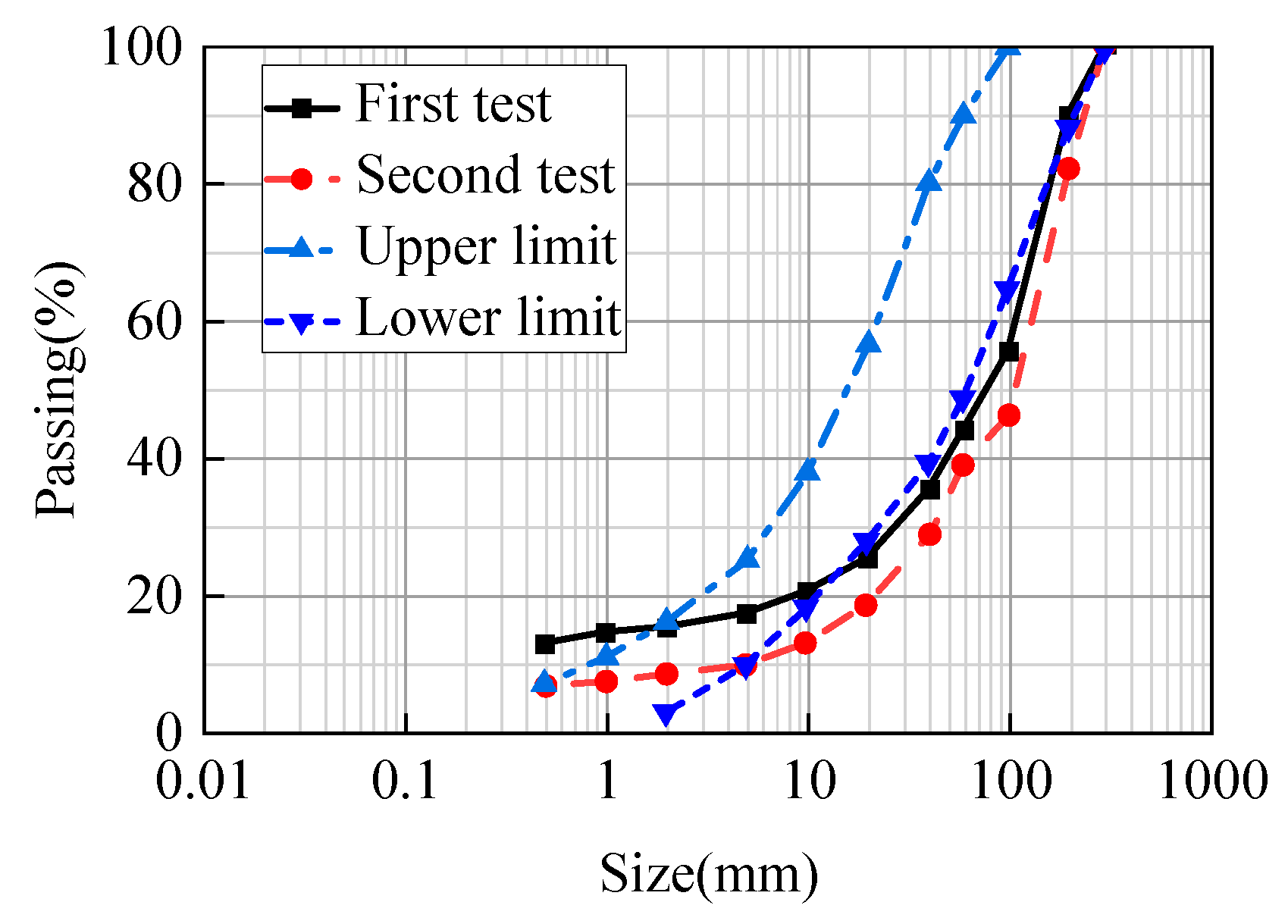
5.2. Simulation Results Analysis
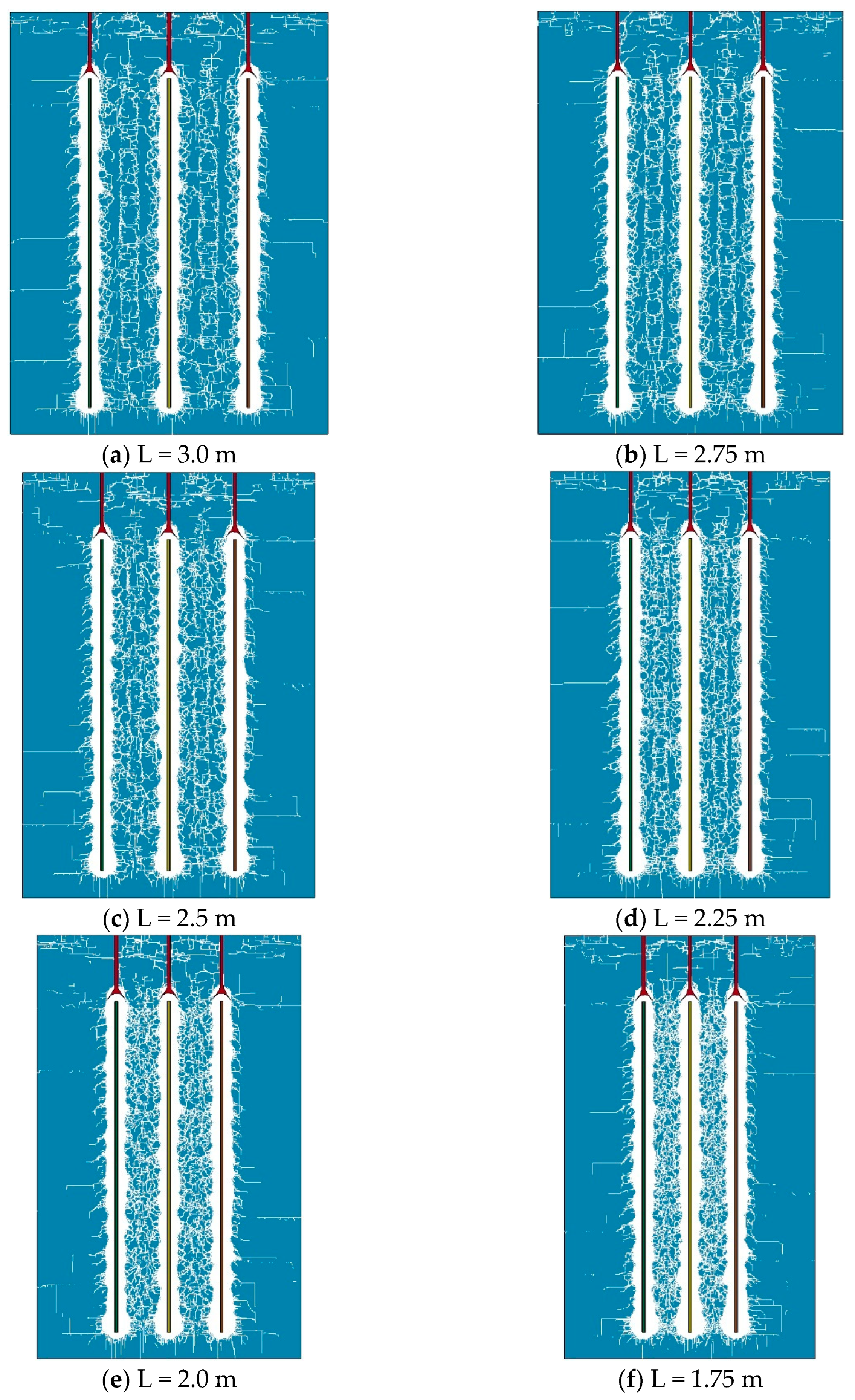
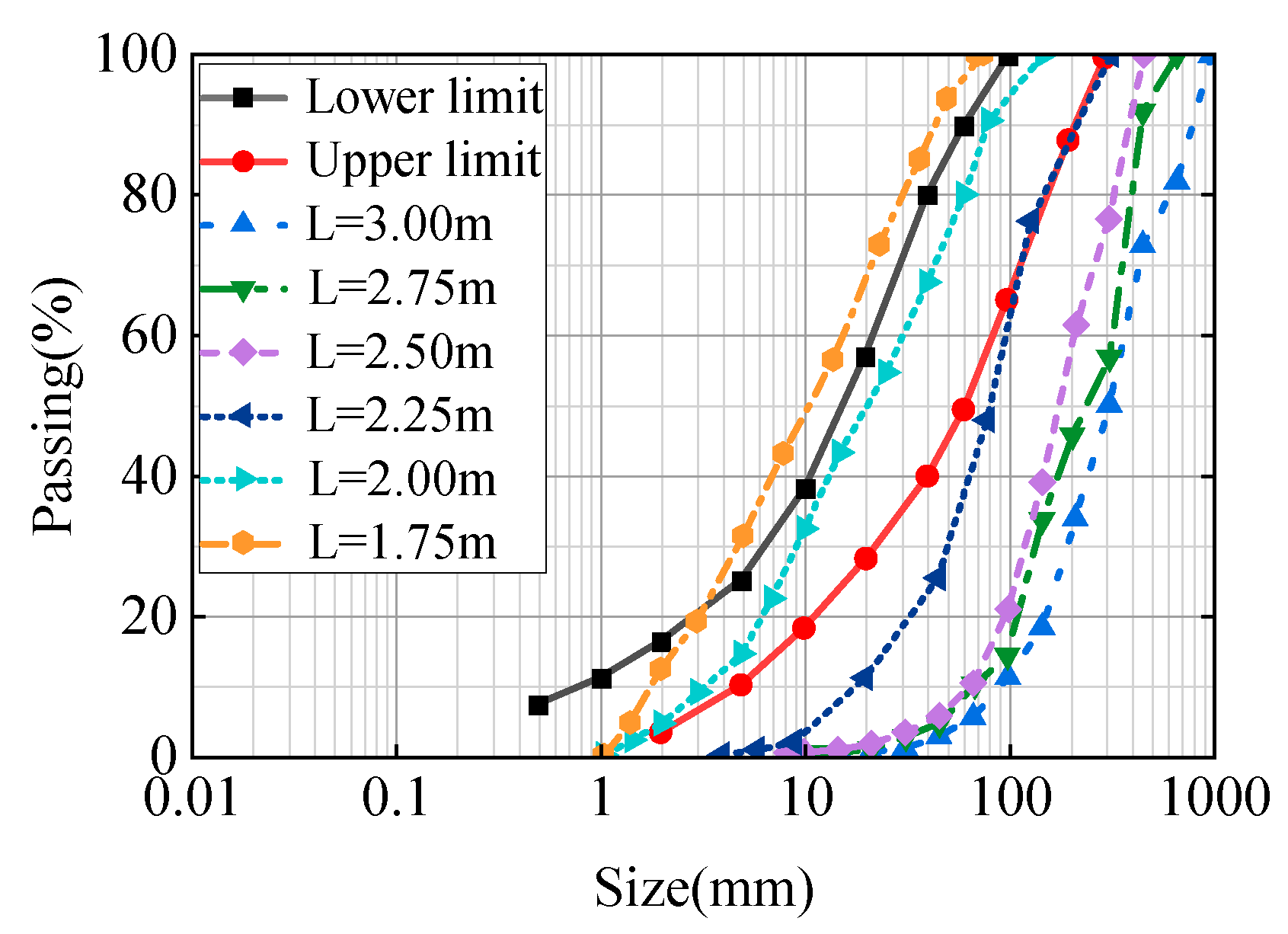
6. Case Study
7. Conclusions
- (1)
- A new simulation and analysis method for rock blasting fragmentation is proposed. The finite element analysis software LS-DYNA was used to simulate rock blasting fragmentation, and the resulting fragmentation images were imported into WipFrag for statistical analysis. This approach offers valuable insights for optimizing blasting parameters.
- (2)
- Due to the directional effects along the cylindrical charge, the explosive loading on blast hole wall first increases and then stabilizes. Furthermore, the detonation processes are different, with varying charging structures. Therefore, it is essential to select charge structures based on the specific site conditions.
- (3)
- The proposed simulation and analysis method was validated though onsite blasting experiments. The fragmentation effects from the simulation and image analysis were used to provide recommendations for optimizing rock blasting parameters.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Yan, P.; Zhou, W.; Lu, W.; Chen, M.; Zhou, C. Simulation of bench blasting considering fragmentation size distribution. Int. J. Impact Eng. 2016, 90, 132–145. [Google Scholar] [CrossRef]
- Baranowski, P.; Kucewicz, M.; Gieleta, R.; Stankiewicz, M.; Konarzewski, M.; Bogusz, P. Fracture and fragmentation of dolomite rock using the JH-2 constitutive model: Parameter determination, experiments and simulations. Int. J. Impact Eng. 2020, 140, 103543. [Google Scholar] [CrossRef]
- An, H.M.; Liu, H.Y.; Han, H.; Zheng, X.; Wang, X.G. Hybrid finite-discrete element modelling of dynamic fracture and resultant fragment casting and muck-piling by rock blast. Comput. Geotech. 2017, 81, 322–345. [Google Scholar] [CrossRef]
- Gheibie, S.; Aghababaei, H.; Hoseinie, S.H.; Pourrahimian, Y. Modified Kuz-Ram fragmentation model and its use at the Sungun Copper Mine. Int. J. Rock Mech. Min. Sci. 2009, 46, 967–973. [Google Scholar] [CrossRef]
- Yilmaz, O. Rock factor prediction in the Kuz–Ram model and burden estimation by mean fragment size. Geomech. Energy Environ. 2023, 33, 100415. [Google Scholar] [CrossRef]
- Ouchterlony, F.; Sanchidrián, J.A.; Moser, P. Percentile fragment size predictions for blasted rock and the fragmentation–energy fan. Rock Mech. Rock Eng. 2017, 50, 751–779. [Google Scholar] [CrossRef]
- Ouchterlony, F. The Swebrec function: Linking fragmentation by blasting and crushing. Min. Technol. 2005, 114, 29–44. [Google Scholar] [CrossRef]
- Schenk, F.; Tscharf, A.; Mayer, G.; Fraundorfer, F. Automatic muck pile characterization from UAV images. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 4, 163–170. [Google Scholar] [CrossRef]
- Bamford, T.; Esmaeili, K.; Schoellig, A.P. A deep learning approach for rock fragmentation analysis. Int. J. Rock Mech. Min. Sci. 2021, 145, 104839. [Google Scholar] [CrossRef]
- Ramezani, M.; Nouranian, S.; Bell, I.; Sameti, B.; Tafazoli, S. Fast rock segmentation using artificial intelligence to approach human-level accuracy. J. Explos. Eng. 2017, 34, 28–32. [Google Scholar]
- Sanchidrián, J.A.; Segarra, P.; Ouchterlony, F.; López, L.M. On the accuracy of fragment size measurement by image analysis in combination with some distribution functions. Rock Mech. Rock Eng. 2009, 42, 95–116. [Google Scholar] [CrossRef]
- Yi, C.; Johansson, D.; Greberg, J. Effects of in-situ stresses on the fracturing of rock by blasting. Comput. Geotech. 2018, 104, 321–330. [Google Scholar] [CrossRef]
- Xie, L.X.; Lu, W.B.; Zhang, Q.B.; Jiang, Q.H.; Wang, G.H.; Zhao, J. Damage evolution mechanisms of rock in deep tunnels induced by cut blasting. Tunn. Undergr. Space Technol. 2016, 58, 257–270. [Google Scholar] [CrossRef]
- Xie, L.X.; Lu, W.B.; Zhang, Q.B.; Jiang, Q.H.; Chen, M.; Zhao, J. Analysis of damage mechanisms and optimization of cut blasting design under high in-situ stresses. Tunn. Undergr. Space Technol. 2017, 66, 19–33. [Google Scholar] [CrossRef]
- Tao, J.; Yang, X.G.; Li, H.T.; Zhou, J.W.; Fan, G.; Lu, G.D. Effects of in-situ stresses on dynamic rock responses under blast loading. Mech. Mater. 2020, 145, 103374. [Google Scholar] [CrossRef]
- Tao, J.; Yang, X.G.; Li, H.T.; Zhou, J.W.; Qi, S.C.; Lu, G.D. Numerical investigation of blast-induced rock fragmentation. Comput. Geotech. 2020, 128, 103846. [Google Scholar] [CrossRef]
- Pál, G.; Varga, I.; Kun, F. Emergence of energy dependence in the fragmentation of heterogeneous materials. Phys. Rev. E 2014, 90, 062811. [Google Scholar] [CrossRef]
- Diehl, A.; Carmona, H.A.; Araripe, L.E.; Andrade, J.S., Jr.; Farias, G.A. Scaling behavior in explosive fragmentation. Phys. Rev. E 2000, 62, 4742. [Google Scholar] [CrossRef]
- Wittel, F.; Kun, F.; Herrmann, H.J.; Kröplin, B.H. Fragmentation of shells. Phys. Rev. Lett. 2004, 93, 035504. [Google Scholar] [CrossRef]
- Bamford, T.; Esmaeili, K.; Schoellig, A.P. A real-time analysis of post-blast rock fragmentation using UAV technology. Int. J. Min. Reclam. Environ. 2017, 31, 439–456. [Google Scholar] [CrossRef]
- Chang, X.; Shan, Y.; Zhang, Z.; Tang, C.; Ru, Z. Behavior of propagating fracture at bedding interface in layered rocks. Eng. Geol. 2015, 197, 33–41. [Google Scholar] [CrossRef]
- Chen, D.F.; Feng, X.T.; Xu, D.P.; Jiang, Q.; Yang, C.X.; Yao, P.P. Use of an improved ANN model to predict collapse depth of thin and extremely thin layered rock strata during tunnelling. Tunn. Undergr. Space Technol. 2016, 51, 372–386. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, W.; Shi, W.; Hao, G.; Liu, X.; Mei, J. Experimental study of parameters of tunneling blasting in jointed layered rock mass. J. China Univ. Min. Technol. 2019, 48, 1248–1255. [Google Scholar] [CrossRef]
- Lisjak, A.; Grasselli, G.; Vietor, T. Continuum-discontinuum analysis of failure mechanisms around unsupported circular excavations in anisotropic clay shales. Int. J. Rock Mech. Min. Sci. 2014, 65, 96–115. [Google Scholar] [CrossRef]
- Xie, L.X.; Yang, S.Q.; Gu, J.C.; Zhang, Q.B.; Lu, W.B. JHR constitutive model for rock under dynamic loads. Comput. Geotech. 2019, 108, 161–172. [Google Scholar] [CrossRef]
- Itasca Consulting Group, Inc. Three-Dimensional Distinct Element Code: User’s Guide; Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 2003. [Google Scholar]
- Gao, W.; Zhang, J.; Li, C.; Cheng, L.; Liu, P. Study on Muck Pile Shape of Open-Pit Bench Blasting Based on PFC. Shock Vib. 2023, 2023, 2859668. [Google Scholar] [CrossRef]
- Yu, R.; Zhang, Z.; Gao, W.; Li, C.; Wu, C. Numerical simulation of rock mass blasting vibration using particle flow code and particle expansion loading algorithm. Simul. Model. Pract. Theory 2023, 122, 102686. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, J.; Cai, J.; Hefny, A.M. UDEC modelling on wave propagation across fractured rock masses. Comput. Geotech. 2008, 35, 97–104. [Google Scholar] [CrossRef]
- Ning, Y.; Yang, J.; An, X.; Ma, G. Modelling rock fracturing and blast-induced rock mass failure via advanced discretisation within the discontinuous deformation analysis framework. Comput. Geotech. 2011, 38, 40–49. [Google Scholar] [CrossRef]
- Ning, Y.; Yang, J.; Ma, G.; Chen, P. Modelling rock blasting considering explosion gas penetration using discontinuous deformation analysis. Rock Mech. Rock Eng. 2011, 44, 483–490. [Google Scholar] [CrossRef]
- Lee, E.L.; Hornig, H.C.; Kury, J.W. Adiabatic Expansion of High Explosive Detonation Products (No. UCRL-50422); Univ. of California Radiation Lab. at Livermore: Livermore, CA, USA, 1968. [Google Scholar]
- Riedel, W.; Thoma, K.; Hiermaier, S.; Schmolinske, E. Penetration of reinforced concrete by BETA-B-500 numerical analysis using a new macroscopic concrete model for hydrocodes. In Proceedings of the 9th International Symposium on the Effects of Munitions with Structures, Berlin-Strausberg, Germany, 3–4 May 1999; Volume 315, pp. 315–322. [Google Scholar]
- Zhou, H.; Gao, Q.; Fan, Y.; Lu, W.; Wang, Y.; Yang, Y.; Leng, Z. Analysis of causes of vibration differences induced by different kinds of blastholes based on the interpretation of blasting parameters: A case study in dam foundation excavation. Rock Mech. Rock Eng. 2023, 56, 7237–7254. [Google Scholar] [CrossRef]
- Knock, C.; Davies, N. Blast waves from cylindrical charges. Shock Waves 2013, 23, 337–343. [Google Scholar] [CrossRef]
- Saadatmand Hashemi, A.; Katsabanis, P. The effect of stress wave interaction and delay timing on blast-induced rock damage and fragmentation. Rock Mech. Rock Eng. 2020, 53, 2327–2346. [Google Scholar] [CrossRef]
- Jayasinghe, L.B.; Shang, J.; Zhao, Z.; Goh, A.T.C. Numerical investigation into the blasting-induced damage characteristics of rocks considering the role of in-situ stresses and discontinuity persistence. Comput. Geotech. 2019, 116, 103207. [Google Scholar] [CrossRef]
- Ye, Z.; Chen, M. Characteristics of Peak Load on a Borehole Wall in Water-Coupling Blasting. J. Eng. Mech. 2023, 149, 04022087. [Google Scholar] [CrossRef]
- Chen, M.; Ye, Z.; Lu, W.; Wei, D.; Yan, P. An improved method for calculating the peak explosion pressure on the borehole wall in decoupling charge blasting. Int. J. Impact Eng. 2020, 146, 103695. [Google Scholar] [CrossRef]
- Leng, Z.; Sun, J.; Lu, W.; Xie, X.; Jia, Y.; Zhou, G.; Chen, M. Mechanism of the in-hole detonation wave interactions in dual initiation with electronic detonators in bench blasting operation. Comput. Geotech. 2021, 129, 103873. [Google Scholar] [CrossRef]
- Liu, L.; Lu, W.; Chen, M.; Yan, P.; Wang, G.H. Statistic damage threshold of critical broken rock mass under blasting load. Chin. J. Rock Mech. Eng. 2016, 35, 1133–1140. (In Chinese) [Google Scholar] [CrossRef]












| Numerical Simulation Methods | Software | Advantages | Disadvantages |
|---|---|---|---|
| Finite element method | LS-DYNA | These methods excel in simulating stress waves, loads, vibrations, and damage resulting from explosions. | They are limited in simulating large deformation failures, such as rock ejection. |
| ANTODYN | |||
| ANSYS | |||
| Discrete element method | 3DEC | These methods are capable of simulating phenomena such as rock fragmentation and ejection during blasting. | It is not capable of accurately simulating the detonation process of explosives. |
| DDA | |||
| PFC | |||
| Continuous–discontinuous method | CDEM | These methods effectively simulate the rock failure process under the influence of explosive detonation. | The parameter configuration is complex, computational efficiency is relatively low, and the rock failure criterion has not yet been widely accepted. |
| FDEM | |||
| CDM |
| ρ/(kg∙m−3) | VoD/(m∙s−1) | A1/GPa | B1/GPa | R1 | R2 | E0/GPa |
|---|---|---|---|---|---|---|
| 1100 | 4800 | 214.4 | 0.182 | 4.2 | 0.9 | 4.192 |
| Density/(kg·m−3) | Young’s Modulus/GPa | Poisson’s Ratio | Yield Strength/MPa | Shear Modulus/GPa | Hardening Index β |
|---|---|---|---|---|---|
| 2060 | 2.5 | 0.25 | 245 | 10.5 | 0.5 |
| Blasting Parameter | Content |
|---|---|
| Bench height | 13.5 m |
| Blast hole layout | Rectangle |
| Drilling diameter | 115 mm |
| Drilling angle | 90° |
| Drilling depth | 15 m |
| Blast hole spacing | 3 m |
| Array pitch | 2 m |
| Front resistance line | 2.0 m |
| Explosive type | 2# emulsion explosive |
| The main blasting charge structure | Continuous charging |
| Stemming length | 2.5 m |
| Explosive length | 12.5 m |
| Delayed initiation mode | Digital electronic detonator 17 ms delayed initiation |
| Density/(kg·m−3) | Young’s Modulus/GPa | Poisson’s Ratio | Yield Strength/MPa | Shear Modulus/GPa | Hardening Index β |
|---|---|---|---|---|---|
| 2440 | 2.5 | 0.25 | 245 | 10.5 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Gao, Q.; Jia, Y.; Zhou, H.; Gao, X.; Jiang, W.; Ma, X. Application of Simulation Methods and Image Processing Techniques in Rock Blasting and Fragmentation Optimization. Appl. Sci. 2025, 15, 3365. https://doi.org/10.3390/app15063365
Yang Q, Gao Q, Jia Y, Zhou H, Gao X, Jiang W, Ma X. Application of Simulation Methods and Image Processing Techniques in Rock Blasting and Fragmentation Optimization. Applied Sciences. 2025; 15(6):3365. https://doi.org/10.3390/app15063365
Chicago/Turabian StyleYang, Qing, Qidong Gao, Yongsheng Jia, Haixiao Zhou, Xin Gao, Wei Jiang, and Xiaobo Ma. 2025. "Application of Simulation Methods and Image Processing Techniques in Rock Blasting and Fragmentation Optimization" Applied Sciences 15, no. 6: 3365. https://doi.org/10.3390/app15063365
APA StyleYang, Q., Gao, Q., Jia, Y., Zhou, H., Gao, X., Jiang, W., & Ma, X. (2025). Application of Simulation Methods and Image Processing Techniques in Rock Blasting and Fragmentation Optimization. Applied Sciences, 15(6), 3365. https://doi.org/10.3390/app15063365





