Abstract
In unpredictable scenarios, quadruped robots with behavior-controllable capabilities can often improve their adaptability through interaction with users. In this paper, we propose a behavior-controllable motion control method, integrating user commands with adversarial motion priors, enabling the quadruped robot to achieve behavior-controllable capabilities. Firstly, a motion trajectory library is constructed to provide motion prior knowledge. To obtain stable trajectory data for various motions, optimal control methods are used to generate dynamic trajectories with whole-body dynamic constraints. These trajectory data are then standardized and assigned different weights, resulting in the construction of a motion trajectory library for the quadruped robot. Secondly, an adversarial motion prior network structure combined with user commands is proposed. Reward functions tailored to different motion behaviors are designed to achieve behavior control. This network structure acts as a single-motion prior discriminator, which, compared to a multi-motion prior discriminator, avoids complex architectures. Furthermore, the incorporation of user commands effectively addresses the issue where the single-motion prior discriminator struggles to clearly select actions as the dataset expands. Finally, simulations and comparative experiments are conducted to evaluate the effectiveness of the proposed method.
1. Introduction
Quadruped robots typically exhibit strong mobility on rugged terrains, which are often considered during the initial stages of controller design. Researchers have developed fully autonomous controllers that enable robust mobility [1,2,3]. However, for terrains that are not anticipated in advance, robots equipped with controllable behaviors demonstrate greater adaptability, especially with the support of user intelligence.
To achieve behavior-controllable motion control for quadruped robots, many studies have adopted model-based motion control approaches [4,5,6,7]. These methods leverage dynamic models to predict the robot’s movement, thereby generating precise and predictable motion trajectories, which facilitate the realization of behavior-controllable motion. However, such approaches may suffer from performance degradation due to inaccuracies in simplified models, leading to deviations from the desired actions. Additionally, the computational complexity limits their real-time applicability and broader scope. Moreover, the reliance on predefined models can reduce adaptability when confronted with unforeseen circumstances.
With advancements in computing technologies and intelligent algorithms, deep reinforcement learning (DRL) has emerged as a more adaptive approach for controlling quadruped robots [8,9]. A DRL-based robot controller has enabled a quadruped robot to learn walking in a real-world environment in just 20 min [10]. A behavior-diverse walking controller, named “Walk These Ways”, has achieved the learning of multiple gaits through a single policy, enabling task diversification by adjusting gaits [11]. Robots such as ANYmal and ANYmal-C are capable of walking stably on complex natural terrains [12]. This is made possible by a DRL controller that does not rely on visual information but instead utilizes a teacher–student architecture and a terrain adaptation curriculum during training. Additionally, a behavior decision tree is introduced, which enables the control of various tasks through user commands [13]. By allowing users to adjust the robot’s behavior according to specific needs, the robot can select different gaits or behavior patterns as required, thereby enhancing both adaptability and behavior controllability. However, these methods often depend on the design of complex reward functions to guide the learning process toward the desired control strategies, significantly increasing the difficulty of training.
Data-driven methods aim to reduce the complexity of designing reward functions and improve learning efficiency for various movement behaviors and environments. Motion primitive-based hierarchical reinforcement learning decomposes complex tasks into reusable action primitives, enabling efficient learning and improved generalization to unseen scenarios by leveraging pre-optimized or learned motion modules [14,15,16,17]. An imitation learning method utilizes action snippets as reference data, allowing the agent to mimic these snippets to acquire high-difficulty skills and predict subsequent actions based on images [18]. The Adversarial Motion Priors (AMP) method uses motion prior knowledge to construct an adversarial discriminator [19,20]. The discriminator not only mimics the behaviors of motions in the dataset but also learns the prior distribution of these motions, capturing the naturalness, physical feasibility, and relationships between different actions. Methods based on AMP and teacher–student networks have been employed to train controllers capable of achieving task objectives while exhibiting robustness [21,22]. Additionally, the Multiple Adversarial Motion Priors (Multi-AMP) method incorporates multiple adversarial discriminators to learn various styles and skills from the motion dataset [23]. A wheeled-legged quadruped robot employing this method has successfully implemented different motion pattern transitions in the real world. These data-driven methods reduce the complexity of designing reward functions. By learning multiple diverse styles and skills, the robot can flexibly select and switch behavior patterns based on task requirements, thereby enhancing the diversity and controllability of its behavior. However, the motion datasets used in these methods typically originate from motion capture, which may contain unstable or unsafe actions. Furthermore, the highly structured data generated by motion capture incurs significant costs for data acquisition.
The AMP-based method reduces the complexity of designing numerous complex reward functions [24], but it faces a challenge: when the dataset is expanded or when multiple trajectory data overlap for similar tasks, the policy struggles to select actions with a distinct style, leading to a decrease in behavior controllability. The Multi-AMP method improves behavior controllability by addressing the challenge of switching between different motion styles through the use of multiple discriminators. However, a limitation of Multi-AMP is that its network structure becomes large and scales with the increase in motion reference data, resulting in higher computational demands and greater training complexity.
This paper proposes a control method based on Behavior-Controllable Adversarial Motion Priors (BCAMP) that enables quadruped robots to learn diverse and stable motions while acquiring behavior-controllable capabilities. First, to address the instability and safety concerns associated with motion capture data, optimal control methods are employed to generate dynamic trajectories with strict dynamic constraints. Various trajectory sequences are standardized to construct a quadruped robot motion trajectory library. Second, the method constructs a single adversarial discriminator and designs a network structure for the AMP and reward function tailored to the motion trajectory library. User commands are introduced to adjust the reward function and switch motion behaviors, enabling the policy network to perform multi-task learning and to control the quadruped robot motion behaviors. Finally, the method proposed in this paper is applied to the Unitree A1 quadruped robot, with simulation and comparative experiments conducted for validation.
The construction of this paper is as follows. In Section 2, we provide an in-depth explanation of the process for generating the motion trajectory library. In Section 3, we introduce the comprehensive BCAMP framework, detailing the integration of user commands into the reward function. In Section 4, we present the simulation verification along with comparative experiments, followed by a thorough analysis of the results. Finally, in Section 5, we summarize the conclusions of our work in this study.
2. Generation of Motion Trajectory Library
The process of constructing the motion trajectory library in this paper is illustrated in the yellow part of Figure 1. The motion trajectory library is formed by merging multiple standardized reference trajectory datasets , each assigned a distinct weight , where is derived from reference trajectory datasets through standardization. Different weights are designed to encourage the robot to learn and utilize diverse motion data from the library, rather than focusing solely on a specific action.
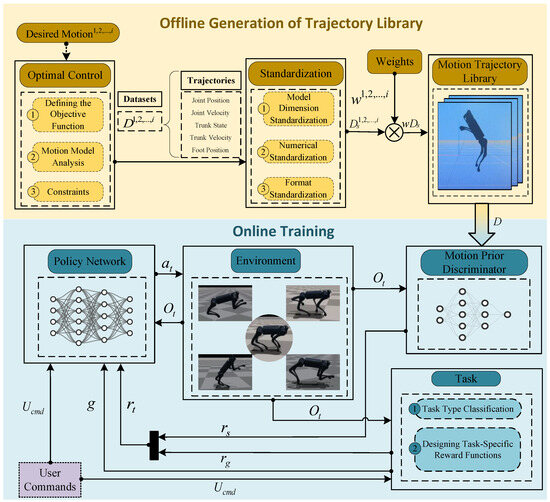
Figure 1.
Overview of BCAMP framework.
Optimal control is used to generate , . k represents the number of reference trajectory datasets, and n is the total number of controlled joints on the robot. Each trajectory includes trunk state; hip, thigh, and calf joint angles; trunk velocity; joint velocities; foot positions and velocities; and represents a time series.
where represents the trunk state of the robot in the world coordinate system; (roll about x-axes), (pitch about y-axes), and (yaw about z-axes) represent the trunk orientation angles; is the trunk velocity of the robot, which includes linear velocity and angular velocity; is the joint positions; is the joint velocities; and is the positions of the robot four feet in the trunk coordinate system.
The quadruped robot model is illustrated in Figure 2. To generate stable quadruped robot motion trajectories, the optimization problem is defined as follows:
where represents the joint torque, and it indicates the sum of all joint torques throughout the entire motion process; and are the joint acceleration and jerk, respectively; and and represent the cost functions, specifically shown in Equations (4) and (5). All constraints represent all the constraints involved in this optimization, as shown in Table 1.
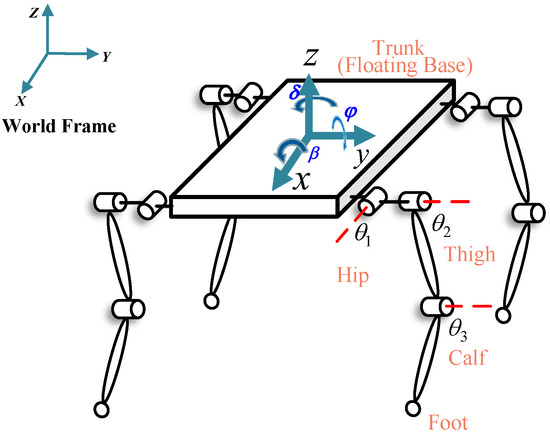
Figure 2.
This is a quadruped robot model. The red dashed lines are the axis of rotation corresponding to the joints. The trunk state is represented in the world coordinate system as , i.e., the floating base state.

Table 1.
Table of all constraints.
2.1. Motion Transformation Model
For common motion patterns of quadruped robots, the overall motion model should be divided into different stages based on changes in contact points. Taking the bipedal standing action as an example, this paper uses the model shown in Figure 3 to describe the stages. The first stage is the quadrupedal standing state, where the front two feet remain in contact with the ground. The second stage is the bipedal standing state, where the front feet have lifted off the ground, and only the rear feet are in contact.

Figure 3.
Model of contact point variation during the bipedal standing motion of a quadruped robot.
To reduce the scale of the optimization problem, the model is simplified from three-dimensional to a two-dimensional sagittal plane model. The simplified trunk state represents the robot position in the X and Z directions and its pitch angle. The simplified joint positions represent the joint angles of the thigh and calf for both the front and rear leg. The simplified foot position represents the foot positions of both feet. The simplified overall state is represented by .
2.2. Motion Trajectory Generation
To optimize the trajectories for common movement actions of a quadruped robot, the continuous-time optimization problem is often converted into a discrete-time nonlinear optimization problem [25]. For example, for a bipedal standing motion, the overall optimization time is denoted as T, and N nodes are taken for discretization. The sampling time interval is then given by
In order to generate stable and smooth motion trajectories, the cost function is given by
where is the weight constant, and minimizing this part can result in optimized trajectories that consume less energy.
where is the weight constant, and minimizing this part of the cost function ensures the stability of the trajectory, reducing sudden changes in motion.
For the trunk state and control state, denoted as and , respectively, they are subject to the following hardware constraints:
As shown in Figure 3, we use the following dynamic equations to establish the relationship between the overall state and joint torques:
where represents the mass matrix; represents the selection matrix for joint torques; represents the Coriolis and centrifugal forces; represents the gravity vector; represents the contact Jacobian matrix, where * can refer to either just the rear foot or all two feet, used to constrain the two movement phases separately; is the controlled joint torques; and represents the torques mapped from external forces into the joint space, applied at different contact points (all two feet or rear foot).
The contact constraints are as follows:
where and represent the Jacobian matrices for all two feet contact and rear foot contact, respectively; denotes the drift matrix; and and represent the external force components in the X and Z directions, respectively. Contact constraints are used to ensure that the robot remains stable and does not move when in contact with the ground, while also adhering to physical constraints. These constraints account for not only joint velocities but also the effect of joint accelerations on the overall system dynamics, thereby making the optimization results more realistic and stable.
Although the dynamic constraints ensure that the system satisfies the dynamic equations at each discrete time step, they do not guarantee that the state transitions between two consecutive time steps are consistent with the dynamics model. This could result in physically discontinuous or infeasible trajectories. The time integration constraints are as follows:
For the constraints on the initial and terminal times and states, these are crucial to ensure that the object reaches the desired state within the specified time frame. The initial and terminal state constraints are defined as follows:
where refers to the initial and terminal state constraints for the robot trunk position and velocity, as well as the joint positions and velocities of the controlled joints. In the initial and terminal states, the trunk position and joint positions are determined based on the desired target robot position, while the trunk velocity and joint velocities are set to zero.
2.3. Standardization Processing
The reference trajectory datasets are standardized in three aspects to obtain the standardized reference trajectory datasets . In terms of model dimensions, a simplified quadruped robot model is used prior to the optimal control optimization to reduce both the optimization complexity and the degrees of freedom of the robot. As a result, once the optimization is complete, the data must be expanded. Based on the leg symmetry of the quadruped robot, the data from the simplified model can be appropriately expanded:
where represents the expanded trunk state; represents the expanded joint positions; represents the extended left front foot position; represents the extended right front foot position; represents the extended left rear foot position; represents the extended right rear foot position; represents the foot position Y-axis direction, with a specific value of half the width of the robot trunk; and represents the expanded foot positions. To obtain the correct trajectory data, the data dimensions derived from the simplified two-dimensional sagittal plane model are expanded to the full three-dimensional kinematic space using symmetry constraints (e.g., mirroring sagittal trajectories to lateral joints). The expanded overall state is represented by .
Numerically, since reference trajectories for different actions may have varying scales, the reference trajectory data must be standardized to minimize feature differences, thereby enhancing the stability of subsequent training:
where represents the trajectory features, which can be the expanded overall state , expanded overall velocity , or expanded foot position ; represents the mean; and represents the standard deviation. Based on Equation (13), the numerical standardization of all trajectory features is performed as follows:
In terms of structure, the reference trajectory data are used to train a motion prior discriminator, which evaluates the similarity between the actions generated by the policy network and those in the dataset. The data are organized according to the sorting and dimensions that align with the observation space of the adversarial discriminator, facilitating the application of adversarial learning. After these three standardization steps, the standardized reference trajectory datasets are designed as follows:
where represents the height of the center of mass (CoM) in the world coordinate system; represents the trunk orientation vector (indicating the robot posture); and are the linear velocity and angular velocity of the CoM in the trunk coordinate system; represents the joint positions of the robot joints; represents the joint velocities of the robot joints; and represents the foot positions in the trunk coordinate system.
3. Behavior-Controllable Adversarial Motion Priors
To address the issue where AMP struggles to select actions with a clear style when expanding the dataset or when multiple trajectory datasets cover similar tasks, the BCAMP method extends the AMP framework by incorporating user commands. During training, user commands are only randomly selected from a discrete set of task IDs, and the task IDs are associated with task-specific reward functions, allowing the policy to learn actions with different movement styles. After training, command parameters and user commands can be issued to actively switch between different stylistic actions.
3.1. Controllable Behavior Motion Generation
The process of training controllable behavior motion control in this paper is illustrated in Figure 1, with the blue part representing the online training process of the policy network and the purple part representing the user commands.
Firstly, multiple reference trajectory datasets for different movements are generated through optimal control. After standardization and assignment of weights , standardized trajectory datasets can be obtained. The motion prior discriminator is then trained based on the prior distribution of all motions provided by the standardized reference trajectory datasets and the environmental observations . This discriminator evaluates the similarity between the actions generated by the policy network and those in the trajectory library, encouraging the policy network to generate behaviors that resemble the styles of the standardized reference trajectory datasets . Actions with high similarity receive a higher style reward .
Second, based on the motions in the motion trajectory library, multiple trajectory data that achieve similar movements are classified into different task IDs. User commands , where represents the number of task IDs, serve two purposes. During training, different can adjust the task reward functions to guide the policy network in learning different tasks g. does not require explicit user input but instead enables multi-task learning by randomly generating different values within a range. Higher task rewards given as the robot performance approaches the task requirements. After training, users can input different values to actively switch between different stylistic actions, thus achieving behavior controllability.
The combination of and is used to train the policy network, enabling the robot to achieve task-specific objectives while also adopting movement styles similar to those in the standardized reference trajectory datasets .
3.2. Network Architecture
The algorithm presented in this paper combines BCAMP with Proximal Policy Optimization (PPO), enabling rapid training and the generation of high-quality policies. The PPO algorithm [26] is a policy-based DRL algorithm that uses the Actor–Critic framework [27]. The Actor network, Critic network, and motion prior discriminator are each implemented using neural networks. Both the Actor and Critic networks are implemented with three fully connected hidden layers, with the layer sizes being 512, 256, and 128 neurons, respectively. The motion prior discriminator is implemented with two fully connected hidden layers, containing 1024 and 521 neurons.
The inputs to the motion prior discriminator include the environmental observations and the standardized reference trajectory data . Here, consists of time series trajectories for all actions, and extracts the state of a particular action at time t. and can be expressed as follows:
It can be found that and have the same format because is intentionally defined in the same format as , which facilitates the learning of the discriminator.
The Actor–Critic networks both take as input the 51-dimensional observation, which includes environmental observations , command parameters , and user commands . Here, is used to describe the robot movement commands, including trunk linear velocity in the X and Y directions, trunk angular velocity, and the absolute height of the trunk CoM; is used to describe different movement behaviors of the robot.
The Actor network outputs an action in the action space, with a control frequency of 33.3 Hz. After scaling and processing based on the default joint positions, the underlying joints receive the command and execute the movement. The Critic network outputs a value estimate for the actions generated by the Actor network, guiding the Actor network to update towards a more optimal policy direction.
3.3. User Command-Integrated Reward Shaping
In the learning setup of BCAMP, it is necessary to design a reward function that takes into account both the style reward and the task reward , as shown below:
where and are the weights for the style reward and the task reward, respectively.
The style reward comes from the motion prior discriminator learning process. The optimization objective of the motion prior discriminator is designed as
where represents the determination of whether a state transition comes from a real sample in the reference trajectory datasets D, or if it is an action generated by the policy network. Here, represents the motion prior discriminator parameterized by ; represents the expectation calculation for a state transition , with these state transition pairs drawn from the motion trajectory library D; is the expectation calculation for samples from the actions generated by the policy network; and is the gradient of the discriminator with respect to its parameters . The first two terms in the equation encourage the discriminator to distinguish between real actions and generated actions, while the last term is a gradient penalty to ensure that the discriminator does not produce excessively large gradients during training, which helps with training stability. The gradient penalty is .
The style reward is defined as
The objective of the policy network in this paper is to enable the quadruped robot to learn and execute actions based on the standardized reference trajectory datasets . We propose a hierarchical reward structure, where user commands (e.g., discrete task IDs) dynamically activate only the relevant task reward functions during training. For example, tasks such as walking, running, jumping, and bipedal standing are categorized into three types, distinguished by user commands . When , the robot performs walking or running tasks; when , the robot performs jumping tasks; when , the robot performs bipedal standing tasks. Importantly, the corresponding rewards are calculated and accumulated only when these specific are issued. This hierarchical reward structure reduces the trial-and-error process, as each task’s rewards are independently optimized during their active phases. To achieve these three tasks, the following task reward functions are set for training:
- When , tracking linear velocity reward :
- When , tracking angle velocity reward :
- When , tracking angle velocity reward :
- When , CoM absolute height reward :
- When , trunk posture reward :
4. Simulation, Experiment, Analysis
4.1. Optimal Control Trajectories
In this paper, a nonlinear programming problem is formulated using CasADi [28], and the dynamics equations are constructed using Pinocchio [29]. Through optimization, the motion trajectory of the simplified quadruped robot model is obtained. Using jumping and bipedal standing as examples, the simulation parameters and the robot initial states are set identically for both optimizations, with a motion period of 1 s. Figure 4 shows the optimized joint angle curves for jumping and bipedal standing actions, and Figure 5 provides snapshots of the optimized jumping and bipedal standing actions. It can be observed that the joint position curves generated by the optimal control method are smooth, and the resulting motions are stable.
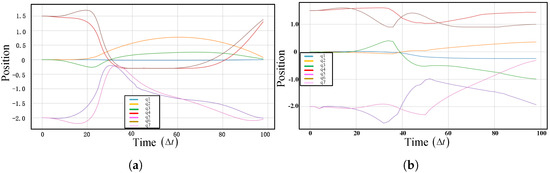
Figure 4.
Optimized action joint position curves. (a) Optimized joint position curve for jumping action. (b) Joint position curve for bipedal standing action, where q1, q2, …, q7 represent the X and Z directions of the trunk’s position, the trunk’s pitch angle, and the joint angles of the front and rear thighs and calves, respectively. These curves depict the simplified overall state as it changes over time.
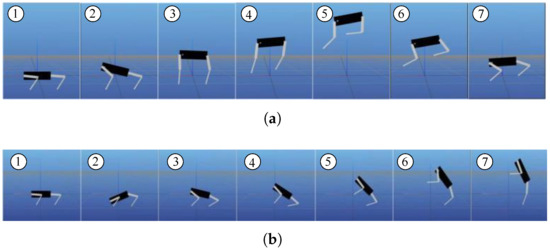
Figure 5.
Optimized action snapshots. (a) A snapshot of a simplified quadruped robot performing a jumping action. (b) A snapshot of a simplified quadruped robot bipedal standing on its rear foot.
4.2. Simulation Environment
The simulation environment is based on Python 3.8 and Isaac Gym [30], with the quadruped robot being Unitree A1. The environment rendering frequency was set to 200 Hz, while the controller control frequency was 33.3 Hz.
4.3. Training Results
The DRL training in this paper was conducted on a computer with a Central Processing Unit (CPU) of Intel i7-9700k and a Graphics Processing Unit (GPU) of NVIDIA GeForce RTX 2080 Ti.
The BCAMP model was trained by 2048 robots in parallel, and after 10,000 model iterations, the learning of actions from the motion trajectory library was accomplished. The weights of the reward functions involved in Section 3.3 are shown in Table 2, the hyperparameters involved in the training are shown in Table 3, and the mean reward is depicted in Figure 6. The mean reward value gradually increased and began to converge around 4000 iterations. The results indicate that the quadruped robot, trained with BCAMP, completed tasks well and received high rewards under different movement commands.

Table 2.
Reward function weights.

Table 3.
BCAMP framework training hyperparameters.
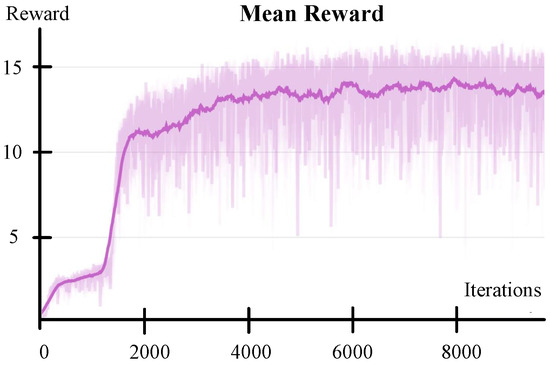
Figure 6.
The mean reward evolves over the training iterations.
To verify the training effectiveness, the trained BCAMP controller was applied in the simulation environment, and the movement of the quadruped robot was recorded, as shown in Figure 7. The policy was trained into a motion controller with various movement skills, allowing the robot to perform walking, running, jumping, and bipedal standing movements in the scene by issuing command parameters and user commands. It also enabled active switching between different stylistic actions.
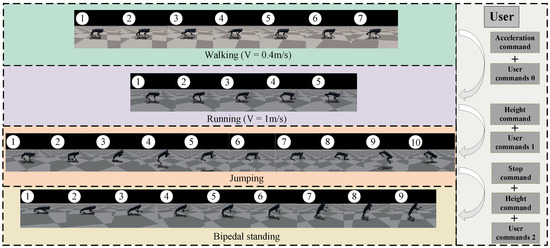
Figure 7.
Active switching of quadruped robot actions.
In summary, the BCAMP successfully completed the training, and the trained controller effectively achieved active switching between walking, running, jumping, and bipedal standing actions, demonstrating the effectiveness of the BCAMP.
4.4. Controllable Behavior Comparison Experiment
To verify the behavior controllability of BCAMP, AMP was used as the control group for comparison experiments. The experiments involved training both BCAMP and AMP with consistent reference trajectory libraries and hyperparameters, and a stepped obstacle was added to the simulation environment for analysis.
The controller trained with BCAMP received both command parameters and user commands, while the AMP-trained controller only accepted command parameters. Analyzing Figure 8, when the robot wanted to overcome the obstacle, the AMP controller, upon receiving command parameters to increase the height of the CoM, chose the bipedal standing action but could not actively switch to the jumping action, eventually leading to a fall. In contrast, Figure 9 shows that the BCAMP controller, when approaching the obstacle, received the same command parameter to increase the height of CoM along with a user command representing the jumping action. In this case, the robot successfully used the jumping action to clear the obstacle.

Figure 8.
AMP obstacle-crossing action snapshot.

Figure 9.
BCAMP obstacle-crossing action snapshot.
The AMP controller, when faced with both jumping and bipedal standing actions that involve raising the height of CoM, failed to select the appropriate action for obstacle clearance. On the other hand, the BCAMP controller actively switched between actions using user commands, successfully completing the obstacle-crossing task. In conclusion, this experiment demonstrates that training with BCAMP enables controllable behavior in quadruped robots, significantly improving their traversability and adaptability.
4.5. Training Speed Comparison
To further validate the performance of BCAMP proposed in this paper, PPO was used as a control group for comparison. The control experiments were conducted in the same environment, with specific parameter designs shown in Table 4.

Table 4.
PPO algorithm hyperparameters.
Using the PPO alone provides no prior knowledge, and the policy network can only be guided by the reward function for motion control. Given the complexity of designing the reward function, the following comparison experiments focus solely on training for the bipedal standing action.
In Figure 10, the PPO accumulates rewards very slowly within the first 6300 iterations, after which it rapidly accumulates reward values and gradually converges around 8000 iterations. As shown in Figure 11, the BCAMP quickly accumulates rewards within 2000 iterations and then gradually converges. The difference in the final reward values after convergence is due to the different designs of the reward functions and their corresponding weights, which does not affect the analysis of the algorithms’ performance. The motion prior knowledge provided by BCAMP effectively reduces the time spent by the robot exploring strategies at the beginning of training, allowing the robot to learn effective bipedal standing actions more quickly, thus improving the training speed.
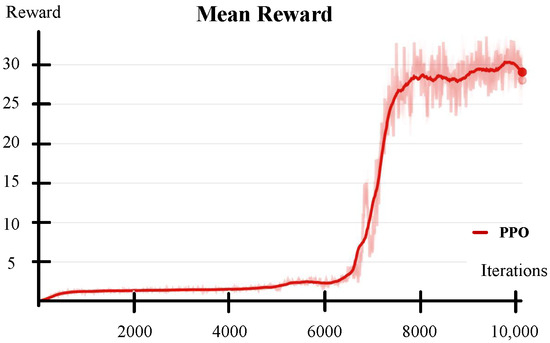
Figure 10.
Mean reward for training bipedal standing action with PPO.
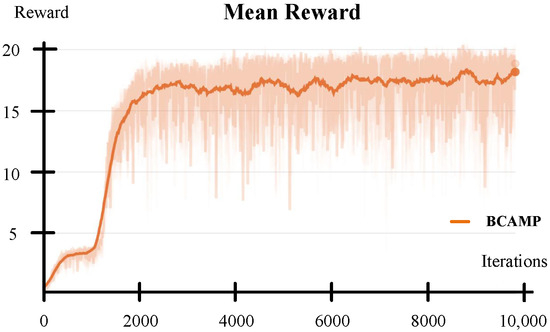
Figure 11.
Mean reward for training bipedal standing action with BCAMP.
To measure whether both algorithms performed well during the training of the quadruped robot, a comparison of the training effects was conducted. Combining Figure 12 and Figure 13, it can be observed that when training the bipedal standing action using only the PPO, after the front feet leave the ground, the robot rear feet are separated front and back to maintain balance. When the rear feet are standing apart, the distribution of the CoM and stability are affected, resulting in an unnatural overall bipedal standing posture compared to the BCAMP.

Figure 12.
Motion snapshot of training bipedal standing action with PPO.

Figure 13.
Motion snapshot of training bipedal standing action with BCAMP.
In summary, the experiments demonstrate the effectiveness of the method proposed in this paper for generating actions in quadruped robots, showing improvements in training speed and the naturalness of movements when compared to the PPO.
5. Conclusions
This paper presents a quadruped robot motion control method based on BCAMP. Simulation training using the BCAMP method was conducted, and the results demonstrate effective behavior-controllable motion, validating the efficacy of the proposed control method. Comparative obstacle-crossing experiments with the AMP algorithm showed that BCAMP enables behavior-controllable capabilities, facilitating successful obstacle crossing and improving the robot’s adaptability. This verifies the necessity of the proposed method in terms of behavior controllability. Furthermore, comparative experiments with the PPO algorithm were conducted, and the results indicate that the proposed method outperforms PPO in terms of reward convergence speed (approximately three times faster) and the naturalness of the generated actions.
Author Contributions
Conceptualization, Y.P., Z.C., L.Z. and X.W.; methodology, Y.P., Z.C. and L.Z.; software, Y.P. and Z.C.; validation, Y.P.; formal analysis, Y.P.; writing—original draft preparation, Y.P.; writing—review and editing, Y.P. and Z.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Beijing Advanced Innovation Center for Intelligent Robots and Systems, grant number: 00921917001.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lee, J.; Hwangbo, J.; Wellhausen, L.; Koltun, V.; Hutter, M. Learning quadrupedal locomotion over challenging terrain. Sci. Robot. 2020, 5, eabc5986. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Park, J.H. Impedance control of quadruped robot and its impedance characteristic modulation for trotting on irregular terrain. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 175–180. [Google Scholar] [CrossRef]
- Tsounis, V.; Alge, M.; Lee, J.; Farshidian, F.; Hutter, M. DeepGait: Planning and Control of Quadrupedal Gaits Using Deep Reinforcement Learning. IEEE Robot. Autom. Lett. 2020, 5, 3699–3706. [Google Scholar] [CrossRef]
- Di Carlo, J.; Wensing, P.M.; Katz, B.; Bledt, G.; Kim, S. Dynamic Locomotion in the MIT Cheetah 3 Through Convex Model-Predictive Control. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Dario Bellicoso, C.; Gehring, C.; Hwangbo, J.; Fankhauser, P.; Hutter, M. Perception-less terrain adaptation through whole body control and hierarchical optimization. In Proceedings of the 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), Cancun, Mexico, 15–17 November 2016; pp. 558–564. [Google Scholar] [CrossRef]
- Kim, D.; Carlo, J.D.; Katz, B.; Bledt, G.; Kim, S. Highly Dynamic Quadruped Locomotion via Whole-Body Impulse Control and Model Predictive Control. arXiv 2019, arXiv:1909.06586. [Google Scholar]
- Bellicoso, C.D.; Jenelten, F.; Gehring, C.; Hutter, M. Dynamic Locomotion Through Online Nonlinear Motion Optimization for Quadrupedal Robots. IEEE Robot. Autom. Lett. 2018, 3, 2261–2268. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Li, T.; Lambert, N.; Calandra, R.; Meier, F.; Rai, A. Learning Generalizable Locomotion Skills with Hierarchical Reinforcement Learning. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 413–419. [Google Scholar] [CrossRef]
- Smith, L.M.; Kostrikov, I.; Levine, S. A Walk in the Park: Learning to Walk in 20 Minutes With Model-Free Reinforcement Learning. arXiv 2022, arXiv:2208.07860. [Google Scholar]
- Margolis, G.B.; Agrawal, P. Walk These Ways: Tuning Robot Control for Generalization with Multiplicity of Behavior. arXiv 2022, arXiv:2212.03238. [Google Scholar]
- Miki, T.; Lee, J.; Hwangbo, J.; Wellhausen, L.; Koltun, V.; Hutter, M. Learning robust perceptive locomotion for quadrupedal robots in the wild. Sci. Robot. 2022, 7, eabk2822. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Kumar, A.; Pathak, D. Legs as Manipulator: Pushing Quadrupedal Agility Beyond Locomotion. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 5106–5112. [Google Scholar] [CrossRef]
- Radac, M.B. Trajectory tracking within a hierarchical primitive-based learning approach. Entropy 2022, 24, 889. [Google Scholar] [CrossRef] [PubMed]
- Merel, J.; Hasenclever, L.; Galashov, A.; Ahuja, A.; Pham, V.; Wayne, G.; Teh, Y.W.; Heess, N. Neural probabilistic motor primitives for humanoid control. arXiv 2018, arXiv:1811.11711. [Google Scholar]
- Goddard, Z.C.; Wardlaw, K.; Williams, K.; Parish, J.; Mazumdar, A. Utilizing reinforcement learning to continuously improve a primitive-based motion planner. J. Aerosp. Inf. Syst. 2022, 19, 468–479. [Google Scholar] [CrossRef]
- Radac, M.B.; Precup, R.E. Three-level hierarchical model-free learning approach to trajectory tracking control. Eng. Appl. Artif. Intell. 2016, 55, 103–118. [Google Scholar] [CrossRef]
- Peng, X.B.; Kanazawa, A.; Malik, J.; Abbeel, P.; Levine, S. SFV: Reinforcement learning of physical skills from videos. ACM Trans. Graph. 2018, 37, 178. [Google Scholar] [CrossRef]
- Peng, X.B.; Ma, Z.; Abbeel, P.; Levine, S.; Kanazawa, A. AMP: Adversarial motion priors for stylized physics-based character control. ACM Trans. Graph. 2021, 40, 144. [Google Scholar] [CrossRef]
- L’Erario, G.; Hanover, D.; Romero, A.; Song, Y.; Nava, G.; Viceconte, P.M.; Pucci, D.; Scaramuzza, D. Learning to Walk and Fly with Adversarial Motion Priors. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; pp. 10370–10377. [Google Scholar]
- Wu, J.; Xin, G.; Qi, C.; Xue, Y. Learning Robust and Agile Legged Locomotion Using Adversarial Motion Priors. IEEE Robot. Autom. Lett. 2023, 8, 4975–4982. [Google Scholar] [CrossRef]
- Peng, T.; Bao, L.; Humphreys, J.; Delfaki, A.M.; Kanoulas, D.; Zhou, C. Learning Bipedal Walking on a Quadruped Robot via Adversarial Motion Priors. arXiv 2024, arXiv:2407.02282. [Google Scholar]
- Vollenweider, E.; Bjelonic, M.; Klemm, V.; Rudin, N.; Lee, J.; Hutter, M. Advanced Skills through Multiple Adversarial Motion Priors in Reinforcement Learning. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 5120–5126. [Google Scholar] [CrossRef]
- Escontrela, A.; Peng, X.B.; Yu, W.; Zhang, T.; Iscen, A.; Goldberg, K.; Abbeel, P. Adversarial Motion Priors Make Good Substitutes for Complex Reward Functions. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 25–32. [Google Scholar] [CrossRef]
- Bock, H.; Plitt, K. A Multiple Shooting Algorithm for Direct Solution of Optimal Control Problems. IFAC Proc. Vol. 1984, 17, 1603–1608. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Sutton, R.S.; McAllester, D.; Singh, S.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. In Proceedings of the 12th International Conference on Neural Information Processing Systems, Cambridge, MA, USA, 29 November–4 December 1999; NIPS’99. pp. 1057–1063. [Google Scholar]
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi: A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Carpentier, J.; Saurel, G.; Buondonno, G.; Mirabel, J.; Lamiraux, F.; Stasse, O.; Mansard, N. The Pinocchio C++ library: A fast and flexible implementation of rigid body dynamics algorithms and their analytical derivatives. In Proceedings of the 2019 IEEE/SICE International Symposium on System Integration (SII), Paris, France, 14–16 January 2019; pp. 614–619. [Google Scholar] [CrossRef]
- Makoviychuk, V.; Wawrzyniak, L.; Guo, Y.; Lu, M.; Storey, K.; Macklin, M.; Hoeller, D.; Rudin, N.; Allshire, A.; Handa, A.; et al. Isaac Gym: High Performance GPU-Based Physics Simulation For Robot Learning. arXiv 2021, arXiv:2108.10470. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).