Fault Diagnosis Across Aircraft Systems Using Image Recognition and Transfer Learning
Abstract
1. Introduction
1.1. Background
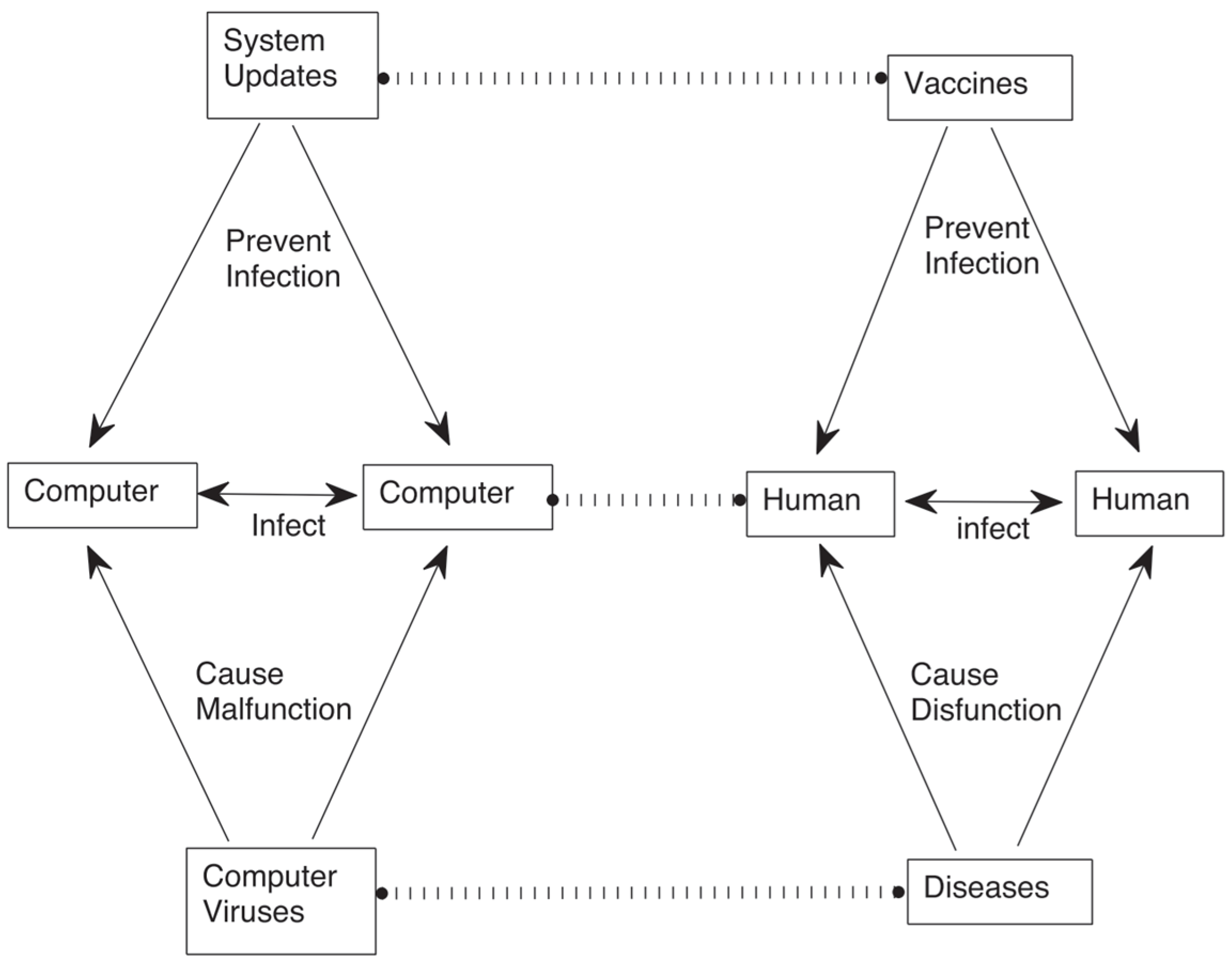
1.2. The Application of Transfer Learning in Solving MRO Challenges
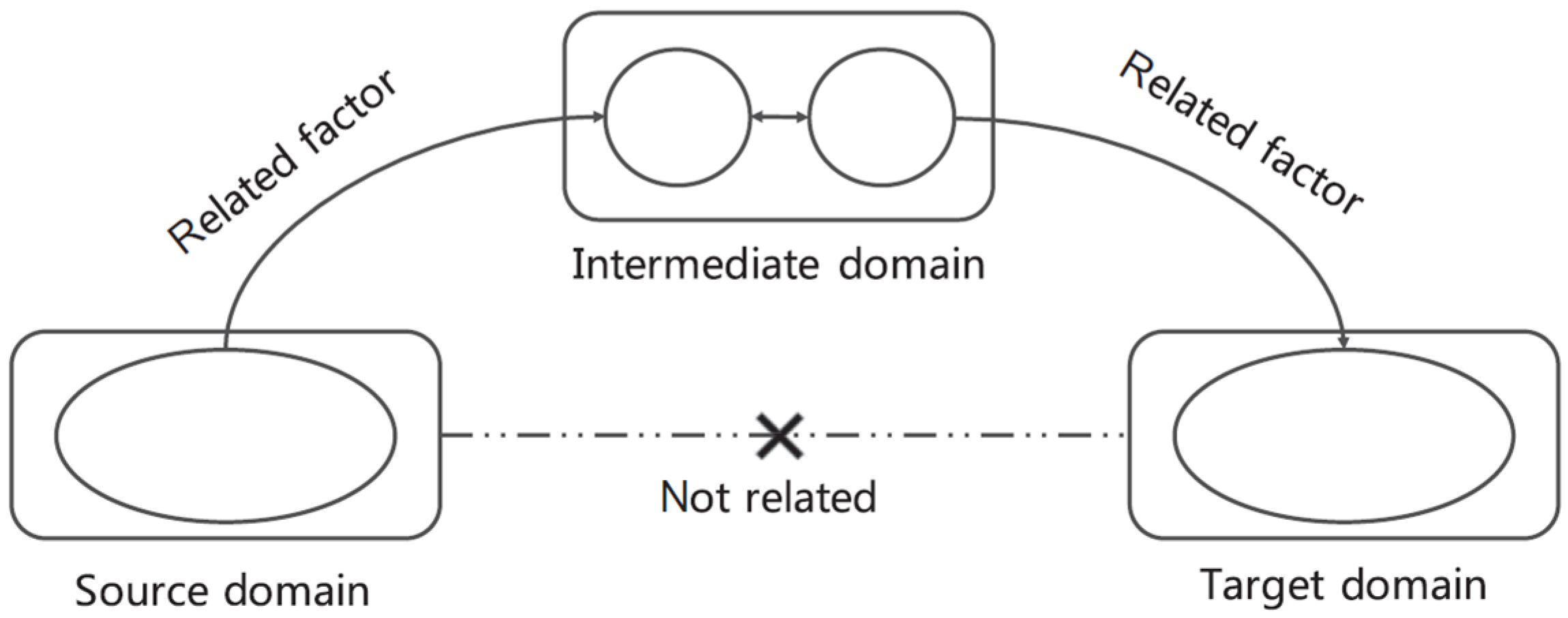
1.3. The Potential of Cross-System Transfer Learning
2. Datasets
2.1. ECS Description
2.2. APU Description
2.3. Fuel System Description
2.4. Dataset Comparison
3. Methodology
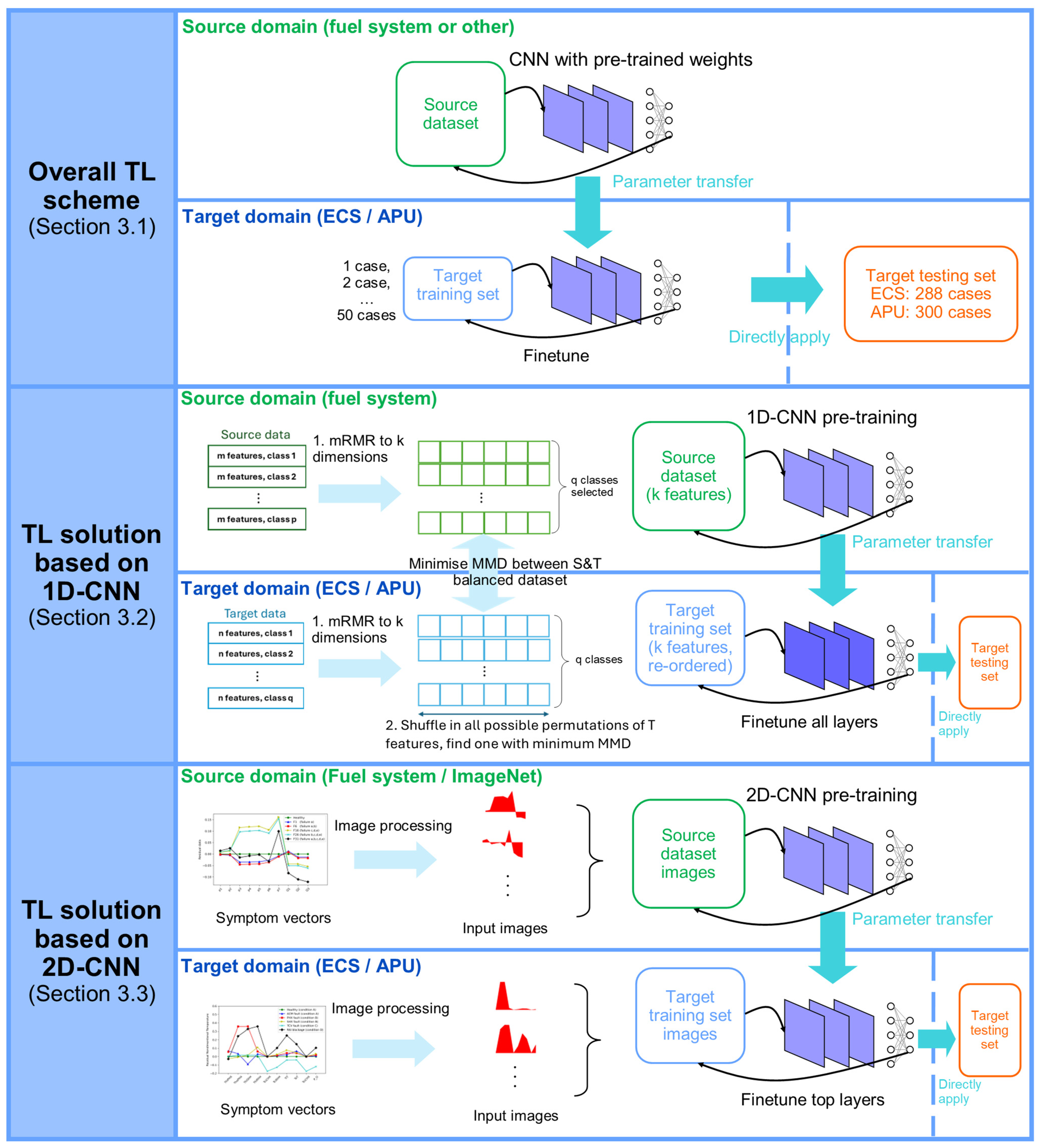
3.1. Transfer Learning Problem
3.2. Transfer Learning Solution Based on 1D-CNN
3.3. Transfer Learning Solution Based on 2D-CNN
3.3.1. From Image Classification to Fault Diagnosis
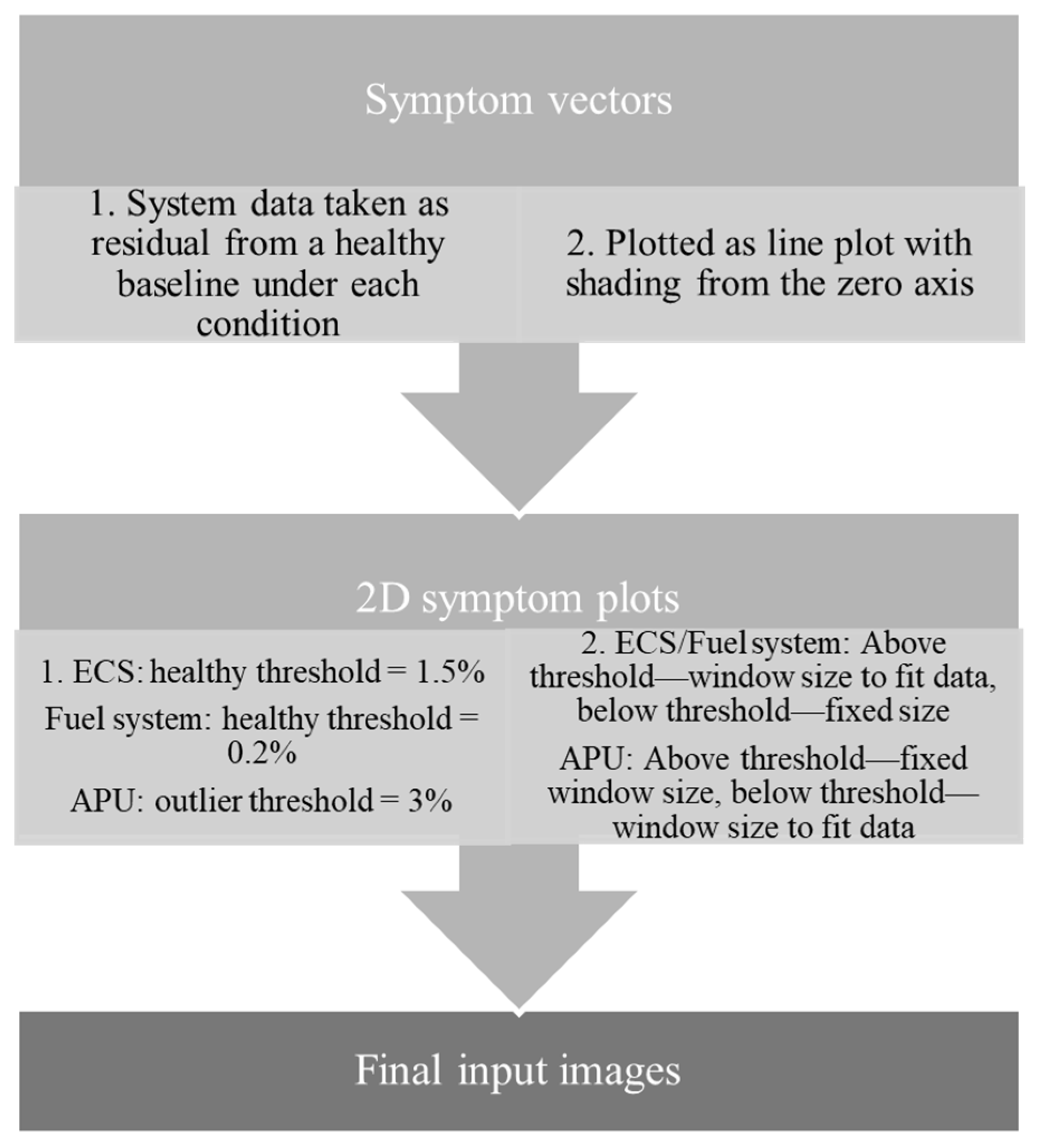
3.3.2. Image Preparation
4. Results and Analysis
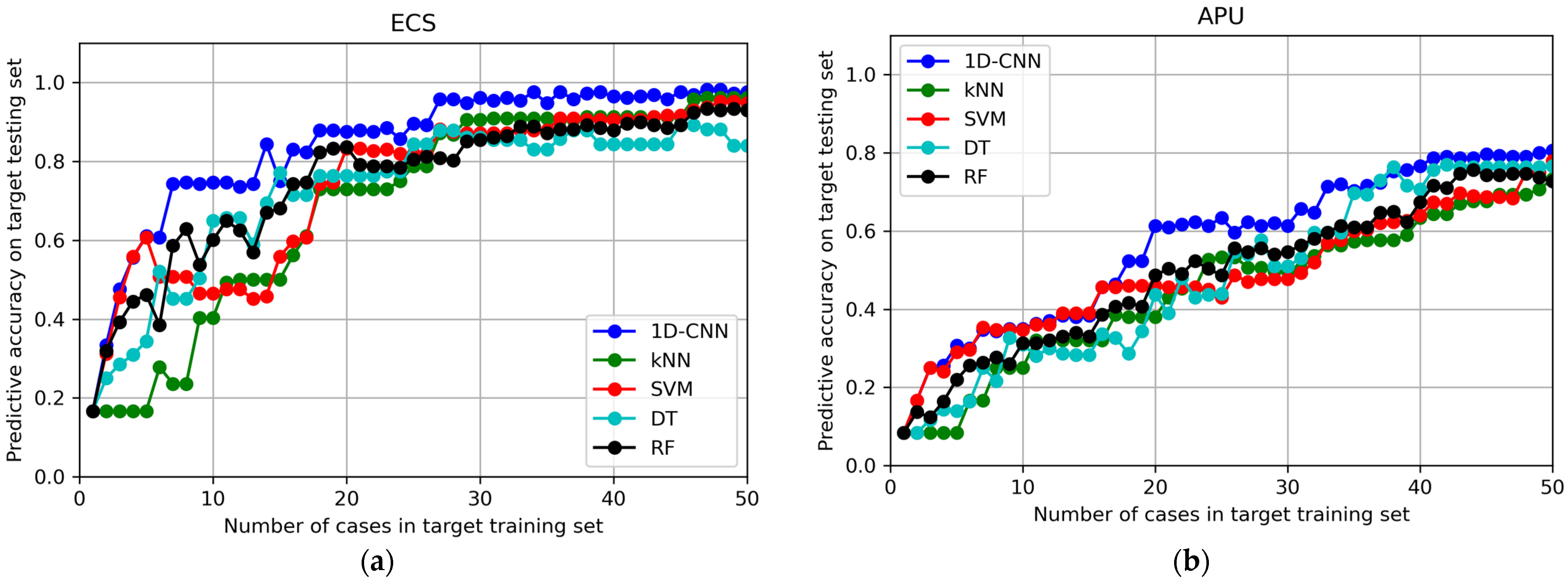
4.1. Baseline Result from Non-TL Methods
4.2. Result from TL Methods
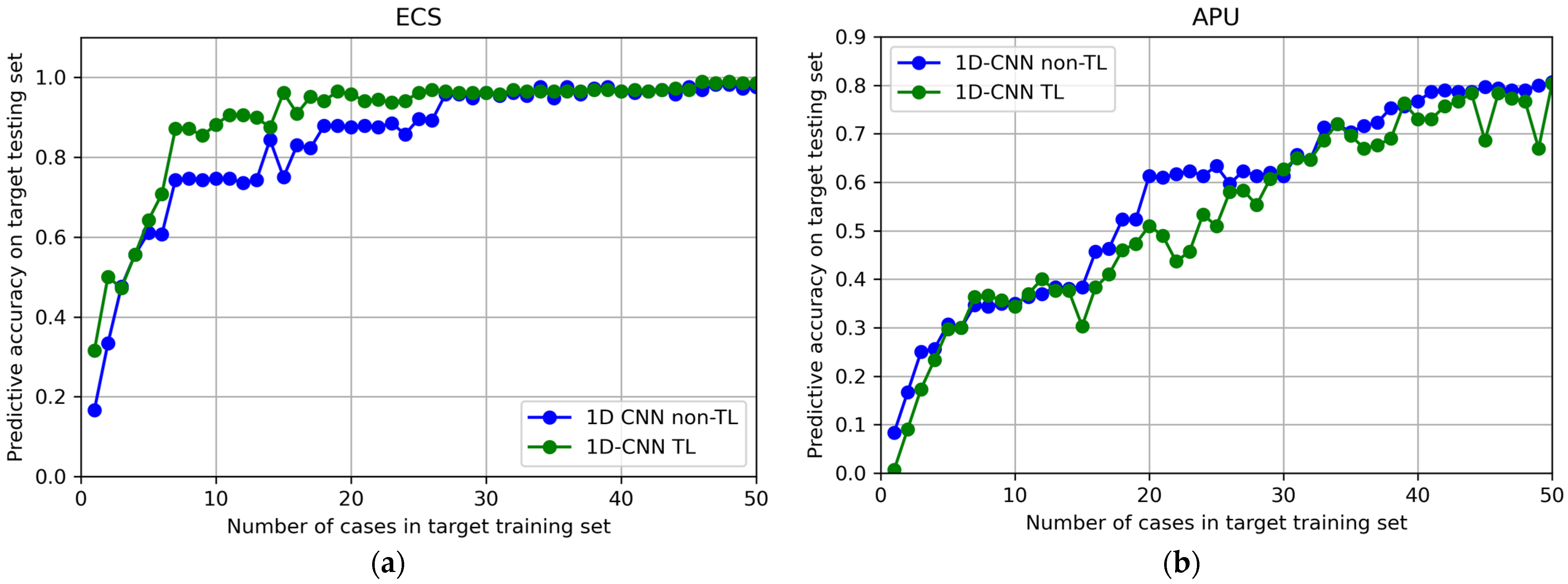
4.2.1. Results from TL Method Based on 1D-CNN
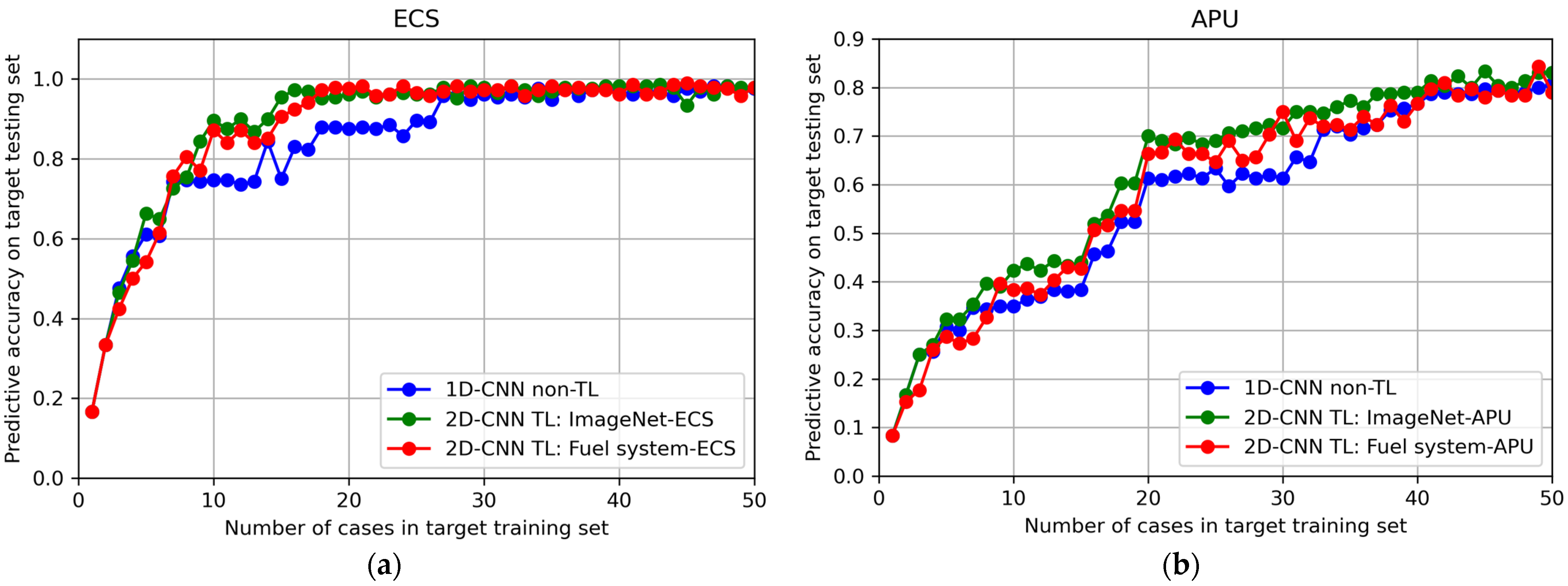
4.2.2. Results from TL Method Based on 2D-CNN
5. Explanation and Evaluation of Results
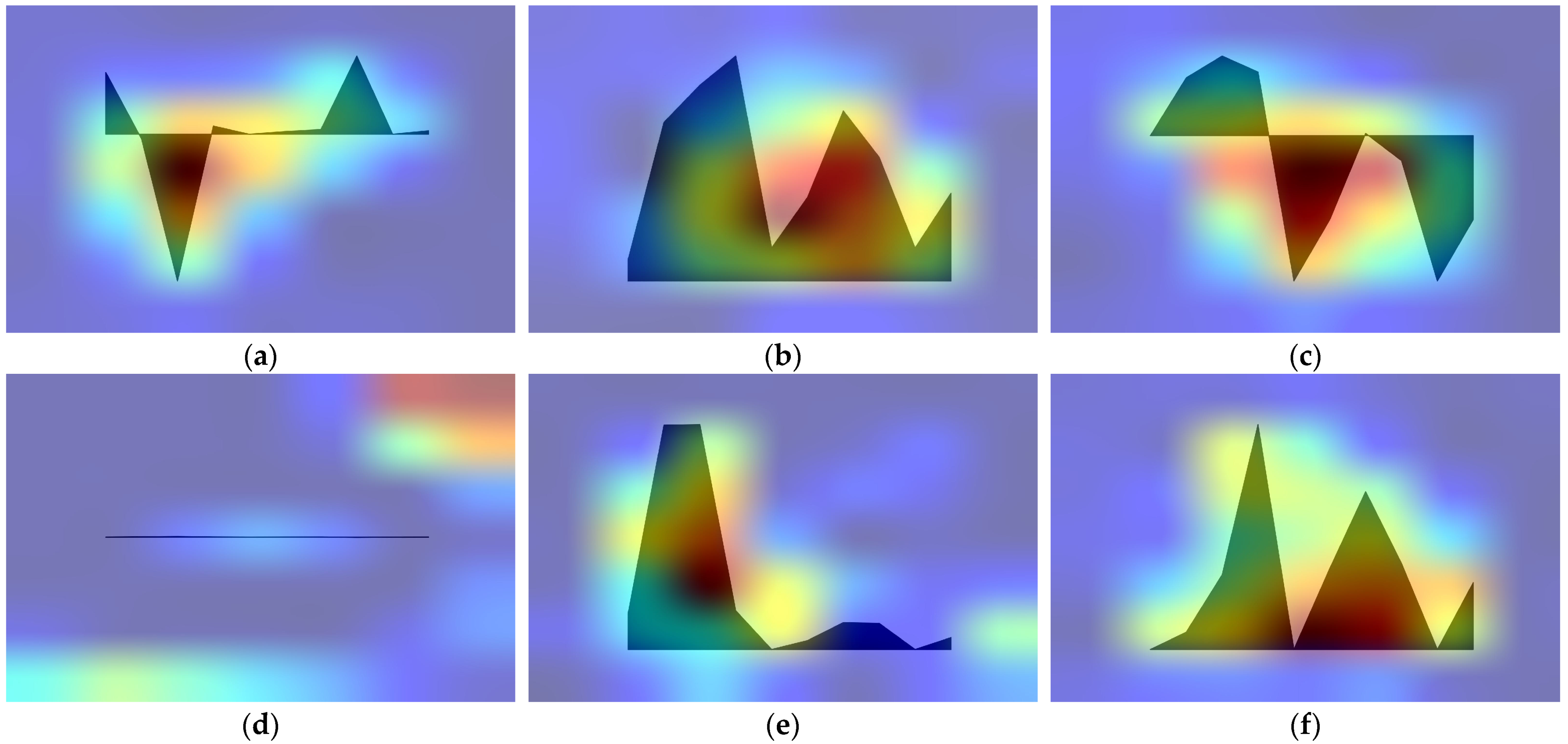
5.1. Grad-CAM Visualisation for 2D-CNN TL Result
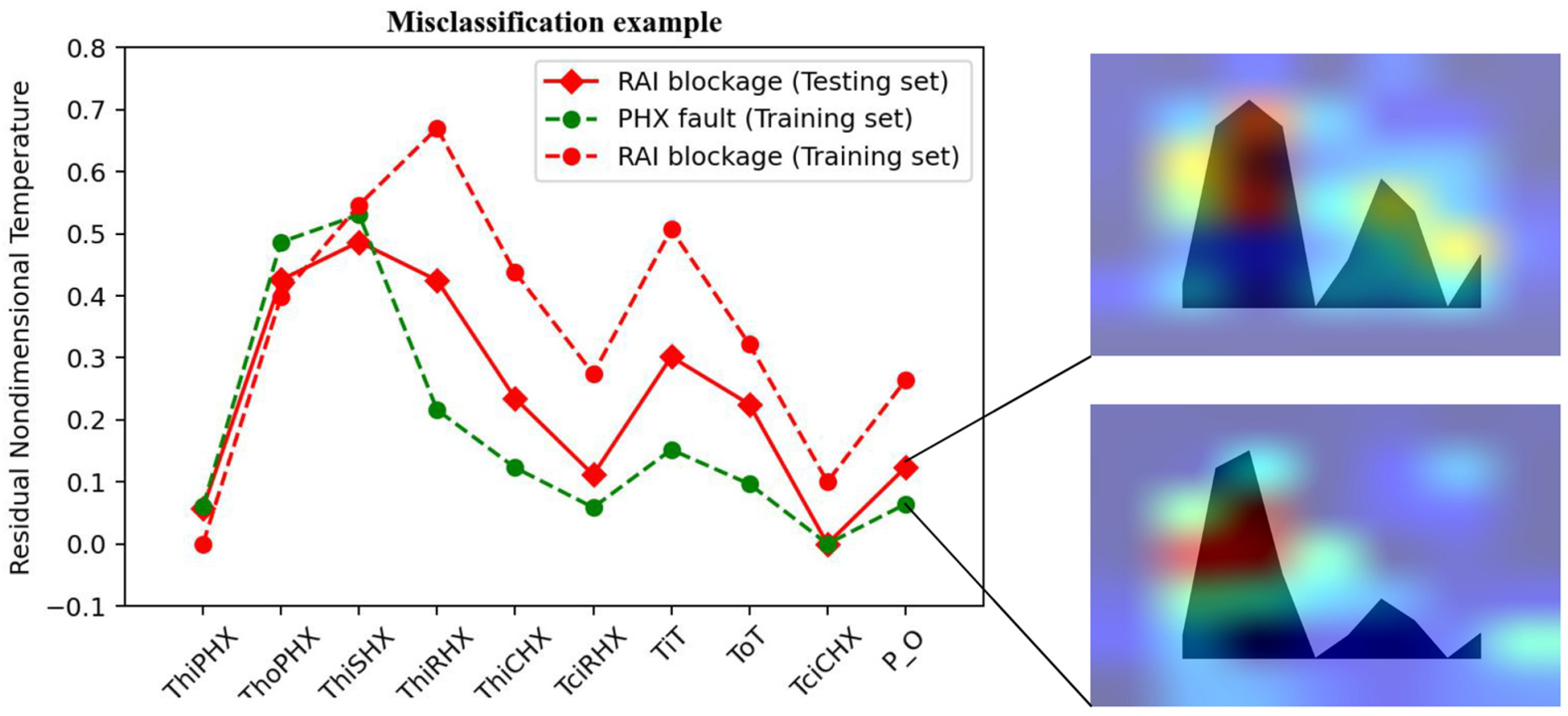
5.2. Specific Case Analysis
5.3. Performance of TL Method over Complex Fault Patterns
6. Conclusions and Future Work
6.1. Conclusions
6.2. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACS | Attitude Control System |
| AI | Artificial Intelligence |
| APU | Auxiliary Power Unit |
| AVR | Automatic Voltage Regulator |
| CBM | Condition-Based Maintenance |
| CNN | Convolutional Neural Network |
| DT | Decision Tree |
| ECS | Environmental Control System |
| ETC | Electronic Turbine Controller |
| EV | Excitation Voltage |
| FMV | Fuel Metering Valve |
| FOHE | Fuel–Oil Heat Exchanger |
| Grad-CAM | Gradient-Weighted Class Activation Mapping |
| HPWS | High-Pressure Water Separator |
| IFD | Intelligent Fault Diagnosis |
| IVHM | Integrated Vehicle Health Management |
| kNN | k-Nearest Neighbours |
| LCV | Load Control Valve |
| ML | Machine Learning |
| MMD | Maximum Mean Discrepancy |
| mRMR | Minimum Redundancy Maximum Relevance |
| MRO | Maintenance Repair and Overhaul |
| PACK | Passenger Air Conditioner |
| PHX | Primary Heat Exchanger |
| PV | PACK Valve |
| RAI | Ram Air Inlet |
| RF | Random Forest |
| SESAC | Simscape ECS Simulation under All Conditions |
| SHX | Secondary Heat Exchanger |
| SVM | Support Vector Machine |
| TCV | Temperature Control Valve |
| TL | Transfer Learning |
| TTL | Transitive Transfer Learning |
References
- International Air Transport Association (IATA). Airline Maintenance Cost Executive Commentary FY2023 Data [Online]. 2025. Available online: https://www.iata.org/contentassets/bf8ca67c8bcd4358b3d004b0d6d0916f/fy2023-mcx-report_public.pdf (accessed on 15 March 2025).
- Aviation MRO Spend Grows Amid Rising Costs and Supply Chain [Online]. Available online: https://www.oliverwyman.com/our-expertise/insights/2024/apr/mro-survey-2024-aviation-mro-grows-amid-rising-costs-supply-chain-woes.html (accessed on 18 January 2025).
- Jennions, I.K. Integrated Vehicle Health Management: Perspectives on an Emerging Field; SAE International: Warrendale, PA, USA, 2011. [Google Scholar] [CrossRef]
- Verhagen, W.J.C.; Santos, B.F.; Freeman, F.; van Kessel, P.; Zarouchas, D.; Loutas, T.; Yeun, R.C.K.; Heiets, I. Condition-Based Maintenance in Aviation: Challenges and Opportunities. Aerospace 2023, 10, 762. [Google Scholar] [CrossRef]
- Ezhilarasu, C.M.; Angus, J.; Jennions, I.K. Toward the Aircraft of the Future: A Perspective from Consciousness. J. Artif. Intell. Conscious. 2023, 10, 249–290. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, Y.; Dai, W.; Pan, S.J. Transfer Learning; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, R.; Yang, Y.; Yin, J.; Li, Y.; Li, Y.; Xu, M. Cross-Domain Fault Diagnosis Using Knowledge Transfer Strategy: A Review. IEEE Access 2019, 7, 129260–129290. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Azari, M.S.; Flammini, F.; Santini, S.; Caporuscio, M. A Systematic Literature Review on Transfer Learning for Predictive Maintenance in Industry 4.0. IEEE Access 2023, 11, 12887–12910. [Google Scholar] [CrossRef]
- Guo, L.; Lei, Y.; Xing, S.; Yan, T.; Li, N. Deep Convolutional Transfer Learning Network: A New Method for Intelligent Fault Diagnosis of Machines with Unlabelled Data. IEEE Trans. Ind. Electron. 2019, 66, 7316–7325. [Google Scholar] [CrossRef]
- Li, B.; Zhao, Y.P.; Chen, Y.B. Learning transfer feature representations for gas path fault diagnosis across gas turbine fleet. Eng. Appl. Artif. Intell. 2022, 111, 104733. [Google Scholar] [CrossRef]
- He, M.; Cheng, Y.; Wang, Z.; Gong, J.; Ye, Z. Fault Location for spacecraft ACS system using the method of transfer learning. In Proceedings of the Chinese Control Conference, CCC, Shanghai, China, 26–28 July 2021; Volume 2021, pp. 4561–4566. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Q. Transfer learning by structural analogy. In Proceedings of the National Conference on Artificial Intelligence, San Francisco, CA, USA, 7–11 August 2011; Volume 1, pp. 513–518. [Google Scholar]
- Tan, B.; Song, Y.; Zhong, E.; Yang, Q. Transitive transfer learning. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; Volume 2015, pp. 1155–1164. [Google Scholar] [CrossRef]
- Jennions, I.; Ali, F.; Miguez, M.E.; Escobar, I.C. Simulation of an aircraft environmental control system. Appl. Therm. Eng. 2020, 172, 114925. [Google Scholar] [CrossRef]
- Skliros, C.; Ali, F.; Jennions, I. Experimental investigation and simulation of a Boeing 747 auxiliary power unit. J. Eng. Gas Turbine Power 2020, 142, 081005. [Google Scholar] [CrossRef]
- Li, J.; King, S.; Jennions, I. Intelligent Multi-Fault Diagnosis for a Simplified Aircraft Fuel System. Algorithms 2025, 18, 73. [Google Scholar] [CrossRef]
- Jennions, I.; Ali, F. Assessment of heat exchanger degradation in a Boeing 737-800 environmental control system. J. Therm. Sci. Eng. Appl. 2021, 13, 061015. [Google Scholar] [CrossRef]
- Jia, L.; Ezhilarasu, C.M.; Jennions, I.K. Cross-Condition Fault Diagnosis of an Aircraft Environmental Control System (ECS) by Transfer Learning. Appl. Sci. 2023, 13, 13120. [Google Scholar] [CrossRef]
- Skliros, C.; Ali, F.; Jennions, I. Fault simulations and diagnostics for a Boeing 747 Auxiliary Power Unit. Expert Syst. Appl. 2021, 184, 115504. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, T. Deep Convolutional Neural Network Using Transfer Learning for Fault Diagnosis. IEEE Access 2021, 9, 43889–43897. [Google Scholar] [CrossRef]
- Shao, S.; McAleer, S.; Yan, R.; Baldi, P. Highly Accurate Machine Fault Diagnosis Using Deep Transfer Learning. IEEE Trans. Ind. Inf. 2019, 15, 2446–2455. [Google Scholar] [CrossRef]
- Ruhi, Z.M.; Jahan, S.; Uddin, J. A novel hybrid signal decomposition technique for transfer learning based industrial fault diagnosis. Ann. Emerg. Technol. Comput. 2021, 5, 37–53. [Google Scholar] [CrossRef]
- Liu, J.; Hou, L.; Zhang, R.; Sun, X.; Yu, Q.; Yang, K.; Zhang, X. Explainable fault diagnosis of oil-gas treatment station based on transfer learning. Energy 2023, 262, 125258. [Google Scholar] [CrossRef]
- ImageNet [Online]. Available online: https://www.image-net.org/ (accessed on 21 October 2024).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Pedregosa, F.; Michel, V.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Vanderplas, J.; Cournapeau, D.; Varoquaux, G.; Gramfort; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Keras. Deep Learning for Humans [Online]. Available online: https://keras.io/ (accessed on 21 October 2024).
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization. Int. J. Comput. Vis. 2016, 128, 336–359. [Google Scholar] [CrossRef]
- Brito, L.C.; Susto, G.A.; Brito, J.N.; Duarte, M.A.V. Fault Diagnosis using eXplainable AI: A transfer learning-based approach for rotating machinery exploiting augmented synthetic data. Expert Syst. Appl. 2023, 232, 120860. [Google Scholar] [CrossRef]
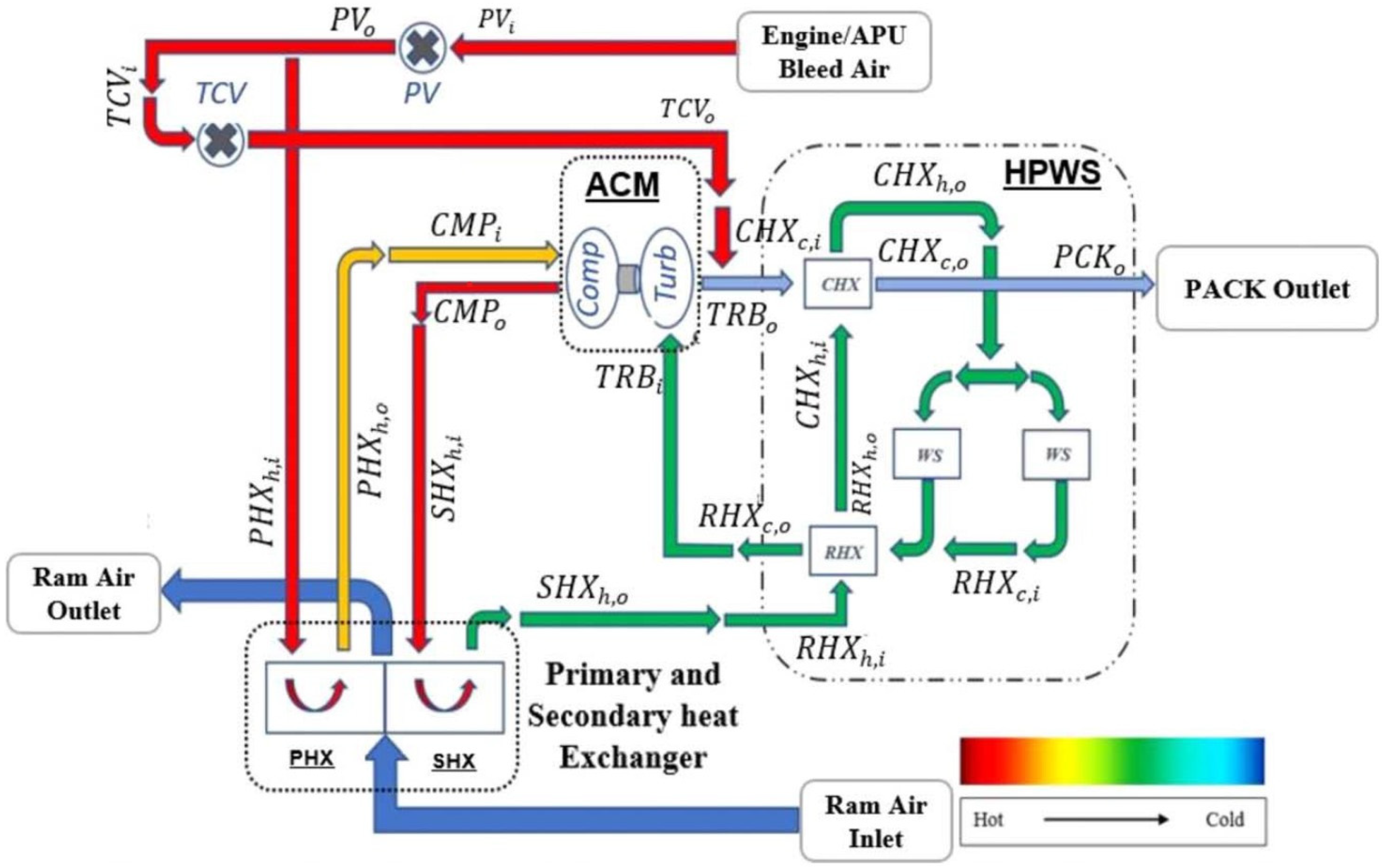
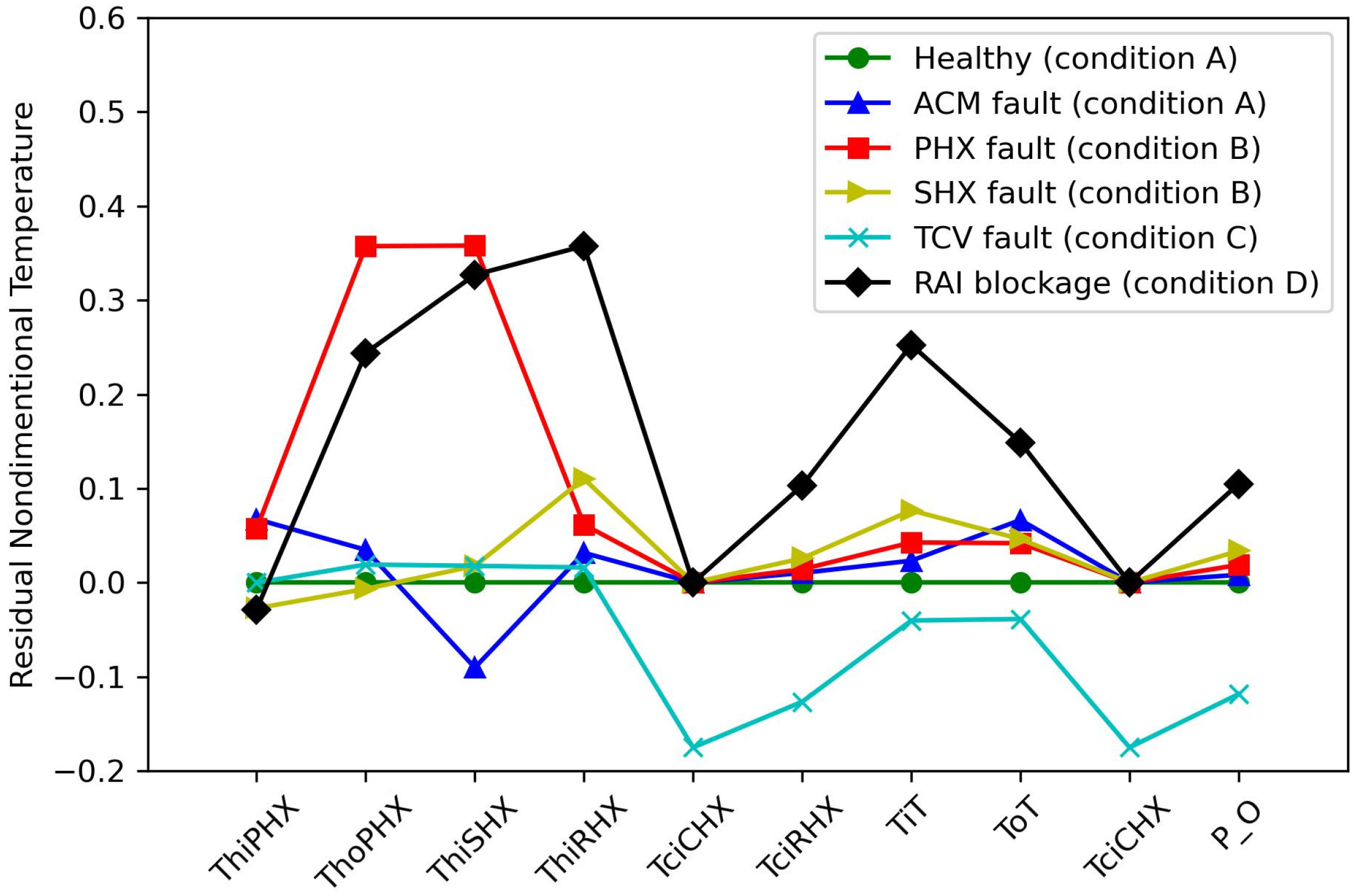

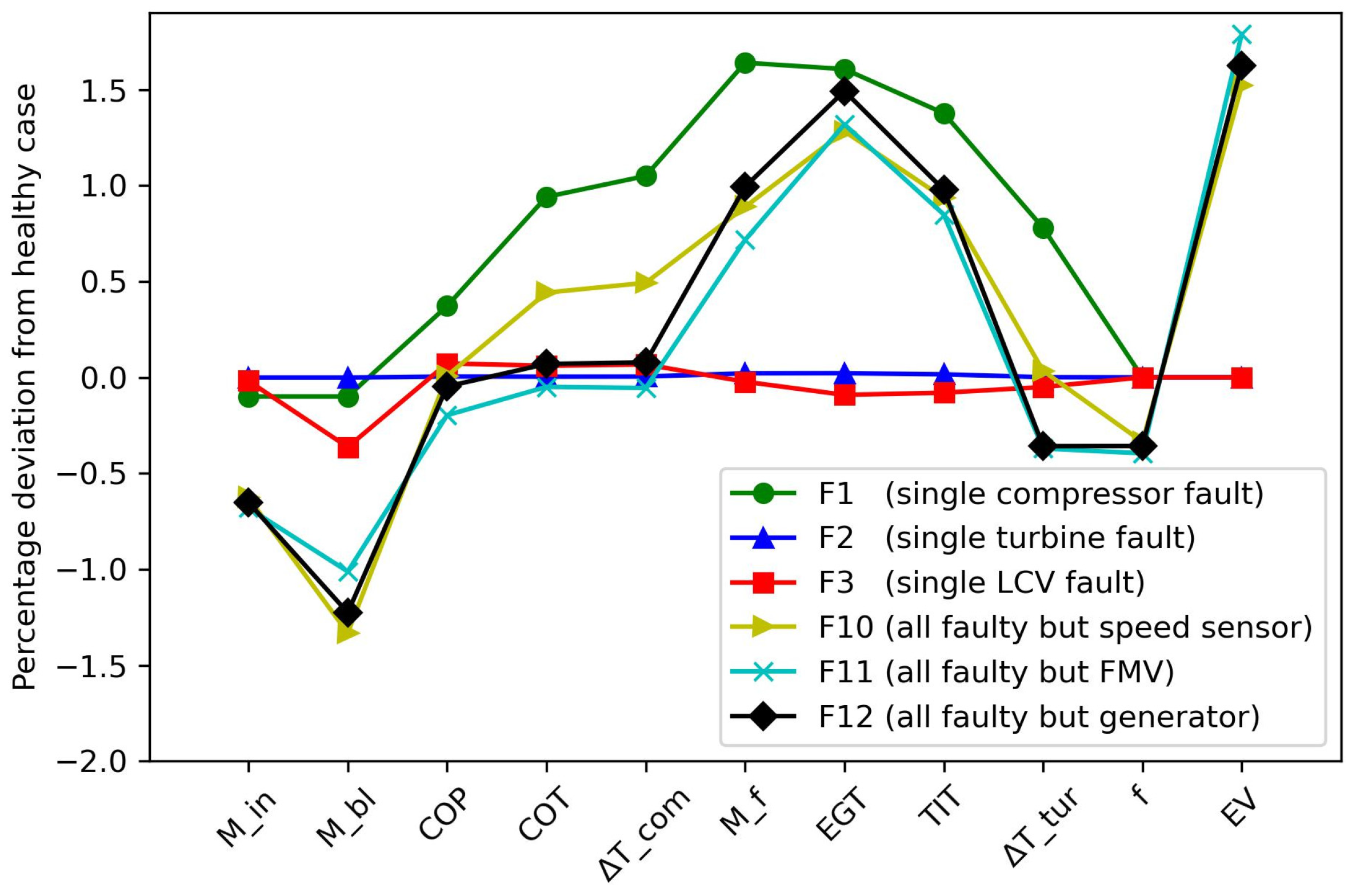
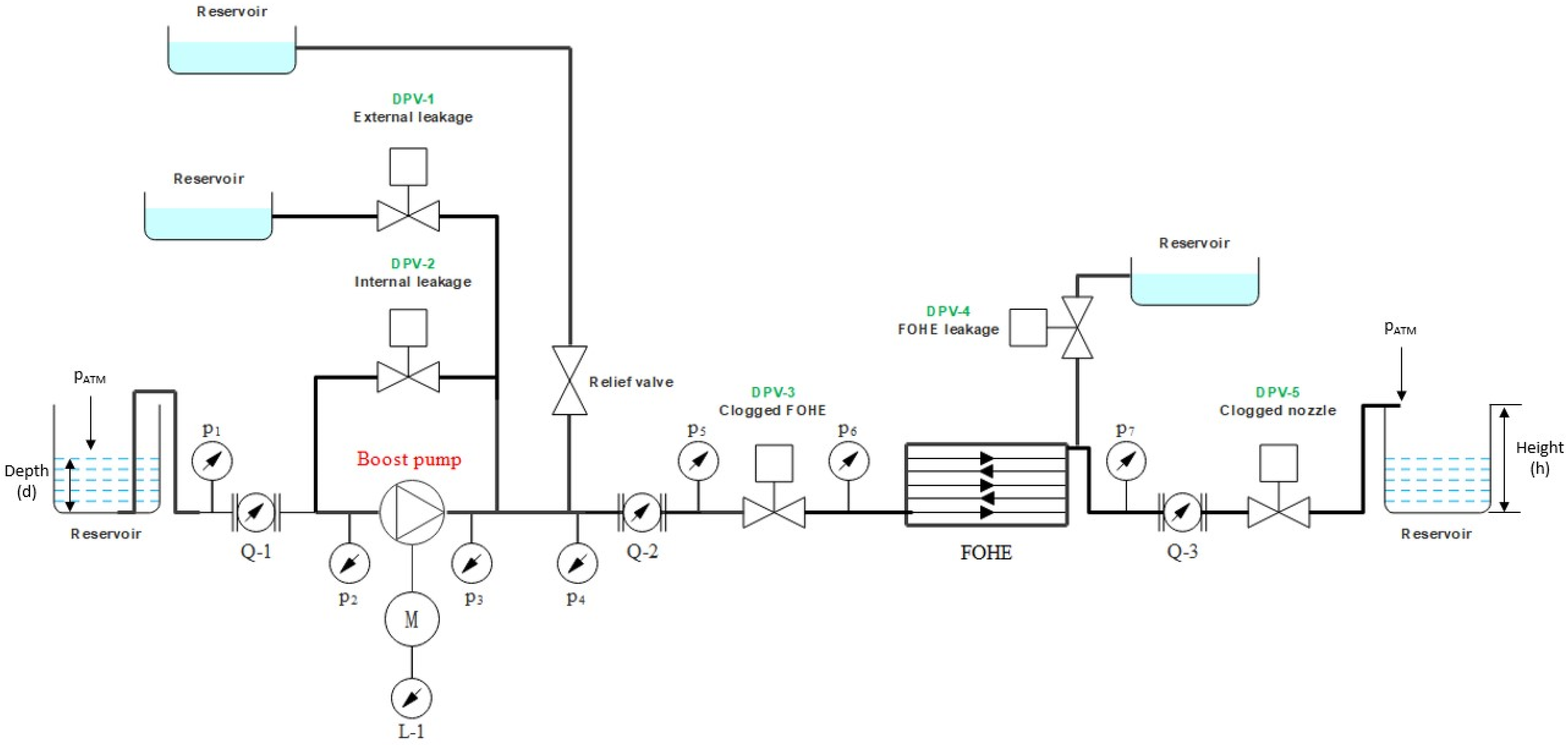


| ECS [19] | APU [20] | Fuel System [17] | |
|---|---|---|---|
| Number and nature of parameters | 10 temperatures | 3 mass flow rates, 5 temperatures, 1 pressure, 2 electric signals, 1 frequency | 7 pressures, 3 volumetric flow rates |
| Operating condition | Ground running (Condition A), 28k ft cruise (Condition B), 35k ft cruise (Condition C), 41k ft cruise (Condition D) | Single condition | Single condition |
| Number of cases collected | 288 | 300 | 3989 |
| Components where fault is inserted (failure modes) | ACM (Fouling/blockage) PHX (Fouling/blockage) SHX (Fouling/blockage) TCV (Deviation from commanded position) RAI door (Blockage) | Compressor (Reduced efficiency) Turbine (Reduced efficiency) LCV (Deviation from commanded position) Speed sensor (Positive bias) FMV (Sticking valve) Generator (Increased stator resistance) | Boost pump (External leakage—failure a) Boost pump (Internal leakage—failure b) FOHE (Clogging—failure c) FOHE (Leakage—failure d) Nozzle (Clogging—failure e) |
| Health states considered | 1 healthy state | F1-F6: single fault of each component | 1 Healthy state |
| 5 single fault states for each component | F7-F11: one component healthy, all others faulty | F1-F5: 1 component faulty, all others healthy | |
| F12: all components faulty | F6-F15: 2 components faulty, all others healthy | ||
| F16-F25: 3 components faulty, all others healthy | |||
| F26-F30: 4 components faulty, one healthy | |||
| F31: all 5 components faulty |
| ML Classifiers | Key Parameters |
|---|---|
| kNN | n_neighbors = 3 |
| SVM | kernel = ‘linear’, decision_function_shape = ‘ovo’ |
| DT | max_depth = 4, criterion = ‘entropy’ |
| RF | n_estimators = 30, max_depth = 4, criterion = ‘entropy’ |
| Deep networks | Information of layers |
| 1D-CNN | Input layer Conv1D layer (filters = 16, kernel_size = 4, padding = ‘causal’) Conv1D layer (filters = 32, kernel_size = 6, padding = ‘causal’) Conv1D layer (filters = 64, kernel_size = 8, padding = ‘causal’) MaxPooling1D layer Flatten layer Dense layer (units = no. classes, activation = ‘softmax’) |
| 2D-CNN | Base model: ResNet101 from Keras Applications, pooling = ‘max’ Top layers: Flatten layer Dense layer (units = 256, activation = ‘relu’) Dense layer (units = no. classes for the target systems, activation = ‘softmax’) |
| Method (Non-TL) | Average Predictive Accuracy (%) for Testing Set | |
|---|---|---|
| 1–30 Cases in ECS Training Set | 1–50 Cases in APU Training Set | |
| 1D-CNN | 76.48 | 56.92 |
| kNN | 54.36 | 44.81 |
| SVM | 63.16 | 48.96 |
| DT | 64.21 | 48.24 |
| RF | 65.96 | 49.25 |
| Method | Average Predictive Accuracy (%) for Testing Set | Minimum Number of Cases in Training Set to Reach | ||
|---|---|---|---|---|
| 1–30 Cases in ECS Training Set | 1–50 Cases in APU Training Set | 95% Accuracy in ECS Testing Set | 75% Accuracy in APU Testing Set | |
| 1D-CNN non-TL baseline | 76.48 | 56.92 | 27 | 40 |
| 2D-CNN TL solution with ImageNet in source domain | 83.38 | 61.96 | 15 | 34 |
| 2D-CNN TL solution with fuel system in source domain | 81.96 | 58.95 | 18 | 40 |
| Method | Average Accuracy over Single Fault Cases Only | Average Accuracy over Multiple Fault Cases Only | Average Accuracy over All Cases |
|---|---|---|---|
| 1D CNN non-TL baseline | 94.00% | 50.00% | 72.00% |
| 2D CNN TL: ImageNet–APU | 99.33% | 52.66% | 76.00% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, L.; Ezhilarasu, C.M.; Jennions, I.K. Fault Diagnosis Across Aircraft Systems Using Image Recognition and Transfer Learning. Appl. Sci. 2025, 15, 3232. https://doi.org/10.3390/app15063232
Jia L, Ezhilarasu CM, Jennions IK. Fault Diagnosis Across Aircraft Systems Using Image Recognition and Transfer Learning. Applied Sciences. 2025; 15(6):3232. https://doi.org/10.3390/app15063232
Chicago/Turabian StyleJia, Lilin, Cordelia Mattuvarkuzhali Ezhilarasu, and Ian K. Jennions. 2025. "Fault Diagnosis Across Aircraft Systems Using Image Recognition and Transfer Learning" Applied Sciences 15, no. 6: 3232. https://doi.org/10.3390/app15063232
APA StyleJia, L., Ezhilarasu, C. M., & Jennions, I. K. (2025). Fault Diagnosis Across Aircraft Systems Using Image Recognition and Transfer Learning. Applied Sciences, 15(6), 3232. https://doi.org/10.3390/app15063232






