The Bearing Performance and Sectional Design Method of Yielding U-Shaped Steel Support
Abstract
1. Introduction
2. Analysis of Typical On-Site Failure Modes of Yielding U-Shaped Steel Support
2.1. Project Overview
2.2. Typical Failure Analysis
- The bending moment at the nodes is large and is difficult to yield. The cable clamp nodes are designed near the bent parts of the support. At this position, the bending moment is large, and the cable clamp nodes are in an open state, making it difficult for the nodes to retract and yield.
- Stress concentration occurs at the nodes, resulting in structural tearing. The failures at the cable clamp nodes are mostly manifested as the tearing of the support, the fracture of screw rods, the outward turning of cable clamps, and the breakage of clamping plates. The main reason is that the combined structure at the nodes is complex, stress concentration occurs easily, and structural failures are prone to happen at the nodes.
- The support is subjected to asymmetric forces, resulting in buckling failures. Under the action of asymmetric loads, the support as a whole shows asymmetric failure characteristics. The deformation on the side of the small coal pillar is greater than that on the side of the solid rib. Straight-leg buckling and shoulder bending of the support occur, and the bearing capacity of the support is difficult to be fully exerted.
3. Indoor Experimental Research on the Bearing Performance of Yielding U-Shaped Steel Support
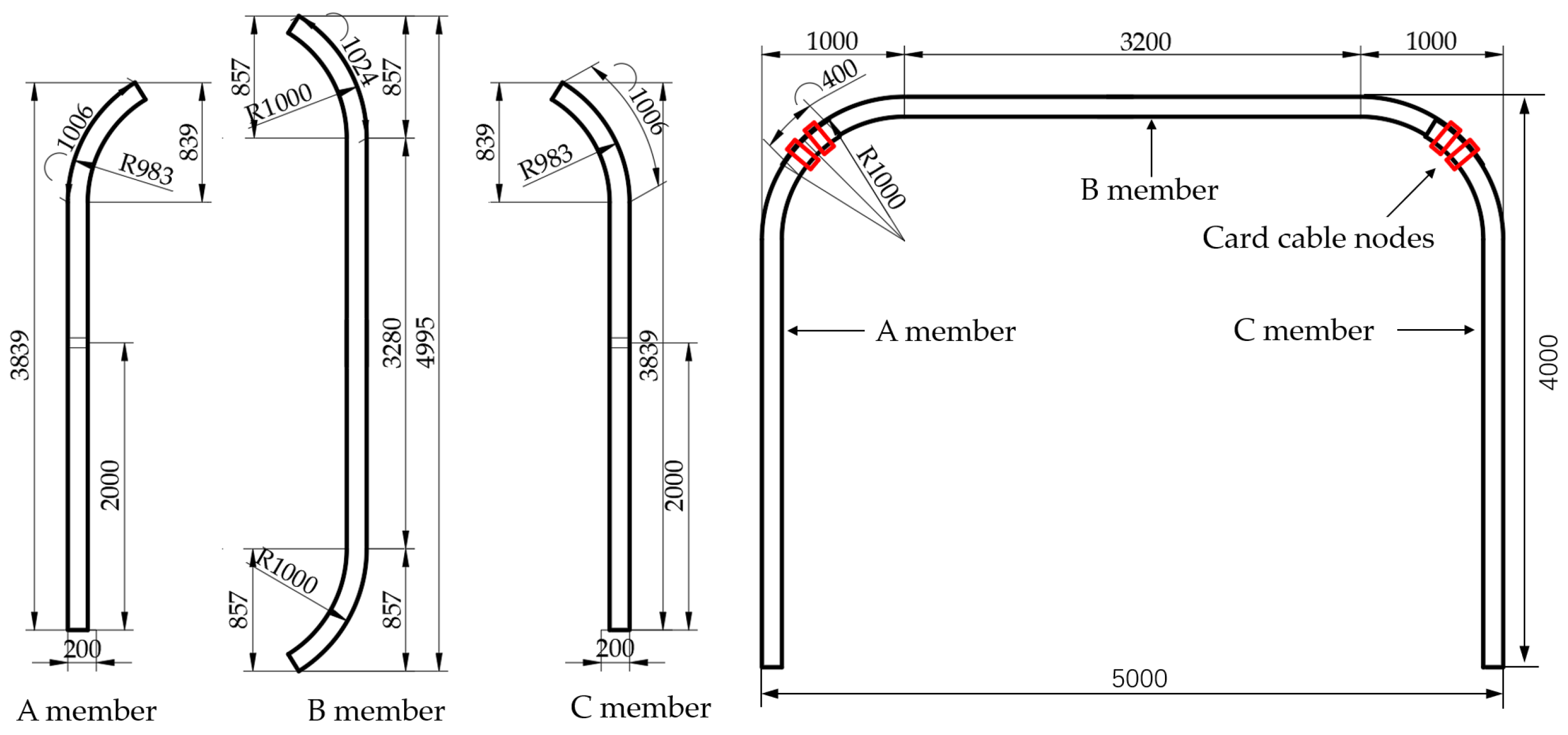
3.1. Experimental Scheme
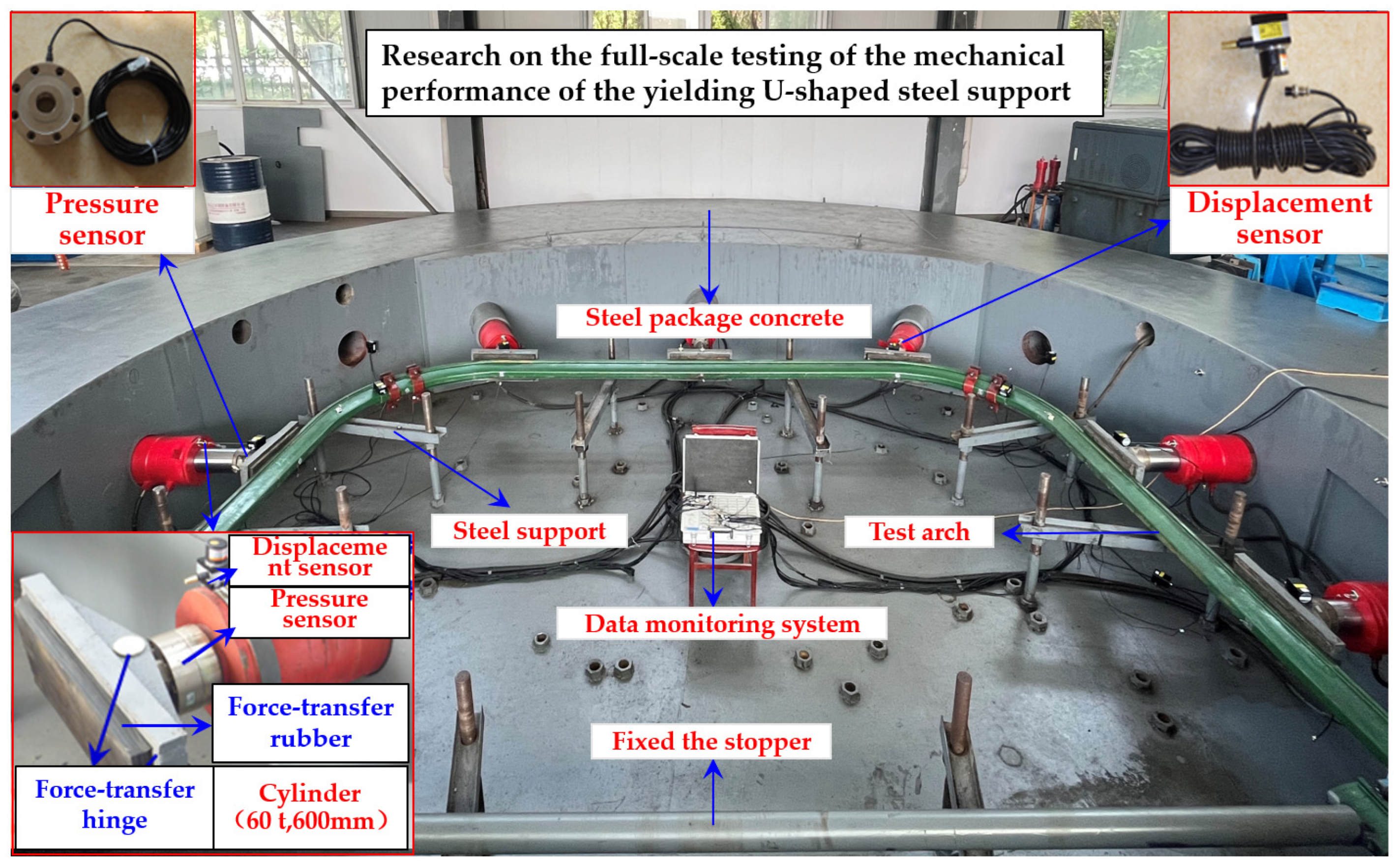
3.1.1. Experimental System
3.1.2. Loading Scheme
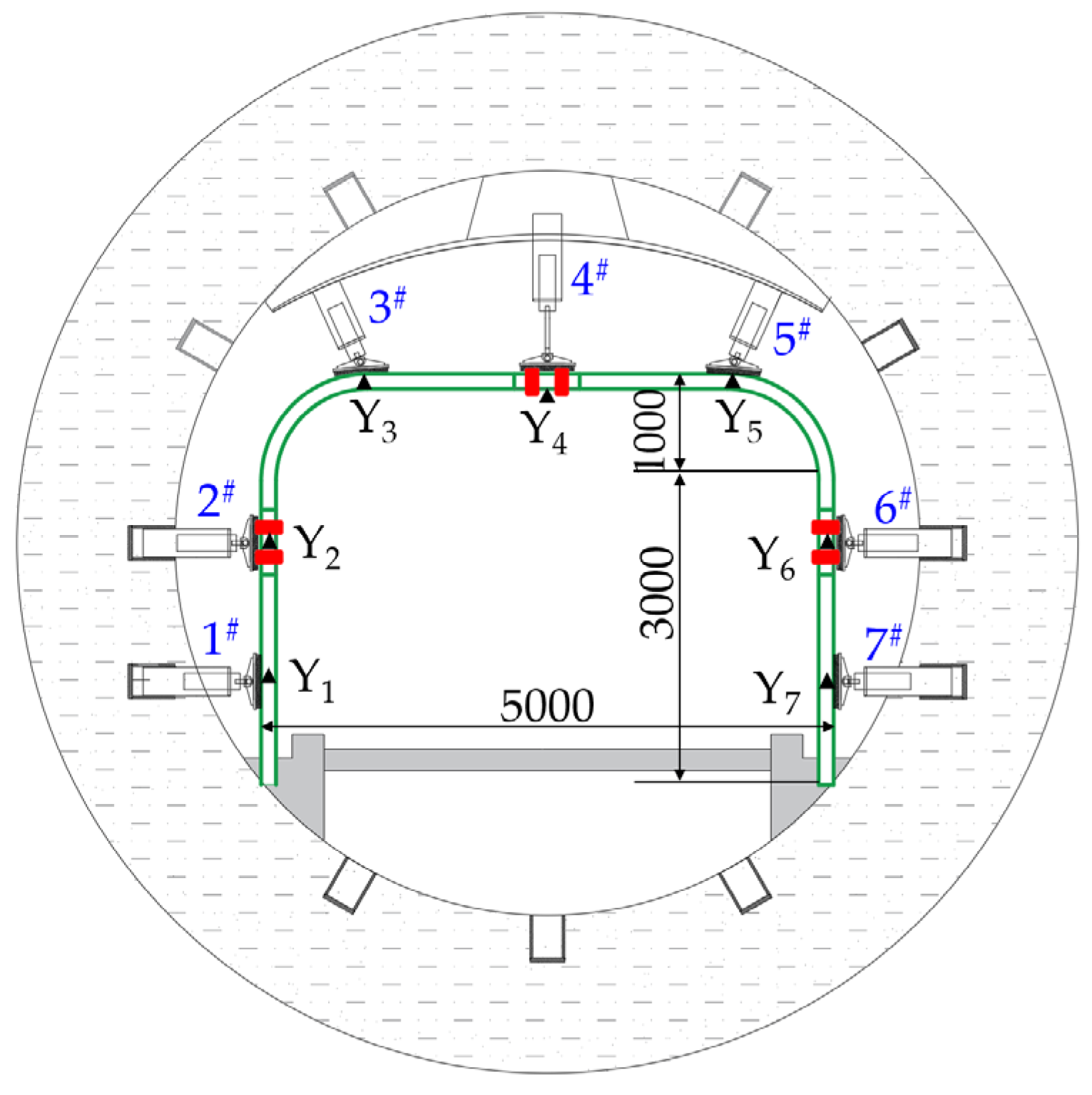
3.1.3. Monitoring Scheme
3.2. Analysis of Test Results
3.2.1. Analysis of the Deformation and Yielding Process
- Analysis of Support Deformation
- 2.
- Analysis of Node Yielding
3.2.2. Analysis of Support Bearing Capacity
4. Analysis of the Influence Mechanism on the Bearing Performance of Yielding U-Shaped Steel Support
4.1. Experimental Scheme and Model Establishment
4.2. Analysis of the Influence Mechanism on Bearing Performance
4.2.1. Influence Analysis of Load Forms
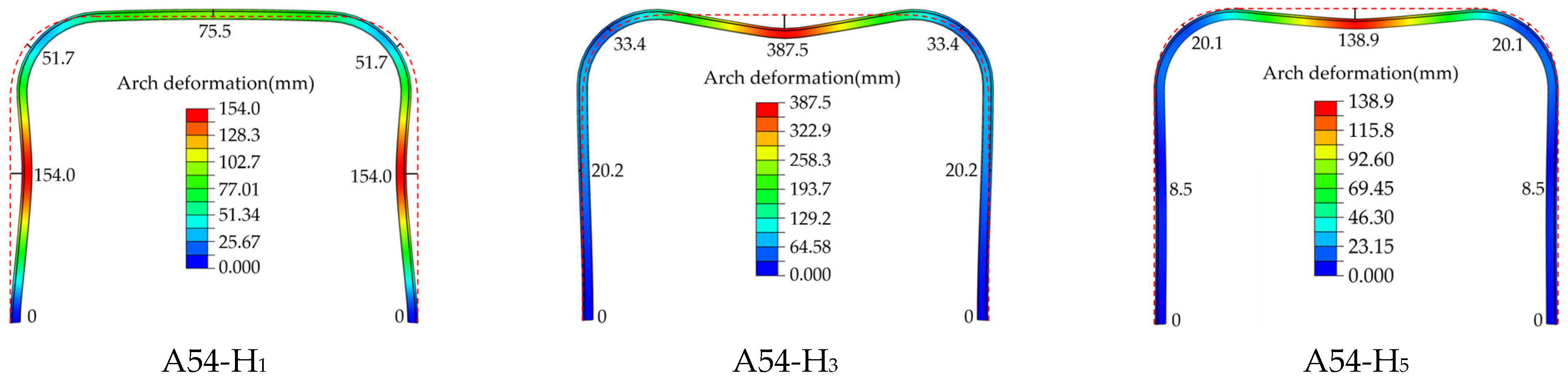
- Analysis of Support Deformation under Different Stress Modes
- 2.
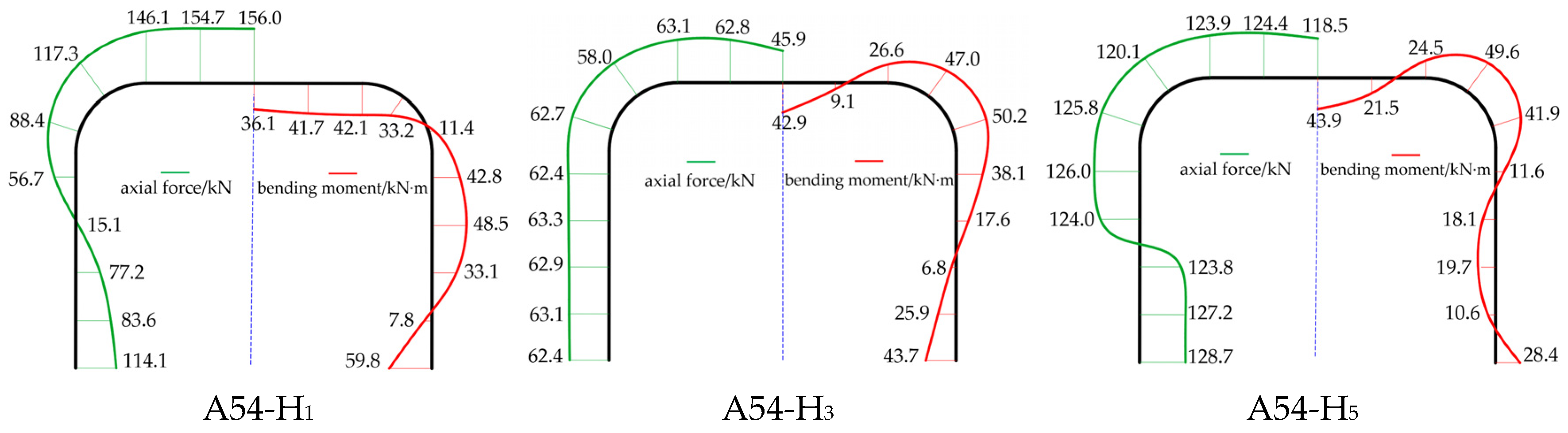
- Analysis of the Internal Forces of Support under Different Stress Modes
- 3.
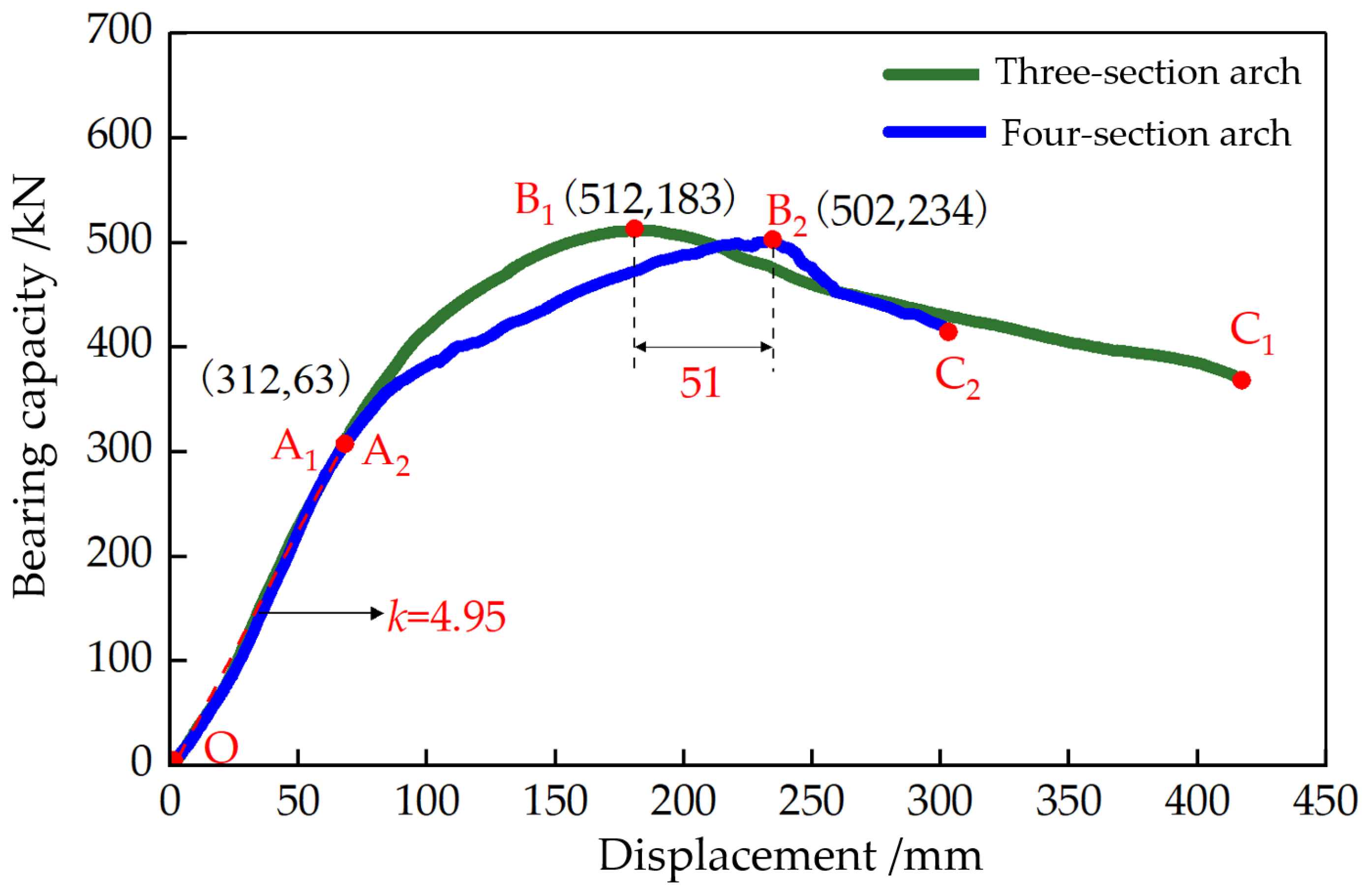
- Analysis of Bearing Capacity–Displacement
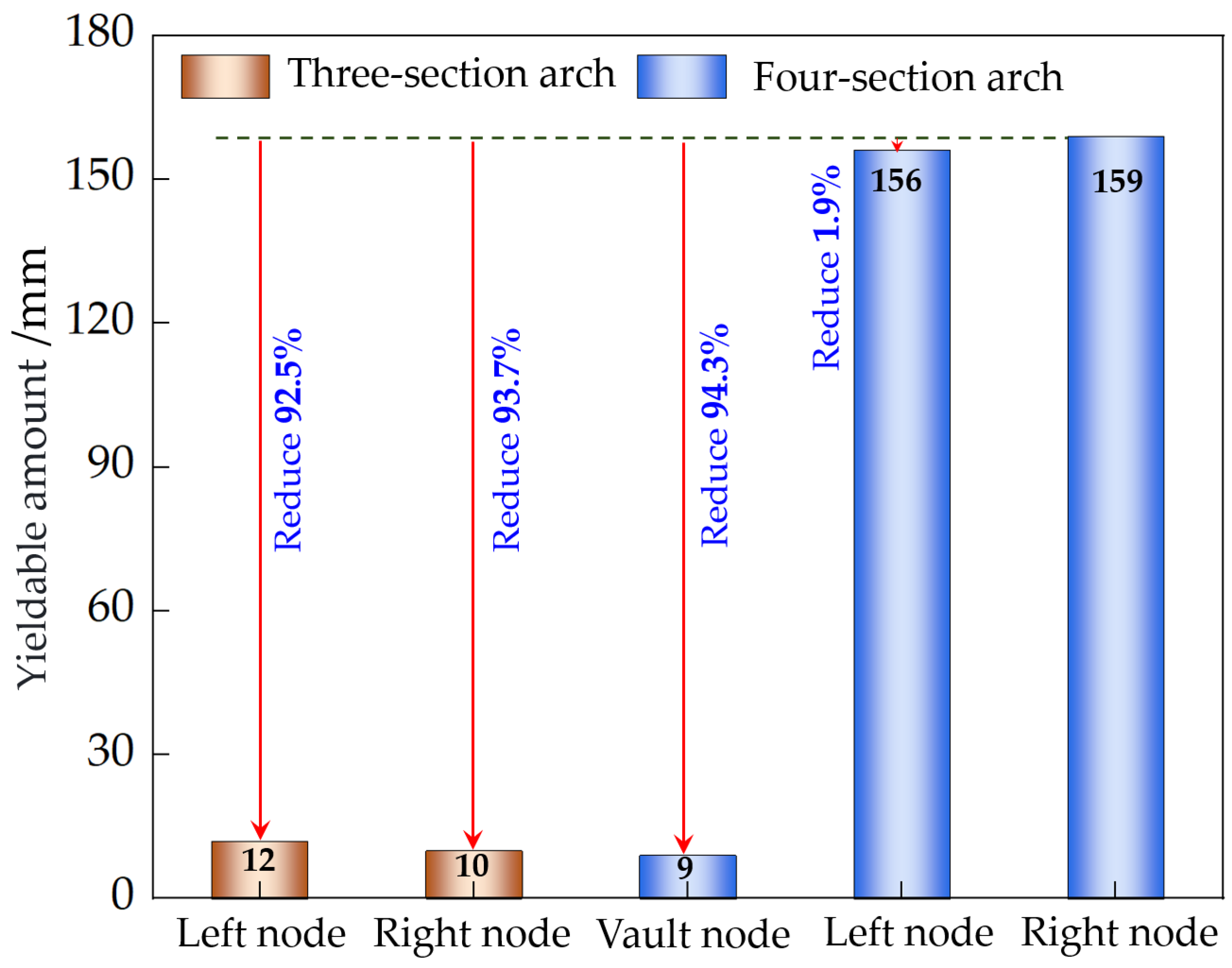
4.2.2. Analysis of the Influence of Section Forms
- Analysis of Support Deformation
- 2.
- Analysis of Support Internal Forces
- 3.
- Analysis of Bearing Capacity–Displacement
4.3. Principles of Sectional Design and Engineering Recommendations
4.3.1. Principles of Sectional Design
4.3.2. Engineering Recommendations
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, M.C.; Wang, Q. Excavation compensation method and key technology for surrounding rock control. Eng. Geol. 2022, 307, 106784. [Google Scholar] [CrossRef]
- Xie, Z.Z.; He, Z.; Xiang, Z.; Zhang, N.; Su, J.B.; Li, Y.L.; Zhang, C.H. Deformation failure characteristics and maintenance control technologies of high-stress crossing-seam roadways: A case study. Appl. Sci. 2024, 13, 4442. [Google Scholar] [CrossRef]
- Liu, C.; Li, H.M. Numerical simulation of realistic top coal caving intervals under different top coal thicknesses in longwall top coal caving working face. Sci. Rep. 2021, 11, 13254. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; He, M.C.; Yang, J.; Gao, H.K.; Jiang, B.; Yu, H.C. Study of a no-pillar mining technique with automatically formed gob-side entry retaining for longwall mining in coal mines. Int. J. Rock Mech. Min. Sci. 2018, 110, 1–8. [Google Scholar] [CrossRef]
- Wu, X.Z.; Jiang, Y.J.; Li, B. Influence of joint roughness on the shear behaviour of fully encapsulated rock bolt. Rock Mech. Rock Eng. 2018, 51, 953–959. [Google Scholar] [CrossRef]
- Huang, Y.B.; Jiang, B.; Ma, Y.K.; Wei, H.Y.; Zang, J.C.; Gao, X. Study on Asymmetric Failure and Control Measures of Lining in Deep Large Section Chamber. Energies 2021, 14, 4075. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, B.; Pan, R.; Li, S.C.; He, M.C.; Sun, H.B.; Qin, Q.; Yu, H.C.; Luan, Y.C. Failure mechanism of surrounding rock with high stress and confined concrete support system. Int. J. Rock Mech. Min. Sci. 2018, 102, 89–100. [Google Scholar] [CrossRef]
- Wang, J.; Tai, L.; Li, C.; Qu, Q.; Yu, X.; Liu, Y.; Yao, W. Research on high-strength economic support technology for soft rock roadway with roof drenching under thin bedrock irregular surface. Appl. Sci. 2024, 14, 9428. [Google Scholar] [CrossRef]
- Huang, Y.B.; Wang, Q.; Gao, H.K.; Jiang, Z.H.; Li, K.; Chen, K. Failure mechanism and construction process optimization of deep soft rock chamber group. J. China Univ. Min. Technol. 2021, 50, 69–78. [Google Scholar]
- Hafeezur, R.; Abdul, M.N.; J-joo, K.; Han-Kyu, Y. Empirical Evaluation of Rock Mass Rating and Tunneling Quality Index System for Tunnel Support Design. Appl. Sci. 2018, 8, 782. [Google Scholar] [CrossRef]
- Waclawik, P.; Kukutsch, R.; Konicek, P.; Ptacek, J.; Kajzar, V.; Nemcik, J.; Stas, L.; Soucek, K.; Vavro, M. Stress State Monitoring in the Surroundings of the Roadway Ahead of Longwall Mining. Procedia Eng. 2017, 191, 560–567. [Google Scholar] [CrossRef]
- Bednarek, Ł.; Majcherczyk, T. An analysis of rock mass characteristics which influence the choice of support. Geomech. Eng. 2020, 21, 31–377. [Google Scholar]
- Ptacek, J.; Konicek, P.; Stas, L.; Waclawik, P.; Kukutsch, R. The rotation of principal axes and changes of stress due to mine induced stresses. Can. Geotech. J. 2015, 52, 1440–1447. [Google Scholar] [CrossRef]
- Hou, C. Roadway Metal Supports; Coal Industry Press: Beijing, China, 1989; pp. 21–34. [Google Scholar]
- Xiao, F. Study on the Joint Support Mechanism of U-Shaped Steel Shrinkable Support in Weak Surrounding Rock Roadway; Southwest Jiaotong University: Chengdu, China, 2007. [Google Scholar]
- Li, X.F.; Wang, C.B.; Wang, H.L.; Diao, B. Experimental study on the bearing characteristics of U-shaped steel enclosed shrinkable steel frame. J. Zhejiang Univ. (Eng. Sci.) 2017, 51, 2355–2364. [Google Scholar]
- Xu, L.M.; Pan, Y.S.; Chen, J.Q.; Liu, K.L.; Wang, A.W. Experimental study on friction properties and optimization of U-shaped steel bracket joints. J. China Coal Soc. 2018, 43, 2992–2998. [Google Scholar]
- Xu, L.M.; Zhang, J.Z.; Guo, R.X.; Li, T.H.; Qin, Z.J.; Wang, A.W.; Sheng, J.Q.; Xiao, Y.H.; Chen, J.Q.; Liu, K.L. Analysis of U-Shaped Steel Failure Characteristics in Rock Burst Roadway and Design of Stable Structure and Constant Resistance O-Shed. Adv. Civ. Eng. 2023, 60, 9246508. [Google Scholar] [CrossRef]
- Xie, W.B.; Jing, S.G.; Wang, T.; Ren, Y.K.; Zhang, N. U-shaped steel bracket structure stability and its control technology. Chin. J. Rock Mech. Eng. 2010, 29, 3743–3748. [Google Scholar]
- Yao, Z.S. Research on improving the overall bearing capacity of U-shaped steel brackets. Mine Press. Roof Manag. 2000, 1, 41–43+89. [Google Scholar]
- Wang, Q.Z.; Liu, G.Q.; Li, N.; Ye, H.W.; Lei, T. Analysis of bearing performance and instability characteristics of U-shaped steel bracket under different load conditions. J. Min. Saf. Eng. 2023, 40, 448–457+466. [Google Scholar]
- Ma, Z.Q.; Jiang, Y.D.; Li, Y.W.; Yang, Y.M. Extremely soft coal seam roadway borehole pressure relief and U-shaped steel synergistic control. J. China Coal Soc. 2015, 40, 2279–2286. [Google Scholar]
- Jiao, Y.Y.; Song, L.; Wang, X.Z.; Amoussou, C.A. Improvement of the U-shaped steel sets for supporting the roadways in loose thick coal seam. Int. J. Rock Mech. Min. Sci. 2013, 60, 19–25. [Google Scholar] [CrossRef]
- Horyl, P.; Šňupárek, R.; Maršálek, P. Behaviour of frictional joints in steel arch yielding supports. Arch. Min. Sci. 2014, 59, 781–792. [Google Scholar] [CrossRef][Green Version]
- Jarosław, B. Tests of Friction Joints in Mining Yielding Supports Under Dynamic Load. Arch. Min. Sci. 2011, 56, 303–318. [Google Scholar]
- Bednarek, Ł.; Małkowski, P.; Niedbalski, Z.; Mucha, K. Steel Arch and Rock Bolt Support in Terms of the Gateroad Stability Maintaining behind the Longwall Face. Appl. Sci. 2024, 14, 3594. [Google Scholar] [CrossRef]
- Rotkegel, M. The conditions for proper operation of the arch-rectangular support. Arch. Min. Sci. 2019, 64, 213–222. [Google Scholar] [CrossRef]
- Wang, J. Research on the Mechanism and Application of Constant Resistance and Large Deformation Support in Deep Rock Roadway of Tangkou Coal Mine; China University of Mining and Technology (Beijing): Beijing, China, 2011. [Google Scholar]
- Jiang, B.; Xin, Z.X.; Zhang, X.F.; Deng, Y.S.; Wang, M.Z.; Li, S.D.; Ren, W.T. Mechanical properties and influence mechanism of confined concrete arches in high-stress tunnels. Int. J. Min. Sci. Technol. 2023, 33, 829–841. [Google Scholar] [CrossRef]
- Jiang, B.; Wang, M.Z.; Wang, Q.; Guo, Y.R.; Deng, Y.S.; Xu, C.J.; Yao, L.D. Theoretical study of bearing capacity calculation model for multi-segment confined concrete arch and design method in underground. J. Environ. Earth Sci. 2024, 83, 203. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Y.; Xin, Z.X.; Wei, H.Y.; Jiang, B.; Wang, M.Z.; Li, D.H.; Feng, Y.X.; Zhao, M.W. Study on mechanical properties and section design method of confined concrete arch. J. Min. Saf. Eng. 2023, 40, 243–250. [Google Scholar]
- GB/T4697-2017; Hot-Rolled Steel Sections for Support in Mine Tunnels. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, National Standardization Administration of China. China Standards Press: Beijing, China, 2017.






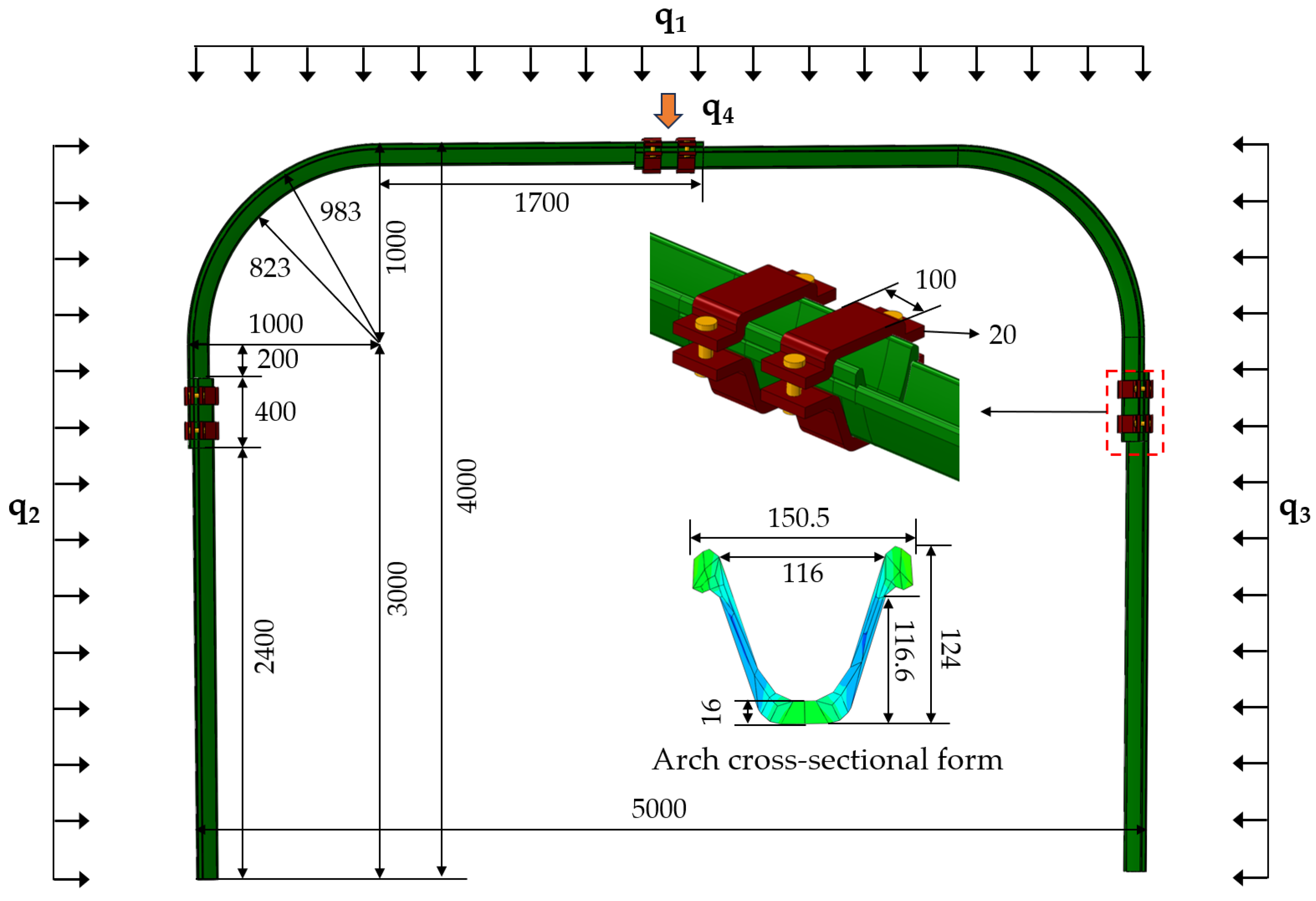

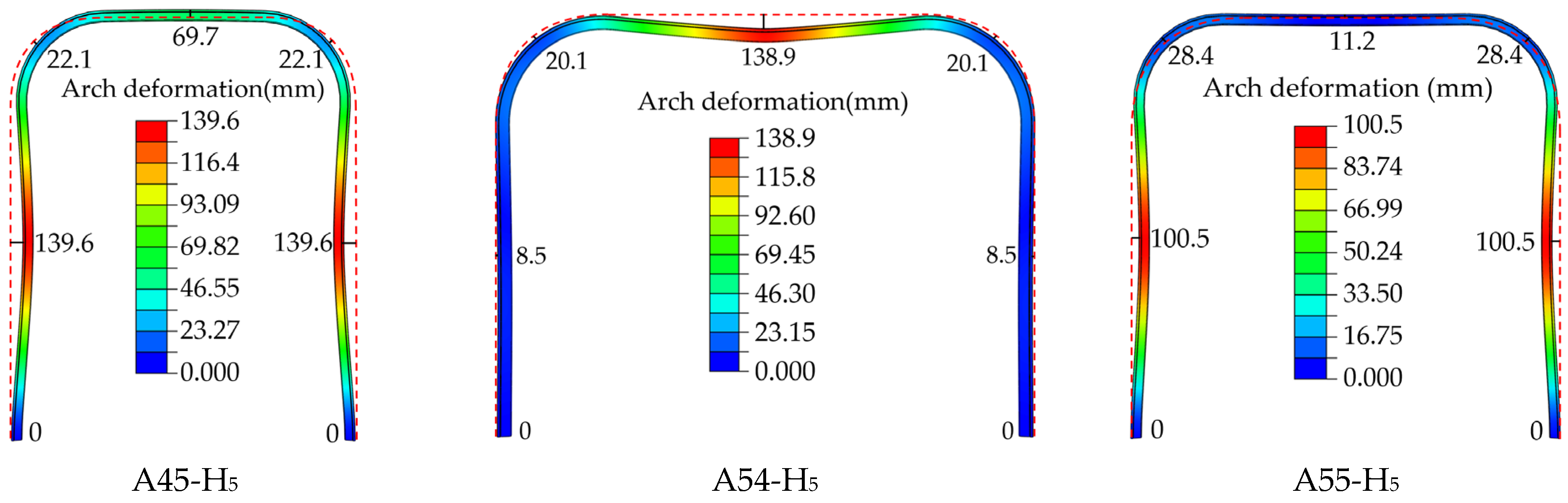
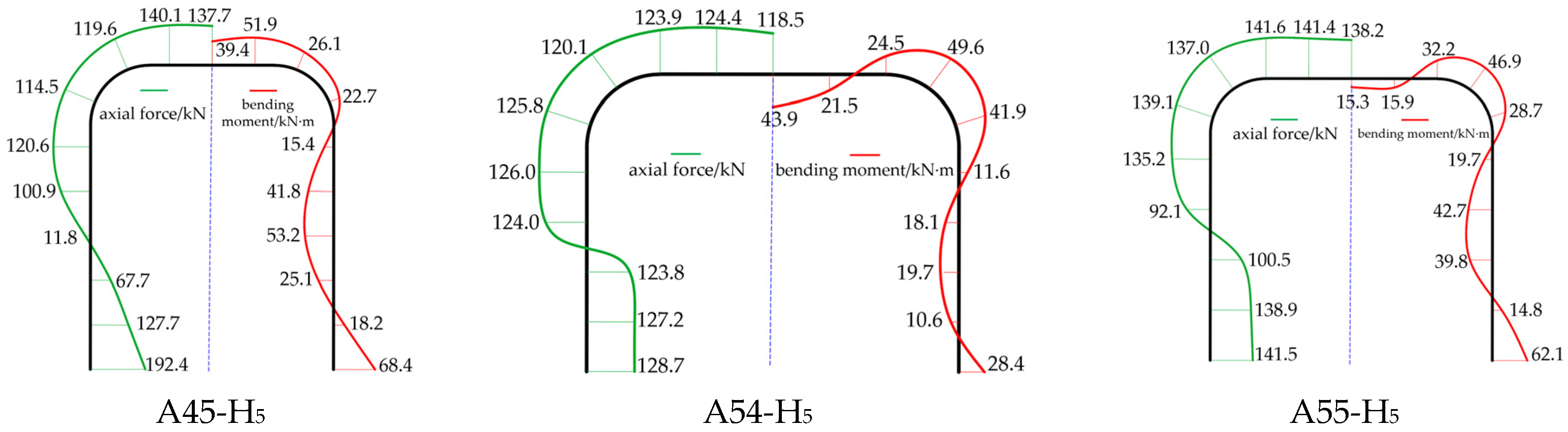


| Proposal Number | Aspect Ratio (L:H) | Load Form (q1:q2:q3/q4) |
|---|---|---|
| A54-H1 | 5:4 | 1:3:3 |
| A54-H2 | 3:1:1 | |
| A54-H3 | q4 = 20 | |
| A54-H4 | 1:3:1 | |
| A54-H5 | 1:1:1 | |
| A45-H5 | 4:5 | |
| A55-H5 | 5:5 |
| Section Area (cm2) | Theoretical Weight (kg/m) | Moment of Inertia (cm4) | Radius of Inertia (cm) | Cross-Section Modulus (cm3) | Static Moment (cm) | |||
|---|---|---|---|---|---|---|---|---|
| S | M | Ix | Iy | ix | iy | Wx | Wx | Sx |
| 37 | 29 | 612 | 771 | 4.07 | 4.57 | 106 | 102 | 212.91 |
| Material | Density (kg/m) | Elastic Modulus (GPa) | Poisson’s Ratio | Yield Strength (MPa) | Tensile Strength (MPa) |
|---|---|---|---|---|---|
| 20MnVK (Baowu Steel Group (Shanghai, China)) | 7850 | 210 | 0.3 | 390 | 570 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Zhang, Y.; Xue, H.; Tian, H.; Li, Y. The Bearing Performance and Sectional Design Method of Yielding U-Shaped Steel Support. Appl. Sci. 2025, 15, 3203. https://doi.org/10.3390/app15063203
Huang Y, Zhang Y, Xue H, Tian H, Li Y. The Bearing Performance and Sectional Design Method of Yielding U-Shaped Steel Support. Applied Sciences. 2025; 15(6):3203. https://doi.org/10.3390/app15063203
Chicago/Turabian StyleHuang, Yubing, Yacong Zhang, Haojie Xue, Hongdi Tian, and Yangyang Li. 2025. "The Bearing Performance and Sectional Design Method of Yielding U-Shaped Steel Support" Applied Sciences 15, no. 6: 3203. https://doi.org/10.3390/app15063203
APA StyleHuang, Y., Zhang, Y., Xue, H., Tian, H., & Li, Y. (2025). The Bearing Performance and Sectional Design Method of Yielding U-Shaped Steel Support. Applied Sciences, 15(6), 3203. https://doi.org/10.3390/app15063203






