Mechanical Performance and Stress Redistribution Mechanisms in Photovoltaic Support Connections: A Finite-Element-Driven Design Optimization Study
Abstract
1. Introduction
2. Methodology
- (1)
- Experimental analysis was conducted on the steel materials used in the project, and the results indicated that the section dimensions and mechanical properties of the support components largely conformed to the design requirements.
- (2)
- The load calculations in the structural design process were examined, and a comparison was made between the major load values for photovoltaic supports as specified in Chinese codes [23,24,32], American codes [19,20], and Eurocodes [21,22]. Additionally, SAP2000 was used to analyze the load-bearing capacity and deformation of the photovoltaic supports.
- (3)
- The finite element analysis (FEA) software ABAQUS (V6.14-5) was used to analyze the impact of different component connection designs on the deformation of photovoltaic supports. Innovative joint connections were proposed to optimize the structural design of the photovoltaic supports.
3. Load Analysis of Photovoltaic Support
3.1. Load Calculation
- (1)
- Weight of photovoltaic panels
- (2)
- Wind load
- (3)
- Snow load
- (4)
- The construction load was considered to be 1 kN and was applied to the most unfavorable position of the photovoltaic supports to ensure a conservative design approach.
- (5)
- According to NB/T 10115-2018, the longitudinal wind load, which acts along the longitudinal direction of the array due to longitudinal wind, must be considered. The value of the longitudinal wind load is calculated as 0.1Awh, where A represents the horizontal projection area of the photovoltaic panel and wh is the wind pressure at the height h of the photovoltaic panel.
3.2. Analysis and Results
- (1)
- Frame elements with predefined steel sections were employed to simulate the main load-bearing members, with section properties automatically calculated by the built-in section database.
- (2)
- Rigid body constraints (6-DOF coupling) were assigned between different steel components, achieved through SAP2000’s Body Constraint command with all translational and rotational degrees of freedom constrained.
- (3)
- Material properties were defined according to the strength grades of different steel components. The fixed restraints with zero displacement tolerance were used as the boundary conditions of the bottom of the concrete column.
4. Finite Element Analysis
4.1. Model Establishment
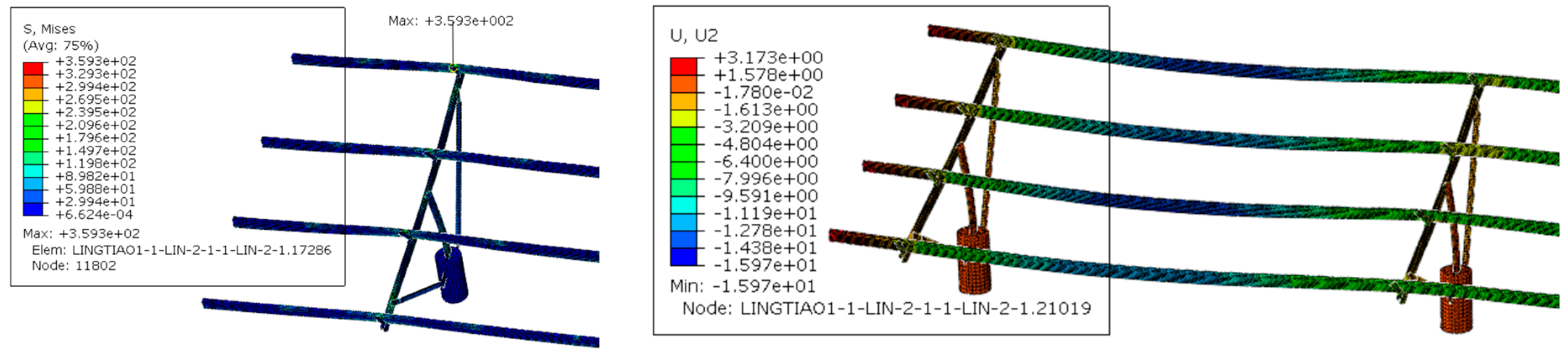
4.2. Damage Analysis
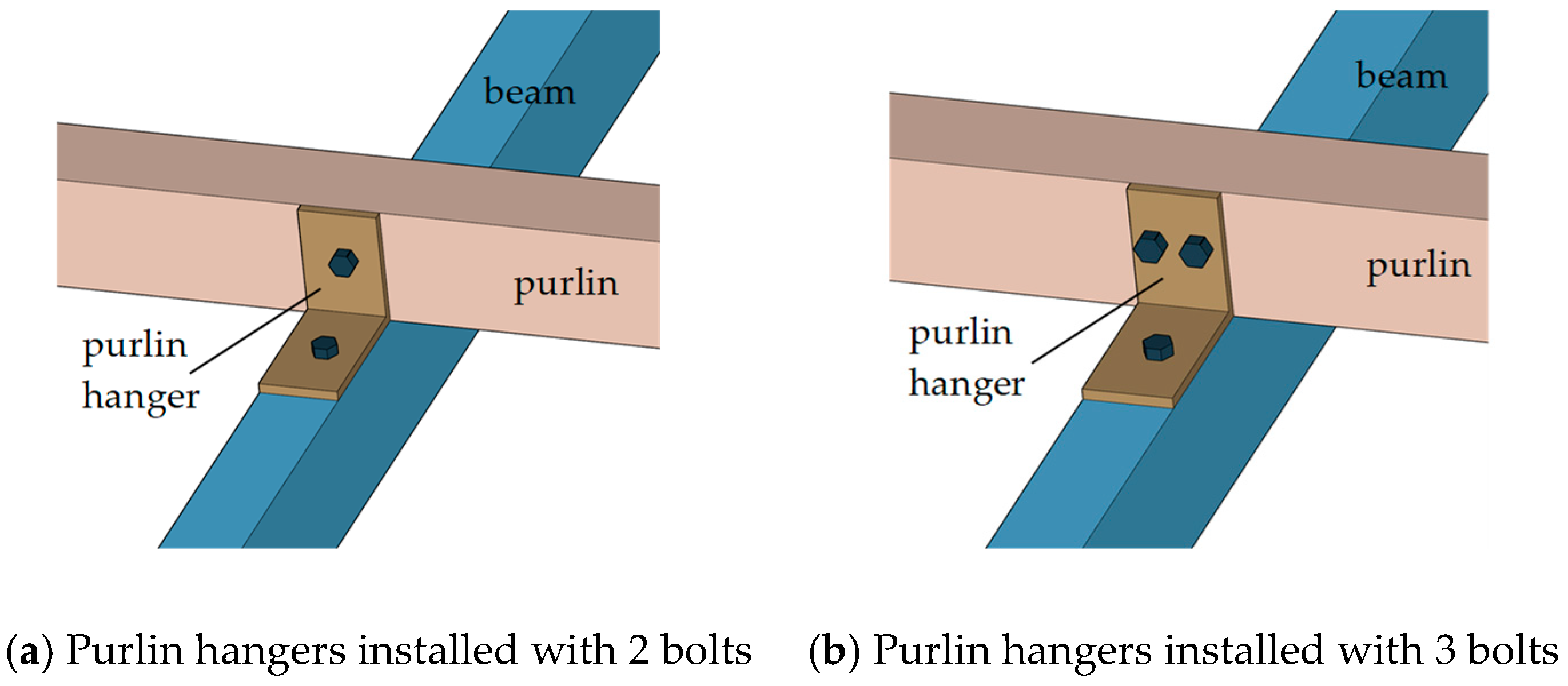
4.3. Optimization Analysis of Purlin Hangers
4.4. Optimization Analysis of Braces
5. Conclusions
- (1)
- Significant differences in wind load calculations for photovoltaic supports arise from variations in the partial coefficients and load action modes between different design codes. The maximum stress calculated using Chinese codes was less than 82% of that obtained with American codes and Eurocodes, indicating a less conservative approach.
- (2)
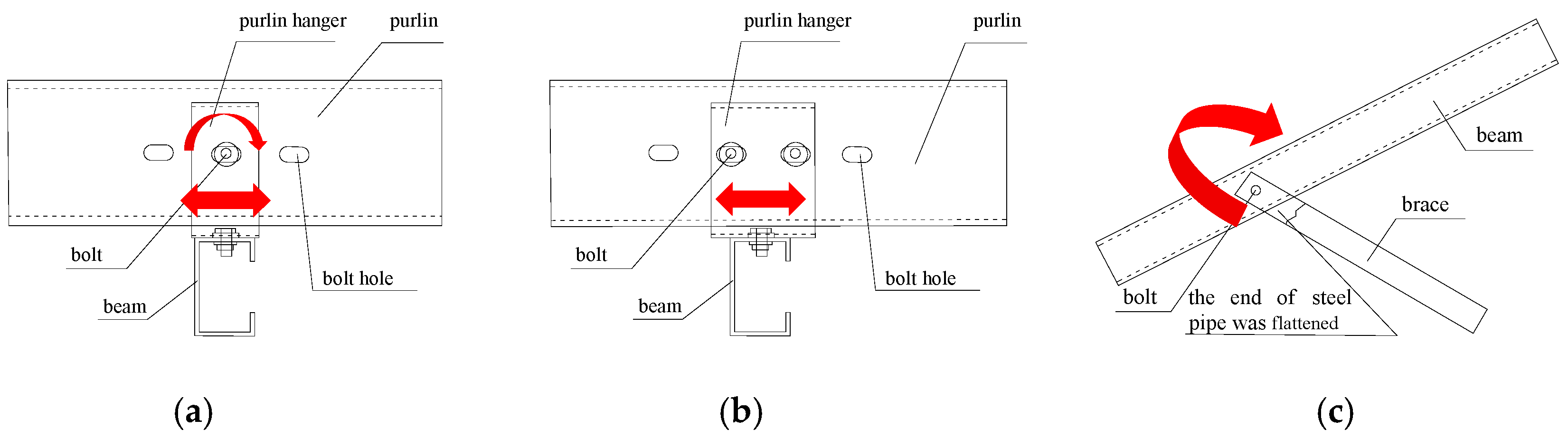
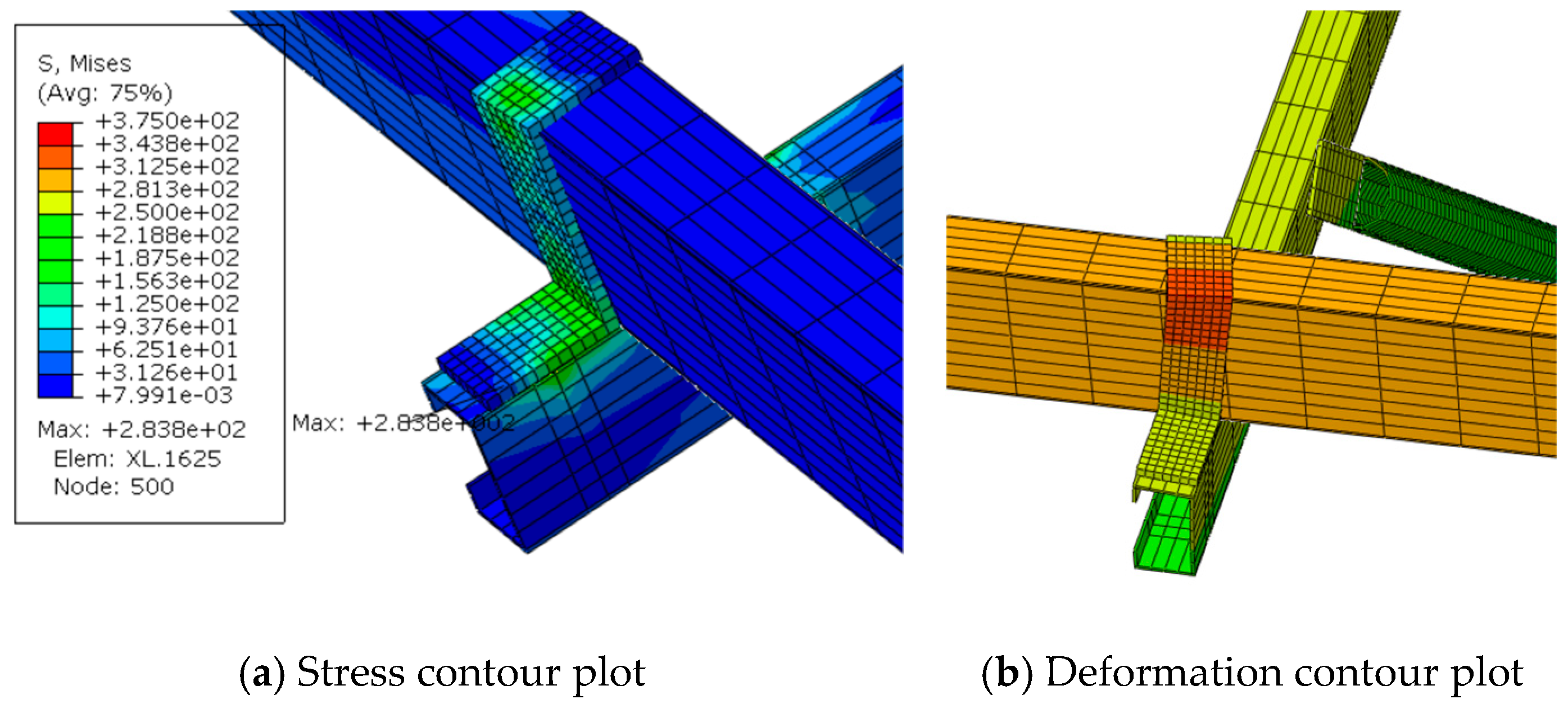
- The on-site damage observations and finite element analysis results both demonstrated that using two bolts to connect the beam and purlin at the purlin hanger position is unreliable. The node connection must be strengthened with at least three bolts recommended to secure the purlin hangers.
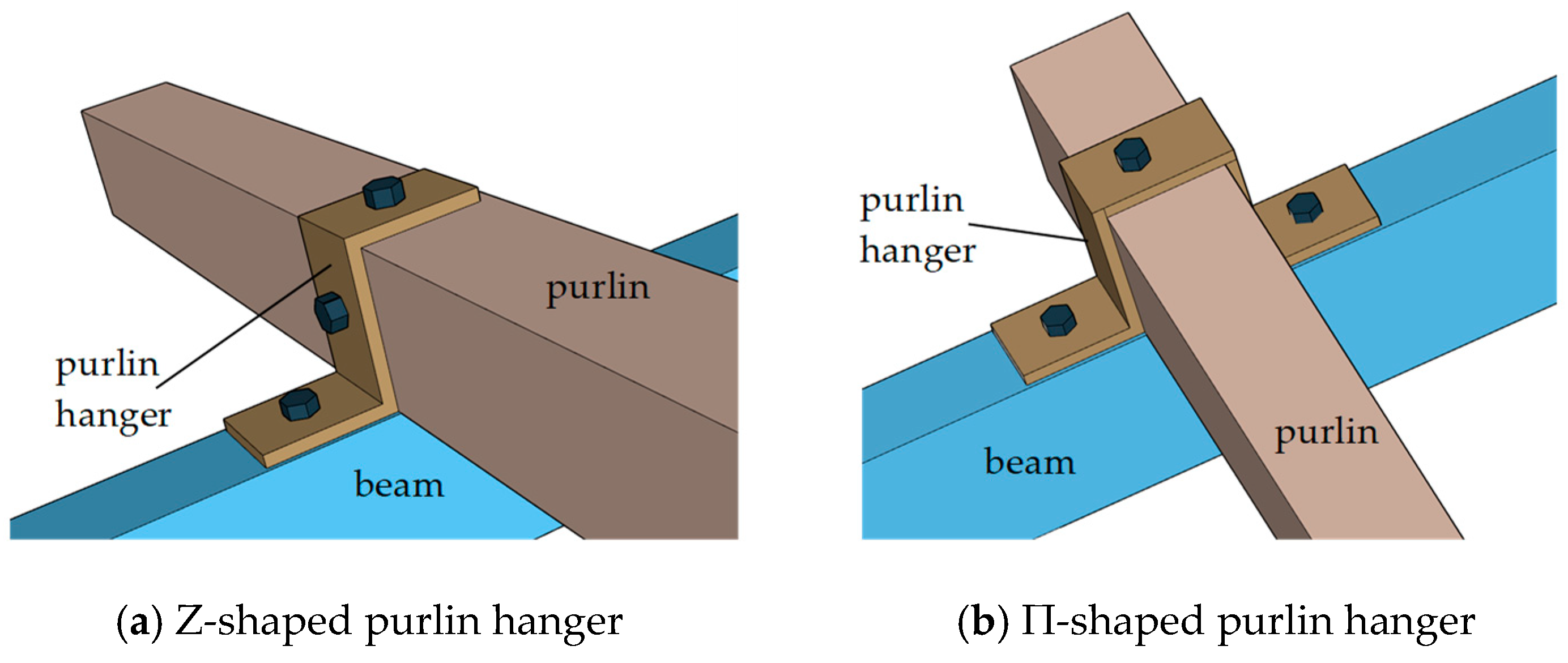
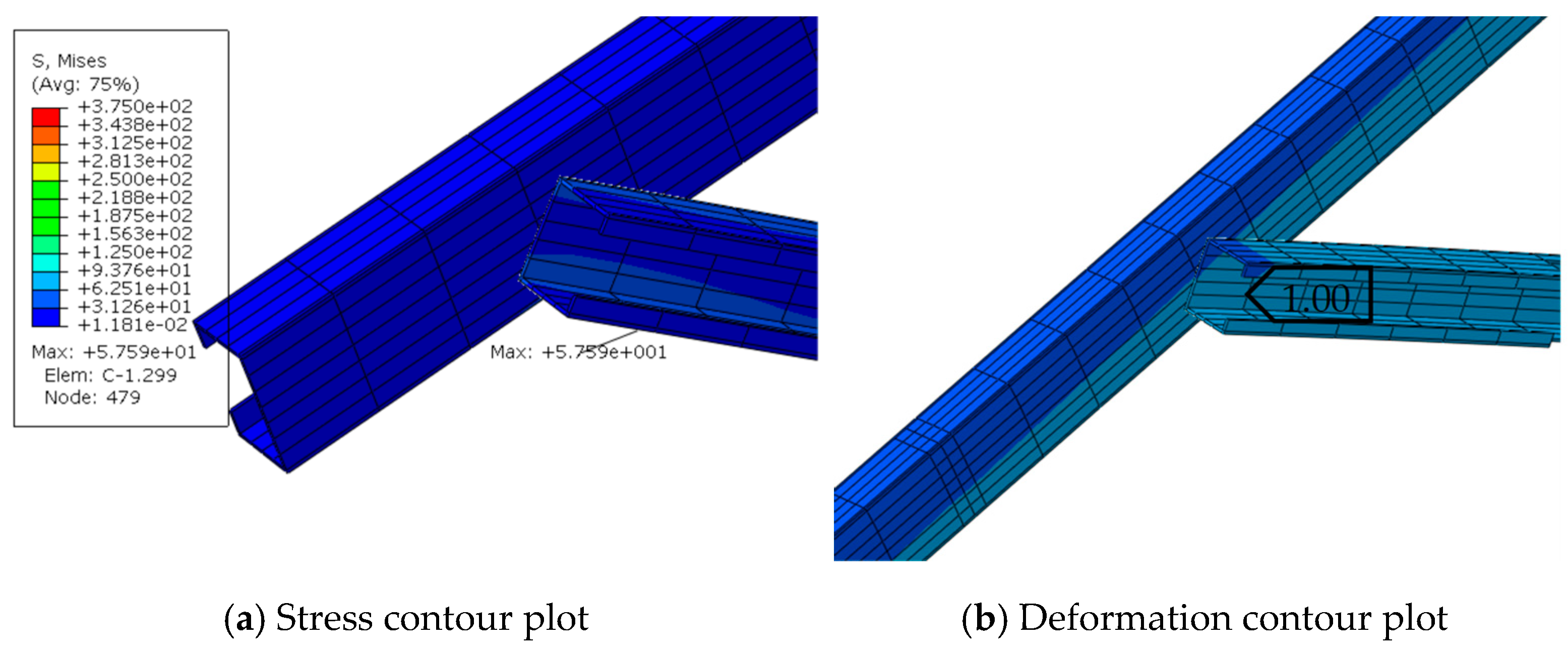
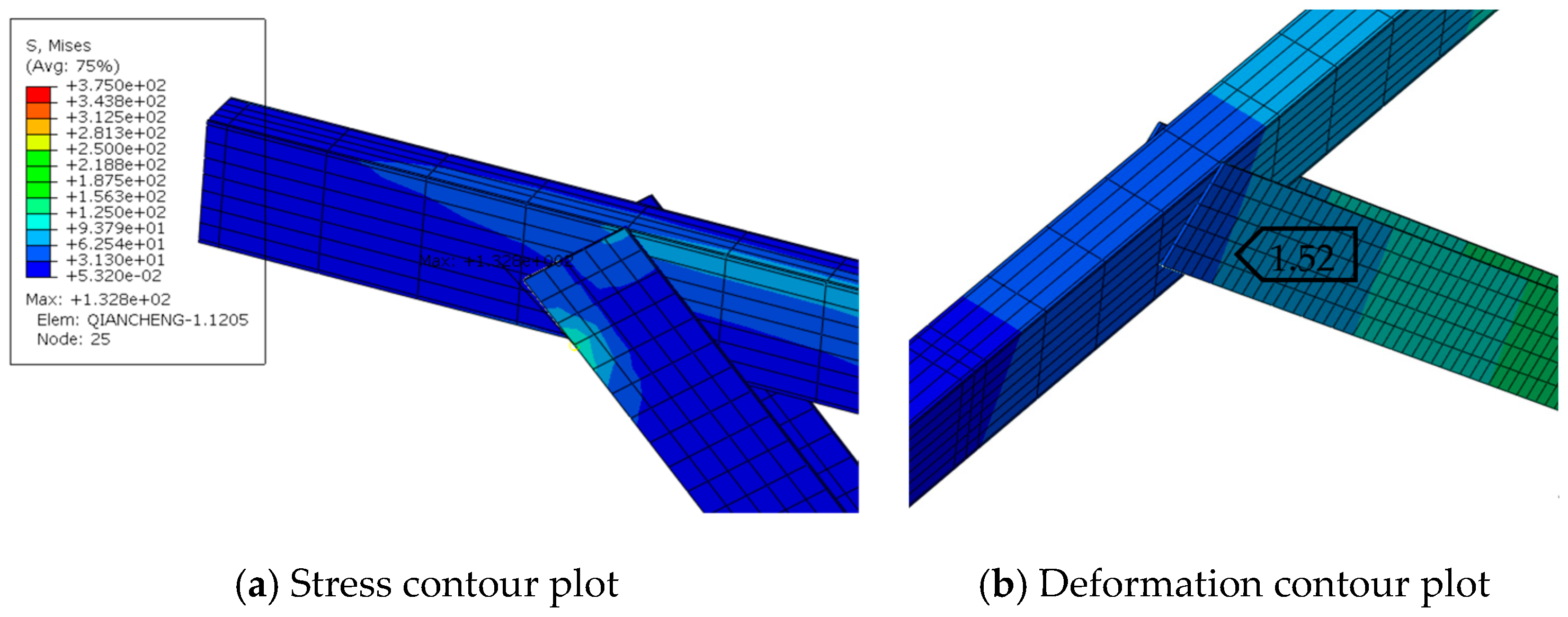
- (3)
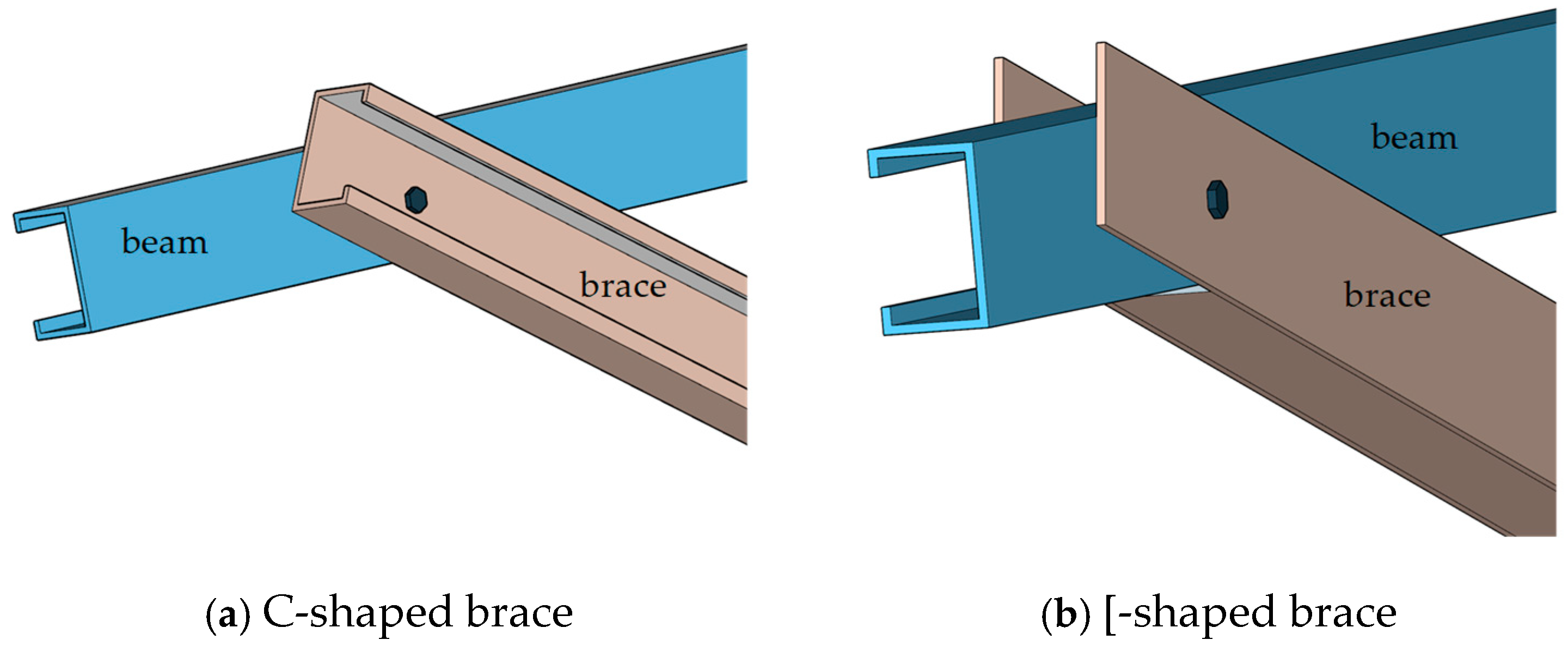
- Thin-walled circular pipes used as braces for photovoltaic supports can lead to further deformation in the joint connection due to the reduced stiffness of their flattened ends when beam deformation occurs as a result of purlin hanger displacement. Z-shaped and Π-shaped purlin brackets are recommended for connecting beams and purlin, as they reduce purlin bracket deformation while preventing excessive stress in L-shaped purlin brackets. C-shaped steel is recommended for use as the support material, offering ease of construction and enhanced safety and reliability. The newly proposed joint connection results in minimal additional steel usage.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, T.Y.; Tian, Y.J.; Zhang, Z.M.; Yu, J.Q. Study on the Coupling and Coordination Relationship Between Urban Living Environment and Economic Development. Buildings 2024, 14, 3914. [Google Scholar] [CrossRef]
- Damiri, D.J.; Legino, S.; Amboro, S. Engineering design development of 52,5 KiloWatt peak solar photovoltaic system for industrial Rooftop building. In Proceedings of the 4th Annual Applied Science and Engineering Conference, Bali, Indonesia, 24 April 2019; Volume 1402, p. 033087. [Google Scholar] [CrossRef]
- Song, D.D.; Pei, H.T.; Liu, Y.W.; Wei, H.Y.; Yang, S.F.; Hu, S.G. Review on Legislative System of Photovoltaic Industry Development in China. Energies 2022, 15, 306. [Google Scholar] [CrossRef]
- Jia, Y.T.; Alva, G.; Fang, G.Y. Development and applications of photovoltaic–thermal systems: A review. Renew. Sustain. Energy Rev. 2019, 102, 249–265. [Google Scholar] [CrossRef]
- Mostakim, K.; Hasanuzzaman, M. Global prospects, challenges and progress of photovoltaic thermal system. Sustain. Energy Technol. Assess. 2022, 53, 102426. [Google Scholar] [CrossRef]
- Eum, J.; Choi, H.J. Analysis of Power Enhancement in Facade-BIPV Systems Through Module-Level Power Optimizer: Evaluating Performance Under Shading Conditions. Buildings 2024, 14, 3850. [Google Scholar] [CrossRef]
- Ni, S.Y.; Zhu, N.; Zhang, Z.Y.; Hou, Y.Z.; Li, S.Q. The operational performance of net zero energy wooden structure building in the severe cold zone: A case study in Hailar of China. Energy Build. 2022, 257, 111788. [Google Scholar] [CrossRef]
- Weaver, J. World Has Installed 1TW of Solar Capacity, pv Magazine USA. 2022. Available online: https://www.pv-magazine.com/2022/03/15/humans-have-installed-1-terawatt-of-solar-capacity/ (accessed on 1 March 2022).
- IRENA. World Energy Transition Outlook: 1.5 °C Pathway; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2021. [Google Scholar]
- He, X.H.; Ding, H.; Jing, H.Q.; Wu, X.P.; Wu, X.J. Mechanical characteristics of a new type of cable-supported photovoltaic module system. Sol. Energy 2021, 226, 408–420. [Google Scholar] [CrossRef]
- He, X.H.; Ding, H.; Jing, H.Q.; Zhang, F.; Wu, X.P.; Wu, X.J. Wind-induced vibration and its suppression of photovoltaic modules supported by suspension cables. J. Wind. Eng. Ind. Aerodyn. 2020, 206, 104275. [Google Scholar] [CrossRef]
- Wang, X.X.; Ji, G.J.; Gu, H.; Lv, S.S.; Ni, H.J.; Wang, P.; Chen, K.; Meng, Y. Research and Design of Fixed Photovoltaic Support Structure Based on SAP2000. In Proceedings of the 2nd International Conference on Mechanical, Aeronautical and Automotive Engineering, Singapore, 24–26 February 2018; EDP Sciences: Les Ulis, France, 2018; Volume 166, p. 03002. [Google Scholar] [CrossRef][Green Version]
- Zhang, C.X.; Shen, C.; Wei, S.; Wang, Y.; Lv, G.Q.; Sun, C. A Review on Recent Development of Cooling Technologies for Photovoltaic Modules. J. Therm. Sci. 2020, 29, 1410–1430. [Google Scholar] [CrossRef]
- Giorges, A.G.; Amador, G.J.; Goodman, J. Numerical Study of Wind Loads on Residential Roof-Mounted Solar Photovoltaic Arrays. In Proceedings of the ASME 2014 International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume V06BT07A040. [Google Scholar] [CrossRef]
- Shi, M.; Lu, X.; Jiang, H.Y.; Mu, Q.; Chen, S. Opportunity of rooftop solar photovoltaic as a cost-effective and environment-friendly power source in megacities. iScience 2022, 25, 104890. [Google Scholar] [CrossRef]
- Meglio, E.; Formisano, A. Seismic Design and Analysis of a Cold-Formed Steel Exoskeleton for the Retrofit of an RC Multi-Story Residential Building. Appl. Sci. 2024, 14, 8674. [Google Scholar] [CrossRef]
- Jiang, S.X.; Wang, Y.Z.; Yan, X. Analysis of the differences in the structural design of PV supports in Chinese code, American code and European code. Build. Struct. 2020, 50, 699–703. [Google Scholar] [CrossRef]
- Li, M.G.; Tan, Y.J.; Liu, Y.L. Comparative study of ASCE7-10 and Chinese standards in photovoltaic (PV) mounting system design. Eng. J. Wuhan Univ. 2022, 55, 90–94. [Google Scholar]
- ASCE/SEI7-10; Minimum Design Loads for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2010.
- AISI-S100-16; North American Specification for the Design of Cold-Formed Steel Structural Members. American Iron and Steel Institute: Washington, DC, USA, 2016.
- BS EN 1991-1-4; Eurocode1: Actions on Structures, Part1–4 General Actions, Wind Actions. European Committee for Standardization: Brussels, Belgium, 2005.
- BS EN 1993-1-1; Eurocode 3: Design of Steel Structures-Part 1-1. European Committee for Standardization: Brussels, Belgium, 2005.
- GB 50009-2012; Load Code for the Design of Building Structures. Ministry of Housing and Urban-Rural Construction of the People’s Republic of China: Beijing, China, 2012.
- GB 50017-2017; Standard for Design of Steel Structures. Ministry of Housing and Urban-Rural Construction of the People’s Republic of China: Beijing, China, 2017.
- Wittwer, A.R.; Podestá, J.M.; Castro, H.J.; Mroginski, J.L. Wind loading and its effects on photovoltaic modules: An experimental–Computational study to assess the stress on structures. Sol. Energy 2022, 240, 315–328. [Google Scholar] [CrossRef]
- Ferreira, L.G.G.B.; Alves, A.J.; Domingos, J.L. Analysis of Wind Loading on Photovoltaic Panels Mounting Brackets. In Proceedings of the International Conference on Environment and Electrical Engineering, Palermo, Italy, 12–15 June 2018. [Google Scholar] [CrossRef]
- Qu, Z.; Jiang, C.; Wang, Y.X.; Wang, R.; Zhao, Y.; Yang, S.C. China’s Photovoltaic Development and Its Spillover Effects on Carbon Footprint at Cross-Regional Scale: Insights from the Largest Photovoltaic Industry in Northwest Arid Area. Sustainability 2024, 16, 9922. [Google Scholar] [CrossRef]
- Ding, H.; He, X.H.; Jing, H.Q.; Wu, X.P.; Wu, X.J. Design Method of Primary Structures of a Cost-Effective Cable-Supported Photovoltaic System. Appl. Sci. 2023, 13, 2968. [Google Scholar] [CrossRef]
- Huang, W.S.; Lu, H.Q.; Peng, X.F. Research on optimized design of structure of photovoltaic supporting support. Eng. J. Wuhan Univ. 2018, 51, 72–76. [Google Scholar]
- Udell, M.; Toole, O. Optimal Design of Efficient Rooftop Photovoltaic Arrays. INFORMS J. Appl. Anal. 2019, 49, 281–294. [Google Scholar] [CrossRef]
- Tan, V.; Deng, R.; Egan, R. Solar photovoltaic waste and resource potential projections in Australia, 2022–2050. Resour. Conserv. Recycl. 2024, 202, 107316. [Google Scholar] [CrossRef]
- NB/T 10115-2018; Code for Design of Photovoltaic Modules Support Structures. National Energy Administration: Beijing, China, 2018.
- Aly, A.M. On the evaluation of wind loads on solar panels: The scale issue. Sol. Energy 2016, 135, 423–434. [Google Scholar] [CrossRef]
- Tamura, Y.; Chen, B.; Wu, Y.; Su, N.; Yang, Q.S. Classification of equivalent static wind loads: Comparisons and applications. Reliab. Eng. Syst. 2024, 251, 110403. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Construction of the People’s Republic of China: Beijing, China, 2011.
- Nadeem, G.; Safiee, N.A.; Bakar, N.A.; Karim, I.A.; Nasir, N.A.M. Finite Element Analysis of the Stability of a Sinusoidal Web in Steel and Composite Steel-Concrete Girders. Appl. Sci. 2021, 11, 9277. [Google Scholar] [CrossRef]
- Śledziewski, K.; Górecki, M. Finite element analysis of the stability of a sinusoidal web in steel and composite steel-concrete girders. Materials 2020, 13, 1041. [Google Scholar] [CrossRef] [PubMed]


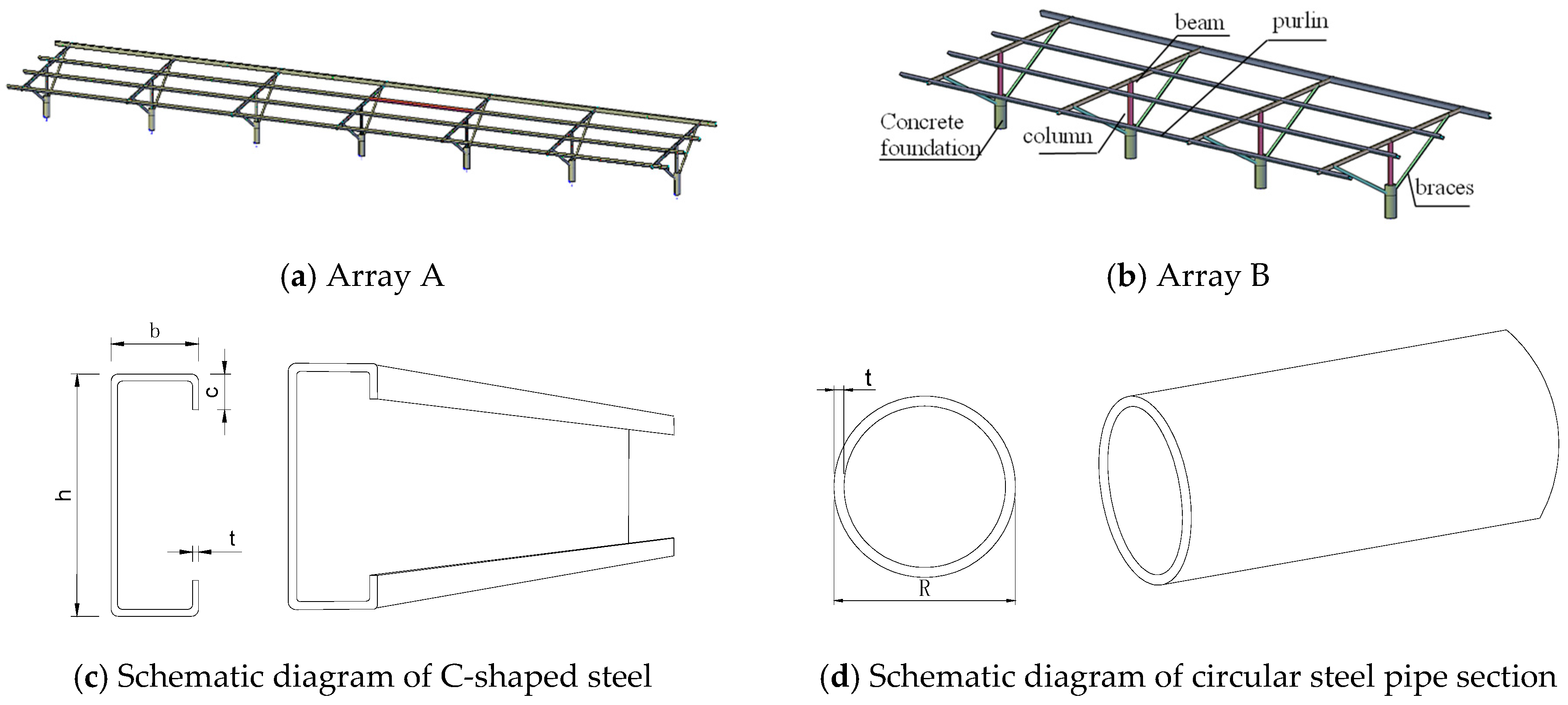



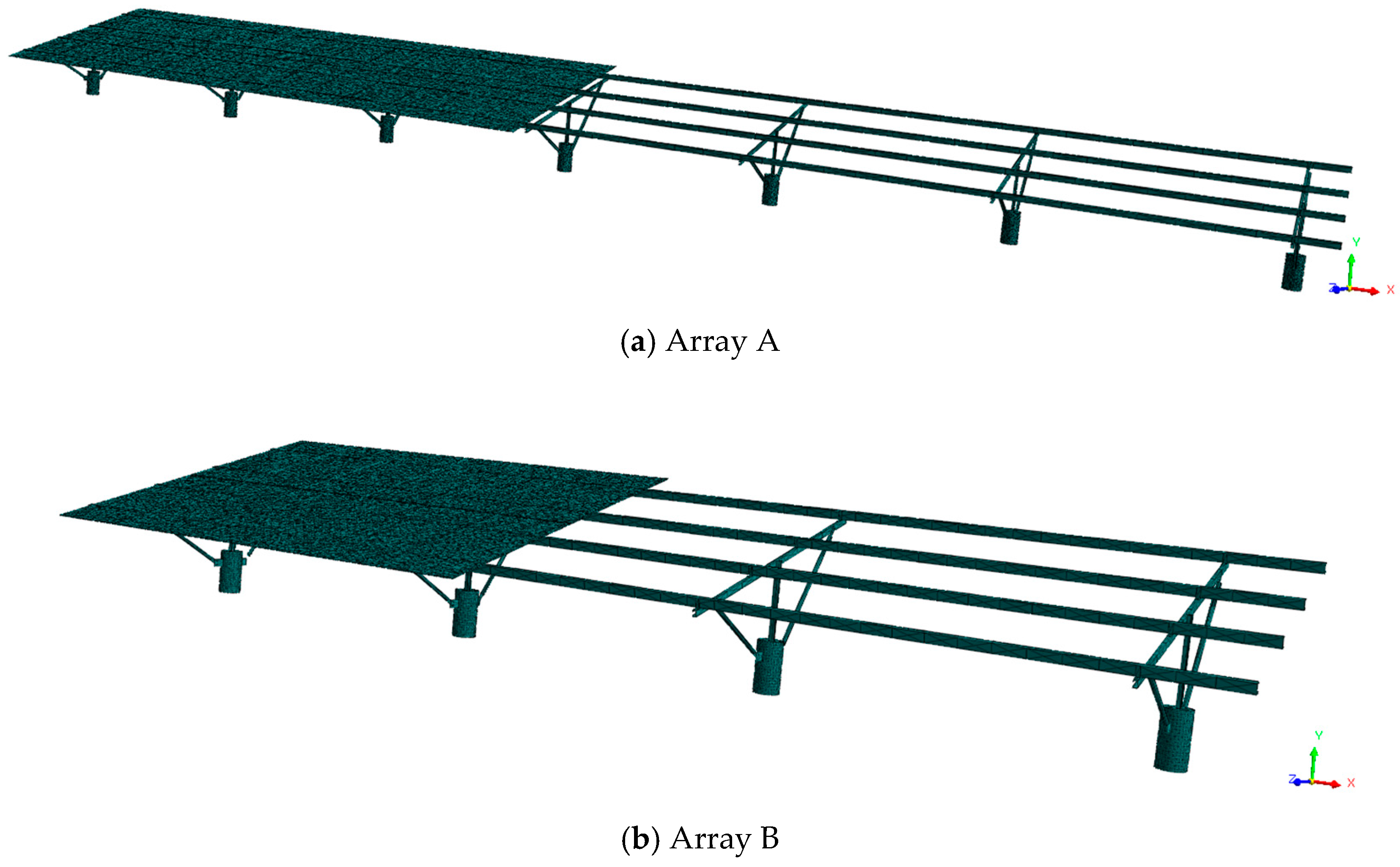


| Chinese Code | American Code | Eurocode |
|---|---|---|
 | 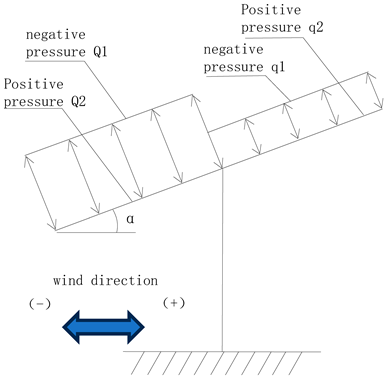 | 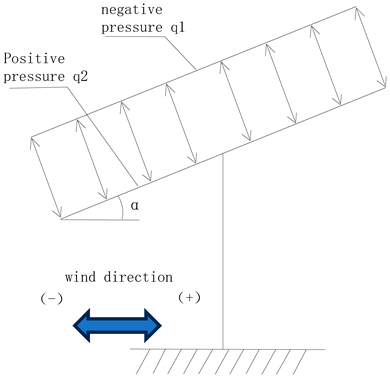 |
| q1 = −0.29 kN/m2 | (Case A: Q1 = −0.36 kN/m2, q1 = −0.52 kN/m2) (Case A: Q2 = 0.52 kN/m2, q2 = 0.64 kN/m2) | q1 = −0.61 kN/m2 |
| q2 = 0.24 kN/m2 | (Case B: Q1 = −0.76 kN/m2, q1 = 0 kN/m2) (Case B: Q2 = 0.72 kN/m2, q2 = 0.24 kN/m2) | q2 = 0.43 kN/m2 |
| Code | Reference Snow Pressure | Exposure Coefficient | Thermal Factor | Shape Factor | Characteristic Value |
|---|---|---|---|---|---|
| Chinese code | 0.4 kN/m2 | / | / | 1.0 | 0.40 kN/m2 |
| American code | 0.4 kN/m2 | 0.8 | 1.2 | 1.0 | 0.27 kN/m2 |
| European code | 0.4 kN/m2 | 1.0 | 1.0 | 0.8 | 0.32 kN/m2 |
| Model | Chinese Codes | American Codes | Eurocodes | |||
|---|---|---|---|---|---|---|
| Stress (MPa) | Deformation (mm) | Stress (MPa) | Deformation (mm) | Stress (MPa) | Deformation (mm) | |
| Array A | 329.3 | −11.53 | 401.5 | −12.75 | 421.6 | −13.29 |
| Array B | 275.1 | −7.82 | 348.2 | −8.54 | 382.5 | −9.28 |
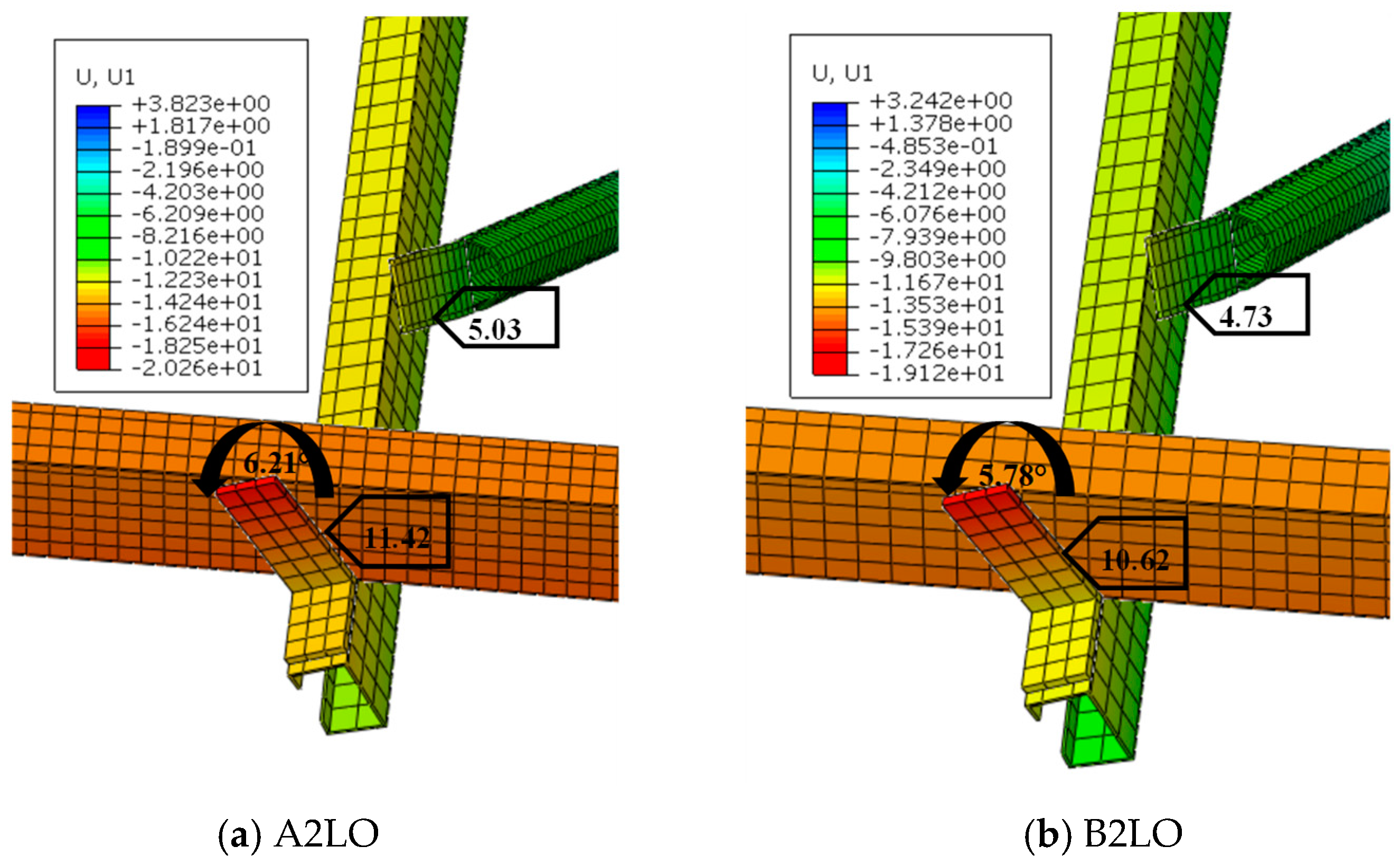
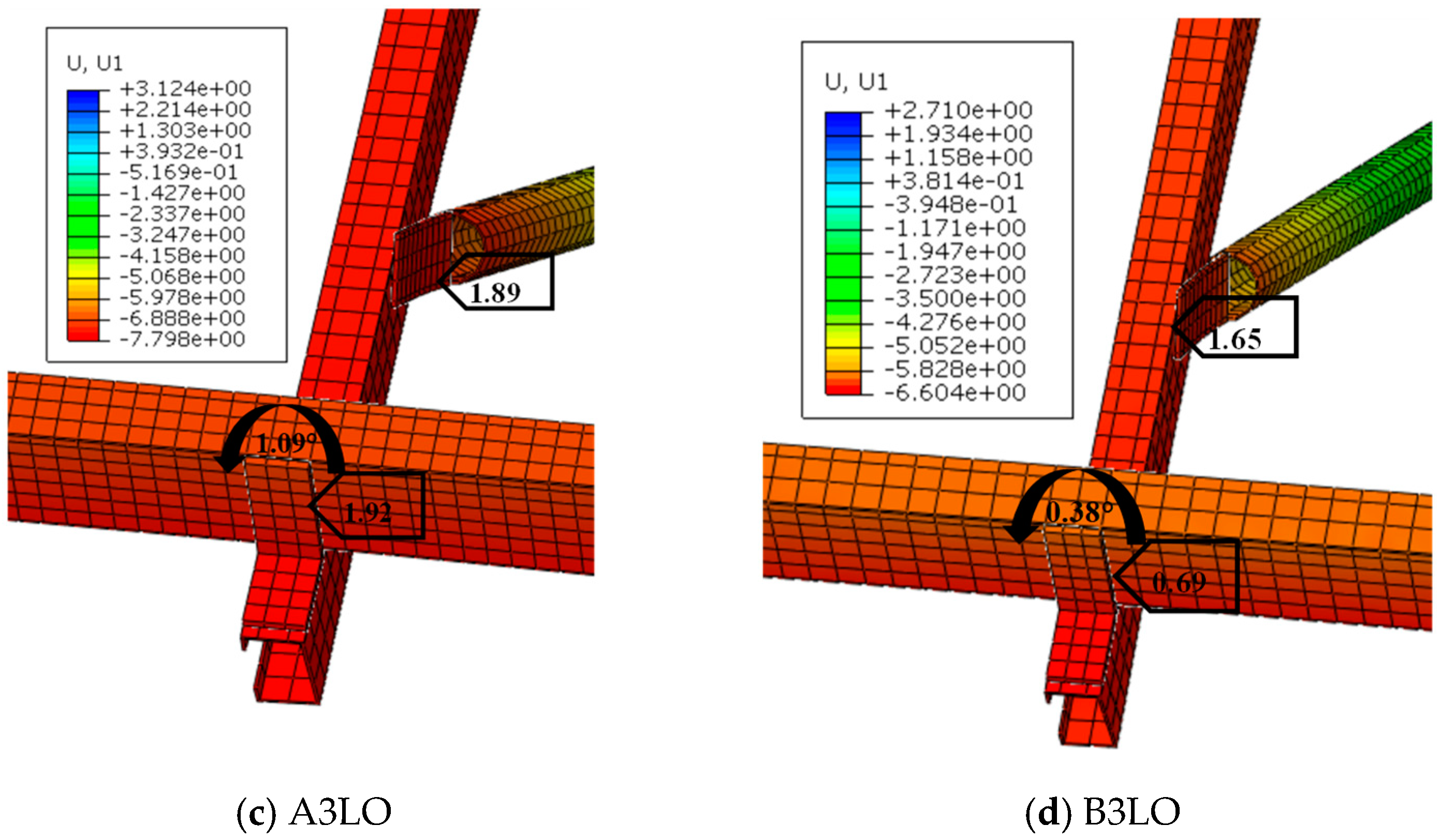
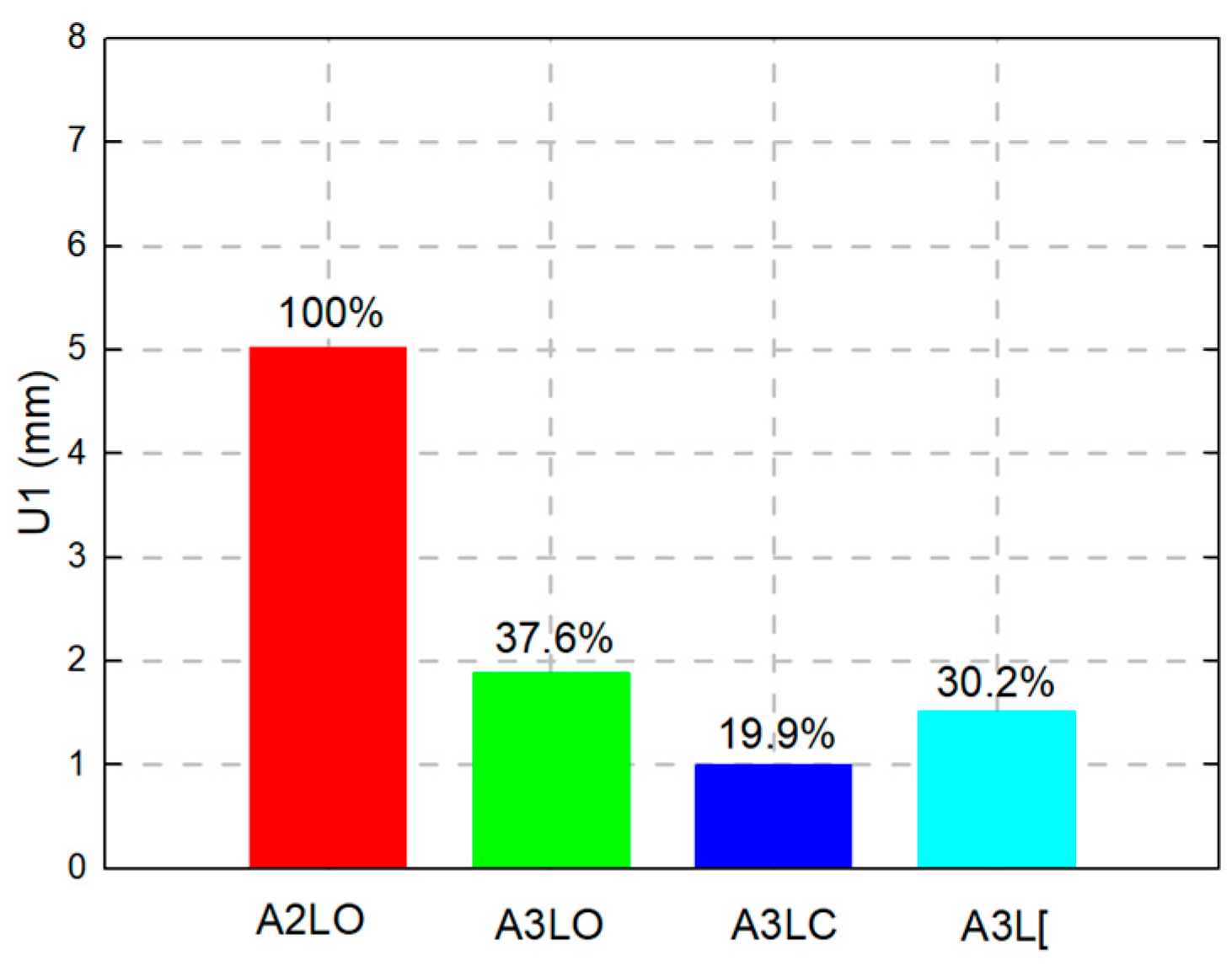
| Model | Stress (MPa) | Ratio of Stress | U1 (mm) | Ratio of U1 |
|---|---|---|---|---|
| A2LO | 359.4 | 1 | 11.42 | 1 |
| A3LO | 351.0 | 0.98 | 1.92 | 0.17 |
| A3ZO | 283.8 | 0.79 | 1.71 | 0.15 |
| A3ΠO | 258.8 | 0.72 | 1.03 | 0.09 |
| Type of Purlin Hanger | Steel Consumption of One Purlin Hanger | Ratio of One Purlin Hanger | Steel Consumption of Array A | Ratio of Array A |
|---|---|---|---|---|
| L-shaped | 0.324 kg | 1 | 482.372 kg | 1 |
| Z-shaped | 0.418 kg | 1.29 | 485.004 kg | 1.005 |
| Π-shaped | 0.742 kg | 2.29 | 494.076 kg | 1.024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Wang, R.; Liu, J.; Huang, X. Mechanical Performance and Stress Redistribution Mechanisms in Photovoltaic Support Connections: A Finite-Element-Driven Design Optimization Study. Appl. Sci. 2025, 15, 3174. https://doi.org/10.3390/app15063174
Zhang D, Wang R, Liu J, Huang X. Mechanical Performance and Stress Redistribution Mechanisms in Photovoltaic Support Connections: A Finite-Element-Driven Design Optimization Study. Applied Sciences. 2025; 15(6):3174. https://doi.org/10.3390/app15063174
Chicago/Turabian StyleZhang, Deli, Ruwei Wang, Juan Liu, and Xuanming Huang. 2025. "Mechanical Performance and Stress Redistribution Mechanisms in Photovoltaic Support Connections: A Finite-Element-Driven Design Optimization Study" Applied Sciences 15, no. 6: 3174. https://doi.org/10.3390/app15063174
APA StyleZhang, D., Wang, R., Liu, J., & Huang, X. (2025). Mechanical Performance and Stress Redistribution Mechanisms in Photovoltaic Support Connections: A Finite-Element-Driven Design Optimization Study. Applied Sciences, 15(6), 3174. https://doi.org/10.3390/app15063174






