Abstract
To address the limitations of traditional concrete barriers in practical applications, this study proposes a novel semi-assembled concrete barrier utilizing ultra high performance concrete (UHPC) as the barrier shell material. The thin shell of the barrier is prefabricated using UHPC and filled with normal concrete (NC) to form a protective structure. Finite element software is employed to simulate collisions between three models and the barrier, and the barrier safety is preliminarily assessed according to the Standard for Safety Performance Evaluation of Highway Barriers. A full-scale vehicle collision test validated the model, and an analysis was conducted. The results demonstrate that the established model exhibits a high accuracy. The peak value of the 25 ms collision force in this simulation can be used as the basis for static load design. None of the three vehicles exhibited overriding or riding phenomena nor did they deviate from their guide frames, and following collisions with three different vehicles, no overall damage was observed on the semi-assembled barrier. Occupant impact velocity (OIV) remained below 12 m/s, while occupant ride-down acceleration (ORA) stayed under 200 m/s2. The barrier meets SB protection-level requirements; thus, the findings can offer theoretical support for promoting the widespread adoption of this new type of barrier.
1. Introduction
As a critical component of road safety facilities, barriers contribute to preventing vehicles from crossing central dividers or breaching roadside barriers, thereby mitigating potential harm to occupants. Among the various types of barriers, concrete barriers stand out for their robust protective abilities and cost-effectiveness, which effectively reduce casualties and property damage. Generally deployed along highways, concrete barriers serve as essential protective structures, which effectively contain vehicles within road boundaries following collisions.
Numerous scholars have extensively researched the optimization of structural designs and materials for concrete barriers to improve their protective performance [1,2,3]. Yang et al. [4] proposed a movable concrete barrier, surpassing traditional concrete and W-beam barriers, thereby effectively reducing occupant injuries. Hasan Jasim Mohammed and Zain [5] proposed the new concrete barrier, comprising expanded polystyrene concrete as the outer material and plain concrete as the inner material. Their verification met the collision requirements for concrete barriers through experiments and simulations. Song et al. [6,7] embedded foam concrete and recycled foam concrete as buffer materials in reinforced concrete barriers. This demonstrated buffer capacity in simulations and numerical calculations.
The investigations discussed herein primarily utilized ordinary reinforced concrete as the main barrier material. These barriers are typically installed using cast-in-place or prefabrication processes. Cast-in-place concrete barriers involve the cumbersome process of installing scaffolding, formwork, steel bars, and on-site pouring, which leads to slow construction progress and quality challenges. Prefabricated concrete barriers have been developed to address these shortcomings. This can significantly improve construction efficiency and material quality [8,9]. However, the weight of prefabricated barriers poses transportation and assembly challenges, particularly for longer sections such as the 4 m SB-level barrier, which can weigh up to 4 tons. This results in increased costs and on-site assembly difficulty. Moreover, ordinary reinforced concrete lacks sufficient resistance to salt corrosion, freeze–thaw cycles, and carbonation, which leads to reduced durability, particularly in coastal areas and snowy regions [10]. Additionally, the higher repair costs of concrete barriers further compound these challenges. Therefore, developing new semi-assembled concrete barrier products with extended lifespans and simplified installation processes is imperative.
In 1994, de Larrard and Sedran [11] proposed the groundbreaking concept of ultra-high-performance concrete (UHPC). He achieved this by utilizing a low water–binder ratio of 0.14, resulting in a compressive strength of 236 MPa after steam curing for 4 d at 90 °C. UHPC has garnered widespread attention owing to its exceptionally high mechanical properties [12,13,14], extremely low porosity [15,16], remarkable durability [17,18,19,20], and superior impact resistance [21], which far exceed those of normal concrete. It thereby exhibits profound application prospects in infrastructure (bridge, municipal, power, water) engineering applications, construction applications, structural repairs and strengthening et al. [22,23,24].
Based on the aforementioned research, it is evident that integrating UHPC into the prefabrication process of semi-assembled barriers as the barrier shell material can fully exploit its characteristics, such as high strength, exceptional toughness, and outstanding durability. The prefabricated construction method involves fabricating the barrier shell offsite and then transporting it to the construction site for splicing. Filling the interior of the UHPC shell with NC significantly reduces the barrier’s weight and transportation costs. The barrier is filled with NC without the use of reinforcing steel, reducing the cost of reinforcing steel and the cost of tying, and its initial cost is about 10% lower than the cast-in-place concrete barrier; compared with the precast concrete barrier, the weight of the barrier is greatly reduced, and its cost is about 20% lower than that of the assembled concrete barrier. Compared to traditional concrete barriers, the barrier exhibits superior durability. It can effectively resist damage from frost expansion and de-icing salts, thereby significantly reducing the structural degradation of the barrier. This improvement effectively mitigates the economic losses and resource wastage associated with the frequent repairs.
To verify the safety performance of the proposed barrier, a vehicle–barrier coupling simulation model was developed using LS-DYNA R11.0. finite element software. The material constitutive model of UHPC in the numerical simulation was calibrated using the conventional triaxial test. Following the Standard for Safety Performance Evaluation of Highway Barriers (JTG B05-01-2013) [25], collision test simulations were conducted for the three models with a protective energy of 280 kJ (SB protective grade). The feasibility of the newly developed UHPC semi-assembled barrier was further verified through full-scale collision tests involving real vehicles, which provided theoretical support for its widespread adoption and application.
2. Structural Characteristics of Barrier
The newly developed semi-assembled UHPC barrier comprised several prefabricated UHPC shell segments, internally filled concrete, dowel bars, connecting rods, and supporting blocks. It is a separate barrier (Figure 1). The geometric shape of the barrier refers to the general diagram of ‘Design Rules for Highway Traffic Safety Facilities’ (JTG D81-2017) [26], which is an F-shaped slope. The UHPC shell segment is 4 m long and the shell thickness is 30 mm. The top is reserved with an internal concrete filling hole, the reserved port spacing is 2 m, and the size is 100 mm × 300 mm. The barrier segments are connected longitudinally by steel bars. The segments are connected by dowel bars at the expansion joints. The barrier segments other than the expansion joints are connected by connecting rods. Both ends of the connecting rods are poured into the segments. The size of the connecting rods is Φ22 × 600 (mm). The supporting block is set at the center of the segment and the connection of adjacent segments is every 2 m on the back of the barrier. The size of the supporting block is 400 × 400 × 100 (mm), and it is prefabricated with ordinary concrete.
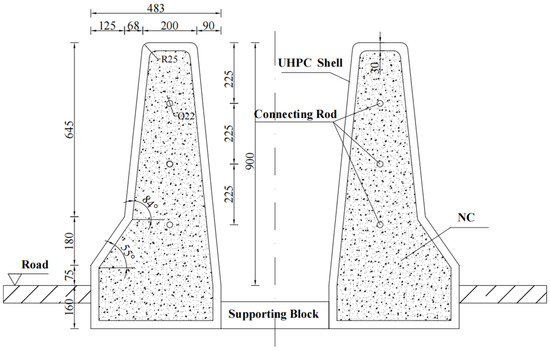
Figure 1.
Schematic of semi-assembled barrier sections.
The cement used in UHPC was Ordinary Portland Cement Type (P.O. 52.5), produced by Jidong Cement Factory in Tangshan, China. Silica fume (SF) was produced by Henan Borun Casting Materials Co. (Zhengzhou, China), with a particle size range of 0.10~0.15 μm, a specific surface area of 21 m2/g, and a SiO2 content of 98.1%. Limestone powder (LP) was produced by Lingshou Dehang Mineral Products Co. (Shijiazhuang, China). The quartz powder (QP) had a particle size of 2000 mesh and a density of 2.65 (g/cm3). In this study, sand (S) was used at three levels, 20–40 mesh, 40–70 mesh, and 70–120 mesh, with a ratio of 5:2:3. A polycarboxylate superplasticizer (SP) with a water reduction rate of 26% was used in the test, which was produced by Suzhou Fuke Technology Co., Ltd. (Suzhou, China). The steel fiber was copper-plated straight steel fiber with a length of 12 mm and a diameter of 0.2 mm. The test water was laboratory tap water. The water–cement ratio was 0.165. To reduce the auto shrinkage of UHPC and improve its crack resistance and durability, expansive additives (EA) and antifoaming admixtures (AFA) were added in this study. The cement used in NC was Ordinary Portland Cement Type (P.O. 42.5). The coarse aggregate (C) was crushed stone with a particle size of 5–10 mm. The mix proportion of concrete is provided in Table 1.

Table 1.
Recipes of the developed UHPC (kg/m3).
The compressive strength of NC and UHPC used in the barrier was tested, yielding a 28 d strength of 30.9 MPa and 142.48 MPa. The tensile strength test of the UHPC and NC was conducted using a universal testing machine. The average values of the three test blocks were obtained. The tensile strengths of UHPC and NC were 9.81 MPa and 300 MPa.
To provide reliable material parameters for the finite element simulations of barrier collisions, a conventional triaxial test of the UHPC was conducted using a rock thermal–hydraulic–mechanical (THM)-coupled microcomputer servo triaxial test system (Figure 2). The radial pressure σ3 was set to 0, 5, 10, 15, and 20 MPa, respectively. Three specimens for each σ3 were utilized for the test, and the average results of the three specimens were taken for analysis. Uniaxial compression tests were conducted at a radial pressure of 0 MPa, with only axial loading to determine the uniaxial mechanical properties of UHPC. The test results are presented in Table 2.

Figure 2.
Conventional triaxial test.

Table 2.
Triaxial compressive test results (MPa).
3. Collision Simulation System
Safety performance evaluations of barriers are mainly conducted using full-scale collision tests or numerical simulations. However, full-scale crash tests of real vehicles are expensive and time-consuming. Many researchers have used the finite element software LS-DYNA [27] to study the safety of barriers and have proven the rationality of the simulation [28,29,30]. These results can be used as a reference for real vehicle collision tests.
3.1. Finite Element Modeling of Barrier
According to the two-dimensional structure size diagram of the barrier (Figure 1), a finite element model of the 40 m barrier was established. Solid elements were used to simulate the UHPC shells, internal concrete, connecting rods, and dowel bars. A shell element was used to simulate the ground and support blocks. The thickness of the UHPC shell was 30 mm, and the length of each section of the barrier shell was 4 m, for a total of 10 sections. The length of each section of the internal concrete was 20 m, for a total of two sections. The three-dimensional size of barrier solid elements at the collision location was about 30 mm; the bidirectional size of the shell elements was about 250 mm.
The Holmquist–Johnson–Cook (HJC) model was used to simulate UHPC and NC, and the calibration of the relevant parameters is presented in Section 3.2. The connecting rods and dowel bars were simulated using the MAT-PLASTIC-KINEMATIC. The keyword *Constrained-Lagrange-In-Solid was used to connect them with the internal concrete. The size of the support block placed at the interface between the two UHPC shells was 400 mm × 400 mm × 100 mm, and a rigid material model was used in this simulation to simplify the simulation and constrain its six degrees of freedom. In this finite element simulation, pavement deformation was ignored, and the pavement was treated as rigid; therefore, the ground adopted a rigid material model and its six degrees of freedom were also constrained.
3.2. Introduction of the HJC Constitutive Model
The HJC model was used in this study since it is suitable for concrete subjected to large strains, high strain rates, and high pressures [31] and is widely used by researchers.
Holmquist et al. [31] proposed a value method to determine the original values of basic, damage pressure, and strength parameters in the HJC model of NC by combining experimental data with curve fitting methods. For UHPC, these parameters in the HJC model were calibrated based on mechanical property tests and recommended values found in the related literature [32,33,34,35].
- Basic physical parameters: , T, G, K
The uniaxial compressive strength and tensile strength T of the UHPC are presented in the test results in Section 2. MPa, T = 9.8 MPa, E = 45.7 GPa, Poisson’s ratio v = 0.2, and ρ = 2.54 g/cm3 were used in this study. The shear modulus G and bulk modulus K were determined using the following formulae:
The calculation can be obtained as follows: G = 32.64 GPa; K = 25.38 GPa.
- 2.
- Strength parameters: A, B, N, C, SFmax
B and N are the fracture strength of the material at the normalized strain rate * = 1.0 s−1, which can be determined by the conventional triaxial test of UHPC. Ignoring the influence of damage parameter D in the elastic stage, the yield surface equation of can be simplified to
In Equation (3),
, are the axial and radial pressures of the conventional triaxial test in Section 2, respectively. Xiong Yibo et al. [34] derived the dimensionless cohesive strength A based on the interrelationship between the Mises criterion and the Mohr–Coulomb criterion in the π-plane in plastic yield surface theory:
where K is the slope of the linear relationship curve obtained from the conventional triaxial test, which can be obtained by linear fitting. K = 4.00, A = 0.25. Curve fitting using the triaxial test results and Equation (3) yields B = 2.49, N = 1.08. Owing to the lack of experimental data, this study takes the initial values of C = 0.007 and SFmax = 7.0, as recommended by Holmquist et al. [31].
- 3.
- Equation of State (EOS) parameters: Pcrush, μcrush, Plock, μlock, K1, K2, and K3
The parameters of the EOS were mainly determined based on Hugoniot test data. Owing to the lack of experimental data, the original values proposed by Holmquist et al. [31] were used in this study, K1 = 85 GPa, K2 = −171 GPa, K3 = 208 GPa. , , can be determined according to the following equations:
Currently, there are few experimental studies on the of UHPC. The values of for different strengths were obtained by interpolation as in Equation (9) and substituting fc′ = 142.48 MPa can be obtained by substituting Plock = 1.00 GPa [35,36]. can be calculated according to Equation (10), where is the original density of concrete, is the density of concrete after the pores in the concrete are compacted. In this study, the porosity of UHPC is taken to be 6.35% [37], that is, 1 − ρ0/ρgrain = 6.35%, μlock = ρgrain/ρ0 − 1 = 0.068.
- 4.
- Damage parameters: D1, D2, EFMIN
The damage constants, taken as the damage parameters for UHPC with a 2% fiber admixture, were obtained from the literature [32], specifically: D1 = 0.061, D2 = 1.0, EFMIN = 0.016. The HJC parameters for NC were obtained using the method and original values proposed by Holmquist et al. [31] and are not repeated here. The parameters of the HJC model for both NC and UHPC are listed in Table 3.

Table 3.
HJC parameters of UHPC and NC.
3.3. Vehicle Finite Element Modeling
According to the relevant requirements of the Standard for Safety Performance Evaluation of Highway Barriers (JTG B05-01-2013) for vehicles, the SB-level collision test requires real vehicle collisions of a 1.5-ton car, 10-ton bus, and 18-ton truck. The relevant parameters and collision requirements of the three models are listed in Table 4. The collision points of the vehicle were located at one-third of the starting point of the barrier along the driving direction.

Table 4.
Vehicle model parameters.
In this study, simulation models of the three types of vehicles were established. The three vehicle models all use a section shell to simulate the vehicle body and a section solid to simulate the engine and tire. MAT-ELASTIC (MAT-1), MAT-PIECEWISE-LINEAR-PLASTICITY (MAT-24), and MAT-RIGID (MAT-20) were used to simulate the material of the vehicles. The keywords Spot Wold, Rigid-Body, and Extra Nodes Set connected the vehicle components.
To ensure the reliability and effectiveness of the vehicle model used in the collision simulation analysis, the selected vehicle finite element model was verified using a frontal collision test before the collision analysis. A rigid wall was set 20 cm from the front of the vehicle bumper, and the vehicle impacted the rigid wall vertically at a speed of 50 km/h. The rigid wall simulates the ground and the rigid wall being collided [38]. Figure 3 shows the finite element frontal collision experiment diagram and energy change curve of the three models. The deformation of the vehicle components during the collision process was reasonable, and no element distortion or penetration occurred. The collision effect in the simulation experiment was reasonable. After analysis of the three models, the hourglass energy of the collision model was 4%, 2%, and 4% of the initial total energy of the system, respectively, which was less than 5% of the total energy. Therefore, the frontal collision test simulation results were reliable, and the vehicle model could be used for further simulation analyses.
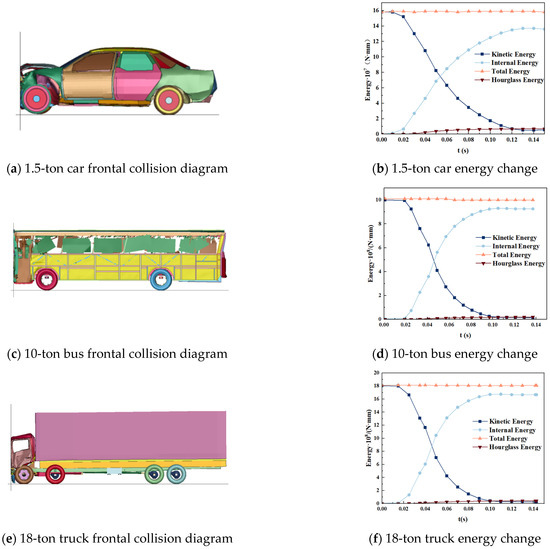
Figure 3.
Frontal collision diagram and energy change.
3.4. Collision System Settings
Given that the collision process between a vehicle and a barrier is very complicated, it is difficult to determine the contact direction of each contact surface of the vehicle body. Therefore, contacts between the concrete barrier and the car were modeled using the Contact-Automatic-Single-Surface command, which is based on the penalty function method, does not need to set the master and slave surfaces, and can effectively control the proportion of hourglass energy in the total energy. Contact-Automatic-surface-to-Surface was used between the barrier and ground, wheel and ground, ground and support block, and resistance block and barrier. The contacts between the UHPC shell and the internal NC were modeled using Contact-Automatic-surface-to-Surface. To conform to the actual situation, gravity was applied to the simulation environment, and the gravitational acceleration was 9.8 m/s2. The overall model of the vehicle barrier is shown in Figure 4 (using a 10-ton bus as an example). The collision coordinate system takes the vehicle driving direction in the x direction (longitudinal), the width direction as the y coordinate (transverse), and the z direction perpendicular to the x–y plane.
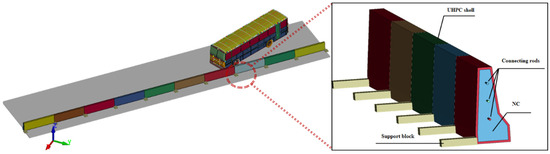
Figure 4.
A 10-ton bus–barrier coupling model.
4. Full-Scale Collision Test
The crash test was conducted at the test site of Beijing Shen Hua Da Transportation Engineering Inspection Co. in Beijing, China. On the day of the test, the temperature was 28 °C, the humidity was between 23% and 41%, and the test road surface was dry and without water accumulation. The test vehicle was accelerated by the hammer traction method and was in a completely free-running state within a distance of 10 m before the collision. The test vehicles did not exceed the service life, and all the equipment of the vehicles met the technical requirements for normal driving. In order to meet the requirements of the total mass of the test vehicle, the loads were evenly placed on the vehicle and fixed with the body.
5. Analysis of the Crash Simulation Results
The safety protection performance of the barrier was preliminarily analyzed for barrier orientation and buffering function. An actual safety performance evaluation was conducted through a full-scale collision test, and the computer simulation results were compared with the full-scale vehicle crash test results to verify the feasibility of the newly semi-assembled barrier.
5.1. Impact Force
In this study, the collision forces of the three vehicles colliding with a newly assembled barrier during the simulation process were extracted (Figure 5). It can be seen from the figure that the peak value of the collision force of the car to the barrier was larger than that of the first collision of the bus and the truck. This is because of the small height of the car. The body directly collides with the barrier, and the stiffness of the body material is large, resulting in a large collision force. The first collision between the bus and truck was caused by a crash between the tire and barrier. The tire has a specific elasticity, and the climbing phenomenon can consume some of the energy, which reduces the collision force between the vehicle and the barrier to some extent.
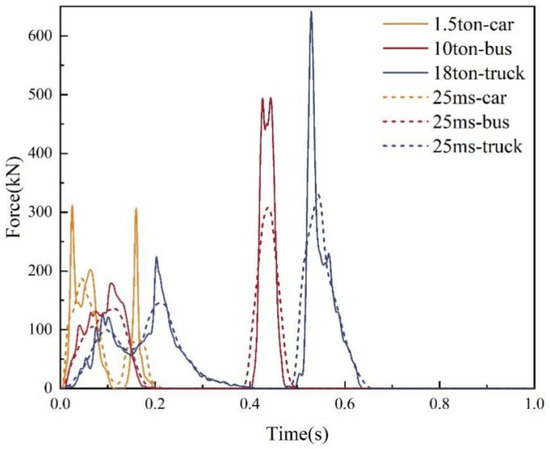
Figure 5.
Time history of the barrier collision force.
The Design Guidelines for Highway Safety Facilities (JTG D81-2017) [26] provide a vehicle collision load formula (Equation (11)) to calculate the theoretical collision force, which has been used in several countries to obtain the design load using the predicted lateral impact force [39]. In the United States, the predicted lateral impact force by this method has been compared with the magnitude of the measured impact force in the crash test, and the prediction accuracy of the formula was found to be ±20%. The relevant parameters of the three models are listed in Table 5.

Table 5.
Parameters of Equation (11).
In which:
- FXmax—Maximum lateral force acting on the barrier by a vehicle (kN);
- m—Mass of vehicle (kg);
- v1—Velocity of vehicle (m/s);
- θ—Collision angle of vehicle (°);
- C—Distance of the vehicle’s center of gravity from the front bumper (m);
- b—Half of the vehicle width (m);
- D—Maximum lateral dynamic deformation value of the barrier (m), D = 0 for concrete barrier.
According to the calculations in Equation (11) and Table 5, the theoretical collision forces of the three models are 189, 333, and 313 kN, respectively. Considering that the magnitude of the collision force changes dynamically when a car collides with a barrier, the peak dynamic load generally exceeds the static design load [40]. In this study, the 25 ms average of the collision forces for the three models was extracted (Figure 5). The peaks of the 25 ms collision force F25ms of the three models were 182, 307, and 324 kN, respectively. The errors compared to the theoretical collision force were 3.8%, 7.8%, and 3.4%, respectively, which were all within 20%. Therefore, it is considered reliable to use the peak of the 25 ms collision force as a reference value for the static load design.
5.2. Barrier Guiding Ability
The Standard for Safety Performance Evaluation of Highway Barriers (JTG B05-01-2013) proposes that if the vehicle does not overturn after the collision and the wheel track after the vehicle leaves the departure point does not cross the straight-line F when passing through the guidance exit frame, the barrier guidance function is considered to be good (Figure 6). The reliability of the numerical simulation was qualitatively evaluated by comparing the trajectory obtained from the full-scale vehicle crash test with that obtained from the numerical simulation.
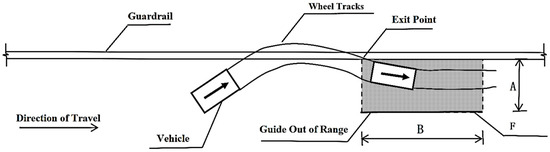
Figure 6.
Vehicle track guided exit frame for a standard section of barrier.
Where
VW—Total width of the vehicle (m); VL—total length of the vehicle (m).
For car A = 2.2 + VW + 0.16 VL (m); B = 10 (m)
For bus and truck A = 4.4 + VW + 0.16 VL (m), B = 20 (m)
- A 1.5-ton car
Figure 7 shows a comparison of the full-scale vehicle crash test results with the vehicle trajectory obtained from the numerical simulation. The car began to collide with the barrier at 0.02 s. The wheel climbed up along the inclined surface of the lower part of the barrier. The car began to turn owing to the blocking effect of the barrier. At 0.15 s, the front of the car completed the steering and slipped along the slope, away from the barrier. Simultaneously, owing to the inertia of the car body, a tail flick occurred, the rear side of the car body rebounded after colliding with the barrier, and the car continued to move forward by turning the left front wheel. Subsequently, the car fell back to the ground in approximately 0.8 s, owing to its gravity.
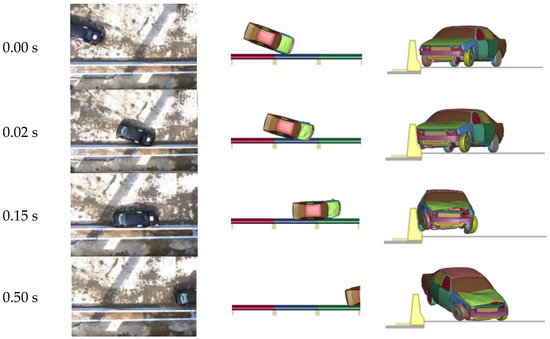

Figure 7.
Comparison of test and simulation of vehicle trajectory for the car.
Over the entire process, the vehicle moved away quickly, and there was no phenomenon of overriding or riding over the barrier. The simulation results of the vehicle trajectory agree well with the experimental results. However, the vehicle traveled differently after the collision with the barrier. In the full-scale vehicle crash test, the car gradually moved away from the barrier after the collision and continued to travel along the exit angle. In the numerical simulation (Figure 8), the car traveled longitudinally along the barrier after the collision. The main reason for this difference is that in the numerical simulation, the right front wheel was held dead after the collision with the barrier and could not continue to rotate, resulting in the vehicle not being able to control the steering and could only move forward under the effect of inertia. This phenomenon may occur in actual collisions, that is, vehicle collisions may cause tire blowouts or vehicle steering lockups.
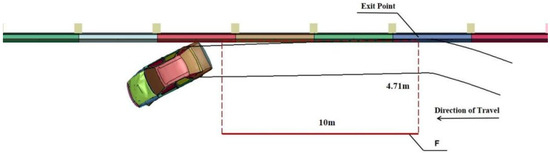
Figure 8.
Trajectory diagram of the 1.5-t car (m).
According to the calculation in Equation (12), for a 1.5-t car, A = 4.71 m, B = 10 m. The trajectory of the car is illustrated in Figure 8. Following the collision with the barrier, the car did not deviate from the guiding exit frame, nor did it pose a threat to adjacent vehicles in the same direction. This indicates that the barrier effectively served its guiding function.
- 2.
- A 10-ton medium bus
Figure 9 compares the collision barrier of the medium-sized bus with the barrier, showing the vehicle trajectory obtained from numerical simulation. After colliding with the barrier, the right front wheel of the bus climbed along the slope of the collision surface of the barrier, causing deformation of the front bumper. Subsequently, owing to gravity, the medium-sized bus returned to the ground along the slope, completing the steering by 0.4 s. At 0.45 s, the inertia of the bus caused the body to flail, resulting in the rear of the vehicle colliding with the barrier, squeezing and slightly overturning but not overturning the barrier. By 1 s into the collision, the bus began to drive away from the barrier, swiftly completing the steering and departure process. According to the calculation in Equation (13), A = 8.29 m, B = 20 m for a 10-ton bus. The running track of the bus is shown in Figure 10. After the bus collided with the barrier, it remained almost parallel to the barrier and did not exit the guide exit frame. After the collision, the barrier did not endanger the driving of adjacent vehicles in the same direction, indicating that the barrier had a good guiding function.
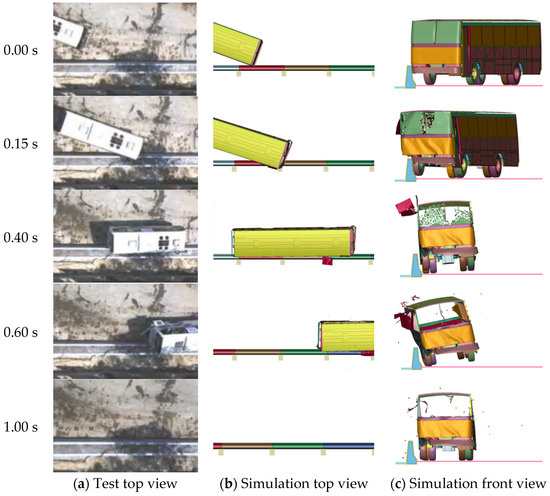
Figure 9.
Comparison of test and simulation of vehicle trajectory for the bus.
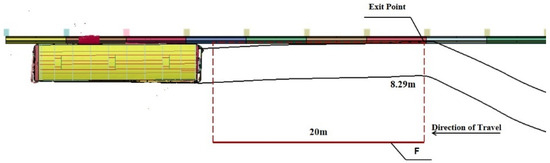
Figure 10.
Trajectory diagram of the 10-ton bus (m).
- 3.
- An 18-t truck
The vehicle trajectory obtained from the test and numerical simulation of the truck is shown in Figure 11; when the truck collided with the barrier, its front bumper was squeezed and deformed. Then, the right front wheel began to climb to a small extent. During this process, the truck turned gradually. The front-right chassis of the cargo compartment contacted the barrier and was scraped from the top of the barrier. The scrape length was approximately 4 m. After 0.4 s, the track’s front wheel was out of the barrier to complete steering, and the body was almost at the level of the barrier. Owing to the high center of gravity of the carriage, under the action of inertia, the right rear wheel hit the barrier at 0.52 s, and the barrier experienced a secondary collision. The carriage was slightly overturned. The truck then slowly fell back to the ground owing to gravity, and the front wheel was not pulled in the right direction. After 1.3 s, the vehicle’s rear broke away from the barrier and ran almost parallel to it.
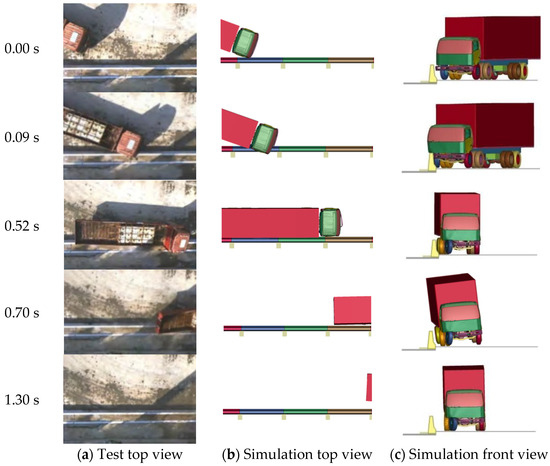
Figure 11.
Comparison of test and simulation of vehicle trajectory for the truck.
According to the formulas, in the calculation in Equation (13), A = 8.71 m and B = 20 m for an 18-ton truck. The trajectory of the 18-ton truck is illustrated in Figure 12. After the truck collides with the barrier, it remains within the guiding exit frame but veers out at an angle nearly parallel to the barrier. This indicates an effective guiding function by the barrier.
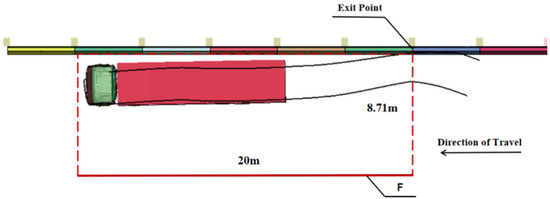
Figure 12.
Trajectory diagram of the 18-t truck (m).
Overall, the newly assembled barrier had good blocking and guiding functions for all three models, and the numerical simulation results were in good agreement with the real vehicle crash test results.
5.3. Vehicle Damage
Figure 13 compares the vehicle damage caused after the real vehicle test and numerical simulation collision. As shown in Figure 13a,b, the car’s front bumper was damaged in both cases. The right headlight was damaged and detached, and the right front side of the vehicle’s body was scratched and damaged. After the collision test, the front bumper of the bus was squeezed and deformed, the collision side of the vehicle body was scratched and damaged, and the tail of the collision side was squeezed and deformed, owing to the secondary collision (Figure 13c,d). In Figure 13e,f, the truck’s front bumper was deformed by crushing against the barrier, and scratches and damage were observed on the crash side of the body. In conclusion, the numerical simulation results are in good agreement with the test results.

Figure 13.
Damage diagram of the truck.
5.4. Barrier Damage
In the real-vehicle collision test, following the vehicle collision barrier, the barrier did not appear to endure overall damage, only scratch damage, a scratch length of about 4.73 m, which did not affect the continued use of the barrier. After testing, the maximum lateral dynamic deformation value of the barrier was 0 m.
After the collision, the contact between the barrier shell and the internal filler concrete was examined, as shown in Figure 14. The bond between the UHPC shell and the internal concrete was good, indicating that the UHPC shell and the internal concrete was a synergistic force during the collision.

Figure 14.
Barrier section after collision.
5.5. Buffering Function
The buffer function of the barrier is primarily evaluated based on the acceleration and speed of the center of gravity of a 1.5-t car. The key indicators include the occupant ride-down acceleration (ORA) and occupant impact velocity (OIV). Acceleration during a vehicle collision is crucial for directly evaluating driver safety. Effective energy absorption and buffering by the barrier can reduce speed changes during collisions, thereby enhancing vehicle safety.
According to the Standard for Safety Performance Evaluation of Highway Barriers (JTG B05-01-2013) [25], the longitudinal and lateral ORA at the driver’s position should be less than 200 m/s2. Moreover, the longitudinal and lateral OIV of occupant collisions should be less than 12 m/s. The ORA can be directly obtained using post-processing software. OIV refers to the instantaneous speed at which an occupant collides with the barrier inside a vehicle during a small vehicle collision. This can be calculated using the following formula:
where
- OIVx—X direction component of occupant impact velocity;
- OIVy—Y direction component of occupant impact velocity;
- ax—Vehicle acceleration in the X direction;
- ay—Vehicle acceleration in the Y direction;
- t0—The moment of impact, determined as the smaller of tx and ty, which are calculated by the following equations when an occupant comes into contact with the interior of the vehicle:
- ORA
Post-processing software was used to extract the ORA in the X and Y directions at the center of gravity of a 1.5-ton car during a collision, as illustrated in Figure 15a,b. In the finite element simulation, the peak acceleration of the occupant in the X direction was 93.2 m/s2, and in the Y direction it was 172.7 m/s2. These values were compared with data obtained from a full-scale vehicle crash test, where the peak acceleration in the X direction was 88.5 m/s2, and in the Y direction it was 170.9 m/s2. The relative errors between the simulation and the actual peak acceleration in the X and Y directions were 5.3% and 1.0%, respectively, both meeting the specification requirements as they were less than 200 m/s2. The errors were within a reasonable range. Thus, it can be concluded that the ORA in the simulation results aligns well with the ORA obtained in the real vehicle collision test.
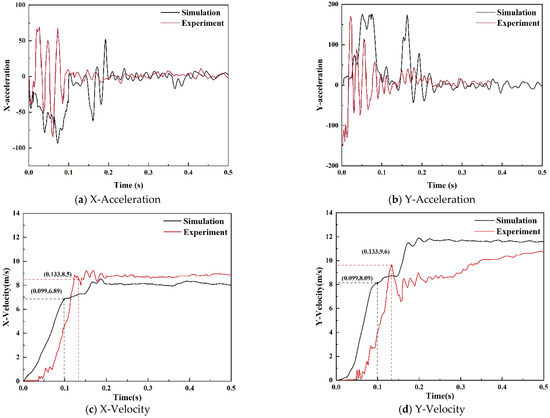
Figure 15.
Acceleration test and simulation results.
- 2.
- OIV
According to Equations (16) and (17), the theoretical displacement curves of the occupant’s head in the X and Y directions during the vehicle collision in the numerical simulation can be obtained (as shown in Figure 16), with tx = 0.142 s and ty = 0.099 s. Therefore, the occupant collision time t0 is taken as 0.099 s. Using Equations (14) and (15), the acceleration curves are integrated, yielding the occupant collision speeds in the X and Y directions in the numerical simulation, which were subsequently compared with the results of the real vehicle collision test (Figure 15c,d).
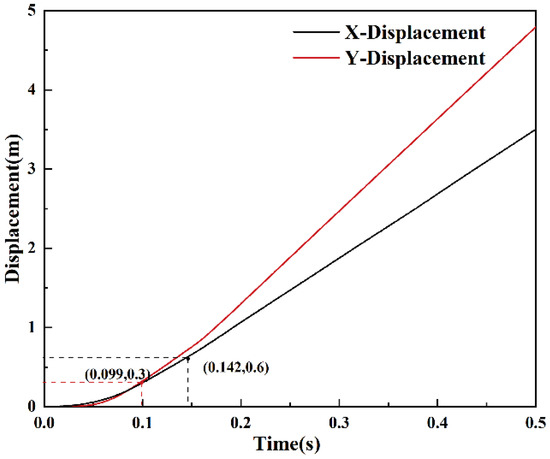
Figure 16.
Displacement in the simulation.
In the finite element simulation, when t0 = 0.099 s, OIVx = 6.89 m/s, and OIVy = 8.09 m/s. In the full-scale vehicle crash test, the measured collision times t0 = 0.133 s, OIVx = 8.50 m/s, OIVy = 9.60 m/s. The relative errors between the simulation and the actual peak acceleration in the X and Y directions were 18.9% and 15.7%. The simulation results were less than 12 m/s and met the specification requirements. However, the simulation results were lower than the X and Y-direction occupant impact velocities in the real vehicle collisions, possibly owing to differences in friction between the tires and the ground, friction between the vehicle and the barrier, and vehicle material properties.
6. Conclusions
In this study, a new semi-assembled barrier based on UHPC was developed, and a finite element simulation of the collision process of the newly semi-assembled barrier was performed using the nonlinear explicit dynamics software LS-DYNA. A full-scale collision test of a real vehicle was conducted and its results were compared with the numerical simulation results. The following conclusions can be drawn:
- The collision force between the three models and the barrier was extracted and analyzed, and the average collision force peak of 25 ms was compared with the theoretical collision force, which has high consistency. It is considered that the peak value of the 25 ms collision force in this simulation can be used as the basis for static load design.
- A collision simulation of a new semi-assembled barrier was performed. It was found that the barrier provided good guidance and reduced damage to the occupant.
- After collision, the barrier did not show overall damage, which does not affect the continued use of the barrier. The maximum lateral dynamic deformation value of the barrier was 0 and the UHPC shell and the NC were in synergistic force during the collision.
- Whether numerical simulation or real vehicle crash test, the ORA and OIV were less than the standard allowable values, suggesting that the new semi-assembled barrier had a good buffering function for the vehicle.
- The collision test results for the real vehicles were in good agreement with the simulation results by LS-DYNA software. This suggests that finite element simulation can predict real outcomes to some extent, which can serve as a basis for full-scale collision tests, potentially reducing unnecessary investments in such tests. The research findings can offer theoretical support for promoting the widespread adoption of this new type of barrier.
In view of the limitations of the numerical model described in the previous section, it is not yet possible to comprehensively simulate failures, such as tire shedding and tire blowout, that may occur during actual collisions. Therefore, subsequent studies will focus on further optimization of the vehicle numerical model, while the safety performance under different working conditions will be considered more systematically to ensure that the simulation results are more reliable and realistic.
Author Contributions
Methodology, L.L.; Software, W.X.; Formal analysis, W.X.; Investigation, L.L. and L.S.; Resources, R.H.; Data curation, Z.L.; Writing—review & editing, Z.L.; Visualization, L.S.; Funding acquisition, R.H. All authors have read and agreed to the published version of the manuscript.
Funding
The work was also supported by Fundamental Research Program of Shanxi Province (Shanxi Transportation Holdings Group Co., Ltd.) (No. 202303011221002); by Key Laboratory of Highway Construction & Maintenance Technology in Loess Region, Ministry of Transport, PRC (KLTLR-Y23-4); by 2023 Shanxi Graduate Student Innovation Project (2023KY252).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Author Lin Liao and Litao Shen were employed by the company “Shanxi Transportation Technology R&D Co., Ltd.” and “Shanxi Transportation Research Institute Group Co., Ltd.”. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The sponsors had no role in the design, execution, interpretation, or writing of the study.
References
- Zhang, P. Numerical Simulation on Crash worthiness of New Type of Rigid barrier. China J. Highw. Transp. 2009, 22, 31–36. (In Chinese) [Google Scholar]
- Dinnella, N.; Chiappone, S.; Guerrieri, M. The innovative “NDBA” concrete safety barrier able to withstand two subsequent TB81 crash tests. Eng. Fail. Anal. 2020, 115, 104660. [Google Scholar] [CrossRef]
- Chen, F.; Rasmussen, J.D.; Bielenberg, R.W.; Lechtenberg, K.A.; Faller, R.K.; Linzell, D.G. Experimental and numerical investigation on deflection and behavior of portable construction barrier subjected to vehicle impacts. Eng. Struct. 2021, 235, 112071. [Google Scholar] [CrossRef]
- Yang, J.; Xu, G.; Cai, C.S.; Kareem, A. Crash performance evaluation of a new movable median barrier on highways. Eng. Struct. 2019, 182, 459–472. [Google Scholar] [CrossRef]
- Mohammed, H.J.; Zain, M.F.M. Experimental application of EPS concrete in the new prototype design of the concrete barrier. Constr. Build. Mater. 2016, 124, 312–342. [Google Scholar] [CrossRef]
- Song, X.M.; Pan, P.Y.; Rong, Y.W.; Tang, M. Protection Performance of New Fabricated barrier Based on Collision Simulation. J. South China Univ. Technol. (Nat. Sci. Ed.) 2021, 49, 41–49. (In Chinese) [Google Scholar]
- Jiang, L.; Wang, K.; Fang, H.; Chen, B.; Zhu, L.; Zhang, Q.; Zhang, X. Protection performance of a novel anti-collision barrier with recycled foamed concrete under vehicle collision. Eng. Struct. 2024, 305, 117795. [Google Scholar] [CrossRef]
- Yee, A.A.; Hon, D. Structural and Economic Benefits of Precast/Prestressed Concrete Construction. PCI J. 2001, 46, 34–42. [Google Scholar] [CrossRef]
- Hu, X.; Xue, W.; Lv, Y. Seismic behavior of a new type of precast concrete shear wall using UHPC connections at boundary elements. Eng. Struct. 2024, 302, 117468. [Google Scholar] [CrossRef]
- Yuan, Q.; Shi, C.; De Schutter, G.; Audenaert, K.; Deng, D. Chloride binding of cement-based materials subjected to external chloride environment—A review. Constr. Build. Mater. 2009, 23, 1–13. [Google Scholar] [CrossRef]
- de Larrard, F.; Sedran, T. Optimization of ultra-high-performance concrete by the use of a packing model. Cem. Concr. Res. 1994, 24, 997–1009. [Google Scholar] [CrossRef]
- Shafieifar, M.; Farzad, M.; Azizinamini, A. Experimental and numerical study on mechanical properties of Ultra High Performance Concrete (UHPC). Constr. Build. Mater. 2017, 156, 402–411. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Banthia, N. Mechanical properties of ultra-high-performance fiber-reinforced concrete: A review. Cem. Concr. Compos. 2016, 73, 267–280. [Google Scholar] [CrossRef]
- Vaitkevičius, V.; Šerelis, E.; Vaičiukynienė, D.; Raudonis, V.; Rudžionis, Ž. Advanced mechanical properties and frost damage resistance of ultra-high performance fiber reinforced concrete. Constr. Build. Mater. 2016, 126, 26–31. [Google Scholar] [CrossRef]
- Yu, R.; Zhou, F.J.; Yin, T.Y.; Wang, Z.Y.; Ding, M.; Liu, Z.; Leng, Y.; Gao, X.; Shui, Z. Uncovering the approach to develop ultra-high performance concrete (UHPC) with dense meso-structure based on rheological point of view: Experiments and modeling. Constr. Build. Mater. 2021, 271, 121500. [Google Scholar] [CrossRef]
- Fan, D.Q.; Rui, Y.; Liu, K.N.; Tan, J.H.; Shui, Z.; Wu, C.; Wang, S.; Guan, Z.; Hu, Z.; Su, Q. Optimized design of steel fibres reinforced ultra-high performance concrete (UHPC) composites: Towards to dense structure and efficient fibre application. Constr. Build. Mater. 2021, 273, 121698. [Google Scholar] [CrossRef]
- Alkaysi, M.; El-Tawil, S.; Liu, Z.; Hansen, W. Effects of silica powder and cement type on durability of ultra high performance concrete (UHPC). Cem. Concr. Compos. 2016, 66, 47–56. [Google Scholar] [CrossRef]
- Li, J.Q.; Wu, Z.M.; Shi, C.J.; Yuan, Q.; Zhang, Z. Durability of ultra-high performance concrete—A review. Constr. Build. Mater. 2020, 255, 119296. [Google Scholar] [CrossRef]
- Chen, Y.X.; Yu, R.; Wang, X.P.; Chen, J.; Shui, Z.H. Evaluation and optimization of Ultra-High Performance Concrete (UHPC) subjected to harsh ocean environment: Towards an application of Layered Double Hydroxides (LDHs). Constr. Build. Mater. 2018, 177, 51–62. [Google Scholar] [CrossRef]
- Sohail, M.G.; Kahraman, R.; Al Nuaimi, N.; Gencturk, B.; Alnahhal, W. Durability characteristics of high and ultra-high performance concretes. J. Build. Eng. 2021, 33, 101669. [Google Scholar] [CrossRef]
- Yu, R.; Zhang, J.J.; Liu, K.N.; Liao, M.Z.; Shui, Z.H.; Zeng, M.; Hu, F.; Hou, D.; Wang, X. Evaluation and regulation of Ultra-High Performance Concrete (UHPC) crack resistance based on physicochemical multi-factor coupling approach. Constr. Build. Mater. 2021, 301, 124100. [Google Scholar] [CrossRef]
- Luo, S.; Zhao, H.; Qiao, D.Q.; Liao, Z.; Hu, Z.; Zhou, C. Experimental and numerical investigation on deck system of a 102 m simply supported prestressed UHPC box-girder highway bridge. Eng. Struct. 2024, 316, 118601. [Google Scholar] [CrossRef]
- Liu, B.X.; Zhang, R.Z. Review of Mechanical Properties and Application on Ultra-High Performance Concrete, 2024th ed.; School of Highway, Chang’an University: Xi’an, China, 2024; pp. 35–44. [Google Scholar] [CrossRef]
- Hong, L.J.; Li, Z.Y.; Peng, Y. Application of lightweight steel-UHPC composite beam in bridge emergency repair. Adv. Bridge Eng. 2024, 5, 19. [Google Scholar] [CrossRef]
- JTG B05-01-2013; Standard for Performance Evaluation of Highway Barrier. China Communications Press: Beijing, China, 2013. (In Chinese)
- JTG D81-2017; Design Guidelines for Highway Safety Facilities. Ministry of Transport of the People’s Republic of China: Beijing, China, 2017. (In Chinese)
- LSTC—Livermore Software Technology Corporation. LS-DYNA Keyword User’s Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2013. [Google Scholar]
- Miller, P.; Iii, J.F.C. Computer Simulations of Roadside Crash Cushion Impacts. J. Transp. Eng. 1997, 123, 370–376. [Google Scholar] [CrossRef]
- Ren, Z.; Vesenjak, M. Computational and experimental crash analysis of the road safety barrier. Eng. Fail. Anal. 2004, 12, 963–973. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, L.; Liu, Z.; Fan, W.; Wu, X.; Wen, G. Crash analysis and evaluation of a new separate W-beam barrier on highways using the finite element method. Eng. Struct. 2023, 278, 115551. [Google Scholar] [CrossRef]
- Holmquist, T.J.; Johnson, G.R.; Cook, W.H. A Computational Constitutive Model for Concrete Subjected to Large Strains, High Strain Rates and High Pressures. In Warhead Mechanisms, Terminal Ballistics; ADPA: Brussels, Belgium, 1993; Volume 2, pp. 591–600. [Google Scholar]
- Wan, W.; Yang, J.; Xu, G.; Liu, Y. Determination and evaluation of Holmquist-Johnson-Cook constitutive model parameters for ultra-high-performance concrete with steel fibers. Int. J. Impact Eng. 2021, 156, 103966. [Google Scholar] [CrossRef]
- Liu, J.; Liu, C.; Qu, K.; Li, J.; Wu, C. Calibration of Holmquist Johnson Cook (HJC) model for projectile penetration of geopolymer-based ultra-high performance concrete (G-UHPC). Structures 2022, 43, 149–163. [Google Scholar] [CrossRef]
- Xiong, Y.B.; Chen, J.J.; Hu, Y.L.; Wang, W.P. Determining Failure Surface Parameters of the Johnson-Holmquist Concrete Constitutive Model. Acta Armamentarii 2010, 31, 746–751. (In Chinese) [Google Scholar]
- Ren, L.; Yu, X.; Zheng, M.; Xue, Z.; Wu, B.; He, Y. Evaluation of typical dynamic damage models used for UHPC based on SHPB technology. Eng. Fract. Mech. 2022, 269, 108562. [Google Scholar] [CrossRef]
- Hanchak, S.J.; Forrestal, M.; Young, E.; Ehrgott, J. Perforation of concrete slabs with 48 MPa (7 ksi) and 140 MPa (20 ksi) unconfined compressive strengths. Int. J. Impact Eng. 1992, 12, 1–7. [Google Scholar] [CrossRef]
- Ghafari, E.; Costa, H.; Júlio, E.; Portugal, A.; Durães, L. Optimization of UHPC by adding nanomaterials. In Proceedings of the 3rd International Symposium on UHPC and Nanotechnology for High Performance Construction Materials, Kassel, Germany, 7–9 March 2012; pp. 71–78. [Google Scholar]
- National Crash Analysis Center (NCAC). Available online: https://www.nhtsa.gov/crash-simulation-vehicle-models (accessed on 10 February 2025).
- Sun, S.; Li, H.; Zhu, C.; Mei, K.; Jiang, H.; Sun, Y.; Huang, H. Study on the anti-collision performance of basalt fiber reinforced polymer beam–column barrier. Compos. Struct. 2021, 276, 114588. [Google Scholar] [CrossRef]
- Lei, Z.B. The Crashworthiness of Structure with Large Displacement and Large Deformation. Doctoral Dissertation, Central South University, Changsha, China, 2004. (In Chinese). [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).