Study on Vertical Uplift Resistance Characteristics of Pre-Drilled Planted Piles in Boulder Strata

Abstract

Pre-drilled composite planted piles are a commonly used construction method, but there is currently limited research on the load-bearing characteristics of piles penetrating boulders. Therefore, a new type of pre-drilled composite planted pile suitable for sites with isolated boulders has been developed. Using transparent soil technology, vertical uplift bearing capacity tests were conducted on pre-drilled piles to investigate the uplift capacity and load transfer mechanism of piles with boulders. Additionally, a discrete–continuous coupled 3D numerical model was employed to analyze the influence of boulder position on the pile’s uplift bearing capacity. The results indicate that the ultimate uplift bearing capacity of piles with boulders in the pile body is approximately twice that of piles without boulders, and this difference decreases with the increase of the distance between boulder and the pile end; under ultimate uplift loading, the pile end of a pile containing boulders contributes approximately 32% of the uplift bearing capacity, whereas the pile end without boulders contributes almost no uplift capacity; the presence of boulders increases the cross-sectional diameter of the pile, providing additional vertical support from the overlying soil, thereby significantly enhancing the ultimate uplift bearing capacity of the pile. Additionally, the boulder also increases the pathways for load transfer to the surrounding soil, further expanding the impact area on the soil surrounding the piles. Parameter analysis of the position of the boulder in the pile body reveals that under various conditions (boulder distances from the pile tip of 0, 50, 100, and 150 mm), both the ultimate uplift bearing capacity and the angle of the sliding failure surface decrease gradually as the depth of boulder decreases. This study provides a novel solution for pile foundation construction in similar boulder strata.

1. Introduction

As urbanization accelerates and infrastructure construction rapidly develops, the demand for foundation reinforcement is increasing, particularly in land reclamation and rock dumping projects, where the frequency of boulders has risen, significantly impacting engineering projects [1,2,3]. Piling technology has been widely used due to its effectiveness in improving the bearing capacity and stability of weak foundations, as well as its minimal environmental impact during construction [4,5,6,7,8,9,10]. Traditional methods for dealing with boulders, such as avoidance, excavation, blasting, and multi-pile integration, are only suitable for situations with fewer boulders and are difficult to implement [11,12,13].

Past research on pre-drilled piles has primarily focused on settlement and deformation under vertical loads, with less emphasis on studies regarding uplift bearing capacity [14,15,16]. However, in geological conditions such as sandy soils, sand, or strata containing boulders, the uplift performance of piles tends to be significantly compromised. In boulder-stratum environments, the discontinuous pile–soil interface and the difficulty in mobilizing end-bearing resistance leads to a reduction in the anti-floating capacity of the pile foundation. Therefore, investigating the uplift characteristics of piles under these conditions can provide a scientific basis for engineering design, ensuring the reliability of pile foundations in such challenging geological environments. The geological conditions are complex, as traditional pre-drilled piles may fail to meet the bearing capacity requirements. Many scholars have investigated the use of pre-drilled piles to form rock-embedded piles or enlarged base piles to enhance bearing capacity [17,18,19]. Mary et al. [20] conducted experimental studies using a half-space small-scale 1 g model and Particle Image Velocimetry (PIV) technology to examine the uplift behavior of enlarged base piles in layered strata. The results indicated that anchoring the pile base in deeper, stronger strata facilitates an increase in the pile’s uplift capacity. In a study by Ahmed et al. [21], through model tests, the uplift capacity of both open-ended piles and enlarged base piles in sandy soil was evaluated, and the experimental results showed that as the relative density of the sand increases, the uplift capacity of the enlarged base piles significantly improves. The study found that anchoring the pile base in deeper, stronger strata helps increase uplift capacity, and enlarging the base area of the pile also contributes to better load-bearing capacity. However, the above methods do not fully consider the influence of boulders and their potential load-bearing effects during the pile formation and construction processes.

Considering that many laboratory tests are time-consuming, labor-intensive, and may lead to difficulties in data acquisition and limited reproducibility, many scholars [22,23,24] have adopted a research approach that combines laboratory tests with numerical simulations. FLAC3D and PFC3D each have their advantages in numerical simulations of pile foundations in geotechnical engineering. Lu et al. [25] used FLAC3D to numerically simulate the cement–soil mixing pile composite foundation, verifying that FLAC3D 7.0 is suitable for handling large deformations and nonlinear problems. Zhao et al. [26] employed the discrete element analysis software PFC3D 6.0 to investigate the pile–soil–cap interaction problem related to the pile cap effect, observing the micromechanical mechanisms of granular materials. Zhou et al. [27] conducted laboratory tests to study the bearing capacity of offshore wind turbine piles and then used PFC3D numerical simulations to establish models corresponding to the laboratory tests, validating their microparameters. The simulation results were in good agreement with the laboratory test results, accurately reflecting the interaction between the pile and clay during the shearing process. The coupled FLAC3D-PFC3D model, which combines the advantages of continuous and discrete media, is suitable for multi-scale complex problems and can simultaneously simulate macroscopic deformation and micromechanical behavior. Gao et al. [28] used FLAC3D-PFC3D coupling to analyze the stability during the contact process between piles and soil, studying the micro-deformation of the surrounding soil, stress distribution, and changes in the pile itself during pile penetration. Tan et al. [29] employed a coupled continuous–discontinuous medium numerical model to simulate the deformation and failure process of a single gravel pile under load in an indoor model test. Guo et al. [30] established a coupled finite element–discrete numerical model and combined it with experimental measurements to investigate the bearing capacity and deformation of a series of composite piles.

Previous pile foundation studies have predominantly utilized field tests [31], laboratory soil tests [32], and numerical simulations [33], but have offered limited observations of internal soil deformation. Transparent soil technology enables the visualization of internal soil deformations, facilitating in-depth studies of the interactions between pile foundations and soil. Ni et al. [34] conducted indoor model experiments using transparent soil to investigate the compaction-induced deformations of soil during the installation of rectangular piles. Hird et al. [35] examined the bearing capacity of threaded and helical piles in soft soil layers through transparent soil model tests, focusing on the influence range on soil and the direction of soil movement. Existing studies have employed transparent soil technology to explore the impact of pile foundations on soil, demonstrating the practicality and reliability of this technique.

To mitigate the effects of boulders on projects, a method involving pre-drilling followed by the insertion of high-strength concrete precast piles is employed, integrating the boulders into the load-bearing system. This method sets the drilling location in the core region of the boulder, allowing for the construction of piles that share the load with the boulder, resulting in a new type of pre-drilled composite pile. This method combines the advantages of embedded piles and enlarged base piles, making it suitable for boulder-rich strata. Previous studies, such as that by Liao et al. [36], have investigated the load-bearing capacity and load transfer mechanisms of piles when the boulder is located at the pile tip, without considering the contributions of boulders positioned at different elevations along the pile shaft to the uplift capacity of the pile.

This study aims to fill the research gap regarding new pre-drilled composite piles when boulders are located at various positions along the pile shaft. Based on transparent soil technology, destructive uplift tests were conducted on planted piles and piles containing boulders to analyze the load transfer mechanism of the piles, the interaction between the piles and the surrounding soil, and the development pattern of the sliding failure surface angle. Concurrently, a discrete–continuous coupled 3D numerical model was established to analyze in comparison with the uplift test results and investigate the effects of different boulder locations along the pile body on the load-bearing capacity of the piles and the sliding rupture surfaces. This study may provide valuable references for the handling of large boulders within boulder strata.

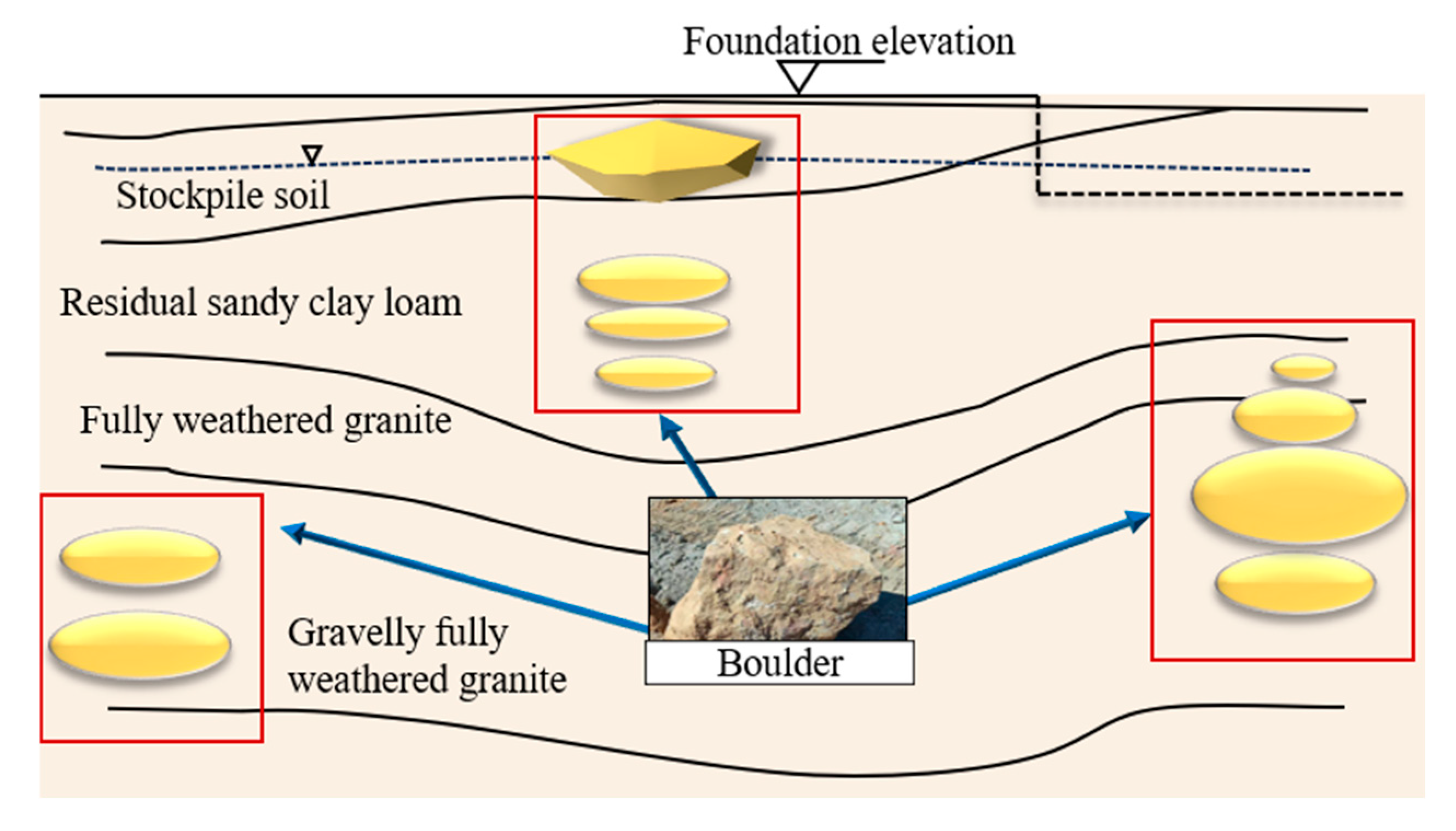
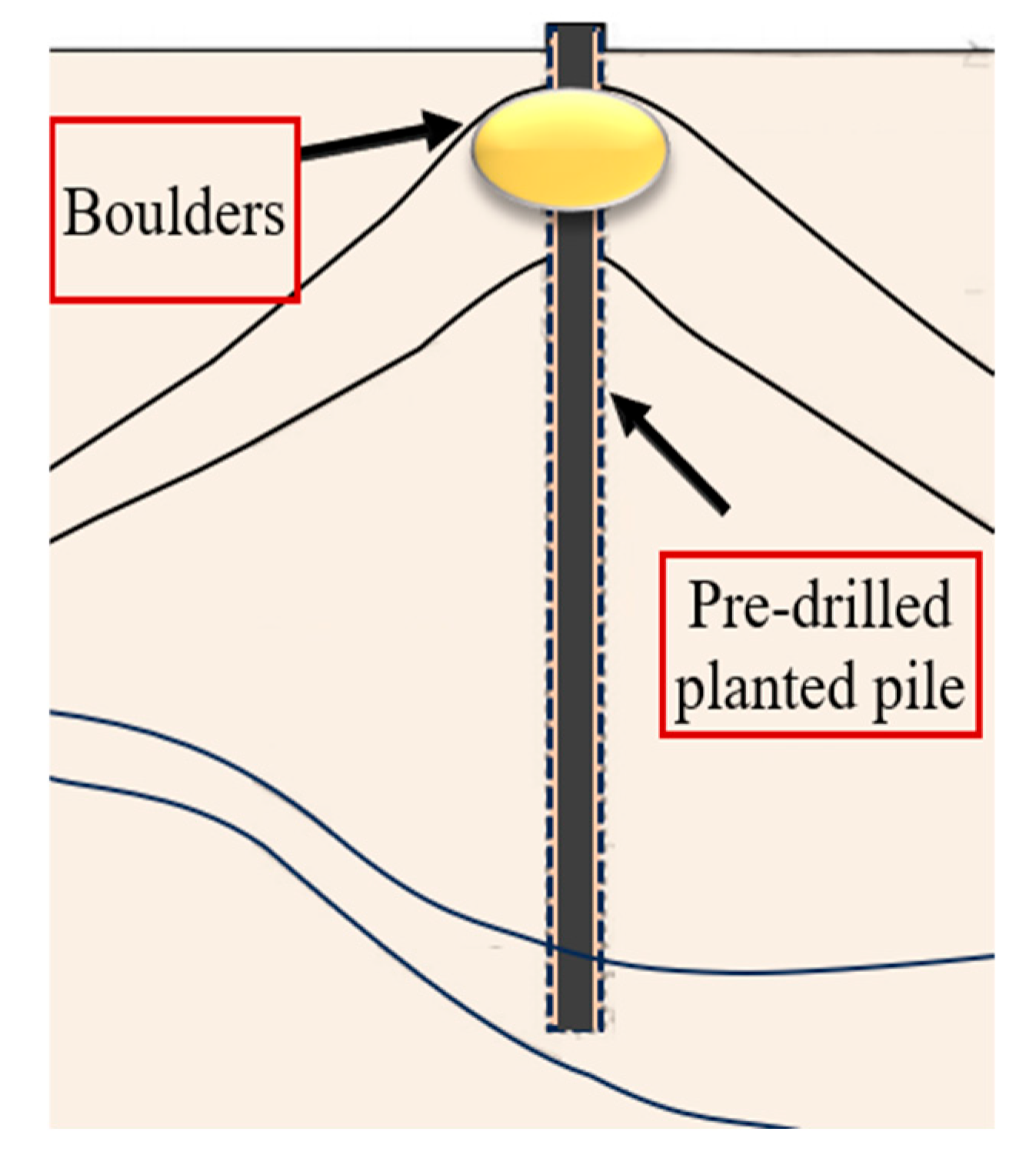
2. Project Overview

The Xiamen New Sports Center is a municipal sports facility located in the eastern new town outside the main island of Xiamen City, Fujian Province, China. The construction site is characterized by complex conditions, with boulders of varying sizes and shapes distributed across the area. The distribution and burial depth of these boulders are random, and boulders can also be found at varying depths in the same location, as shown in Figure 1, the red boxed sections are boulders.

According to the geotechnical investigation report for the New Sports Center project [37], the design and construction in areas with boulders should consider their adverse effects. The design employs concrete composite pipe piles to treat the site and utilizes drilled root-planting pile construction. Drilled root-planting pile construction involves pre-drilled holes at specified locations, pouring in concrete, and then implanting precast pipe piles into the concrete to form a new type of composite pile foundation. Since boulders are commonly distributed within the depth range of the base piles, they should be incorporated into the load-bearing system rather than removed artificially. During the pre-drilled process, boulders are drilled alongside the formation of holes so that pipe piles can be inserted and concrete poured last. The schematic diagram of pre-drilled planted piles in boulder fields is shown in Figure 2, the red box is the name of the arrow pointing to the object.

3. Design of the Planted Pile Model Tests Based on Transparent Soil

3.1. The Planted Pile Model Test Device and Transparent Soil Formulation

The model test apparatus, as shown in Figure 3, mainly comprises a model box, loading system, and imaging and information collection and processing systems, among others. Referring to Ni [34], the width of the model box was determined to be 200 mm to achieve maximum transparency of the transparent soil. Considering the size effect from related literature [38], the internal dimensions of the box were set as 400 mm in length, 200 mm in width, and 450 mm in height, constructed using 5 mm thick transparent acrylic sheets. The experimental loading system consists of a reaction frame, pull rope, fixed pulleys, loading platform, and weights. The load application was achieved by increasing the number of weights. Two fixed pulleys were secured at designated locations on the reaction frame: one for positioning the model box (the center point of the model box, with distances of 200 mm and 100 mm from the edges) and the other for determining the load application position. A rope was passed through the pulleys, connecting the toggles at the top of the piles to the weight trays (where the experimental weights were placed). The imaging system includes a laser, a digital camera, a DH3816 static strain testing system, and a notebook.

The transparent soil used in this experiment is composed of a mixture of fused quartz sand, n-dodecane, and No. 15 white oil. The transparency of transparent soil is primarily determined by the degree of refractive index matching between the particles and the liquid. A closer match in refractive indices results in higher transparency, while ensuring uniform particle distribution, thorough mixing, and adequate degassing during preparation. The refractive indices of the three materials at a room temperature of 23 °C are shown in

Table 1. Transparent soil preparation materials and their refractive index.

Material	Refractive Index
Fused quartz sand	1.4585
N-dodecane	1.4215
No. 15 white oil	1.460

.

The volume ratio of n-dodecane to No. 15 white oil is estimated using Equation (1):

$$A\mathit{x}+B\mathit{y}=C\left(\mathit{x}+\mathit{y}\right)$$

(1)

where $A$ is the refractive index of n-dodecane, $B$ is the refractive index of No. 15 white oil, $C$ is the refractive index of fused quartz sand, and $\mathit{x}/\mathit{y}$ is the volume ratio of dodecane to No. 15 white oil.

N-dodecane and No. 15 white oil are mixed in a volume ratio of 1:24.67 to create a pore solution. After ensuring thorough mixing, the refractive index of the mixture was measured using an Abbe refractometer. The proportions of the two liquids were adjusted based on the observed refractive index until it reached 1.4585, which is equivalent to the refractive index of quartz sand. Once configured, the porous solution was poured into a model box lined with quartz sand, and after thorough mixing, approximately 30 min of vacuum treatment was conducted. After the vacuum treatment, the model box was placed in a thermostatic chamber at 23 °C for 24 h to ensure the soil particles within the box were adequately consolidated and any remaining air bubbles were expelled.

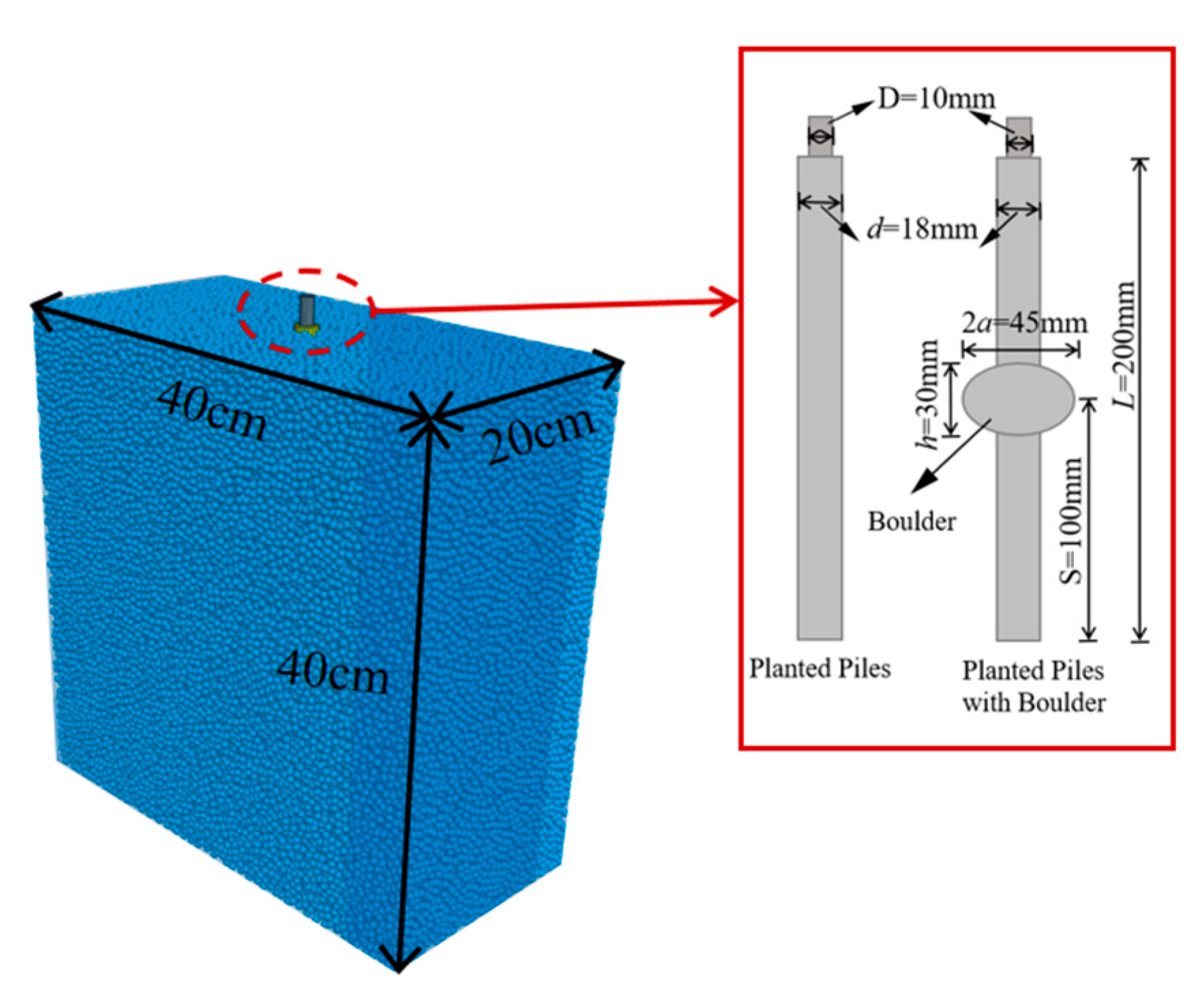
3.2. Pile Planted Model and Test Program

Two conditions are established: one without boulders in the pile body (Condition 1) and another with boulders located in the pile body (Condition 2), to comparatively analyze the impact of boulders on the bearing capacity of planted piles. In the model tests, the core pile of the foundation pile model was made of a hollow aluminum tube, while the outer concrete of the pile was composed of epoxy resin. To prevent laser reflections from the aluminum tube that could affect observation and image capture, the surface of the aluminum tube was coated with black paint. The construction of the pile planting model is illustrated in Figure 4, the red boxes are strain gauges. After the surface coating dries, a layer of quartz sand is wrapped around the outer surface of the pile to simulate realistic pile formation effects. Based on the engineering planted pile prototype, the model pile size was determined according to the geometric similarity ratio of 1:100, and the model pile parameters are shown in

Table 2. Dimensional parameters for modeled piling.

Condition	Pile Type	Core Pile Outer Diameter D1/mm	Core Pile Wall Thickness t1/mm	Caliber D/mm	Core Pile Wall Thickness t2/mm	Pile Length L/mm
1	Planted piles without boulder	10 mm	1.5 mm	18 mm	4 mm	200 mm
2	Planted piles with boulder	10 mm	1.5 mm	18 mm	4 mm	200 mm

.

An ellipsoid was selected as the shape of the model boulder, with the long axis, short axis, and thickness measuring 22.5 mm, 15.0 mm, and 30.0 mm, respectively. A cylindrical hole with a diameter of 18 mm was reserved on the surface of boulder to accommodate the inserted foundation pile and was fabricated using transparent resin through 3D printing. The boulder model was also cast monolithically with the planted pile model using epoxy resin that simulates concrete material.

Displacement gauges were employed to measure the settlement displacement of the weight tray, thereby obtaining the uplift displacement at the pile head. To obtain the axial force distribution along the pile, seven monitoring sections were arranged along the longitudinal direction on the exterior surface of the aluminum tube and the epoxy resin, with intervals of 3 cm, and 120-1AA miniature strain gauges were attached.

During the experimental process, loading was applied incrementally by adding weights to the top of the pile. After each loading stage, the next level of loading could proceed only if the following condition was met: the displacement at the pile top was less than 0.01 mm within 20 min and the axial force of the pile remained stable. If, under a certain loading stage, the displacement at the pile top exceeded twice that of the previous loading stage, or if a distinct inflection point appeared on the load–displacement curve, the loading test was terminated. During the transparent soil test loading process, photographs were taken of the core area surrounding the model pile, and the images were analyzed using PIVLab 2022a software to obtain the displacement field distribution of the soil around the pile.

4. Numerical Modeling

4.1. Model Construction

The numerical model mainly consists of two parts: the pile and the soil. FLAC3D is capable of accurately describing stress and strain distribution as well as the nonlinear deformation behavior of piles. Therefore, the pile structure is modeled using FLAC3D solid elements. On the other hand, PFC3D can capture the interactions between soil particles, discontinuities, and complex large deformation behaviors of soil. As a result, the soil is modeled using PFC3D sphere elements, and the boulder uses PFC3D rigid clusters, creating a coupled domain in the contact area between the pile and the soil. The dimensions of the numerical simulation are consistent with those of the experiment.

The soil is simulated by particles with a diameter ranging from 3 to 5 mm, totaling 160,000 particles. The friction coefficient between particles is set to 0.4, while the friction coefficient between particles and wall elements is set to 0.1. The numerical calculation model is illustrated in Figure 5, the red box shows the dimensional details of the pile.

4.2. Constitutive Model and Material Parameters

The top of the model is a free surface, the bottom is fixed, and the sides are in a sliding constraint state. Firstly, the PFC3D spherical elements are preloaded to obtain a free field model. Then, particles at the positions of boulders and pile insertions are removed from the free field model to generate the boulders and pile models. Finally, tensile stress is applied to the surface of the pile foundations to simulate the forces experienced during the extraction process. The contact model for the soil units employs the elastic model in PFC3D, with key parameters as shown in

Table 3. PFC3D linear contact parameters.

Name	Unit	Effective Modulus E MPa	Stiffness Ratio - -	Friction Coefficient F -
Soil–soil	Ball–Ball	100	1.5	0.4
Soil–boulder	Ball–Ball	50	1.5	0.3
Soil–pile	Ball–Ball	50	1.5	0.5
Pile–boulder	Ball–Ball	500	1.5	0.7

. The specific parameters of the model are listed in

Table 4. FLAC3D model parameters.

Name	Constitutive Model	Weight Density γ kN/m3	Elastic Modulus E GPa	Poisson’s Ratio - -	Cohesion c kPa	Friction Angle φ °
The core pile	Elasticity	27	70	0.33	-	-
The outer concrete	Elasticity	12	2	0.38	-	-

.

5. Calculation Results and Analysis

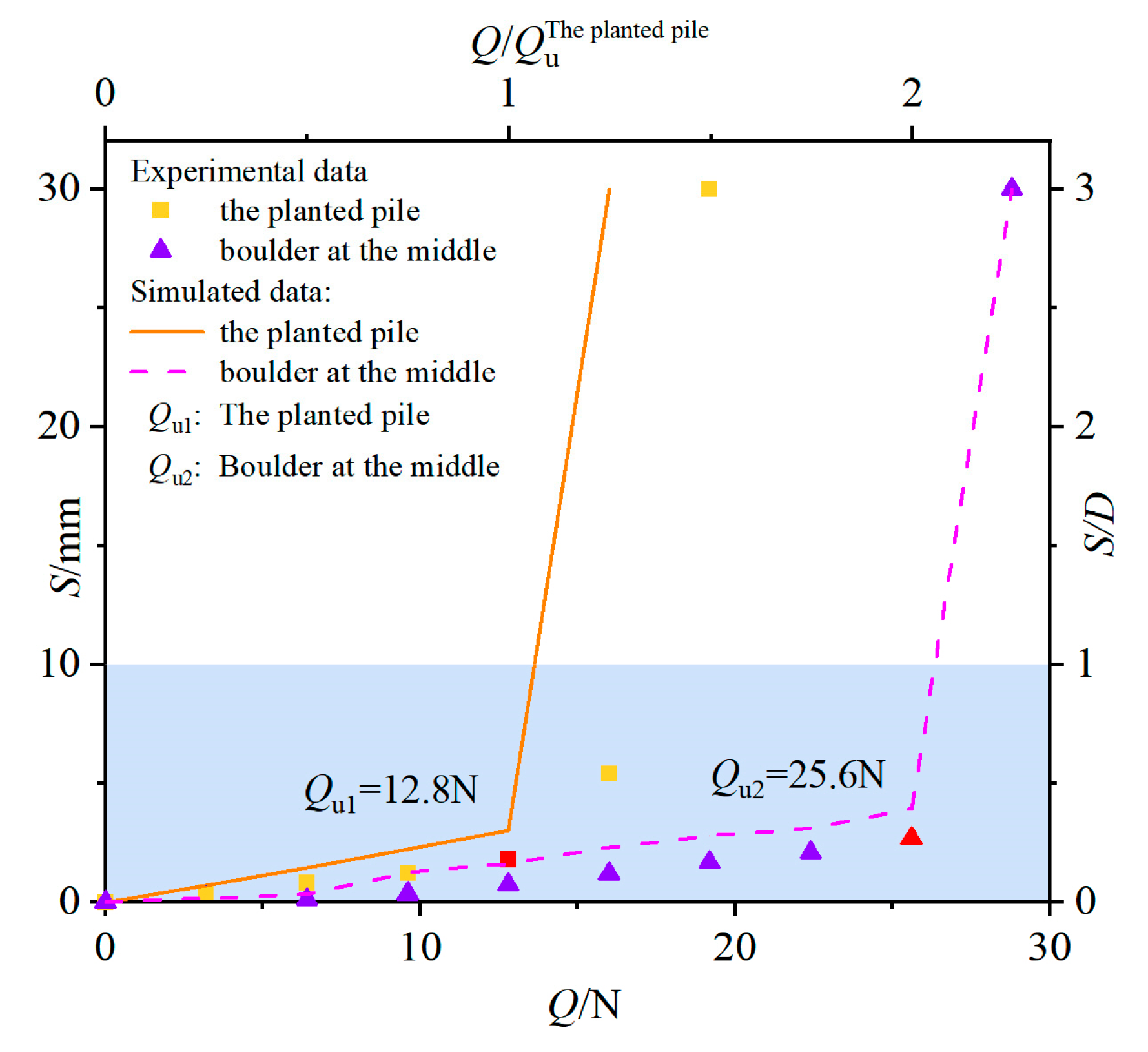
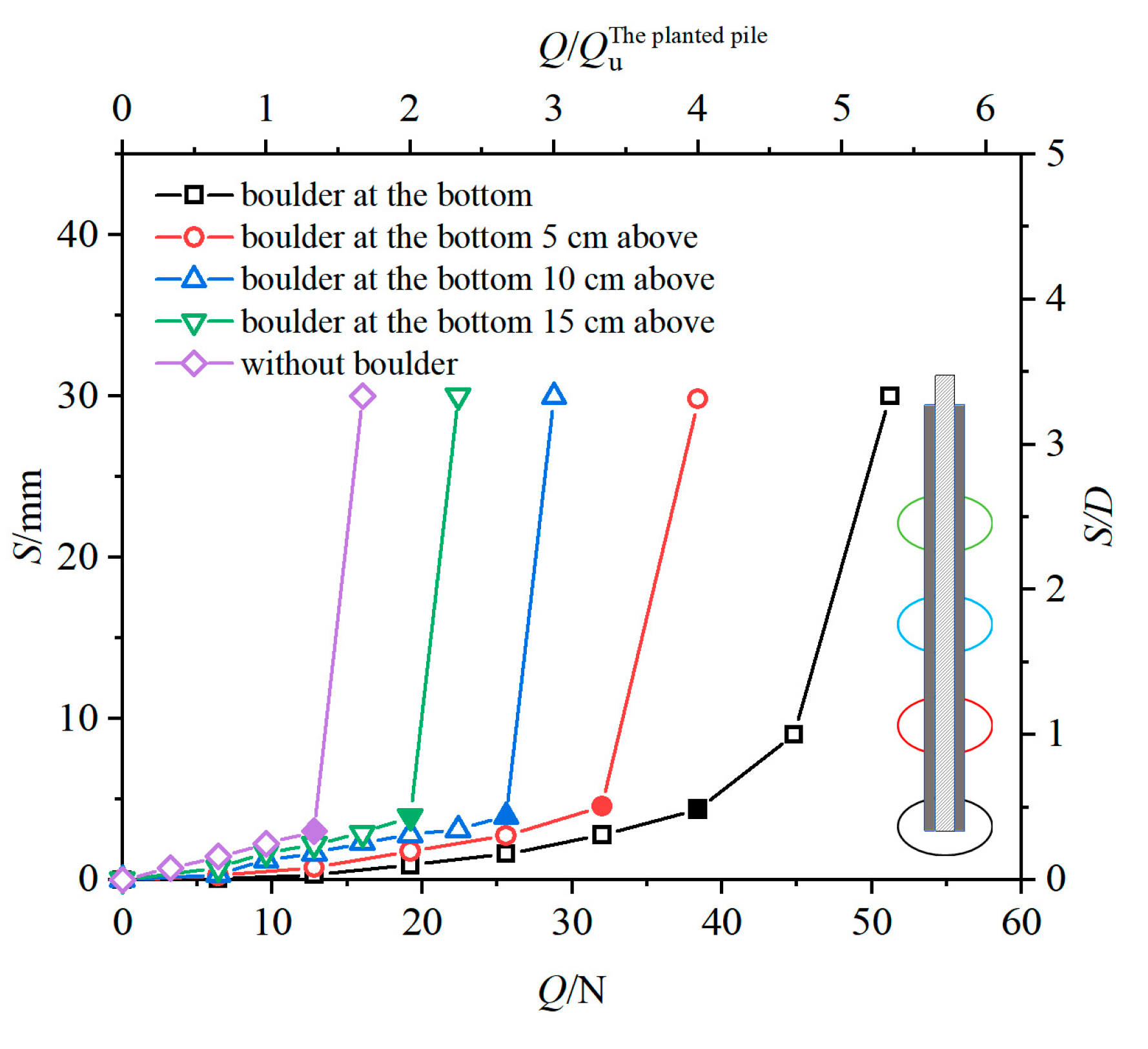
5.1. Q-S Curve Analysis

Figure 6 displays the load–displacement (Q-S) curve of the pile under vertical loading, derived from experimental data and numerical simulations. The numerical results are consistent with the experimental results, thereby validating the high accuracy of the numerical simulation. The Q-S curves for both conditions exhibit similar trends, with distinct inflection points (marked in red in the figure). Before the inflection point, the pile head displacement increases gradually with the applied load; after the inflection point, the displacement increases abruptly, and the pile undergoes rapid uplift.

The red-marked inflection points in Figure 6 represent the ultimate uplift resistance of the pile. The Q-S curves of the piles generally exhibit a consistent abrupt pattern, with their characteristics closely related to the presence of boulders. The Q-S curve for Condition 2 is more gradual. Specifically, for Condition 1, the load at the inflection point is 12.8 N, with a corresponding pile head displacement of 2 mm; for Condition 2, the load at inflection point is 25.6 N, with a corresponding displacement of 2.7 mm. Clearly, the pile in Condition 2 can withstand a greater uplift load. Under the same applied load (12.8 N), the uplift displacement of the pile in Condition 2 is only 1.2 mm, whereas the pile in Condition 1 reaches its ultimate uplift displacement of 2 mm. Under the same applied load (12.8 N), the uplift displacement of the pile in Condition 2 is only 1.2 mm, whereas the pile in Condition 1 reaches its ultimate uplift displacement of 2 mm. This phenomenon can be attributed to the increased cross-sectional area due to the presence of a boulder, which enhances the vertical support provided by the overlying soil, enabling the pile with the boulder to withstand greater uplift loads.

The ultimate uplift resistance of the pile in Condition 2 (25.6 N) is approximately twice that of the pile in Condition 1 (12.8 N), while the corresponding pile head displacement (2.7 mm) is about 1.35 times that of the pile in Condition 1 (2 mm). This indicates that boulders significantly enhance the uplift resistance of the pile and reduce the uplift displacement. The boulders act as load-sharing components, becoming an integral part of the pile-bearing system, not only providing greater load-bearing capacity but also significantly increasing the side friction resistance.

5.2. Axial Force Transmission Analysis of the Core Pile

By calculating the strain at various sections of the core pile under different pile head loads, the axial force distribution along the core pile is obtained, as shown in Figure 6. The results show that under the applied load, the upper section of the core pile plays a dominant role. As the load increases, the upper load is transmitted downward along the pile shaft and transferred to the surrounding soil through the outer concrete. When a boulder is present in the pile, the load can also be transmitted to the boulder through the outer concrete and ultimately to the surrounding soil.

To counteract the uplift tendency of the core pile, the outer concrete layer exerts downward frictional resistance on the core pile. The axial force curves at different pile sections exhibit varying rates of decrease, with their slopes directly reflecting the magnitude of the frictional resistance. Figure 7a displays the change in axial force along the core pile under Condition 1. It can be observed that the axial force decreases gradually with depth, reaching a minimal value near zero at the pile tip, indicating that the end resistance is negligible, and the load is primarily borne by side friction. Within 3 cm from the pile top, the rate of decrease of the axial force curve of the core pile is the greatest, because under loading, the core pile undergoes deformation due to tensile forces at the pile head, resulting in the displacement difference between the core pile and the outer concrete at the head being maximized, leading to significant internal friction resistance at the head. As the depth increases, the displacement difference between the core pile and the outer concrete gradually decreases, and the internal friction resistance correspondingly diminishes and stabilizes, indicating a strong cohesion between the concrete and pipe pile and good compatibility of deformation between the core pile and outer concrete. In Condition 2 (Figure 7b), the axial force of the pile also decreases with depth. However, due to the presence of boulder, the cross-sectional diameter of the pile increases, providing greater vertical support force from the overlying soil and increasing the contact area with the surrounding soil, thereby expanding the pathways for load transfer to the surrounding soil. Consequently, in the region where boulders are present, the axial force along the core pile decreases sharply. When the uplift load reaches the ultimate uplift resistance of 25.6 N, the pile tip contributes approximately 32% of the total uplift resistance.

Under both conditions, the load is transferred from the pile head to the pile tip, and the axial force of the core pile decreases in depth, with the axial force at the pile bottom being small and the axial force of the pile approaching zero, indicating that the end resistance is negligible, and the load is primarily borne by side friction. However, the presence of a boulder provides additional vertical support and pathways for load transfer, thus offering some end resistance to the pile, enhancing its uplift capacity.

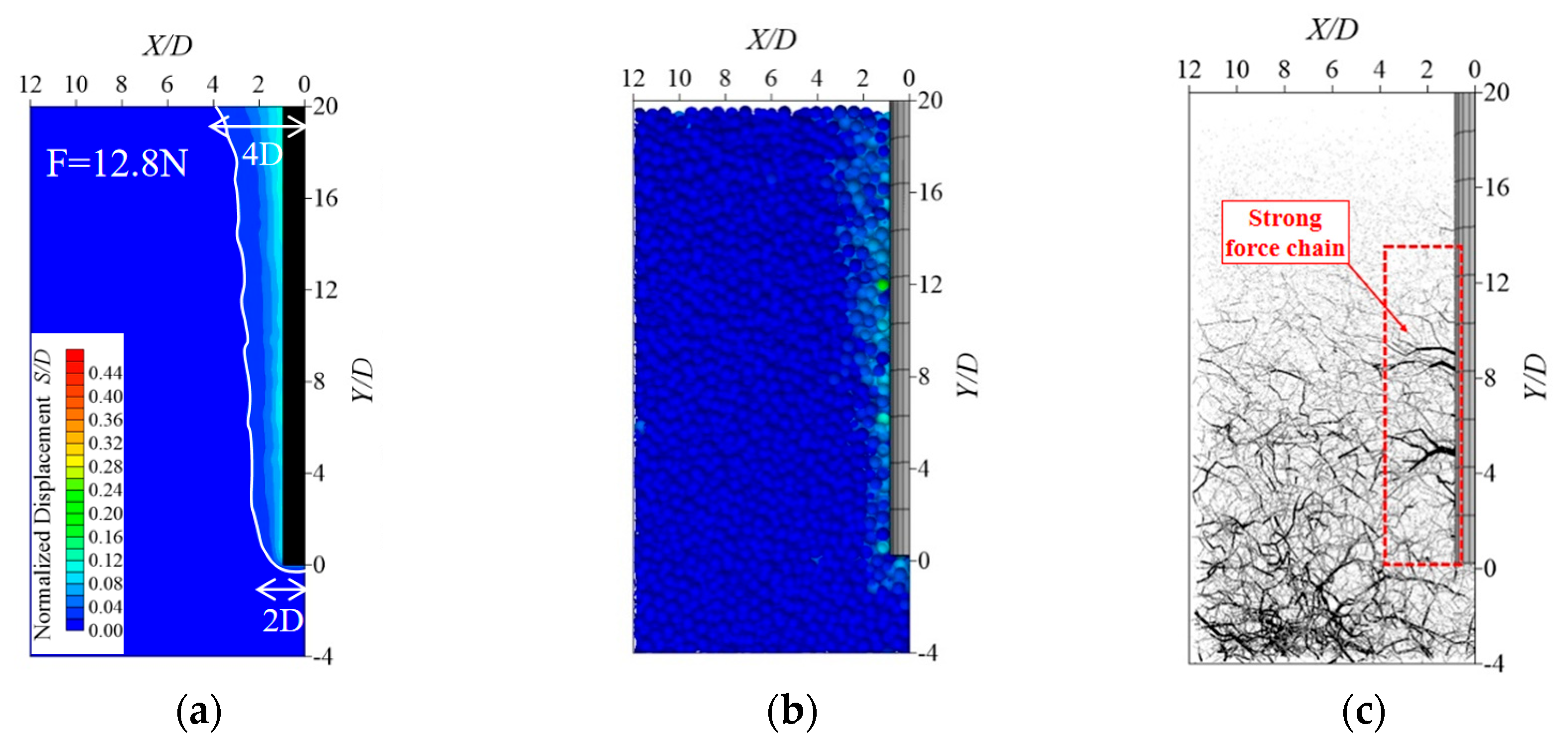
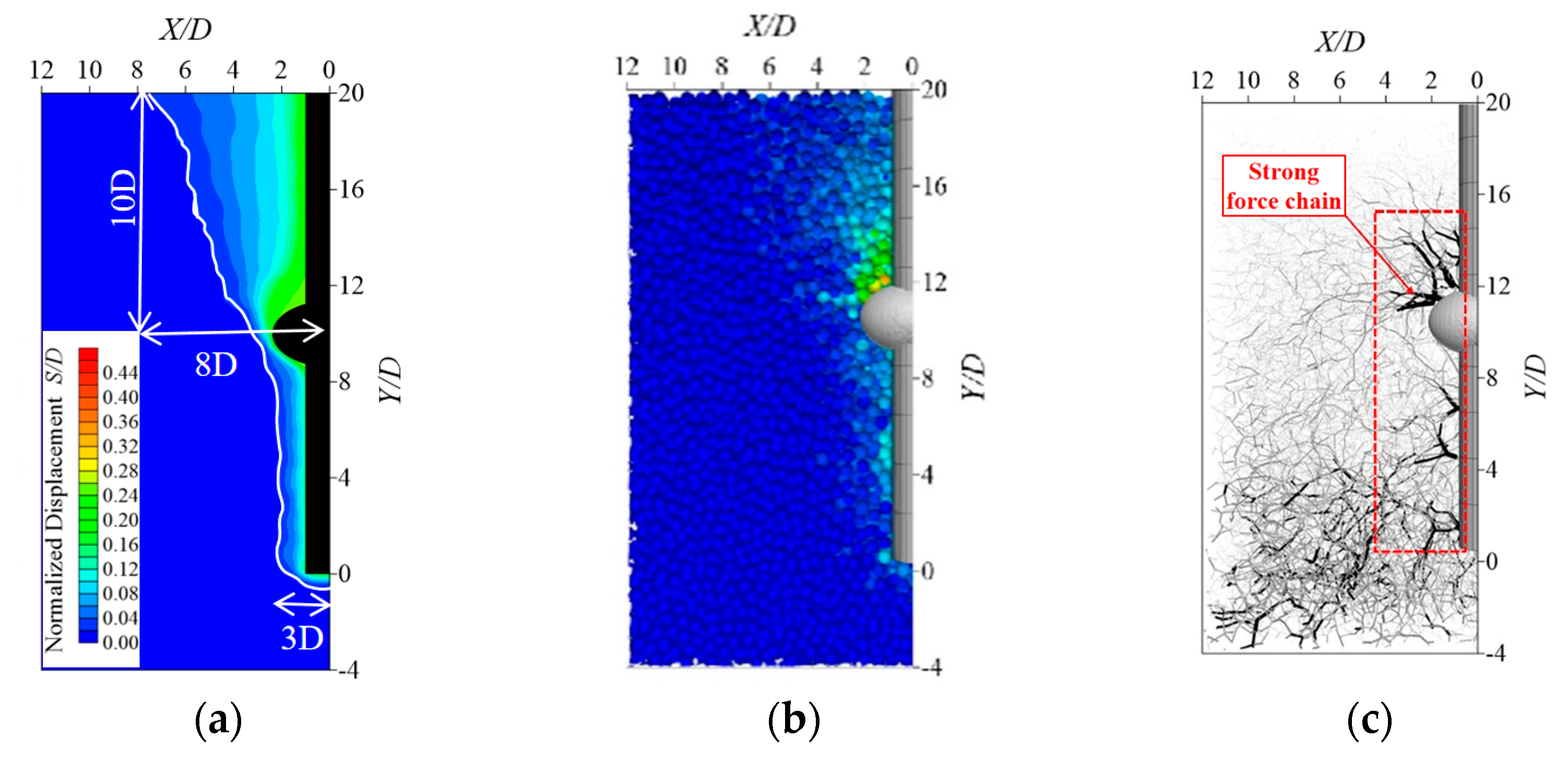
5.3. Soil Displacement Field Analysis

Figure 8 and Figure 9 show the displacement cloud map of the soil and the force chain diagram of soil particles under the action of ultimate bearing capacity. In the figure, X and Y represent the horizontal and vertical distances from the center of the pile head, respectively, both normalized by the diameter D of the core pile.

Under the action of ultimate load, the influence of the planted pile in Condition 1 on the soil in the Y direction is not significant; however, in the X direction, the range of soil influence is approximately from 0D to 4D, with the displacement field distribution presenting an inverted triangular shape. The soil displacement decreases gradually in the horizontal direction away from the center of the pile, with the maximum displacement occurring at the pile head and decreasing progressively along the pile depth. For Condition 2, the range of influence on the soil in the Y direction is primarily within the length of the pile shaft, approximately 10D, whereas in the X direction, the influence range is about twice that of Condition 1, reaching 8D. This is because the boulder increases the contact area between the pile and the soil, resulting in greater compression between the pile and the soil, which amplifies the horizontal displacement component of the soil above boulder and extends the influence range of the pile tip on the surrounding soil. Due to the shallow burial depth of the boulder, the sliding failure surface of the pile forms earlier, resulting in the largest impact range on the soil in the X direction at the ground surface. The displacement distribution of the soil below the boulder tends to align with that of piles without boulders. The force chain diagram of the pile shows that the strong force chain area in Condition 1 appears deep within the pile, where the side friction resistance at greater depths fully exerts its effect under the ultimate load. In Condition 2, the strong force chain area is in the soil particles above the boulder and those in contact with the pile shaft, confirming that during the uplift process, boulders can provide more side friction resistance and uplift resistance, effectively counteracting the uplift load.

This phenomenon further confirms the positive influence of the boulder on the mechanical performance of the pile, particularly in enhancing uplift resistance and optimizing load transfer mechanisms. It is also worth noting that the presence of the boulder increases the bearing capacity of the pile and correspondingly expands its influence on the surrounding soil. Therefore, when the cross-sectional area of the boulder is approximately four times that of the pile and it is in the middle of the pile, attention should be paid to the impact of the pile on other piles in engineering practice, with a recommended spacing greater than 8D.

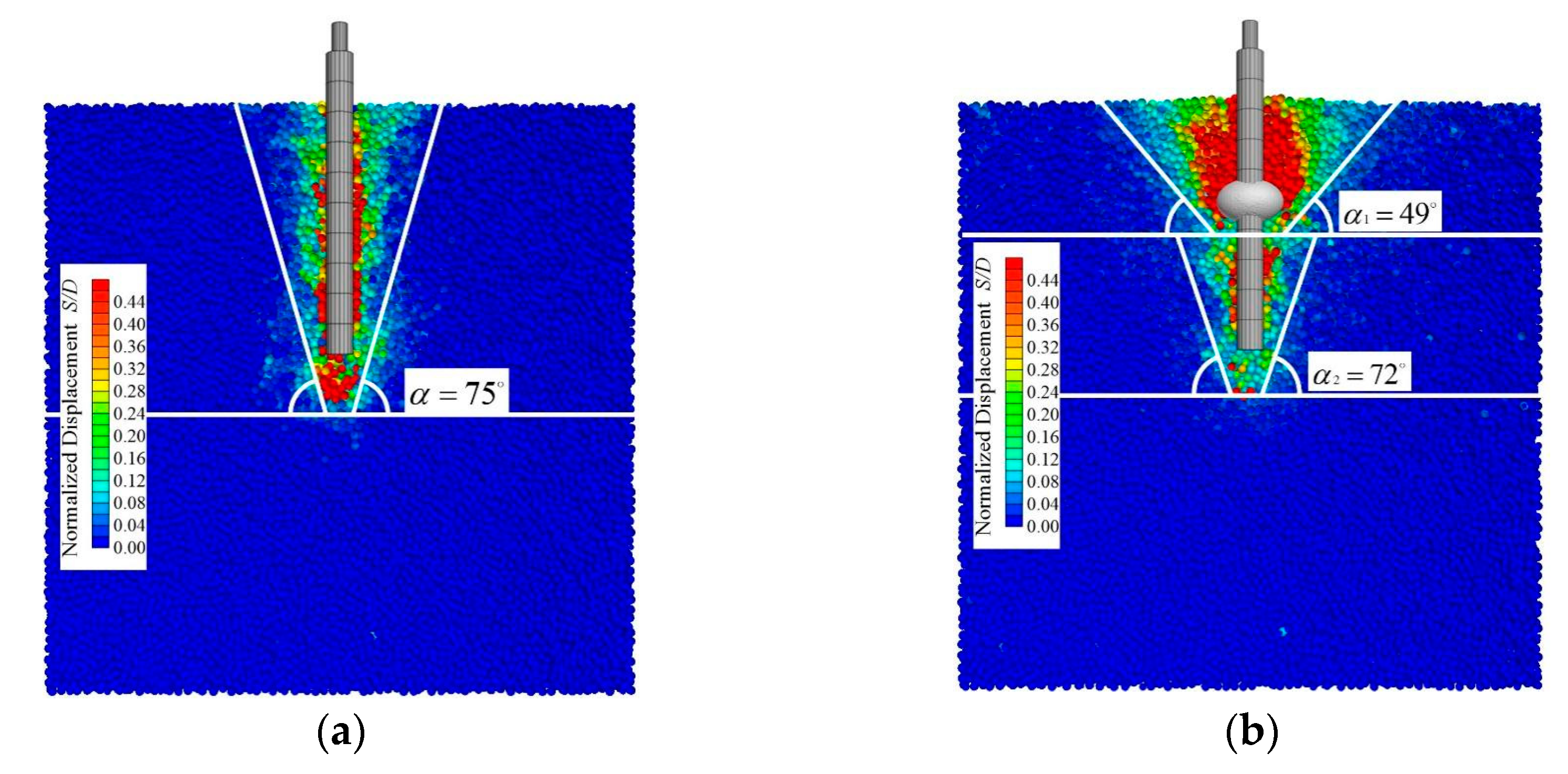
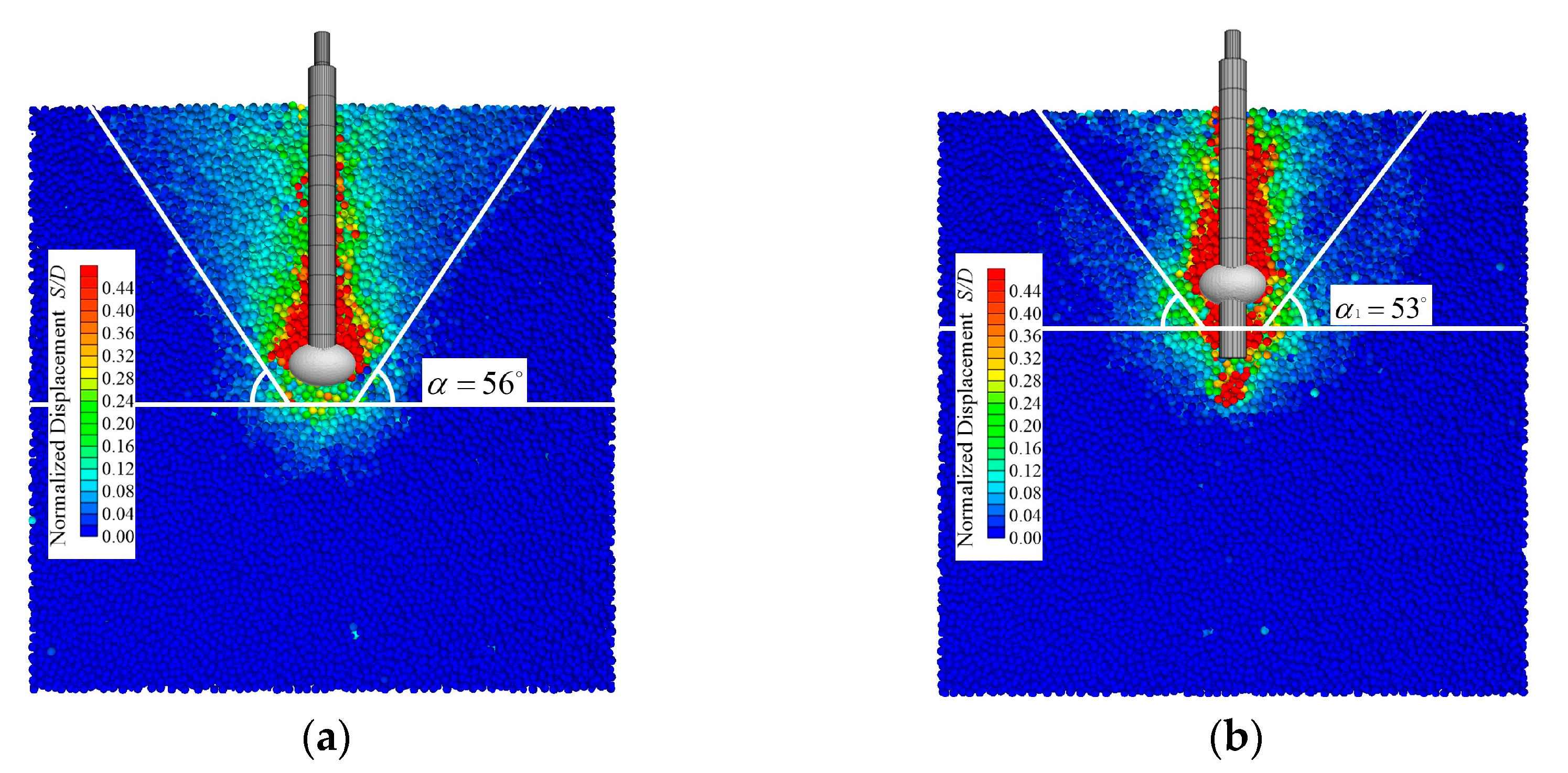
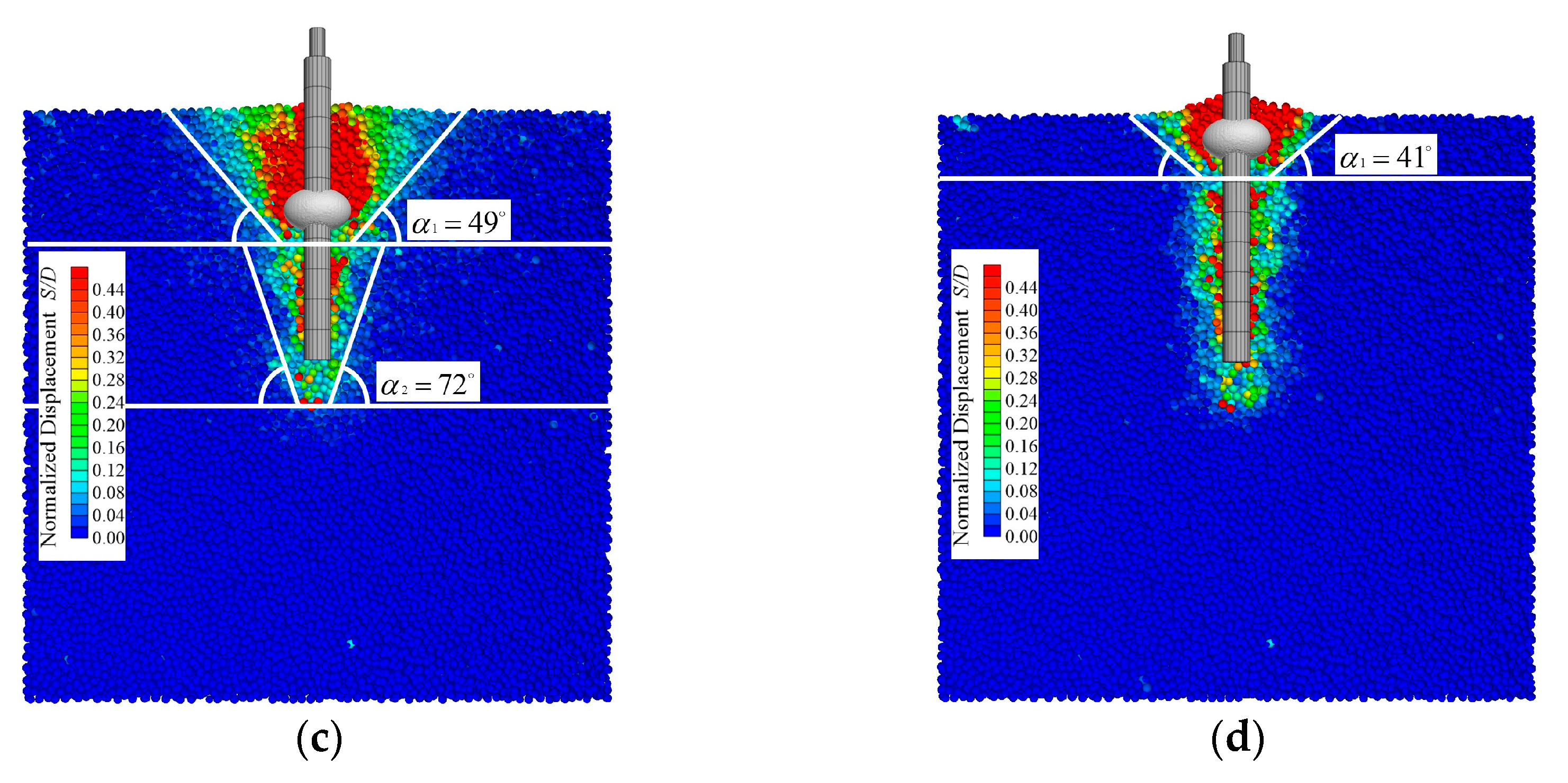
5.4. Analysis of Shear Damage Slip Fracture Surfaces and Surface Deformation

The shear failure sliding surface of the soil refers to the slipping surface formed during shear failure around the pile, which typically develops along a path of relatively lower shear strength within the soil. The ultimate load in this study is defined as the applied load just before the abrupt increase in pile head displacement (at the inflection point). Considering that the surrounding soil may not have fully deformed at this time, the paper presents the sliding failure surface morphology during the 3D displacement of the uplift of the pile, as obtained from numerical simulations (Figure 10).

Figure 10a shows the sliding failure surface for Condition 1, where the angle between the sliding surface and the horizontal plane is 75°, indicating that the influence of the pile on the soil is primarily concentrated in a narrow region along the pile shaft. Figure 9b presents the sliding failure surface for Condition 2, where the boulder is in the pile; thus, the sliding surface can be divided into two parts, above and below the boulder. Below the boulder, the movement of the soil is influenced by the boulder, resulting in a decrease in the sliding surface angle from 75° to 72°. Simultaneously, the angle of the sliding surface of the soil above the boulder diminishes from 75° to 49°. The presence of the boulder significantly affects the morphology of the sliding failure surface during the uplift of the pile, leading to changes in the angle of the sliding surface.

Figure 11 illustrates the surface deformation characteristics under different conditions. When the uplift displacement of the pile is 3D, the sliding failure surface has extended to the ground surface. In this case, the influence range of surface uplift for Condition 1 extends up to 7.5D, as shown in Figure 10a, while for Condition 2, it expands to 13D. The presence of the boulder provides the pile with more pathways for load transfer and resistance, significantly increasing both the uplift load and displacement, thus enhancing the pile’s influence on the soil, as illustrated in Figure 11b. Thus, for the same upward displacement, the range of surface uplift is influenced by the presence of a boulder. The influence range of piles containing a boulder on the ground surface is larger. This may be attributed to the boulder enabling the pile to withstand greater uplift forces, thereby subjecting the surrounding soil to higher stress and affecting a wider area. It is also worth noting that the presence of the boulder increases the bearing capacity of the pile and correspondingly expands its influence on the surrounding soil. Therefore, when the cross-sectional area of the boulder is approximately four times that of the pile and it is located in the middle of the pile, attention should be paid to the impact of the pile on other piles in engineering practice, with a recommended spacing greater than 8D.

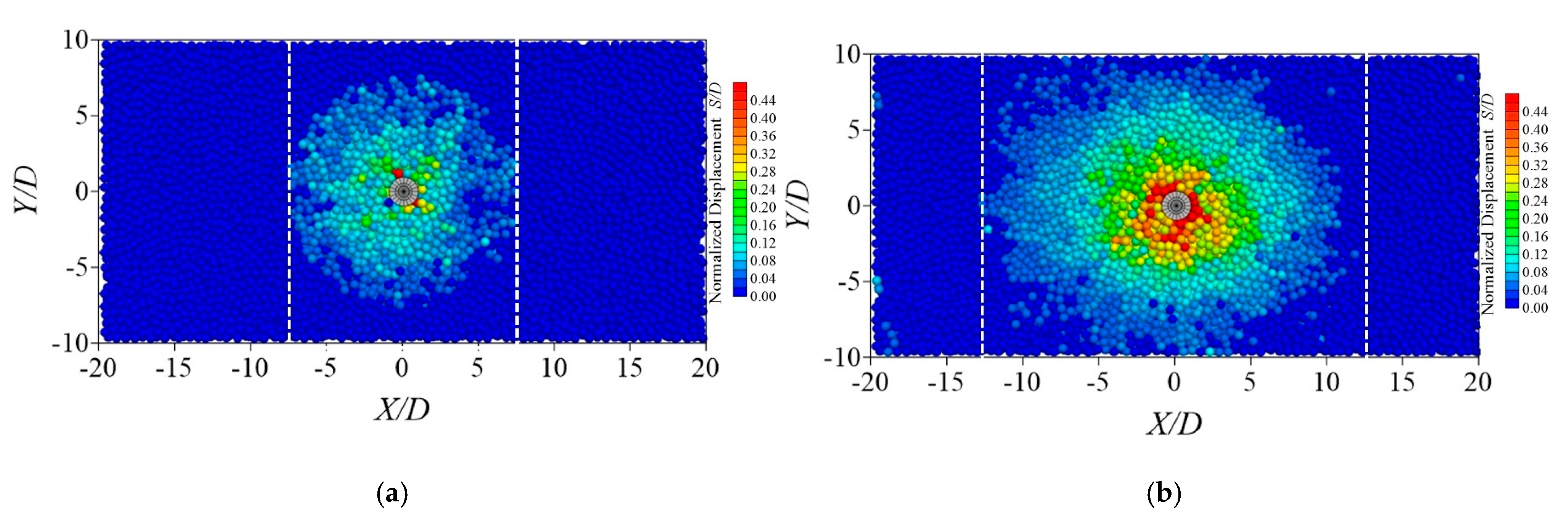
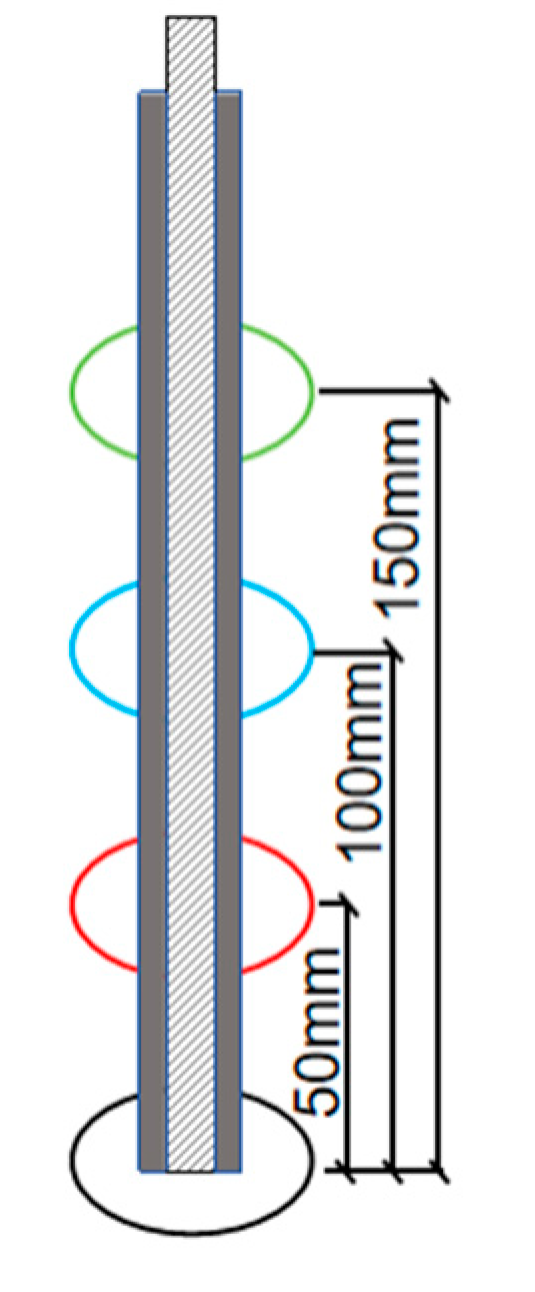
6. Analysis of the Influence of Boulder Position

To further examine the effect of boulder position on the angle between the sliding failure surface and the horizontal plane, as well as its influence range, numerical simulations were conducted for boulders located at distances of 0, 50, 100, and 150 mm from the pile tip, compared with piles without boulders. The position of the boulder along the pile is illustrated in Figure 12, circles in the picture represent boulders, different colors are used to distinguish isolated stones in different locations.

Figure 13 shows the relationship between the uplifting load and displacement of the pile under different boulder burial depth conditions, circles in the picture represent boulders, different colors are used to distinguish isolated stones in different locations. It can be observed from Figure 13 that, compared to piles without boulders, the presence of a boulder at each position enhances the uplift capacity of the pile. With the same load at the pile head, the boulder caused the pile head displacements to decrease to varying degrees, and the deeper the boulder is buried, the lesser the pile head displacement. Additionally, as boulder position increases along the depth of the pile, the Q-S curve gradually becomes gentler, yet all exhibit a steep drop-off type of curve.

The Q-S curve indicates that the boulder increases the contact area with the surrounding soil, thereby utilizing the pressure from the overlying soil to resist the uplift load. As the burial depth of the boulder increases, the thickness of the overlying soil also increases, enabling greater side friction and resistance, which in turn raises the ultimate uplift capacity of the pile, indicating that the contribution of the boulder to the pile’s bearing capacity increases with burial depth. Notably, when the boulder is located at the pile tip, its contribution to the pile’s bearing capacity is greater compared to other positions of the boulder. As the boulder moves from the pile bottom to the pile top, the ultimate uplift resistance values are 38.4 N, 32 N, 25.6 N, and 19.2 N, representing increases of 3 times, 2.5 times, 2 times, and 1.5 times compared to piles without a boulder, respectively.

Figure 14 illustrates the morphology of the sliding failure surface of the pile during uplift under different burial depth conditions of the boulder. As observed in Figure 14, as the position of boulder moves from the pile bottom to the top, the angle between the sliding surface and the horizontal plane decreases from 56° when boulder is at the pile tip to 41° when boulder is located 150 mm above the pile bottom. At the same time, the horizontal influence range of the sliding surface extending to the ground surface gradually reduces as the burial depth of boulder decreases. In the vertical direction, the closer the boulder is to the ground surface, the greater the height of the ground uplift caused by the pile during uplift, while the extent of the uplift decreases correspondingly.

In this study, the bearing characteristics of grouted piles in a boulder stratum were analyzed using a combination of transparent soil scaled-down laboratory tests and coupled PFC-FLAC numerical simulations. The results provided valuable insights into the micro-scale deformation, stress distribution, and dynamic response. However, due to the errors associated with the scale effect in the scaled-down tests, the findings are still subject to certain limitations. Future work will focus on conducting large-scale tests and optimizing the experimental equipment to enhance the accuracy and universality of the research results.

7. Conclusions

This study, based on actual engineering problems in the Xiamen region of China, employs transparent soil technology to conduct non-intrusive pull-out model tests. It compares two scenarios—with and without a boulder—to investigate the influence mechanism of the boulder on pile bearing capacity, the influence range of the pile on surrounding soil, and the development of sliding failure surfaces. Additionally, FLAC3D-PFC3D numerical simulations are used to analyze the relationship between the contribution of the boulder to pile bearing capacity and their position along the pile. The study concludes with the following findings:

(1)

The presence of boulders significantly enhances the overall bearing capacity of the pile. Specifically, boulders increase the effective cross-sectional diameter of the pile, providing additional vertical support. Additionally, boulders enhance load transfer pathways to the surrounding soil and expand the contact area, thereby extending the influence range of the pile on the surrounding soil.

(2)

During the pulling process of the planted pile, the vertical impact depth on the soil primarily concentrates within the length range of the pile body. The presence of boulders modifies the morphology and horizontal influence range of the soil displacement field. Under extreme uplift loads, the displacement field of the surrounding soil for piles without boulders exhibits an “inverted triangle” distribution, with the maximum horizontal influence range on the surface soil being approximately four times the pile diameter (4D). However, when a boulder is positioned within the pile, the displacement field around the pile shows an overall distribution of two “inverted trapezoids” with the horizontal influence range on the soil expanding from 6D above a boulder to 8D at the surface.

(3)

The presence of the isolated boulder can amplify the impact on the surrounding soil during the uplift failure of a grouted pile. When the cross-sectional area of an isolated boulder is approximately four times that of the pile and it is in the middle section of the pile, the distance to adjacent piles should be greater than eight times the pile diameter in engineering practice.

(4)

The presence of a boulder alters the angle of the sliding failure surface of the pile, and as the burial depth of a boulder decreases, the angle of the sliding failure surface also gradually reduces. When the boulder is at distances of 0, 50, 100, and 150 mm from the end of the pile, the angles of the sliding failure surface of the pile are 56°, 53°, 49°, and 41°, respectively, whereas under the condition without a boulder, it is 75°.

(5)

Boulders significantly enhance the ultimate uplift bearing capacity of the pile. When a boulder is at distances of 0, 50, 100, and 150 mm from the end of the pile, the uplift bearing capacity of the pile increases by 3, 2.5, 2, and 1.5 times, respectively, compared to the piles without boulder. This is attributed to the additional uplift resistance provided by the overburden from the boulder. The thicker the overburden, the greater the vertical resistance, thereby significantly improving the uplift bearing capacity of the planted pile.

(6)

When the boulder is embedded in the middle or lower part of the pile, their effect on enhancing the bearing capacity of the pile is more pronounced. Therefore, in practical engineering, when considering the inclusion of the boulder in the bearing system, priority should be given to the boulder located near the design depth of the pile, with a preference for the boulder positioned at the pile tip.