Abstract
The subject of the analysis is a modified auxetic structure in the form of rotating rectangles, which exhibit large negative Poisson’s ratio values. The structure modification consisted of introducing rotational axes on the surfaces of structural units near the corners of the rectangles. Such a system had previously unknown relationships between Poisson’s coefficient and parameters in the form of the quotient of the lengths of the sides of the rectangle, the position of the axis of rotation, and the degree of opening of the structure. Poisson’s coefficient is always −1 for square units, while it takes numerical values in a wide range of negative and positive values for rectangular units. Based on geometric relationships, formulas were determined to calculate the linear size of the structure and the values of Poisson’s ratio. It is shown that depending on the quotient of the lengths of the sides of the rectangle, the structures can lose their auxetic properties. For elongated rectangles (structures with a/b = 2.5), extremely high negative values of Poisson’s ratio are obtained but only for small changes in linear dimensions, and with greater stretching, the structure loses auxetic properties. Such a tendency occurs for a large group of structures of systems composed of rotating rectangles. The physical structures built provide an experimental complement to the research conducted.
1. Introduction
Auxetic structures are primarily mathematical concepts that have been given graphical form. Thanks to simulation studies, it has been discovered that they may have unusual mechanical properties that one would like to exploit. The technique awaits the applications of auxetics, and the community awaits the benefits of it. Numerous review papers present various aspects of auxetics and theoretically possible potential applications [1,2,3,4].
Auxetic structures can be used to produce advanced lightweight cellular materials for the aerospace, automotive, and construction industries [5], including in sandwich panels [6] and similar sandwich structures [7], for creating efficient structures for energy absorption [8,9], and for applications in biomedical engineering [10], especially in bone tissue and blood vessel engineering and as a stent [11]. Since 2000, there have been more than 105 review-type publications on auxetics, where the mentioned potential applications are a natural motivation for the analysis of auxetic structures. The idea is to exploit the effect of multidirectional expansion when structures are stretched and the effect of vertical and horizontal contraction when they are compressed.
A special group of mechanical metamaterials are so-called structures of rotating geometric figures, with squares, rectangles, triangles, or rhombuses appearing as unit cells. These structures in the form of computer graphics were first proposed by Retsch [12,13] in 1965. However, it is only since 2000 that these structures have been popularized by Grima groups, where in a very large number of publications, they have been subjected to careful analysis, e.g., [14,15,16], and it has been shown that, rotating structures have a negative Poisson’s ratio. A particular advantage of such structures is that their auxetic behavior was also illuminated in many other publications devoted to structures of rotating squares [17,18,19,20,21], or rotating rectangles [22,23,24,25]. Structures of rotating geometric figures are created by regularly arranging two-dimensional unit cells connected by corners.
The idea is to use the effect of multidirectional expansion when structures are stretched and the effect of vertical and horizontal contraction when they are compressed.
In publications, subjecting a representative number of unity cells in the structure to theoretical analysis is customary. Such an ideal image of auxetic structures has no relation to the practiced construction of these structures. Especially in all previous constructions, the connections of unit cells are the weak points of the structures because the damaging stresses pile up. In addition, the changes in the linear dimensions of such structures under tension or compression are small. These changes are those that the elastic properties of the materials of elementary cell connections allow.
The subject of the study is the known structures of rotating rectangles, which are characterized by the possibility of obtaining large negative values of Poisson’s ratio. For these structures, a simple and proven modification [26] was used, which consists of connecting rectangular elementary cells with axes of rotation. In this solution, the corners of the unit cells are overlapped, with the position of the axis of rotation passing through the overlapped corners being an important geometric parameter of the modified structures. The distance of the axis of rotation from the edge of the unit cell was defined as the x parameter. When such structures are stretched or compressed, the structural units not only rotate and the angles between adjacent sides change, but the units also move, which leads to planar expansion or contraction, which is an auxetic behavior. The structure deforms not only by the relative rotation of the squares but also by their translation.
This paper presents a mathematical analysis and experimental design of rotating rectangular structures with a large number of unit cells. This engineering approach to auxetic structures is technique-friendly and promotes the development of applications. However, it deviates from popular virtual-world simulation studies and applies to real meta-materials.
2. Mathematical Analysis of Modified Structures of Rotating Rectangles
Modified structures of rotating rectangles are formed by assembling unity cells in the form of a continuum, the linear dimensions of which can be theoretically calculated according to simple geometric relationships [27]. The above relationships for calculating the component sections are used to determine the size of structures X1 and X2, both in closed and open positions (Figure 1).
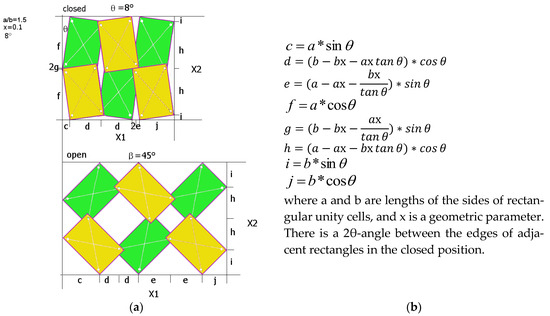
Figure 1.
The smallest unit of the modified structure of rotating squares in the closed position and in the open position (a), as well as the relationships of the lengths of the sections needed to calculate the dimensions of the structure (b).
The above relationships for calculating the component sections are used to determine the size of structures X1 and X2, both in closed and open positions.
The parameter x given in the formulas determines the position of the axis of rotation, with the distance of the axis of rotation from the edge b being a × x. It can be shown that the parameter x must satisfy the following condition:
Otherwise, the structures become immobile, and the rectangles block each other.
Based on the calculated values of X1 and X2, you can calculate Poisson’s ratio, corresponding to the transition from the initial position to the selected final position, such as from closed to open positions. The open position corresponds to the maximum stretch of the structure.
Poisson’s ratio is determined from the following relationship derived from the axial displacement:
Figure 2 shows the theoretically calculated values of Poisson’s ratio depending on the relative elongation of the structure for structures with different values of the parameter a/b and the geometric parameter x.
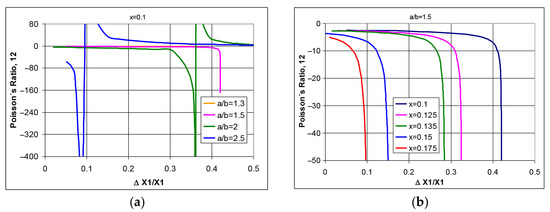
Figure 2.
Change in Poisson’s ratio as a function of elongation (a) for different values of the parameter a/b (x = 0.1) and (b) for different values of the geometric parameter x (a/b = 1.5).
The functional waveforms shown in Figure 2 show that certain values of Poisson’s ratio can be obtained depending on the size of rectangular unity cells. For rectangular elemental cells satisfying the condition a/b < 2, it is possible to obtain auxetic properties for the structure in the whole range of changes in linear dimensions. On the other hand, for unity cells for which a/b ≥ 2, the tested structures can show negative values of Poisson’s ratio only for certain ranges of changes in linear dimensions, e.g., in tension without reaching the maximum opening. For a fixed value of the parameter a/b, e.g., for a/b = 1.5, changing the position of the axis of rotation strongly affects the negative value of Poisson’s ratio. The farther the axis of rotation is located from the edge (the geometric parameter x increases, Figure 2b), the smaller the elongations, but at the same time, the larger the negative values of Poisson’s ratio become. It should be noted that as the structure is stretched, Poisson’s ratio changes. This means that not only does the structure’s geometry determine its value but also the amount of strain measured by the change in opening angle or linear dimensions.
3. Physical Structures of Modified Rotating Rectangular Structures
Numerous physical models were developed to illustrate the functioning of the modified structures of rotating rectangles and confirm the derived theoretical relationships. Structures were fabricated from different materials by means of assembly: a rigid material (laminated plate) and a material showing good flexibility (thin steel sheet).
Photographs of these exhibits are shown below, along with calculated and theoretical changes in elongation and corresponding Poisson’s ratio.
3.1. Structures Made of Flexible Rectangular Elementary Cells
This group of physical models was made by assembling laser-cut rectangles from elastic-elastic steel sheets, and structures with different numbers of unit cells were made from them.
For a symmetrical structure (n = m = 6) in which the straights satisfy the condition a/b = 2 (Figure 3), auxetic and non-auxetic ranges are obtained, with maximum negative values of Poisson’s ratio for horizontal elongation exceeding 36% and corresponding horizontal elongation of about 0.04%. With further stretching of the structure, positive values of Poisson’s ratio are obtained and the structure loses its auxetic properties. Similar behavior was obtained for the structure expanded to 8 × 13 (Figure 4). For the structure of the asymmetric structure (m ≠ n), the dependence of Poisson’s coefficient on linear expansion is identical to that for the symmetric structure (m = n).
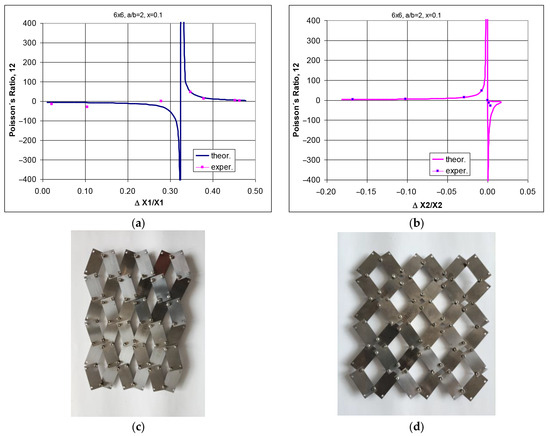
Figure 3.
Theoretical waveforms of Poisson’s ratio for structure 6 × 6, a/b = 2, x = 0.1 as a function of elongation in stretching of the structure (a,b), and photographs of structures 6 × 6 (c,d) in closed and open positions, respectively.
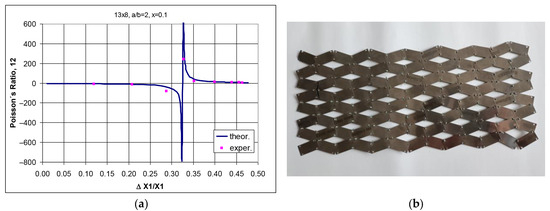

Figure 4.
Theoretical waveforms of Poisson’s ratio for structure 13 × 8, a/b = 2, x = 0.1 as a function of elongation in tension of the structure (a), and photographs of structure 8 × 13 in two closed positions (b,c) and in an open position (d), respectively.
It is particularly characteristic that with a continuous change in elongation, Poisson’s ratio changes continuously up to the limit value at which there is a step change in the value of Poisson’s ratio from a negative value to a positive value. The results of its auxetic behavior for the assembled structure of the asymmetric structure (m > n) are shown in Figure 4.
For extended asymmetrical structures, the image in the closed position depends on the arrangement of the rectangular units. Figure 4b,c are about 13 × 8 structures in a closed position. When it is stretched, open positions are obtained in both cases (Figure 4d). Also, in this case, after expansion to about 32% is achieved, the value of Poisson’s coefficient experiences discontinuity and undergoes a step change from extremely large negative values to positive values.
3.2. Structures from Rigid Rectangular Elementary Cells
In this group of experiments, structures assembled from rectangular unit cells with different parameters a/b and with a fixed geometric parameter x were compared.
Extended structures with small clearances at joints become unstable, and this instability can be significantly reduced by installing double-layer structures (Figure 5). Such structures can act as screens with variable clearance.
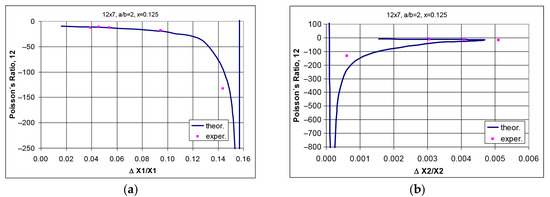

Figure 5.
Theoretical waveforms of Poisson’s ratio for structure 12 × 7, a/b = 2, x = 0.125 as a function of tensile elongation for the auxetic range (a) and for the entire tensile range of the structure (b), and photographs of structure 12 × 7 in two positions: closed (c) and in the open position (d), respectively.
Figure 5a shows the range of occurrence of auxetic behavior for 12 × 7 structures with parameters a/b = 2 and x = 0.125. It is characteristic that for such structures, Poisson’s ratio reaches extremely high negative values for correspondingly large values of linear elongation horizontally and with vertical elongation going to zero.
It can be seen from the presented relation in Figure 5b that when the structure is stretched, it initially exhibits an auxetic behavior. It loses its auxetic properties after exceeding the specific elongation for this geometry. However, this is not related to a right angle between the edges. In this case, the maximum value of Poisson’s ratio occurs for an angle of 64° and at an elongation of ΔX1/X1 = 0.156.
For example, when stretching the structure with parameters 10 × 8, a/b = 1.6, x = 0.125 (Figure 6), the maximum negative value of Poisson’s coefficient for horizontal elongation ΔX1/X1 = 0.2909 was obtained, and the vertical elongation ΔX1/X1 = 0.0087 was obtained, which corresponds to an angle between edges of about 94°.
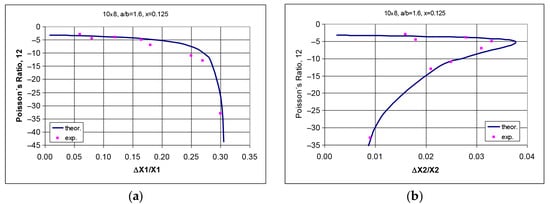

Figure 6.
Theoretical waveforms of Poisson’s ratio for structure 10 × 8, a/b = 1.6, x = 0.125 for the auxetic range in tension as a function of horizontal elongation (a) and as a function of vertical elongation (b), and photographs of structure 8 × 10 in two positions: closed (c) and open (d), respectively.
In the elaborate structures shown, the connections of elementary cells play a special role. While in structures of low abundance, cyclic stretching and compression (transition from closed to open positions and vice versa) do not require effort; a corresponding force is required for structures of higher abundance. This conclusion, although obvious, places new requirements on the modified structure of rotating rectangles. Of course, the bearing of the rectangular connections of the unity cells is needed.
To summarize, a good agreement between theoretical and experimental values was obtained in the case of tensile experiments for both structures. However, for the reverse action, there were some differences. Theoretical and experimental relationships are close to each other for structures assembled from rigid rectangular unity cells. Still, there were deviations in compression for structures made from flexible unity cells, consisting of (bulging) warping of the structure.
4. Discussion
The present work effectively investigates the occurrence of mechanical phase transitions in auxetic structures. In this way, the concept of phase transition has also been extended to mechanics to distinguish the behavior of structures at different stages of the deformation process. Considering the mathematical aspects of phase transition, it can be stated, similarly to Ehrefest’s concept, that mechanical phase transitions occur when a discontinuity of Poisson’s ratio changes is obtained with a continuous change of dimensions, e.g., elongation.
Assuming that the metamaterial phase transition concerns changes in the sign of Poisson’s ratio (from negative to positive) with a continuous change in the linear dimensions of the structure, it was discovered that this predicted phenomenon occurs in modified structures of rotating rectangles. These structures are, therefore, partially auxetic. It has been known so far that metamaterial structures in the form of a system of rectangular unit cells can obtain large negative values of Poisson’s ratio. This property has been emphasized in well-known publications [15,22,23,24]. It was also predicted that Poisson’s ratio could change sign [28,29,30], i.e., change from negative to positive values, although, as noted, this requires large dimensional changes in the structures. It has been investigated theoretically and practically that compliant structures subjected to loading can only undergo slight dimensional changes, which are limited by elastic properties. With larger deformations, they are destroyed. One of the known proposals to remove this shortcoming was the introduction of articulated gratings [31] but without practical implementation.
It should be emphasized that although the occurrence of a metamaterial phase transition has been demonstrated in theory, it has not been realized in a realistic way for metamaterial structures.
In order to ensure the proper functioning of structures subjected to tension and compression, a solution was proposed for a stable connection of rigid structural elements, ensuring high values of linear expansion in the longitudinal or transverse direction. By using a structural modification that connects elementary cells with rotational axes, auxetic properties that depend on geometric parameters (a/b and x) and the degree of deformation are achieved. In particular, it is necessary to consider the relationship between the degree of deformation and Poisson’s ratio in these structures. It should be noted that the structure of the rotating squares does not show this effect.
The movement of the structure from the initial to the final position and the associated change in dimensions determine the value of this complex parameter, Poisson’s ratio.
Based on the study of rotating rectangular structures, it has been confirmed that for fixed parameters a/b and x, Poisson’s ratio does not depend on the number of unit cells. Increasing the number of unit cells keeps Poisson’s ratio constant.
For modified structures, the change of one of the geometric parameters (a/b or x) can be selected in such a way as to obtain a structure with the intended auxetic properties. For example, increasing the quotient a/b from 1.6 to 2 (with a constant geometric parameter x) results in a smaller range of linear dimension changes in the auxetic area, while the negative Poisson’s ratio increases sharply. However, for the parameters a/b = 2 and x = 0.1, negative and positive Poisson’s ratios were obtained, thus creating a partially auxetic structure with a phase transition. The phase transition can be controlled by selecting structure parameters (a/b and x).
Like most phase transitions, mechanical phase transitions are also rapid. At the moment of transition, the system has discontinuities in Poisson’s ratio. For a certain elongation value, an infinitely large negative and infinitely large positive value of Poisson’s ratio is reached, which also means that one of the linear dimensions of the stretched structure undergoes zero dimensional change. After the phase transition, there is a monotonic change in one of the dimensions and a non-monotonic change in the other.
This may illustrate a certain type of mechanism responsible for instability or phase transitions in mechanical metamaterials as researched in work [32].
Structures that exhibit negative and positive Poisson’s ratios belong to metamaterials undergoing phase transitions. In theory, its occurrence has already been demonstrated [15,28,29,30,31,32,33], but it has not been presented realistically for metamaterial structures. It should be added that work is underway on the realistic representation of phase transitions in mechanical metamaterials. Work [33] has found a relationship between Poisson’s ratio and Young’s modulus value, which can be treated as a change in Poisson’s ratio depending on the type of material from which the unit cells are made.
Composites with different Poisson’s ratios can also be designed by grading the effect in a tunable metamaterial [34] and by combining auxetic metamaterials with non-auxetic materials [33,35]. This new class of phase transformation in phase-transforming mechanical metamaterials, which combines the liquid–vapor phase transition and phase-transforming mechanical metamaterials (PMMs), may have practical significance, e.g., in sensor technology [34].
The results obtained in this work confirmed that this phenomenon of phase transformation in mechanical metamaterials can realistically occur for the structure of rotating rectangles. Also, work [36] confirmed the realistic occurrence of phase transformations in a similar structure of connected equilateral right-angled triangles and right-angled trapezoids.
5. Conclusions
In summary, a modified structure of rotating rectangles was designed and produced for which a metamaterial mechanical phase transition was determined. This modified structure behaves stably with large changes in dimensions.
Modified structures of rotating rectangles, built from rectangular unit cells with selected a/b and x parameters, show the occurrence of a metamaterial phase transition. It consists of changing Poisson’s ratio from positive to negative values while continuously changing the dimensions of the structure. This means that, for example, when the structure is stretched, the elongation of the structure in both orthogonal directions initially increases. Then, with a further continuous increase in elongation in one direction, the elongation in the direction perpendicular to it decreases.
For low values of the parameter x (position of the axis of rotation), this effect occurs for a/b ≥ 2 (ratio of the length of the sides of the rectangular unit cell). However, larger values of this parameter (x > 0.1) can also appear for less elongated rectangular unit cells.
Measurements on real physical models confirmed the calculated theoretical values and measured values of linear dimension changes for areas of auxetic behavior of structures. In this respect, the work sets the direction for the mass production of auxetic structures for applications requiring large negative Poisson’s ratios and small elongations in the direction perpendicular to the force causing the deformation of the structure.
An additional but no less important feature of such a modified structure of rotating rectangles (or squares) is the independence of Poisson’s ratio from the elastic properties of the unit cells. Poisson’s ratio only depends on the change in linear dimensions of the modified structure and is, therefore, related to a new class of mechanical metamaterials. This example of auxetic structures has a Poisson’s ratio that is not related to material properties but only results from movement of the structure. Poisson’s ratio here is, therefore, purely geometrical.
The proposed structures can be used to build a structure that, given a certain change in Poisson’s ratio, will exhibit the expected auxetic behavior with the required dimensional changes. This type of structure may be needed in applications where a large negative Poisson’s ratio is required, and the change in dimensions in one direction is small.
The article presents the design and development of a modified metamaterial structure that can be used in robotics.
Such modified structures of rotating rectangles composed of numerous unit cells made of rigid materials can also exhibit a predetermined degree of deformation, e.g., tensile expansion. For this reason, they can also be used as metamaterials for the study of buckling and fracture mechanics. This is particularly important because only real physical structures allow us to understand their macroscopic mechanical properties. Only the bulk behavior of a metamaterial can indicate its auxetics and stability, which is the starting point for potential and expected applications.
Author Contributions
J.P. came up with the idea presented here, including the model and geometric relationships, prepared the first draft of the manuscript, and constructed physical models used as proof. M.P. arranged the editing and proofreading of the work. All authors have read and agreed to the published version of the manuscript.
Funding
The present paper was financed partly by the Polish Ministry of Education and Science within statutory activity.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
Special thanks go to Jacek Palka for his help in implementing unit cells.
Conflicts of Interest
The authors declare no conflicts of interest. The study is part of a strategic area of interest covering the analysis and assembly of auxetic systems.
References
- Fischer, S.C.L.; Hillen, L.; Eberl, C. Review. Mechanical Metamaterials on the Way from Laboratory Scale to Industrial Applications: Challenges for Characterization and Scalability. Materials 2020, 13, 3605. [Google Scholar] [CrossRef] [PubMed]
- Luo, C.; Han, C.Z.; Zhang, X.Y.; Zhang, X.G.; Ren, X.; Xie, Y.M. Design, manufacturing and applications of auxetic tubular structures: A review. Thin-Walled Struct. 2021, 163, 107682. [Google Scholar] [CrossRef]
- Veerabagu, U.; Palza, H.; Quero, F. Review: Auxetic Polymer-Based Mechanical Metamaterials for Biomedical Applications. ACS Biomater. Sci. Eng. 2022, 8, 2798–2824. [Google Scholar] [CrossRef] [PubMed]
- Wallbanks, M.; Khan, M.F.; Bodaghi, M.; Triantaphyllou, A.; Serjouei, A. Topical Review. On the design workflow of auxetic metamaterials for structural applications. Smart Mater. Struct. 2022, 31, 023002. [Google Scholar] [CrossRef]
- Zhang, W.-M.; Li, Z.-Y.; Yang, J.-S.; Ma, L.; Lin, Z.; Schmidt, R.; Schröder, K.-U. A lightweight rotationally arranged auxetic structure with excellent energy absorption performance. Mech. Mater. 2022, 166, 104244. [Google Scholar] [CrossRef]
- Imbalzano, G.; Linforth, S.; Ngo, T.D.; Lee, P.V.S.; Tran, P. Blast resistance of auxetic and honeycomb sandwich panels: Comparisons and parametric designs. Compos. Struct. 2018, 183, 242–261. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, J.; Kong, X.; Xu, Y.; Chen, Y.; Zhu, J.; Jin, F.; Wang, P. An Innovative Auxetic Honeycomb Sandwich Tube: Fabrication and Mechanical Properties. Polymers 2022, 14, 4369. [Google Scholar] [CrossRef]
- Zhang, W.; Yin, H.; Wu, Y.; Jin, Q.; Wu, L.; Wen, G.; Liu, J.; Wu, X. A novel auxetic 3D lattice structure for enhancing energy absorption. Compos. Struct. 2023, 326, 117620. [Google Scholar] [CrossRef]
- Francisco, M.B.; Pereira, J.L.J.; Oliver, G.A.; da Silva, L.R.R.; Cunha, S.S., Jr.; Gomes, G.F. A review on the energy absorption response and structural applications of auxetic structures. Mech. Adv. Mater. Struct. 2022, 29, 5823–5842. [Google Scholar] [CrossRef]
- Rose, S.; Siu, D.; Zhu, J.D.; Roufail, R. Auxetics in Biomedical Applications: A Review. J. Min. Mater. Charact. Eng. 2023, 11, 27–35. [Google Scholar] [CrossRef]
- Wang, H.; Lyu, Y.; Bosiakov, S.; Zhu, H.; Ren, Y. A review on the mechanical metamaterials and their applications in the field of biomedical engineering. Front. Mater. 2023, 10, 1273961. [Google Scholar] [CrossRef]
- Resch, R.D. Geometrical Device Having Articulated Relatively Movable Sections. U.S. Patent 3,201,894, 24 August 1965. [Google Scholar]
- Resch, R.D. Self-Supporting Structural Unit Having a Series of Repetitious Geometrical Modules. U.S. Patent 3,407,558, 29 October 1968. [Google Scholar]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 2000, 19, 1563–1565. [Google Scholar] [CrossRef]
- Grima, J.N.; Alderson, A.; Evans, K.E. Negative Poisso’s Ratios from Rotating Rectangles. Comput. Methods Sci. Technol. 2004, 10, 137–145. [Google Scholar] [CrossRef]
- Grima-Cornish, J.N.; Grima, J.N.; Attard, D. Mathematical modeling of auxetic systems: Bridging the gap between analytical models and observation. Int. J. Mech. Mater. Eng. 2021, 16, 4. [Google Scholar] [CrossRef]
- Acuna, D.; Gutierrez, F.; Silva, R.; Palza, H.; Nunez, A.S.; During, G. Auxetic behavior on demand: A three steps recipe for new designs. Commun. Phys. 2022, 5, 113. [Google Scholar] [CrossRef]
- Broeren, F.G.J.; van der Wijk, V.; Herder, J.L. Spatial pseudo-rigid body model for the analysis of a tubular mechanical metamaterial. Math. Mech. Solids 2020, 25, 305–316. [Google Scholar] [CrossRef]
- Rauf, A.M.; Bernardo, J.S.; Follmer, S. Electroadhesive Auxetics as Programmable Layer Jamming Skins for Formable Crust Shape Displays. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation, (ICRA), London, UK, 29 May–2 June 2023; pp. 2591–2597. [Google Scholar] [CrossRef]
- Sorrentino, A.; Castagnetti, D.; Mizzi, L.; Spaggiari, A. Rotating squares auxetic metamaterials with improved strain tolerance. Smart Mater. Struct. 2021, 30, 035015. [Google Scholar] [CrossRef]
- Ali, M.N.; Busfield, J.J.C.; Rehman, I.U. Auxetic oesophageal stents: Structure and mechanical properties. J. Mater. Sci. Mater. Med. 2014, 25, 527–553. [Google Scholar] [CrossRef]
- Liang, Y.; Huang, J.; Qu, J.; Huang, J.; Hui, D. Research on the auxetic behavior and mechanical properties of periodically rotating graphene nanostructures. Nanotechnol. Rev. 2022, 11, 1733–1743. [Google Scholar] [CrossRef]
- Slann, A.; White, W.; Scarpa, F.; Boba, K.; Farrow, I. Cellular plates with auxetic rectangular perforations. Phys. Status Solidi 2015, 252, 1533–1539. [Google Scholar] [CrossRef]
- Williams, J.J.; Smith, C.W.; Evans, K.E.; Lethbridge, Z.D.A.; Walton, R.I. An analytical model for producing negative Poisson’s ratios and its application in explaining off-axis elastic properties of the NAT-type zeolites. Acta Mater. 2007, 55, 5697–5707. [Google Scholar] [CrossRef]
- Warisaya, K.; Sato, J.; Tachi, T. Freeform Auxetic Mechanisms Based on Corner Connected Tiles. J. Int. Assoc. Shell Spat. Struct. J. IASS 2022, 63, 263–271. [Google Scholar] [CrossRef]
- Plewa, J.; Plonska, M.; Lis, P. Investigation of Modified Auxetic Structures from Rigid Rotating Squares. Materials 2022, 15, 2848. [Google Scholar] [CrossRef] [PubMed]
- Plewa, J.; Płonska, M. Studies of auxetic structures assembled from rotating rectangles. Materials 2024, 17, 731. [Google Scholar] [CrossRef]
- Clark, J.B.; Hastie, J.W.; Kilhlborg, L.H.E.; Metselaar, R.; Thackeray, M.M. Definitions of Terms Relating to Phasetransitions of the Solid State. Pure Appl. Chem. 1994, 66, 577–594. [Google Scholar] [CrossRef]
- Wang, L.; Ulliac, G.; Wang, B.; Martinez, J.A.I.; Dudek, K.K.; Laude, V.; Kadic, M. 3d auxetic metamaterials with elastically-stable continuous phase transition. Adv. Sci. 2022, 9, 2204721. [Google Scholar] [CrossRef]
- Bonetti, E.; Fabrizio, M.; Frémond, M. A Phase Transition Model Describing Auxetic Materials. In Solvability, Regularity, and Optimal Control of Boundary Value Problems for PDEs; Springer: Cham, Switzerland, 2017; pp. 77–95. [Google Scholar] [CrossRef]
- Hunt, G.W.; Dodwell, T.J. Complexity in phase transforming pin-jointed auxetic lattices. Proc. R. Soc. A 2019, 475, 20180720. [Google Scholar] [CrossRef]
- Podestá, J.M.; Rossi, N.; Huespe, A.E. Design of Elastic Metamaterials with Volumetric Phase Transitions. Asoc. Argentina Mec. Comput. 2023, XL, 869. [Google Scholar]
- Zhong, Y.; Tang, W.; Xu, H.; Qin, K.; Yan, D.; Fan, X.; Qu, Y.; Li, Z.; Jiao, Z.; Yang, H.; et al. Phase-transforming mechanical metamaterials with dynamically controllable shape-locking performance. Natl. Sci. 2023, 10, nwad192. [Google Scholar] [CrossRef]
- Ben-Yelun, I.; Gómez-Carano, G.; San Millán, F.J.; Sanz, M.Á.; Montáns, F.J.; Saucedo-Mora, L. GAM: General Auxetic Metamaterial with Tunable 3D Auxetic Behavior Using the Same Unit Cell Boundary Connectivity. Materials 2023, 16, 3473. [Google Scholar] [CrossRef]
- Peng, X.-L.; Soyarslan, C.; Bargmann, S. Phase contrast mediated switch of auxetic mechanism in composites of infilled re-entrant honeycomb microstructure. Extrem. Mech. Lett. 2020, 35, 100641. [Google Scholar] [CrossRef]
- Lim, T.-C. Auxetic metamaterial inspired by the seesaw motion. J. Mech. 2024, 40, 368–376. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).