Epilepsy Diagnosis Analysis via a Multiple-Measures Composite Strategy from the Viewpoint of Associated Network Analysis Methods
Abstract
1. Introduction
2. Methodology
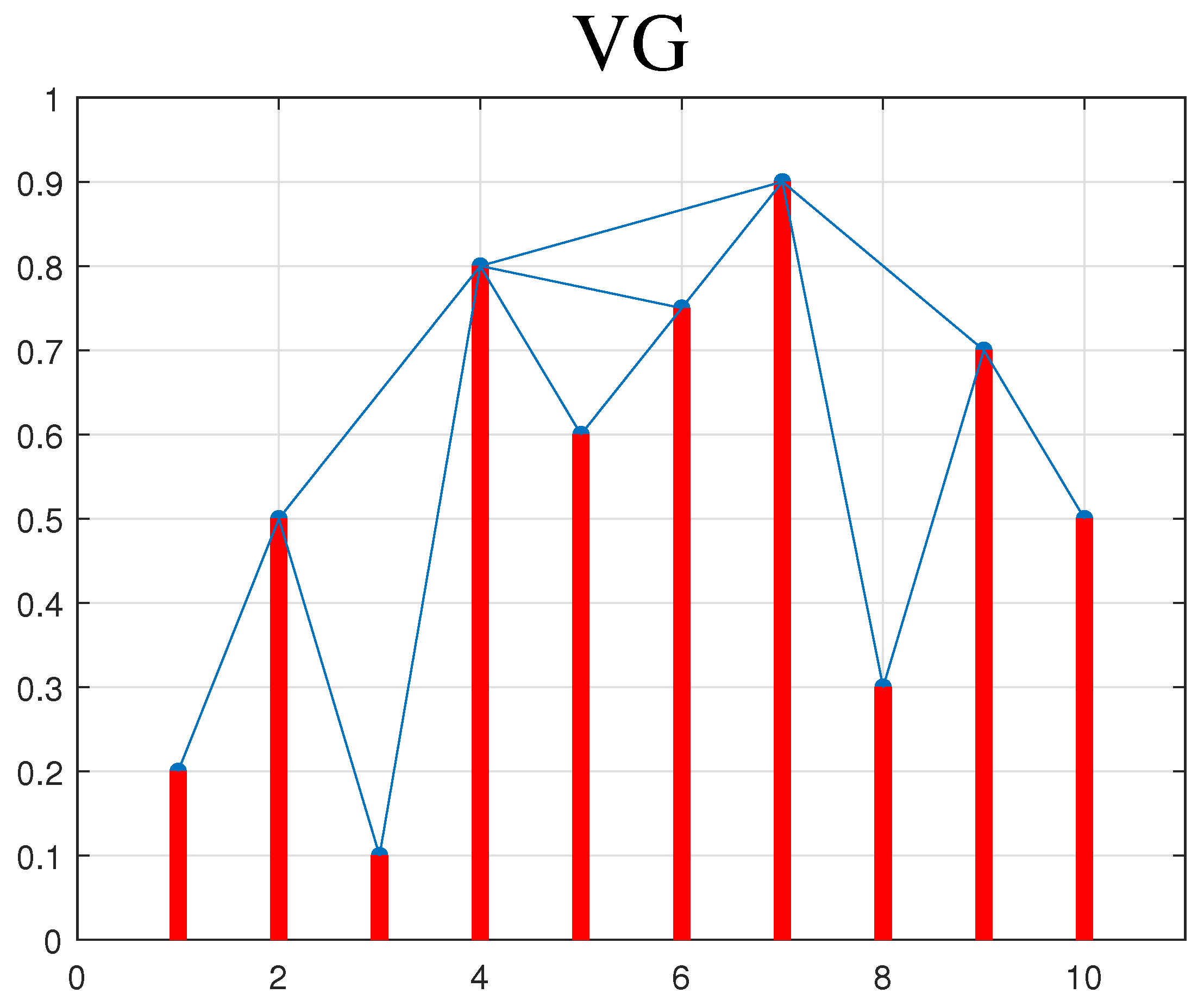
2.1. Visibility Graph (VG)
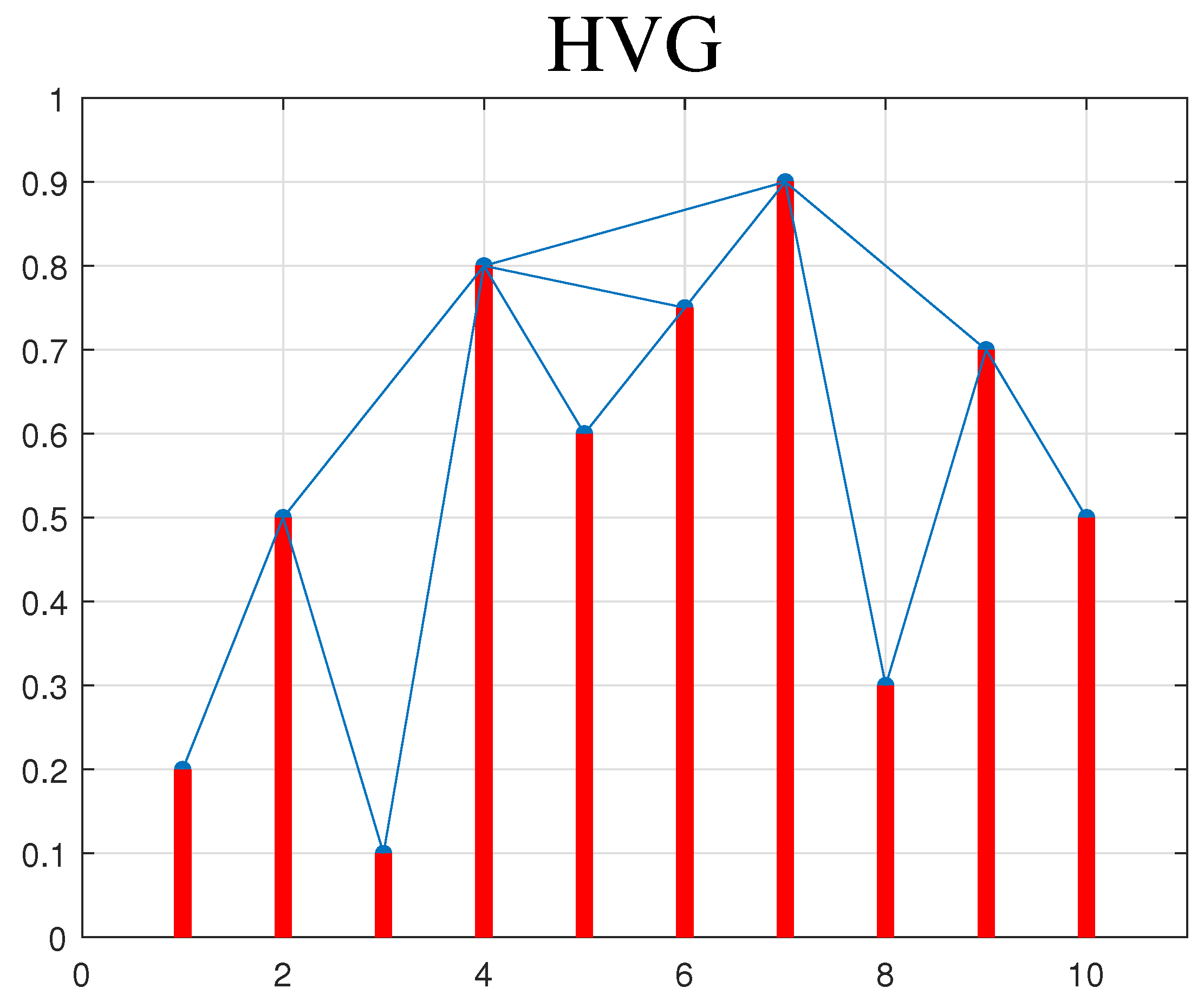
2.2. Horizontal Visibility Graph (HVG)
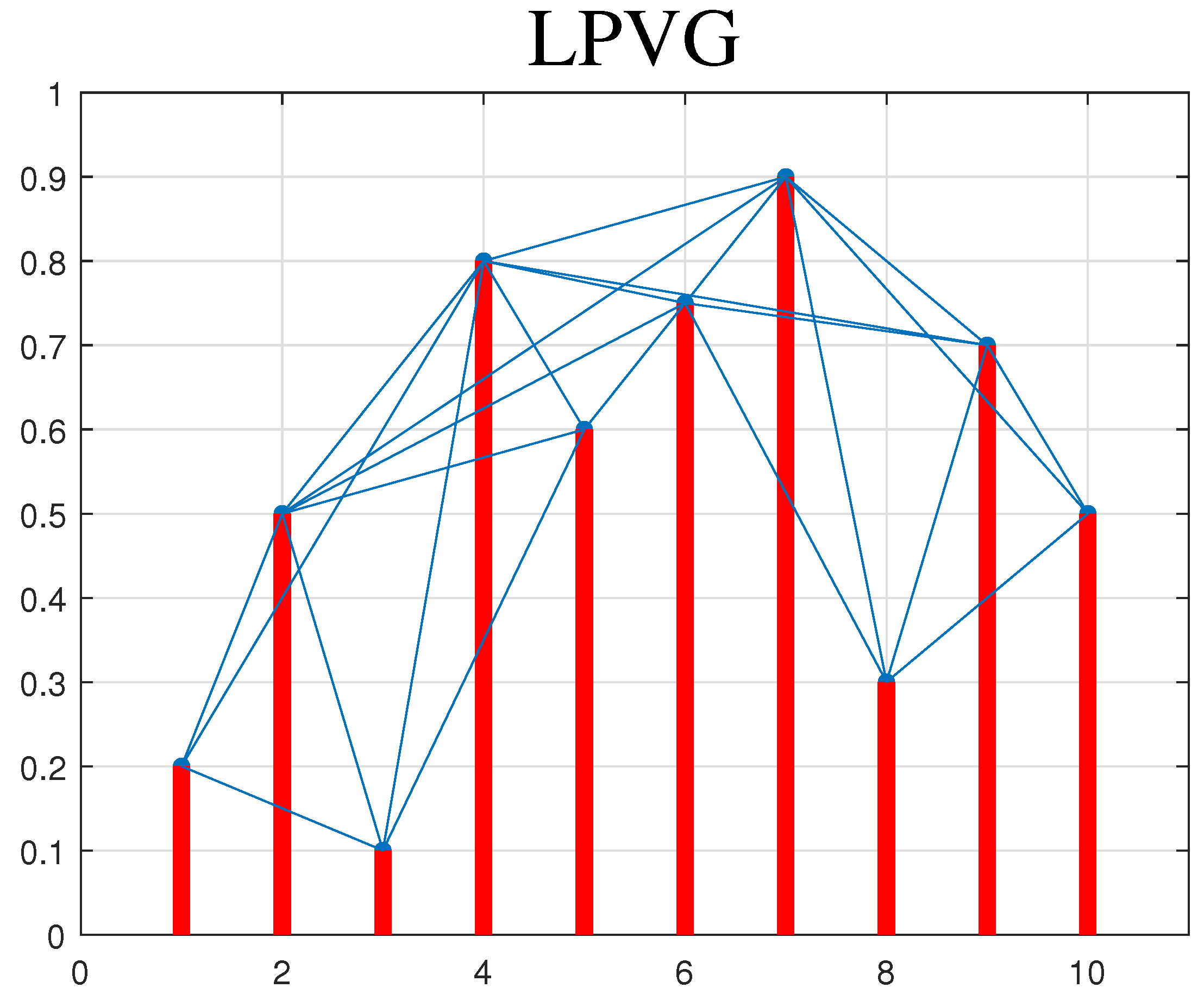
2.3. Limited Penetrable Visibility Graph (LPVG)
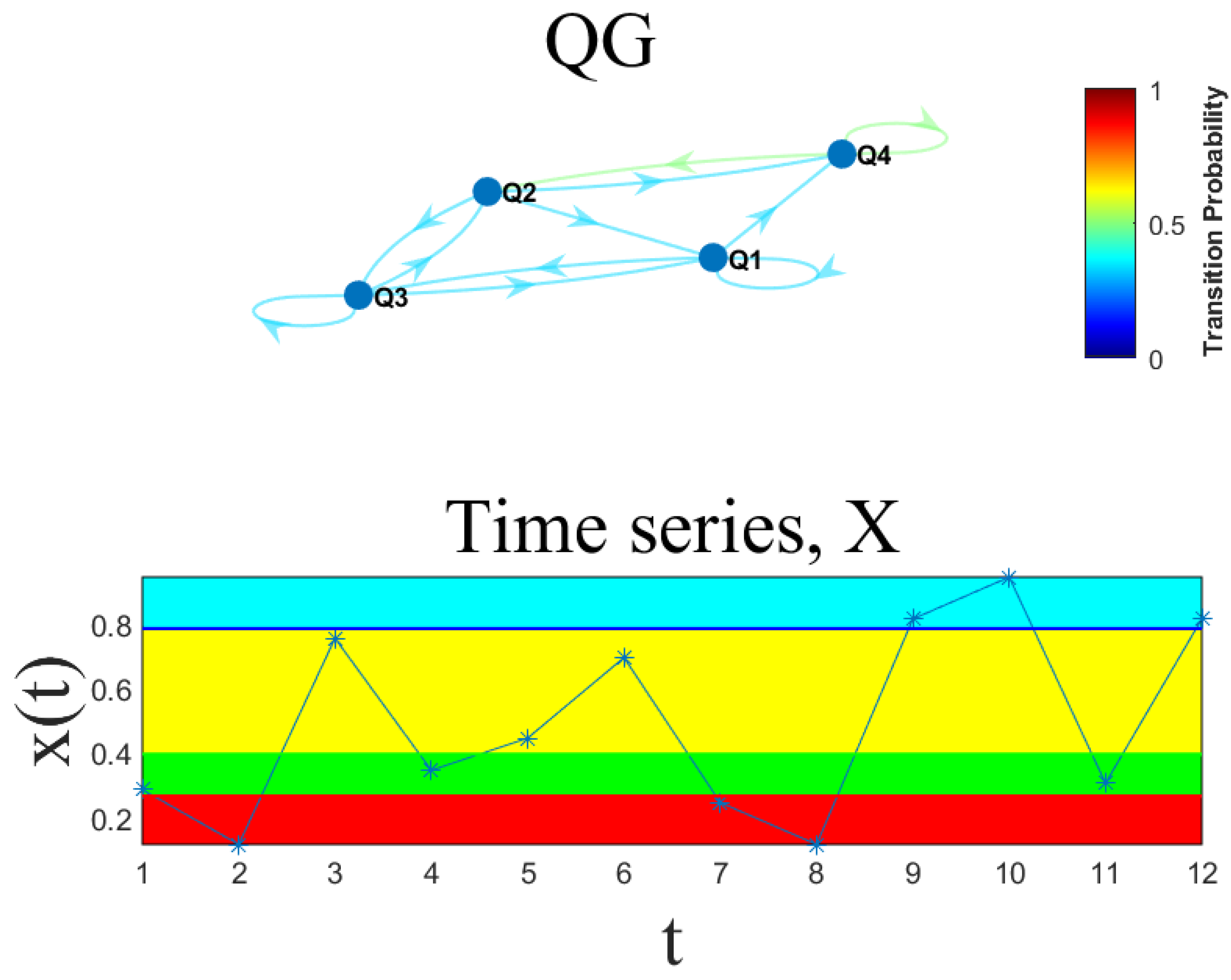
2.4. Quantile Graphs (QGs)
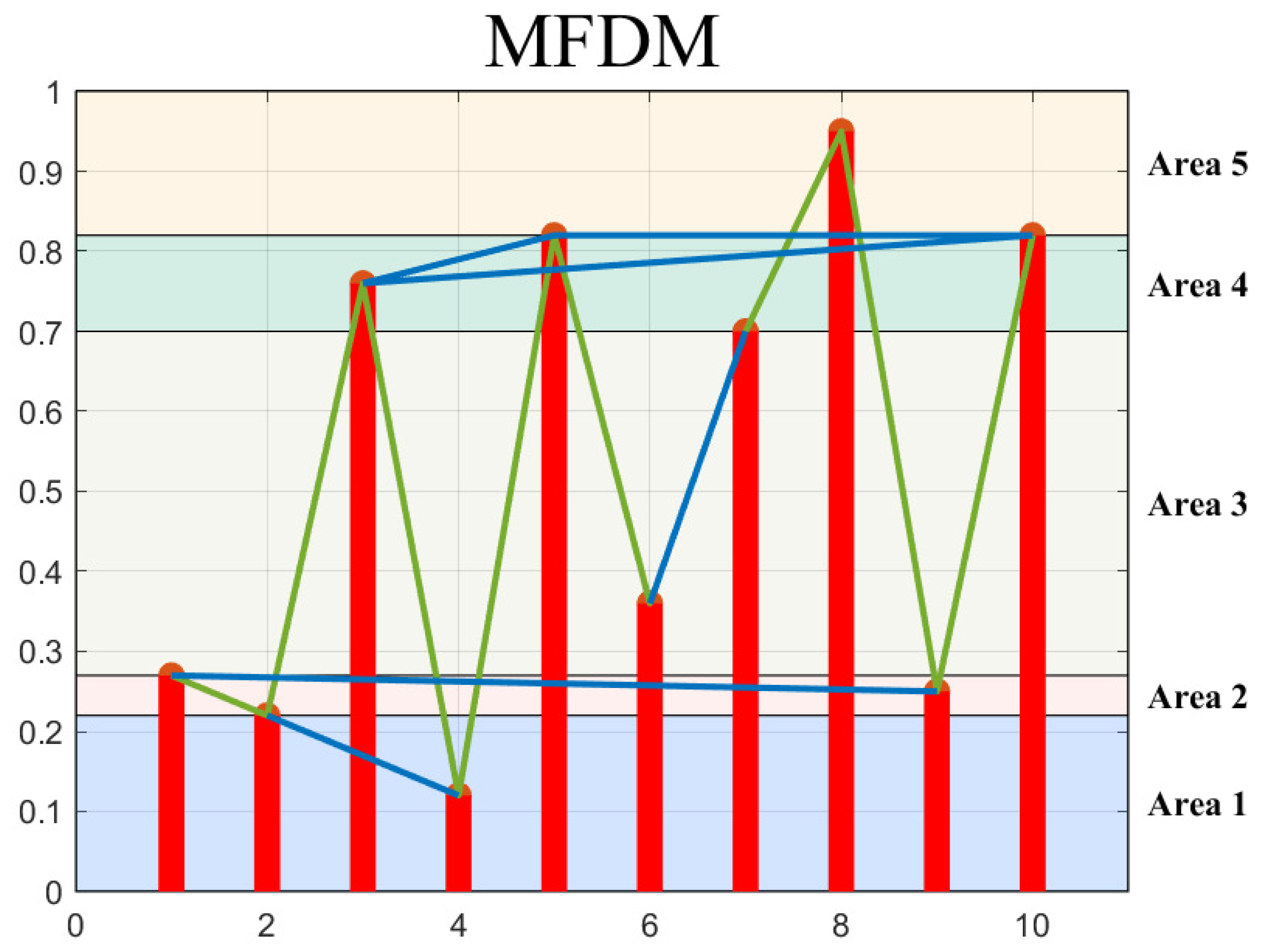
2.5. Modified Frequency Degree Method (MFDM)
3. Main Framework, Dataset, and Feature Extraction Overview
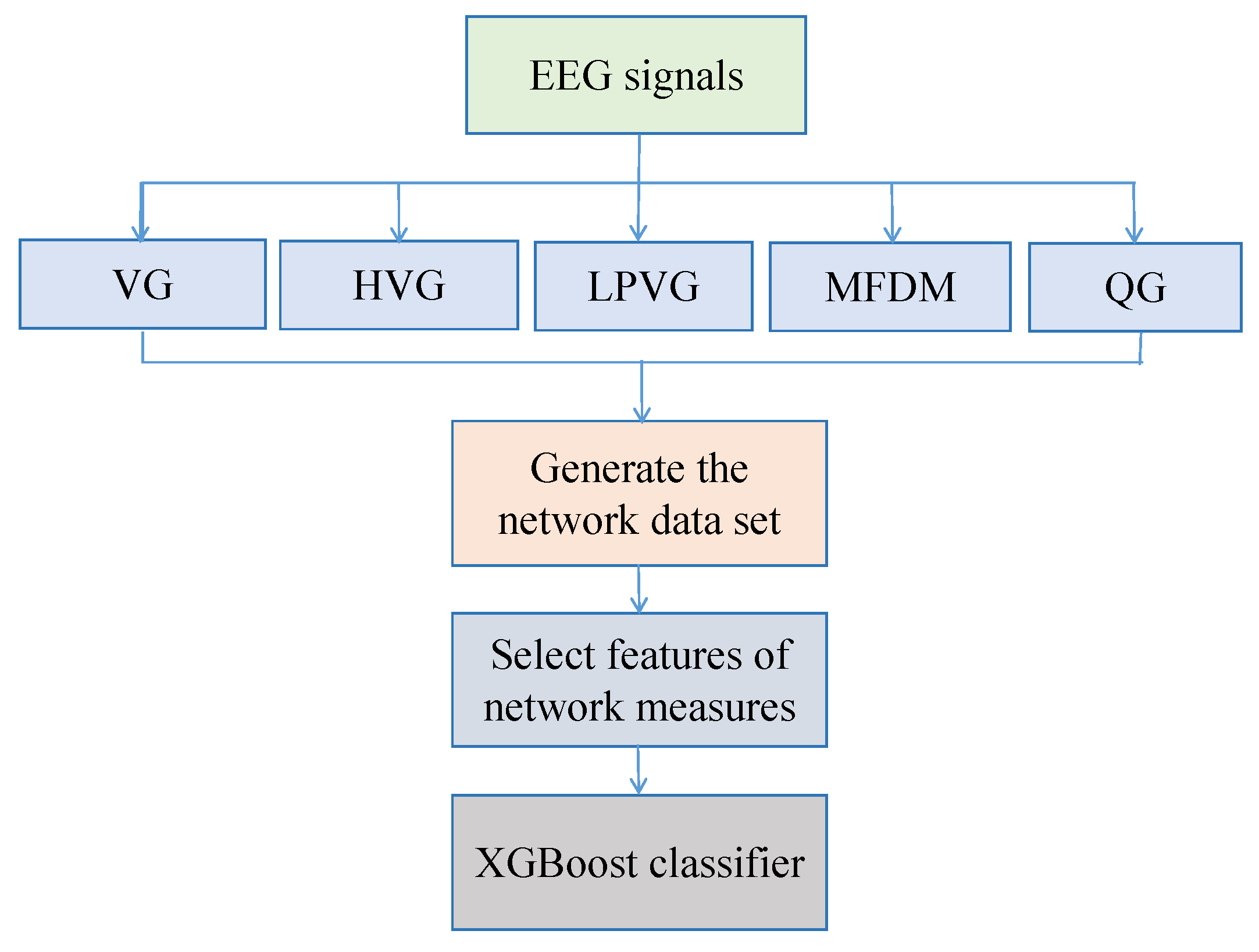
3.1. Main Framework
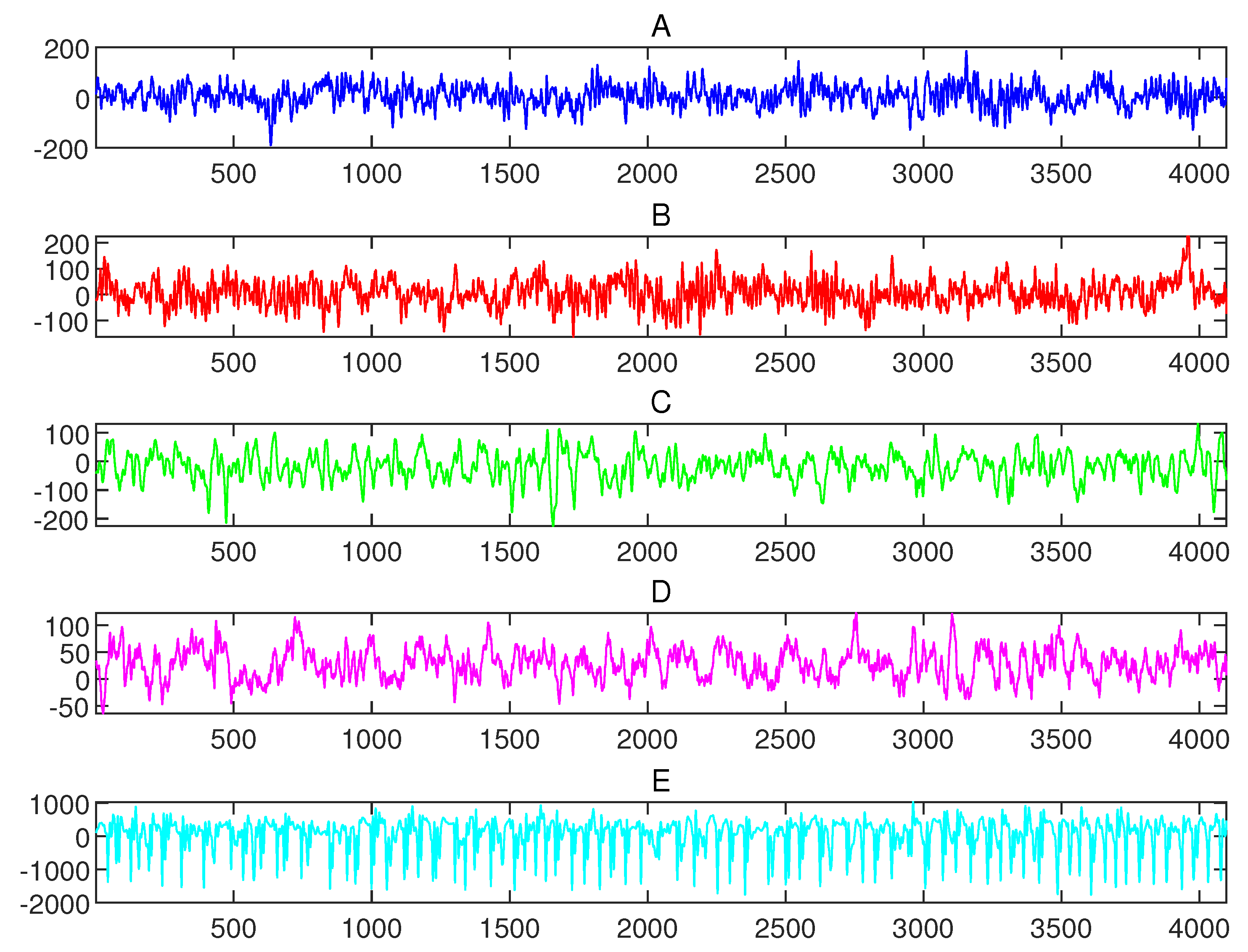
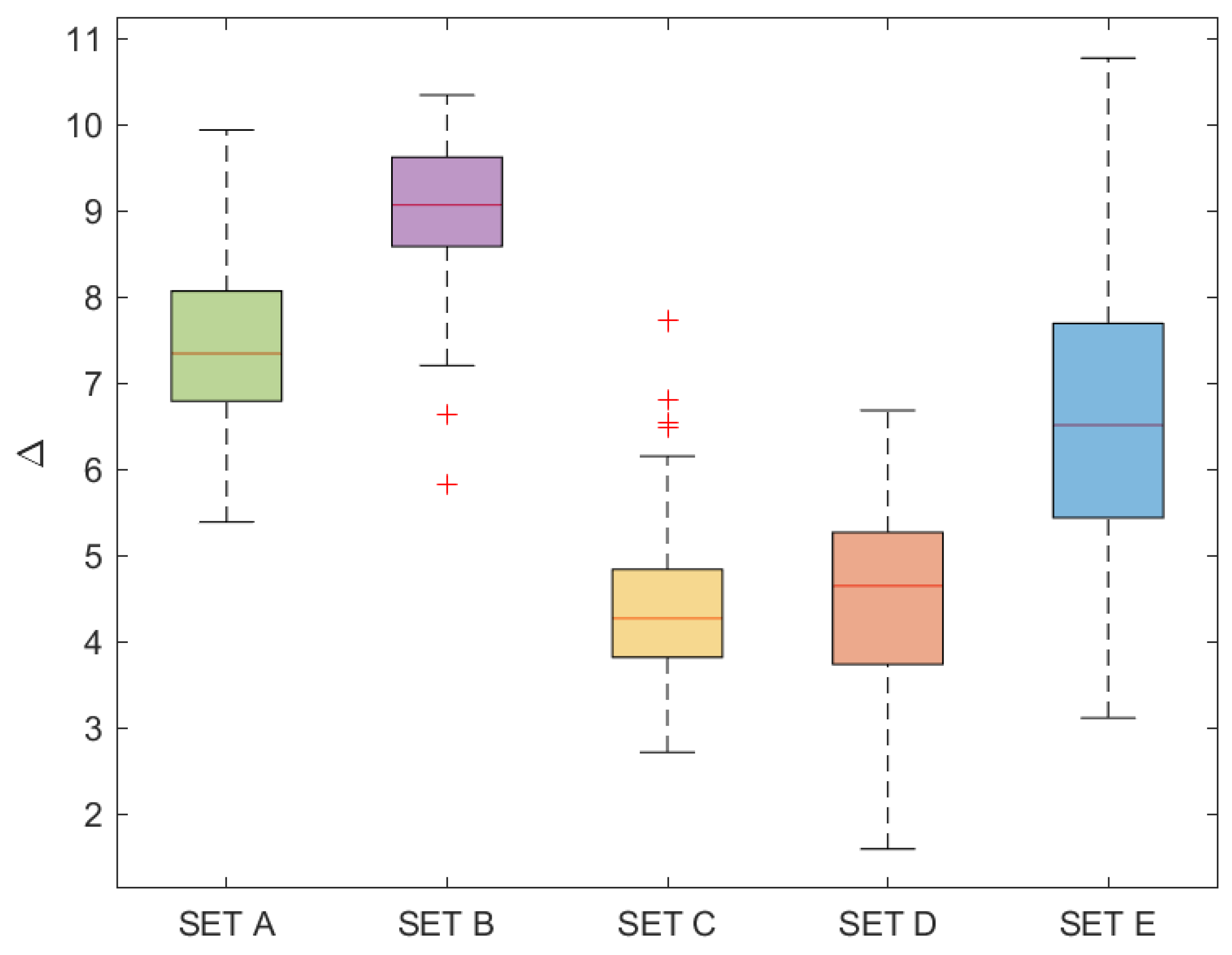
3.2. Dataset Used in Numerical Experiments
3.3. Feature Extraction
| Algorithm 1 ANOVA feature concatenation |
|
- VG: average degree (); the maximum degree(); average clustering coefficient (); density: (); global efficiency: (); and average path length: ().
- HVG: average degree (); the maximum degree (); average clustering coefficient (); density: (); global efficiency: (); network diameter (); and average path length: ().
- LPVG: average degree (); the maximum degree (); average clustering coefficient (); density: (); global efficiency: (); and average path length: ().
- MFDM: average degree (); the maximum degree (); average clustering coefficient (); density: (); global efficiency: (); network diameter (); average path length: ().
- QG: and average jump length ().
3.4. Model Evaluation Index
4. Classification Effect on the Dataset
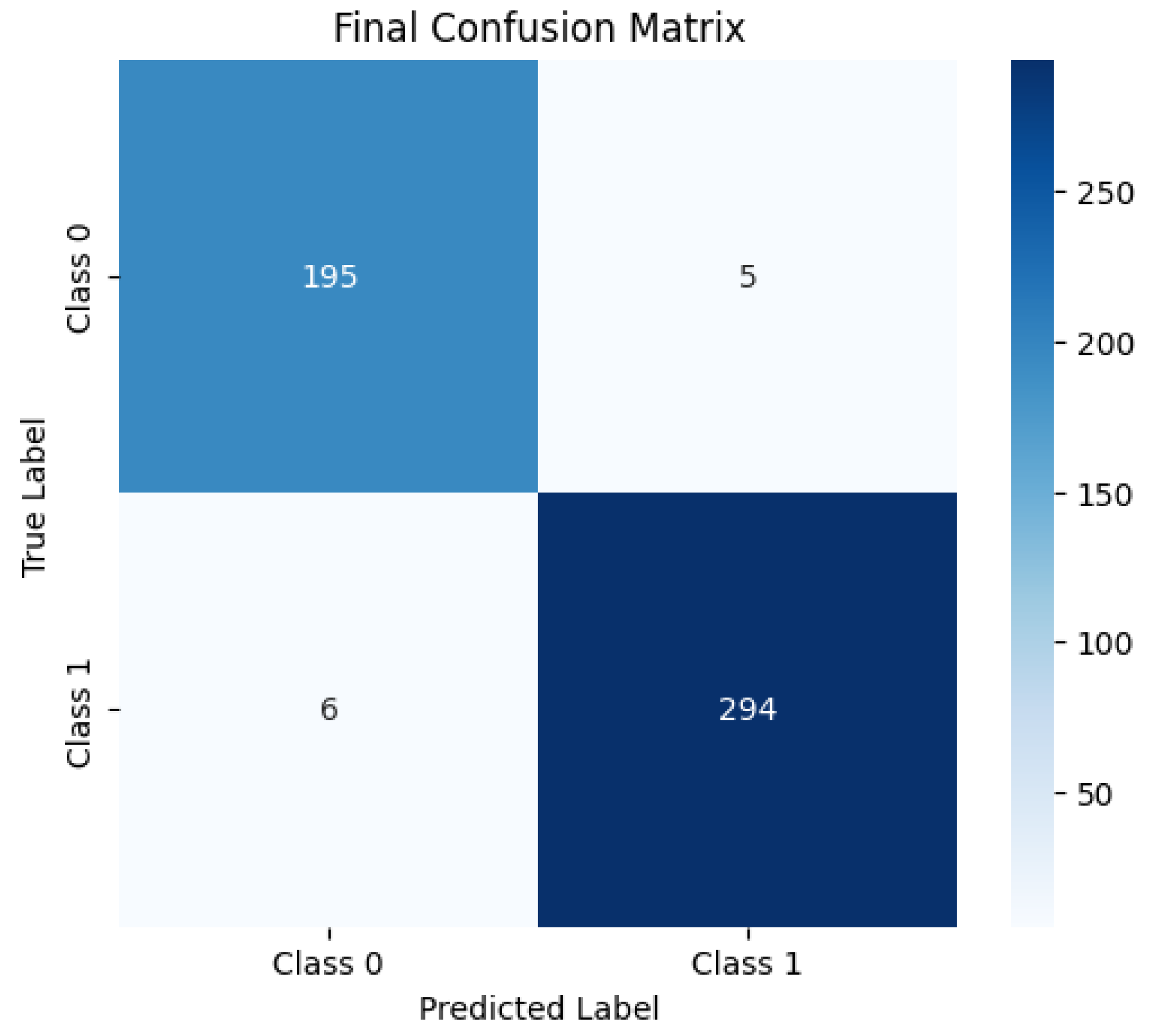
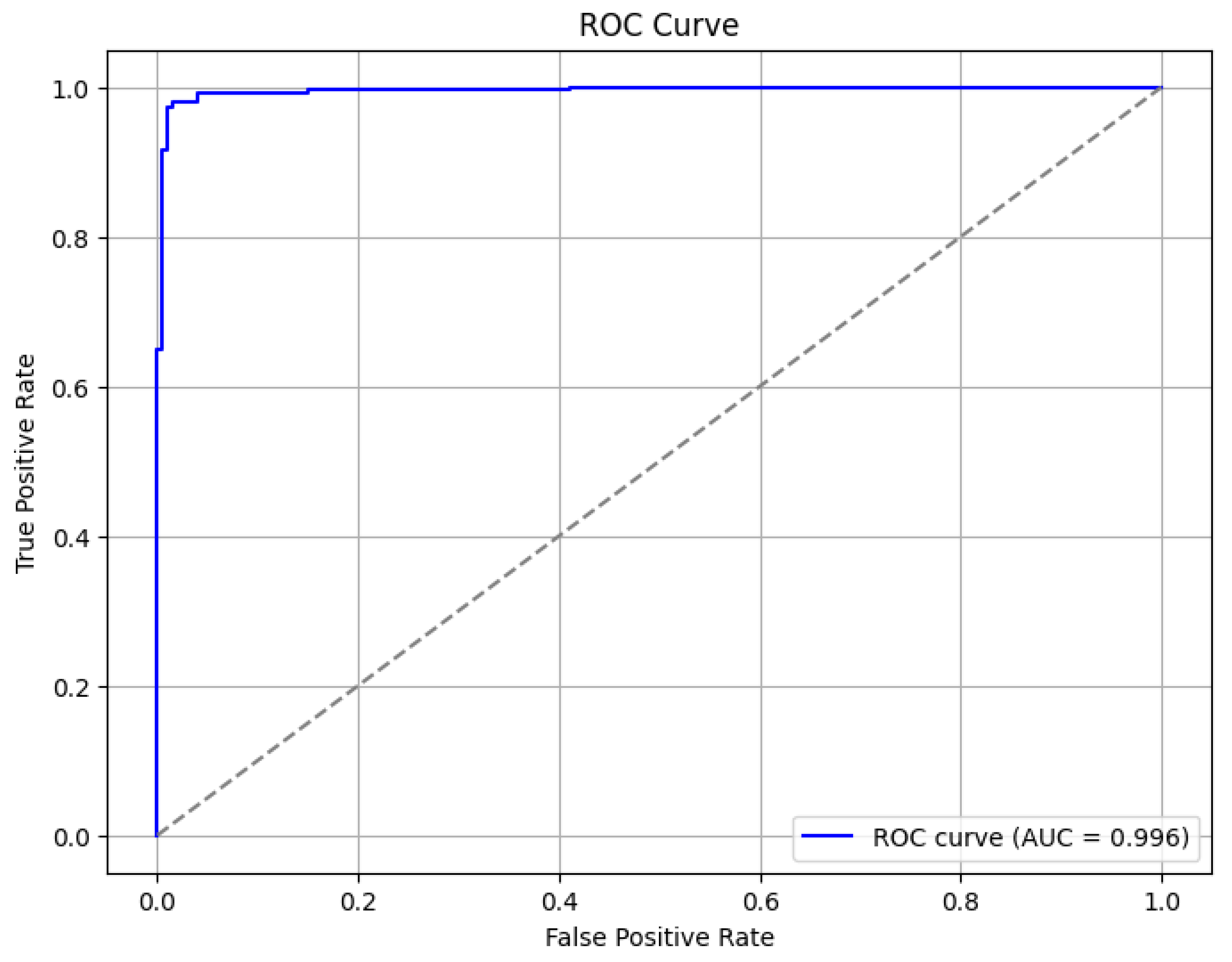
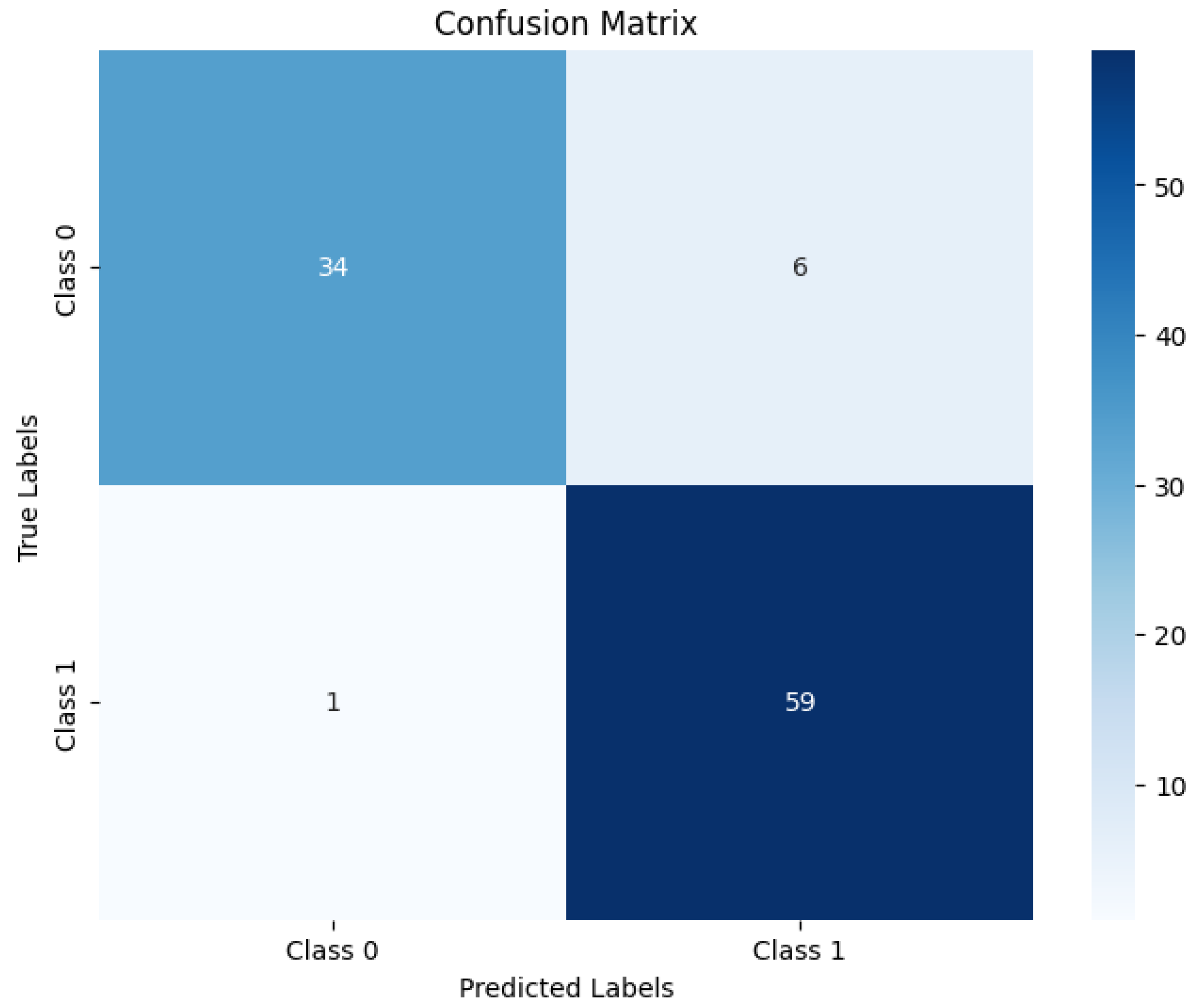
4.1. Classification Effect on Binary Classification Dataset
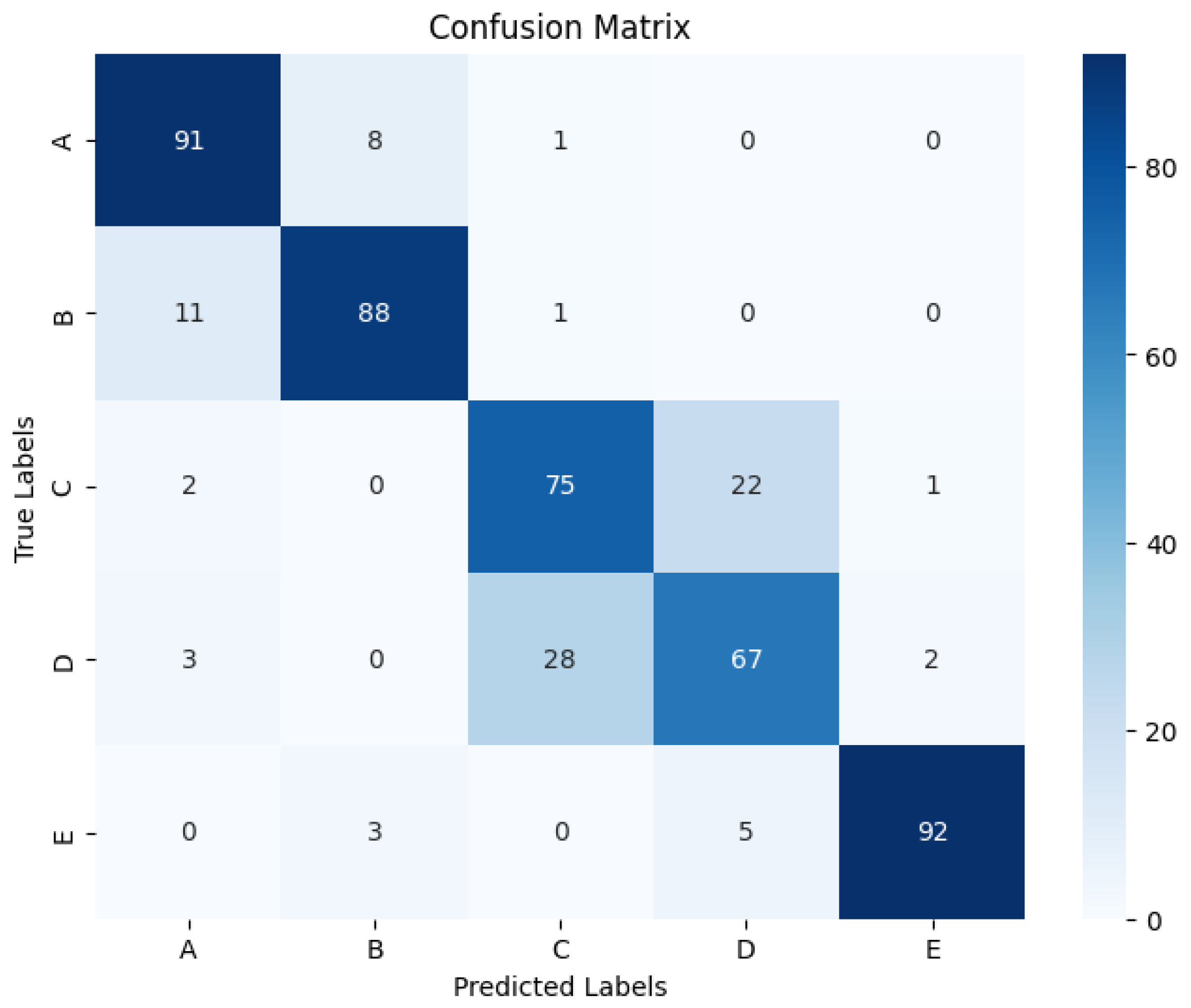
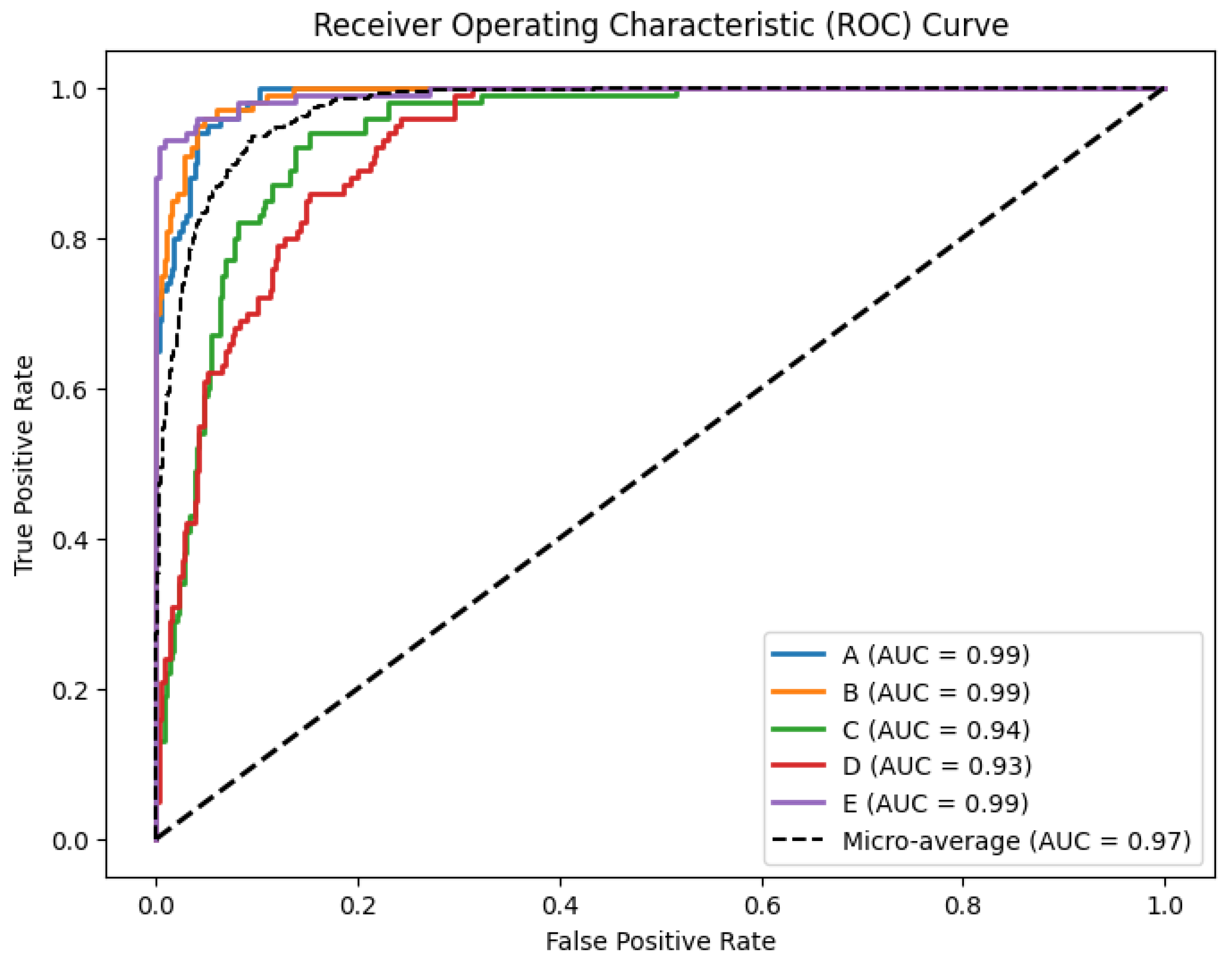
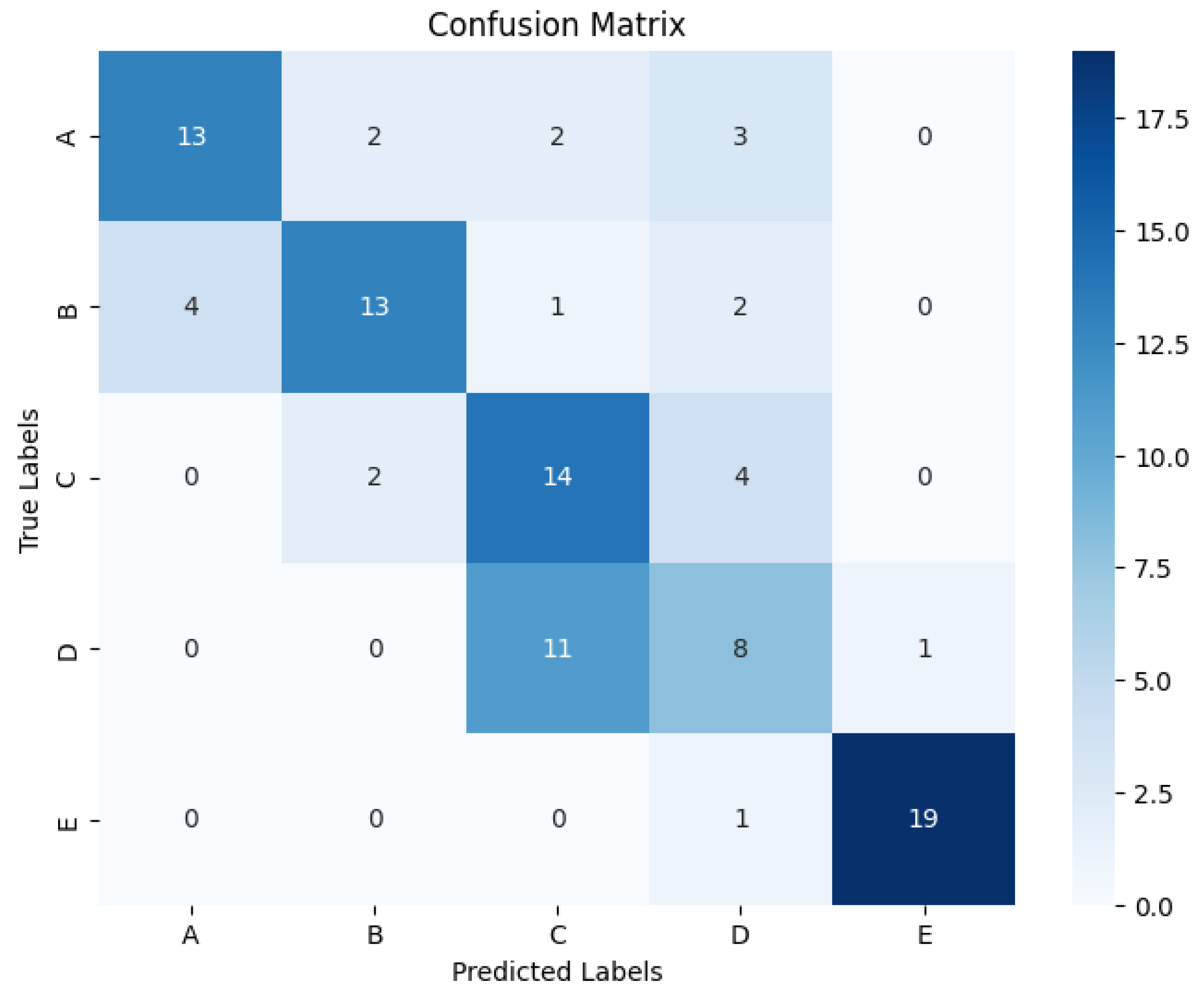
4.2. Classification Effect on Five Classification Datasets
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Taha, M.A.; Morren, J.A. The role of artificial intelligence in electrodiagnostic and neuromuscular medicine: Current state and future directions. Muscle Nerve 2024, 69, 260. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Long, X.; Arends, J.B.; Aarts, R.M. EEG analysis of seizure patterns using visibility graphs for detection of generalized seizures. J. Neurosci. Methods 2017, 290, 85. [Google Scholar] [CrossRef] [PubMed]
- Pineda, A.M.; Ramos, F.M.; Betting, L.E.; Campanharo, A.S. Quantile graphs for EEG-based diagnosis of Alzheimer’s disease. PLoS ONE 2020, 15, e0231169. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Wang, H.; Xu, H.; Bao, S.; Li, L. A modified markov transition probability-based network constructing method and its application on nonlinear time series analysis. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020. [Google Scholar]
- Samiei, S.; Ghadiri, N.; Ansari, B. A complex network approach to time series analysis with application in diagnosis of neuromuscular disorders. arXiv 2021, arXiv:2108.06920. [Google Scholar]
- Cai, Q.; Gao, Z.; An, J.; Gao, S.; Grebogi, C. A graph-temporal fused dual-input convolutional neural network for detecting sleep stages from EEG signals. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 777. [Google Scholar] [CrossRef]
- Veeranki, Y.R.; Ganapathy, N.; Swaminathan, R. Non-parametric classifiers based emotion classification using electrodermal activity and modified Hjorth features. In Public Health and Informatics; IOS Press: Amsterdam, The Netherlands, 2021; pp. 163–167. [Google Scholar]
- Vicchietti, M.L.; Ramos, F.M.; Betting, L.E.; Campanharo, A.S. Computational methods of EEG signals analysis for Alzheimer’s disease classification. Sci. Rep. 2023, 13, 8184. [Google Scholar] [CrossRef] [PubMed]
- Hramov, A.E.; Maksimenko, V.; Koronovskii, A.; Runnova, A.E.; Zhuravlev, M.; Pisarchik, A.N.; Kurths, J. Percept-related EEG classification using machine learning approach and features of functional brain connectivity. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 093110. [Google Scholar] [CrossRef] [PubMed]
- Lacasa, L.; Luque, B.; Ballesteros, F.; Luque, J.; Nuno, J.C. From time series to complex networks: The visibility graph. Proc. Natl. Acad. Sci. USA 2008, 105, 4972–4975. [Google Scholar] [CrossRef] [PubMed]
- Luque, B.; Lacasa, L.; Ballesteros, F.; Luque, J. Horizontal visibility graphs: Exact results for random time series. Phys. Rev. E 2009, 80, 046103. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Jin, N.; Gao, Z.; Luo, Y. Limited penetrable visibility graph for establishing complex network from time series. Acta Phys. Sin. 2012, 61, 030506. [Google Scholar] [CrossRef]
- Campanharo, A.S.; Sirer, M.I.; Malmgren, R.D.; Ramos, F.M.; Amaral, L.A.N. Duality between time series and networks. PLoS ONE 2011, 6, e23378. [Google Scholar] [CrossRef] [PubMed]
- Campanharo, A.S.; Doescher, E.; Ramos, F.M. Automated EEG signals analysis using quantile graphs. In Advances in Computational Intelligence: 14th International Work-Conference on Artificial Neural Networks, IWANN 2017, Cadiz, Spain, June 14-16, 2017, Proceedings, Part II 14; Springer: New York, NY, USA, 2017. [Google Scholar]
- Li, X.; Yang, D.; Liu, X.; Wu, X.M. Bridging time series dynamics and complex network theory with application to electrocardiogram analysis. IEEE Circuits Syst. Mag. 2012, 12, 33. [Google Scholar] [CrossRef]
- Niu, H.; Liu, J. Associated network family of the unified piecewise linear chaotic family and their relevance. Chin. Phys. B 2025. online in advance. [Google Scholar] [CrossRef]
- Andrzejak, R.G.; Schindler, K.; Rummel, C. Nonrandomness, nonlinear dependence, and nonstationarity of electroencephalographic recordings from epilepsy patients. Phys. Rev. E—Stat. Nonlinear, Soft Matter Phys. 2012, 86, 046206. [Google Scholar] [CrossRef] [PubMed]
- Alotaiby, T.N.; Alshebeili, S.A.; Alshawi, T.; Ahmad, I.; El-Samie, F.E.A. EEG seizure detection and prediction algorithms: A survey. EURASIP J. Adv. Signal Process. 2014, 2014, 1. [Google Scholar] [CrossRef]
- Barabási, A.L. Network science. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120375. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E. Complex systems: A survey. arXiv 2011, arXiv:1112.1440. [Google Scholar]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.-U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175. [Google Scholar] [CrossRef]
- Zhou, Z. Machine Learning; Springer: Singapore, 2021. [Google Scholar]
- Wang, L.; Arends, J.B.; Long, X.; Cluitmans, P.J.; van Dijk, J.P. Seizure pattern-specific epileptic epoch detection in patients with intellectual disability. Biomed. Signal Process. Control 2017, 35, 38. [Google Scholar] [CrossRef]
- Goutte, C.; Gaussier, E. A probabilistic interpretation of precision, recall and F-score, with implication for evaluation. In European Conference on Information Retrieval; Springer: Berlin/Heidelberg, Germany, 2005; pp. 345–359. [Google Scholar]
- Schwenke, C.; Schering, A.G. True positives, true negatives, false positives, false negatives. In Wiley StatsRef: Statistics Reference Online; Wiley Online Library: Berlin, Germany, 2014. [Google Scholar]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K. Xgboost: Extreme gradient boosting. R Package Version 0.4-2 2015, 1, 1–4. [Google Scholar]




| Feature | p-Value |
|---|---|
| Method | Accuracy | Balanced Accuracy | F1 Score | Precision | Recall | Specificity | MCC | Cohen’s Kappa | Hamming Loss | Jaccard Index |
|---|---|---|---|---|---|---|---|---|---|---|
| VG | 0.882 | 0.879 | 0.901 | 0.908 | 0.893 | 0.865 | 0.755 | 0.755 | 0.118 | 0.820 |
| HVG | 0.934 | 0.931 | 0.945 | 0.944 | 0.947 | 0.915 | 0.862 | 0.862 | 0.066 | 0.896 |
| LPVG | 0.928 | 0.928 | 0.939 | 0.952 | 0.927 | 0.930 | 0.851 | 0.851 | 0.072 | 0.885 |
| MFDM | 0.840 | 0.833 | 0.867 | 0.864 | 0.870 | 0.795 | 0.666 | 0.666 | 0.160 | 0.765 |
| QG | 0.796 | 0.784 | 0.832 | 0.821 | 0.843 | 0.725 | 0.572 | 0.572 | 0.204 | 0.713 |
| Ours | 0.978 | 0.978 | 0.982 | 0.983 | 0.98 | 0.975 | 0.954 | 0.954 | 0.020 | 0.964 |
| Rank | Model Type | Accuracy (%) | Total Cost | Preset | Prediction Speed (obs/s) | Training Time (s) |
|---|---|---|---|---|---|---|
| 1 | Ensemble | 97.6 | 12 | Custom Ensemble | 274.21 | 168.61 |
| 2 | SVM | 97.4 | 13 | Custom SVM | 20,898.55 | 41.13 |
| 3 | Ensemble | 97.4 | 13 | Bagged Trees | 2703.39 | 3.53 |
| 4 | Neural Network | 97.2 | 14 | Custom Neural Network | 17,686.34 | 165.26 |
| 5 | Tree | 97.2 | 14 | Custom Tree | 13,993.02 | 17.42 |
| 6 | SVM | 97.2 | 14 | Cubic SVM | 14,767.65 | 1.11 |
| 7 | Kernel | 97.2 | 14 | SVM Kernel | 17,235.55 | 1.84 |
| 8 | Neural Network | 97.0 | 15 | Trilayered Neural Network | 17,110.86 | 1.03 |
| 9 | Tree | 96.8 | 16 | Fine Tree | 22,969.39 | 1.72 |
| 10 | Tree | 96.8 | 16 | Medium Tree | 21,404.11 | 3.76 |
| 11 | SVM | 96.8 | 16 | Medium Gaussian SVM | 12,757.80 | 2.04 |
| 12 | Ensemble | 96.8 | 16 | RUSBoosted Trees | 6180.08 | 2.12 |
| 13 | Ensemble | 96.6 | 17 | Subspace KNN | 924.60 | 3.72 |
| 14 | Neural Network | 96.6 | 17 | Medium Neural Network | 21,523.24 | 4.87 |
| 15 | SVM | 96.4 | 18 | Quadratic SVM | 15,984.76 | 1.40 |
| 16 | KNN | 96.2 | 19 | Custom KNN | 4506.50 | 18.77 |
| 17 | KNN | 96.2 | 19 | Fine KNN | 7484.53 | 3.06 |
| 18 | Neural Network | 96.2 | 19 | Narrow Neural Network | 16,441.53 | 1.68 |
| 19 | Neural Network | 96.2 | 19 | Wide Neural Network | 22,565.42 | 1.03 |
| 20 | Neural Network | 96.2 | 19 | Bilayered Neural Network | 20,544.01 | 1.62 |
| 21 | KNN | 96.0 | 20 | Weighted KNN | 8537.68 | 2.07 |
| 22 | Kernel | 96.0 | 20 | Logistic Regression Kernel | 16,205.77 | 1.09 |
| 23 | Tree | 95.8 | 21 | Coarse Tree | 16,004.92 | 2.09 |
| 24 | SVM | 95.8 | 21 | Linear SVM | 12,219.59 | 2.11 |
| 25 | Logistic Regression | 95.4 | 23 | Logistic Regression | 4623.44 | 3.51 |
| 26 | KNN | 95.2 | 24 | Medium KNN | 7554.55 | 1.69 |
| 27 | Naive Bayes | 94.8 | 26 | Custom Naive Bayes | 2382.31 | 63.52 |
| 28 | Naive Bayes | 94.8 | 26 | Kernel Naive Bayes | 1967.08 | 3.54 |
| 29 | KNN | 94.8 | 26 | Cosine KNN | 7863.22 | 0.83 |
| 30 | SVM | 94.6 | 27 | Fine Gaussian SVM | 12,950.65 | 0.79 |
| 31 | KNN | 94.6 | 27 | Cubic KNN | 5804.98 | 0.95 |
| 32 | Discriminant | 92.4 | 38 | Custom Optimizable Discriminant | 9477.07 | 28.42 |
| 33 | Naive Bayes | 92.4 | 38 | Gaussian Naive Bayes | 4518.48 | 3.67 |
| 34 | SVM | 91.2 | 44 | Coarse Gaussian SVM | 14,743.48 | 1.92 |
| 35 | Ensemble | 90.6 | 47 | Subspace Discriminant | 1371.42 | 3.28 |
| 36 | Discriminant | 89.4 | 53 | Linear Discriminant | 12,721.64 | 1.16 |
| 37 | KNN | 86.6 | 67 | Coarse KNN | 7719.47 | 2.57 |
| 38 | Ensemble | 60.0 | 200 | Boosted Trees | 19,922.38 | 2.83 |
| Method | Accuracy | Balanced Accuracy | F1 Score | Precision | Recall | Specificity | MCC | Cohen’s Kappa | Hamming Loss | Jaccard Index |
|---|---|---|---|---|---|---|---|---|---|---|
| VG | 0.568 | 0.568 | 0.571 | 0.576 | 0.568 | 0.892 | 0.460 | 0.460 | 0.432 | 0.406 |
| HVG | 0.728 | 0.728 | 0.728 | 0.729 | 0.728 | 0.932 | 0.660 | 0.660 | 0.272 | 0.592 |
| LPVG | 0.594 | 0.594 | 0.596 | 0.603 | 0.594 | 0.899 | 0.493 | 0.493 | 0.406 | 0.430 |
| MFDM | 0.470 | 0.470 | 0.469 | 0.469 | 0.470 | 0.868 | 0.338 | 0.338 | 0.530 | 0.309 |
| QG | 0.438 | 0.438 | 0.436 | 0.435 | 0.438 | 0.860 | 0.298 | 0.298 | 0.562 | 0.291 |
| Ours | 0.824 | 0.824 | 0.823 | 0.823 | 0.824 | 0.956 | 0.780 | 0.780 | 0.176 | 0.715 |
| Rank | Model Type | Accuracy (%) | Total Cost | Preset | Prediction Speed (obs/s) | Training Time (s) |
|---|---|---|---|---|---|---|
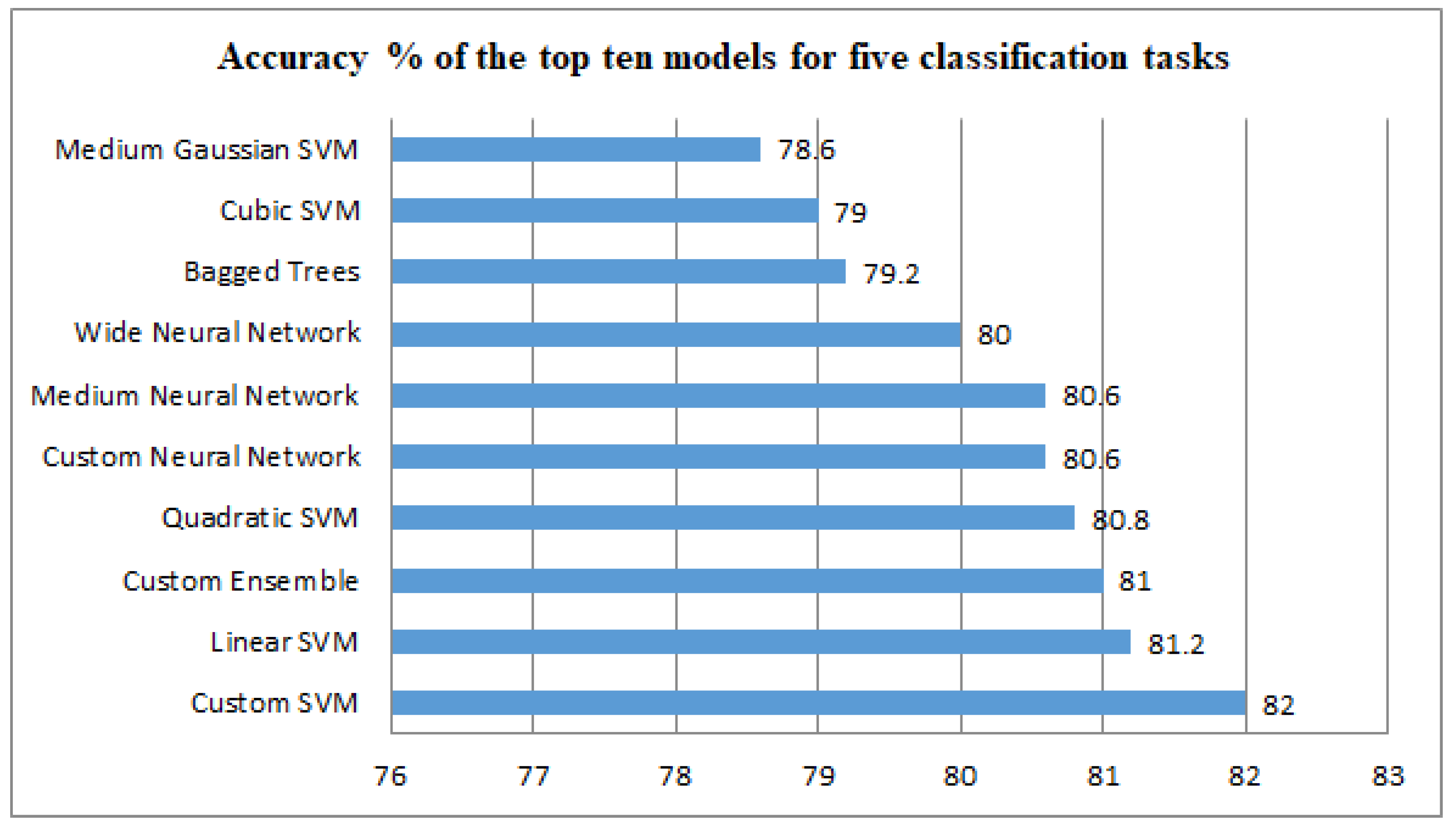
| 1 | SVM | 82.0 | 90 | Custom SVM | 10,505.95 | 249.81 |
| 2 | SVM | 81.2 | 94 | Linear SVM | 3907.47 | 4.57 |
| 3 | Ensemble | 81.0 | 95 | Custom Ensemble | 3021.87 | 88.07 |
| 4 | SVM | 80.8 | 96 | Quadratic SVM | 3794.01 | 4.37 |
| 5 | Neural Network | 80.6 | 97 | Custom Neural Network | 21,322.14 | 261.35 |
| 6 | Neural Network | 80.6 | 97 | Medium Neural Network | 10,889.95 | 4.83 |
| 7 | Neural Network | 80.0 | 100 | Wide Neural Network | 22,057.92 | 2.10 |
| 8 | Ensemble | 79.2 | 104 | Bagged Trees | 2281.52 | 5.26 |
| 9 | SVM | 79.0 | 105 | Cubic SVM | 3244.70 | 4.26 |
| 10 | SVM | 78.6 | 107 | Medium Gaussian SVM | 2875.67 | 4.03 |
| 11 | Ensemble | 78.2 | 109 | Boosted Trees | 2966.54 | 3.95 |
| 12 | Tree | 77.8 | 111 | Fine Tree | 5292.95 | 8.34 |
| 13 | Tree | 77.8 | 111 | Custom Tree | 8286.84 | 25.31 |
| 14 | Neural Network | 77.8 | 111 | Narrow Neural Network | 13,850.45 | 5.43 |
| 15 | Neural Network | 77.6 | 112 | Trilayered Neural Network | 14,166.03 | 7.04 |
| 16 | Neural Network | 77.4 | 113 | Bilayered Neural Network | 13,540.19 | 5.83 |
| 17 | KNN | 76.8 | 116 | Custom KNN | 6235.37 | 26.83 |
| 18 | Kernel | 76.4 | 118 | Custom Kernel | 5609.94 | 10.26 |
| 19 | Ensemble | 74.8 | 126 | Subspace Discriminant | 1279.07 | 4.06 |
| 20 | KNN | 74.6 | 127 | Weighted KNN | 4769.25 | 2.09 |
| 21 | Kernel | 74.6 | 127 | Custom Kernel | 5119.61 | 5.70 |
| 22 | Tree | 74.4 | 128 | Medium Tree | 11,200.87 | 0.97 |
| 23 | Ensemble | 74.2 | 129 | RUSBoosted Trees | 2949.14 | 3.89 |
| 24 | Ensemble | 73.8 | 131 | Subspace KNN | 893.56 | 5.70 |
| 25 | Discriminant | 72.2 | 139 | Optimizable Discriminant | 7123.51 | 30.54 |
| 26 | Discriminant | 72.2 | 139 | Linear Discriminant | 11,343.24 | 3.04 |
| 27 | Naive Bayes | 71.6 | 142 | Custom Naive Bayes | 967.91 | 111.53 |
| 28 | Naive Bayes | 71.6 | 142 | Custom Naive Bayes | 822.89 | 7.32 |
| 29 | KNN | 71.6 | 142 | Fine KNN | 5459.71 | 3.28 |
| 30 | KNN | 71.0 | 145 | Cosine KNN | 4489.38 | 2.32 |
| 31 | SVM | 70.4 | 148 | Coarse Gaussian SVM | 5785.77 | 5.28 |
| 32 | KNN | 70.0 | 150 | Medium KNN | 4529.33 | 1.64 |
| 33 | KNN | 69.0 | 155 | Cubic KNN | 3553.80 | 2.20 |
| 34 | Naive Bayes | 67.0 | 165 | Gaussian Naive Bayes | 2288.75 | 2.76 |
| 35 | SVM | 67.0 | 165 | Fine Gaussian SVM | 2990.76 | 4.15 |
| 36 | Tree | 65.2 | 174 | Coarse Tree | 11,090.56 | 3.89 |
| 37 | KNN | 58.6 | 207 | Coarse KNN | 4593.06 | 1.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, H.; Mu, T.; Wang, Y.; Huang, J.; Liu, J. Epilepsy Diagnosis Analysis via a Multiple-Measures Composite Strategy from the Viewpoint of Associated Network Analysis Methods. Appl. Sci. 2025, 15, 3015. https://doi.org/10.3390/app15063015
Niu H, Mu T, Wang Y, Huang J, Liu J. Epilepsy Diagnosis Analysis via a Multiple-Measures Composite Strategy from the Viewpoint of Associated Network Analysis Methods. Applied Sciences. 2025; 15(6):3015. https://doi.org/10.3390/app15063015
Chicago/Turabian StyleNiu, Haoying, Tiange Mu, Yuting Wang, Jiayang Huang, and Jie Liu. 2025. "Epilepsy Diagnosis Analysis via a Multiple-Measures Composite Strategy from the Viewpoint of Associated Network Analysis Methods" Applied Sciences 15, no. 6: 3015. https://doi.org/10.3390/app15063015
APA StyleNiu, H., Mu, T., Wang, Y., Huang, J., & Liu, J. (2025). Epilepsy Diagnosis Analysis via a Multiple-Measures Composite Strategy from the Viewpoint of Associated Network Analysis Methods. Applied Sciences, 15(6), 3015. https://doi.org/10.3390/app15063015






