Multi-Granularity Temporal Knowledge Graph Question Answering Based on Data Augmentation and Convolutional Networks
Abstract
1. Introduction
2. Related Work
2.1. Knowledge Graph Embedding Models
2.2. Temporal Knowledge Graph Question Answering
2.3. Deep Learning and Time Series
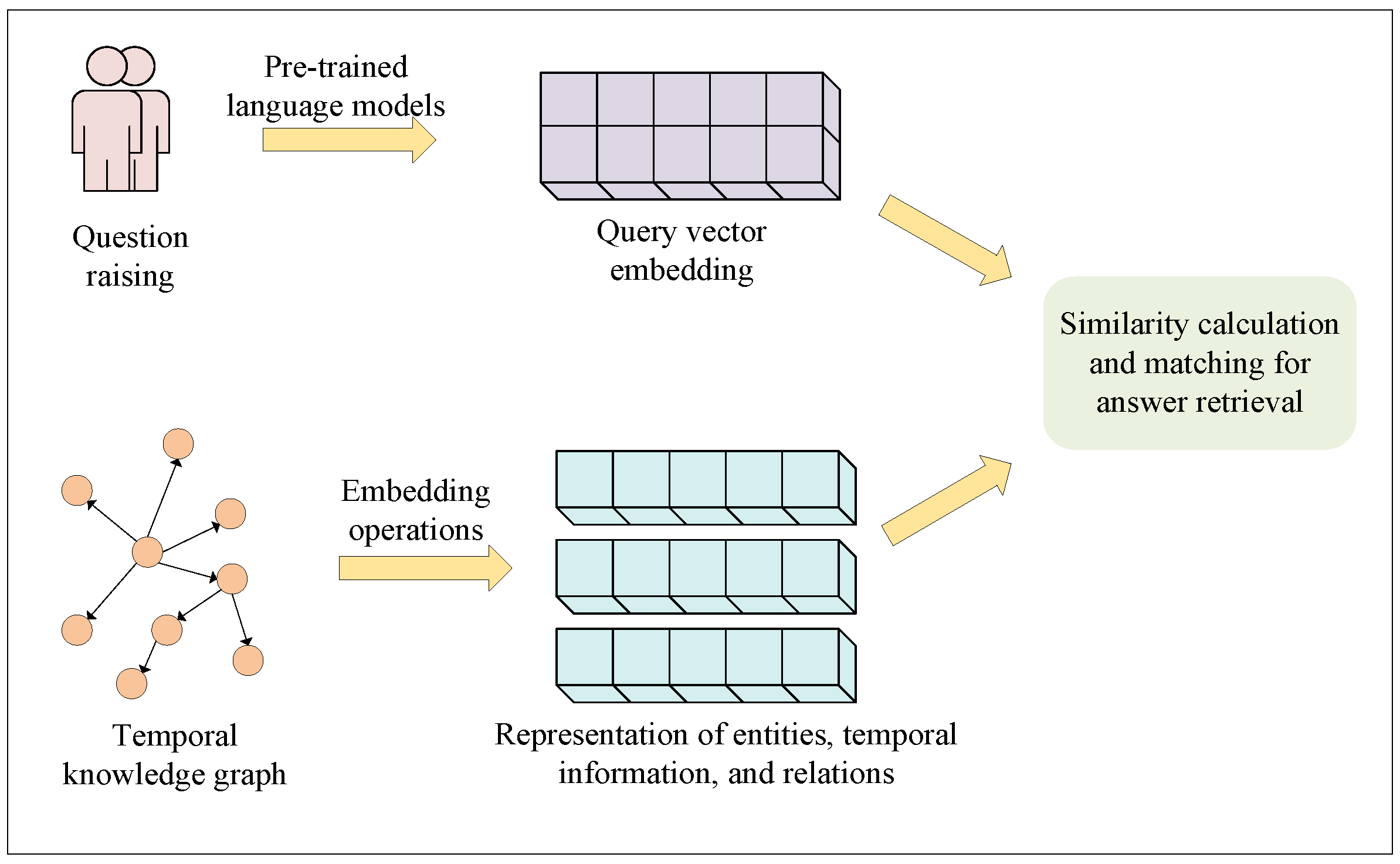
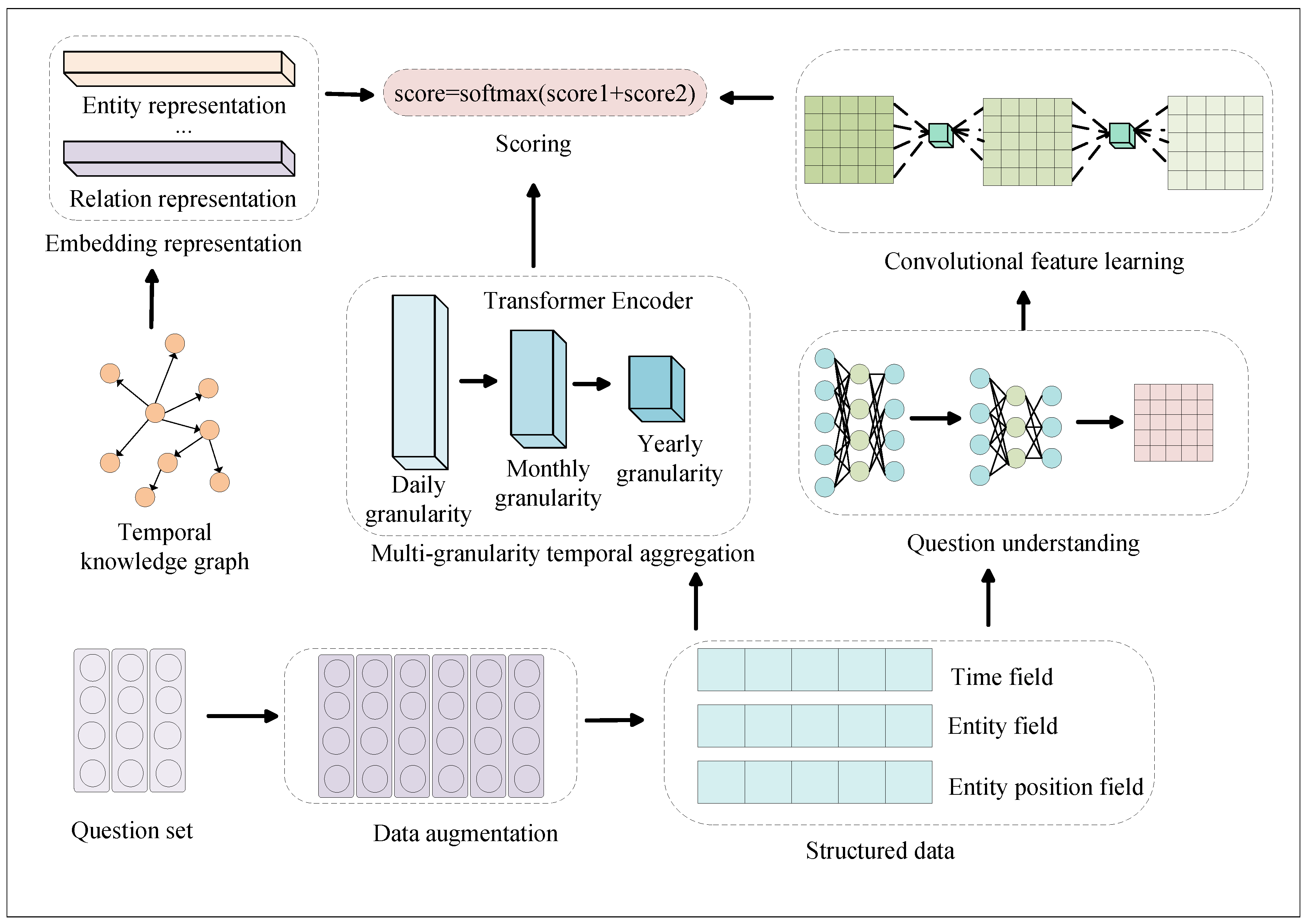
3. MTQADC Model
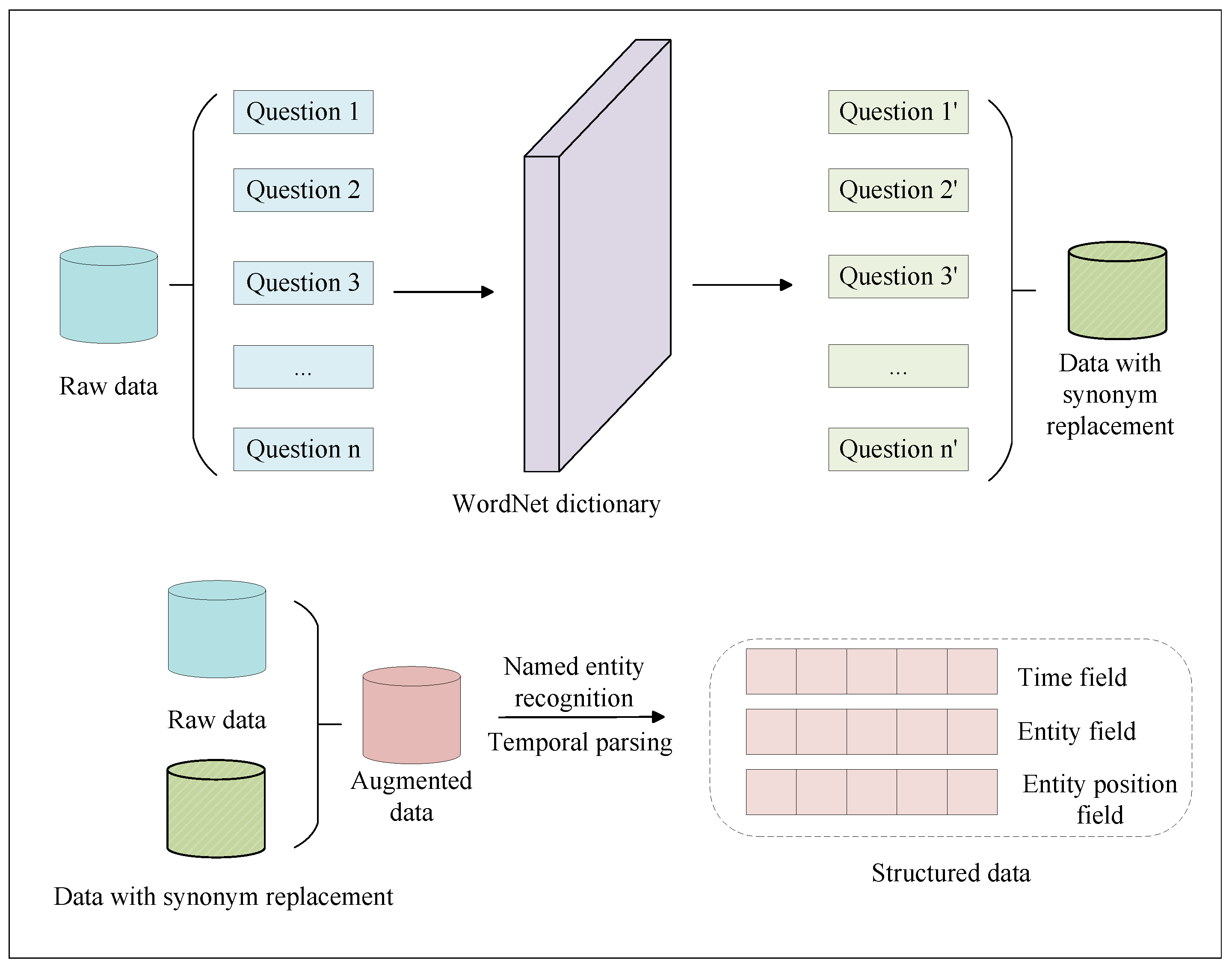
3.1. Data Processing Module
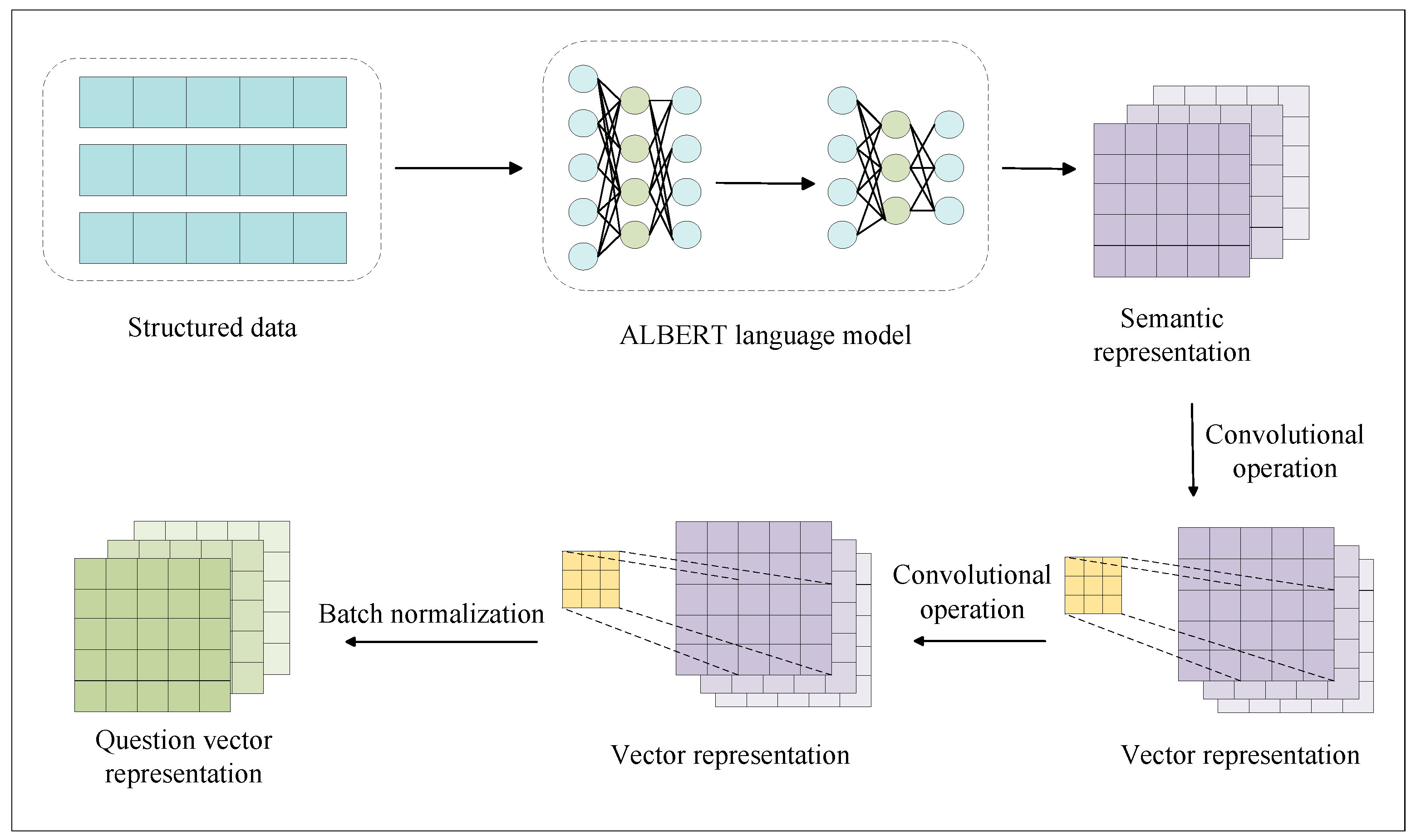
3.2. Feature Extraction Module
3.3. Convolutional Feature Learning Module
3.4. Scoring Module
4. Experiments and Analysis
4.1. Dataset
4.1.1. Multi-Granularity Time Dataset
4.1.2. Single-Granularity Time Dataset
4.2. Evaluation Metrics
4.3. Experiment Parameters
4.4. Comparison Models
4.5. Experimental Results and Analysis
4.5.1. Comparative Experimental Results and Analysis
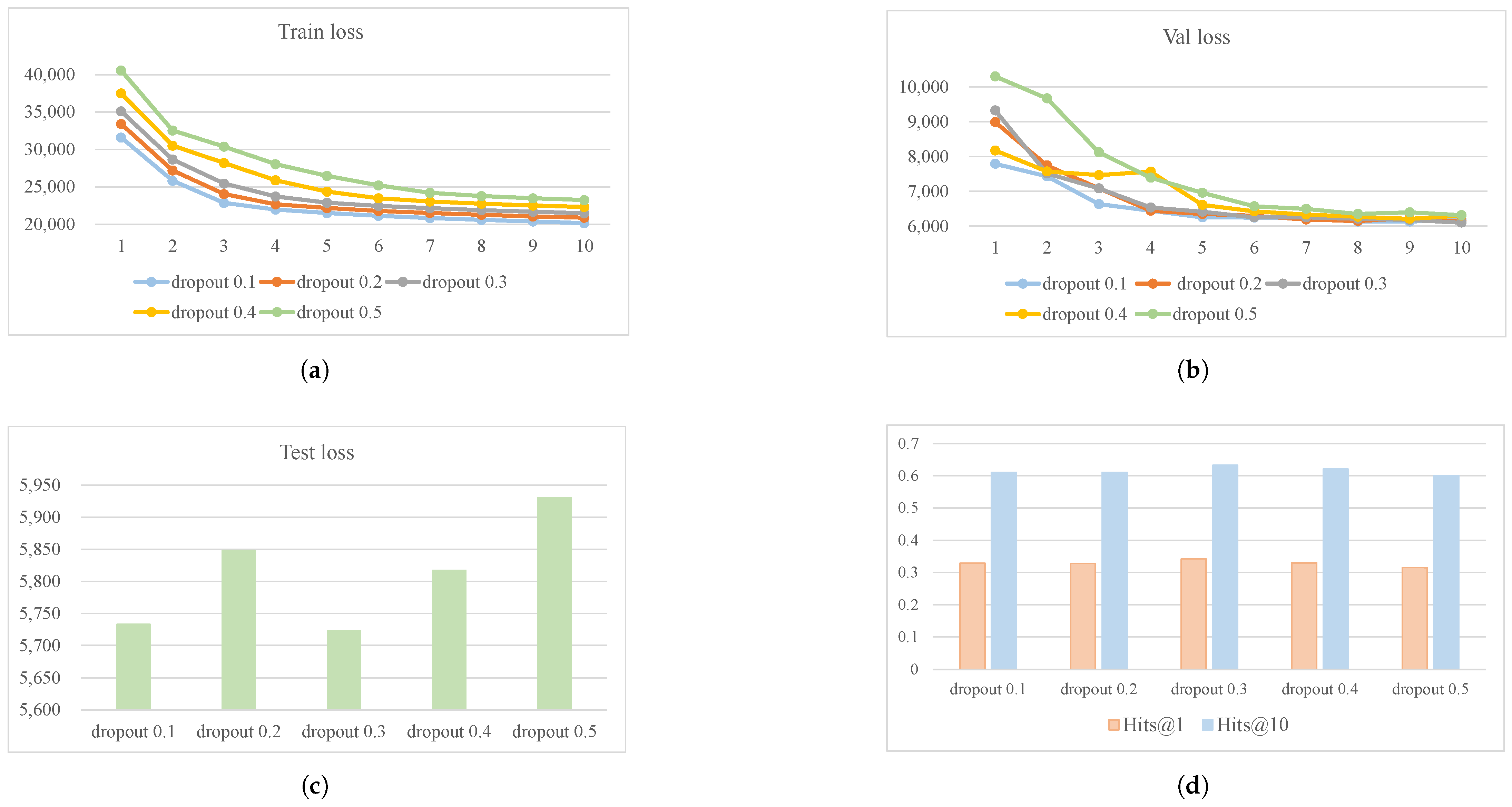
4.5.2. Impact of Dropout Rate on Experiments
4.5.3. Ablation Experiment Results and Analysis
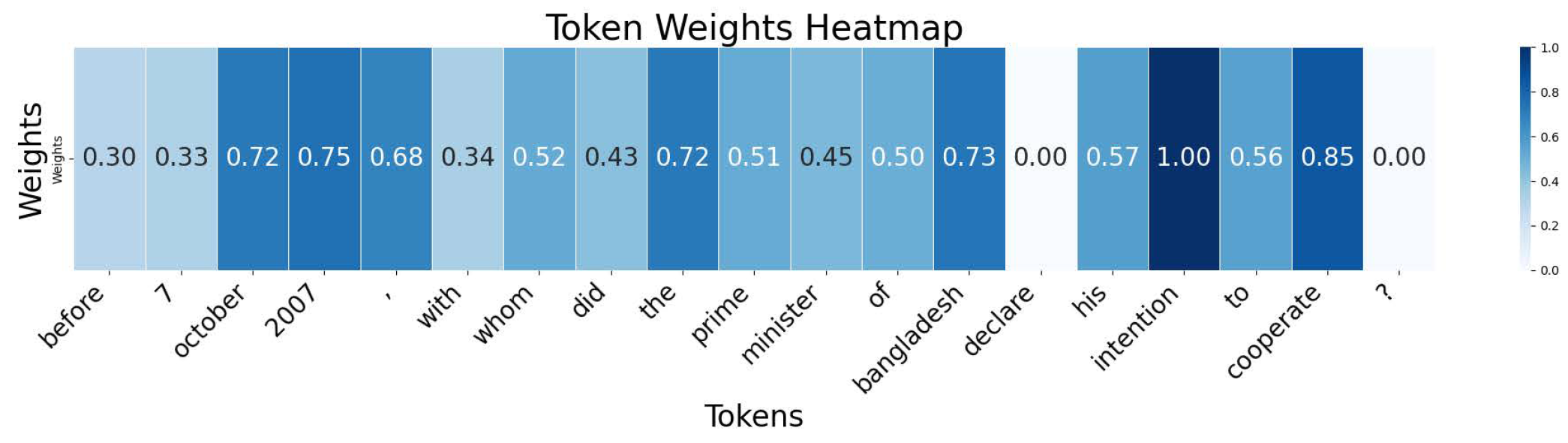
4.5.4. Justification and Interpretability
4.5.5. Error Analysis
4.5.6. Scalability and Computational Complexity
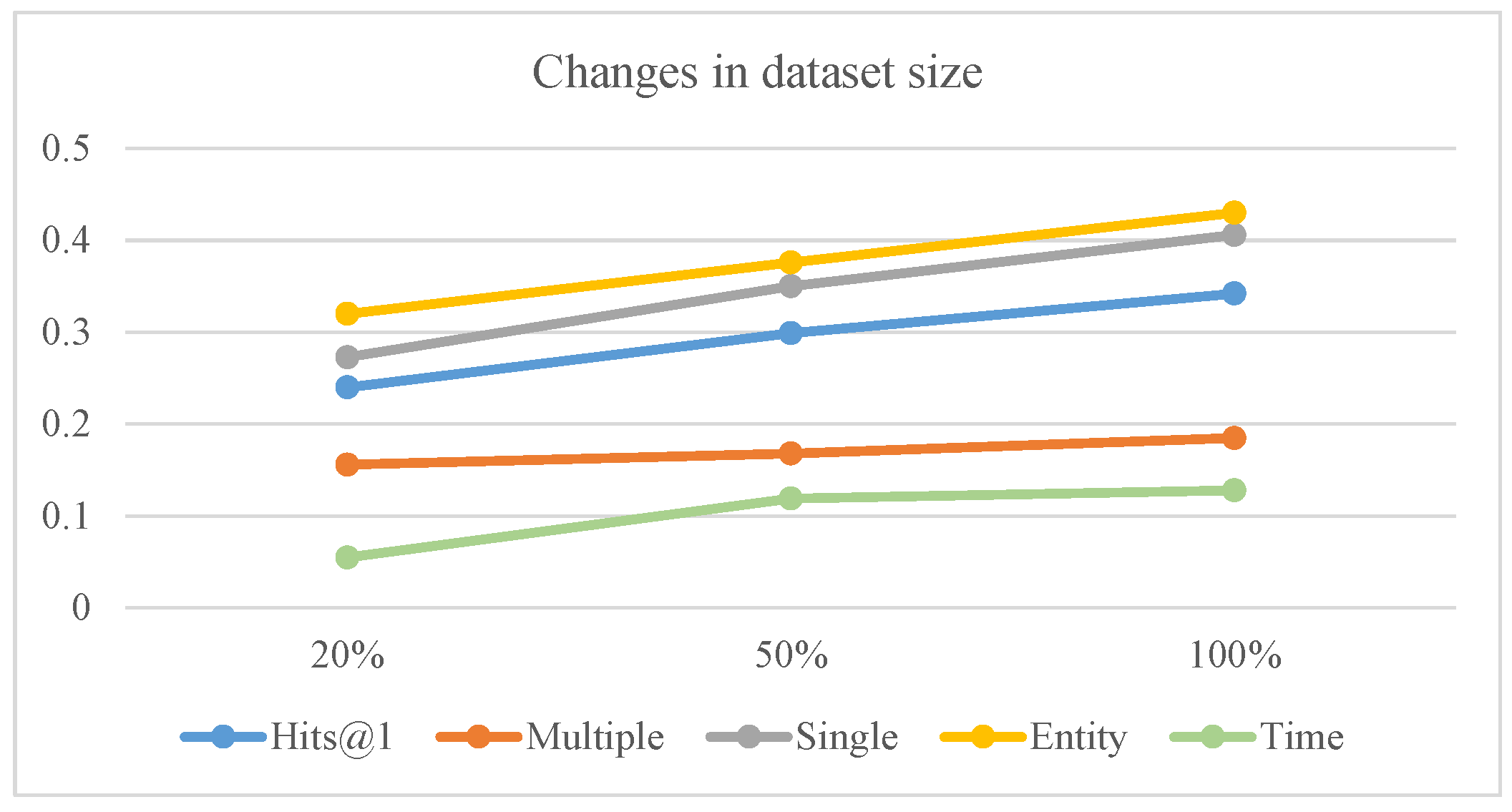
4.5.7. Broader Applicability and Generalization
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, M.; Peng, S.; Yang, M.; Li, N.; Wang, H.; Qiao, L.; Mi, H.; Wen, Z.; Xu, T.; Liu, L. IIAS: An Intelligent Insurance Assessment System through Online Real-time Conversation Analysis. In Proceedings of the IJCAI, Montreal, QC, Canada, 19–27 August 2021; pp. 5036–5039. [Google Scholar]
- Tai, C.Y.; Huang, L.Y.; Huang, C.K.; Ku, L.W. User-centric path reasoning towards explainable recommendation. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, 11–15 July 2021; pp. 879–889. [Google Scholar]
- Leblay, J.; Chekol, M.W. Deriving validity time in knowledge graph. In Proceedings of the Companion Proceedings of the Web Conference, Lyon, France, 23–27 April 2018; pp. 1771–1776. [Google Scholar]
- Jia, Z.; Abujabal, A.; Saha Roy, R.; Strötgen, J.; Weikum, G. Tempquestions: A benchmark for temporal question answering. In Proceedings of the Companion Proceedings of the Web Conference, Lyon, France, 23–27 April 2018; pp. 1057–1062. [Google Scholar]
- Saxena, A.; Chakrabarti, S.; Talukdar, P. Question Answering Over Temporal Knowledge Graphs. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), Virtual Event, 1–6 August 2021; pp. 6663–6676. [Google Scholar]
- Mavromatis, C.; Subramanyam, P.L.; Ioannidis, V.N.; Adeshina, A.; Howard, P.R.; Grinberg, T.; Hakim, N.; Karypis, G. Tempoqr: Temporal question reasoning over knowledge graphs. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual Event, 22 February–1 March 2022; Volume 36, pp. 5825–5833. [Google Scholar]
- Chen, Z.; Liao, J.; Zhao, X. Multi-granularity temporal question answering over knowledge graphs. In Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Toronto, QC, Canada, 9–14 July 2023; pp. 11378–11392. [Google Scholar]
- Jia, Z.; Abujabal, A.; Saha Roy, R.; Strötgen, J.; Weikum, G. Tequila: Temporal question answering over knowledge bases. In Proceedings of the 27th ACM International Conference on Information and Knowledge Management, Torino, Italy, 22–26 October 2018; pp. 1807–1810. [Google Scholar]
- Ding, W.; Chen, H.; Li, H.; Qu, Y. Semantic Framework based Query Generation for Temporal Question Answering over Knowledge Graphs. In Proceedings of the 2022 Conference on Empirical Methods in Natural Language Processing, Abu Dhabi, United Arab Emirates, 7–11 December 2022; pp. 1867–1877. [Google Scholar]
- Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating embeddings for modeling multi-relational data. In Proceedings of the NIPS’13: 27th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; Volume 26. [Google Scholar]
- Wang, Z.; Zhang, J.; Feng, J.; Chen, Z. Knowledge graph embedding by translating on hyperplanes. In Proceedings of the AAAI Conference on Artificial Intelligence, Quebec City, QC, Canada, 27–31 July 2014; Volume 28. [Google Scholar]
- Trouillon, T.; Welbl, J.; Riedel, S.; Gaussier, É.; Bouchard, G. Complex embeddings for simple link prediction. In Proceedings of the International Conference on Machine Learning, PMLR, New York, NY, USA, 20–22 June 2016; pp. 2071–2080. [Google Scholar]
- Nickel, M.; Tresp, V.; Kriegel, H.P. A three-way model for collective learning on multi-relational data. In Proceedings of the ICML, Bellevue, WA, USA, 28 June–2 July 2011; Volume 11, pp. 3104482–3104584. [Google Scholar]
- Yang, B.; Yih, S.W.t.; He, X.; Gao, J.; Deng, L. Embedding Entities and Relations for Learning and Inference in Knowledge Bases. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Jain, P.; Rathi, S.; Mausam; Chakrabarti, S. Temporal Knowledge Base Completion: New Algorithms and Evaluation Protocols. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), Virtual, 16–20 November 2020; pp. 3733–3747. [Google Scholar]
- Lacroix, T.; Obozinski, G.; Usunier, N. Tensor Decompositions for Temporal Knowledge Base Completion. arXiv 2020, arXiv:2004.04926. [Google Scholar]
- Shang, C.; Wang, G.; Qi, P.; Huang, J. Improving Time Sensitivity for Question Answering over Temporal Knowledge Graphs. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Dublin, Ireland, 22–27 May 2022; pp. 8017–8026. [Google Scholar]
- Jia, Z.; Pramanik, S.; Saha Roy, R.; Weikum, G. Complex temporal question answering on knowledge graphs. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, New York, NY, USA, 1–5 November 2021; pp. 792–802. [Google Scholar]
- Jiao, S.; Zhu, Z.; Wu, W.; Zuo, Z.; Qi, J.; Wang, W.; Zhang, G.; Liu, P. An improving reasoning network for complex question answering over temporal knowledge graphs. Appl. Intell. 2023, 53, 8195–8208. [Google Scholar] [CrossRef]
- Graves, A.; Graves, A. Long short-term memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. In Proceedings of the NIPS 2014 Workshop on Deep Learning, Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Lai, G.; Chang, W.C.; Yang, Y.; Liu, H. Modeling long-and short-term temporal patterns with deep neural networks. In Proceedings of the the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 95–104. [Google Scholar]
- Shih, S.Y.; Sun, F.K.; Lee, H.y. Temporal pattern attention for multivariate time series forecasting. Mach. Learn. 2019, 108, 1421–1441. [Google Scholar] [CrossRef]
- Kitaev, N.; Kaiser, L.; Levskaya, A. Reformer: The Efficient Transformer. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Zhang, L.; Aggarwal, C.; Qi, G.J. Stock price prediction via discovering multi-frequency trading patterns. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 2141–2149. [Google Scholar]
- Vaswani, A. Attention is all you need. In Proceedings of the NIPS’17: 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Hou, M.; Xu, C.; Li, Z.; Liu, Y.; Liu, W.; Chen, E.; Bian, J. Multi-granularity residual learning with confidence estimation for time series prediction. In Proceedings of the ACM Web Conference, Lyon, France, 25–29 April 2022; pp. 112–121. [Google Scholar]
- Févry, T.; Soares, L.B.; Fitzgerald, N.; Choi, E.; Kwiatkowski, T. Entities as Experts: Sparse Memory Access with Entity Supervision. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), Virtual, 16–20 November 2020; pp. 4937–4951. [Google Scholar]
- Lan, Z. Albert: A lite bert for self-supervised learning of language representations. arXiv 2019, arXiv:1909.11942. [Google Scholar]
- Saxena, A.; Tripathi, A.; Talukdar, P. Improving multi-hop question answering over knowledge graphs using knowledge base embeddings. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Virtual, 5–10 July 2020; pp. 4498–4507. [Google Scholar]
- Raffel, C.; Shazeer, N.; Roberts, A.; Lee, K.; Narang, S.; Matena, M.; Zhou, Y.; Li, W.; Liu, P.J. Exploring the limits of transfer learning with a unified text-to-text transformer. J. Mach. Learn. Res. 2020, 21, 1–67. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]



| Category | Subcategory | Train | Dev | Test |
|---|---|---|---|---|
| Single | Equal | 135,890 | 18,983 | 17,311 |
| Before/After | 75,340 | 11,665 | 11,073 | |
| First/Last | 72,252 | 11,097 | 10,480 | |
| Multiple | Equal Multi | 16,893 | 3213 | 3207 |
| After First | 43,305 | 6499 | 6266 | |
| Before Last | 43,107 | 6532 | 6247 | |
| Total | 386,787 | 57,979 | 54,584 |
| Train | Dev | Test | |
|---|---|---|---|
| Entity Answer | 225,672 | 19,362 | 19,524 |
| Time Answer | 124,328 | 10,638 | 10,476 |
| Simple Entity | 90,651 | 7745 | 7812 |
| Simple Time | 61,471 | 5197 | 5046 |
| Before/After | 23,869 | 1982 | 2151 |
| First/Last | 118,556 | 11,198 | 11,159 |
| Time Join | 55,453 | 3878 | 3832 |
| Total | 350,000 | 30,000 | 30,000 |
| ALBERT | EmbedKGQA | T5 | GPT-2 | |
|---|---|---|---|---|
| Large Language Model | yes | yes | yes | yes |
| Embedding Operations | no | yes | yes | yes |
| Temporal Aggregation | no | no | yes | yes |
| Convolutional Network | no | no | no | no |
| Data Augmentation | no | no | no | no |
| CronKGQA | CTRN | MultiQA | MTQADC | |
|---|---|---|---|---|
| Large Language Model | yes | yes | yes | yes |
| Embedding Operations | yes | yes | yes | yes |
| Temporal Aggregation | yes | yes | yes | yes |
| Convolutional Network | no | no | no | yes |
| Data Augmentation | no | no | no | yes |
| Model | Hits@1 | Hits@10 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Overall | Question Type | Answer Type | Overall | Question Type | Answer Type | |||||
| Multiple | Single | Entity | Time | Multiple | Single | Entity | Time | |||
| ALBERT | 0.108 | 0.086 | 0.116 | 0.139 | 0.032 | 0.484 | 0.415 | 0.512 | 0.589 | 0.228 |
| EmbedKGQA | 0.206 | 0.134 | 0.235 | 0.290 | 0.001 | 0.459 | 0.439 | 0.467 | 0.648 | 0.001 |
| T5 | 0.279 | 0.175 | 0.322 | 0.379 | 0.036 | 0.560 | 0.497 | 0.585 | 0.707 | 0.201 |
| GPT-2 | 0.283 | 0.161 | 0.333 | 0.362 | 0.091 | 0.586 | 0.489 | 0.625 | 0.702 | 0.304 |
| CronKGQA | 0.279 | 0.134 | 0.337 | 0.328 | 0.156 | 0.608 | 0.453 | 0.671 | 0.696 | 0.392 |
| CTRN | 0.307 | 0.177 | 0.359 | 0.387 | 0.110 | 0.611 | 0.507 | 0.653 | 0.723 | 0.338 |
| MultiQA | 0.293 | 0.159 | 0.347 | 0.349 | 0.157 | 0.635 | 0.519 | 0.682 | 0.733 | 0.396 |
| MTQADC | 0.342 | 0.185 | 0.406 | 0.430 | 0.128 | 0.633 | 0.532 | 0.674 | 0.742 | 0.369 |
| Model | Equal | Before/After | Equal Multi | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Day | Month | Year | Day | Month | Year | Day | Month | Year | |
| ALBERT | 0.069 | 0.082 | 0.132 | 0.221 | 0.277 | 0.308 | 0.103 | 0.144 | 0.144 |
| EmbedKGQA | 0.200 | 0.336 | 0.218 | 0.392 | 0.518 | 0.511 | 0.145 | 0.321 | 0.263 |
| T5 | 0.418 | 0.365 | 0.239 | 0.611 | 0.637 | 0.637 | 0.201 | 0.319 | 0.284 |
| GPT-2 | 0.49 | 0.33 | 0.247 | 0.556 | 0.572 | 0.599 | 0.173 | 0.289 | 0.28 |
| CronKGQA | 0.425 | 0.389 | 0.331 | 0.375 | 0.474 | 0.450 | 0.295 | 0.333 | 0.251 |
| CTRN | 0.522 | 0.337 | 0.288 | 0.592 | 0.611 | 0.604 | 0.192 | 0.293 | 0.296 |
| MultiQA | 0.445 | 0.393 | 0.350 | 0.379 | 0.548 | 0.525 | 0.308 | 0.321 | 0.283 |
| MTQADC | 0.619 | 0.376 | 0.314 | 0.640 | 0.707 | 0.723 | 0.160 | 0.308 | 0.313 |
| Model | Hits@1 | Hits@10 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Overall | Question Type | Answer Type | Overall | Question Type | Answer Type | |||||
| Multiple | Single | Entity | Time | Multiple | Single | Entity | Time | |||
| MTQADC | 0.342 | 0.185 | 0.406 | 0.430 | 0.128 | 0.633 | 0.532 | 0.674 | 0.742 | 0.369 |
| w/o Data Augmentation | 0.321 | 0.160 | 0.386 | 0.409 | 0.105 | 0.615 | 0.527 | 0.615 | 0.740 | 0.311 |
| w/o Convolutional Networks | 0.303 | 0.164 | 0.359 | 0.381 | 0.113 | 0.607 | 0.503 | 0.650 | 0.721 | 0.331 |
| w/o Temporal Aggregation | 0.320 | 0.175 | 0.378 | 0.417 | 0.083 | 0.607 | 0.518 | 0.644 | 0.735 | 0.298 |
| Question | Answer | Predicted Answer | Answer Type | Time | qtype | qlable | |
|---|---|---|---|---|---|---|---|
| 1 | When did Adji Otheth Ayassor first visit China? | ‘8 April 2009’ | ‘27 April 2009’, ‘8 April 2009‘, ‘Laos’ | time | day | first_last | Single |
| 2 | Who would wish to visit Oman on the same month of the Businessperson of Uzbekistan? | ‘Saudi Arabia’ | ‘Iran’, ‘Mahmoud Ahmadinejad’, ‘United Arab Emirates’ | entity | month | equal_multi | Multiple |
| 3 | In which month did Don McKinnon visit Swaziland? | ‘December 2006’ | ‘14 December 2006’, ‘7 November 2005’, ‘17 August 2009’ | time | month | equal | Single |
| 4 | Before China, with whom did the UN Security Council last express its willingness to negotiate? | ‘France’ | ‘Japan’, ‘Iran’, ‘China’ | entity | day | before_last | Multiple |
| 5 | Who was the first to praise China after Lawrence Cannon? | ‘Ma Ying Jeou’ | ‘Japan’, ‘South Korea’, ‘Vietnam’ | entity | day | after_first | Multiple |
| Model | Hits@1 | Hits@10 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Overall | Question Type | Answer Type | Overall | Question Type | Answer Type | |||||
| Complex | Simple | Entity | Time | Complex | Simple | Entity | Time | |||
| EmbedKGQA | 0.288 | 0.286 | 0.290 | 0.411 | 0.057 | 0.672 | 0.632 | 0.725 | 0.850 | 0.341 |
| CronKGQA | 0.647 | 0.392 | 0.987 | 0.699 | 0.549 | 0.884 | 0.802 | 0.992 | 0.898 | 0.857 |
| TempoQR Soft | 0.799 | 0.655 | 0.990 | 0.876 | 0.653 | 0.957 | 0.930 | 0.993 | 0.972 | 0.929 |
| TempoQR Hard | 0.918 | 0.864 | 0.990 | 0.926 | 0.903 | 0.978 | 0.967 | 0.993 | 0.980 | 0.974 |
| MTQADC Soft | 0.771 | 0.607 | 0.989 | 0.847 | 0.628 | 0.958 | 0.931 | 0.990 | 0.974 | 0.926 |
| MTQADC Hard | 0.875 | 0.789 | 0.990 | 0.903 | 0.822 | 0.977 | 0.964 | 0.991 | 0.980 | 0.971 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Su, L.; Wu, L.; Jiang, D. Multi-Granularity Temporal Knowledge Graph Question Answering Based on Data Augmentation and Convolutional Networks. Appl. Sci. 2025, 15, 2958. https://doi.org/10.3390/app15062958
Lu Y, Su L, Wu L, Jiang D. Multi-Granularity Temporal Knowledge Graph Question Answering Based on Data Augmentation and Convolutional Networks. Applied Sciences. 2025; 15(6):2958. https://doi.org/10.3390/app15062958
Chicago/Turabian StyleLu, Yizhi, Lei Su, Liping Wu, and Di Jiang. 2025. "Multi-Granularity Temporal Knowledge Graph Question Answering Based on Data Augmentation and Convolutional Networks" Applied Sciences 15, no. 6: 2958. https://doi.org/10.3390/app15062958
APA StyleLu, Y., Su, L., Wu, L., & Jiang, D. (2025). Multi-Granularity Temporal Knowledge Graph Question Answering Based on Data Augmentation and Convolutional Networks. Applied Sciences, 15(6), 2958. https://doi.org/10.3390/app15062958






