Mamba-DQN: Adaptively Tunes Visual SLAM Parameters Based on Historical Observation DQN
Abstract
1. Introduction
2. Related Work
2.1. Visual SLAM
2.2. Visual SLAM Adaptation
2.3. Deep Reinforcement Learning
2.4. States Space Models
3. Method
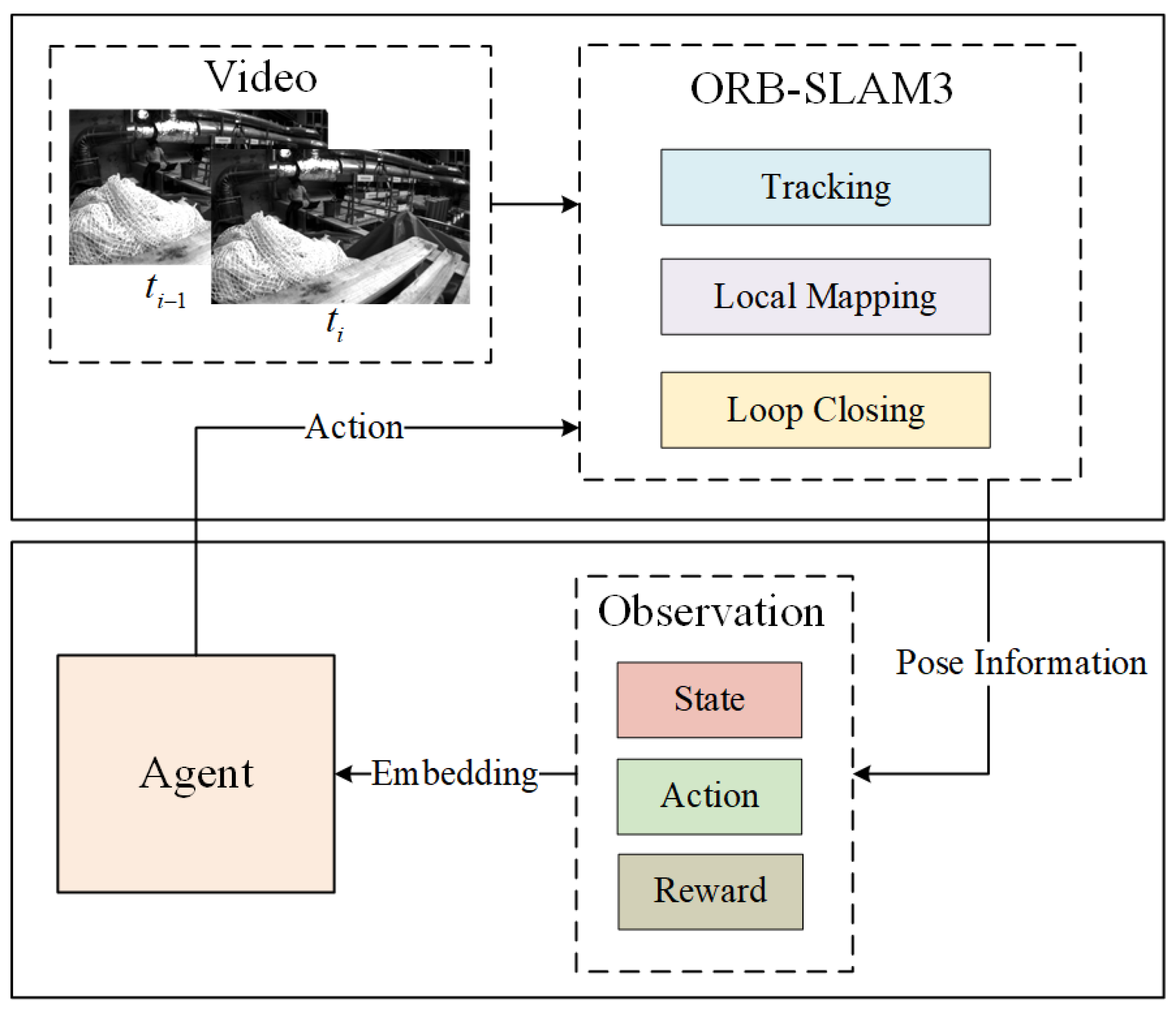
3.1. Problem Summary
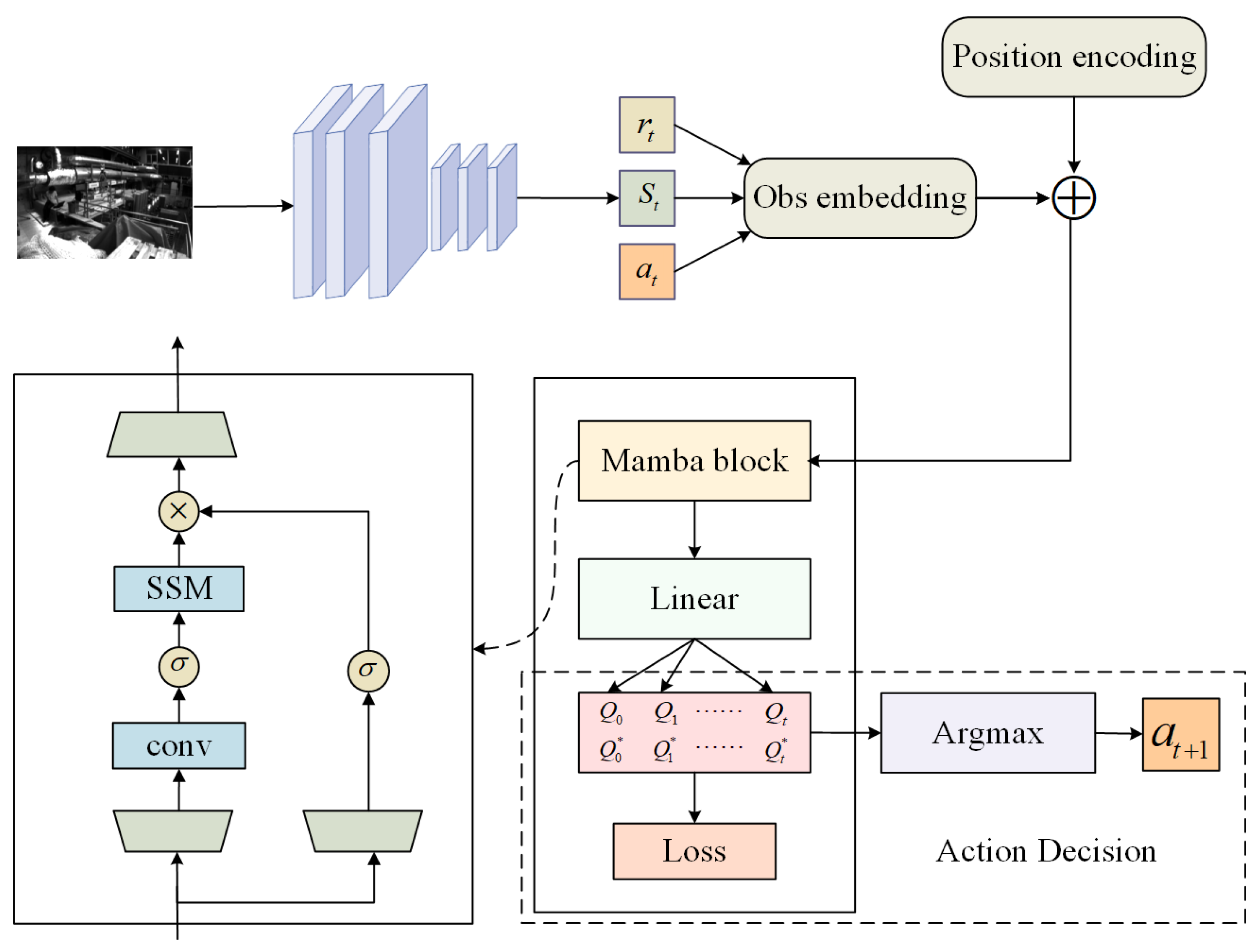
3.2. Mamba-DQN Agent
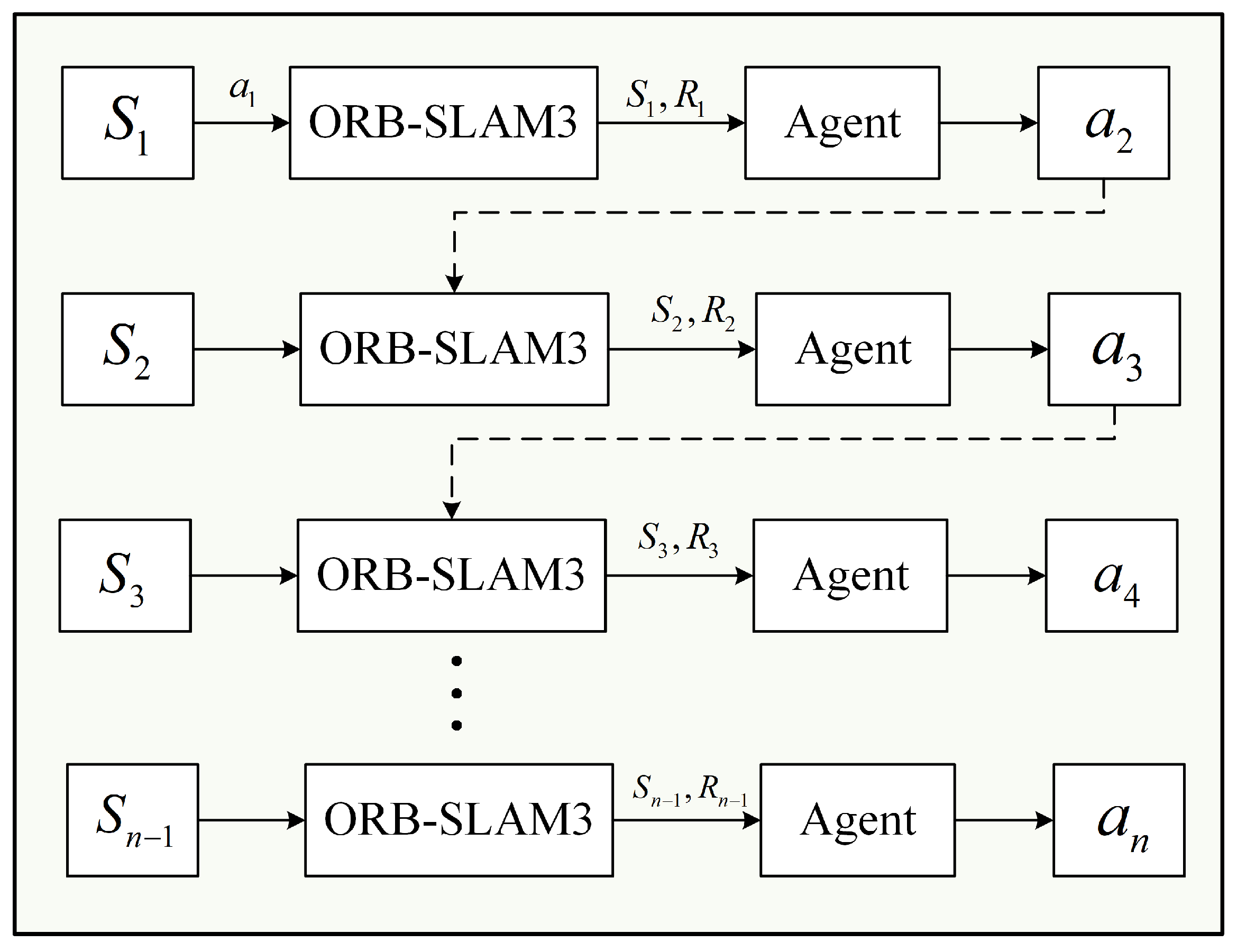
3.2.1. Mamba-DQN Interaction
| Algorithm 1 Mamba-DQN |
|
3.2.2. Computational Analysis of Mamba-DQN
- (1)
- Time Complexity Analysis
- Sequence processing complexity:
- State update: .
- Output calculation: .
- (2)
- Memory Complexity Analysis
- Parameter storage: the parameter matrices in the Mamba module, including , , , and , require storage space of approximately , where d is the hidden state dimension.
- Experience replay buffer: storing the historical observation sequence requires memory, where represents the size of a single observation.
- Hidden States: the SSM computation process requires storing the hidden state for each time step, with a memory requirement of .
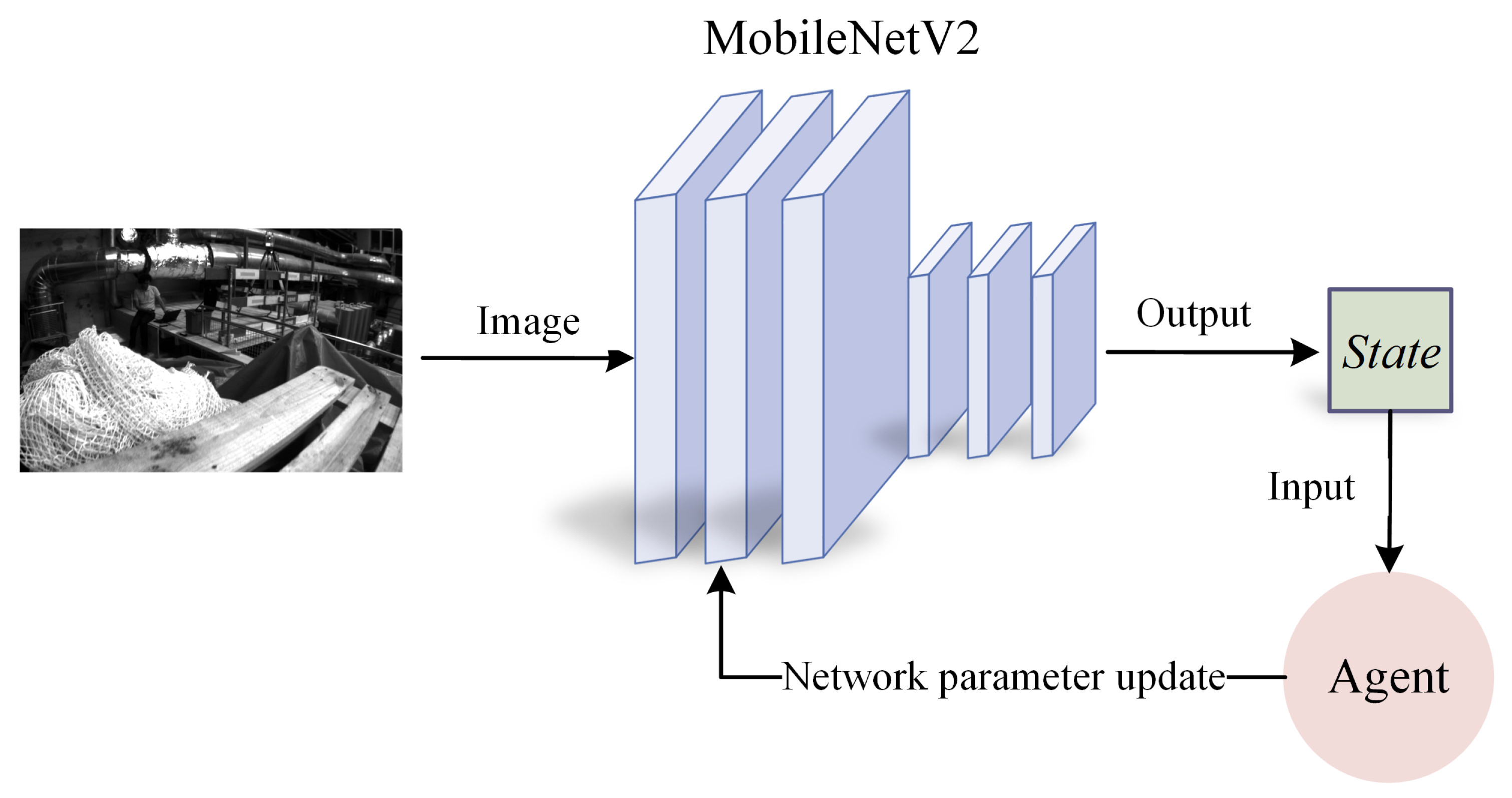
3.3. State Space Design
3.4. Reward Function Design
3.5. Action Space Design
3.5.1. Analysis of Parameters (Action) Selection
3.5.2. Definition of Action Space
4. Experiments
4.1. DataSets
4.2. Analysis of Experimental Results
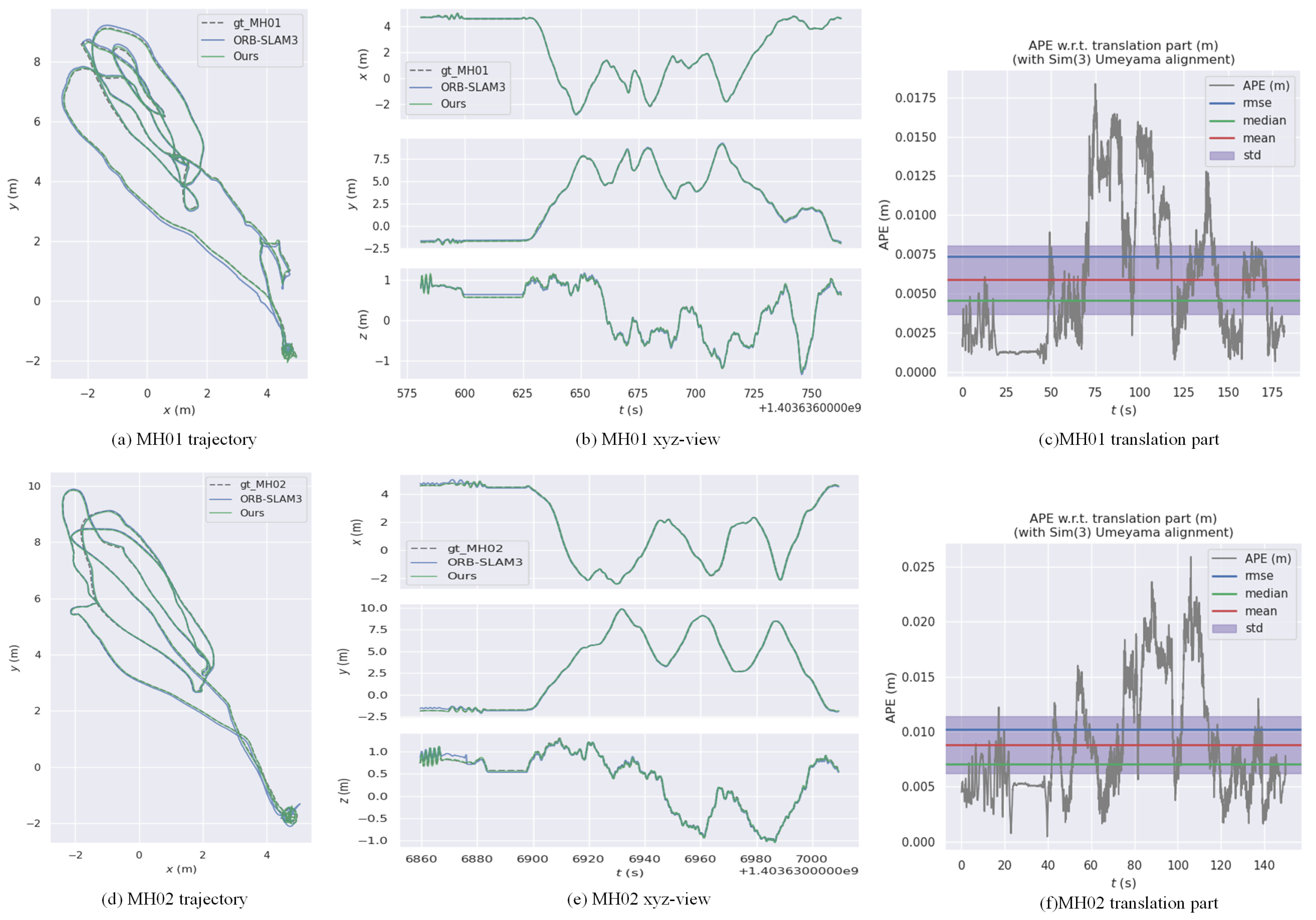
4.2.1. Result1: EUROC
4.2.2. Result2: TUM-VI
4.2.3. Result3: Memory Usage and Time Performance
4.2.4. Result4: Ablation Experiment
- (1)
- Ablation Study on Different Observation Modules
- (2)
- Ablation Study on Historical Observation Window Size
5. Discussion
Failure Case Analysis
- Scene complexity: In the V102 and V201 sequences, rapid camera motion combined with complex lighting conditions led to failures in the Mamba historical observer’s learning process, preventing it from effectively updating the observation model, as shown in Figure 8a,b.
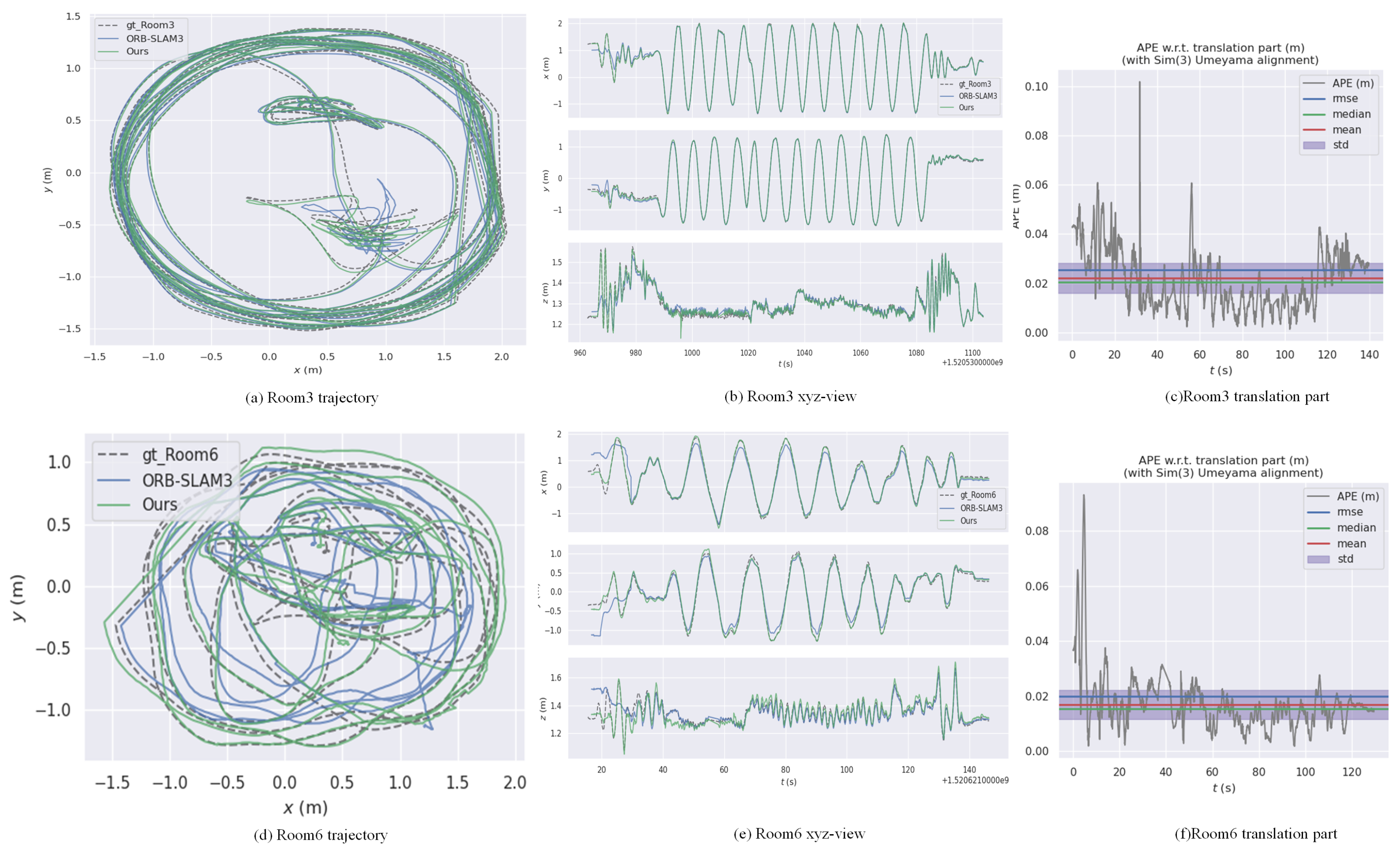
- Feature sparsity: In the Corridor5 sequence, our method achieved an RMSE of 0.040 m, while DDPG-SLAM achieved 0.010 m and SL-SLAM 0.009 m. The corridor environment, characterized by repetitive textures and relatively flat walls, resulted in suboptimal feature extraction and tracking. Additionally, image distortion further exacerbated this issue, leading to the Mamba historical observer’s failure to properly learn from historical experiences. These issues are illustrated in Figure 8c,d, where distortion is particularly evident during the feature extraction process.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SLAM | Simultaneous Localization and Mapping |
| ATE | Absolute Trajectory Error |
| DQN | Deep Q-Network |
| AR | Augmented Reality |
| VR | Virtual Reality |
| CNN | Convolutional Neural Network |
| DDPG | Deep Deterministic Policy Gradient |
| 3D | Three-dimensional |
| ORB | Oriented fast and Rotated Brief |
| RMSE | Root Mean Square Error |
| DDQN | Double Deep Q-Network |
| A3C | Asynchronous Advantage Actor-Critic |
| PPO | Proximal Policy Optimization |
| DRQN | Deep Recurrent Q-Network |
References
- Teed, Z.; Lipson, L.; Deng, J. Deep patch visual odometry. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023; Volume 36. [Google Scholar]
- Chen, Y.; Inaltekin, H.; Gorlatova, M. AdaptSLAM: Edge-Assisted Adaptive SLAM with Resource Constraints via Uncertainty Minimization. In Proceedings of the IEEE INFOCOM 2023–IEEE Conference on Computer Communications, New York, NY, USA, 17–20 May 2023; pp. 1–10. [Google Scholar]
- Messikommer, N.; Cioffi, G.; Gehrig, M.; Scaramuzza, D. Reinforcement Learning Meets Visual Odometry. In Proceedings of the European Conference on Computer Vision (ECCV), Milan, Italy, 29 September–4 October 2024; pp. 76–92. [Google Scholar]
- Khalufa, A.; Riley, G.; Luján, M. A dynamic adaptation strategy for energy-efficient keyframe-based visual SLAM. In Proceedings of the International Conference on Parallel and Distributed Processing Techniques and Applications (PDPTA), Las Vegas, NV, USA, 24–27 June 2019; Arabnia, H.R., Ed.; CSREA Press: Las Vegas, NV, USA, 2019; pp. 3–10. [Google Scholar]
- Kuo, J.; Muglikar, M.; Zhang, Z.; Scaramuzza, D. Redesigning SLAM for arbitrary multi-camera systems. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Virtual Conference, 31 May–31 August 2020; pp. 2116–2122. [Google Scholar]
- Gao, W.; Huang, C.; Xiao, Y.; Huang, X. Parameter adaptive of visual SLAM based on DDPG. J. Electron. Imaging 2023, 32, 053027. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Aglave, P.; Kolkure, V.S. Implementation of high performance feature extraction method using Oriented FAST and Rotated BRIEF algorithm. Int. J. Res. Eng. Technol. 2015, 4, 394–397. [Google Scholar]
- Mur-Artal, R.; Tardós, J.D. ORB-SLAM2: An open-source SLAM system for monocular, stereo, and RGB-D cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.; Tardós, J.D. ORB-SLAM3: An accurate open-source library for visual, visual–inertial, and multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Tateno, K.; Tombari, F.; Laina, I.; Navab, N. CNN-SLAM: Real-time dense monocular SLAM with learned depth prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6243–6252. [Google Scholar]
- Teed, Z.; Deng, J. Droid-SLAM: Deep visual SLAM for monocular, stereo, and RGB-D cameras. Adv. Neural Inf. Process. Syst. 2021, 34, 16558–16569. [Google Scholar]
- Bhowmik, A.; Gumhold, S.; Rother, C.; Brachmann, E. Reinforced feature points: Optimizing feature detection and description for a high-level task. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 4948–4957. [Google Scholar]
- Chandio, Y.; Khan, M.A.; Selialia, K.; Garcia, L.; DeGol, J.; Anwar, F.M. A neurosymbolic approach to adaptive feature extraction in SLAM. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; pp. 4941–4948. [Google Scholar]
- Zhou, L.; Wang, M.; Zhang, X.; Qin, P.; He, B. Adaptive SLAM methodology based on simulated annealing particle swarm optimization for AUV navigation. Electronics 2023, 12, 2372. [Google Scholar] [CrossRef]
- Jia, Y.; Luo, H.; Zhao, F.; Jiang, G.; Li, Y.; Yan, J.; Jiang, Z.; Wang, Z. Lvio-fusion: A self-adaptive multi-sensor fusion SLAM framework using actor-critic method. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 286–293. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; Xing, E.P., Jebara, T., Eds.; JMLR.org: Beijing, China, 2014; pp. 387–395. [Google Scholar]
- Hausknecht, M.; Stone, P. Deep recurrent q-learning for partially observable MDPs. In Proceedings of the 2015 AAAI Fall Symposium Series, Arlington, VA, USA, 12–14 November 2015. [Google Scholar]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the 2018 International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018; pp. 1587–1596. [Google Scholar]
- Vaswani, A. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017. [Google Scholar]
- Parisotto, E.; Song, F.; Rae, J.; Pascanu, R.; Gulcehre, C.; Jayakumar, S.; Jaderberg, M.; Kaufman, R.L.; Clark, A.; Noury, S.; et al. Stabilizing transformers for reinforcement learning. In Proceedings of the International Conference on Machine Learning, Vienna, Austria, 12–18 July 2020; pp. 7487–7498. [Google Scholar]
- Chen, L.; Lu, K.; Rajeswaran, A.; Lee, K.; Grover, A.; Laskin, M.; Abbeel, P.; Srinivas, A.; Mordatch, I. Decision transformer: Reinforcement learning via sequence modeling. Adv. Neural Inf. Process. Syst. 2021, 34, 15084–15097. [Google Scholar]
- Hu, S.; Shen, L.; Zhang, Y.; Tao, D. Graph decision transformer. arXiv 2023, arXiv:2303.03747. [Google Scholar]
- Yamagata, T.; Khalil, A.; Santos-Rodriguez, R. Q-learning decision transformer: Leveraging dynamic programming for conditional sequence modelling in offline RL. In Proceedings of the 40th International Conference on Machine Learning, Hawaii Convention Center, Honolulu, HI, USA, 23–29 July 2023; pp. 38989–39007. [Google Scholar]
- Esslinger, K.; Platt, R.; Amato, C. Deep Transformer Q-Networks for Partially Observable Reinforcement Learning. arXiv 2022, arXiv:2206.01078. [Google Scholar]
- Chebotar, Y.; Vuong, Q.; Hausman, K.; Xia, F.; Lu, Y.; Irpan, A.; Kumar, A.; Yu, T.; Herzog, A.; Pertsch, K.; et al. Q-transformer: Scalable offline reinforcement learning via autoregressive q-functions. In Proceedings of the Conference on Robot Learning, Atlanta, GA, USA, 6–9 November 2023; pp. 3909–3928. [Google Scholar]
- Hu, S.; Shen, L.; Zhang, Y.; Chen, Y.; Tao, D. On transforming reinforcement learning with transformers: The development trajectory. IEEE Trans. Pattern Anal. Mach. Intell. 2024. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhang, L.; Wu, W.; Zhu, Y.; Zhao, D.; Chen, C. Meta-DT: Offline Meta-RL as Conditional Sequence Modeling with World Model Disentanglement. Adv. Neural Inf. Process. Syst. 2025, 37, 44845–44870. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. Trans. Asme J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Dao, T.; Gu, A. Transformers are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality. In Proceedings of the Forty-First International Conference on Machine Learning (ICML), Vienna, Austria, 21–27 July 2024; pp. 1–10. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar]
- Umeyama, S. Least-squares estimation of transformation parameters between two point patterns. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 376–380. [Google Scholar] [CrossRef]
- Tang, L.; Tang, W.; Qu, X.; Han, Y.; Wang, W.; Zhao, B. A Scale-Aware Pyramid Network for Multi-Scale Object Detection in SAR Images. Remote Sens. 2022, 14, 973. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, L. SA-FPN: An effective feature pyramid network for crowded human detection. Appl. Intell. 2022, 52, 12556–12568. [Google Scholar] [CrossRef]
- Yang, X.; Liu, L.; Wang, N.; Gao, X. A two-stream dynamic pyramid representation model for video-based person re-identification. IEEE Trans. Image Process. 2021, 30, 6266–6276. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, Y.; Cheng, Z.; Song, Z.; Tang, C. Multi-scale spatial pyramid attention mechanism for image recognition: An effective approach. Eng. Appl. Artif. Intell. 2024, 133, 108261. [Google Scholar] [CrossRef]
- Kumar, A.; Park, J.; Behera, L. High-speed stereo visual SLAM for low-powered computing devices. IEEE Robot. Autom. Lett. 2023, 9, 499–506. [Google Scholar] [CrossRef]
- Guo, X.; Lyu, M.; Xia, B.; Zhang, K.; Zhang, L. An Improved Visual SLAM Method with Adaptive Feature Extraction. Appl. Sci. 2023, 13, 10038. [Google Scholar] [CrossRef]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. SuperPoint: Self-Supervised Interest Point Detection and Description. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 1–10. [Google Scholar]
- Cai, Z.; Ou, Y.; Ling, Y.; Dong, J.; Lu, J.; Lee, H. Feature Detection and Matching with Linear Adjustment and Adaptive Thresholding. IEEE Access 2020, 8, 189735–189746. [Google Scholar] [CrossRef]
- Burri, M.; Nikolic, J.; Gohl, P.; Schneider, T.; Rehder, J.; Omari, S.; Achtelik, M.; Siegwart, R. The EuRoC micro aerial vehicle datasets. Int. J. Robot. Res. 2016, 35, 103–111. [Google Scholar] [CrossRef]
- TUM Visual-Inertial Dataset. Available online: https://cvg.cit.tum.de/data/datasets/visual-inertial-dataset (accessed on 6 September 2024).
- Forster, C.; Pizzoli, M.; Scaramuzza, D. SVO: Fast semi-direct monocular visual odometry. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 15–22. [Google Scholar]
- Xiao, Z.; Li, S. SL-SLAM: A robust visual-inertial SLAM based deep feature extraction and matching. arXiv 2024, arXiv:2405.03413. [Google Scholar]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]


| Parameters (--) | MH01 | MH02 | MH03 | MH04 |
|---|---|---|---|---|
| 1.1-0.9-8 | 0.010 | 0.024 | 0.026 | 0.143 |
| 1.3-0.7-7 | 0.031 | 0.087 | 0.059 | 0.058 |
| 1.4-0.9-9 | 0.027 | 0.024 | 0.042 | 0.072 |
| 1.2-0.6-9 | 0.018 | 0.063 | 0.086 | 0.146 |
| 1.2-0.8-8 | 0.010 | 0.069 | 0.057 | 0.055 |
| 1.2-0.8-4 | 0.015 | 0.019 | 0.043 | 0.084 |
| SVO [45] | ORB-SLAM3 | DDPG-SLAM [6] | DROID-SLAM [12] | Ours | |
|---|---|---|---|---|---|
| MH01 | 0.100 | 0.016 | 0.008 | 0.013 | 0.007 |
| MH02 | 0.120 | 0.027 | 0.011 | 0.014 | 0.010 |
| MH03 | 0.410 | 0.028 | 0.023 | 0.022 | 0.018 |
| MH04 | 0.420 | 0.138 | 0.011 | 0.043 | 0.007 |
| V102 | 0.210 | 0.015 | 0.016 | 0.012 | 0.038 |
| V201 | 0.110 | 0.023 | 0.021 | 0.017 | 0.120 |
| V202 | 0.110 | 0.029 | 0.022 | 0.013 | 0.019 |
| VINS-Mono [47] | ORB-SLAM3 | DDPG-SLAM [6] | SL-SLAM [46] | Ours | |
|---|---|---|---|---|---|
| Corridor1 | 0.630 | 0.040 | 0.021 | 0.086 | 0.011 |
| Corridor2 | 0.950 | 0.020 | 0.019 | 0.062 | 0.014 |
| Corridor3 | 1.560 | 0.031 | 0.200 | 0.039 | 0.018 |
| Corridor5 | 0.170 | 0.030 | 0.010 | 0.009 | 0.040 |
| Room2 | 0.070 | 0.020 | 0.028 | - | 0.028 |
| Room3 | 0.110 | 0.040 | 0.030 | - | 0.025 |
| Room4 | 0.040 | 0.010 | 0.020 | - | 0.046 |
| Room5 | 0.200 | 0.020 | 0.010 | - | 0.009 |
| Room6 | 0.080 | 0.040 | - | - | 0.019 |
| VINS-Mono [47] | ORB-SLAM3 | Ours | |
|---|---|---|---|
| magistrale1 | 2.19 | 1.13 | 0.81 |
| magistrale2 | 3.11 | 0.63 | 0.49 |
| magistrale3 | 0.40 | 4.89 | 0.98 |
| outdoors1 | 74.96 | 70.79 | 30.62 |
| outdoors2 | 133.46 | 14.98 | 12.92 |
| outdoors3 | 36.99 | 39.63 | 26.87 |
| slides1 | 0.68 | 0.97 | 0.53 |
| slides2 | 0.84 | 1.06 | 0.42 |
| slides3 | 0.69 | 0.69 | 0.43 |
| Agent Type | Memory Usage (MB) |
|---|---|
| DQN with Mamba | 728.4 |
| DQN Without Mamba | 529.6 |
| ORB_SLAM3 | DDPG_SLAM [6] | Ours | |
|---|---|---|---|
| MH01 | 199 | 223 | 220 |
| MH02 | 162 | 183 | 163 |
| MH04 | 106 | 118 | 107 |
| V202 | 123 | 137 | 123 |
| Corridor2 | 366 | 381 | 373 |
| Corridor5 | 344 | 349 | 349 |
| Room2 | 158 | 171 | 158 |
| Room5 | 154 | 168 | 156 |
| Agent | MH01 | V202 | Corridor2 | Room5 | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE | Time | RMSE | Time | RMSE | Time | RMSE | Time | |
| Without Mamba | ||||||||
| - | 0.016 | 220 | 0.029 | 123 | 0.040 | 374 | 0.020 | 154 |
| DQN | 0.013 | 221 | 0.029 | 124 | 0.014 | 375 | 0.026 | 156 |
| DRL + Mamba | ||||||||
| DDQN + Mamba | 0.015 | 224 | 0.021 | 123 | 0.012 | 374 | 0.013 | 156 |
| A3C + Mamba | 0.007 | 228 | 0.020 | 128 | 0.010 | 375 | 0.008 | 157 |
| PPO + Mamba | 0.010 | 232 | 0.018 | 132 | 0.009 | 384 | 0.009 | 158 |
| Ours | 0.007 | 220 | 0.019 | 123 | 0.011 | 373 | 0.009 | 156 |
| DQN + Attention | ||||||||
| DRQN | 0.012 | 242 | 0.020 | 134 | 0.013 | 395 | 0.010 | 169 |
| DQN + Transformer | 0.008 | 252 | 0.020 | 146 | 0.015 | 400 | 0.024 | 177 |
| Dataset | BatchSize = 15 | BatchSize = 30 | BatchSize = 60 | |||
|---|---|---|---|---|---|---|
| RMSE | Time (s) | RMSE | Time (s) | RMSE | Time (s) | |
| MH01 | 0.028 | 220 | 0.007 | 220 | 0.008 | 249 |
| MH02 | 0.039 | 162 | 0.010 | 163 | 0.009 | 185 |
| V202 | 0.024 | 123 | 0.019 | 123 | 0.019 | 135 |
| Corridor2 | 0.044 | 372 | 0.014 | 373 | 0.012 | 426 |
| Corridor5 | 0.054 | 351 | 0.047 | 349 | 0.047 | 385 |
| Room2 | 0.035 | 158 | 0.028 | 158 | 0.026 | 172 |
| Room5 | 0.026 | 155 | 0.009 | 156 | 0.009 | 186 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Huang, C.; Huang, X.; Wu, W. Mamba-DQN: Adaptively Tunes Visual SLAM Parameters Based on Historical Observation DQN. Appl. Sci. 2025, 15, 2950. https://doi.org/10.3390/app15062950
Ma X, Huang C, Huang X, Wu W. Mamba-DQN: Adaptively Tunes Visual SLAM Parameters Based on Historical Observation DQN. Applied Sciences. 2025; 15(6):2950. https://doi.org/10.3390/app15062950
Chicago/Turabian StyleMa, Xubo, Chuhua Huang, Xin Huang, and Wangping Wu. 2025. "Mamba-DQN: Adaptively Tunes Visual SLAM Parameters Based on Historical Observation DQN" Applied Sciences 15, no. 6: 2950. https://doi.org/10.3390/app15062950
APA StyleMa, X., Huang, C., Huang, X., & Wu, W. (2025). Mamba-DQN: Adaptively Tunes Visual SLAM Parameters Based on Historical Observation DQN. Applied Sciences, 15(6), 2950. https://doi.org/10.3390/app15062950






