Abstract
Bioconvection can be defined as an aggregation pattern-generating phenomenon characterized by the collective behavior of swimming microorganisms in response to external influences and self-induced fluid flow, and it has attracted significant interest in the study of microalgae. This review aims to provide a comprehensive examination of this phenomenon in a concentrated population of suspended microalgae definable as nonlinear dynamical systems (i.e., generators of spatial and temporal patterns), describing and clarifying the underlying mechanisms, ecological implications, and possible biotechnological applications in different fields for the improvement of bioreactor design for biomass cultivation, wastewater treatment, or bioremediation. The most influential models used to capture the complexity of bioconvection are perused in order to explore the intricate interplay of internal and external influences (biological, physical, and environmental) governing pattern formation dynamics alongside recent advancements in modeling techniques and experimental approaches.
1. Introduction
In 1911, Wager [1] described in fine detail the aggregation behavior of the unicellular alga Euglena viridis and defined it as the mechanical result of the action of gravity combined with the cohesive force acting upon microorganisms heavier than water, which comes into play as soon as the microalgae are in a sufficiently crowded condition to allow gravity to act [1]. On the basis of his observation of the seasonal and diurnal behaviors of Euglena, the British botanist performed some experiments to follow the appearance and evolution of the aggregation network in different kinds of vessels. He examined the influences of light, vessel shape and depth, exposure to air, temperature, and specific gravity. He described the aggregation phenomenon as the result of a constant cyclic movement downwards and upwards. If cells are present in large numbers, as is the case when the conditions for aggregation are fulfilled, they soon become massed together; their freedom of movement gradually becomes more and more impeded, and very soon, they find themselves sinking downwards under gravitational influence due to the specific gravity of the living Euglena being greater than that of water. This downward movement through the water generates a movement in the opposite direction. The friction between the cell stream and the water sets up a vortical motion by which many of the cells become separated from the main mass; once free, but still with a vertical orientation, they swim upwards again, where they will soon experience mass conditions leading again to sinking. It is in this way that the cyclic downward and upward movements persisting during aggregation are maintained. He concluded that aggregation, though not necessarily involving communication between cells, is of benefit to Euglena in that it results in a constant dissemination of the cells through the liquid environment and prevents accumulation in such dense masses that would have a detrimental effect on their existence by interfering with their assimilative and respiratory functions. Wager observed that aggregation also occurs in the dark, relatively quickly, with cells forming more irregular and distantly spaced groups with respect to light conditions, and attributed it to mechanical forces, including gravity and cohesive forces acting on the single organisms that are heavier than water.
About 50 years later, Platt [2] coined the term “bioconvection” to describe these peculiar patterns formed in shallow suspension by the collective behavior of swimming organisms [2]. Platt observed that under certain conditions, suspensions of swimming microorganisms that are denser than the fluid they swim in, such as the ciliate Tetrahymena pyriformis, would spontaneously form regular patterns, such as polygonal cells or parallel bands. He noted that many microorganisms, such as certain algae and protozoa, show a directional bias and tend to swim upward. As these organisms concentrate near the upper surface of the fluid, they create a top-heavy, unstable density distribution, which in turn leads to convection, where denser fluid (containing more organisms) sinks, while less dense fluid rises, creating circulation patterns that resemble the Benard cells typical of thermal convection (hence the term bioconvection pattern) [3,4]. The requirement of a minimum critical depth and a minimum critical density for pattern formation support the resemblance to Benard cells, with the density of motile organisms being the analog of the energy input in the thermal case [5,6,7]. Confirming what was already stated by Wager, Platt [2] concluded that the combination of upward swimming and fluid convection results in self-organized patterns visible at the macroscopic scale. To date, the detailed descriptions provided by Wager [1] and Platt [2] are still valid and representative of bioconvection in single-celled swimming microorganisms.
This remarkable macroscopic phenomenon represents a fundamental aspect of microbial ecology since microorganisms constitute a major part of the world’s biomass, and their population dynamics (replication and decay, accumulation, and dispersal) modulate and regulate their own lives, the lives of the larger creatures that feed on them, and eventually the climate, and this holds especially true in the case of microalgae since they play pivotal roles in nutrient cycling, primary productivity, and ecosystem stability [8,9,10,11]. Bioconvection in microalgae has emerged as a subject of increasing interest due to its ecological significance and biotechnological potential. A suspension of microalgae can be defined as an “active medium”, i.e., an aggregate of elements capable of independently moving and interacting with each other, where microalgae are single-celled microorganisms which are motile, i.e., self-propelled, and so small that inertial effects can be ignored in describing their locomotion [12,13,14,15]. They interact with their physical environment as individuals and as a population, and in both cases, the dynamics can provide benefits to the organisms, either improving their growth or increasing their chance of survival [16]. The interaction produces the key features of bioconvection, i.e., distinct patterns of different shapes, arising from the interplay between the upward swimming of the microalgae and the downward fluid flow driven by their collective motion [17]. In bioconvection, microalgae are both the driving force for convective instabilities and the markers allowing the visualization of the flow; hence, they provide a unique tool for studying and understanding the mechanisms driving the phenomenon, which is crucial for unraveling its ecological implications and harnessing its applications in environmental and industrial settings (optimizing light distribution in photobioreactors, reducing reliance on mechanical mixing, improving nutrient distribution within the medium, and enhancing the photobioreactor’s overall efficiency and productivity) [18,19,20].
Many mathematical models have been formulated to explain bioconvection in microalgae and the pattern formation characterizing it in fluid flows within non-porous and porous media, all of them analyzing the combination of the different physical parameters that elicit the phenomenon, such as non-equilibrium processes, dynamic instabilities, gravity, taxis, and diffusion [21,22,23]. This review will provide details of some of these models, paying particular attention to those based on the Turing reaction–diffusion model, a purely mathematical model that can explain spatial pattern formation during development [24,25]. Though the goal of Turing was not merely uncovering the principle of two-dimensional pattern formation, but a principle that explains morphogenesis in general, his model is powerful in generating patterns; hence, its equations can also be applied to the description of microalgal patterns formed in bioconvection. We will describe how Turing’s framework connects to bioconvection by integrating the reaction–diffusion equations of his model with the self-organization phenomena that characterize the behavior of algal populations.
2. Models
While Platt did not provide a formal mathematical model in his paper [2], his description and explanation of bioconvection were crucial in establishing the field and inspiring future research and modeling efforts. In this section, we will describe some of the models developed from experimental observations to analyze the bioconvection phenomenon and simulate the different patterns generated by the collective motion of two microalgae, i.e., Chlamydomonas and Euglena, the microorganisms of choice due to their complex behavior and multifaceted potentialities as cell models in photobiology [26,27,28,29,30,31] and as sources of active biomolecules [32,33,34,35].
We will not go into full detail of the complex mathematical formulations at the basis of the various models since this is beyond the scope of this review; still, we will provide simplified forms of the equations used by the authors to describe their approach.
One of the most influential modern models for bioconvection was developed by Pedley and Kessler in the 1990s [17,36], often referred to as the Pedley–Kessler continuum model formulated for dilute suspensions of swimming microorganisms with asymmetric mass distributions [17,36]. It treats the suspension as a continuous medium rather than focusing on individual microorganisms, combining fluid dynamics with the behavior of swimming microorganisms, and accounting for randomness in swimming direction by incorporating gyrotaxis (orientation due to balance between viscous and gravitational torques) [37,38,39].
The model used a Fokker–Planck equation analogous to that obtained for colloid suspensions in the presence of rotational Brownian motion [40,41] and was tested on swimming cells of Chlamydomonas nivalis. The Fokker–Planck equation [42] for bioconvection describes the probability distribution of microorganism positions and velocities in a fluid, where the organisms exhibit both random motion and directed swimming behavior (often in response to stimuli). The general form is
where p is the probability density function, v is the fluid velocity, D is the diffusion coefficient representing the random motion of the organisms, Vs is their swimming velocity, t is time, and ∇ is the gradient operator.
This equation combines advection (second term), diffusion (third term), and active swimming (fourth term) to model how populations of swimming microorganisms distribute themselves in fluid environments.
A key consideration is that while this model is powerful for understanding bulk behaviors and patterns in microorganism suspensions, it may not be suitable for studying phenomena that depend heavily on individual organism characteristics or interactions. The model’s success with Chlamydomonas nivalis suggests that it works well for similar swimming microorganisms, but careful validation would be needed for application to other species. The Pedley–Kessler continuum model may not be fully applicable when suspensions become too dense or when strong chemical gradients are present. It may also become limited in the case of interactions of multiple species since it does not account for cell–cell signaling or chemical communication, so it may not capture complex behavioral responses to environmental cues. Still, its computational efficiency enables the simulation of large-scale systems and makes it suitable for studying collective behavior.
Extensions and refinements of this model have been proposed afterwards. Hill and Pedley [42] further developed and renewed the new continuum model of 1992 [17], stressing the rational aspect of the formulation, i.e., its systematical derivation from scientific data. They provided nonlinear extensions of previous models, introducing the effects of transport and dispersion by the flow, known as the “taxis” function (a biased motile response of the microorganism to directional stimuli). With the assumption that the cell volume fraction is low enough for hydrodynamic or cell–cell interactions to be neglected, the authors described the models for dilute suspensions of the unicellular, bottom-heavy alga Chlamydomonas nivalis as this organism exhibits the key behaviors the model was designed to capture—specifically phototaxis, negative gravitaxis (swimming upward against gravity), and gyrotaxis (orientation due to the balance between viscous and gravitational torques on the cell). The model was also tested on the bacteria Bacillus subtilis, oxygen-consuming organisms that become active swimmers when the oxygen concentration in the environment exceeds a critical value. Since they swim up oxygen gradients (oxytaxis) and are denser than the surrounding medium, their swimming behavior leads to bioconvective instability.
The mathematical framework these authors developed for C. nivalis can be synthesized into the following governing equations:
- Continuity equation (conservation of cells):
- Fluid conservation (incompressibility):
- Momentum equation (Navier–Stokes with cell density effects):
where n is the cell concentration, u is the fluid velocity, Vg is the gyrotactic swimming velocity, D is the cell diffusivity tensor, is the fluid density, P is the pressure, g is the gravitational acceleration, α is the relative density difference parameter, μ is the fluid viscosity, and k is the unit vector in the vertical direction. The mathematical constraints of this model limit its applicability to Newtonian fluids, taking into account only small perturbations from equilibrium; therefore, the model may not capture strongly nonlinear behaviors.
The model created by Hill and Pedley [42] captures cell transport through both advection and diffusion, the flow of the fluid driven by density differences, the directed swimming response to stimuli, and the coupling between cell distribution and fluid motion. It is only valid for dilute suspensions where cell–cell interactions are negligible, and where cell morphologies or swimming patterns are simple and constant.
The main drawback of this model is that it does not account for cell division or death and for complex behavioral responses to multiple stimuli. Moreover, by assuming uniform cell properties across the population, it ignores potential chemical signaling between cells. Though representing a significant advance in understanding bioconvection, the model by Hill and Pedley may need modification for systems with strong cell–cell interactions or complex behavioral responses.
Within the framework of Pedley and Kessler [17], Williams and Bees [43] presented three novel approaches aiming to integrate the effects of two important behavioral traits, phototaxis and gyrotaxis, in the descriptive model of bioconvection in cell suspensions and their impact on pattern formation.
The three proposed models take into consideration different aspects of cell swimming behavior: the swimming speed as a function of light intensity; the adjustment of the center-of-mass offset in response to light by modulating the symmetric flagellar beat; and a new reactive torque due to phototaxis, induced by an asymmetric flagellar beat pattern.
The first model is named Photokinesis–Gyrotaxis. It focuses on how light intensity affects swimming velocity (Vs) while maintaining normal gravitaxis and gyrotaxis behaviors. Its photokinetic description is based on the assumption that the swimming velocity, vs, varies linearly with light intensity I according to
where Ic is the critical intensity, and ξ = Vn/Ic (Vn is the swimming speed in the dark). Cells swim forward when I < Ic, stop at I = Ic, and swim backward when I > Ic.
This relatively simple linear equation makes this model computationally efficient and easy to implement in existing gyrotaxis models; its low computational overhead allows for large-scale simulations, such as photobioreactors for algal cultivation, by predicting cell distribution patterns in vertical water columns and by predicting cell behavior in these cultivation systems where light intensity varies. Though it works best for species where the swimming speed is primarily light-dependent, it may need modifications for cells with more complex photoresponses since it assumes a linear relationship between swimming velocity and light intensity, which may not always hold true, and maintains fixed gyrotactic behavior regardless of the light conditions.
The second model is named Light-Dependent Center-of-Mass Offset. It modifies how deterministically cells swim by varying their center-of-mass offset, h (i.e., the distance between the cell’s geometric center and the center of mass), with light intensity. In this case, the center-of-mass offset varies linearly with light intensity according to
where ξ = hn/Ic (hn is the normal offset in the dark).
The maximum offset will be in dark (most deterministic swimming), and the zero offset will be at I = Ic (purely stochastic swimming), while the negative offset will be set at high intensities.
This second model is better suited for species with well-documented center-of-mass changes, and it is the most accurate for studying cell orientation control in photobioreactors and for understanding cell clustering behavior in order to optimize light exposure in dense cell cultures. Its main limit is the linear relationship assumption between the center-of-mass offset and light intensity, which may be oversimplified since it does not account for potential physiological adaptations over time and does not accurately represent all species’ mechanical responses to light; hence, it may require validation for different cell types. Its computational efficiency is moderately complex due to the need to recalculate orientation parameters, and it is more computationally intensive than the first model, but it is still manageable for medium-scale simulations.
The third model is named Reactive Phototactic Torque; it introduces an additional torque (Lp) that responds to both light direction and intensity gradients, and it is induced by an asymmetric flagellar beat pattern. The phototactic torque equation is
where Lp is the total phototactic torque vector, f(I) is the phototactic strength, Co is the unit vector in the direction of cell orientation, ∧ is the vector cross-product operator, π is the unit vector indicating global light direction, ∇ I is the gradient of light intensity, and β₁ and β₂ are two constants.
The model considers two cases:
- (β₁, β₂) = (1, 0): the response to light direction only;
- (β₁, β₂) = (0, H/Is): the response to light gradients only (H is the fluid layer depth).
The torque characteristics are as follows:
- -
- Zero at I = 0 and I = Ic;
- -
- Maximum at I = Ic/2.
In terms of cell behavior, the intensity responses will be as follows:
- -
- No torque in darkness (I = 0);
- -
- No torque at critical intensity (I = Ic);
- -
- Maximum effect at I = Ic/2;
- -
- Positive torque between I = 0 and I = Ic.
Unlike the first two models, which modify existing cell properties (swimming speed and center of mass), this model introduces a new physical mechanism that can work alongside existing cell behaviors. Moreover, thanks to its flexibility, by adjusting β₁ and β₂, it can be investigated how cells respond to either global light direction or local light gradients, or potentially a combination of both. This is the most comprehensive model of the three since it can represent both global and local light responses, and it is flexible enough to accommodate different species’ behaviors. It is also the most computationally intensive since it requires solving more complex vector equations for the accurate determination of multiple parameters (β₁, β₂). Though it may be challenging to validate experimentally and may need optimization for large-scale simulations, it is still excellent for studying complex photo-orientation behaviors in light gradients and useful in designing advanced photobioreactor control systems.
According to the authors, the combination of these three models provides the cells with a valuable, efficient photo-orientation mechanism. The authors also stressed the importance of studying biased swimming microorganisms in layers (as in bioconvection patterns) to exploit the photo-gyrotactic behavior in biofuel production reactors to self-concentrate the cells, to prevent cell interaction with vertical boundaries that may foul the surface, to mix nutrients by bioconvective circulation, and to allow more efficient light penetration into concentrated cell cultures [44,45]. The primary strength of this combined approach is its ability to represent different aspects of cell behavior while maintaining physical relevance. However, users should carefully consider the computational costs versus accuracy needs when implementing these models in practical applications.
In 2013, Kage et al. [46] provided a quantitative description of the whole process of pattern formation and evolution based on long-term observations (over 2 h) of a suspension of Chlamydomonas reinhardtii placed in an experimental chamber illuminated from the bottom with wavelengths longer than 640 nm. These authors described the pattern behavior as a dynamic bioconvection pattern that can reorganize its structure even when appearing stable, and they showed its ability to respond to physiological processes and environmental cues, indicating that the pattern, though it may seem stable, is not stable in steady-state conditions in which upward and downward cell movements are in balance.
Their observations highlighted the following pattern transition characteristics: the wave numbers of steady-state patterns were relatively insensitive to the suspension depth and cell density, the onset pattern wave numbers were highly sensitive to the suspension depth, and the wave numbers decreased with an increasing depth. The physical mechanisms triggering the transition could be changes in the balance between gyrotactic and gravitactic features; enhanced gyrotactic features would lead to larger cell populations accumulating at the bottom, with more cells being entrained in downward plumes, and hence, the formation of concentrated “beams” moving downward. Moreover, changes in shape asymmetry (significantly influenced by flagellar projections and alterations in flagellar beating modes) may increase gyrotactic torque and decrease gravitactic torque.
The authors also observed that pattern wavelength changes correlate with illumination intensity and that red light specifically affects SS2 patterns (steady-state conditions after pattern transition) and not onset or SS1 patterns (steady-state conditions before pattern transition), concluding that these changes may be linked to cellular photosynthetic activity.
All of these characteristics have biological implications since bioconvection may influence cell proliferation, nutrient uptake, gas transport, and photosynthesis, playing a fundamental role in biological functions.
The Kage model has key applications in photobioreactor design, especially long-term continuous production systems, helping in optimizing light distribution by managing cell density gradients for long-term culture stability and predicting pattern transitions that affect productivity.
The main strengths of this model are its long-term dynamics (i.e., capturing pattern evolution over extended periods and accounting for physiological adaptations) and biological integration, carried out by linking physical patterns to photosynthetic activity, cell behavior changes, and physiological responses. While this model is the most valid for flagellated microalgae and similar-sized photosynthetic organisms, under specific conditions (red light illumination, bottom-up lighting, and laboratory-scale), it may need adaptation and modification for different swimming mechanisms and various cell shapes, different lighting configurations, complex reactor geometries, and industrial-scale applications.
More recently, Ramamonij et al. [47] investigated how a population of Chlamydomonas reinhardtii moves in response to a heterogeneous lit environment. They applied a phenomenological law within a Keller–Segel framework, whose two key components are as follows:
- Balance of diffusive and phototactic fluxes
- -
- Diffusive flux: D∇ c, arising from the random motion of cells, where D is the effective diffusion coefficient (0.7–0.9 × 10−7 m2/s), and ∇ c represents the concentration gradient;
- -
- Phototactic flux: cvdrift, which represents directed movement toward/away from light, where vdrift = χ(I)∇I, which represents the drift velocity proportional to the light intensity gradient; χ(I) is the phototactic susceptibility; and ∇I is the light intensity gradient.
- Phototactic susceptibility χ(I): This novel highly nonlinear function quantifies the propensity of cells to migrate in a light intensity gradient and encompasses all phototaxis microscopic mechanisms.
The experimental data reveal three qualitatively different regimes:
No phototactic response: χ(I) = 0 for I < Ith;
Positive phototaxis: χ(I) = αp (1 − I/Icrit)(I/Ith − I1)/(I/Icrit)^(1+m) for Ith < I < Icrit;
Negative phototaxis: χ(I) = αn (1 − II/Icrit) for Icrit < I.
HereIth is the detection threshold intensity (about 1 mW/m2),
Icrit is the critical intensity separating positive and negative phototaxis (~100 W/m2), m is the power-law exponent (1.5 ± 0.2), αp is the positive phototaxis strength (8 ± 5 × 10−17 m4/J), and αn is the negative phototaxis strength (4 ± 2 × 10−11 m4/J).
There are mainly three key innovations in the approach of Ramamonij et al. [47]: (1) a unified framework, which, instead of modeling individual cellular mechanisms (like tumbling frequency or swimming velocity), uses a population-level description, simplifying the complex individual behaviors into a single function χ(I); (2) the experimental validation achieved by measuring χ(I) across seven orders of magnitude of light intensity, showing a clear transition from no response to positive phototaxis to negative phototaxis; and (3) extensions to the classic Keller–Segel chemotaxis (the average behavior of a cell can reflect the chemical gradient with arbitrary accuracy) [48,49,50] by incorporating bioconvection and gyrotactic effects and accounting for spatial heterogeneity in light distribution. The advantages are mainly simplification (reduces complex microscopic behaviors to macroscopic observables, making it easier to measure and validate experimentally); predictive power (successfully predicts pattern formation; captures transition between different regimes; and explains instability mechanisms) and scalability (can be applied to different experimental conditions and works across different spatial scales).
Though the models described so far deal with the effect of phototaxis on fluid flows within non-porous media, bioconvection in porous media also deserves attention since it presents unique and important considerations for both theoretical understanding and practical applications [51,52,53]. This fascinating phenomenon combines biological behavior with fluid dynamics, where the collective motion of microorganisms creates convection patterns within fluid-filled porous materials characterized by a solid matrix containing distributed void spaces or pores, and it is ubiquitous in both natural and engineered contexts, ranging from soil and rock formations to biological tissues, and from foam materials to concrete and ceramics. Also in this case, the basic concept is bioconvection, which occurs when phototactic microorganisms swim with a directional bias. In porous media, these organisms must navigate through interconnected void spaces, and their movement creates density instabilities that lead to convection patterns.
The behavior of bioconvection in porous media is fundamentally shaped by several key characteristics of the medium itself. The porosity φ, defined as the ratio of the void volume to the total volume, determines the space available for fluid flow and organism movement. Permeability K measures how easily fluid can flow through the medium, directly affecting the formation and maintenance of convection patterns. Additionally, tortuosity—the ratio of the actual fluid path length to the straight-line distance—influences both organism movement patterns and the formation of chemical gradients within the system.
The mathematical description of bioconvection in porous media provided by Rajput and Panda [51] requires a comprehensive framework incorporating several key equations.
The system is governed by conservation equations for mass, and the momentum is determined as follows:
In this equation is the fluid density, φ is the porosity of the medium, t is the time, Pe is the pressure above the hydrostatic, μ is the fluid viscosity, K is the permeability of the medium, u is the fluid velocity vector, n is the concentration of microorganisms, is their average volume, g is the gravitational acceleration, ∆ is the density difference between microorganisms and the base fluid, and z is the unit vector in vertical direction.
Swimming orientation and light distribution are intimately coupled through two key equations (swimming orientation and Lambert–Beer law) that work together to describe how microorganisms respond to and affect light conditions in their environment.
The swimming orientation is described by
where So is the mean swimming orientation vector, Ph(I) is the phototaxis function, I is the local light intensity, and z is the unit vector in vertical direction. The phototaxis function determines the vertical orientation of the microorganisms; its values range between −1 and +1, indicating downward swimming for negative values and upward swimming for positive values. The swimming orientation affects the distribution of organisms, which in turn affects light absorption and distribution. Areas with a higher organism concentration will absorb more light, creating shadows for organisms below them, where the light intensity distribution follows the Lambert–Beer law.
So = Ph(I) z
The implications of bioconvection in porous media span multiple fields and applications. In environmental science, this phenomenon plays a crucial role in understanding nutrient cycling in soils, groundwater contamination, and microbial distribution patterns. These processes are fundamental to bioremediation efforts and the overall health of soil and aquatic ecosystems. This phenomenon has particular relevance in marine environments, where it influences sediment ecology and nutrient transport patterns. In industrial applications, bioconvection principles have found significant use in microbial-enhanced oil recovery, where microorganisms are employed to improve oil extraction from reservoirs. The biotechnology sector has leveraged the understanding of these processes to optimize bioreactor design and improve biofilter efficiency, leading to advances in wastewater treatment, biofuel production, and microalgae cultivation. The medical field has also benefited from insights into bioconvection in porous media, particularly in the development of drug delivery systems and the study of bacterial infection patterns. Understanding how microorganisms move through porous biological tissues has improved our ability to design controlled release systems and combat biofilm formation.
To continue with models of bioconvection in non-porous media, special attention has been paid to the bioconvective behavior of Euglena by the group of Suematsu [54], who investigated the effect that light exerts on pattern formation and proposed a model for it. These authors performed experimental observations of the cell behavior in a sealed container schematically divided into a thin upper layer and a thick lower layer and described a novel bioconvective localized pattern induced by positive phototaxis. They derived a two-component system of reaction–diffusion equations with a nonlocal term (this term represented the localization of the pattern since patterns were not formed in the whole container) to model the macroscopic pattern formed by Euglena under stationary illumination, stressing the similarities between this pattern and Rayleigh–Benard convection [5,6,7]. The model considered not only upward swimming due to negative phototaxis and downward sinking due to gravity, but also the diffusion in the two layers of the container due to horizontal swimming and lateral movement in the upper layer based on the nonlocal interaction of cells (“self-shading” effect). It is based on a quasi-one-dimensional system with two layers (upper and lower) and incorporates both vertical and lateral phototaxis. It uses two coupled partial differential equations for population vertical dynamics in the two layers:
- For the upper layer,
- For the lower layer,
where Pᵤ and Pₗ are the cell populations in the upper and lower layers, P = Pᵤ + Pₗ (total population), a and b are constants for downward/upward average velocities, δ is the suspension depth, and Dᵤ and Dₗ are the diffusion coefficients, while C+ and C− represent the lateral phototaxis effects towards the right (+) and left (−) directions.
The equations show that the downward movement (aP2u/δ term) increases with a higher upper-layer population density, while the upward movement (bPl term) is proportional to the lower-layer population, with diffusive spreading being present in both layers (D terms). As for the lateral phototaxis term, it is expressed as follows:
where c is the coefficient relating cell density to light intensity, and λ is the decay length of light propagation.
The lateral phototaxis term (C+(x) − C−(x)) is particularly interesting because it uses a convolution integral to account for light effects from neighboring cells (light scattered from the cells proportional to their density), and an exponential decay (e−|x−y|/λ) that models how light intensity diminishes with distance |x − y| (Lambert–Beer law). This creates a nonlocal interaction between cells through light.
In their model, Suematsu et al. [54] assumed that in the vertical movement, the upward transition rate (b) is much larger than the downward rate (a) due to negative phototaxis from bottom illumination, while the downward transition increases with the total population density. The lateral movement is the result of the cells swimming toward high-density regions in the upper layer because of positive phototaxis, with light scattering by cells creating an attractant effect. The authors also applied the Neumann boundary condition to the populations in both the upper (Pu) and lower (Pl) layers of their system, i.e., zero flux at the boundaries (x = 0 and x = L, where L = system length), i.e., which can be mathematically expressed as
This boundary condition is physically meaningful because it ensures no cells can enter or leave the system through the lateral boundaries, which matches the experimental setup where the suspension is sealed in a container. It would preserve the total number of Euglena cells in the system, which is important for modeling the localized bioconvection pattern while allowing cells to accumulate near the illuminated side due to phototaxis.
Interestingly, for the lateral phototaxis terms (C+ and C−), the authors calculated the boundary conditions assuming Pu = 0 outside the system (x < 0 and x > L). This makes sense physically since there are no cells outside of the sealed container to scatter light and influence the phototactic behavior of cells inside the system.
The model created by Suematsu successfully reproduces key experimental observations, i.e., the formation of localized clusters, the convective flow within clusters, the dependence of cluster spacing on the suspension depth, and the relationship between the number of clusters and cell density. It also demonstrates that localized bioconvection patterns emerge from the combination of vertical negative phototaxis driving upward swimming, lateral positive phototaxis causing cluster formation, and density-dependent downward movement creating convective flow.
Two possible explanations for the changes in the patterns due to light intensity (the destruction of steady states and the prevention of pattern formation) were then given: the first is that motile microorganisms such as Euglena are phototactic, i.e., they swim towards the light source (positive phototaxis) when the total intensity is below a critical value and swim away from the light source (negative phototaxis) when the total intensity is above the critical value. These taxis drive the cells to accumulate at optimal places where the total intensity is close to the critical value. The second explanation is based on absorption and scattering by microorganisms: absorption by the cells reduces the total intensity along the incidence path, while scattering decreases it at a point by deflecting light away from the incidence path but increases it at the same point due to the scattered light arriving at that point from other points in the medium.
Following the experiment on stationary illumination, Suematsu carried out another experiment using spatially homogeneous illumination with light intensity being changed periodically over time [55]. He found that there existed a range of frequencies of the order of 1 Hz (the intrinsic frequency of the rotation of a cell) such that cells of Euglena gracilis failed to form macroscopic patterns. If the illumination frequency was higher than the above range of frequencies, including 1 Hz, patterns were observed. In the case of the illumination frequency being lower than the above range of frequencies, including 1 Hz, patterns were formed intermittently. No detailed explanations were given for this complex dynamical behavior of Euglena, but Suematsu’s experiments and model were analyzed in detail by Tokuta [56], who derived a model of macroscopic patterns valid for both stationary and periodic settings, generated by the collective behavior of the cells depending on the environment. The model integrates cell behavior with mathematical modeling and includes the phenomenon of negative phototaxis, considered not just an individual response but a phenomenon that can influence group dynamics.
For his model, Tokuta relied on Turing’s idea [24] that a system of coupled reaction–diffusion equations can be used to describe the differentiation and spatial pattern formations in biological systems, such as the pigment pattern in the animal kingdom. Turing’s theory says that diffusion could destabilize an otherwise stable steady state of the reaction–diffusion system and subsequently lead to the emergence of new non-uniform spatial patterns. This kind of instability is usually called Turing instability [57,58].
The Turing equations are as follows:
In these equations, (short-ranged activator with slow diffusion) and (long-ranged inhibitor with fast diffusion) are the morphogens (i.e., signaling molecules named the activator and inhibitor that spread through tissue and help control pattern formation during development), which interact in a nonlinear way according to quadratic and cubic terms; is the ratio of the diffusion coefficient of to that of ; is a scaling variable that measures the length scale in the problem; is the Laplacian operator, which describes spatial diffusion; and are the rate constants for interaction terms; and α, β, and γ are rate parameters. The activator automatically enhances its own production, and the inhibitor suppresses the activator’s growth. The differences in the diffusion rates of activator and inhibitor species destabilize the uniform state and lead to the spontaneous emergence of periodic spatial patterns.
In the case of microalgae, the activator could be the cell concentration (the top accumulation of the cells producing density instability), while the inhibitor could be an intrinsic chemical signal linked to redox state changes or a metabolite produced by cell respiration.
Tokuta [56] proved that the experimental system used by Suematsu had Turing instability for coefficients corresponding to stationary and periodic illumination. If a system has Turing instability, an originally homogeneous initial condition may evolve into a spatially non-constant solution, i.e., a convective pattern, which is triggered by spatial disturbances. Therefore, the bioconvection patterns reported by Suematsu can be explained by Turing instability.
The patterns produced by Euglena have an astonishing resemblance with the pigmentation spot patterns of leopard and jaguar generated by Liu et al. [59] using a simple Turing reaction–diffusion model, transformed in such a way that the variables are considered deviations from a steady state rather than actual concentrations of the morphogens, which are the essential elements of the original Turing model. These authors proposed a model with two stages of patterning to explain the temporal evolution of the pigmentation pattern of leopard and jaguar, from spots in the cub (first stage) to rings and rosettes in the adult (second stage).
Figure 1 clarifies this resemblance between the pattern generated by the bioconvective movement of Euglena in a Petri dish and the spot pattern of a leopard: the left panel (a) is a top-view image of the bioconvection pattern of the microalga; the central panel (b) is the binary image of (a), while the right panel (c) shows the spot pattern generated by the application of the Turing equation generated by Liu et al. [59] to simulate the fur pattern characterizing the first stage of growth of the members of the felid family. The spotted pattern shown in (c) was generated using specific values for the parameters, i.e., = 0.45, = 6, α = 0.899, β = −0.91, r2 = 2, r3 = 3.5, and γ = −α.
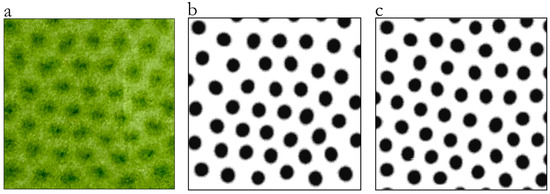
Figure 1.
This figure highlights the resemblance between the pattern generated by the bioconvective movement of Euglena in a Petri dish and the spot pattern of a leopard’s fur: (a) is a top-view image of the bioconvection pattern of the microalga; (b) is a binary image of the bioconvection pattern of the microalga; and (c) shows the spot pattern generated by the Turing equation and simulates the fur pattern characterizing the first stage of growth of the members of the felid family. See the text for details. The images were redrawn after 54 and 59.
3. Conclusions
The remarkable similarity between the algal pattern and the spot pattern of felid fur supports the universal nature of the Turing pattern and the fact that the underlying mathematical principles governing pattern formation in nature are always the same, highlighting their ability to capture a wide range of real-world phenomena and unify our understanding of pattern formation across diverse biological scales and domains [60,61,62,63,64].
Moreover, this similarity strongly suggests that Turing-type reaction–diffusion equations, possibly enhanced with fluid dynamics components, offer the most promising direction for future bioconvection studies. Such mathematical unification can advance practical applications in biomass cultivation by optimizing reactor design, light positioning, and temperature gradients to enhance natural mixing, improve light distribution, and increase mass transfer efficiency [19,65,66,67].
In biomass culturing, bioconvection understanding can improve the design of efficient reactors, optimizing column height to maximize the effects of convective movements and the position of light sources to enhance phototactic responses, using temperature gradients as a taxis to reinforce convection patterns. In these culture devices, mixing can be naturally enhanced by the patterns generated by algal movement, improving nutrient distribution and uptake and reducing boundary layer effects, thus reducing energy costs compared to mechanical mixing [68]. Bioconvection can improve also light exposure since the vertical movement of cells allows for better light distribution throughout the culture, reducing photoinhibition by preventing constant surface exposure and creating light/dark cycles that can enhance photosynthetic efficiency. Moreover, mass transfer benefits will be obtained since the fluid movement can enhance gas exchange (CO2 and O2) [69]. As a bioremediation and wastewater treatment method, bioconvection can increase pollutant removal by improving contact between algae and contaminants through a better distribution of the microorganisms throughout the water column, which in turn leads to a more efficient uptake of heavy metals and organic pollutants. Bioconvection patterns also enhance oxygen transfer to deeper layers, supporting aerobic bacteria that break down organic pollutants and creating micro-zones with varying oxygen levels, supporting diverse microbial communities, thus reducing energy costs for aeration [70,71].
In bioremediation, these models could revolutionize wastewater treatment by predicting optimal conditions for pollutant removal, enhancing oxygen transfer to support diverse microbial communities, and ultimately creating more efficient energy-saving systems that leverage the inherent pattern-forming behaviors of microalgae. The future likely lies in hybrid models that integrate Turing mechanisms with fluid dynamics principles, capturing both pattern formation and the physical movement characteristics of bioconvection.
Author Contributions
Conceptualization, P.G.; data curation, L.B. (Lorenzo Birindelli); writing—original draft preparation, P.G. and L.B. (Laura Barsanti); writing—review and editing, L.B. (Laura Barsanti), P.G. and A.D.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wager, H. On the effect of gravity upon the movements and aggregation of Euglena viridis, Ehrb., and other micro-organisms. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1911, 201, 333–390. [Google Scholar]
- Platt, J.R. “Bioconvection patterns” in cultures of free swimming organisms. Science 1961, 133, 1766–1767. [Google Scholar] [CrossRef] [PubMed]
- Williams, R.J.P.; Fraústo da Silva, J.J.R. The Chemistry of Evolution, 1st ed.; Elsevier Science Ltd.: Oxford, UK, 2006; pp. 77–124. [Google Scholar]
- Kuznetsov, A.V. Bio-thermal convection induced by two different species of microorganisms. Int. Commun. Heat Mass Transf. 2011, 38, 548–553. [Google Scholar] [CrossRef]
- Corcione, M. Rayleigh-Bénard convection heat transfer in nanoparticle suspensions. Int. J. Heat Fluid Flow 2011, 32, 65–77. [Google Scholar] [CrossRef]
- Boffetta, G.; Mazzino, A. Incompressible Rayleigh–Taylor turbulence. Annu. Rev. Fluid Mech. 2017, 49, 119–143. [Google Scholar] [CrossRef]
- Chen, M.; Niu, X.; Yu, P.; Yamasaki, H. Flow behavior and heat transfer characteristics in Rayleigh-Bénard laminar convection with fluid-particle interaction. Int. J. Heat Mass Transf. 2020, 146, 118840. [Google Scholar] [CrossRef]
- Childress, S.; Levandowsky, M.; Spiegel, E.A. Pattern formation in a suspension of swimming microorganisms: Equations and stability theory. J. Fluid Mech. 1975, 69, 591–613. [Google Scholar] [CrossRef]
- Bees, M.A. Advances in Bioconvection. Annu. Rev. Fluid Mech. 2020, 52, 449–476. [Google Scholar] [CrossRef]
- Barsanti, L.; Gualtieri, P. Algae: Anatomy, Biochemistry, and Biotechnology, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Di Nezio, F.; Roman, S.; Buetti-Dinh, A.; Sepúlveda Steiner, O.; Bouffard, D.; Sengupta, A.; Storelli, N. Motile bacteria leverage bioconvection for eco-physiological benefits in a natural aquatic environment. Front. Microbiol. 2023, 14, 1253009. [Google Scholar] [CrossRef] [PubMed]
- Aditi Simha, R.; Ramaswamy, S. Hydrodynamic fluctuations and instabilities in ordered suspensions of self-propelled particles. Phys. Rev. Lett. 2002, 89, 058101. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Ishikawa, T.; Imai, Y. (Eds.) Swimming Microorganisms. In Integrated Nano-Biomechanics; Elsevier: Boston, MA, USA, 2018; pp. 175–216. [Google Scholar]
- Ishikawa, T.; Pedley, T.J. 50-year history and perspective on biomechanics of swimming microorganisms: Part I. Individual behaviours. J. Biomech. 2023, 158, 111706. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, T.; Pedley, T.J. 50-year history and perspective on biomechanics of swimming microorganisms: Part II. Collective behaviours. J. Biomech. 2023, 160, 111802. [Google Scholar] [CrossRef] [PubMed]
- Grover, J.P. Dynamics of competition among microalgae in variable environments: Experimental tests of alternative models. Oikos 1991, 62, 231–243. [Google Scholar] [CrossRef]
- Pedley, T.J.; Kessler, J.O. Hydrodynamic Phenomena in Suspensions of Swimming Microorganisms. Annu. Rev. Fluid Mech. 1992, 24, 313–358. [Google Scholar] [CrossRef]
- Croze, O.A.; Ashraf, E.E.; Bees, M.A. Sheared bioconvection in a horizontal tube. Phys. Biol. 2010, 7, 046001. [Google Scholar] [CrossRef]
- Dervaux, J.; Resta, M.; Capellazzi; Brunet, P. Light-controlled flows in active fluids. Nat. Phys. 2017, 13, 306–312. [Google Scholar] [CrossRef]
- Javadi, A.; Arrieta, J.; Tuval, I.; Polin, M. Photo-bioconvection: Towards light-control of flows in active suspensions. Phil. Trans. R. Soc. A 2020, 378, 20190523. [Google Scholar] [CrossRef]
- Ben-Jacob, E.; Cohen, I.; Levine, H. Cooperative self-organization of microorganisms. Adv. Phys. 2000, 49, 395–554. [Google Scholar] [CrossRef]
- Czirók, A.; Jánosi, I.M.; Kessler, J.O. Bioconvective dynamics: Dependence on organism behaviour. J. Exp. Biol. 2000, 203, 3345–3354. [Google Scholar] [CrossRef]
- Ghorai, S.; Panda, M.K. Bioconvection in an anisotropic scattering suspension of phototactic algae. Eur. J. Mech. B/Fluids 2013, 41, 81–93. [Google Scholar] [CrossRef]
- Turing, A. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 1952, 237, 37–72, 641. [Google Scholar]
- Maini, P.K.; Woolley, T.E. The Turing model for biological pattern formation. In The Dynamics of Biological Systems; Springer: Berlin/Heidelberg, Germany, 2019; pp. 189–204. [Google Scholar]
- Lorenzetti, G.; Barsanti, L.; Birindelli, L.; Gualtieri, P.; Legnaioli, S. Nomen omen: Euglena gracilis possesses a rhodopsin-based photoreceptor. Photochem. Photobiol. 2024; early view. [Google Scholar]
- Barsanti, L.; Evangelista, V.; Passarelli, V.; Frassanito, A.; Gualtieri, P. Fundamental questions and concepts about photoreception and the case of Euglena gracilis. Integr. Biol. 2012, 4, 22–36. [Google Scholar] [CrossRef] [PubMed]
- Tulin, F.; Clark-Cotton, M.R.; Onishi, M. Chlamydomonas. Curr. Biol. 2024, 34, R611–R612. [Google Scholar] [CrossRef] [PubMed]
- Leptos, K.C.; Chioccioli, M.; Furlan, S.; Pesci, A.I.; Goldstein, R.E. Phototaxis of Chlamydomonas arises from a tuned adaptive photoresponse shared with multicellular Volvocine green algae. Phys. Rev. E 2023, 107, 014404. [Google Scholar] [CrossRef]
- Mercatelli, R.; Quercioli, F.; Barsanti, L.; Evangelista, V.; Coltelli, P.; Passarelli, V.; Frassanito, A.; Gualtieri, P. Intramolecular photo-switching and intermolecular energy transfer as primary photoevents in photoreceptive processes: The case of Euglena gracilis. Biochem. Biophys. Res. Commun. 2009, 385, 176–180. [Google Scholar] [CrossRef] [PubMed]
- Akiyama, A.; Ookida, A.; Mogami, Y.; Baba, S.A. Spontaneous alteration of the pattern formation in the bioconvection of Chlamydomonas reinhardtii. J. Jpn. Soc. Microgravity Appl. 2005, 22, 210–215. [Google Scholar]
- Bellido-Pedraza, C.M.; Torres, M.J.; Llamas, A. The Microalgae Chlamydomonas for Bioremediation and Bioproduct Production. Cells 2024, 13, 1137. [Google Scholar] [CrossRef] [PubMed]
- Scartazza, A.; Picciarelli, P.; Mariotti, L.; Curadi, M.; Barsanti, L.; Gualtieri, P. The role of Euglena gracilis paramylon in modulating xylem hormone levels, photosynthesis, and water-use efficiency in Solanum lycopersicum L. Physiol. Plant. 2017, 161, 486–501. [Google Scholar] [CrossRef] [PubMed]
- Kusmic, C.; Barsanti, L.; Di Lascio, N.; Faita, F.; Evangelista, V.; Gualtieri, P. Anti-fibrotic effect of paramylon nanofibers from the WZSL mutant of Euglena gracilis on liver damage induced by CCl₄ in mice. J. Funct. Foods 2018, 46, 538–545. [Google Scholar] [CrossRef]
- Barsanti, L.; Gualtieri, P. Paramylon, a Potent Immunomodulator from WZSL Mutant of Euglena gracilis. Molecules 2019, 24, 3114. [Google Scholar] [CrossRef]
- Pedley, T.J.; Kessler, J.O. A new continuum model for suspensions of gyrotactic micro-organisms. J. Fluid Mech. 1990, 212, 155–182. [Google Scholar] [CrossRef]
- Timm, U.; Okubo, A. Gyrotaxis: A plume model for self-focusing micro-organisms. Bull. Math. Biol. 1994, 56, 187–206. [Google Scholar] [CrossRef]
- Zeng, L.; Jiang, W.; Pedley, T.J. Sharp turns and gyrotaxis modulate surface accumulation of microorganisms. Proc. Natl. Acad. Sci. USA 2022, 119, e2206738119. [Google Scholar] [CrossRef]
- Mandal, A.; Mondal, H.; Tripathi, R. A mathematical model of magneto hydrodynamics unsteady nanofluid flow containing gyrotactic micro-organism through a bidirectional stretching sheet. BioNanoScience 2024, 14, 1410–1427. [Google Scholar] [CrossRef]
- Mori, H. Transport, Collective Motion, and Brownian Motion. Prog. Theor. Phys. 1965, 33, 423–455. [Google Scholar] [CrossRef]
- Das, J.; Mondal, S.; Bag, B.C. Fokker-Planck equation for the non-Markovian Brownian motion in the presence of a magnetic field. J. Chem. Phys. 2017, 147, 164102. [Google Scholar] [CrossRef]
- Hill, N.A.; Pedley, T.J. Bioconvection. Fluid Dyn. Res. 2005, 37, 1. [Google Scholar] [CrossRef]
- Williams, C.R.; Bees, M.A. Photo-gyrotactic bioconvection. J. Fluid Mech. 2011, 678, 41–86. [Google Scholar] [CrossRef]
- Ghorai, S.; Hill, N.A. Penetrative phototactic bioconvection. Phys. Fluids 2005, 17, 074101. [Google Scholar] [CrossRef]
- Ghorai, S.; Hill, N.A. Gyrotactic bioconvection in three dimensions. Phys. Fluids 2007, 19, 054107. [Google Scholar] [CrossRef]
- Kage, A.; Hosoya, C.; Baba, S.A.; Mogami, Y. Drastic reorganization of the bioconvection pattern of Chlamydomonas: Quantitative analysis of the pattern transition response. J. Exp. Biol. 2013, 216, 4557–4566. [Google Scholar] [CrossRef] [PubMed]
- Ramamonjy, A.; Dervaux, J.; Brunet, P. Nonlinear Phototaxis and Instabilities in Suspensions of Light-Seeking Algae. Phys. Rev. Lett. 2022, 128, 258101. [Google Scholar] [CrossRef]
- Keller, E.F.; Segel, L.A. Initiation of Slime Mold Aggregation Viewed as Instability. J. Theor. Biol. 1970, 26, 399–415. [Google Scholar] [CrossRef]
- Keller, E.F.; Segel, L.A. Traveling bands of chemotactic bacteria: A theoretical analysis. J. Theor. Biol. 1971, 30, 377–380. [Google Scholar] [CrossRef] [PubMed]
- Bellomo, N.; Tao, Y.; Winkler, M. Toward a mathematical theory of Keller-Segel models of pattern formation in biological tissues. Math. Models Methods Appl. Sci. 2015, 25, 1663–1763. [Google Scholar] [CrossRef]
- Rajput, S.K.; Panda, M.K. A mathematical modeling of light-induced bioconvection in an isotropic porous medium. Chinese J. Phys. 2024, 91, 792–806. [Google Scholar] [CrossRef]
- Quagliarini, E.; Gregorini, B.; D’Orazio, M. Modelling microalgae biofouling on porous buildings materials: A novel approach. Mater. Struct. 2022, 55, 158. [Google Scholar] [CrossRef]
- Ahmad, S.; Muhammad, A.; Kashif, A. Bioconvection Due to Gyrotactic Microbes in a Nanofluid Flow Through a Porous Medium. Heliyon 2020, 6, e05832. [Google Scholar] [CrossRef]
- Suematsu, N.J.; Awazu, A.; Izumi, S.; Noda, S.; Nakata, S.; Nishimori, H. Localized bioconvection of Euglena caused by phototaxis in the lateral direction. J. Phys. Soc. Jpn. 2011, 80, 064003. [Google Scholar] [CrossRef]
- Suematsu, N.J.; Yamashita, H.; Iima, M. Bioconvection pattern of Euglena under periodical illumination. Front. Cell Dev. Biol. 2023, 11, 1134002. [Google Scholar] [CrossRef]
- Tokuta, Y.M. Negative Phototaxis of Euglena gracilis and Resulting Bioconvection Patterns under Stationary or Rapidly Periodic Illumination. Ph.D. Thesis, Freie Universität, Berlin, Germany, 2019. [Google Scholar]
- Métivier, G.; Rauch, J. Dispersive Stabilization. Bull. Lond. Math. Soc. 2009, 42, 250–262. [Google Scholar] [CrossRef]
- Vittadello, S.T.; Leyshon, T.; Schnoerr, D.; Stumpf, M.P.H. Turing pattern design principles and their robustness. Phil. Trans. R. Soc. A 2021, 379, 20200272. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.T.; Liaw, S.S.; Maini, P.K. Two-stage Turing model for generating pigment patterns on the leopard and the jaguar. Phys. Rev. E 2006, 74, 011914. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.D. A Pre-pattern formation mechanism for animal coat markings. J. Theor. Biol. 1981, 88, 161–199. [Google Scholar] [CrossRef]
- Meinhardt, H. Models of Biological Pattern Formation; Academic Press Inc.: London, UK, 1982. [Google Scholar]
- Liaw, S.S. Phyllotaxis: Its geometry and dynamics. Phys. Rev. E 1998, 57, 4589. [Google Scholar] [CrossRef]
- Liaw, S.S. Turing model for the patterns of lady beetles. Phys. Rev. E 2001, 64, 041909. [Google Scholar] [CrossRef]
- Zhenpeng, G. The hidden order of Turing patterns in arid and semi-arid vegetation ecosystems. Proc. Natl. Acad. Sci. USA 2023, 120, e2306514120. [Google Scholar]
- Geng, P.; Kuznetsov, A.V. Settling of bidispersed small solid particles in a dilute suspension containing gyrotactic micro-organisms. Int. J. Eng. Sci. 2005, 43, 992–1010. [Google Scholar] [CrossRef]
- Geng, P.; Kuznetsov, A.V. Direct numerical simulation of settling of a large solid particle during bioconvection. Int. J. Numer. Methods Fluids 2006, 51, 511–530. [Google Scholar] [CrossRef]
- Geng, P.; Kuznetsov, A.V. Dynamics of large solid particles in bioconvective sedimentation. Int. J. Numer. Methods Fluids 2007, 53, 713–733. [Google Scholar] [CrossRef]
- Thiffeault, J.-L.; Childress, S. Stirring by swimming bodies. Phys. Lett. A 2010, 374, 3487–3490. [Google Scholar] [CrossRef]
- Ahmad, S.; Ashraf, M.; Ali, K. Heat and mass transfer flow of gyrotactic microorganisms and nanoparticles through a porous medium. Int. J. Heat Tech. 2020, 38, 395–402. [Google Scholar] [CrossRef]
- Stewart, T.L.; Fogler, H.S. Biomass plug development and propagation in porous media. Biotechnol. Bioeng. 2001, 72, 353–363. [Google Scholar] [CrossRef] [PubMed]
- Burghelea, T.; Segre, E.; Bar-Joseph, I.; Groisman, A.; Steinberg, V. Chaotic flow and efficient mixing in a microchannel with a polymer solution. Phys. Rev. E 2004, 69, 066305. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).