Abstract
The vehicle routing problem (VRP), as one of the classic combinatorial optimization problems, has garnered widespread attention in recent years. Existing deep reinforcement learning (DRL)-based methods predominantly focus on node information, neglecting the edge information inherent in the graph structure. Moreover, the solution trajectories produced by these methods tend to exhibit limited diversity, hindering a thorough exploration of the solution space. In this work, we propose a novel Edge-Driven Multiple Trajectory Attention Model (E-MTAM) to solve VRPs with various scales. Our model is built upon the encoder–decoder architecture, incorporating an edge-driven multi-head attention (EDMHA) block within the encoder to better utilize edge information. During the decoding process, we enhance graph embeddings with visitation information, integrating dynamic updates into static graph embeddings. Additionally, we employ a multi-decoder architecture and introduce a regularization term to encourage the generation of diverse trajectories, thus promoting solution diversity. We conduct comprehensive experiments on three types of VRPs: (1) traveling salesman problem (TSP), (2) capacitated vehicle routing problem (CVRP), and (3) orienteering problem (OP). The experimental results demonstrate that our model outperforms existing DRL-based methods and most traditional heuristic approaches, while also exhibiting strong generalization across problems of different scales.
1. Introduction
Combinatorial optimization is a fundamental problem in operations’ research, computer science, and applied mathematics [1], which has garnered significant attention in recent years. Vehicle routing problems (VRPs), as a representative combinatorial optimization problem [2,3], have widespread applications in real-world scenarios [4,5,6]. The objective of a VRP can be succinctly described as determining the optimal or shortest route for vehicles to visit all customer nodes [7]. Over the recent few decades, numerous effective approaches have been proposed to address VRPs and their variants [8,9]. Traditional methodologies for solving VRPs can be broadly classified into exact algorithms [10] and heuristic algorithms [11,12]. Exact methods can guarantee the identification of the optimal path; however, they are computationally expensive when dealing with large-scale or complex graphs and are not sensitive to dynamic changes. Heuristic algorithms, such as genetic algorithms [13], ant colony optimization [14,15], and Dirac delta-based methods [16,17,18], leverage heuristic information to guide the search process and can yield good solutions within an acceptable time frame, leading to widespread applications. However, the performance of these algorithms is highly dependent on domain expertise and the design of heuristic functions [19]. Inappropriately designed heuristics may result in inefficient search or suboptimal outcomes.
Recent advancements in deep reinforcement learning (DRL) have significantly transformed the approach to solving combinatorial optimization problems, including vehicle routing problems [20,21]. Early efforts to tackle related challenges, such as the traveling salesman problem (TSP) [8], primarily employed supervised learning techniques [22]. However, recent shifts in research focus have emphasized reinforcement learning, owing to its ability to optimize task objectives directly, without the dependence on large volumes of labeled data. These DRL-based approaches not only enhance solution quality but also maintain computational efficiency within acceptable bounds. In response to the increasing demand for optimal VRP solutions, substantial research has been directed toward end-to-end deep learning models. Notable architectures in this domain include recurrent neural networks (RNNs) [23], graph neural networks (GNNs) [24], and transformer-based models [25,26,27]. Innovations in attention mechanisms have further propelled the development of reinforcement learning frameworks based on encoder–decoder architectures, such as the attention model (AM) [25], which has demonstrated significant improvements in both performance and computational speed. A key advantage of DRL-based approaches lies in their scalability. Once trained, these models can effectively solve problems of varying sizes with identical combinatorial structures, obviating the need for retraining when the problem scale is adjusted. This scalability is particularly valuable in addressing real-world VRP instances, where problem size can fluctuate significantly.
Although notable progress has been made, existing attention-based DRL models still face several limitations. Firstly, they overlook the potential exploitation of edge-related information. The input to VRP often includes not only node information but also edge information between nodes. Traditional attention-based DRL models typically focus on node feature representations and fail to learn edge feature representations, thereby leaving the rich feature information embedded in the graph topology underutilized. Second, existing models exhibit limited sensitivity to state transitions during the decoding process. For instance, AMs [25] leverage graph embeddings to compute context embeddings. However, these graph embeddings are fixed as the average embedding of all nodes within an episode, resulting in static information during the decoding process that fails to capture the dynamic evolution of graph embeddings. This limitation may impair the solution quality. Furthermore, these approaches often struggle to generate sufficiently diverse solution trajectories. A broader range of candidate routes could enhance exploration within the solution space, potentially yielding better routing outcomes. However, current approaches typically rely on a single strategy trained by a single decoder, and this limited variability restricts the model’s ability to explore more optimal routing configurations.
To address the aforementioned issues and limitations, we propose a novel Edge-Driven Multiple Trajectory Attention Model (E-MTAM) for vehicle routing problems, building on the existing encoder–decoder framework. First, we emphasize the integration of edge information by incorporating both edge and node embeddings as inputs to the encoder. This allows the model to capture comprehensive edge feature representations alongside node features. During the encoding phase, we enhance the multi-head attention mechanism driven by edge information, thereby improving the encoder’s capacity to model graph topology and its associated relational data. Next, in the decoding phase, we incorporate dynamic visitation information into static graph embeddings via a mask, allowing graph embeddings to be input into the decoder to evolve in real time in accordance with the visited graph, thereby endowing the decoder with an enhanced capacity to represent dynamic information. Third, our model employs a multi-decoder structure, where the decoders are identical but with non-shared parameters. We introduce regularization loss to encourage these decoders to generate diverse trajectories, which enhances the exploration capacity within the solution space and increases the likelihood of obtaining superior results. Finally, extensive experimental evaluations across three distinct VRP variants demonstrate that our proposed E-MTAM significantly outperforms a range of heuristic algorithms and DRL-based models, highlighting its effectiveness in addressing the complexities of VRP solutions. Our results indicate that E-MTAM not only effectively addresses the conventional TSP but also proves applicable to other types of vehicle routing problems (CVRP and OP), showcasing its potential for application in real-world scenarios.
In general, the main contributions of this work are as follows:
- We propose a model called E-MTAM for VRPs, which effectively incorporates edge information to drive the node encoding process, thereby fully leveraging the rich edge features embedded within the graph topology.
- We combine visitation information with graph embeddings to integrate dynamic information into static graph embeddings, enabling the decoder to perceive real-time changes in the visited graph at each time step.
- We employ a multi-decoder framework and introduce a regularization term to encourage the decoders to generate diverse trajectories, thereby learning distinct routing strategies and fostering a more comprehensive exploration of the solution space.
- We conduct extensive experiments on three distinct VRP variants, and the results demonstrate that our E-MTAM model consistently outperforms a broad spectrum of alternative methods, underscoring its superior performance and robustness.
2. Related Work
2.1. Traditional Methods
Traditional methods for solving VRPs can be broadly divided into exact methods, approximation methods, and heuristic methods. Exact methods, such as Branch-and-Bound [28] and Concorde [29], are prominent solvers specifically designed for the TSP. Although these methods guarantee optimal solutions, they become computationally expensive for large-scale problems due to their exponential time complexity. In contrast, heuristic methods are commonly employed for their practical efficiency, delivering satisfactory solutions within reasonable time constraints. Chen et al. [30] propose a genetic algorithm combined with simulated annealing to address the optimal waiting time and path planning problem, enhancing solution quality for time-varying networks. Zhu et al. [31] propose an improved genetic algorithm based on fuzzy C-means clustering to solve the vehicle routing problem with capacity constraints. Huang et al. [32] propose a mixed integer programming formulation and an ant colony optimization algorithm to solve the vehicle routing problem with a drone (VRPD), achieving significant cost savings and efficiency improvements in parcel delivery. Lei et al. [33] propose a dynamical artificial bee colony algorithm to address the VRPD, achieving new best solutions and demonstrating promising advantages in operational cost minimization. However, these methods often depend on domain-specific customization and expert knowledge [19], and their lack of a solid theoretical foundation can lead to unpredictable performance, making it challenging to generalize across different problem contexts.
2.2. Deep Reinforcement Learning Methods
The application of deep reinforcement learning (DRL) methods has seen a significant rise in recent years for solving complex optimization problems. In response to the growing demand for optimal solutions to VRPs, considerable research has been dedicated to developing end-to-end deep learning models. Key architectures in this area include recurrent neural networks (RNNs), graph neural networks (GNNs), and transformer-based models. A notable advantage of these DRL-based methods is their capacity to handle problems of varying sizes with identical combinatorial structures once trained, thus eliminating the need for retraining when scaling up the problem.
2.2.1. RNN-Based Methods
States in sequence-to-sequence problems are typically inter-related in time or space, such as words in sentences or frames in a video [34]. Vinyals et al. [35] introduce the Pointer Network (PtrNet), incorporating the attention mechanism into a sequence model, which enables the decoder to focus on key embeddings. Bello et al. [36] replace the long short-term memory (LSTM) encoder in PtrNet with element-wise graph embeddings of the input sequence, demonstrating that their method outperforms Vinyals et al.’s approach [35] on TSP100 instances. To generate solutions for VRP instances, this model employed an RNN-based decoder coupled with an attention mechanism. However, the aforementioned works do not leverage the link information in the graph topology, which is crucial for solving graph-based combinatorial optimization problems effectively.
2.2.2. GNN-Based Methods
GNNs are deep learning models specifically designed to address graph-related tasks, enabling end-to-end predictions at the node, edge, and graph levels [35]. Ma et al. [37] integrate GNNs with pointer networks (PtrNet) and train the model using reinforcement learning to solve the traveling salesman problem. Duan et al. [38] propose a graph convolutional network-based model that incorporates both node and edge features, combining reinforcement learning with supervised learning. Other related works are based on graph attention networks (GATs). Gao et al. [39] integrate a modified network based on GATs that learns to design the heuristics with better performance for VRP. Similarly, Lei et al. [24] propose an edge-encoded GAT with a skip connection (residual E-GAT) to better capture the underlying graph topology. These methods incorporate graph information into the model, thereby significantly enhancing the solution quality.
2.2.3. Transformer-Based Methods
Transformers [40] have emerged as the most effective neural network architectures for handling long-term sequential data, thanks to their superior computational efficiency and remarkable performance improvements. Taking full advantage of these benefits, transformer networks are now increasingly applied to solve combinatorial optimization problems. Kool et al. [25] introduced a groundbreaking deep reinforcement learning (DRL)-based framework that leverages self-attention mechanisms to learn constructive routing strategies across a variety of VRP variants. This model, known as the Attention Model (AM), demonstrates significant potential in solving complex routing problems. Building on this approach, Kwon et al. [41] proposed a policy optimization with multiple optima (POMO) strategy, which enhances the robustness of the learned policies, achieving state-of-the-art performance on VRP tasks. Similarly, Xu et al. [26] propose a model based on the encoder–decoder structure, which provides enhanced node embeddings via batch normalization reordering and gate aggregation. Some other works iteratively refine complete solutions by applying local search operators until predefined termination criteria are satisfied. Chen et al. [42] propose NeuRewriter, a model that learns a policy to select heuristics and iteratively improve solutions for combinatorial optimization tasks, demonstrating strong performance in expression simplification, online job scheduling, and vehicle routing problems. Similarly, Ma et al. [43] propose the dual-aspect collaborative transformer (DACT), which learns separate embeddings for node and positional features using a novel cyclic positional encoding, and applies proximal policy optimization with curriculum learning to solve VRPs, outperforming existing transformer-based models. Taken together, these advancements highlight the growing prominence of transformer-based methods in addressing complex optimization challenges across various routing problems.
3. Methodology
3.1. Edge-Driven Diverse Trajectory Attention Model
We present the proposed E-MTAM model in the context of TSP. The model is also applicable to other routing problems, requiring only adjustments to the input, masks, and decoder context vectors [25,41]. TSP is defined on an undirected graph , where node i is represented by the two-dimensional coordinates , for , with m being the total number of nodes. A link from node i to j is denoted as , , and the associated distance information is represented as .
We construct a solution to represent a permutation of all the nodes, where denotes the index of the selected node at step i. Given a problem instance G, the goal of routing problems is to find a solution such that each node is visited exactly once, and the total tour length is minimized.
where denotes the norm. Our E-MTAM model constructs a stochastic policy for a given instance G. Using the chain rule of probability, the selection probability for a tour is parameterized by and is expressed as follows:
Our model leverages the encoder–decoder architecture, similar to the milestone AM [25]. To fully exploit edge information and better capture the dynamics of state transitions, we design an Edge-Driven Multiple Trajectory Attention Model (E-MTAM). Specifically, our E-MTAM incorporates three key modifications: (1) we embed edge information into the multi-head attention layer to effectively learn a representation of the underlying graph topology, which we refer to as edge-driven multi-head attention (EDMHA); (2) we integrate dynamic visitation information into the graph embeddings to be input into the decoder, enabling the decoder to perceive real-time changes in the visited graph; (3) we adopt a multi-decoder structure and introduce a regularization to encourage the decoders to output diverse trajectories, thereby learning distinct routing strategies.
The overall framework of our E-MTAM is illustrated in Figure 1. E-MTAM adopts a transformer-based architecture. The encoder first embeds the initial node features and edge features into node embeddings. Then, each decoder computes m steps and selects the optimal node to visit at each time step, based on the node embeddings and the current context embedding. The entire model is optimized using a policy gradient.
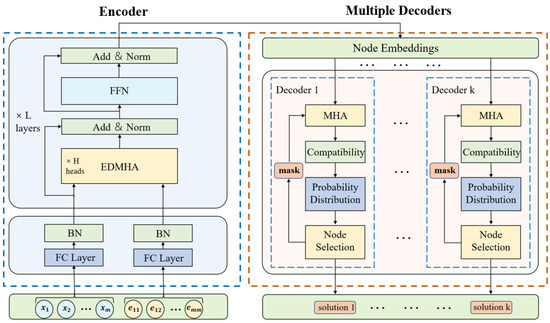
Figure 1.
Overall framework of proposed E-MTAM.
3.2. Encoder
Our encoder model takes a graph as input. Taking TSP as an example, the initial node features can be given as two-dimensional coordinates , while the initial edge features represent the Euclidean distances, where . Before being fed into E-MTAM, these input node and edge features are first mapped into high-dimensional embeddings through a fully connected layer, respectively, as follows:
where , , and are trainable parameters.
The initial node embeddings and edge embeddings are jointly fed into the encoder, and the node embeddings are updated through L attention layers. Each attention layer consists of a multi-head attention (MHA) sublayer and a node-wise feed-forward network sublayer. We denote the node embeddings after the l-th attention layer as , where . In contrast to the conventional multi-head attention used in AM, our E-MTAM employs an edge-driven multi-head attention (EDMHA), which enhances the model’s ability to capture and represent graph topology and relational information more effectively.
As shown in Figure 2, EDMHA fuses edge information with node information and updates them simultaneously, enabling richer node representation learning (we omit the superscript (0) for readability). Specifically, we use node embeddings to compute the query, key, and value vectors, and the conventional compatibility is obtained by taking the dot product of the query and key vectors. Next, we map the edge embeddings to a higher-dimensional space using a fully connected linear layer to obtain , which is then multiplied by the compatibility , followed by a softmax function to compute the attention weights. Finally, we aggregate the neighboring graph information by weighted summation to update the node embeddings .
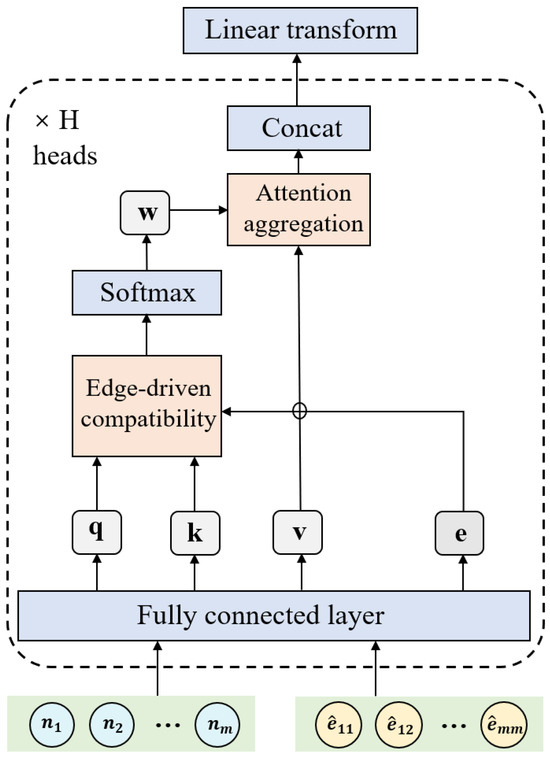
Figure 2.
Edge-driven multi-head attention block.
We leverage the input node embeddings to compute the query, key, and value vectors:
where and are trainable query, key, and value matrices, respectively, for each head h. Subsequently, we incorporate edge information to enhance the conventional compatibility and compute the weight values through a softmax layer:
where and are learnable parameters. Therefore, we can update the node’s representation by aggregating the edge information from its neighborhood connectivity, as computed in
Each head of EDMHA, indexed by h, generates the aggregated node embeddings . We then concatenate and linearly transform these node embeddings to obtain the final output of EDMHA:
where and are trainable parameters; H is the number of multi-head attention.
In the encoder, let denote the output of the -th layer. The output of the l-th EDMHA sublayer can be calculated as follows:
The operations in the feed-forward network (FFN) sublayer are similar. Given the input to the l-th FFN sublayer, the output is defined as
where represents the feed-forward operator, which consists of two learnable linear projections with a ReLU activation function in between. Thus, the final output node embeddings of the encoder are obtained as .
3.3. Decoder
E-MTAM comprises K attention-based decoders, which are structurally identical but do not share parameters. At time step t, each decoder generates a probability value to select the next node to visit, continuing this process until all nodes have been visited. Previous approaches [25,41] typically rely on the entire graph embedding vector produced by the encoder to compute the context embedding , which often fail to capture dynamic state transitions effectively. In this work, we integrate dynamic visitation information into the graph embeddings and propose a context embedding that more effectively captures dynamic information changes. Specifically, we leverage the node embedding generated by the encoder and the subsequent mask produced by the decoder to obtain a masked node embedding . We then aggregate the mean and maximum values of , along with the embeddings of the first and last visited node to construct a context embedding that is more sensitive to dynamic state transitions:
where and are learnable variables, and is the Sigmoid function.
We utilize an MHA module to compute the new context embedding for decoder k at time step t, where the attention values are computed based on and . In this work, we adopt the self-attention mechanism from AM to obtain the attention values. Unlike the MHA in our encoder, the queries in the decoder’s MHA are computed from the context embedding , while the keys and values are derived from the node embeddings :
We then compute the compatibility values for each node based on and the node embedding , and we apply tanh clipping to restrict the output within the range . To prevent revisiting nodes, we set the compatibility values of already visited nodes to according to the mask . Finally, we apply a softmax function to obtain the final output probability for decoder k at time step t to select node i for visitation:
where are learnable weight matrices, and C is a constant.
Subsequently, the action will be sampled based on at each time step t. This process continues until all m nodes are selected. To record the visitation information for each node indexed by , we initialize a mask vector with all elements set to 1 and update it at each time step t:
3.4. Training
At the end of each episode, the K decoders in our E-MTAM generate K distinct solution trajectories, each of which consists of the action sequences produced by a decoder at each time step. To encourage diversity among the decoders and promote the generation of more varied solution trajectories, we incorporate the following regularizer into the training process and propose a to diversify the probability distributions output by each pair of decoders:
For instance, let G be the set of all possible trajectories. Each decoder generates a trajectory with a probability distribution . In the reinforcement learning training framework adopted by E-MTAM, the reward is assigned episodically. To maximize the reward, we optimize the model by policy gradient:
where denotes the baseline estimator, which helps reduce gradient variance and accelerate convergence. As demonstrated in prior works [23,36], the baseline estimator is typically implemented as a copy of the policy network, updated at a lower frequency.
Overall, our E-MTAM accounts for the divergence in outputs from different decoders and establishes a comprehensive training policy, as illustrated in Figure 3. In contrast to the milestone AM, we incorporate the additional loss term, , to promote the diversity of the outputs generated by the decoders. Consequently, the overall training loss is defined as
where is a hyperparameter that balances the influence of .
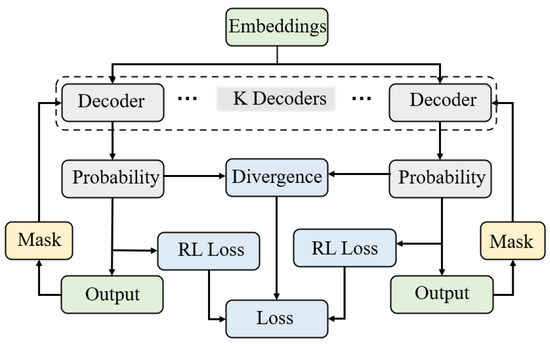
Figure 3.
Training policy of our E-MTAM.
4. Experiments
4.1. Experiment Settings
We focus on three types of VRPs in our experiments: (1) TSP; (2) CVRP; and (3) OP. Generally, the objective of the TSP is to determine the shortest path that starts and ends at a depot while visiting all nodes exactly once. The CVRP, a generalized case of TSP, requires that each vehicle departs from a central depot, visits a set of customer nodes, and completes all delivery tasks within specified capacity constraints. In the OP, each node is associated with a prize value, and the goal is to construct a single path starting and ending at the depot, aiming to maximize the total prize collected while staying within the maximum routing length constraint. Furthermore, following adjustments to the input, masking rules, and decoder context vectors, the model is also capable of addressing other variants of VRP as well as more complex real-world routing challenges.
For each problem, we follow [25,41] to conduct experiments with node sizes of . For each problem instance, the coordinates of the nodes are randomly generated within the region . The vehicle capacities of CVRP are set to for problems with nodes, while the demand at each customer node is assigned values from . For OP, the maximum path length constraints for instances of different node sizes are set to , respectively.
We train the models for 100 epochs, during which 1,280,000 instances are generated in real time with a batch size of 512 per epoch (we specifically generate 320,000 instances and use a batch size of 128 for CVRP50 and CVRP100). We use the rollout baseline as the baseline estimator and employ the Adam optimizer for model training. Additionally, we construct a test set consisting of 1000 instances, which follows the same distribution as the training data. Other relevant hyperparameter settings used in our framework are detailed in Table 1. All our experiments are conducted on an Intel Core i5-12600KF CPU and an NVIDIA GeForce RTX 4060 GPU.

Table 1.
Hyperparameter values.
For evaluation, we consider the average tour length, optimality gap, and running time to assess the performance of a method on a given problem. The optimality gap quantifies the difference between the obtained result and the best result:
where denotes the average tour length across all test instances, while represents the best-known result for the given problem. Similarly, we calculate the optimality gap of OP using the average collected prize and the maximum prize :
We compare our proposed E-MTAM against a range of traditional and DRL-based approaches for solving VRPs. These baselines include the following:
- (1)
- Concorde [29]: a specialized exact solver for solving TSP;
- (2)
- LKH [15]: a state-of-the-art heuristic optimization solver;
- (3)
- Gurobi [44]: a commercial optimization solver;
- (4)
- OR Tools [45]: an open source software suite developed by Google for solving optimization problems such as routing, scheduling, and linear programming;
- (5)
- ACO [46]: a heuristic algorithm inspired by the foraging behavior of ants, used to solve combinatorial optimization problems;
- (6)
- EMA [13]: an evolutionary optimization method designed to solve multiple vehicle routing problems simultaneously, leveraging knowledge transfer between tasks to enhance performance;
- (7)
- PtrNet [35]: a neural model that employs attention to select elements from an input sequence, solving combinatorial problems with variable-sized outputs;
- (8)
- GCN [47]: a graph convolutional network that efficiently builds TSP graph representations and outputs tours through a parallelized beam search;
- (9)
- DACT [43]: a dual-aspect collaborative transformer that improves vehicle routing problems by separately learning node and positional embeddings with a novel cyclic positional encoding method;
- (10)
- AM [25]: a milestone DRL-based model with an attention mechanism and encoder–decoder scheme;
- (11)
- POMO [41]: a state-of-the-art DRL method that achieves competitive performance on various routing problems.
In this work, we focus solely on models that employ greedy selection, eliminating the impact of the sampling strategy on model performance to ensure a fair comparison.
4.2. Comparison Results
Table 2 presents a comparison between our proposed E-MTAM and baseline methods across three typical vehicle routing problems: (1) TSP; (2) CVRP; and (3) OP. Our results demonstrate that E-MTAM consistently outperforms existing state-of-the-art baseline methods. For TSP, E-MTAM achieves the best optimality gaps of 0.26%, 0.35%, and 0.77% for problem sizes of 20, 50, and 100 nodes, respectively. Notably, as the problem size increases, the advantage of E-MTAM becomes more pronounced. For the most challenging TSP100, E-MTAM reduces the gap by 0.65% compared to the second-best method, POMO. This significant advantage is also observed in the CVRP experiments, where E-MTAM achieves gap reductions of 4.26%, 5.11%, and 6.39% compared to the milestone method (AM) for CVRP20, CVRP50, and CVRP100, respectively. In comparison to heuristic algorithms (i.e., ACO and EMA), E-MTAM attains gap reductions of 7.93% and 6.84% for CVRP100 while requiring less computational time. For OP, E-MTAM clearly outperforms other DRL-based methods, achieving the highest reward values of 5.35, 16.06, and 32.85 for OP20, OP50, and OP100, respectively.

Table 2.
Comparison results with exact, heuristic, and DRL-based baselines on TSPs, CVRPs and OPs.
Regarding running time, while the encoder introduces additional computational overhead due to the aggregation of edge information, and the multi-decoder architecture of E-MTAM results in slightly slower computation compared to AM, E-MTAM still outperforms exact and heuristic algorithms by orders of magnitude in terms of speed. Furthermore, compared to other DRL-based methods, E-MTAM strikes a better balance between effectiveness and efficiency.
To facilitate a more comprehensive comparison, we present the training curves of E-MTAM and AM on CVRP20, CVRP50, and CVRP100. As shown in Figure 4, the average tour length of both models steadily decreases during the training process and eventually converges in the later stages, demonstrating the effectiveness of our training framework. Furthermore, E-MTAM exhibits a faster learning speed, although it does not attain a shorter tour length in the early stages (especially on CVRP20 and CVRP50). E-MTAM ultimately delivers superior results across all problems, approaching the best results attained by LKH (indicated by the horizontal dashed line). Notably, as the problem size increases, the advantages of E-MTAM become more pronounced.
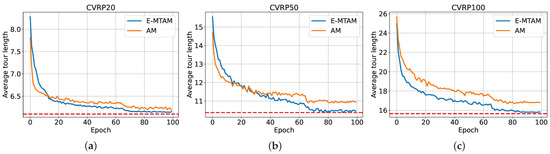
Figure 4.
The average tour length convergency curves on (a) CVRP20, (b) CVRP50 and (c) CVRP100. The horizontal dashed line represents the best result obtained by LKH.
4.3. Generalization Analysis
In practical applications, the number of nodes in problems can vary significantly, making it impractical to train a model from scratch for each possible node configuration. Therefore, models trained on given problems should exhibit generalization capabilities, allowing it to perform well on instances with different node scales. To this end, we analyze the generalization ability of E-MTAM on TSP, CVRP, and OP problems, with AM serving as the baseline. Specifically, the performance of models trained on problems with 20 and 50 nodes is evaluated across problems with 20, 50, and 100 nodes, as presented in Table 3.

Table 3.
Generalization results on TSPs, CVRPs and OPs against AM.
The experimental results demonstrate that our E-MTAM consistently outperforms AM in terms of generalization ability across problems of all scales. Specifically, when models trained on TSP20 are tested on TSP50, E-MTAM achieves a reduction in the optimality gap by 0.53% compared to AM. This reduction reaches 0.87% and 1.23% on CVRP and OP, respectively. Notably, although models trained and tested on the same problem scale perform better than those on different scales, models trained on 50 nodes typically outperform those trained on 20 nodes when confronted with larger problem sizes. In tests on TSP100, CVRP100, and OP100, the best optimality gaps of 4.51%, 4.60%, and 6.51%, respectively, are all achieved by E-MTAM trained on 50 nodes. These results underscore the exceptional generalization capability of the proposed method, highlighting its effectiveness in addressing the complex routing problems encountered in real-world applications.
4.4. Ablation Analysis
4.4.1. Effect of Each Component
The proposed E-MTAM incorporates three innovative components: (1) the EDMHA block; (2) dynamic graph embedding; and (3) the multi-decoder-based JS loss. To investigate the individual and combined effects of these components on model performance, we conducted ablation experiments on TSPs, CVRPs, and OPs, as shown in Table 4, Table 5 and Table 6. Specifically, we start with a vanilla model and progressively integrate the components, evaluating the model’s performance on different problems at each stage. Taking TSP100 as an example, we incorporate the EDMHA block, dynamic graph embedding, and JS loss into the vanilla model and obtain improved routing performance with gaps of 2.45%, 3.22%, and 2.84%, respectively. These correspond to absolute gap reductions of 1.80%, 1.03%, and 1.41% compared to the baseline. For CVRP100, the individual addition of each component leads to gap reductions of 4.92%, 3.77%, and 4.47%, respectively. In the case of OPs, the complete model demonstrates gap reductions of 0.97%, 0.58%, and 0.82% for instances with 20, 50, and 100 nodes, respectively, relative to the baseline. Moreover, paired combinations of these components yield further improvements in performance compared to their individual contributions. These results substantiate the efficacy of incorporating the proposed components in enhancing the performance of the E-MTAM.

Table 4.
Ablation analysis of different components of proposed E-MTAM on TSPs.

Table 5.
Ablation analysis of different components of proposed E-MTAM on CVRPs.

Table 6.
Ablation analysis of different components of proposed E-MTAM on OPs.
4.4.2. Effect of Hyperparameters
We follow the work of [25] to conduct a sensitivity analysis under different learning rates and random seed configurations. Table 7 presents the experimental results for Random Seeds 1234 and 1235 under two learning rate strategies. The results show that, across TSPs, CVRPs, and OPs of varying scales, the variations in average tour lengths and optimality gaps are minimal, demonstrating the robustness and reliability of our method under different hyperparameter settings. Taking CVRP100 as an example, the difference in the optimality gap for E-MTAM across different settings does not exceed 0.19%.

Table 7.
Routing performance of E-MTAM with different learning rate strategies and seeds for TSPs, CVRPs, and OPs.
5. Conclusions
In this work, we propose a novel Edge-Driven Multiple Trajectory Attention Model (E-MTAM) to address VRPs of different scales. Our model is built upon the existing encoder–decoder architecture and employs a deep reinforcement learning approach for routing, eliminating the reliance on manually designed rules. We introduce three pivotal innovations to further improve the routing performance of the model. First, we integrate edge information into the encoder via an edge-driven multi-head attention block, enhancing the model’s ability to capture the graph’s topological structure. Second, we combine visitation information with graph embeddings to incorporate dynamic updates, enabling the decoder to adapt to real-time changes in the graph. Finally, we employ a multi-decoder architecture with a regularization term, encouraging the generation of diverse trajectories and thereby fostering a more comprehensive exploration of the solution space.
We conducted extensive experiments on three types of routing problems: TSP, CVRP, and OP. We evaluate the performance of E-MTAM against a range of traditional and DRL-based methods. The comparison results demonstrate that our proposed E-MTAM significantly outperforms a variety of alternative approaches. Furthermore, generalization experiments demonstrate that our model exhibits stronger generalization capabilities than the baseline method on larger-scale problems. Finally, ablation studies validate the effectiveness of the three key improvements we introduced. Pertaining to future works, we acknowledge that there remains a gap between our E-MTAM and exact algorithms. On the one hand, the utilization of graph topology information in our model is still not fully optimized. Therefore, we will focus on exploring the underlying structure of the graph to enhance this aspect. On the other hand, we plan to incorporate other novel techniques to further optimize our encoder–decoder framework and to extend this solution to more complex variants of the VRP.
Author Contributions
Conceptualization, D.Y. and B.O.; methodology, B.O.; software, Q.G. and Z.Z.; validation, D.Y., B.O. and Q.G.; formal analysis, Z.Z.; investigation, Z.Z.; resources, Q.G.; data curation, B.O.; writing—original draft preparation, B.O.; writing—review and editing, D.Y.; visualization, Q.G.; supervision, H.C.; project administration, H.C.; funding acquisition, D.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant No. 62306232; the Natural Science Basic Research Program of Shaanxi Province under Grant No. 2023-JC-QN-0662; and the State Key Laboratory of Electrical Insulation and Power Equipment under Grant No. EIPE23416.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
We thank Xi’an Jiaotong University for helping us with the Article Processing Charge for the publication of this article in open access.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bengio, Y.; Lodi, A.; Prouvost, A. Machine learning for combinatorial optimization: A methodological tour d’horizon. Eur. J. Oper. Res. 2021, 290, 405–421. [Google Scholar] [CrossRef]
- Baty, L.; Jungel, K.; Klein, P.S.; Parmentier, A.; Schiffer, M. Combinatorial optimization-enriched machine learning to solve the dynamic vehicle routing problem with time windows. Transp. Sci. 2024, 58, 708–725. [Google Scholar] [CrossRef]
- Kim, M.; Park, J.; Kim, J. Learning collaborative policies to solve np-hard routing problems. Adv. Neural Inf. Process. Syst. 2021, 34, 10418–10430. [Google Scholar]
- Guan, Q.; Hong, X.; Ke, W.; Zhang, L.; Sun, G.; Gong, Y. Kohonen self-organizing map based route planning: A revisit. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 7969–7976. [Google Scholar]
- Bogyrbayeva, A.; Yoon, T.; Ko, H.; Lim, S.; Yun, H.; Kwon, C. A deep reinforcement learning approach for solving the traveling salesman problem with drone. Transp. Res. Part C Emerg. Technol. 2023, 148, 103981. [Google Scholar] [CrossRef]
- Tan, K.; Liu, W.; Xu, F.; Li, C. Optimization model and algorithm of logistics vehicle routing problem under major emergency. Mathematics 2023, 11, 1274. [Google Scholar] [CrossRef]
- Bogyrbayeva, A.; Meraliyev, M.; Mustakhov, T.; Dauletbayev, B. Machine learning to solve vehicle routing problems: A survey. IEEE Trans. Intell. Transp. Syst. 2024, 25, 4754–4772. [Google Scholar] [CrossRef]
- Pop, P.C.; Cosma, O.; Sabo, C.; Sitar, C.P. A comprehensive survey on the generalized traveling salesman problem. Eur. J. Oper. Res. 2024, 314, 819–835. [Google Scholar] [CrossRef]
- Kalatzantonakis, P.; Sifaleras, A.; Samaras, N. A reinforcement learning-variable neighborhood search method for the capacitated vehicle routing problem. Expert Syst. Appl. 2023, 213, 118812. [Google Scholar] [CrossRef]
- Zhou, H.; Qin, H.; Cheng, C.; Rousseau, L.M. An exact algorithm for the two-echelon vehicle routing problem with drones. Transp. Res. Part B Methodol. 2023, 168, 124–150. [Google Scholar] [CrossRef]
- Liu, F.; Lu, C.; Gui, L.; Zhang, Q.; Tong, X.; Yuan, M. Heuristics for vehicle routing problem: A survey and recent advances. arXiv 2023, arXiv:2303.04147. [Google Scholar]
- Azad, U.; Behera, B.K.; Ahmed, E.A.; Panigrahi, P.K.; Farouk, A. Solving vehicle routing problem using quantum approximate optimization algorithm. IEEE Trans. Intell. Transp. Syst. 2022, 24, 7564–7573. [Google Scholar] [CrossRef]
- Feng, L.; Zhou, L.; Gupta, A.; Zhong, J.; Zhu, Z.; Tan, K.C.; Qin, K. Solving generalized vehicle routing problem with occasional drivers via evolutionary multitasking. IEEE Trans. Cybern. 2019, 51, 3171–3184. [Google Scholar] [CrossRef]
- Feng, L.; Huang, Y.; Zhou, L.; Zhong, J.; Gupta, A.; Tang, K.; Tan, K.C. Explicit evolutionary multitasking for combinatorial optimization: A case study on capacitated vehicle routing problem. IEEE Trans. Cybern. 2020, 51, 3143–3156. [Google Scholar] [CrossRef]
- Helsgaun, K. An extension of the Lin-Kernighan-Helsgaun TSP solver for constrained traveling salesman and vehicle routing problems. Rosk. Rosk. Univ. 2017, 12, 966–980. [Google Scholar]
- Gomez-Marin, A.; Schmiedl, T.; Seifert, U. Optimal protocols for minimal work processes in underdamped stochastic thermodynamics. J. Chem. Phys. 2008, 129, 024114. [Google Scholar] [CrossRef]
- Bonança, M.V.; Deffner, S. Minimal dissipation in processes far from equilibrium. Phys. Rev. E 2018, 98, 042103. [Google Scholar] [CrossRef]
- Nazé, P. Analytical solution for optimal protocols of weak drivings. J. Stat. Mech. Theory Exp. 2024, 2024, 073205. [Google Scholar] [CrossRef]
- Li, K.; Zhang, T.; Wang, R. Deep reinforcement learning for multiobjective optimization. IEEE Trans. Cybern. 2020, 51, 3103–3114. [Google Scholar] [CrossRef]
- James, J.; Yu, W.; Gu, J. Online vehicle routing with neural combinatorial optimization and deep reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3806–3817. [Google Scholar]
- Wang, C.; Cao, Z.; Wu, Y.; Teng, L.; Wu, G. Deep Reinforcement Learning for Solving Vehicle Routing Problems with Backhauls. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 1–15. [Google Scholar] [CrossRef]
- Bai, R.; Chen, X.; Chen, Z.L.; Cui, T.; Gong, S.; He, W.; Jiang, X.; Jin, H.; Jin, J.; Kendall, G.; et al. Analytics and machine learning in vehicle routing research. Int. J. Prod. Res. 2023, 61, 4–30. [Google Scholar] [CrossRef]
- Nazari, M.; Oroojlooy, A.; Snyder, L.; Takác, M. Reinforcement learning for solving the vehicle routing problem. Adv. Neural Inf. Process. Syst. 2018, 31, 1–11. [Google Scholar]
- Lei, K.; Guo, P.; Wang, Y.; Wu, X.; Zhao, W. Solve routing problems with a residual edge-graph attention neural network. Neurocomputing 2022, 508, 79–98. [Google Scholar] [CrossRef]
- Kool, W.; van Hoof, H.; Welling, M. Attention, Learn to Solve Routing Problems! In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019.
- Xu, Y.; Fang, M.; Chen, L.; Xu, G.; Du, Y.; Zhang, C. Reinforcement learning with multiple relational attention for solving vehicle routing problems. IEEE Trans. Cybern. 2021, 52, 11107–11120. [Google Scholar] [CrossRef]
- Fellek, G.; Farid, A.; Gebreyesus, G.; Fujimura, S.; Yoshie, O. Graph transformer with reinforcement learning for vehicle routing problem. IEEJ Trans. Electr. Electron. Eng. 2023, 18, 701–713. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Montemanni, R.; Novellani, S. Algorithms based on branch and bound for the flying sidekick traveling salesman problem. Omega 2021, 104, 102493. [Google Scholar] [CrossRef]
- Applegate, D.L. The Traveling Salesman Problem: A Computational Study; Princeton University Press: Princeton, NJ, USA, 2006; Volume 17. [Google Scholar]
- Chen, C.M.; Lv, S.; Ning, J.; Wu, J.M.T. A genetic algorithm for the waitable time-varying multi-depot green vehicle routing problem. Symmetry 2023, 15, 124. [Google Scholar] [CrossRef]
- Zhu, J. Solving Capacitated Vehicle Routing Problem by an Improved Genetic Algorithm with Fuzzy C-Means Clustering. Sci. Program. 2022, 2022, 8514660. [Google Scholar] [CrossRef]
- Huang, S.H.; Huang, Y.H.; Blazquez, C.A.; Chen, C.Y. Solving the vehicle routing problem with drone for delivery services using an ant colony optimization algorithm. Adv. Eng. Inform. 2022, 51, 101536. [Google Scholar] [CrossRef]
- Lei, D.; Cui, Z.; Li, M. A dynamical artificial bee colony for vehicle routing problem with drones. Eng. Appl. Artif. Intell. 2022, 107, 104510. [Google Scholar] [CrossRef]
- Li, B.; Wu, G.; He, Y.; Fan, M.; Pedrycz, W. An overview and experimental study of learning-based optimization algorithms for the vehicle routing problem. IEEE/CAA J. Autom. Sin. 2022, 9, 1115–1138. [Google Scholar] [CrossRef]
- Vinyals, O.; Fortunato, M.; Jaitly, N. Pointer networks. Adv. Neural Inf. Process. Syst. 2015, 28, 1–9. [Google Scholar]
- Bello, I.; Pham, H.; Le, Q.V.; Norouzi, M.; Bengio, S. Neural combinatorial optimization with reinforcement learning. arXiv 2016, arXiv:1611.09940. [Google Scholar]
- Ma, Q.; Ge, S.; He, D.; Thaker, D.; Drori, I. Combinatorial optimization by graph pointer networks and hierarchical reinforcement learning. arXiv 2019, arXiv:1911.04936. [Google Scholar]
- Duan, L.; Zhan, Y.; Hu, H.; Gong, Y.; Wei, J.; Zhang, X.; Xu, Y. Efficiently solving the practical vehicle routing problem: A novel joint learning approach. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; pp. 3054–3063. [Google Scholar]
- Gao, L.; Chen, M.; Chen, Q.; Luo, G.; Zhu, N.; Liu, Z. Learn to design the heuristics for vehicle routing problem. arXiv 2020, arXiv:2002.08539. [Google Scholar]
- Vaswani, A. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Kwon, Y.D.; Choo, J.; Kim, B.; Yoon, I.; Gwon, Y.; Min, S. Pomo: Policy optimization with multiple optima for reinforcement learning. Adv. Neural Inf. Process. Syst. 2020, 33, 21188–21198. [Google Scholar]
- Chen, X.; Tian, Y. Learning to perform local rewriting for combinatorial optimization. Adv. Neural Inf. Process. Syst. 2019, 32, 1–12. [Google Scholar]
- Ma, Y.; Li, J.; Cao, Z.; Song, W.; Zhang, L.; Chen, Z.; Tang, J. Learning to iteratively solve routing problems with dual-aspect collaborative transformer. Adv. Neural Inf. Process. Syst. 2021, 34, 11096–11107. [Google Scholar]
- Meindl, B.; Templ, M. Analysis of commercial and free and open source solvers for linear optimization problems. Eurostat Stat. Neth. Proj. ESSnet Common Tools Harmon. Methodol. SDC ESS 2012, 20, 64. [Google Scholar]
- Gunjan, V.K.; Kumari, M.; Kumar, A.; Rao, A.A. Search engine optimization with Google. Int. J. Comput. Sci. Issues 2012, 9, 206. [Google Scholar] [CrossRef]
- Hlaing, Z.C.S.S.; Khine, M.A. Solving traveling salesman problem by using improved ant colony optimization algorithm. Int. J. Inf. Educ. Technol. 2011, 1, 404. [Google Scholar] [CrossRef]
- Joshi, C.K.; Laurent, T.; Bresson, X. An efficient graph convolutional network technique for the travelling salesman problem. arXiv 2019, arXiv:1906.01227. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).