1. Introduction
Closed walls are essential structures in various engineering fields, including mining, civil engineering, and geotechnical engineering. They are designed to prevent the spillage of hazardous materials, such as fragments, chips, and magma, resulting from rock blasting, thereby reducing the risk of injuries, fatalities, and equipment damage during mining operations [
1,
2,
3,
4]. However, in situations such as roof falls, blasting activities, or accidents, shock waves can be generated that may impact the stability of these walls. Therefore, the accurate prediction of the impact of shock waves on closed walls is deemed crucial.
In the field of mining goaf management, the temporary or permanent closure of the goaf through the installation of closed walls is a major type of management measure. Types of closed walls include metal mesh, brick or masonry walls, concrete walls, and reinforced concrete walls. The study of the impact of air shock waves on closed walls due to the collapse of a mining area is a highly relevant and important topic in the field of mining engineering and geotechnical research. Badshah et al. [
5] undertook a comprehensive set of eight blasting experiments involving various masonry wall configurations, namely, unreinforced masonry walls, wire mesh cement-covered masonry walls, and restrained masonry walls. The outcomes of these experiments served as a foundational platform for discerning the dynamic responses exhibited by each distinct masonry system in response to explosive forces. When the roof collapses and generates air shock waves in the goaf, the effect and damage law of the shock wave on the mine seal structure are different from the free field explosion because the underground roadway forms a relatively closed structure [
6]. From the macroscopic perspective, the study of shock wave damage to mine seals concerns the mutual coupling effect between the shock wave and the underground structures [
7]. Qu et al. [
8,
9,
10] found that the overpressure law generated by a gas explosion is related to the propagation distance, cross-sectional area, and initial pressure of the burst source; they analyzed the damage effect of a gas explosion on underground structures. Kallu et al. [
11] investigated the stability of a brick mine containment wall under the conditions of simultaneous blast loading and top and bottom slab displacement, and the results show that the deformation has an important influence on the blast resistance of the containment and should be considered in more detail in the design. Cheng et al. [
12] studied the impact response of blast waves acting on mine structures after complex reflections or bypasses in the roadways by establishing numerical models of different types of bifurcated roadways and cornered roadways in mines.
Given the high cost of acquiring explosion data and the challenges associated with experimental validation, numerical simulation is becoming an increasingly preferred method [
13,
14,
15,
16,
17,
18]. Numerical simulation offers a valuable and cost-effective way to analyze the complex dynamics of masonry structure failure under the impact of blast waves. Numerous scholars have conducted research on the fragment distribution, size, ejection patterns, and damage assessment of unidirectional masonry walls subjected to shock waves through experiments and numerical simulations [
7]. Traditional methods for assessing the stability of closed walls are typically based on hand calculations or simple models, which may overlook the influence of complex geological and engineering conditions on the stability of these walls, resulting in predictions that are less accurate or reliable. Zhang et al. [
13,
19] used numerical simulation to study the propagation law and pressure distribution of shock waves in the bends of a roadway and found that the decay of peak overpressure with distance did not obey the exponential law when air shock waves passed through the bends of the roadway. Utilizing the discrete element method (DEM), Masi et al. [
20] investigated the dynamic response of curved masonry structures under blast loading and the effects of the shear expansion angle and tensile strength on the dynamic structural response of masonry. Edri and Yankelevsky [
21] developed a resistance model and single-degree-of-freedom (SDOF) computational method for unidirectional hollow concrete block-filled brick walls by simulating an unreinforced masonry wall, which can predict the response of this masonry wall under different types of out-of-face static loads. Dong et al. [
22] investigated the damage of the roof impact wave on an ore column using theoretical modeling. Geng et al. [
23] proposed a simulation model of roof fall in an underground mined-out area based on lattice Boltzmann, which provides a new approach for predicting the disaster of roof fall in mined-out areas. Wang et al. [
24,
25,
26] used mathematical methods to carry out a study of stability prediction for the stability of the roof plate of a mined-out area. Zhao et al. [
27] used the numerical software (ANSYS Fluent 2023 R1) of fluid dynamics to simulate and analyze a roof slab fall in a mining goaf area. Xing et al. [
28,
29] established a coupled roof fall/air impact model to study the influence of the roof height on the air velocity of the quarry and the roadway when the roof falls. Rodriguez et al. [
30,
31,
32] investigated the effects of downhole shock waves on different shapes of wave-retarding walls through experiments and numerical simulations. Rajasekar et al. [
33] investigated the effect of different-shaped geometric barriers on mitigating shock waves and their numerical prediction methods using similar simulation experiments and numerical simulations.
Furthermore, recent research has been leaning towards using techniques that combine AI-driven approaches and multi-physics coupling for prediction, yielding many promising results. Sha et al. [
34] utilized a multi-physics coupling prediction model to develop a fluid–solid coupling model based on asymmetric rock strata structures, considering dynamic geological responses (Rock Mechanics and Rock Engineering), achieving a 38% reduction in the prediction error compared to traditional models. Xi, Dongmin, et al. [
35] proposed a cross-mining area transfer learning framework in “Tunnelling and Underground Space Technology” using an AI-driven approach to address small sample problems (achieving a 90% accuracy with only 150 data points); BYD’s mining AI platform employs multi-modal data fusion to integrate microseismic, InSAR, and laser scanning data to predict collapse risks in real time (measured response time < 12 s). Jiang et al. [
36] proposed Physics-Informed Neural Networks (PINNs) using a physics mechanism and data-combined modeling approach. By constructing a PINN model with constitutive constraints for rock mass damage, they achieved a 24% reduction in error compared to purely data-driven methods. These latest approaches have greatly advanced the research in related fields.
Against this backdrop, machine learning methods offer a novel approach to overcome the limitations of numerical simulations. The random forest (RF) algorithm, through its ensemble learning strategy, can efficiently process multi-source heterogeneous data and capture nonlinear relationships between variables. By inputting finite element simulation data as a training set into the RF model, rapid surrogate predictions of the structural response can be achieved. Furthermore, RF models exhibit greater robustness in parameter sensitivity analysis, making them particularly suitable for mining scenarios with complex geological conditions and sparse monitoring data. This paper selects the random forest model precisely because of its complementarity with the finite element method—the latter provides physics-driven, refined simulation data, while the former achieves efficient prediction through a data-driven approach. The combination of these two can provide a multi-scale solution for the stability assessment of retaining walls.
The scholars mentioned above have conducted extensive research on roofing disasters and the stability of the mining zone, yielding significant results. However, there are still many challenges in practical application. Most existing prediction models are complex to build, require a large amount of data to be collected, and are difficult to deploy in practice, and many theoretical analyses and numerical simulations rely on simplified assumptions, often overlooking the complexities of the actual environment, such as material non-homogeneity and variations in the ambient temperature and humidity. Additionally, experimental conditions have some limitations. The experimental research is often limited by experimental conditions and equipment, making it difficult to fully simulate actual working conditions. In particular, large-scale explosion simulation experiments are costly and risky, which further constrains their applicability. Moreover, there is a lack of long-term performance evaluation, as most research focuses on the effects of transient impact and short-term loading, and there is a lack of systematic research on the environmental erosion and fatigue damage suffered by closed walls in the course of long-term use.
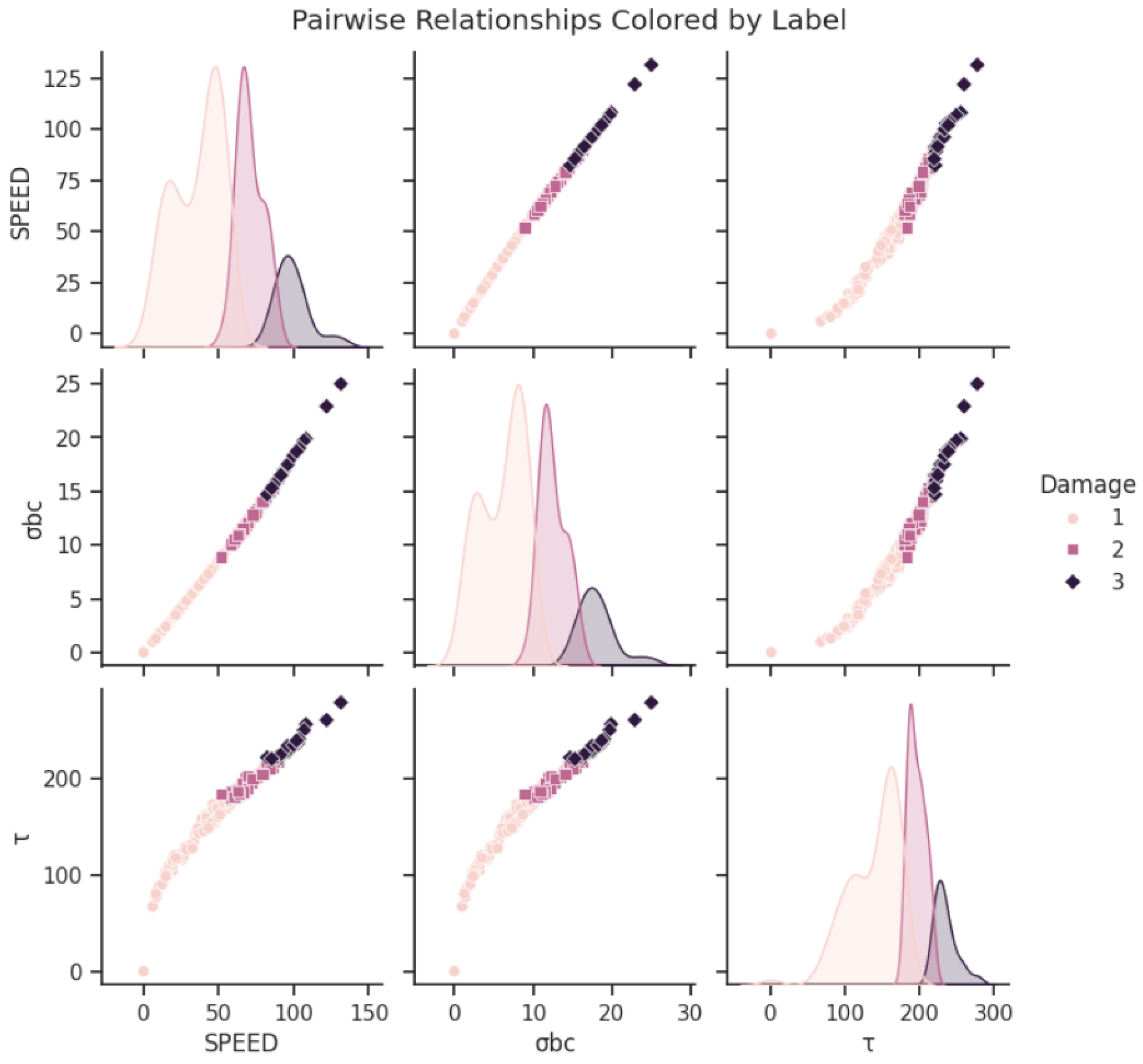
The shock wave generated by a roof fall in a mined-out area seriously affects the quarry stability and personnel safety. To investigate the effects of these shock waves on sealing protection requirements, data on the shock wave sizes generated by roof falls in various mined-out areas and the mechanical parameters of the closed walls were systematically collected. An RF algorithm was employed to fit the influence of the mechanical parameters of the closed walls and the shock wave size on the construction area under their coupled effects. The safety threshold values for the mechanical parameters of the closed walls were accurately predicted under the pressure of shock waves generated by roof falls in different mined-out areas, thereby providing technical guidance for similar engineering practices.
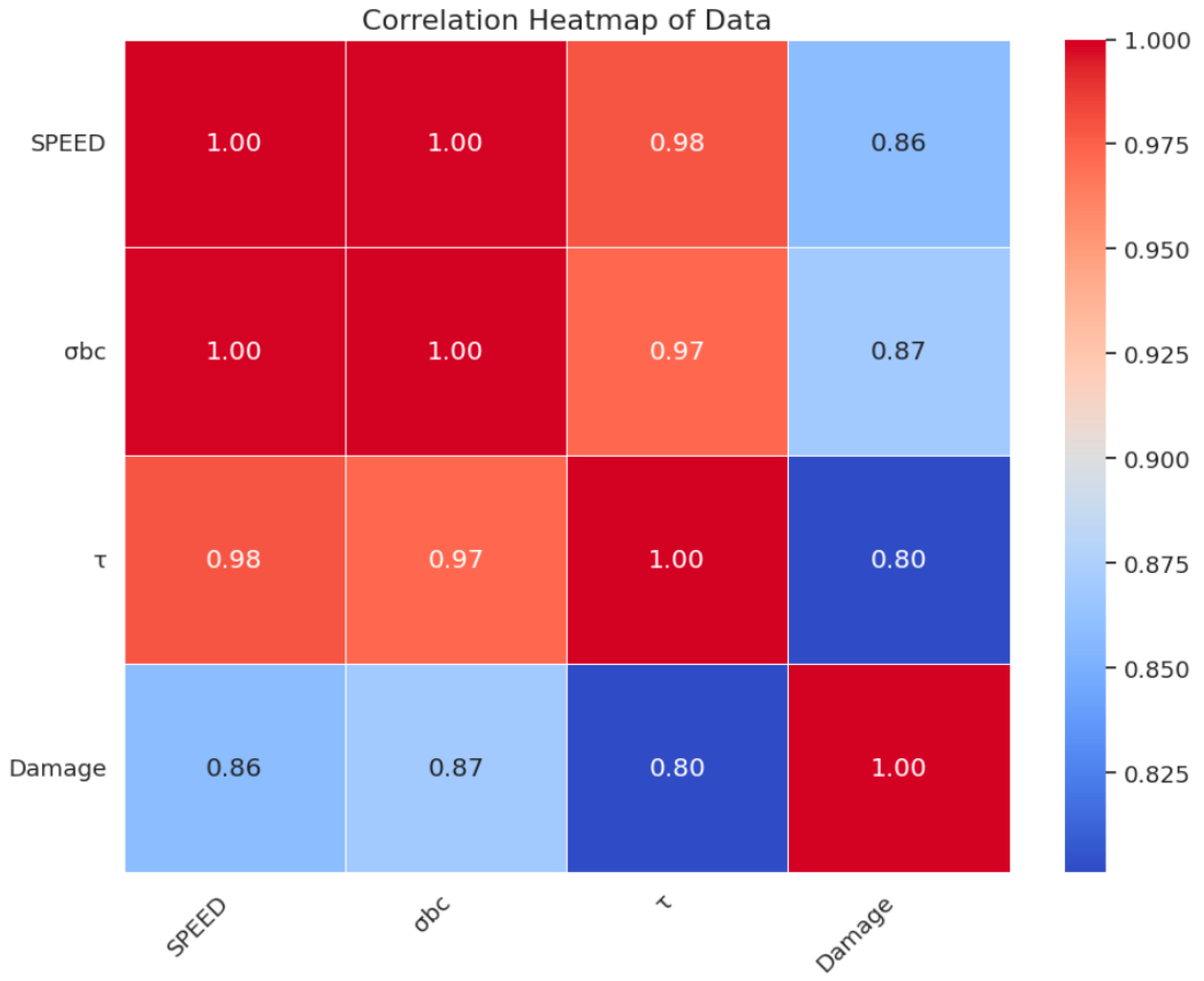
In this study, we propose the following four research hypotheses: (1) the mechanical parameters and shock wave velocity jointly influence the stability of confined walls; (2) the random forest model can effectively capture nonlinear relationships; (3) hyperparameter optimization can significantly improve the model accuracy; (4) the model possesses practical engineering applicability. Based on these hypotheses, a closed wall damage prediction model based on an RF algorithm is proposed, and the hyperparameters are optimized using a grid search to enhance the model prediction performance. A random forest algorithm model is trained for prediction, and the trained machine learning model is further tuned with hyperparameters. The contributions of this research are as follows: (1) the development of an efficient damage prediction model for confined walls; (2) the introduction of a model hyperparameter optimization algorithm combining a grid search method; (3) the proposition of an efficient prediction model based on the random forest algorithm for predicting the extent of damage to confined walls in engineering instances; (4) experimental validation of the proposed model based on actual working conditions.
5. Results and Discussion
5.1. Evaluation Metrics Description
In machine learning, model evaluation is essential and occurs at two levels. First, during the model training process, the training set is used to evaluate the model with different parameters, aiming at optimizing these parameters. Second, once the model is built, it is evaluated using the test set to verify the final performance. This two-tiered approach ensures both effective training and the reliable assessment of the model’s predictive capabilities.
To gain a comprehensive understanding of the performance of the classification model, test sets are often utilized to analyze the detailed predictions through confusion matrices. These matrices display the number of true positives, false positives, true negatives, and false negatives, which helps to deeply analyze the model’s performance in each category and make more targeted adjustments. In binary classification problems, the two categories are classified as positive or negative. In multi-class scenarios, the definitions of positive and negative are relative: any category can be treated as positive, while the remaining categories are considered negative.
All of the results appearing in the model can be categorized into the following four types: (1) true positive (TP) occurs when the true value is positive and the predicted value is also positive; (2) false negative (FN) arises when the true value is positive but the predicted value is negative, representing a Type I error; (3) false positive (FP) occurs when the true value is negative while the predicted value is positive, which is known as a Type II error; and (4) true negative (TN) is when both the true and predicted values are negative.
These four cases can be organized into a table, resulting in what is known as a confusion matrix. While the confusion matrix effectively counts the number of positives and negatives, it can be challenging to evaluate the strengths and weaknesses of the model solely based on case counts, especially with large datasets. Therefore, additional key performance indicators are introduced to provide a more comprehensive assessment.
Precision indicates the proportion of positive predictions made by the model that are actually correct. It measures the probability that a predicted positive outcome is accurate, calculated as the number of true positives (TPs) divided by the sum of true positives and false positives (TPs + FPs).
Recall, also known as sensitivity, measures the proportion of actual positive cases that the model correctly identifies. It is calculated as the number of true positives (TPs) divided by the sum of true positives and false negatives (TPs + FNs). A higher recall indicates that the model is effective at capturing more positive samples, thus reflecting its ability to minimize missed positive cases.
F1-score is the harmonic mean of precision and recall, providing a single metric that balances both aspects of the model performance. It ranges from zero to one, where a higher F1-score indicates a better overall classification quality.
The accuracy, precision, recall, and F1-score are indicated below as follows:
5.2. Hyperparameter Optimization Results
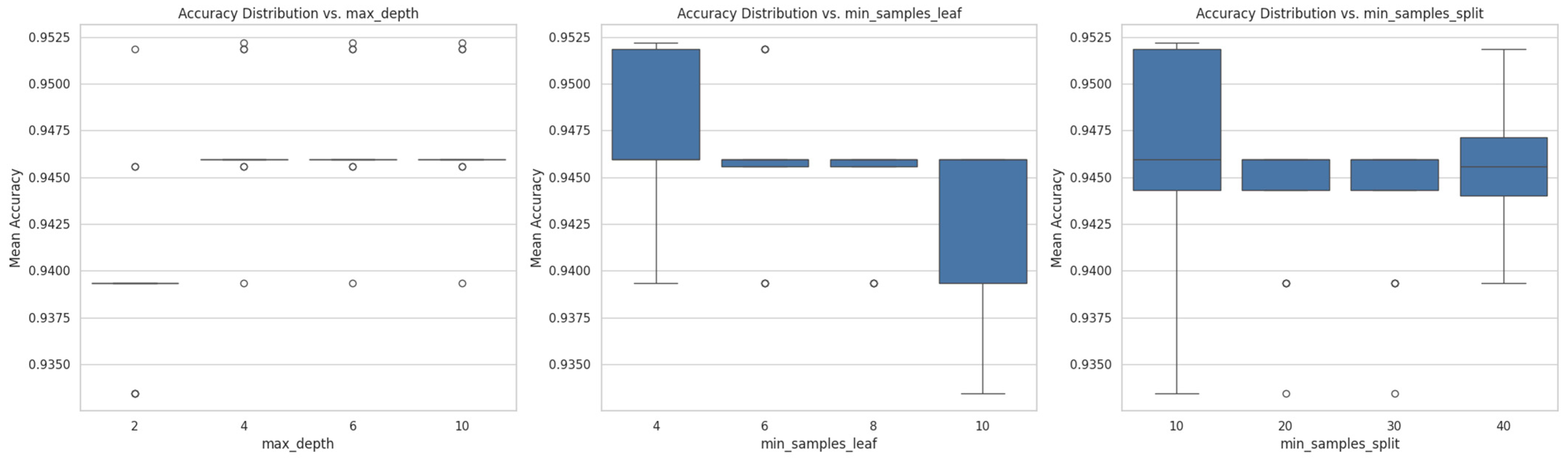
Figure 5 shows the impact curves of various parameters on the model’s accuracy. The curves in the figure were obtained by fixing the x-axis parameter and then calculating the average prediction accuracy of all other parameter combinations. From the figure, it can be seen that the prediction accuracy of n_estimators = 250 is significantly higher than other values. The relatively optimal parameter combination is as follows: n_estimators = 250, max_depth = 4, min_samples_leaf = 4, and min_samples_split = 10, which is consistent with the hyperparameter optimization results.
Since averaging cannot determine the optimality of the selected parameters, we further analyzed the parameters. Taking n_estimators = 250, we analyzed the prediction accuracy of different parameters for max_depth, min_samples_leaf, and min_samples_split. The resulting box plot is shown in
Figure 6. It can be seen that the parameters obtained by hyperparameter optimization are indeed superior to the other parameter combinations. The best combination of parameters for the RF algorithm is shown in
Table 3, with the accuracy being the average accuracy of ten-fold cross-validation. Compared to the parameter combination of n_estimators = 200, max_depth = 0, min_samples_leaf = 4, and min_samples_split = 10, the prediction accuracy of the learning curve and the test curve for this parameter increased from 94.6% to 95.9%.
After grid search hyperparameter optimization, the RF model exhibited significantly improved prediction performance. This method effectively selects the optimal parameters that enhance the accuracy of the model. As a result of this hyperparameter optimization, the RF algorithm achieves more precise predictions, demonstrating its efficacy in refining model performance.
5.3. Performance of Machine Learning Techniques Results
After the hyperparameter optimization, the optimal prediction accuracy and other metrics for the random forest-based closed wall damage prediction model are as shown in
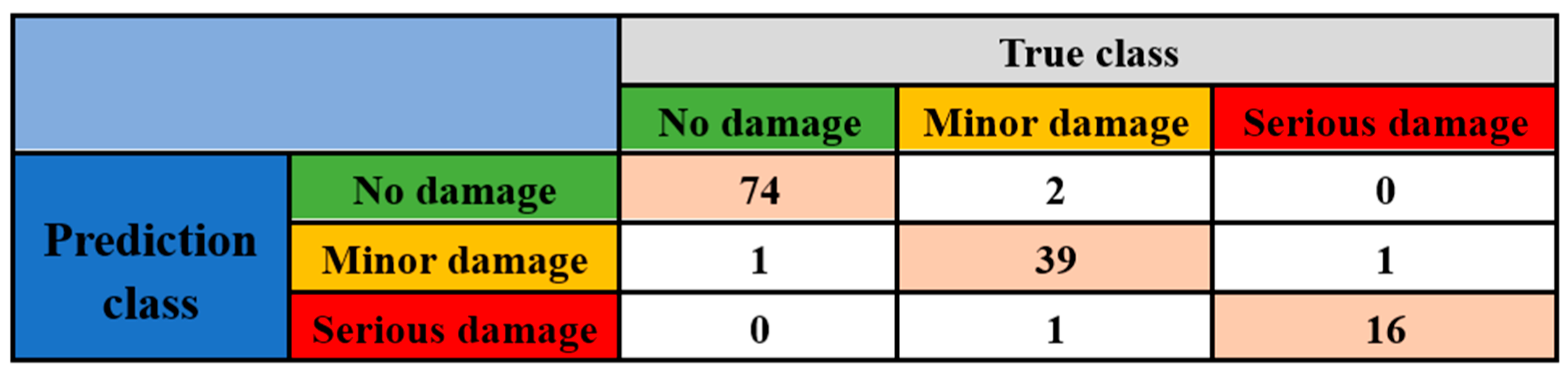
Table 4. The trained RF algorithm achieved an accuracy of 96%, with a prediction accuracy of 0.99 for the no damage class, a recall of 0.97, and an F1 value of 0.98. For the minor damage class, the prediction accuracy is 0.93, the recall is 0.95, and the F1-score is 0.94. In the severe damage category, the prediction accuracy is 0.94, the recall is 0.94, and the F1-score is also 0.94. The weighted averages for the accuracy, recall, and F1-score are 0.95, 0.96, and 0.95, respectively. The model identified six misjudgment groups in the test set, including one for no damage, two for minor damage, and three for serious damage. The confusion matrix for each model is presented in
Figure 7.
The experimental results show that, by using grid search to optimize the hyperparameters, a high prediction accuracy can be achieved with the RF algorithm. Compared to traditional prediction methods, this approach offers comparable predictive performance but is simpler and easier to deploy.
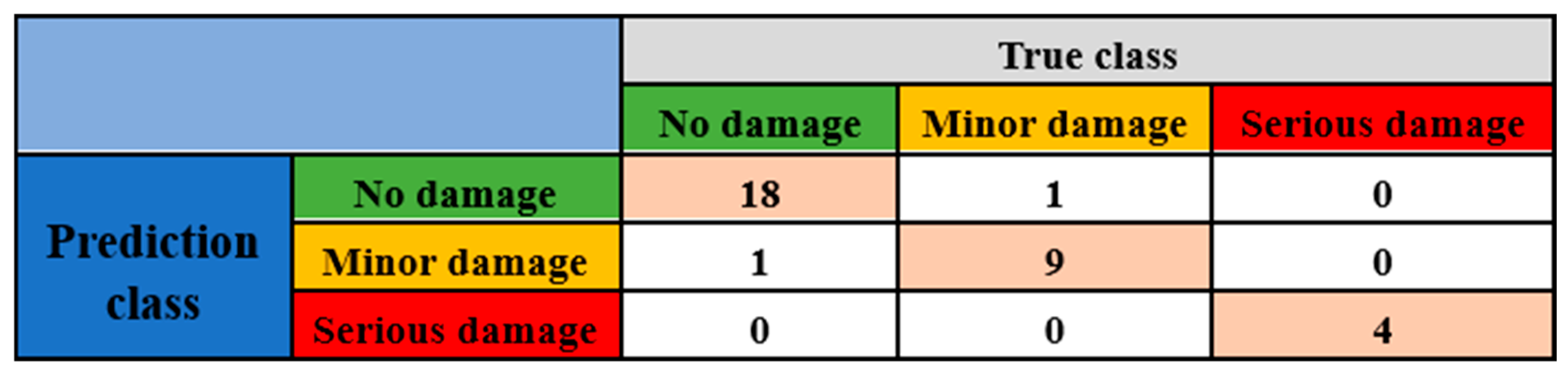
To test the robustness of the algorithm, its performance was validated on the test set. The confusion matrix of the RF model on the test set is shown in
Figure 8. The performance results are shown in
Table 5.
The experimental results on the test set show that the model can still maintain a 95% accuracy on the test set. The performance degradation is not significant, indicating strong robustness.
In this study, a machine learning modeling algorithm for predicting the stability of closed walls was proposed by combining the recent development of the RF model and ML methods. The results obtained in this study will help to encourage the use of machine learning in the prediction of closed wall stability, which can be useful for engineering geology-related fields.
However, the method presented in this paper does not account for the influence of temperature and humidity on the stability of confined walls. Experimental results may vary under different environmental conditions. Future work could explore hybrid modeling incorporating physical models to consider more influencing factors, evaluate the algorithm’s feasibility, and address potential issues accordingly.
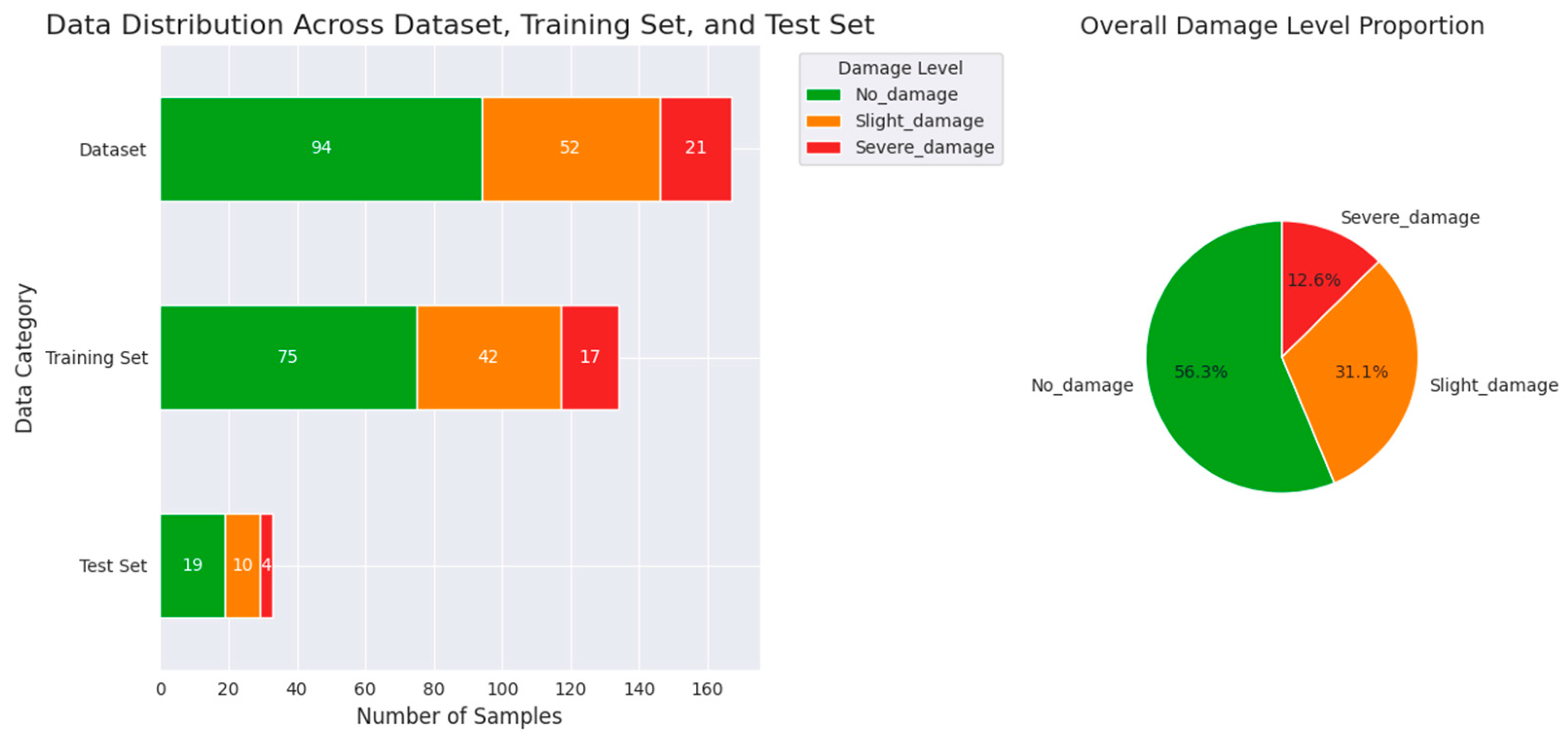
Furthermore, the sample size used in this study was limited to 167 sets. A larger sample size is needed, and future collaborations across different regions could enhance the model’s generalizability. Additional improvements could include expanding the dataset to include multiple mineral types, integrating time-series data to predict the long-term stability, and developing a real-time monitoring system embedded with the model.
Additionally, the model relies on high-quality mechanical parameter inputs. Insufficient on-site monitoring may affect the prediction accuracy. Future research should consider integrating finite element simulation with machine learning and developing a real-time parameter updating system to enhance the algorithm’s robustness and practicality.
7. Conclusions
In this study, the overall process of predicting the impact of shock waves on closed walls using the RF algorithm involves several of the following key steps: data preparation, model selection, hyperparameter optimization, model training, cross-validation, and performance evaluation. A total of 167 data samples, each containing three predetermined key input parameters, were collected to train and validate the RF machine learning model. Based on the introduction of four performance evaluation metrics, namely, the accuracy, precision, recall, and F1-score, within the experimental context of this study, we drew the following conclusions:
- (1)
The analysis of the machine learning-based closed wall stability prediction model reveals that the random forest model demonstrates excellent predictive performance, achieving an accuracy of 94.6%. Following hyperparameter optimization through a grid search, the performance of the optimized random forest model is further enhanced, reaching an impressive accuracy of 95.9%. Compared to other algorithms, the method proposed in this paper does not exhibit a decrease in the prediction performance. Compared to the numerical model of Zhang et al. [
19], the model presented in this paper improves the computational efficiency by approximately 40%.
- (2)
Based on the model established in this study, the three parameters obtained from the experiments (the shock wave velocity, compressive strength, and shear strength) can effectively predict the stability of the closed walls in the project. To verify the reliability of the model, the machine learning prediction model was tested against data from 74 engineering examples and the Duimenshan mining area. The results indicate that the predicted stabilities of the closed walls are basically in line with the actual conditions, confirming that the RF prediction model exhibits superior performance and accuracy.
This high-performance prediction model provides a reliable and efficient tool for accurately assessing the impact of shock waves on closed walls, which is of great significance for theoretical research in the field of engineering geology. It fills a gap in the existing research to some extent by offering a more accurate and efficient prediction method for this specific engineering problem. This practical application not only validates the effectiveness of the model but also provides valuable guidance for real-world engineering projects, such as mine construction and underground engineering, where the stability of closed walls is crucial for ensuring safety and operational efficiency.