Abstract
This paper presents an innovative route planning method for autonomous port tugs, using an evolutionary algorithm with radar fitness assessment. The proposed solution takes into account the specifics of tug operation in a complex port environment, characterized by the presence of numerous static obstacles (port infrastructure, islands) and dynamic obstacles (other vessels). The presented radar fitness assessment method allows for taking into account many optimization criteria, such as route length, number of turn points or safety margin with respect to obstacles. The algorithm was tested in four different navigation scenarios of varying complexity. The results of the research showed that, compared to the classic genetic algorithm, the radar method generates routes with fewer turn points (reduction by 1–2 points) and significantly reduces the total course change (up to 53.6%). Additionally, the routes generated by the radar algorithm consistently maintained a greater safety margin with respect to obstacles. The algorithm is prepared to take advantage of data interchange according to International Maritime Organization’s e-navigation proposal via its VHF Data Exchange System (VDES) messages, which could improve the safety of proposed routes and their efficiency. This gives a basis to use the proposed solution as an autonomous vessels and/or formation control algorithm in future automated transport systems.
1. Introduction
In recent years, we have witnessed the dynamic development of autonomous marine vehicles. Progress in the field of robotics and artificial intelligence has enabled the construction of vessels capable of independently performing complex tasks without human intervention. One of the key aspects of autonomous navigation is planning the optimal route of a ship’s passage.
Port tugs are specialized vessels whose task it is to assist larger ships during maneuvers within the port. Their work is local and takes place in a relatively small area, which translates into specific requirements for planning the passage route. Sea ports are characterized by high traffic density [1,2], as many vessels of different sizes and purposes operate in a limited space, creating a high risk of collision. Tugs must navigate efficiently between them, while at the same time performing precise maneuvers near the assisted ships. Additionally, the port infrastructure includes numerous narrow channels, quays and breakwaters, which significantly restrict freedom of movement. Planning the tug’s route must take into account these obstacles and ensure safe passage through the port.
Recently, more and more port operators have decided to introduce electric or hybrid tugs into service [3]. These vessels are characterized by significantly lower pollutant emissions and allow for reducing the negative impact on the environment. However, this is associated with certain limitations. Electric tugs have a relatively small capacity of energy storage tanks compared to their counterparts with combustion engines. This translates into a limited range and operating time on a single battery charge. Therefore, route planning for an electric tug must be particularly careful and take into account the efficient use of available energy. Suboptimal maneuvers, rapid acceleration or long periods of work under high load can quickly drain the batteries and immobilize the vessel or prevent it from completing the task. The route planning algorithm should minimize energy consumption while ensuring the implementation of the tug’s work schedule. This is a difficult optimization task that requires advanced computational methods.
It should be emphasized that route planning for a full-size autonomous ship is a task requiring special responsibility [4]. It must take into account a number of factors such as energy consumption, travel time, weather conditions, and above all the safety of the vessel and its crew (if present) and the marine environment.
Modern computational methods can find solutions to this problem, which are beneficial in many respects. These include graph-based methods, methods with a potential field or vector field, methods using evolutionary algorithms, methods with an artificial neural network, modifications of classic graph algorithms, or hybrid methods.
Graph-based methods consist in representing the environment in the form of a graph, where the vertices correspond to the possible positions of the vessel, and the edges represent permissible transitions between them. Particularly popular are visibility graphs, which take into account mutual visibility between waypoints, and Voronoi diagrams [5], which divide space into regions based on the distance to obstacles, as well as sampling algorithms using Rapidly exploring Random Tree (RRT) search [6,7,8,9].
Methods using Artificial Potential Fields (APF) and vector fields treat the environment as a force field, where obstacles generate repulsive forces and the destination generates an attractive force. The route is determined by finding a path with the lowest potential energy or following the resultant vector of forces [10,11,12,13,14,15].
Methods based on evolutionary algorithms use mechanisms inspired by biological evolution, such as selection, crossover and mutation, to iteratively improve the population of potential solutions. Among them, we can distinguish ant colony methods (ACO), which imitate the behavior of ant colonies in search of the optimal path [16,17,18] and genetic algorithms (GA), where potential routes are encoded in the form of chromosomes undergoing evolution [19,20,21,22,23].
Artificial neural networks (ANNs) are computational models inspired by the structure and operation of the human brain. A neural network can learn to determine an optimal route based on sample training data and then generalize this knowledge to new cases [24,25,26,27].
Modifications of classical graph algorithms involves algorithms such as Dijkstra or A*, which were were originally used to find the shortest path in a graph. They can be adapted to the problem of ship route planning by appropriately representing the environment and modifying the cost function [5,28,29,30,31].
The increase in computer performance has allowed the use of computationally intensive reinforced learning methods, which are also suitable for calculating passage routes [32,33,34,35,36,37].
Hybrid methods combine the advantages of different computational approaches. For example, a genetic algorithm can be used for global exploration of the solution space, and then its results can be improved by local optimization using potential fields. Such a combination allows for effective searching of the complex space of possible routes. This article presents a method for determining an energy-efficient passage route for an autonomous tugboat, using an evolutionary algorithm with a radar method of fitness assessment. The aim of the algorithm is to determine a passage route that minimizes energy consumption while maintaining the safety of navigation.
2. Determining a Local Passage Route Using Evolutionary Algorithms
Evolutionary algorithms imitate the natural process of adaptation of a population of creatures to changing environmental conditions. As in the case of natural evolution, in its artificial equivalent, evolutionary pressure and the associated selection of the best adapted individuals play a key role.
The individual is the basis for the operation of the evolutionary algorithm, and in the case of a genetic algorithm, which is a very frequently used type of evolutionary algorithm, the basis for the actions is the genome of a given individual. Unlike the genomes of living organisms, the genomes of individuals in evolutionary algorithms contain only the information necessary to solve a given problem. The most commonly used type of genome is a genome with binary coding, consisting of chromosomes containing genes that take the value 0 or 1.
In order to be able to use a genetic algorithm to solve the problem of navigating a ship, the first step is to appropriately encode the variables describing the given problem on the chromosomes. Each variable used in the algorithm must be mapped to the appropriate number of bits, or genes. For example, if one wants to encode the course of a ship as one of 8192 possible values, we need 13 bits. Variables such as speed and turn point coordinates can also be represented as binary strings, where each gene corresponds to one bit of the variable, maintaining the appropriate resolution required by the size of the data.
After the variables have been properly encoded, the genetic algorithm can begin the optimization process. A classic genetic algorithm consists of several basic steps: population initialization, fitness evaluation (objective function), selection, crossover, and mutation.
The process begins with generating an initial population of individuals, where each individual has a random chromosome. The initial population usually consists of several dozen to several hundred individuals, and each genome represents one potential solution to the problem. In order to be able to compare different solutions, the algorithm must determine how well a given individual copes with the navigation task. For this purpose, a fitness function is used, which evaluates how well the genome of a given individual fulfills the assumptions of the problem.
After assessing the fitness of individuals, the algorithm performs a selection, choosing those individuals that will participate in the reproduction process. One of the most commonly used selection mechanisms is roulette wheel selection. In this method, the probability of selecting a given individual is proportional to the value of its fitness—the better the solution, the greater the chance of its selection. Each individual corresponds to a segment of the roulette wheel, with the segment’s size proportional to the individual’s fitness value. In this way, individuals with higher fitness value have a greater chance of participating in subsequent genetic operations.
The selected individuals are subjected to a crossover process, the purpose of which is to exchange genes between them, which gives new solutions. In the simplest variant of crossover (single-point crossover), the chromosomes of two parents are cut at a randomly selected point, and then fragments of chromosomes before and after the cut are exchanged, giving two new offspring individuals. The crossover operation is the first of the key features of a genetic algorithm, combining the features of different individuals, which in turn allows for the exploration of new solutions.
To ensure diversity in the population and avoid the solution getting stuck in a local optimum, the genetic algorithm uses the second key operation—mutation, which is a random change in the values of some genes in the chromosome. For example, if one of the genes in the chromosome has a value of 0, the mutation can change it to 1. Mutation occurs with a certain probability, usually at the level of 1–5%, and allows the algorithm to explore new areas of the solution space that could be missed without this operation.
After the process of crossing and mutation is completed, the new population of individuals replaces the old one. Then, the whole process of fitness assessment, selection, crossing and mutation is repeated for many iterations (generations), until the algorithm’s termination criteria are met, such as reaching a satisfactory solution or reaching a designated number of iterations.
Using an evolutionary algorithm to determine a local route for a ship’s passage involves determining the starting point, which is usually the position of the ship at the start of the calculations, the destination point, and the static and dynamic navigation constraints existing in a given water body.
The initial population of individuals is initiated with randomly determined passage routes, where each is a broken line connecting the starting point of the passage route with the destination point, and each of the route sections has a given speed on this section. The number of individuals, the range of coordinates of the turning points in longitude and latitude, and the range of randomized speeds on each section are the algorithm’s control parameters. Algorithm 1 presents the main steps of the evolutionary algorithm determining the passage route of a ship:
| Algorithm 1: Evolutionary Algorithm calculating the ship navigation route |
| BEGIN | Load navigational data | | Initialize random population, encode data on chromosomes | | LOOP Iteration over set number of iterations | | | Calculate fitness of every individual | | | Select best individuals | | | Crossover best individuals | | | Apply Mutation operators | | Update number of iterations, check if reached maximum | Return result solution END |
In order for the genetic algorithm to effectively determine optimal navigation routes, it is necessary to take into account existing navigation constraints already at the stage of generation and evaluation of individual individuals. Generated routes, although initially created randomly, must be subject to thorough verification to ensure that none of the route sections violate applicable navigation rules, such as avoiding obstacles or following fairways. Each individual representing one route must be checked for compliance with these constraints, and verification includes checking for violations of both static and dynamic constraints. A route may be considered incorrect if any of its sections intersects with terrain obstacles, areas excluded from navigation, or passes dangerously close to any of the ships navigating in a given body of water. In such a case, an individual whose route violates these constraints may be rejected or receive a significantly lower value in the fitness assessment. The most important static constraints include terrain obstacles and related shallows; various objects with known positions such as navigation buoys, breakwaters, mooring piles; dangerous objects such as wrecks and boulders on the bottom; navigation zones requiring specific behavior, e.g., areas temporarily or completely excluded from navigation or waterways with a specific direction and/or speed of movement.
Dynamic restrictions include moving objects in a given water area, primarily other vessels, but also non-ship objects such as icebergs or lost containers.
Due to their invariability over time, static restrictions have a fixed position and dimensions, which can be saved in the form of a digital map and thus used by the algorithm to determine areas that the planned route of passage cannot violate. In order to maintain a certain margin of error in the knowledge of the position of these restrictions, the prohibited area may include the boundaries of known restrictions increased by a certain assumed distance [38].
In turn, dynamic constraints have a certain degree of uncertainty related, firstly, to the methods used on ships to detect and determine the direction of movement of other ships, i.e., radar with ARPA attachment, systems using LIDAR [10,26], optical sensors imaging in visible light and/or infrared [10] and information distributed using the Automatic Identification System (AIS) [39]. The position of the own ship is determined using available GNSS systems, such as GPS [10] and is also burdened with a certain error, while information on speed may come from both the GNSS system and from the log or logs on board the ship. If the generated individual does not meet these conditions, several solutions can be applied. One approach is penalization in the objective function—routes violating constraints are assigned a lower fitness value, which reduces their chances of participating in crossbreeding. Alternatively, such routes can be rejected completely and replaced with new ones, generated randomly or through mutations and crossbreeding of existing individuals.
The fitness evaluation of an individual in the ship route planning algorithm should assess the route’s quality in terms of its traversal efficiency, considering the total route length compared to the shortest path between start and destination points, the travel time, and the number and magnitude of required maneuvers. The second factor in the assessment of fitness is the degree of safety of the designated route, taking into account whether the route does not violate static constraints and whether it bypasses static constraints at an appropriate distance. The safety assessment is usually defined in binary terms and only says whether the route is safe or not. To determine the passage route, it is necessary to know the starting and ending points. The length of the route Lr consisting of n sections is equal to the sum of the lengths of the sections of this route:
where
Li—length of i-th section, and
n—number of route sections.
During the route, the ship will change course after reaching the turning points, and the total change in course θk expressed in degrees will be equal to:
where
θk—course change at of k-th waypoint, and
n—number of route sections.
Assuming that the ship’s speed on a given section of the route will be constant, the total time to complete the route tt will be the sum of the products of the speed on a given section and its length:
where
Li—length of i-th section, and
vi—ship speed while travelling the i-th section.
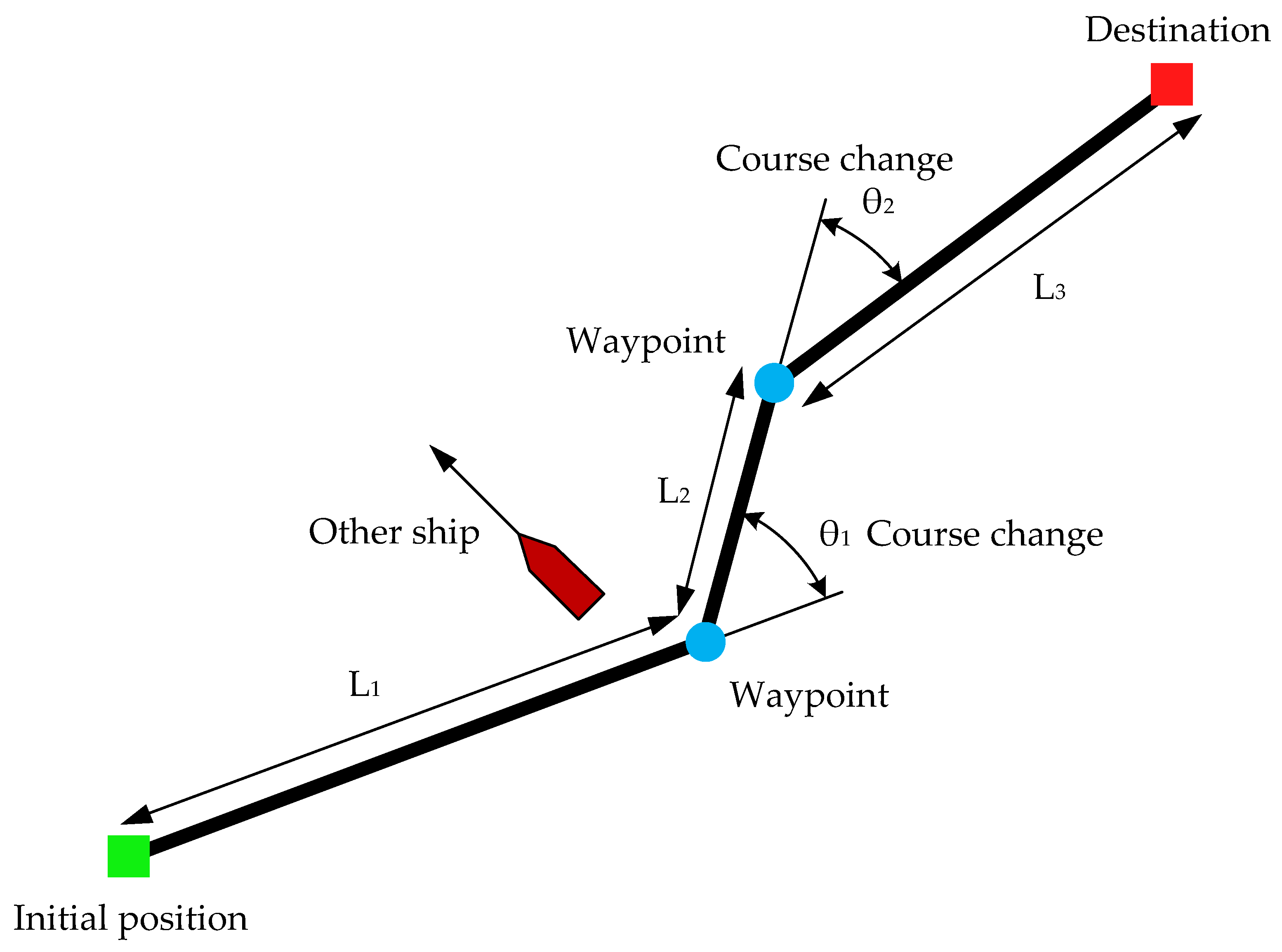
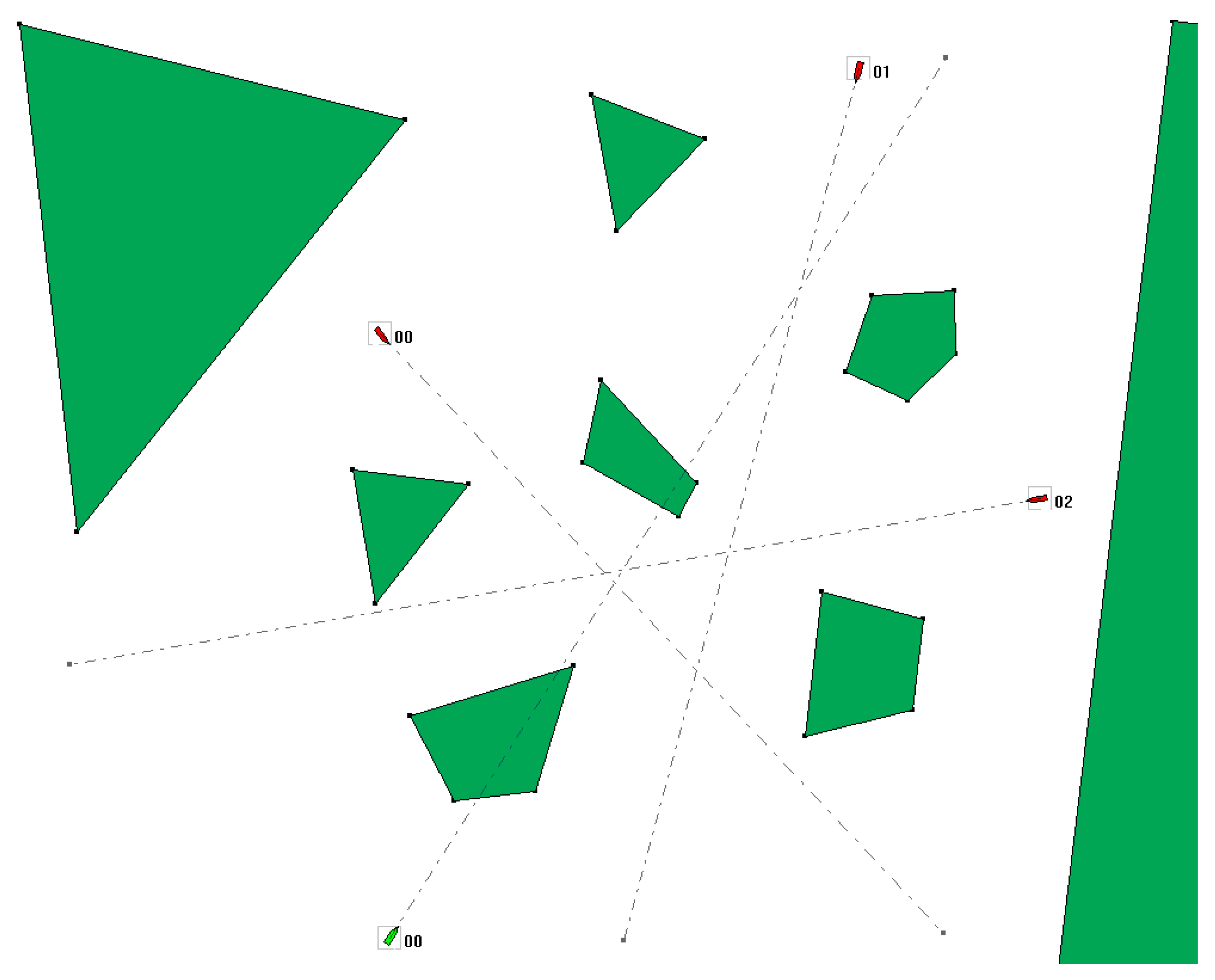
Figure 1 shows an example route between two points, consisting of 3 sections and 2 waypoints. One other ship is also visible, crossing the planned course. The need to avoid it is dictated by the rules of the Convention on the International Regulations for Preventing Collisions at Sea (COLREG) [40], which specify the behavior of ships when meeting during navigation.
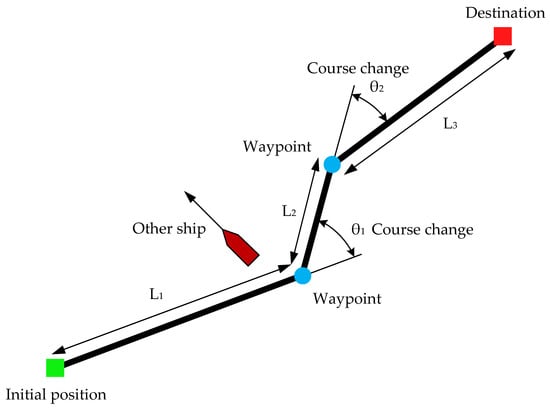
Figure 1.
Diagram of elements used to determine the passage route.
3. Evolutionary Algorithm Determining a Local Passage Route Using a Radar Method of Fitness Estimation
The presented algorithm is an extension of the classic genetic algorithm, in which instead of a simple method of assessing fitness, an innovative method based on a radar chart was used. The principle of operation of this method is based on the assessment of the surface area encompassed by the radar chart of the parameters of a given passage route represented by an individual included in the population undergoing evolution. The advantage of this method is the possibility of easily introducing many criteria for assessing the fitness of individuals, which allows the algorithm to be adapted to the specific conditions of determining a given local route.
The presented algorithm uses five criteria for assessing the fitness of a given individual. The first criterion is the number n of waypoints of the passage route, the second is the length of the route Lr, the third is the total course change θk, the fourth is the time tt required to cover the route, and the fifth criterion is the minimum approach distance to any of the static or dynamic constraints, calculated as a multiple of the minimum distance from a given constraint that must not be violated.
Algorithm 2 presents a description of the individual steps for the evolutionary algorithm with the radar fitness evaluation method.
| Algorithm 2: Evolutionary Algorithm with Radar Plot Fitness Evaluation calculation steps |
| BEGIN | Load navigational data | | Initialize random population, encode data on chromosomes | | LOOP Iteration over set number of iterations | | | LOOP Calculate fitness of every individual: | | | | (a) Get number of route sections n for individual | | | | (b) Calculate length of route for indicidual according to Equation (1) | | | | (c) Calculate total course change θk according to Equation (2) | | | | (d) Get speed for each route section, calculate route time tt according to (3) | | | | (e) Find the minimal distances to static and dynamic constraints | | | Calculate radar plot area with data from steps (a) to (e) | | | Select best individuals | | | Crossover best individuals | | | Apply Mutation operators | | Update number of iterations, check if reached maximum | Return result solution END |
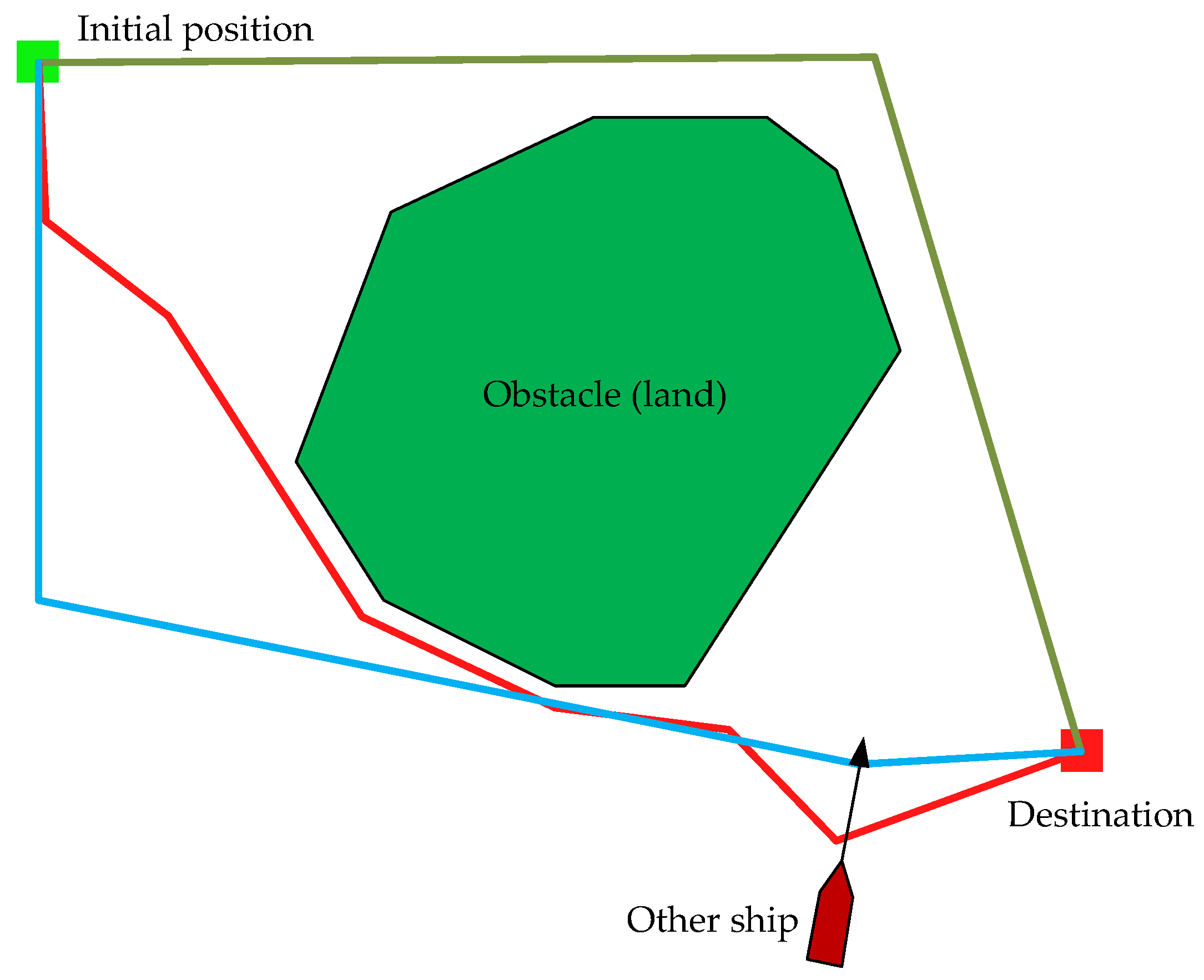
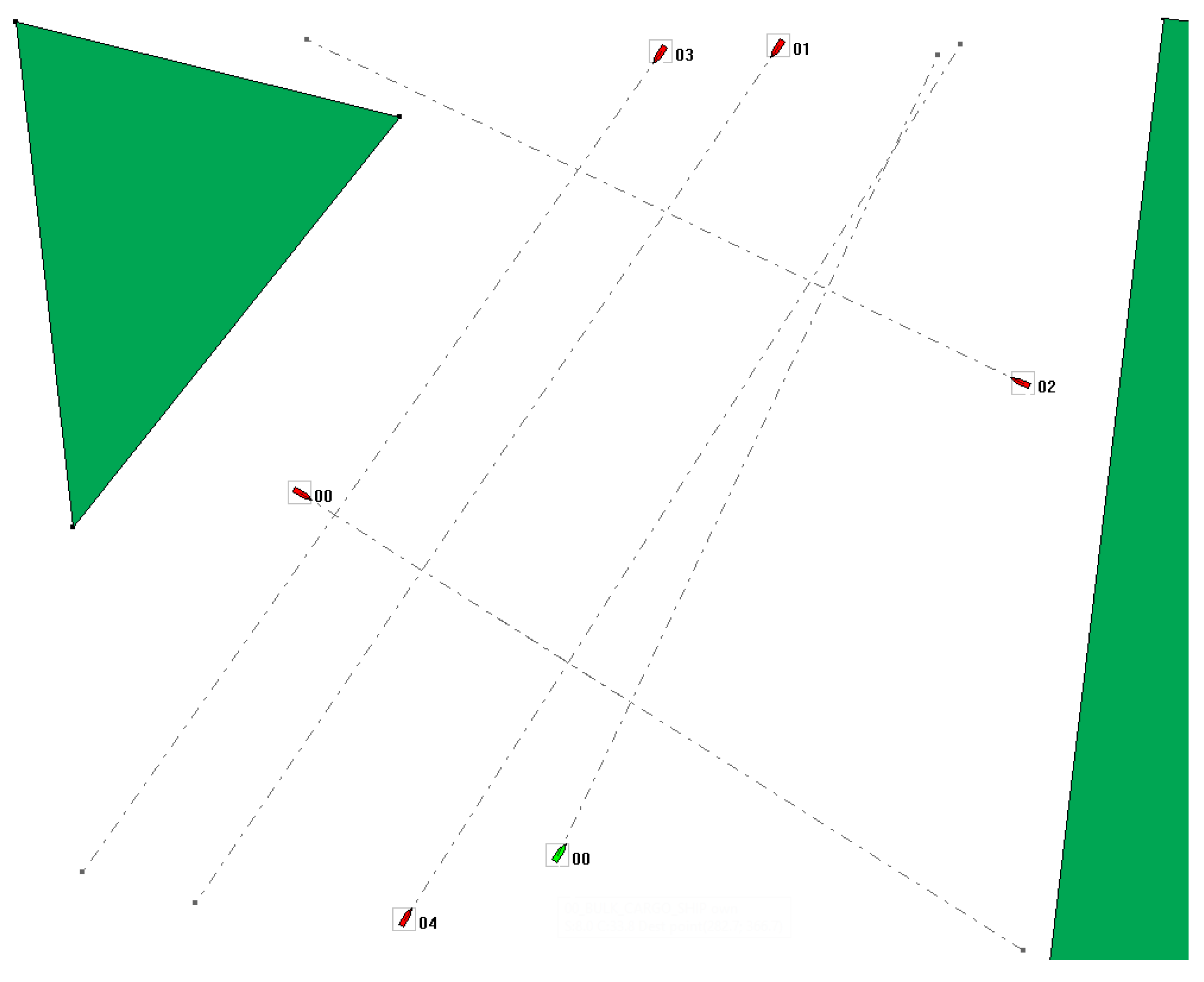
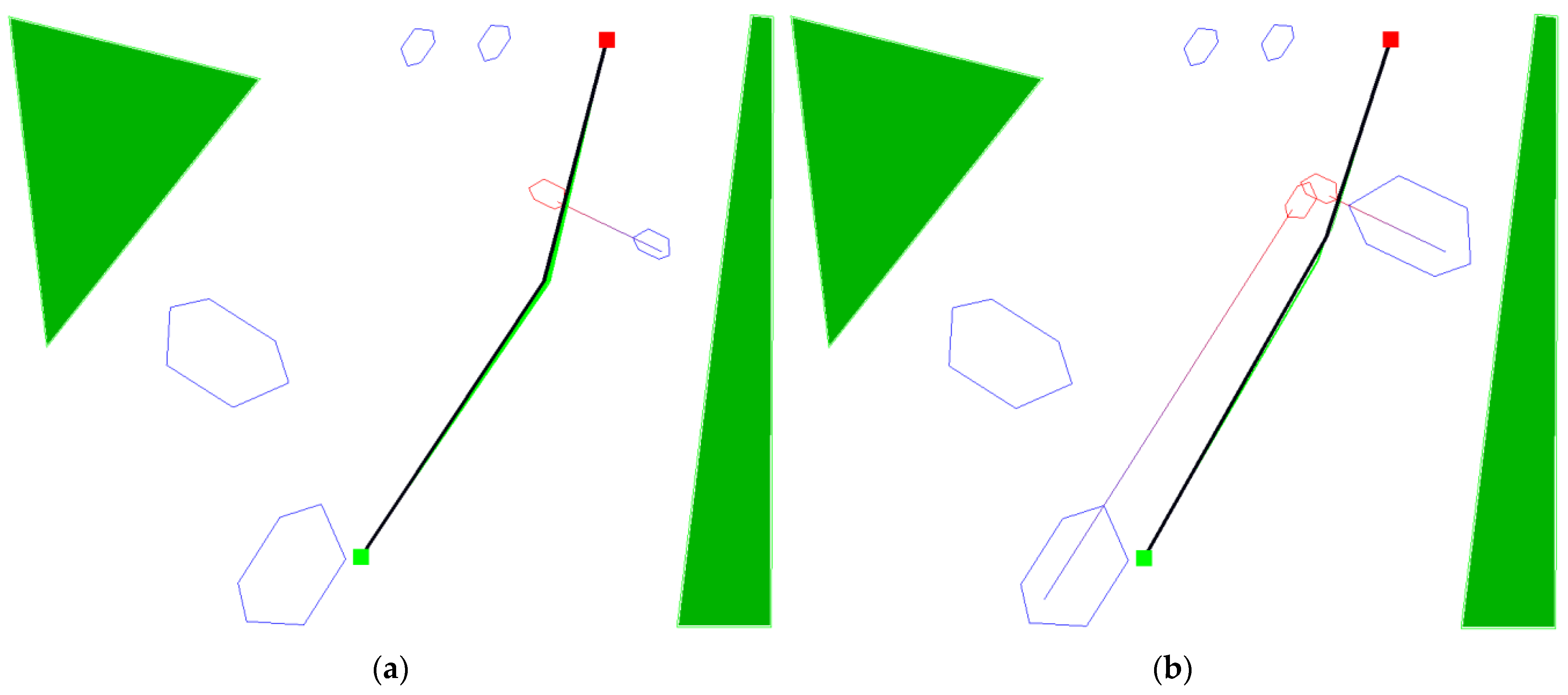
Figure 2 shows the course of three hypothetical navigation routes, while Figure 3 shows the corresponding radar chart showing the degree of fitness of individuals corresponding to these routes.
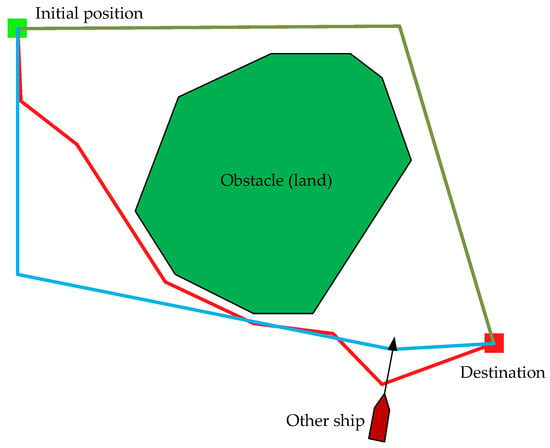
Figure 2.
Examples of 3 individuals representing navigation routes subject to fitness assessment using the radar method.
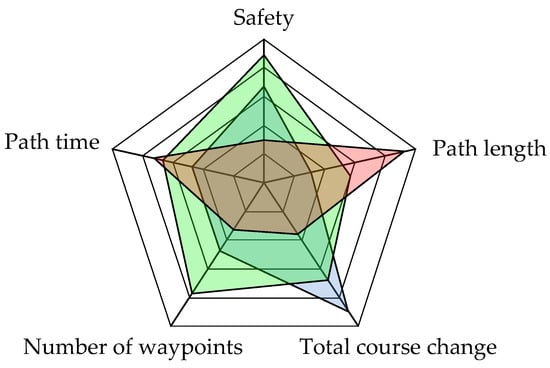
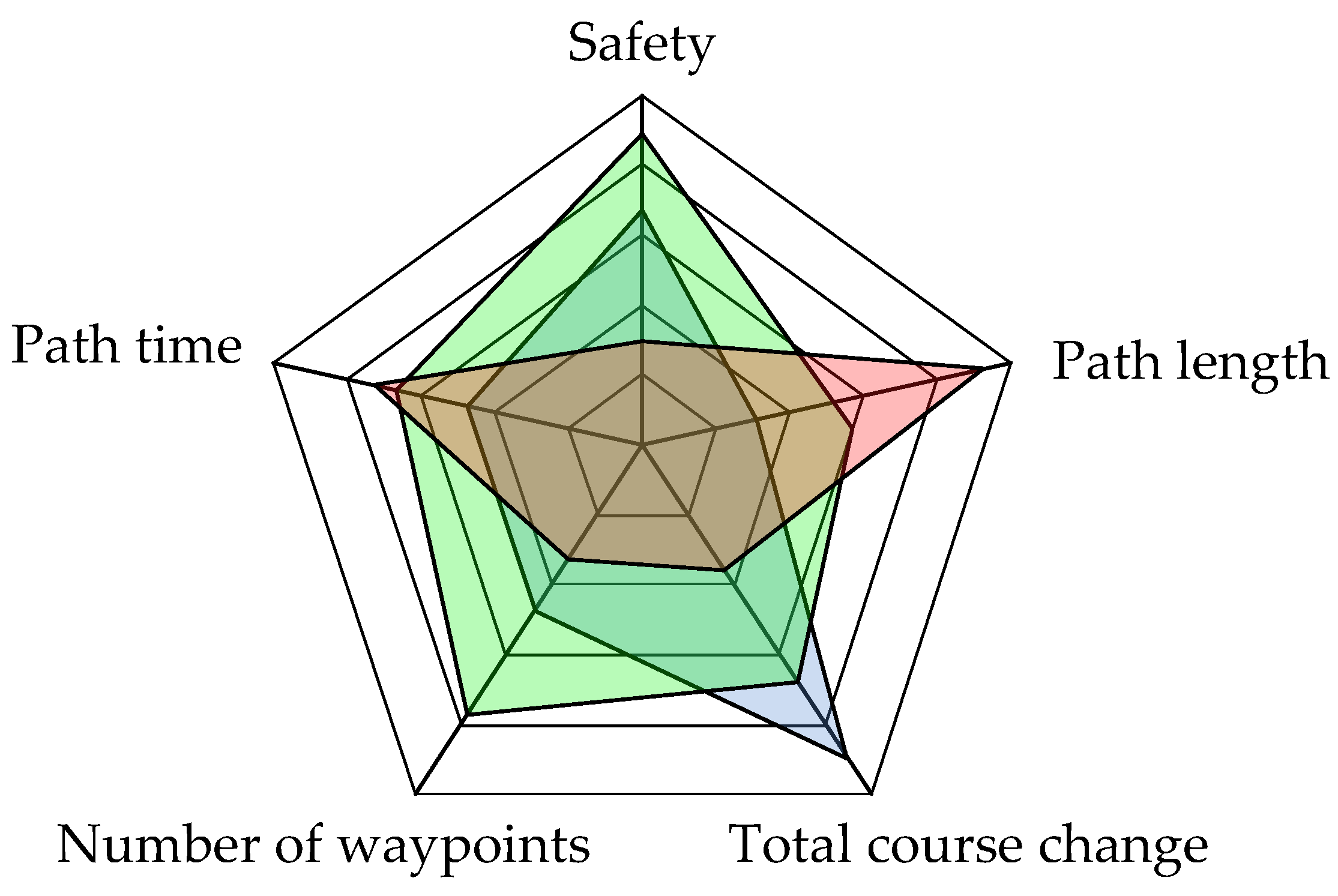
Figure 3.
Principle of calculating fitness values based on the radar chart surface.
The presented radar chart using five criteria is only a basic chart. It is possible to extend the scope of optimization with additional parameters, e.g., change in the ship’s speed or the impact of environmental conditions such as sea currents, wind, shallow waters, on the ship’s motion resistance.
The presented routes are marked with the colors: red, blue and green. The red route is characterized by the shortest distance to cover, but it contains many turning points and the associated change in course is also large. A large number of maneuvers led to the route covered the fastest, but at the expense of safety, because it runs quite close to navigational restrictions—land and one other ship.
The second route, marked in blue, has fewer turning points, but they are performed at a large angle, which also resulted in an extension of the route and the time required to cover the route.
The last route represented in green has only one turning point and despite a slightly longer route than the blue route, it does not have to perform an anti-collision maneuver with the other ship, because it leads from the other side of a static navigational obstacle—an island.
Despite not having the shortest distance to cover, the route marked in green is characterized by the best degree of adaptation, due to the largest field on its radar chart. The blue route is characterized by a medium degree, and the red route by the smallest.
This method of representation allows for a quick visual analysis of the results obtained when testing a selected set of rules that comprise a radar chart, which makes it possible to quickly compare several sets of rules and select the one that is characterized by the best results for a given type of navigation situation.
4. Results
The described algorithm was tested on four navigation situations, taking place in restricted waters, in the presence of both static and dynamic constraints. In the case of all maps presented in this chapter, north is at the top of the figure. The parameters of the distances covered and course changes are presented in Table 1 and Table 2 placed at the end of the chapter.

Table 1.
Navigational data for the presented situations.

Table 2.
Summary of each situation solution with total path distance, and total course change.
The research presented in this chapter uses the proprietary marine navigation environment simulator. The simulator environment uses cooperating programs written in C++, the first one is used to prepare and introduce changes to existing navigation situations, the second program performs calculations related to the evolutionary algorithm being studied and the movement of dynamic objects. The last element of the environment is a simulator enabling full simulation of ship movement during the situation designed in the first program. The simulation includes the dynamics of the movement of all ships related to their physical dimensions, weight, draft, as well as hydrometeorological disturbances affecting the hull related to waves, wind and sea current, described by their: speed, course, and variability in time.
The marine navigation environment simulator enables the collection of data on the movement of each unit during the simulation. In the presented research, the screenshots visible in Figures 4, 6, 8 and 10 come from the program preparing the navigation situation. The green shapes visible on them are static navigational restrictions—land, while free space is a body of water available for free navigation.
The second program used in this study was used to perform calculations according to the algorithm presented in Algorithm 2, and also to visualize the results, which resulted in screenshots visible in Figures 5, 7, 9 and 11, as well as data in Table 1. The visualization has an analogous color scheme, only replacing the icon of the initial position of the own ship with a green square, and the target position with a red square. The route resulting from the calculations, represented by the best-adapted individual, is presented with a thick broken line in black.
The program performing calculations related to evolutionary algorithms and visualizing their work has the ability to switch between the tested algorithms, in this case between the algorithms described in Algorithm 1 and Algorithm 2, which allowed for a comparison of their work.
4.1. Situation 1
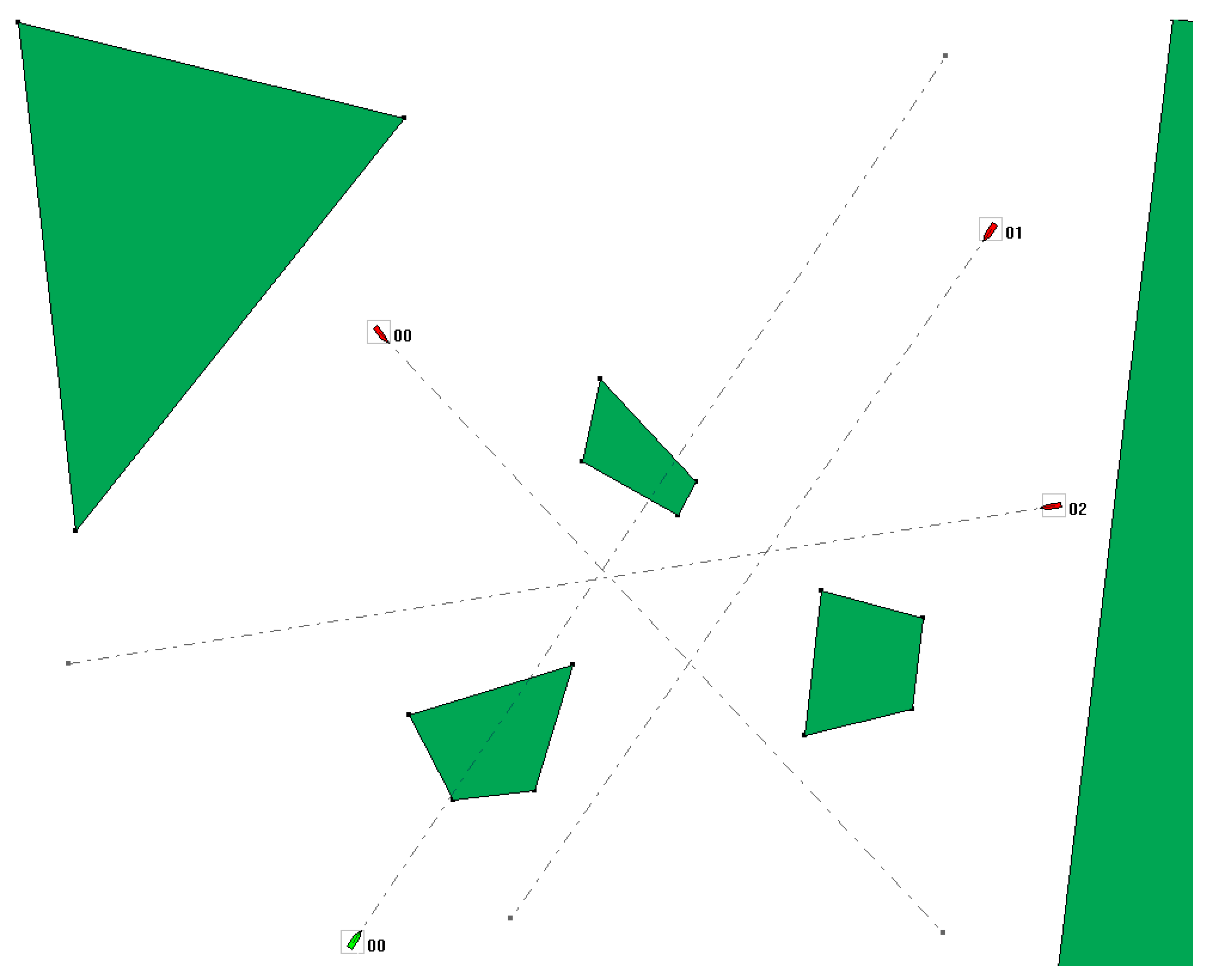
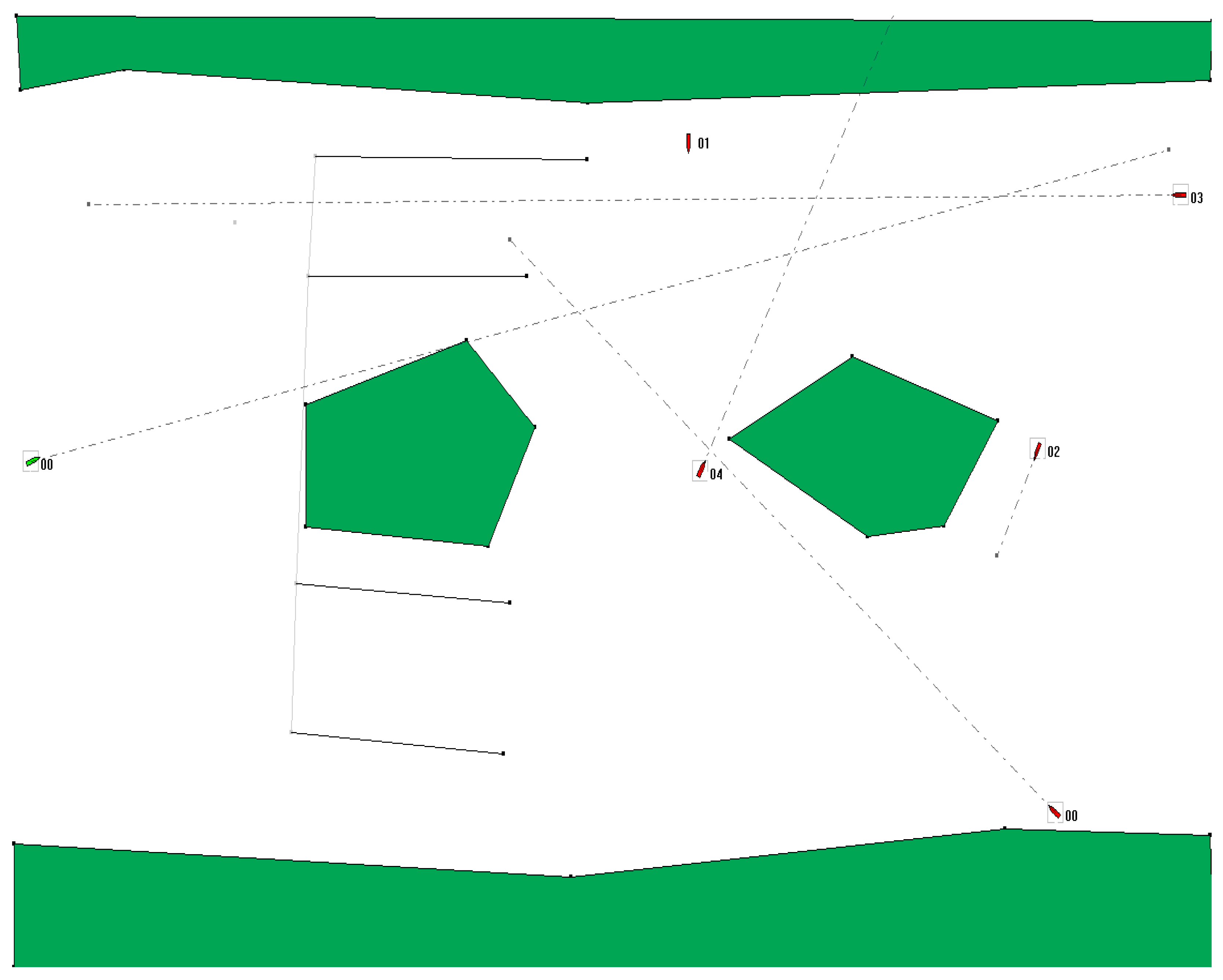
The view of the water area at the beginning of the first situation is shown in Figure 4. The situation takes place in waters restricted to the northwest and east, and there are three small islands in the middle of the water area.
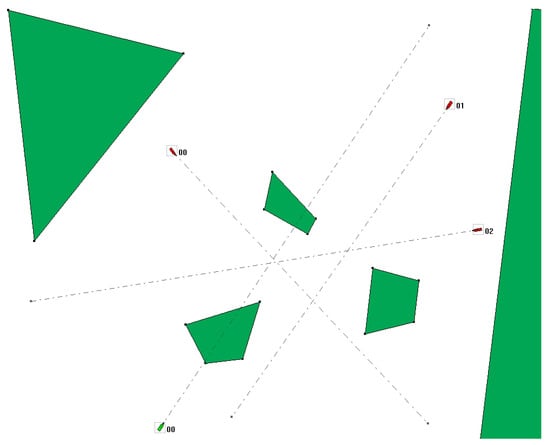
Figure 4.
Situation 1, a strait with 3 islands and 3 other ships.
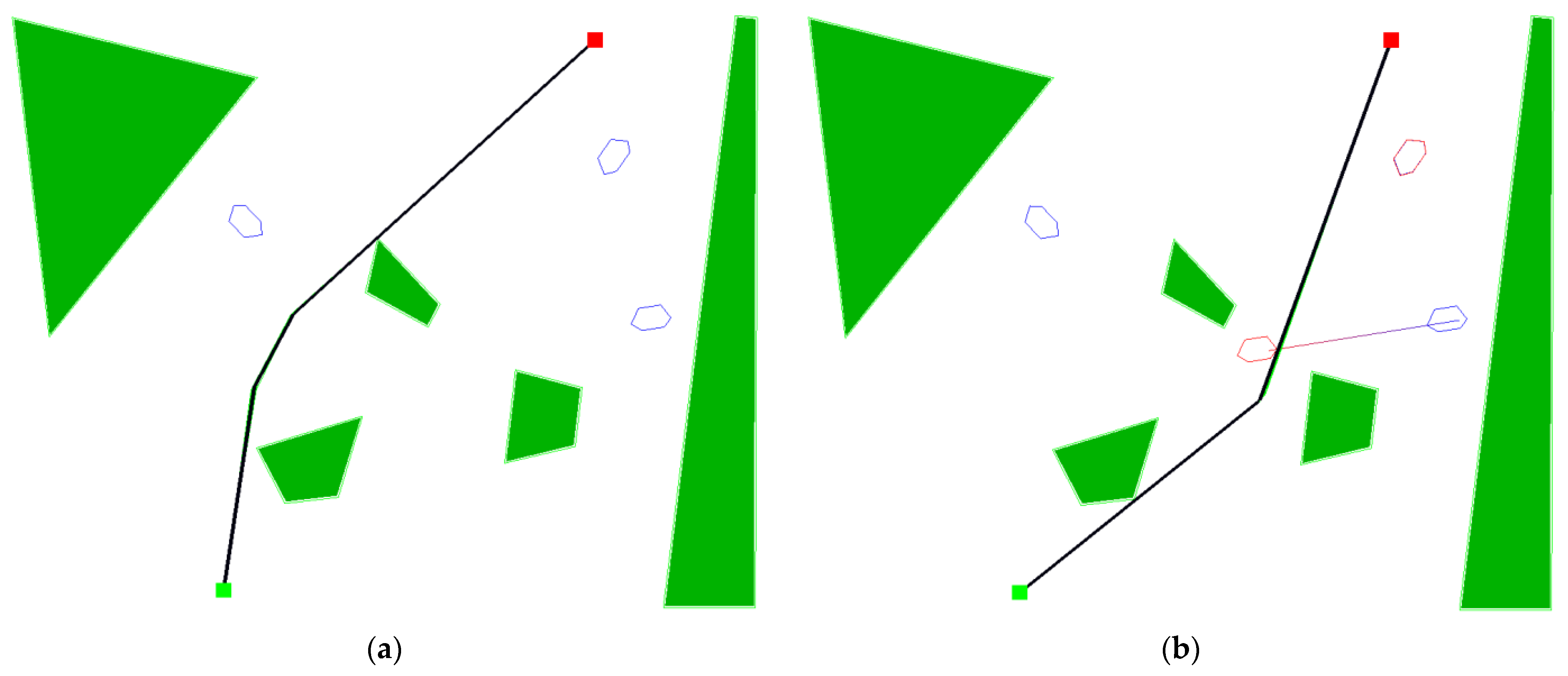
The tug considered is located in the southern part of the water area and is represented by a green icon. The dashed line connects the initial position of the tug with the destination point and indicates its initial course. The three other ships present in the water area are represented by red icons and their initial course and destination points are also marked. Unlike the ship considered, the other ships do not maneuver, they are only moving navigational obstacles, moving at a constant speed. Figure 5 shows a graphical view of the solution to navigation situation no. 1.
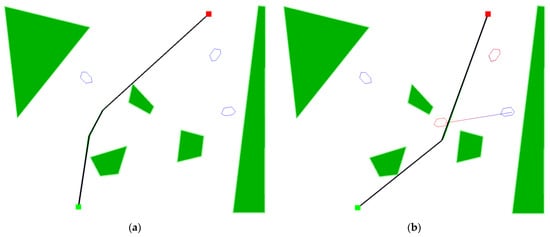
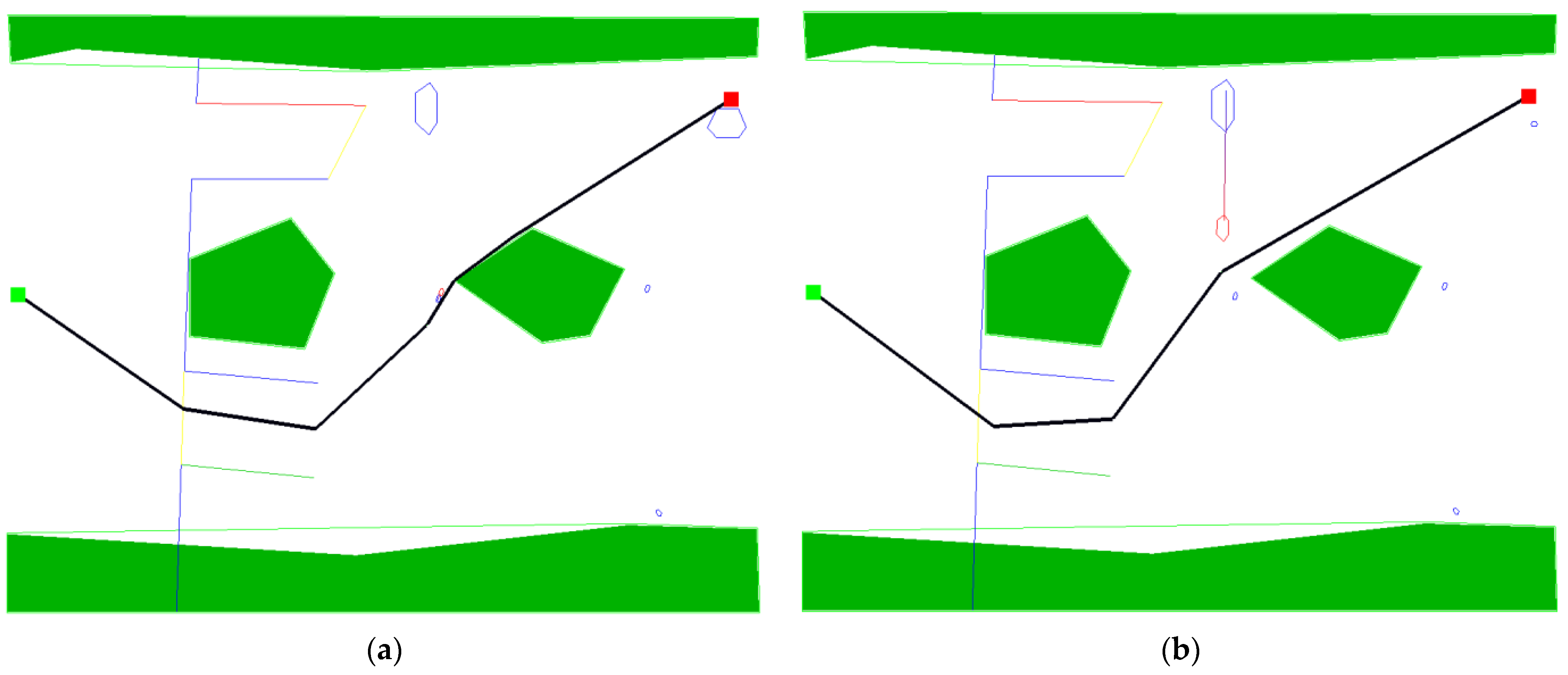
Figure 5.
Situation 1 solutions. (a) Solution with a classic fitness method, and (b) solution with a radar fitness method.
The navigation routes proposed by both versions of the evolutionary algorithm have a similar shape, but the route (a) obtained from the algorithm with the classic fitness assessment method has one less turning point and runs in the immediate vicinity of one of the islands. In comparison, the algorithm using the radar method found a shorter route, using only 1 turning point, placed in such a way as to pass one of the moving other ships behind its stern, which is considered a safer maneuver than passing in front of its bow. The route proposed by the postulated algorithm also requires 24.7% fewer course changes, compared to the classic algorithm.
The colored hexagons visible in Figure 5 symbolize the safety domains, the violation of which is considered to be the risk of collision. The blue domains show the initial position of other ships, while the red ones show the position of the other ship in the event of approaching or intersecting the proposed passage route with the predicted route of the other ship.
4.2. Situation 2
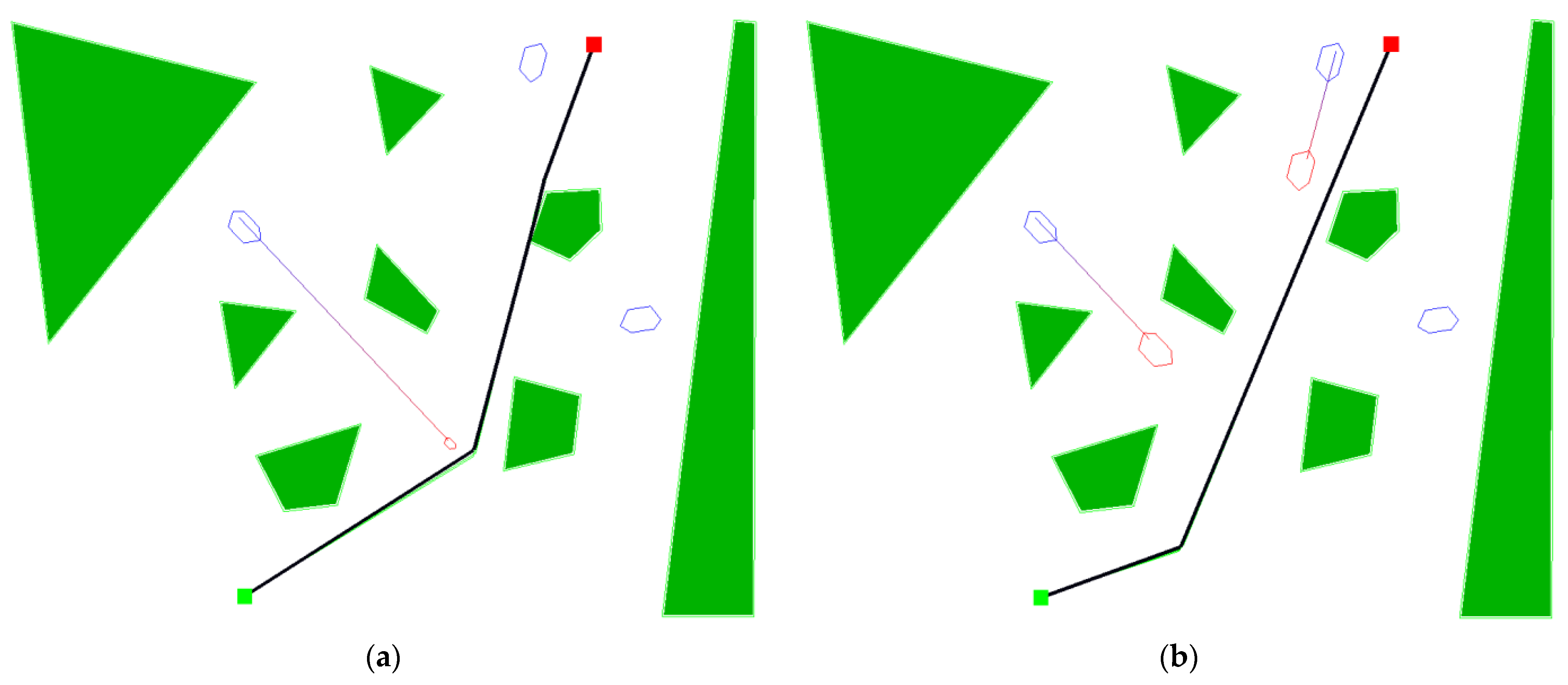
Figure 6 shows the view of the water area at the beginning of the second situation. The number of islands in the middle of the water area was increased to six, and the routes of three other ships were changed. Compared to situation 1, the water area of situation no. 2 is more limited.
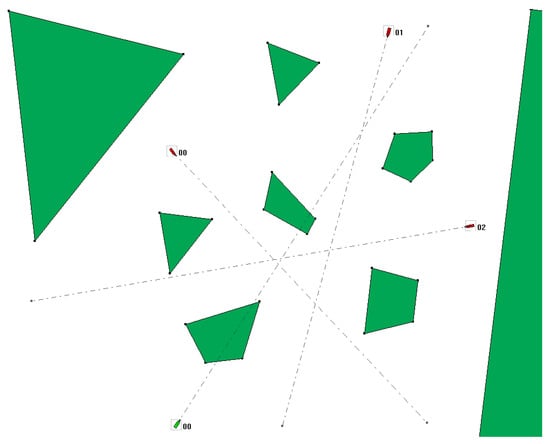
Figure 6.
Situation 2, a strait with 6 islands and 3 other ships.
The considered tugboat starts the journey in a similar orientation to situation 1, but its course intersects a larger ship sailing from the north.
The solution proposed by the algorithm with the classic method of assessing the fitness again determined a route with two turning points, one more than the radar algorithm. Again, the classic algorithm determined a route that is slightly longer and passes very close to one of the islands. Determining the first turning point farther from the other ship sailing to the southeast means that when this course and the planned route intersect, the tugboat is already far away. The route proposed by the algorithm with the radar assessment gives a smaller approach distance with this ship, but it is several times longer than the length of the domain of this ship. This route brings the tug close to the second vessel heading southwest, but the vessels pass each other in opposite directions by about 1 domain width as shown in Figure 7.
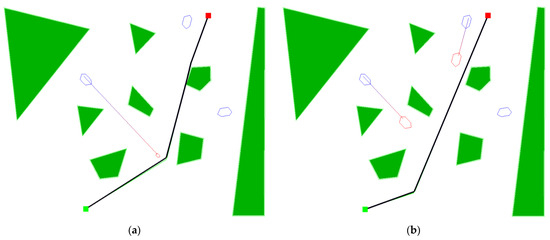
Figure 7.
Situation 2 solutions. (a) Solution with a classic fitness method, and (b) solution with a radar fitness method.
4.3. Situation 3
Figure 8 shows the view of the water area at the beginning of the third situation. The water area is devoid of islands, but the number of other ships has been increased to five, including one ship sailing slightly faster than the tugboat, on its left side.
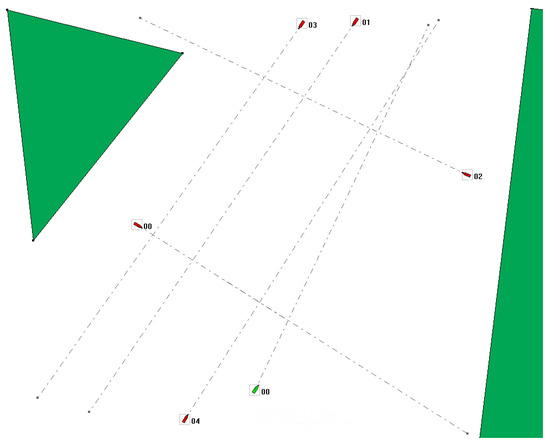
Figure 8.
Situation 3, a clear strait with 5 other ships.
In this case, both solutions have only one turning point, but the solution proposed by the radar algorithm determined the turning point with a course change of over 50% smaller than the classic algorithm, and again with a slightly shorter total distance as can be seen in Figure 9.
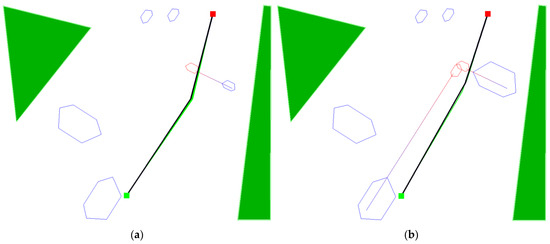
Figure 9.
Situation 3 solutions. (a) Solution with a classic fitness method, and (b) solution with a radar fitness method.
4.4. Situation 4
For the purposes of situation 4, a new water area was prepared, limited by land to the north and south, containing 2 islands in the middle. Additionally, fairways were designated around the western of the islands, directing the movement of ships: north to the west, and south to the east. In addition to the tugboat, there were five other ships in the water area, including two moving near the eastern island at low speed as shown in Figure 10 and Figure 11.
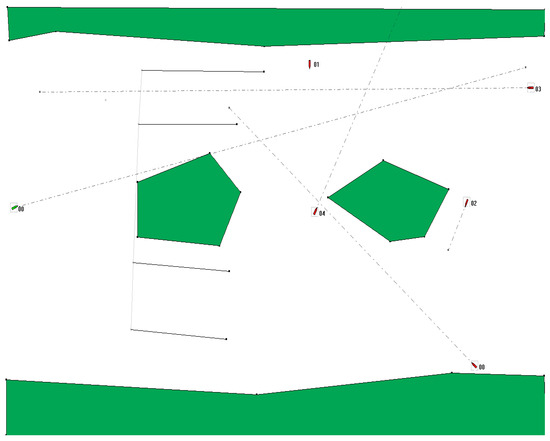
Figure 10.
Situation 4, a strait with 5 other ships, 2 islands and a defined fairway around 1 of the islands.
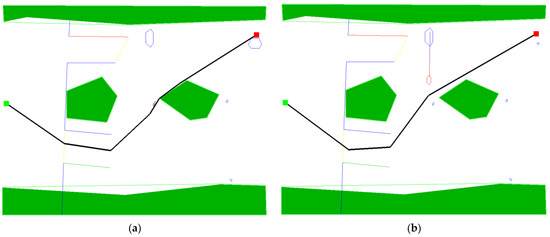
Figure 11.
Situation 4 solutions. (a) Solution with a classic fitness method, and (b) solution with a radar fitness method.
As in situations 1 and 2, the evolutionary algorithm using the classic fitness assessment method proposed a route very close to one of the islands, with two more waypoints than the route proposed by the postulated radar algorithm. This time, the route determined by the second algorithm is slightly longer, but still requires a smaller total change in course, and is also much further from obstacles, so from a navigational point of view it will be considered safer.
Table 1 contains navigation parameters—course and distance to be covered, for all sections of the navigation routes presented above. The values in the waypoint column indicate the number of the next turn point, with the value 0 assumed for the starting point.
Table 2 presents the aggregate values of the total length of the routes determined by the evolutionary algorithm using both the classic fitness assessment method and the proposed radar method. Table 2 also contains the value of the relative change in the length of the route determined using the radar method, compared to the route determined by the classic fitness assessment algorithm.
5. Discussion
The conducted research has shown that the use of an evolutionary algorithm with a radar-based fitness assessment method allows for the effective determination of safe routes for an autonomous tugboat in restricted waters and in situations similar to those encountered in ports and their roadsteads. Compared to the classic evolutionary algorithm, the solutions proposed by the radar-based algorithm for assessing the degree of adaptation are characterized by:
- Fewer route turn points—in situations 1, 2 and 4, the radar-based algorithm generated routes 1–2 turn points shorter than the classic method,
- Reduction in the total course change—particularly visible in situations 1 (24.7%) and 3 (53.6%), which translates into lower energy consumption,
- Maintaining safer distances from static obstacles—the routes generated by the radar algorithm consistently bypassed islands with a greater safety margin,
- Comparable or slightly shorter total route length—differences in route lengths ranged from −0.8% to +0.97%.
The proposed evolutionary algorithm with an innovative method of fitness determination using a radar plot is intended for use in controlling autonomous marine vehicles, as well as entire formations of such vehicles, while other methods described in the literature so far are usually intended only to support decision-making by navigators of the ship It should be emphasized that the presented algorithm makes decisions taking into account both static and dynamic constraints, unlike many algorithms described in the literature, focusing mainly on the movement of other ships, entirely omitting static constraints.
The innovation of the proposed algorithm is manifested in the possibility of quickly changing the set of criteria for assessing fitness, by replacing a set of one radar plot coefficients with another, or by adding new radar plot coefficients, depending on the change in the nature of the navigation situation.
It is worth noting that the radar-based algorithm demonstrated particular effectiveness in highly complex situations (situation 4), where, despite a greater number of navigation constraints, it was able to determine a safer route with a similar total length. The solutions generated by the proposed algorithm have parameters similar to the solutions proposed in a given situation by professional navigators.
When applying the described algorithm in a real ship, it would be necessary to take into account the situation when one of the other ships changes the parameters of its movement. The most effective tool for identifying such a situation is the AIS system, where information about the course and speed is sent by the ship in an open form, which allows for a quick determination that a significant change in its movement has occurred. The ARPA (Automatic Radar Plotting Aids) attachment to the navigation radar is an another device that allows obtaining data on the course and speed of moving objects in the environment, and therefore also on their significant changes. In such a case, the calculations can be repeated, taking into account the new parameters of the other ships’ motion and the new starting position.
An improvement in the case of recalculation could be introduction of another criterion for fitness assessment, taking into account maintaining the initial course and speed of the own ship for a certain period of time. This would allow maintaining a predictable course of movement and would limit maneuvering to the minimum necessary to react to the change in the situation. This approach is consistent with the ideas processed in the IMO within the e-navigation initiative [41] and related proposals for the real-time communication system VHF Data Exchange System (VDES). According to the proposal, one of the VDES mechanisms allows for the broadcasting of parameters of the intended passage route in advance, to allow other participants of maritime traffic to take this information into account in their route planning At the same time, any similar information from other ships would allow for a more precise prediction of their future maneuvers, which would help the algorithm to determine a route that would not have to be modified in the future.
A complete knowledge of the intentions of all users of the water area would enable a significant improvement in safety, and would provide the possibility of a global reduction in energy consumption by all participants. Even partial knowledge of the future routes of several participants in a given navigation situation may allow the route planning algorithm to propose a route that will be subject to at most minor changes.
Finally, the proximity of other ships whose routes are known in advance may, for the reasons mentioned above, be subject to a more lenient assessment due to the criterion of the distance of closest approach.
The proposed method of radar fitness assessment in the evolutionary algorithm is a promising solution to the problem of route planning for autonomous port tugs. In the case of electric-powered ships, it is also possible to introduce additional criteria related to the characteristic features of this drive, i.e., limited energy reserves, variable energy prices available on land, or the impact of the power level demanded from the propulsion system on its durability. For example, choosing a slightly longer route that does not require rapid acceleration will result in lower energy consumption and lower heat losses in the propulsion system battery, which will result in a lower maximum temperature and, to some extent, extend the total operating time of the energy storage.
Supposing that as a result of the work of the evolutionary algorithm in a specific navigation situation, several equivalent solutions would appear, criteria such as those mentioned above could decide to the benefit of the shipowner, allowing the implementation of tasks in a way that would lower operational costs (OPEX).
The main advantages of the described method are:
- Generating routes requiring fewer, and less aggressive maneuvers,
- Increased safety margin with respect to obstacles, and
- Maintaining the optimal route length.
Further work may focus on the following issues:
- Testing the algorithm in real conditions,
- Optimization of the radar method parameters,
- Consideration of additional criteria related to energy consumption, and
- Integration with other vessels’ motion prediction systems, and with communication systems proposed within the e-navigation strategy [41] developed within the International Maritime Organization.
Author Contributions
Conceptualization, W.K. and A.Ł.; methodology, W.K. and A.Ł.; software, W.K. and A.Ł.; writing—original draft preparation, W.K. and A.Ł.; writing—review and editing, W.K. and A.Ł.; supervision, A.Ł. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the research project No. WE/2025/PZ/08, Electrical Engineering Faculty, Gdynia Maritime University, Poland.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Przybylowski, A.; Suchanek, M.; Miszewski, P. COVID-19 Pandemic Impact on a Global Liner Shipping Company Employee Work Digitalization. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2022, 16, 759–765. [Google Scholar] [CrossRef]
- Abramowicz-Gerigk, T.; Burciu, Z.; Gerigk, M.K.; Jachowski, J. Monitoring of Ship Operations in Seaport Areas in the Sustainable Development of Ocean–Land Connections. Sustainability 2024, 16, 597. [Google Scholar] [CrossRef]
- MUC, A.; Iwaszkiewicz, J.; Piechowski, L. Single-phase Cascade Inverter Controlled by Signals Calculated on the Basis of the Haar Wavelet. Electrotech. Rev. 2023, 1, 232–235. [Google Scholar] [CrossRef]
- CZECH, P. Autonomous vehicles: Basic issues. Sci. J. Silesian Univ. Technol. Ser. Transp. 2018, 100, 15–22. [Google Scholar] [CrossRef]
- Niu, H.; Lu, Y.; Savvaris, A.; Tsourdos, A. Efficient Path Planning Algorithms for Unmanned Surface Vehicle. IFAC-PapersOnLine 2016, 49, 121–126. [Google Scholar] [CrossRef]
- Zaccone, R.; Martelli, M.; Figari, M. A COLREG-Compliant Ship Collision Avoidance Algorithm. In Proceedings of the IEEE European Control Conference-ECC2019, Naples, Italy, 25–28 June 2019; pp. 2530–2535. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, D.; Gu, J.; Li, F. A Path-Planning Strategy for Unmanned Surface Vehicles Based on an Adaptive Hybrid Dynamic Stepsize and Target Attractive Force-RRT Algorithm. J. Mar. Sci. Eng. 2019, 7, 132. [Google Scholar] [CrossRef]
- Cao, S.; Fan, P.; Yan, T.; Xie, C.; Deng, J.; Xu, F.; Shu, Y. Inland Waterway Ship Path Planning Based on Improved RRT Algorithm. J. Mar. Sci. Eng. 2022, 10, 1460. [Google Scholar] [CrossRef]
- Yu, J.; Chen, Z.; Zhao, Z.; Yao, P.; Xu, J. A traversal multi-target path planning method for multi-unmanned surface vessels in space-varying ocean current. Ocean. Eng. 2023, 278, 114423. [Google Scholar] [CrossRef]
- Mousazadeh, H.; Jafarbiglu, H.; Abdolmaleki, H.; Omrani, E.; Monhaseri, F.; Abdollahzadeh, M.-r.; Mohammadi-Aghdam, A.; Kiapei, A.; Salmani-Zakaria, Y.; Makhsoos, A. Developing a navigation, guidance and obstacle avoidance algorithm for an Unmanned Surface Vehicle (USV) by algorithms fusion. Ocean. Eng. 2018, 159, 56–65. [Google Scholar] [CrossRef]
- Wang, H.; Ban, X. Research on Autonomous Collision Avoidance Method of Unmanned Surface Vessel in the Circumstance of Moving Obstacles. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 501–506, ISBN 978-988-15639-5-8. [Google Scholar]
- Iswanto, I.; Ma’arif, A.; Wahyunggoro, O.; Imam, A. Artificial Potential Field Algorithm Implementation for Quadrotor Path Planning. Int. J. Adv. Comput. Sci. Appl. 2019, 10, 575–585. [Google Scholar] [CrossRef]
- Park, M.G.; Lee, M.C. A new technique to escape local minimum in artificial potential field based path planning. KSME Int. J. 2003, 17, 1876–1885. [Google Scholar] [CrossRef]
- MUC, A.; Kasprowicz, A.; Bielecka, A.; Mysiak, P.; Iwaszkiewicz, J. The influence of the reference potential on the operation of the pulse formation system of a 12-pulse controlled rectifier. Electrotech. Rev. 2024, 1, 234–237. [Google Scholar] [CrossRef]
- Lyu, H.; Yin, Y. COLREGS-Constrained Real-time Path Planning for Autonomous Ships Using Modified Artificial Potential Fields. J. Navig. 2019, 72, 588–608. [Google Scholar] [CrossRef]
- Xinchi, T.; Huajun, Z.; Wenwen, C.; Peimin, Z.; Zhiwen, L.; Kai, C. A Research on Intelligent Obstacle Avoidance for Unmanned Surface Vehicles. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, November 30–2 December 2018; pp. 1431–1435. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, T.; Wang, D. Path Planning Algorithm of Unmanned Ship Based on Improved Ant Colony. In Proceedings of the 2023 4th International Conference on Computers and Artificial Intelligence Technology (CAIT), Macau, Macao, 13–15 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 193–199, ISBN 979-8-3503-2671-0. [Google Scholar]
- Jialin, L.I.; Jianqiang, Z. Global path planning of unmanned boat based on improved ant colony algorithm. In Proceedings of the 2021 4th International Conference on Electron Device and Mechanical Engineering (ICEDME), Guangzhou, China, 19–21 March 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 176–179, ISBN 978-1-6654-3596-3. [Google Scholar]
- Kim, H.; Kim, S.-H.; Jeon, M.; Kim, J.; Song, S.; Paik, K.-J. A study on path optimization method of an unmanned surface vehicle under environmental loads using genetic algorithm. Ocean. Eng. 2017, 142, 616–624. [Google Scholar] [CrossRef]
- Xin, J.; Zhong, J.; Yang, F.; Cui, Y.; Sheng, J. An Improved Genetic Algorithm for Path-Planning of Unmanned Surface Vehicle. Sensors 2019, 19, 2640. [Google Scholar] [CrossRef]
- Fiskin, R.; Atik, O.; Kisi, H.; Nasibov, E.; Johansen, T.A. Fuzzy domain and meta-heuristic algorithm-based collision avoidance control for ships: Experimental validation in virtual and real environment. Ocean. Eng. 2021, 220, 108502. [Google Scholar] [CrossRef]
- Arzamendia, M.; Gregor, D.; Reina, D.G.; Toral, S.L. An evolutionary approach to constrained path planning of an autonomous surface vehicle for maximizing the covered area of Ypacarai Lake. Soft Comput. 2019, 23, 1723–1734. [Google Scholar] [CrossRef]
- Seghir, M.M. Safe Ship’s Control in a Fuzzy Environment Using a Genetic Algorithm. Solid State Phenom. 2011, 180, 70–75. [Google Scholar] [CrossRef]
- Praczyk, T. Neural anti-collision system for Autonomous Surface Vehicle. Neurocomputing 2015, 149, 559–572. [Google Scholar] [CrossRef]
- Wang, R.; Li, D.; Miao, K. Optimized Radial Basis Function Neural Network Based Intelligent Control Algorithm of Unmanned Surface Vehicles. J. Mar. Sci. Eng. 2020, 8, 210. [Google Scholar] [CrossRef]
- Sorial, M.; Mouawad, I.; Simetti, E.; Odone, F.; Casalino, G. Towards a Real Time Obstacle Detection System for Unmanned Surface Vehicles. In Proceedings of the OCEANS 2019 MTS/IEEE SEATTLE, Seattle, WA, USA, 27–31 October 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Wang, R.; Miao, K.; Li, Q.; Sun, J.; Deng, H. The path planning of collision avoidance for an unmanned ship navigating in waterways based on an artificial neural network. Nonlinear Eng. 2022, 11, 680–692. [Google Scholar] [CrossRef]
- Naeem, W.; Irwin, G.W.; Yang, A. COLREGs-based collision avoidance strategies for unmanned surface vehicles. Mechatronics 2012, 22, 669–678. [Google Scholar] [CrossRef]
- Casalino, G.; Turetta, A.; Simetti, E. A three-layered architecture for real time path planning and obstacle avoidance for surveillance USVs operating in harbour fields. In Proceedings of the OCEANS 2009-EUROPE, Bremen, Germany, 11–14 May 2009; pp. 1–8. [Google Scholar] [CrossRef]
- Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D.; Khan, A. A constrained A* approach towards optimal path planning for an unmanned surface vehicle in a maritime environment containing dynamic obstacles and ocean currents. Ocean. Eng. 2018, 169, 187–201. [Google Scholar] [CrossRef]
- Neumann, T. Vessels Route Planning Problem with Uncertain Data. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2016, 10, 459–464. [Google Scholar] [CrossRef]
- Zhao, L.; Szakas, T.; Churley, M.; Lucas, D. Multi-class multi-residue analysis of pesticides in edible oils by gas chromatography-tandem mass spectrometry using liquid-liquid extraction and enhanced matrix removal lipid cartridge cleanup. J. Chromatogr. A 2019, 1584, 1–12. [Google Scholar] [CrossRef]
- Perera, L.P. Deep Learning Toward Autonomous Ship Navigation and Possible COLREGs Failures. J. Offshore Mech. Arct. Eng. 2020, 142, 2256. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, X.; Zheng, Y.; Du, A.Y. An Autonomous Path Planning Model for Unmanned Ships Based on Deep Reinforcement Learning. Sensors 2020, 20, 426. [Google Scholar] [CrossRef]
- Chen, C.; Chen, X.-Q.; Ma, F.; Zeng, X.-J.; Wang, J. A knowledge-free path planning approach for smart ships based on reinforcement learning. Ocean. Eng. 2019, 189, 106299. [Google Scholar] [CrossRef]
- Li, L.; Wu, D.; Huang, Y.; Yuan, Z.-M. A path planning strategy unified with a COLREGS collision avoidance function based on deep reinforcement learning and artificial potential field. Appl. Ocean. Res. 2021, 113, 102759. [Google Scholar] [CrossRef]
- Ai, B.; Jia, M.; Xu, H.; Xu, J.; Wen, Z.; Li, B.; Zhang, D. Coverage path planning for maritime search and rescue using reinforcement learning. Ocean. Eng. 2021, 241, 110098. [Google Scholar] [CrossRef]
- Liu, Y.; Bucknall, R.; Zhang, X. The fast marching method based intelligent navigation of an unmanned surface vehicle. Ocean. Eng. 2017, 142, 363–376. [Google Scholar] [CrossRef]
- Gao, M.; Shi, G.-Y. Ship-Collision Avoidance Decision-Making Learning of Unmanned Surface Vehicles with Automatic Identification System Data Based on Encoder—Decoder Automatic-Response Neural Networks. J. Mar. Sci. Eng. 2020, 8, 754. [Google Scholar] [CrossRef]
- International Maritime Organization. Convention on the International Regulations for Preventing Collisions at Sea; International Maritime Organization: London, UK, 1972. [Google Scholar]
- International Maritime Organization. E-Navigation. Available online: https://www.imo.org/en/OurWork/Safety/Pages/eNavigation.aspx (accessed on 19 November 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).