Torque/Speed Equilibrium Point Monitoring of an Aircraft Hybrid Electric Propulsion System Through Accelerometric Signal Processing
Abstract
:1. Introduction
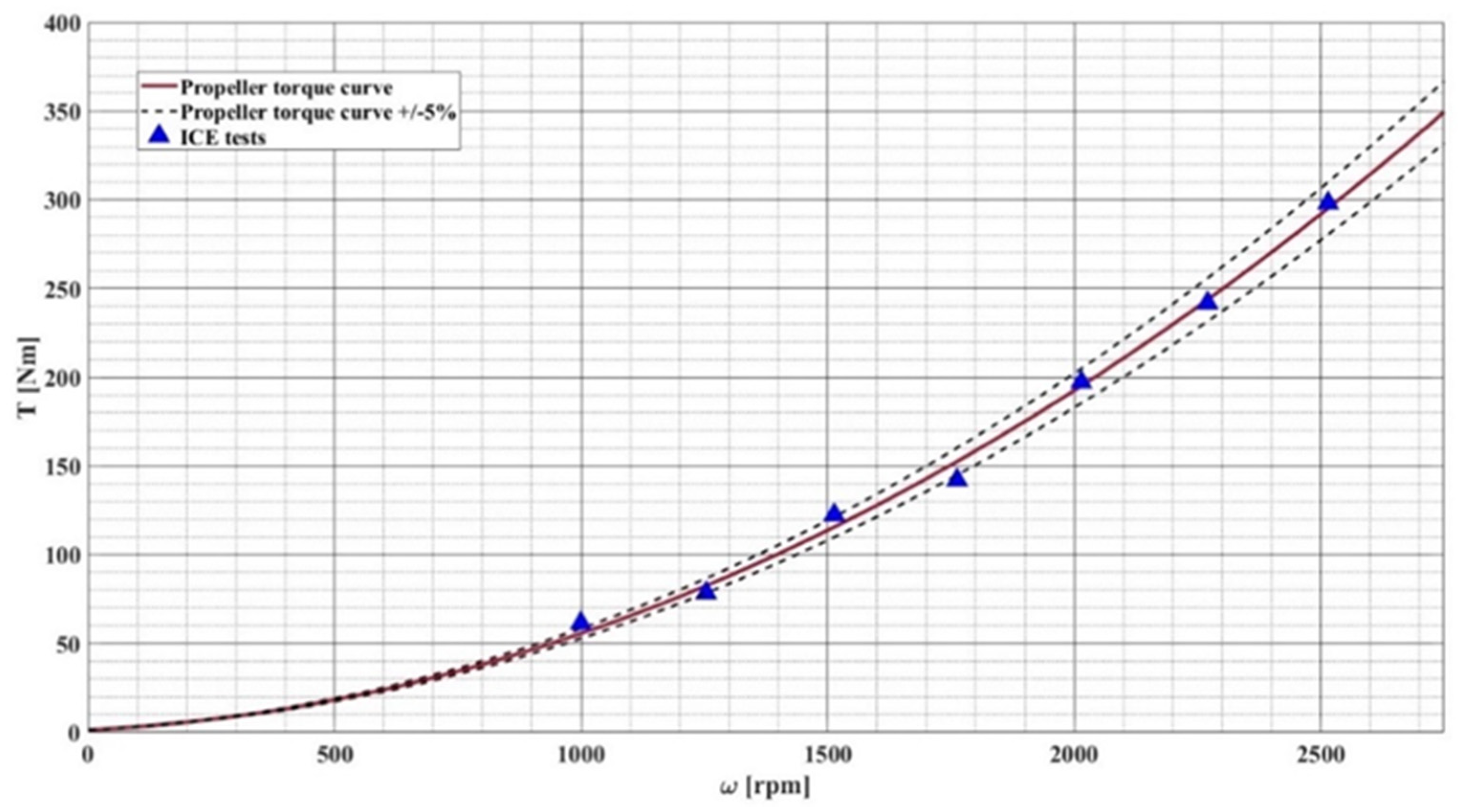
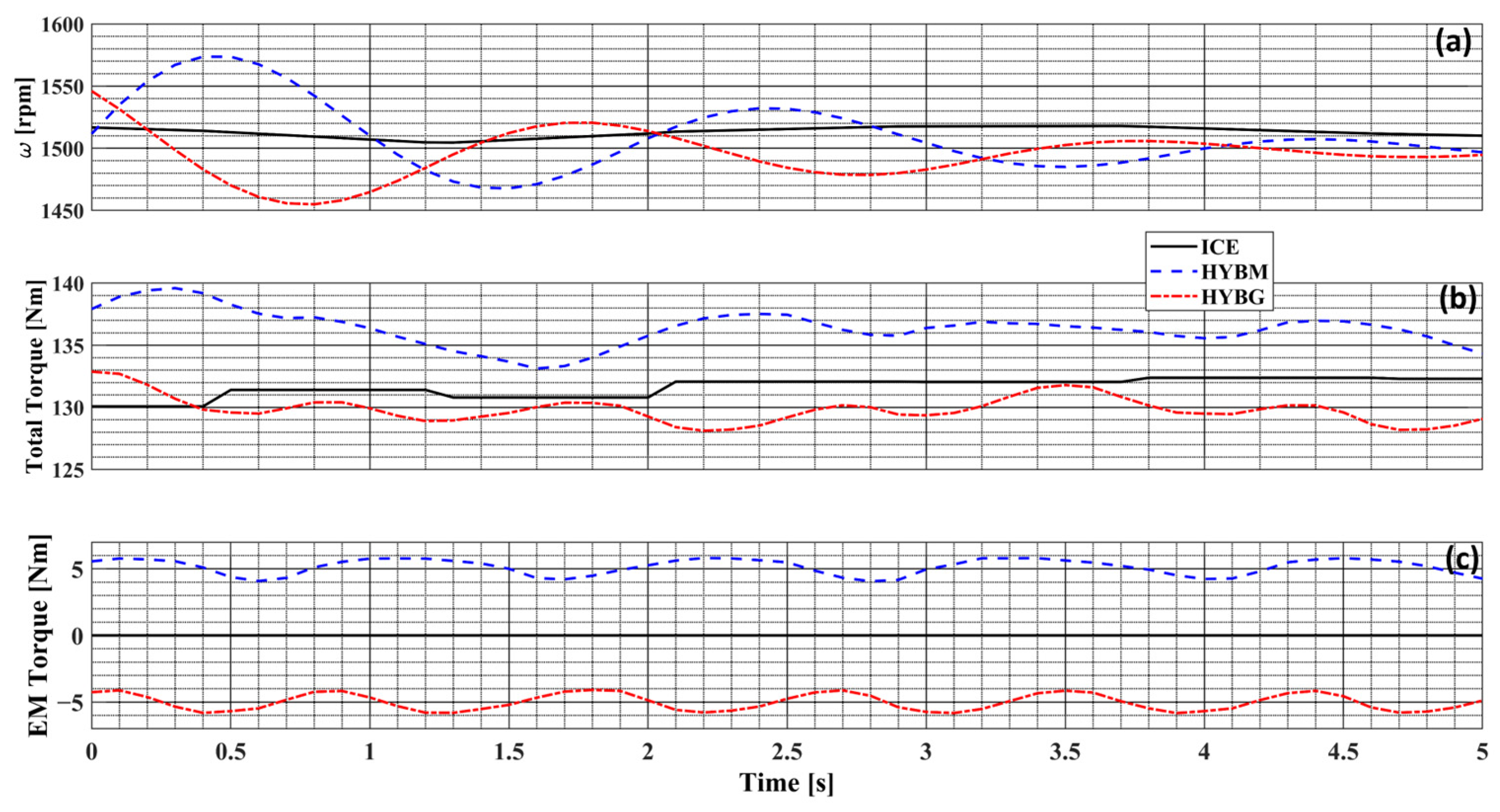
2. HEPS Architecture and Testing Protocol
- ICE: only the ICE contributes to balancing the propeller resistance torque ( and );
- HYBM: the EM operates as a motor, contributing to balancing the propeller resistance torque ( and );
- HYBG: the EM operates as a generator to recharge the batteries, and the ICE must balance both the propeller and the EM torque ( e )
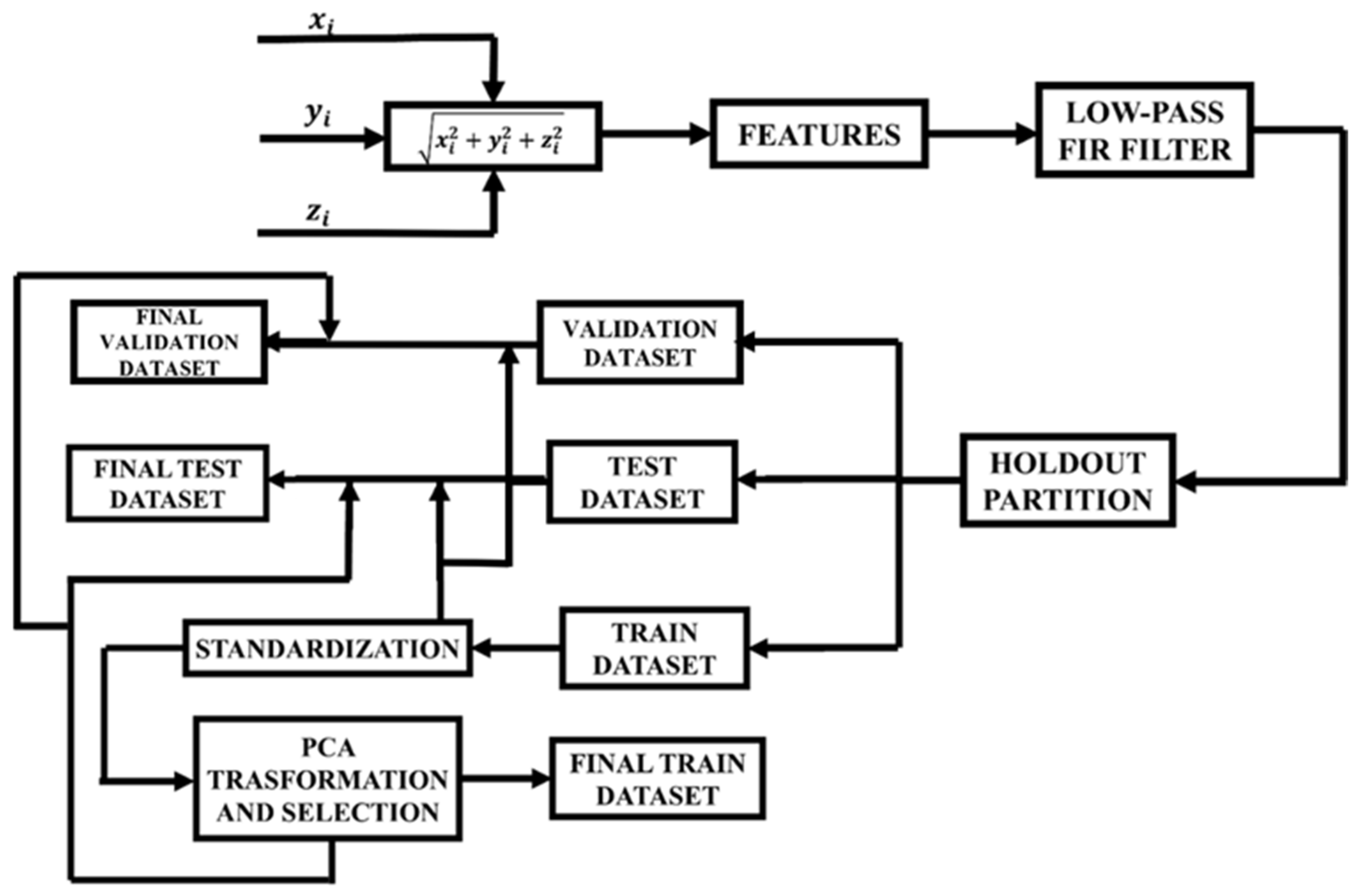
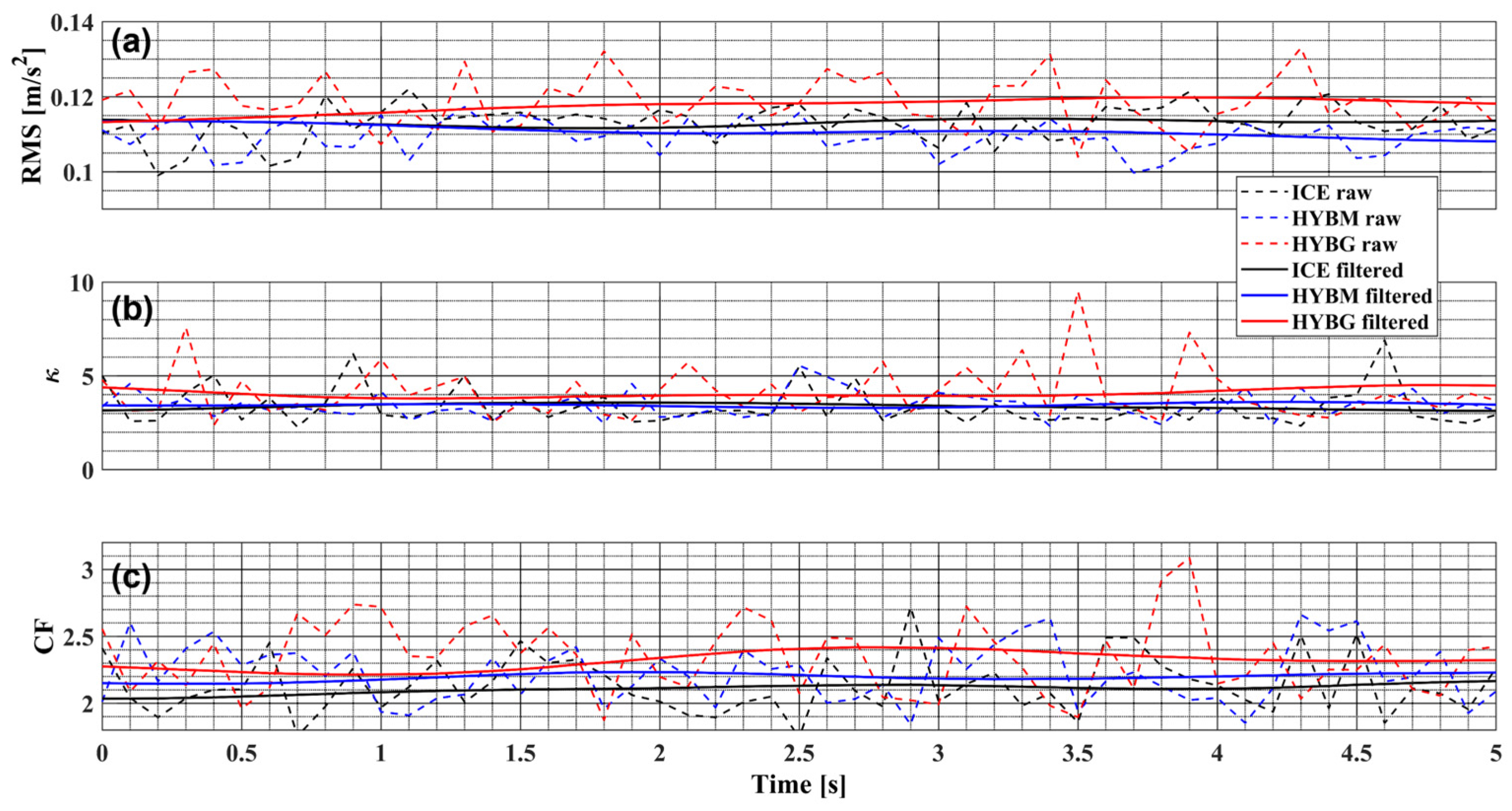
3. Vibration-Based Monitoring Technique: Development Steps
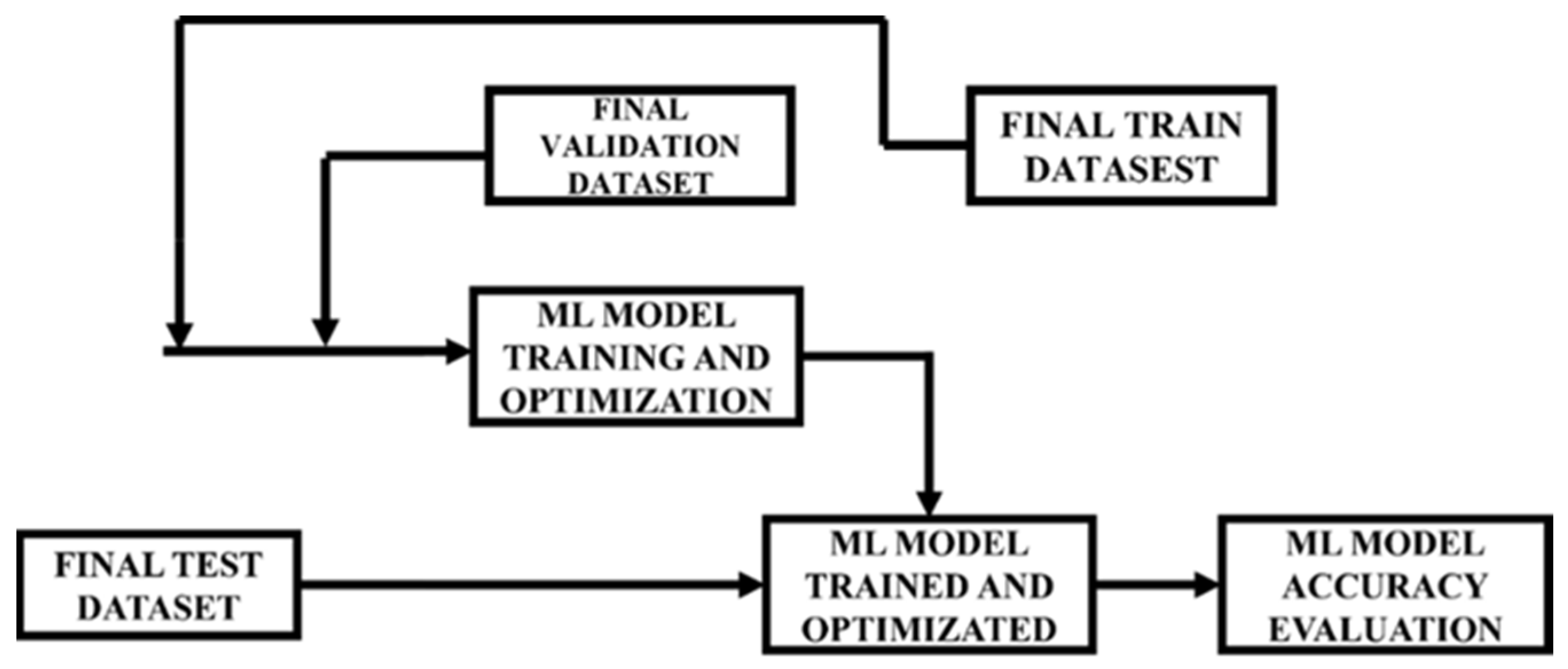
4. Feedforward Neural Network and RMS
- An input layer with a number of neurons equal to the number of inputs;
- An output layer with a number of neurons equal to the number of outputs;
- A few hidden layers and corresponding nodes defined through a hyperparameter optimization process.
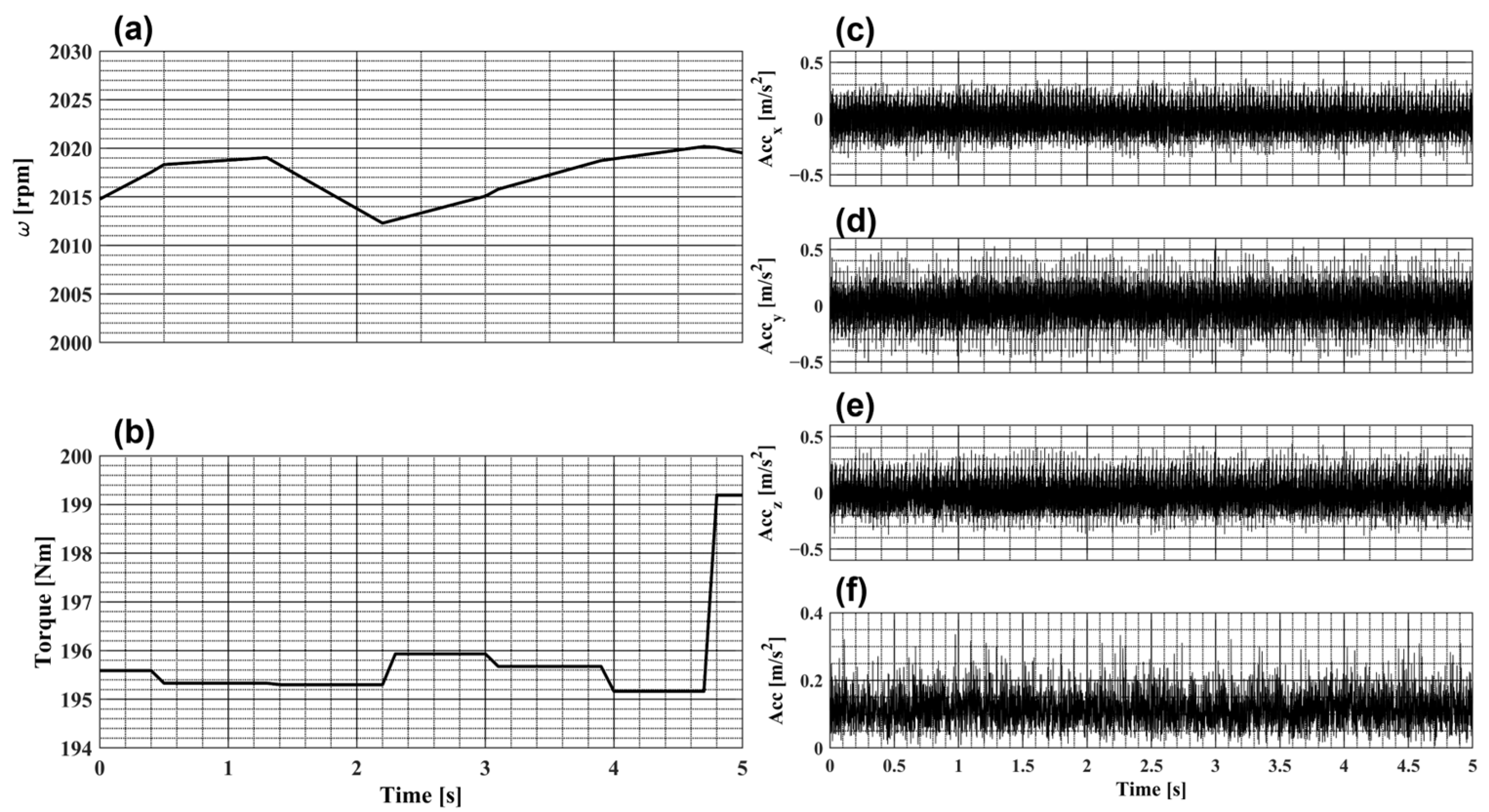
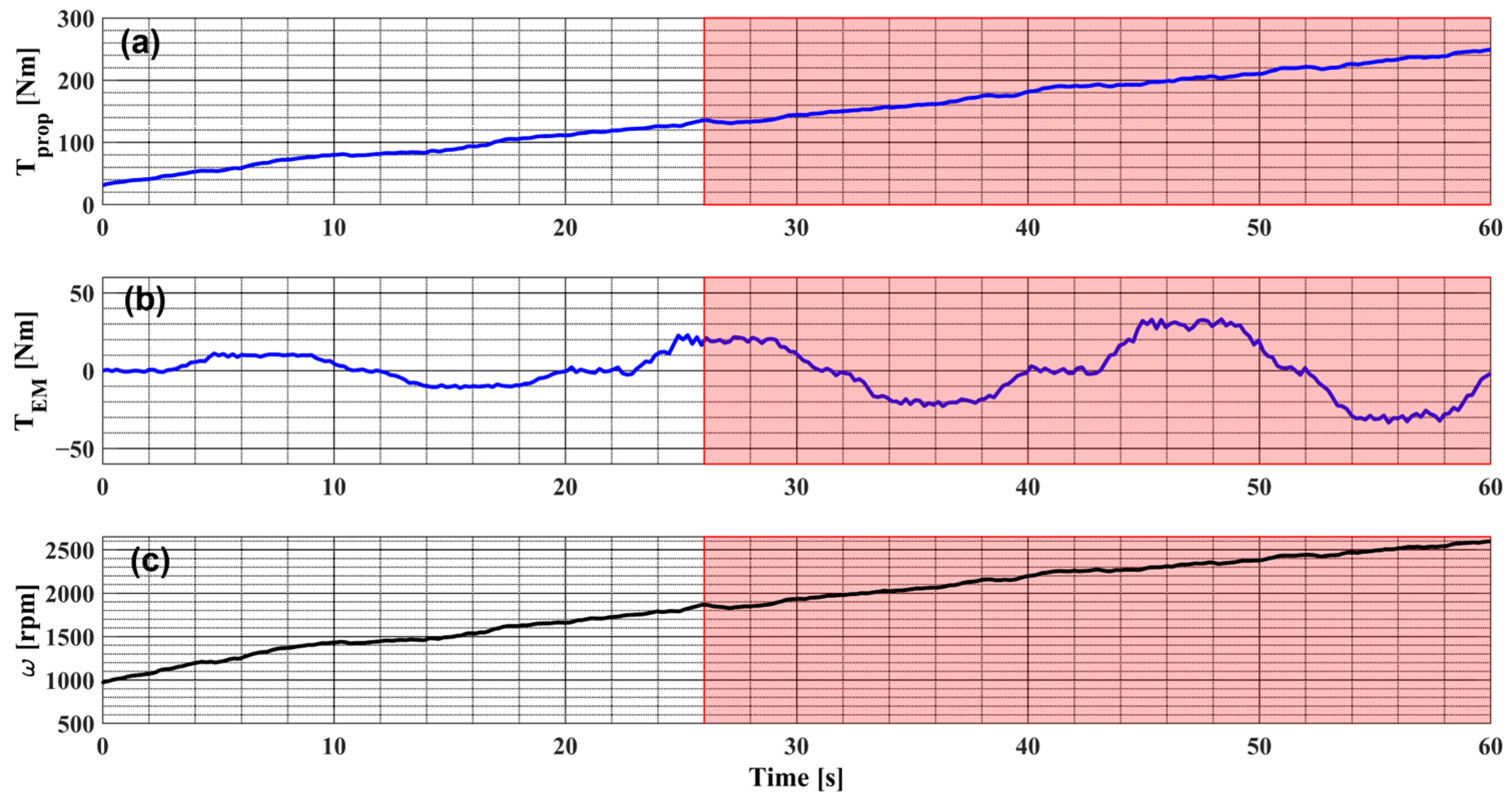
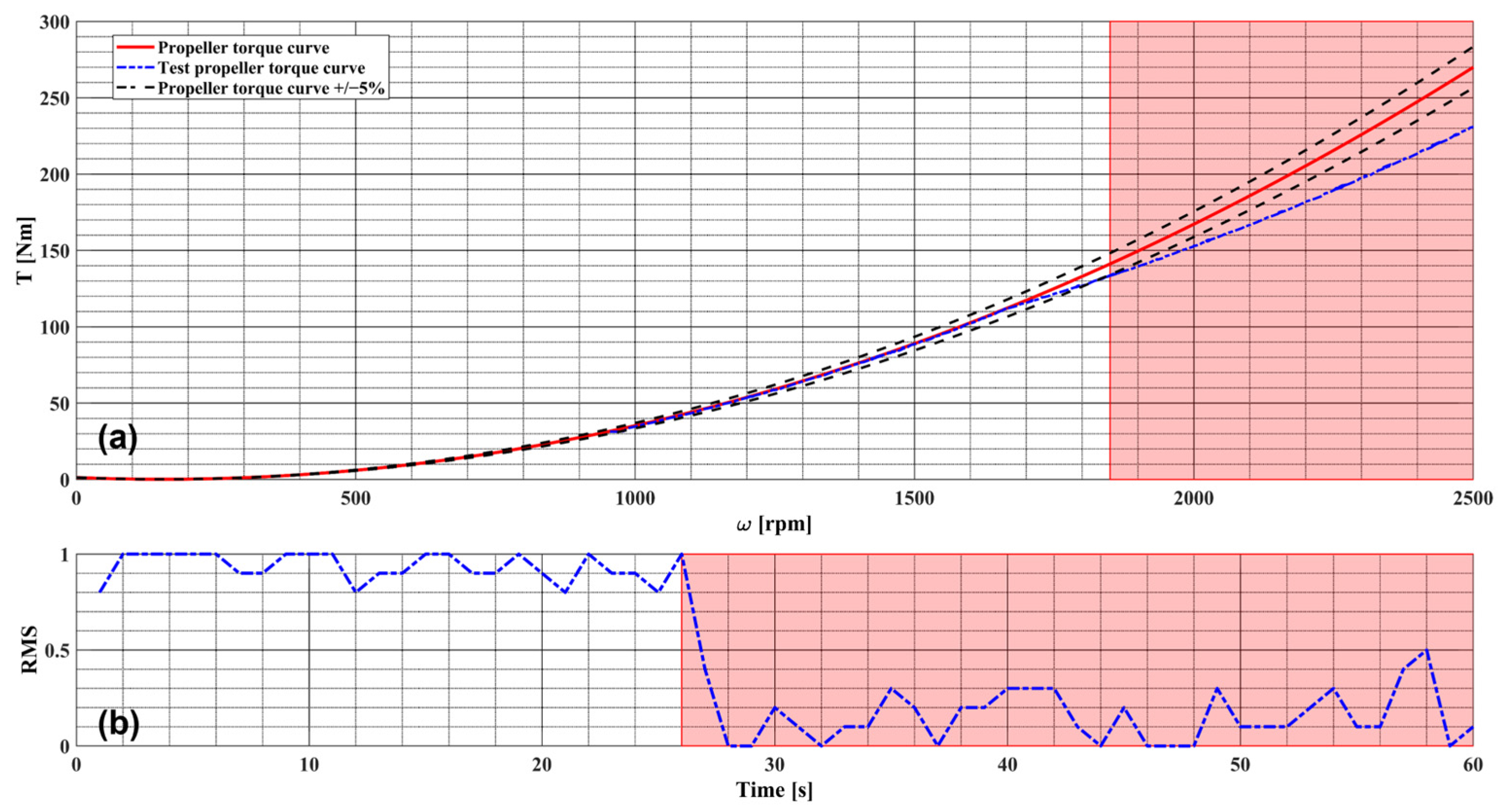
5. Results and Discussion
- When the propeller torque curve was inside the ±5% limits (range 0–25 s), the RMS trend was toward 1 with a mean of 0.94;
- When the propeller torque curve was outside the ±5% limits (range 26–60 s), the RMS value was toward 0 with a mean of 0.29.
6. Conclusions
- The equilibrium point position was inside the ±5% limits of the propeller torque curve;
- The equilibrium point position was outside the ±5% limits of the propeller torque curve.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tiboni, M.; Remino, C.; Bussola, R.; Amici, C. A review on vibration-based condition monitoring of rotating machinery. Appl. Sci. 2022, 12, 972. [Google Scholar] [CrossRef]
- Aherwar, A. An investigation on gearbox fault detection using vibration analysis techniques: A review. Aust. J. Mech. Eng. 2012, 10, 169–183. [Google Scholar] [CrossRef]
- Kirankumar, M.V.; Lokesha, M.; Kumar, S.; Kumar, A. Review on Condition Monitoring of Bearings using vibration analysis techniques. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 376, p. 012110. [Google Scholar]
- Mohd Ghazali, M.H.; Rahiman, W. Vibration analysis for machine monitoring and diagnosis: A systematic review. Shock Vib. 2021, 2021, 9469318. [Google Scholar] [CrossRef]
- Bianchini, A.; Rossi, J.; Antipodi, L. A procedure for condition-based maintenance and diagnostics of submersible well pumps through vibration monitoring. Int. J. Syst. Assur. Eng. Manag. 2018, 9, 999–1013. [Google Scholar] [CrossRef]
- Niola, V.; Savino, S.; Quaremba, G.; Cosenza, C.; Spirto, M.; Nicolella, A. Study on the dispersion of lubricant film from a cylindrical gearwheels with helical teeth by vibrational analysis. WSEAS Trans. Appl. Theor. Mech. 2021, 16, 274–282. [Google Scholar] [CrossRef]
- Cosenza, C.; Malfi, P.; Nicolella, A.; Niola, V.; Savino, S.; Spirto, M. Experimental approach to study the tribological state of gearwheel through vision devices. Int. J. Mech. Control 2023, 24, 61–68. [Google Scholar]
- McFadden, P.D.; Toozhy, M.M. Application of synchronous averaging to vibration monitoring of rolling element bearings. Mech. Syst. Signal Process. 2000, 14, 891–906. [Google Scholar] [CrossRef]
- Hu, C.; Smith, W.A.; Randall, R.B.; Peng, Z. Development of a gear vibration indicator and its application in gear wear monitoring. Mech. Syst. Signal Process. 2016, 76, 319–336. [Google Scholar] [CrossRef]
- De Azevedo, H.D.; de Arruda Filho, P.H.; Araújo, A.M.; Bouchonneau, N.; Rohatgi, J.S.; De Souza, R.M. Vibration monitoring, fault detection, and bearings replacement of a real wind turbine. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 3837–3848. [Google Scholar] [CrossRef]
- Ni, Q.; Ji, J.C.; Feng, K.; Halkon, B. A novel correntropy-based band selection method for the fault diagnosis of bearings under fault-irrelevant impulsive and cyclostationary interferences. Mech. Syst. Signal Process. 2021, 153, 107498. [Google Scholar] [CrossRef]
- Niola, V.; Quaremba, G.; Avagliano, V. Vibration monitoring of gear transmission. In WSEAS International Conference. Proceedings. Mathematics and Computers in Science and Engineering (No. 5); WSEAS: Athens, Greece, 2009. [Google Scholar]
- Bartelmus, W.; Zimroz, R. Vibration condition monitoring of planetary gearbox under varying external load. Mech. Syst. Signal Process. 2009, 23, 246–257. [Google Scholar] [CrossRef]
- Niola, V.; Quaremba, G. The Gear Whine Noise: The influence of manufacturing process on vibro-acoustic emission of gear-box. In Proceedings of the 10th WSEAS International Conference, Recent Researches in Communications, Automation, Signal Processing, Nanotechnology, Astronomy and Nuclear Physics, Athens, Greece, 20 February 2011. [Google Scholar]
- Romagnuolo, L.; Frosina, E.; Amoresano, A.; Quaremba, G.; Spirto, M.; Senatore, A. Instability measurement of cavitation conditions in a spool valve through the definition of a cavitation instability index. Flow Meas. Instrum. 2023, 91, 102366. [Google Scholar] [CrossRef]
- Casoli, P.; Pastori, M.; Scolari, F.; Rundo, M. A vibration signal-based method for fault identification and classification in hydraulic axial piston pumps. Energies 2019, 12, 953. [Google Scholar] [CrossRef]
- Saxena, A.; Saad, A. Evolving an artificial neural network classifier for condition monitoring of rotating mechanical systems. Appl. Soft Comput. 2007, 7, 441–454. [Google Scholar] [CrossRef]
- Praveenkumar, T.; Sabhrish, B.; Saimurugan, M.; Ramachandran, K.I. Pattern recognition based on-line vibration monitoring system for fault diagnosis of automobile gearbox. Measurement 2018, 114, 233–242. [Google Scholar] [CrossRef]
- Wang, W.; Ismail, F.; Golnaraghi, F. A neuro-fuzzy approach to gear system monitoring. IEEE Trans. Fuzzy Syst. 2004, 12, 710–723. [Google Scholar] [CrossRef]
- Wang, W. An enhanced diagnostic system for gear system monitoring. IEEE Trans. Syst. Man Cybern. Part B 2008, 38, 102–112. [Google Scholar] [CrossRef]
- Zhang, M.; Cui, H.; Li, Q.; Liu, J.; Wang, K.; Wang, Y. An improved sideband energy ratio for fault diagnosis of planetary gearboxes. J. Sound Vib. 2021, 491, 115712. [Google Scholar] [CrossRef]
- Zhan, Y.; Makis, V. A robust diagnostic model for gearboxes subject to vibration monitoring. J. Sound Vib. 2006, 290, 928–955. [Google Scholar] [CrossRef]
- Shao, Y.; Mechefske, C.K. Gearbox vibration monitoring using extended Kalman filters and hypothesis tests. J. Sound Vib. 2009, 325, 629–648. [Google Scholar] [CrossRef]
- Siano, D.; Panza, M.A. Diagnostic method by using vibration analysis for pump fault detection. Energy Procedia 2018, 148, 10–17. [Google Scholar] [CrossRef]
- Feng, K.; Ji, J.C.; Ni, Q.; Beer, M. A review of vibration-based gear wear monitoring and prediction techniques. Mech. Syst. Signal Process. 2023, 182, 109605. [Google Scholar] [CrossRef]
- Tang, Z.; Guo, J.; Wang, Y.; Xu, W.; Bao, Y.; He, J.; Zhang, Y. Automated seismic event detection considering faulty data interference using deep learning and Bayesian fusion. Comput. Aided Civ. Infrastruct. Eng. 2024. Available online: https://onlinelibrary.wiley.com/doi/full/10.1111/mice.13377 (accessed on 26 December 2024).
- Wang, H.; Xu, J.; Sun, C.; Yan, R.; Chen, X. Intelligent fault diagnosis for planetary gearbox using time-frequency representation and deep reinforcement learning. IEEE/ASME Trans. Mechatron. 2021, 27, 985–998. [Google Scholar] [CrossRef]
- Li, Z.; Yan, X.; Wang, X.; Peng, Z. Detection of gear cracks in a complex gearbox of wind turbines using supervised bounded component analysis of vibration signals collected from multi-channel sensors. J. Sound Vib. 2016, 371, 406–433. [Google Scholar] [CrossRef]
- Feng, K.; Smith, W.A.; Randall, R.B.; Wu, H.; Peng, Z. Vibration-based monitoring and prediction of surface profile change and pitting density in a spur gear wear process. Mech. Syst. Signal Process. 2022, 165, 108319. [Google Scholar] [CrossRef]
- Laissaoui, A.; Bouzouane, B.; Miloudi, A.; Hamzaoui, N. Perceptive analysis of bearing defects (Contribution to vibration monitoring). Appl. Acoust. 2018, 140, 248–255. [Google Scholar] [CrossRef]
- Loutas, T.H.; Sotiriades, G.; Kalaitzoglou, I.; Kostopoulos, V. Condition monitoring of a single-stage gearbox with artificially induced gear cracks utilizing on-line vibration and acoustic emission measurements. Appl. Acoust. 2009, 70, 1148–1159. [Google Scholar] [CrossRef]
- Delvecchio, S.; Bonfiglio, P.; Pompoli, F. Vibro-acoustic condition monitoring of Internal Combustion Engines: A critical review of existing techniques. Mech. Syst. Signal Process. 2018, 99, 661–683. [Google Scholar] [CrossRef]
- Kar, C.; Mohanty, A.R. Monitoring gear vibrations through motor current signature analysis and wavelet transform. Mech. Syst. Signal Process. 2006, 20, 158–187. [Google Scholar] [CrossRef]
- Kar, C.; Mohanty, A.R. Vibration and current transient monitoring for gearbox fault detection using multiresolution Fourier transform. J. Sound Vib. 2008, 311, 109–132. [Google Scholar] [CrossRef]
- Amoresano, A.; Niola, V.; Quaremba, A. A sensitive methodology for the EGR optimization: A perspective study. Int. Rev. Mech. Eng. 2012, 6, 1082–1088. [Google Scholar]
- Zhang, L.; Lin, Y.; Yang, X.; Chen, T.; Cheng, X.; Cheng, W. From sample poverty to rich feature learning: A new metric learning method for few-shot classification. IEEE Access 2024, 12, 124990–125002. [Google Scholar] [CrossRef]
- Niola, V.; Rossi, C. Video acquisition of a robot arm trajectories in the work space. WSEAS Trans. Comput. 2005, 4, 830–836. [Google Scholar]
- Niola, V.; Rossi, C.; Savino, S.; Troncone, S. An underactuated mechanical hand: A first prototype. In Proceedings of the 2014 23rd International Conference on Robotics in Alpe-Adria-Danube Region (RAAD), Smolenice, Slovakia, 3–5 September 2014; pp. 1–6. [Google Scholar]
- Malfi, P.; Nicolella, A.; Spirto, M.; Cosenza, C.; Niola, V.; Savino, S. Motion sensing study on a mobile robot through simulation model and experimental tests. WSEAS Trans. Appl. Theor. Mech. 2022, 17, 79–85. [Google Scholar] [CrossRef]
- Penta, F.; Rossi, C.; Savino, S. An underactuated finger for a robotic hand. Int. J. Mech. Control 2014, 15, 63–68. [Google Scholar]
- Ma, S.; Wang, S.; Zhang, C.; Zhang, S. A method to improve the efficiency of an electric aircraft propulsion system. Energy 2017, 140, 436–443. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, S.; Ma, S. An energy efficiency optimization method for fixed pitch propeller electric aircraft propulsion systems. IEEE Access 2019, 7, 159986–159993. [Google Scholar] [CrossRef]
- Song, Z.; Liu, C. Energy efficient design and implementation of electric machines in air transport propulsion system. Appl. Energy 2022, 322, 119472. [Google Scholar] [CrossRef]
- Epstein, A.H.; O’Flarity, S.M. Considerations for reducing aviation’s CO2 with aircraft electric propulsion. J. Propuls. Power 2019, 35, 572–582. [Google Scholar] [CrossRef]
- Mercer, C.; Haller, W.; Tong, M. Adaptive engine technologies for aviation CO2 emissions reduction. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006; p. 5105. [Google Scholar]
- Kuśmierek, A.; Galiński, C.; Stalewski, W. Review of the hybrid gas-electric aircraft propulsion systems versus alternative systems. Prog. Aerosp. Sci. 2023, 141, 100925. [Google Scholar] [CrossRef]
- Fentaye, A.D.; Zaccaria, V.; Kyprianidis, K. Aircraft engine performance monitoring and diagnostics based on deep convolutional neural networks. Machines 2021, 9, 337. [Google Scholar] [CrossRef]
- Krajček, K.; Nikolić, D.; Domitrović, A. Aircraft performance monitoring from flight data. Teh. Vjesn. 2015, 22, 1337–1344. [Google Scholar]
- Antoni, J.; Griffaton, J.; André, H.; Avendano-Valencia, L.D.; Bonnardot, F.; Cardona-Morales, O.; Castellanos-Dominguez, G.; Daga, A.P.; Leclère, Q.; Vicuña, C.M.; et al. Feedback on the Surveillance 8 challenge: Vibration-based diagnosis of a Safran aircraft engine. Mech. Syst. Signal Process. 2017, 97, 112–144. [Google Scholar] [CrossRef]
- Herzog, J.P.; Hanlin, J.; Wegerich, S.W.; Wilks, A.D. High performance condition monitoring of aircraft engines. In Turbo Expo: Power for Land, Sea, and Air; ASME: New York, NY, USA, 2005; Volume 46997, pp. 127–135. [Google Scholar]
- Ghazi, G.; Gerardin, B.; Gelhaye, M.; Botez, R.M. New adaptive algorithm development for monitoring aircraft performance and improving flight management system predictions. J. Aerosp. Inf. Syst. 2020, 17, 97–112. [Google Scholar] [CrossRef]
- Léonard, O.; Borguet, S.; Dewallef, P. Adaptive estimation algorithm for aircraft engine performance monitoring. J. Propuls. Power 2008, 24, 763–769. [Google Scholar] [CrossRef]
- Bieber, M.; Verhagen, W.J.; Cosson, F.; Santos, B.F. Generic Diagnostic Framework for Anomaly Detection—Application in Satellite and Spacecraft Systems. Aerospace 2023, 10, 673. [Google Scholar] [CrossRef]
- Fornaro, E.; Cardone, M.; Dannier, A. A comparative assessment of hybrid parallel, series, and full-electric propulsion systems for aircraft application. IEEE Access 2022, 10, 28808–28820. [Google Scholar] [CrossRef]
- Fornaro, E.; Cardone, M.; Dannier, A. Hybrid Electric Aircraft Model Based on ECMS Control. In Proceedings of the 2022 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Sorrento, Italy, 22–24 June 2022; pp. 865–870. [Google Scholar]
- Niola, V.; Fornaro, E.; Spirto, M.; Malfi, P.; Melluso, F. A Comparison Between Different Hybrid Electric Propulsion System Configurations by Means of Vibrational Analysis and Fuel Consumption. In Proceedings of the International Conference of IFToMM ITALY; Springer: Cham, Switzerland, 2024; pp. 452–460. [Google Scholar]
- McCormick, B.W. Aerodynamics, Aeronautics, and Flight Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1994. [Google Scholar]
- Neuvo, Y.; Cheng-Yu, D.; Mitra, S. Interpolated finite impulse response filters. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 563–570. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. IJCAI 1995, 14, 1137–1145. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006; Volume 2, pp. 5–43. [Google Scholar]
- Jolliffe, I.T. Principal Component Analysis for Special Types of Data; Springer: New York, NY, USA, 2002; pp. 338–372. [Google Scholar]
- Zeng, L. Prediction and classification with neural network models. Sociol. Methods Res. 1999, 27, 499–524. [Google Scholar] [CrossRef]
- Féraud, R.; Clérot, F. A methodology to explain neural network classification. Neural Netw. 2002, 15, 237–246. [Google Scholar] [CrossRef]
- Joy, T.T.; Rana, S.; Gupta, S.; Venkatesh, S. Batch Bayesian optimization using multi-scale search. Knowl. Based Syst. 2020, 187, 104818. [Google Scholar] [CrossRef]
- Joy, T.T.; Rana, S.; Gupta, S.; Venkatesh, S. Hyperparameter tuning for big data using Bayesian optimisation. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 2574–2579. [Google Scholar]
- Večeř, P.; Kreidl, M.; Šmíd, R. Condition indicators for gearbox condition monitoring systems. Acta Polytech. 2005, 45, 35–43. [Google Scholar] [CrossRef] [PubMed]
- Ram, B.; Mishra, S.K.; Lai, K.K.; Rajković, P. Quantum Limited Memory Broyden Fletcher Goldfarb Shanno Method. In Unconstrained Optimization and Quantum Calculus; Springer Nature: Singapore, 2024; pp. 125–138. [Google Scholar]


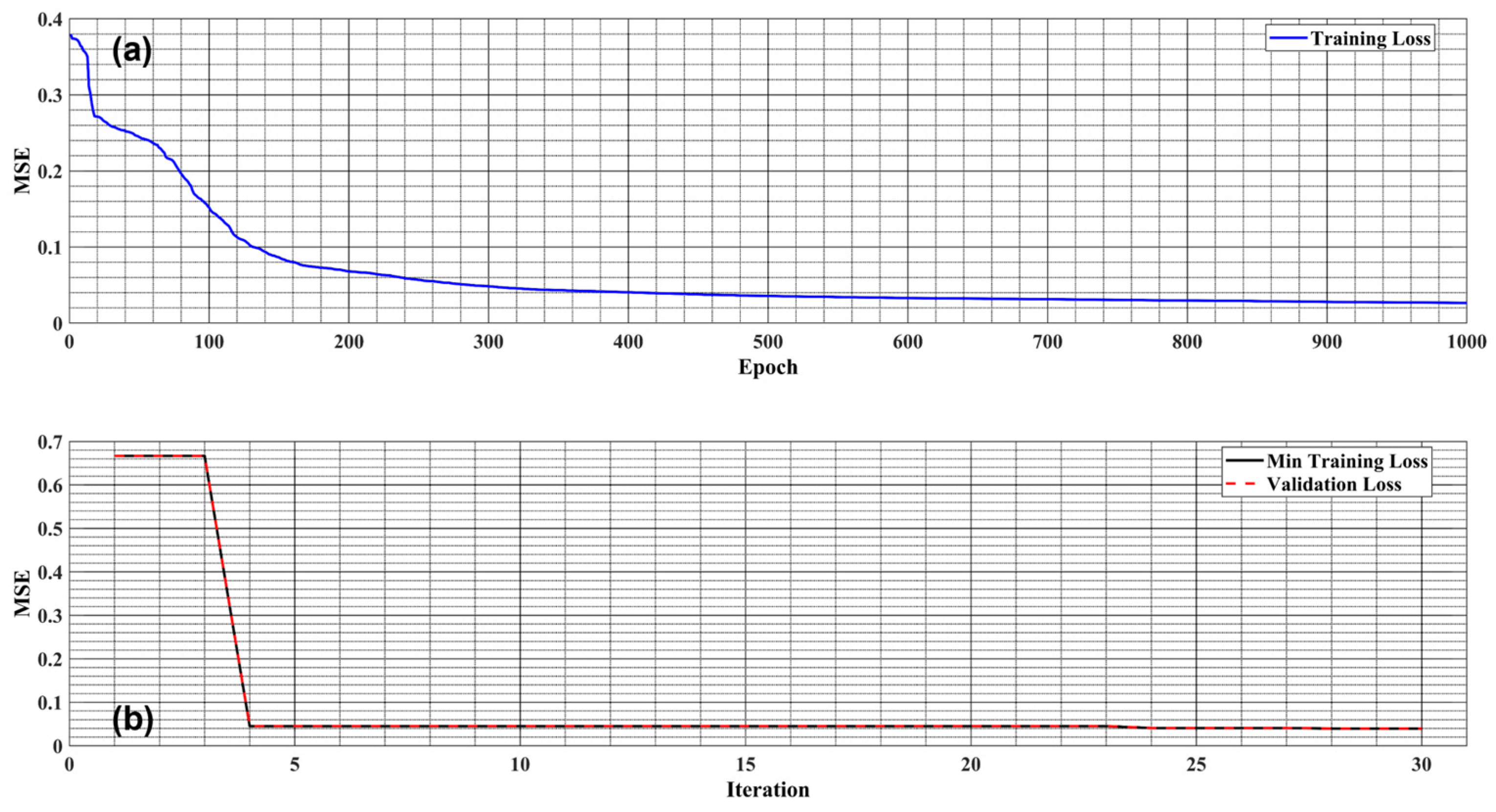

| Hyperparameter | Range | Optimized |
|---|---|---|
| Input Layer Neurons | / | 3 |
| Output Layer Neurons | / | 3 |
| Input Layer Activation Function | / | ReLu |
| Output Layer Activation Function | / | SoftMax |
| Hidden Layer | 3 | |
| First Hidden Layer Neurons | 145 | |
| Second Hidden Layer Neurons | 32 | |
| Third Hidden Layer Neurons | 204 | |
| Hidden Layer Activation Function | ReLu, Tanh, Softmax, Sigmoid | Tanh |
| Regularization Parameter | ||
| FNN Train Epoch | / | 1000 |
| FNN Train Loss Function | / | MSE |
| Batch Size | / | 32 |
| Learning Rate | ||
| Optimization Algorithm | / | Quasi-Newton BFGS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niola, V.; Cosenza, C.; Fornaro, E.; Malfi, P.; Melluso, F.; Nicolella, A.; Savino, S.; Spirto, M. Torque/Speed Equilibrium Point Monitoring of an Aircraft Hybrid Electric Propulsion System Through Accelerometric Signal Processing. Appl. Sci. 2025, 15, 2135. https://doi.org/10.3390/app15042135
Niola V, Cosenza C, Fornaro E, Malfi P, Melluso F, Nicolella A, Savino S, Spirto M. Torque/Speed Equilibrium Point Monitoring of an Aircraft Hybrid Electric Propulsion System Through Accelerometric Signal Processing. Applied Sciences. 2025; 15(4):2135. https://doi.org/10.3390/app15042135
Chicago/Turabian StyleNiola, Vincenzo, Chiara Cosenza, Enrico Fornaro, Pierangelo Malfi, Francesco Melluso, Armando Nicolella, Sergio Savino, and Mario Spirto. 2025. "Torque/Speed Equilibrium Point Monitoring of an Aircraft Hybrid Electric Propulsion System Through Accelerometric Signal Processing" Applied Sciences 15, no. 4: 2135. https://doi.org/10.3390/app15042135
APA StyleNiola, V., Cosenza, C., Fornaro, E., Malfi, P., Melluso, F., Nicolella, A., Savino, S., & Spirto, M. (2025). Torque/Speed Equilibrium Point Monitoring of an Aircraft Hybrid Electric Propulsion System Through Accelerometric Signal Processing. Applied Sciences, 15(4), 2135. https://doi.org/10.3390/app15042135








