Research on the Time Series Prediction of Acoustic Emission Parameters Based on the Factor Analysis–Particle Swarm Optimization Back Propagation Model
Abstract
1. Introduction
2. Materials and Methods
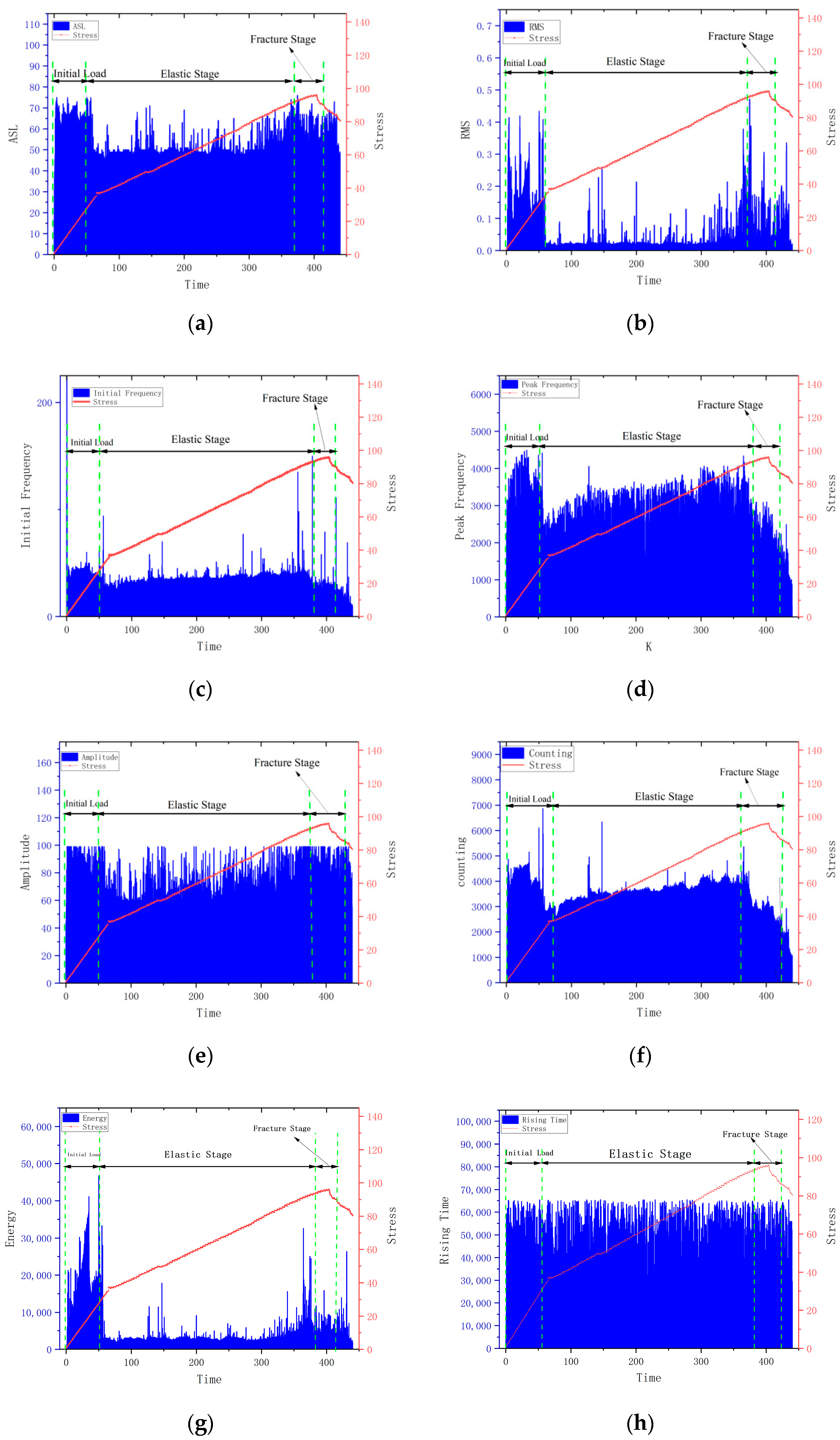
2.1. Determination of Acoustic Emission Parameters
2.2. Data Preprocessing
2.2.1. Adaptability Analysis
2.2.2. Extraction of Common Factors
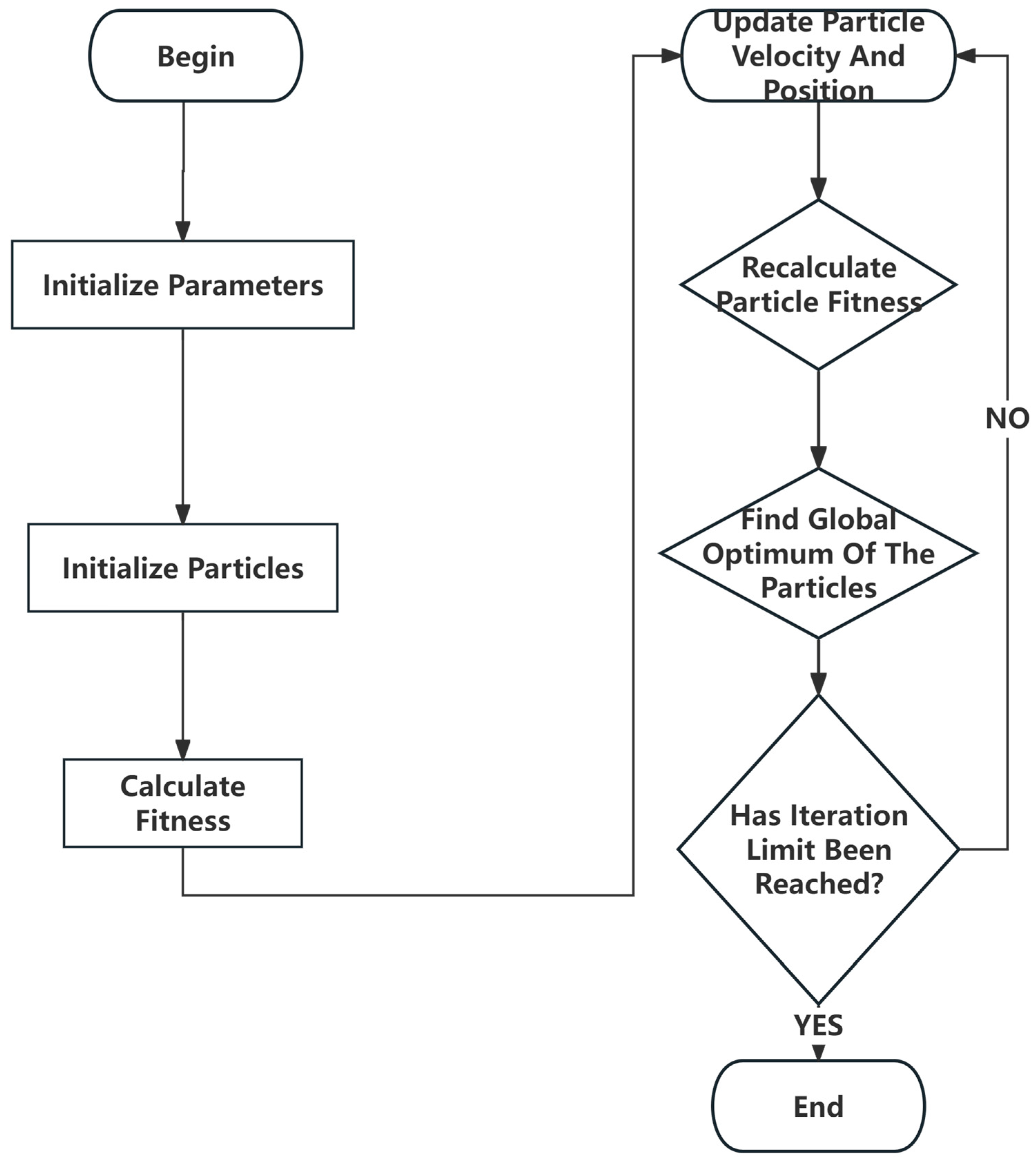
2.3. Particle Swarm Optimization (PSO) Algorithm
2.4. Backpropagation Neural Network
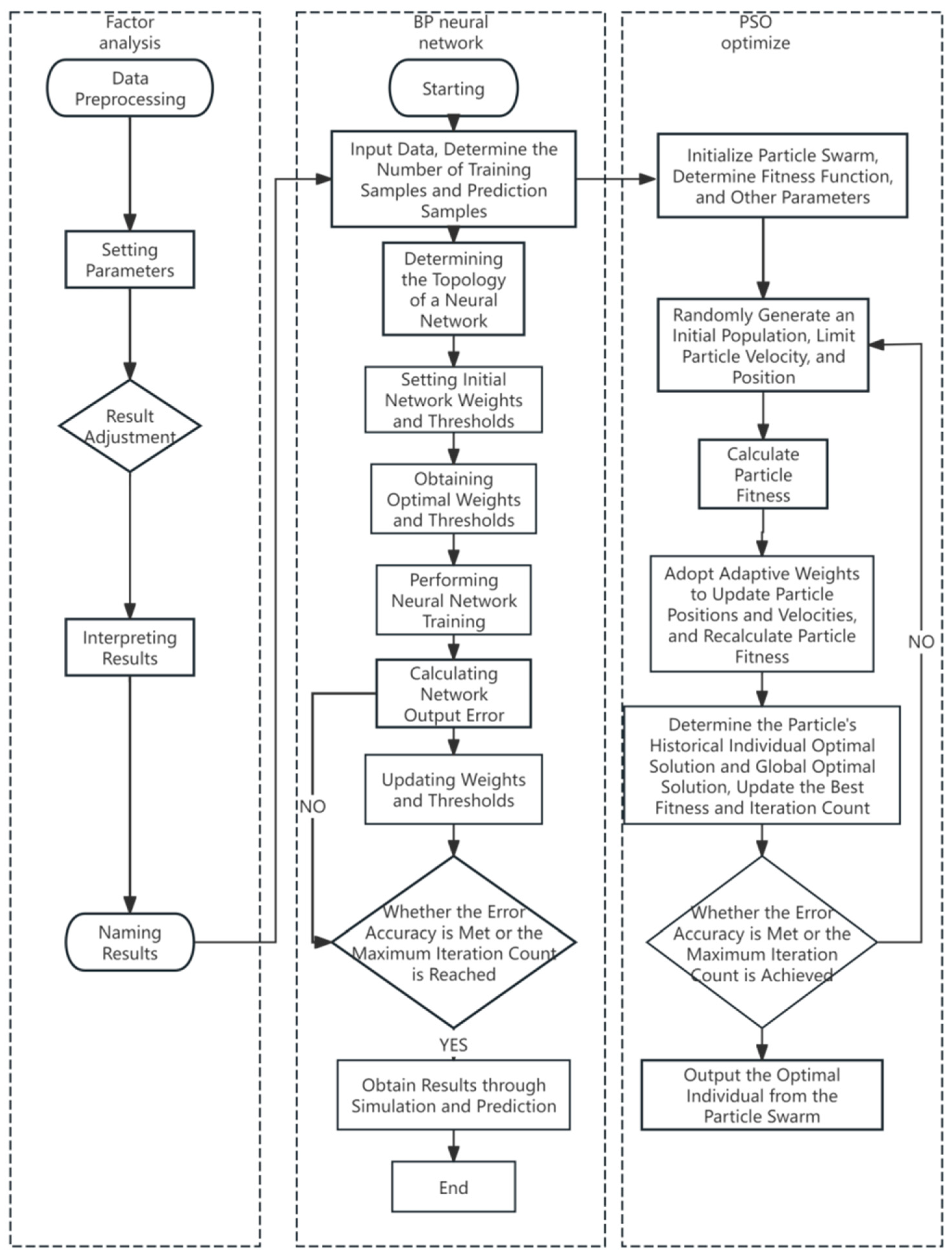
3. Model Construction
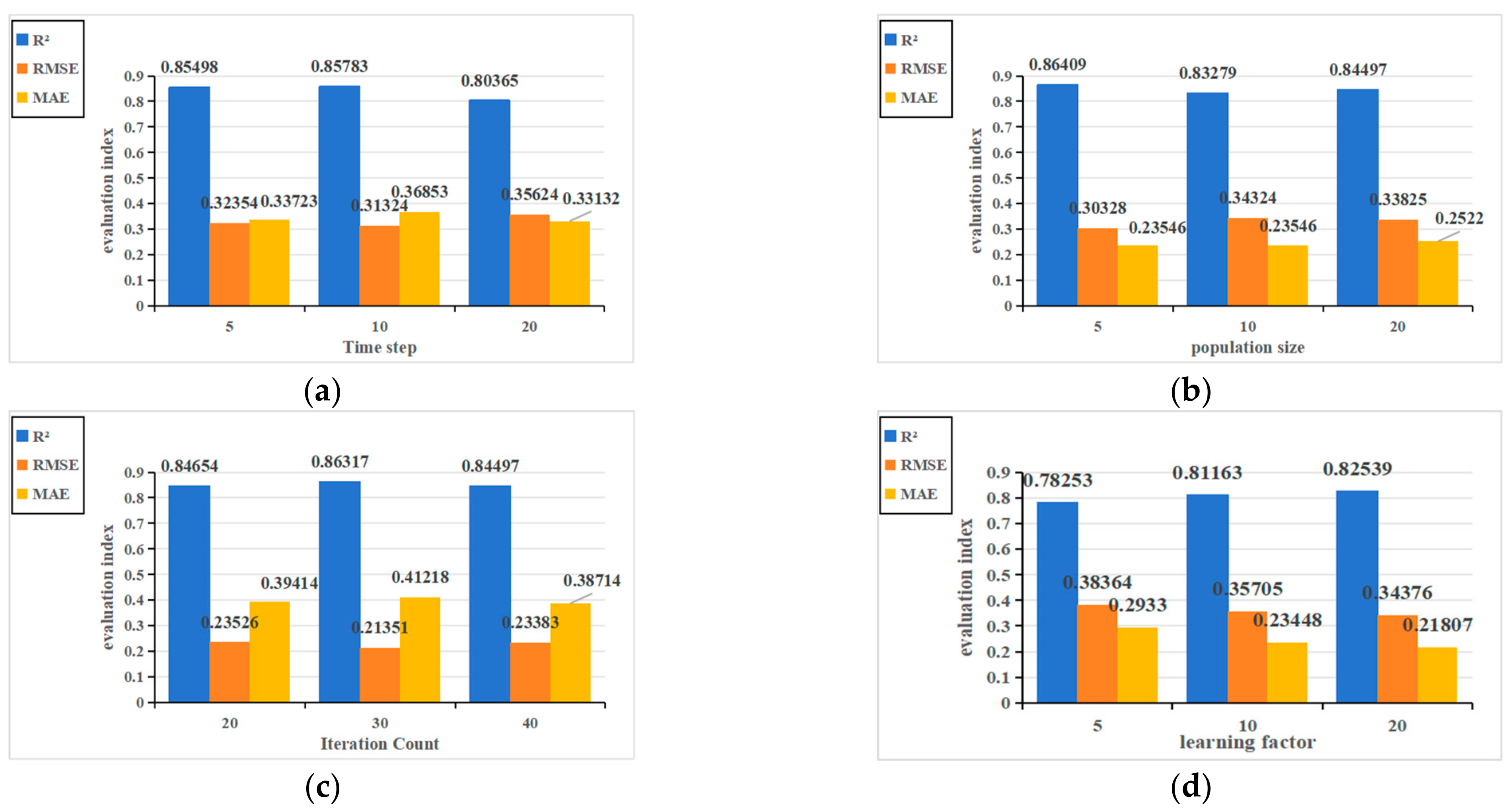
3.1. Hyperparameter Optimization
3.2. FA-PSOBP Construction of Optimized Model
4. Result and Discussion
4.1. Prediction Performance Comparison
4.2. Discussion
5. Conclusions
5.1. Acoustic Emission (AE) Signal Analysis for Rockburst Prediction
5.2. Factor Analysis for AE Time Series
5.3. Improved FA-PSOBP Model for AE Time Series Prediction
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hoek, E.; Kaiser, P.K.; Bawden, W.F. Support of Underground Excavations in Hard Rock; Taylor and Francis, CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Wang, S.; Huang, L.; Li, X. Analysis of rockburst triggered by hard rock fragmentation using a conical pick under high uniaxial stress. Tunn. Undergr. Space Technol. 2020, 96, 103195. [Google Scholar] [CrossRef]
- Prabhat, B.S.M.; Shakil, M.; Aibing, J. A comprehensive review of intelligent machine learning based predicting methods in long-term and short-term rock burst prediction. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2023, 142, 105434. [Google Scholar]
- Song, Z.; Cheng, Y.; Yang, T.; Huo, R.; Wang, J.; Liu, X.; Zhou, G. Analysis of compression failure and acoustic emission characteristics of limestone under permeability-stress coupling. J. China Coal Soc. 2019, 44, 2751–2759. (In Chinese) [Google Scholar]
- Ohtsu, M.; Grosse, C. Acoustic Emission Testing: Basics for Research-Applications in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Cheng, Y.; Song, Z.; Xu, Z.; Yang, T.; Tian, X. Failure mechanism and infrared radiation characteristic of hard siltstone induced by stratification effect. J. Mt. Sci. 2024, 21, 700–716. [Google Scholar] [CrossRef]
- Glazer, S. Mine Seismology: Data Analysis and Interpretation; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Hu, X.; Su, G.; Chen, G.; Mei, S.; Feng, X.; Mei, G.; Huang, X. Experiment on Rockburst Process of Borehole and Its Acoustic Emission Characteristics. Rock Mech. Rock Eng. 2019, 52, 783–802. [Google Scholar] [CrossRef]
- Su, G.; Shi, Y.; Feng, X.; Jiang, J.; Zhang, J.; Jiang, Q. True-Triaxial Experimental Study of the Evolutionary Features of the Acoustic Emissions and Sounds of Rockburst Processes. Rock Mech. Rock Eng. 2018, 51, 375–389. [Google Scholar] [CrossRef]
- Mei, F.; Hu, C.; Li, P.; Zhang, J. Study on main Frequency precursor characteristics of Acoustic Emission from Deep buried Dali Rock explosion. Arab. J. Geosci. 2019, 12, 645. [Google Scholar] [CrossRef]
- He, S.; Song, D.; Li, Z.; He, X.; Chen, J.; Li, D.; Tian, X. Precursor of Spatio-temporal Evolution Law of MS and AE Activities for Rock Burst Warning in Steeply Inclined and Extremely Thick Coal Seams Under Caving Mining Conditions. Rock Mech. Rock Eng. 2019, 52, 2415–2435. [Google Scholar] [CrossRef]
- Li, J.; Liu, D.; He, M.; Guo, Y.; Wang, H. Experimental investigation of true triaxial unloading rockburst precursors based on critical slowing-down theory. Bull. Eng. Geol. Environ. 2023, 82, 65. [Google Scholar] [CrossRef]
- Jia, Y.; Lu, Q.; Shang, Y. Rockburst prediction using particle swarm optimization algorithm and general regression neural network. Chin. J. Rock Mech. Eng. 2013, 32, 343–348. [Google Scholar]
- Zhao, Z.; Gross, L. Using supervised machine learning to distinguish microseismic from noise events. In Proceedings of the SEG International Exposition and Annual Meeting, Houston, TX, USA, 24–29 September 2017; p. SEG-2017-17727697. [Google Scholar]
- Wang, Y. Prediction of rockburst risk in coal mines based on a locally weighted C4.5 algorithm. IEEE Access 2021, 9, 15149–15155. [Google Scholar] [CrossRef]
- Liang, W.; Sari, A.; Zhao, G.; McKinnon, S.D.; Wu, H. Short-term rockburst risk prediction using ensemble learning methods. Nat. Hazards 2020, 104, 1923–1946. [Google Scholar] [CrossRef]
- Ke, B.; Khandelwal, M.; Asteris, P.G.; Skentou, A.D.; Mamou, A.; Armaghani, D.J. Rock-burst occurrence prediction based on optimized Naïve Bayes models. IEEE Access 2021, 9, 91347–91360. [Google Scholar] [CrossRef]
- Wu, S.; Wu, Z.; Zhang, C. Rock burst prediction probability model based on case analysis. Tunn. Undergr. Space Technol. 2019, 93, 103069. [Google Scholar] [CrossRef]
- Xue, Y.; Bai, C.; Qiu, D.; Kong, F.; Li, Z. Predicting rockburst with database using particle swarm optimization and extreme learning machine. Tunn. Undergr. Space Technol. 2020, 98, 103287. [Google Scholar] [CrossRef]
- Zhili, T.; Xue, W.; Qianjun, X. Rockburst prediction based on oversampling and objective weighting method. J. Tsinghua Univ. (Sci. Technol.) 2021, 61, 543–555. [Google Scholar]
- Papadopoulos, D.; Benardos, A. Enhancing machine learning algorithms to assess rock burst phenomena. Geotech. Geol. Eng. 2021, 39, 5787–5809. [Google Scholar] [CrossRef]
- Yin, X.; Liu, Q.; Huang, X.; Pan, Y. Real-time prediction of rockburst intensity using an integrated CNN-Adam-BO algorithm based on microseismic data and its engineering application. Tunn. Undergr. Space Technol. 2021, 117, 104133. [Google Scholar] [CrossRef]
- Jian, Z.; Shi, X.Z.; Huang, R.D.; Qiu, X.Y.; Chong, C. Feasibility of stochastic gradient boosting approach for predicting rockburst damage in burst-prone mines. Trans. Nonferrous Met. Soc. China 2016, 26, 1938–1945. [Google Scholar]
- Pu, Y.; Apel, D.B.; Hall, R. Using machine learning approach for microseismic events recognition in underground excavations: Comparison of ten frequently-used models. Eng. Geol. 2020, 268, 105519. [Google Scholar] [CrossRef]
- Ma, K.; Shen, Q.Q.; Sun, X.Y.; Ma, T.H.; Hu, J.; Tang, C.A. Rockburst prediction model using machine learning based on microseismic parameters of Qinling water conveyance tunnel. J. Cent. South Univ. 2023, 30, 289–305. [Google Scholar] [CrossRef]
- Zhang, H.; Zeng, J.; Ma, J.; Fang, Y.; Ma, C.; Yao, Z.; Chen, Z. Time series prediction of microseismic multi-parameter related to rockburst based on deep learning. Rock Mech. Rock Eng. 2021, 54, 6299–6321. [Google Scholar] [CrossRef]
- Di, Y.; Wang, E. Rock burst precursor electromagnetic radiation signal recognition method and early warning application based on recurrent neural networks. Rock Mech. Rock Eng. 2021, 54, 1449–1461. [Google Scholar] [CrossRef]
- Di, Y.; Wang, E.; Li, Z.; Liu, X.; Huang, T.; Yao, J. Comprehensive early warning method of microseismic, acoustic emission, and electromagnetic radiation signals of rock burst based on deep learning. Int. J. Rock Mech. Min. Sci. 2023, 170, 105519. [Google Scholar] [CrossRef]
- Hu, L.; Feng, X.T.; Yao, Z.B.; Zhang, W.; Niu, W.J.; Bi, X.; Feng, G.L.; Xiao, Y.X. Rockburst time warning method with blasting cycle as the unit based on microseismic information time series: A case study. Bull. Eng. Geol. Environ. 2023, 82, 121. [Google Scholar] [CrossRef]



| KMO and Bartlett’s Test | ||
|---|---|---|
| Kaiser–Meyer–Olkin Measure of Sampling Adequacy | 0.842 | |
| Bartlett’s test of sphericity | Approximate Chi-Square | 151,302.068 |
| Degree of freedom | 45 | |
| Significance | 0.000 | |
| Ingredients | Initial Eigenvalues | Extract the Sum of Squares of the Loadings | Sum of the Rotating Load Squares | ||||
|---|---|---|---|---|---|---|---|
| Total | Percentage Variance | Accumulate % | Total | Percentage Variance | Accumulate % | Total | |
| 1 | 5.696 | 56.955 | 56.955 | 5.696 | 56.955 | 56.955 | 4.104 |
| 2 | 1.476 | 14.756 | 71.711 | 1.476 | 14.756 | 71.711 | 2.509 |
| 3 | 1.019 | 10.186 | 81.898 | 1.019 | 10.186 | 81.898 | 1.577 |
| 4 | 0.462 | 4.625 | 86.523 | ||||
| 5 | 0.443 | 4.427 | 90.950 | ||||
| 6 | 0.343 | 3.433 | 94.383 | ||||
| 7 | 0.298 | 2.981 | 97.364 | ||||
| 8 | 0.132 | 1.317 | 98.681 | ||||
| 9 | 0.094 | 0.937 | 99.618 | ||||
| 10 | 0.038 | 0.382 | 100.000 | ||||
| Parameter | Y1 (Energy-Related) | Y2 (Time-Related) | Y3 (Frequency-Related) |
|---|---|---|---|
| Energy (d3) | 0.92 | 0.15 | 0.08 |
| Amplitude (d5) | 0.88 | 0.21 | 0.12 |
| Average Signal Strength (d8) | 0.85 | 0.18 | 0.09 |
| Duration (d4) | 0.13 | 0.91 | 0.07 |
| Rise Time (d1) | 0.11 | 0.89 | 0.05 |
| Ringing Count (d2) | 0.24 | 0.83 | 0.14 |
| Peak Frequency (d9) | 0.08 | 0.12 | 0.95 |
| Initial Frequency (d10) | 0.09 | 0.07 | 0.93 |
| RMS Voltage (d7) | 0.76 | 0.31 | 0.22 |
| Average Frequency (d6) | 0.18 | 0.27 | 0.82 |
| Number | Comprehensive Indicator Y | ||
|---|---|---|---|
| Measured Value | Predicted Value | Relative Error | |
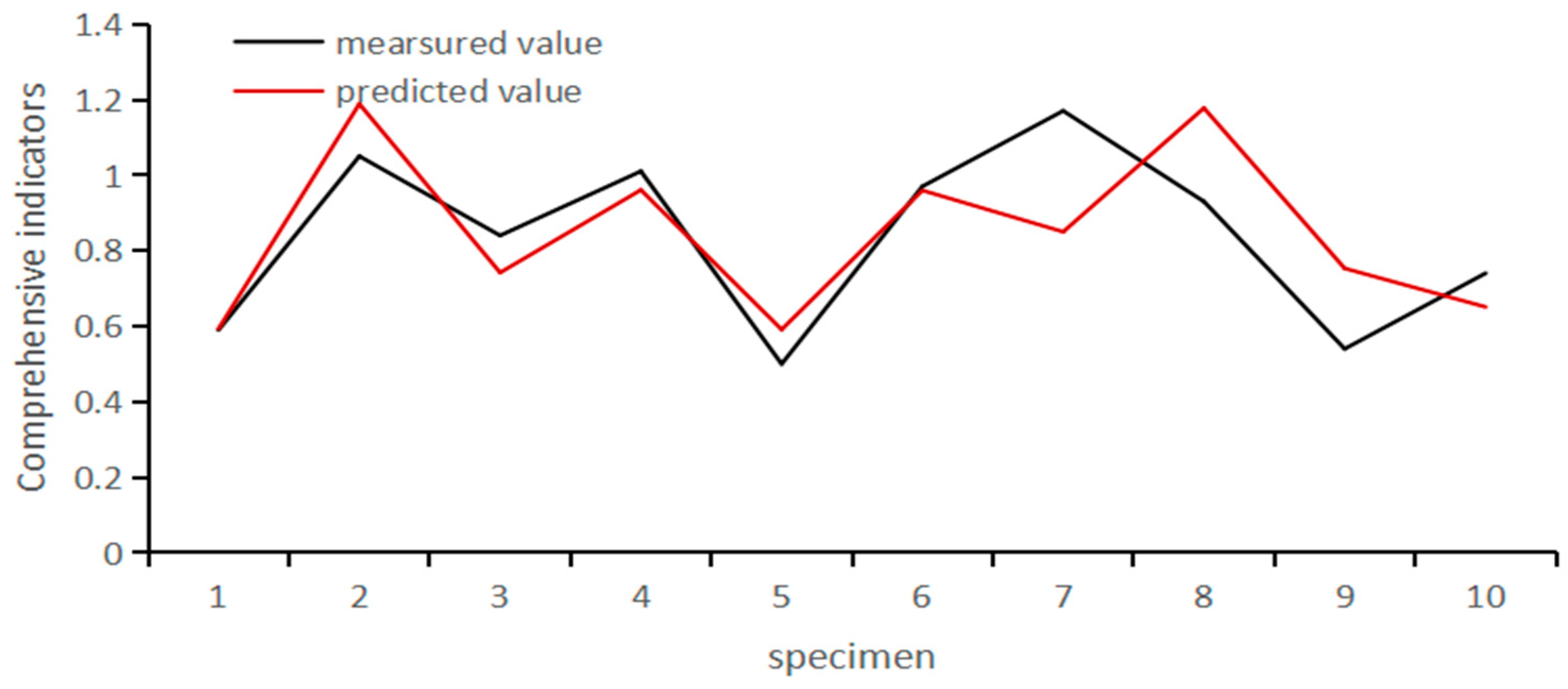
| 191 | 0.59 | 0.593268406 | 0.55% |
| 192 | 1.05 | 1.188406557 | 14.54% |
| 193 | 0.84 | 0.741827053 | 11.61% |
| 194 | 1.01 | 0.960578817 | 4.89% |
| 195 | 0.5 | 0.59110598 | 18.23% |
| 196 | 0.97 | 0.959367536 | 1.03% |
| 197 | 1.17 | 0.849890528 | 27.35% |
| 198 | 0.93 | 1.177363619 | 25.80% |
| 199 | 0.54 | 0.652859941 | 20.37% |
| 200 | 0.74 | 0.650975516 | 12.16% |
| Average Relative Error % | 13.653% | ||
| Title 1 | R2 | Mean Relative Error |
|---|---|---|
| FA-PSOBP | 0.864 | 13.65% |
| LSTM | 0.845 | 18.76% |
| CNN | 0.744 | 21.44% |
| SVM | 0.782 | 19.88% |
| Random Forest | 0.721 | 23.12% |
| Title 1 | R2 | Mean Relative Error |
|---|---|---|
| FA-PSOBP | 0.864 | 13.65% |
| BP | 0.714 | 22.27% |
| GA-BP | 0.824 | 19.18% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, X.; Wang, M. Research on the Time Series Prediction of Acoustic Emission Parameters Based on the Factor Analysis–Particle Swarm Optimization Back Propagation Model. Appl. Sci. 2025, 15, 1977. https://doi.org/10.3390/app15041977
Xie X, Wang M. Research on the Time Series Prediction of Acoustic Emission Parameters Based on the Factor Analysis–Particle Swarm Optimization Back Propagation Model. Applied Sciences. 2025; 15(4):1977. https://doi.org/10.3390/app15041977
Chicago/Turabian StyleXie, Xuebin, and Meng Wang. 2025. "Research on the Time Series Prediction of Acoustic Emission Parameters Based on the Factor Analysis–Particle Swarm Optimization Back Propagation Model" Applied Sciences 15, no. 4: 1977. https://doi.org/10.3390/app15041977
APA StyleXie, X., & Wang, M. (2025). Research on the Time Series Prediction of Acoustic Emission Parameters Based on the Factor Analysis–Particle Swarm Optimization Back Propagation Model. Applied Sciences, 15(4), 1977. https://doi.org/10.3390/app15041977






