Prototypical Graph Contrastive Learning for Recommendation
Abstract
1. Introduction
- A novel preference prototype-based feature augmentation contrastive learning recommendation framework is proposed.
- A preference learning module is proposed to enrich prototype information, along with a prototype filtering network to regulate feature augmentation, improving the model’s stability.
- Compared with existing prototype-based methods, ProtoRec achieves maximum gains of up to 16.8% and 20.0% in recall@k and NDCG@k on three real-world datasets. Additional experiments were performed to further analyze the rationale behind ProtoRec.
2. Preliminaries
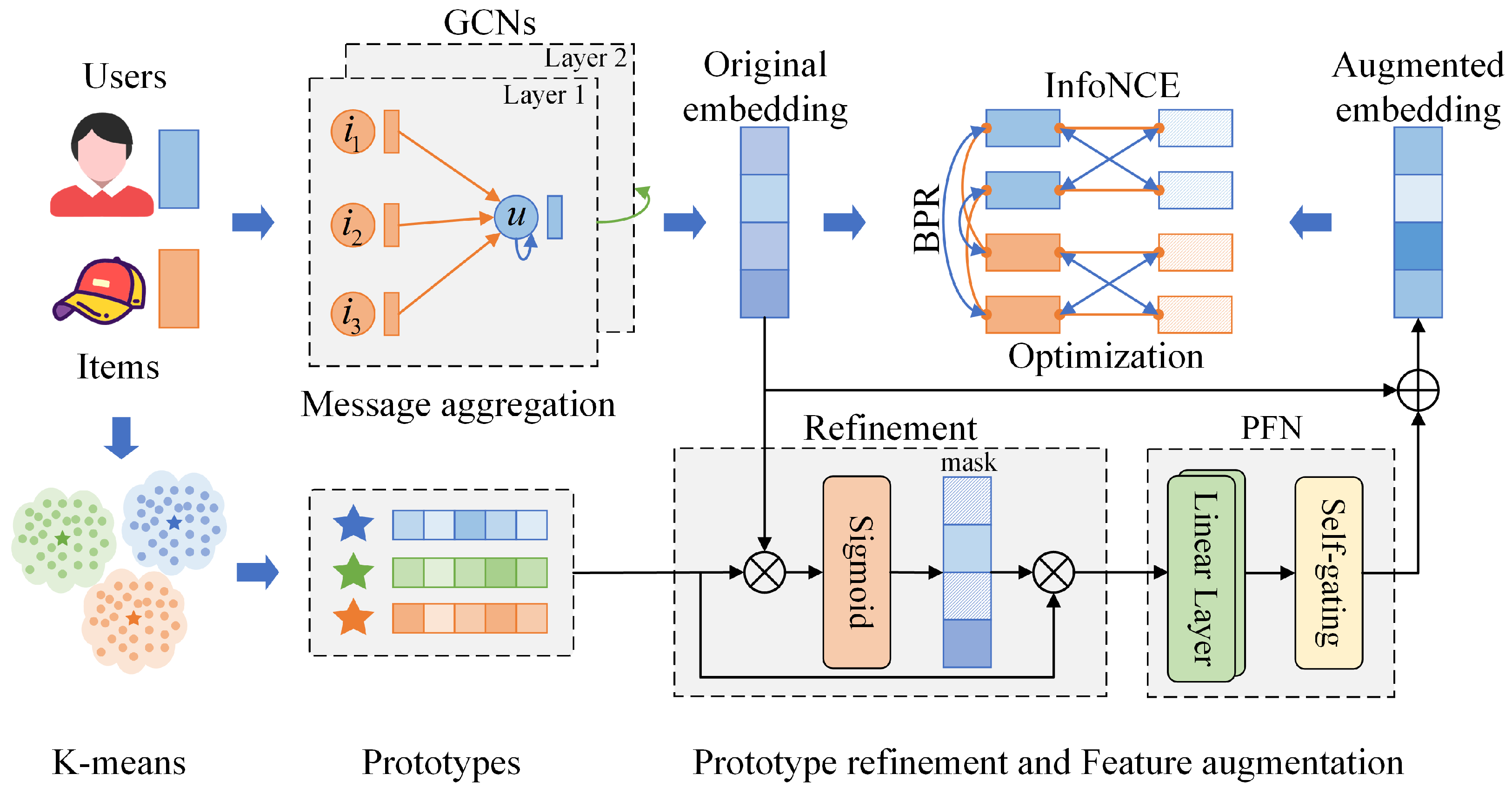
3. Methodology
3.1. Graph Neural Network Backbone
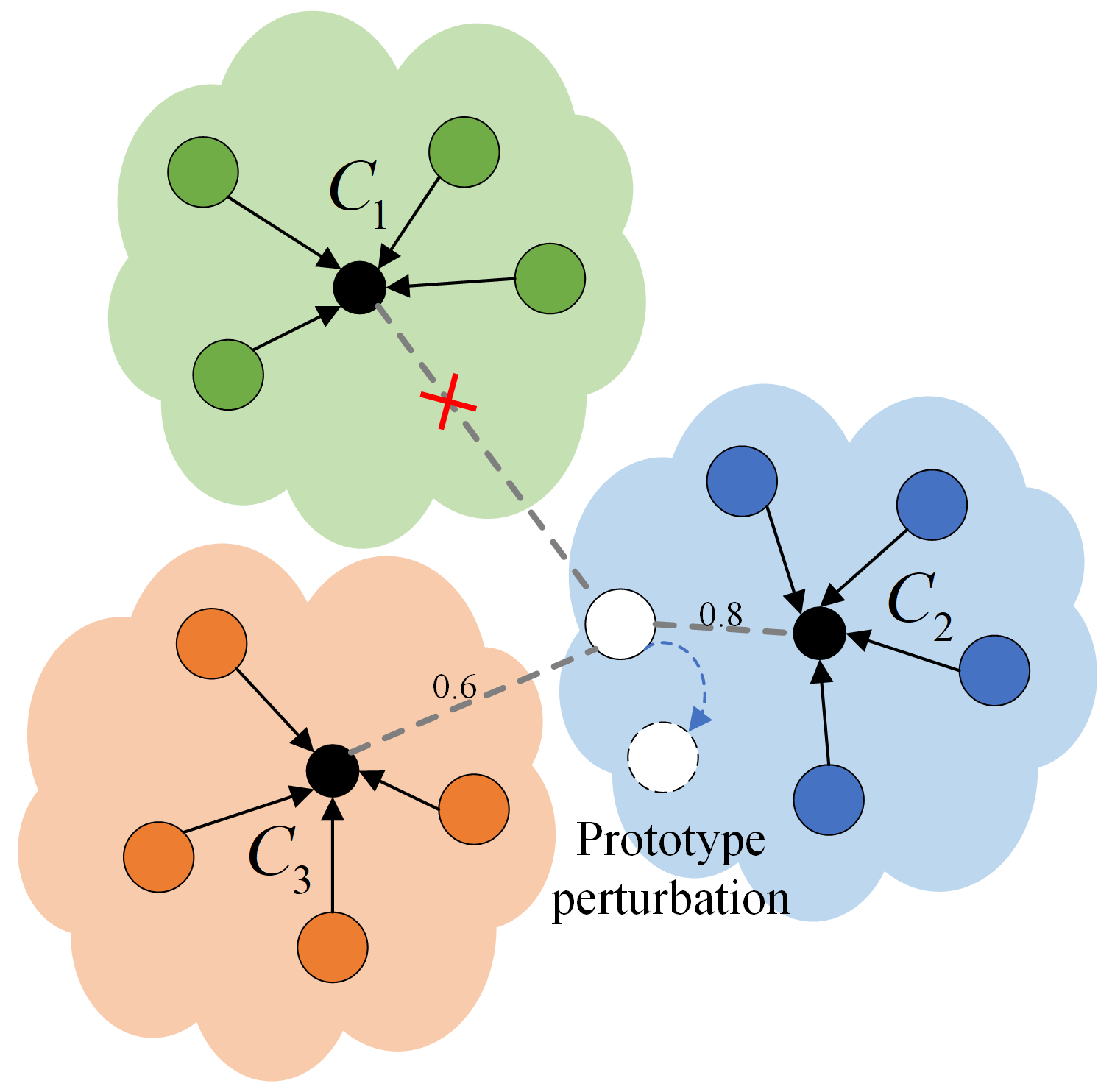
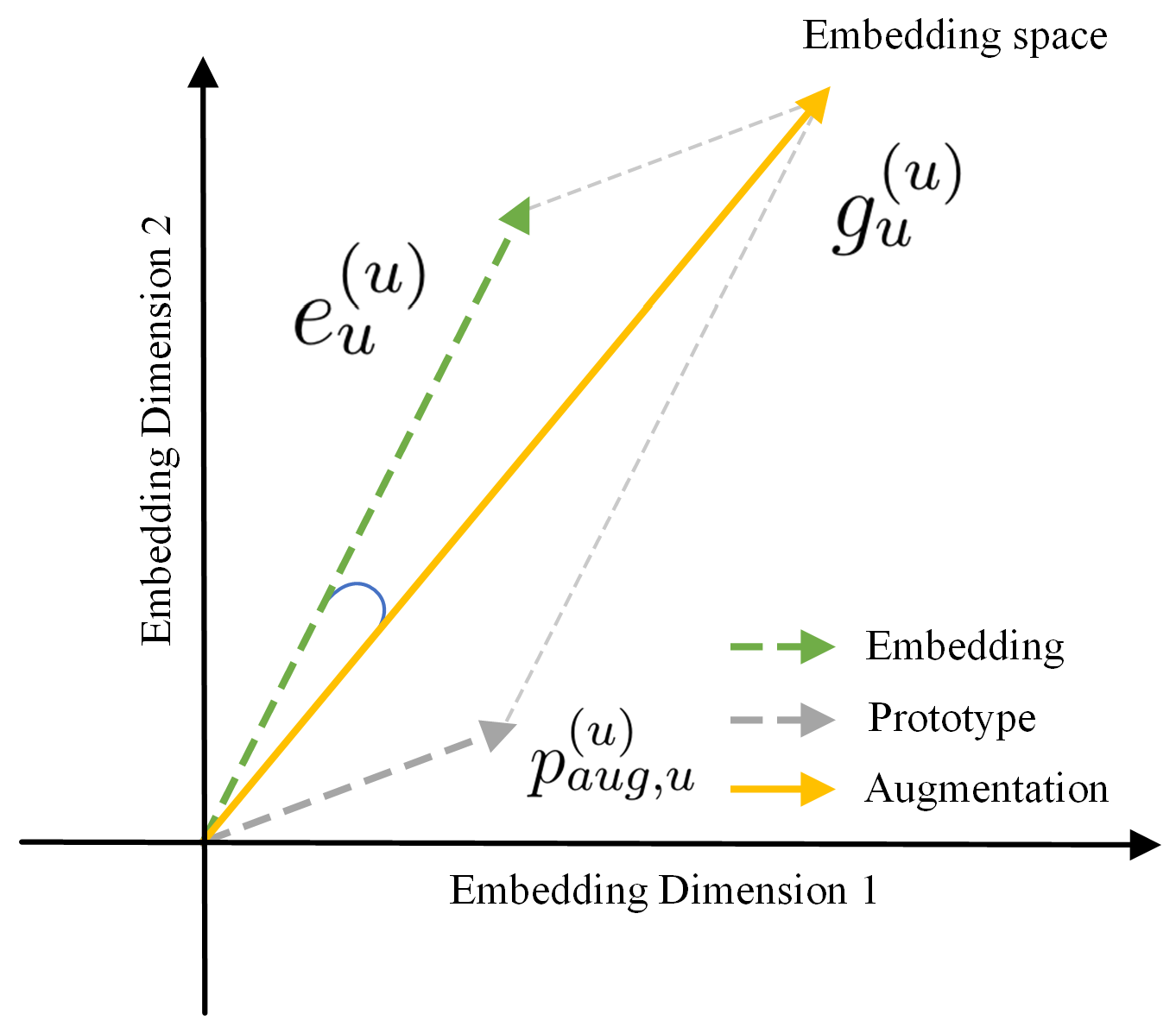
3.2. Prototype Generation and Feature Augmentation
3.3. Optimization
3.4. Algorithm Complexity
| Algorithm 1 Prototypical Graph Contrastive Learning for Recommendation (ProtoRec) |
|
4. Experiments
- RQ1: How does ProtoRec perform in top-k recommendation compared to other baselines?
- RQ2: How uniform are the embeddings learned by ProtoRec?
- RQ3: How do the key components influence ProtoRec, and how is the performance of the proposed variants?
- RQ4: How do various hyperparameter settings impact ProtoRec’s performance?
- RQ5: How robust is ProtoRec to different types of noise?
4.1. Experimental Settings
4.1.1. Datasets and Metrics
4.1.2. Baselines
- Graph-based collaborative filtering methods.
- LightGCN [4] is the primary choice for the graph convolutional network backbone in current recommendation models, capable of capturing collaborative information in interaction graphs in a lightweight manner.
- DirectAU [23] optimizes embedding alignment and uniformity through a loss function and theoretically reveals the rationality of this approach for optimizing recommendation performance.
- Self-supervised learning methods.
- LightGCL [12] constructs perturbed views through random singular value decomposition and employs a dual-view approach for CL.
- SGL [5] proposes random strategies to drop nodes and edges in the graph for CL.
- SimGCL [10] introduces a feature augmentation method constructed by adding uniform noise to learned embeddings.
- SCCF [24] decomposes the contrastive learning loss into two processes, making embeddings more compact and more dispersed, thereby enhancing the ability of contrastive learning to capture high-order connectivity information.
- RecDCL [25] integrates batch-wise contrastive learning to enhance the robustness of representations and feature-wise contrastive learning to eliminate redundant solutions in user–item positive samples, thereby optimizing the uniformity of embeddings.
- AdaGCL [26] dynamically reconstructs the interaction graph and denoises the data based on the learned embeddings, and it constructs contrastive learning using the embeddings learned from both processes.
- Prototype-based recommendation methods.
4.2. Performance Comparison (RQ1)
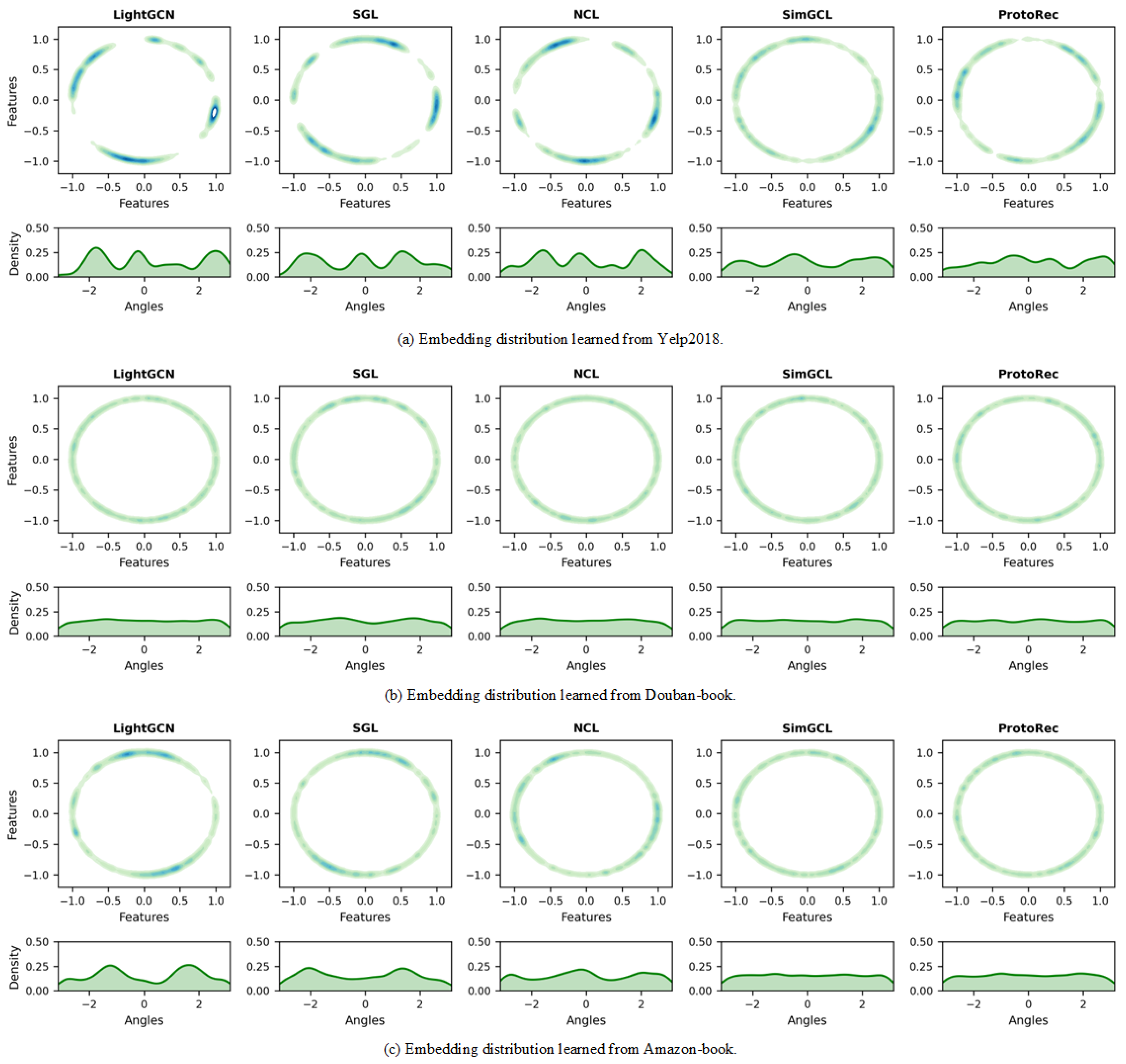
4.3. Uniformity Study (RQ2)
4.4. Ablation Study (RQ3)
4.5. Hyperparameter Analysis (RQ4)
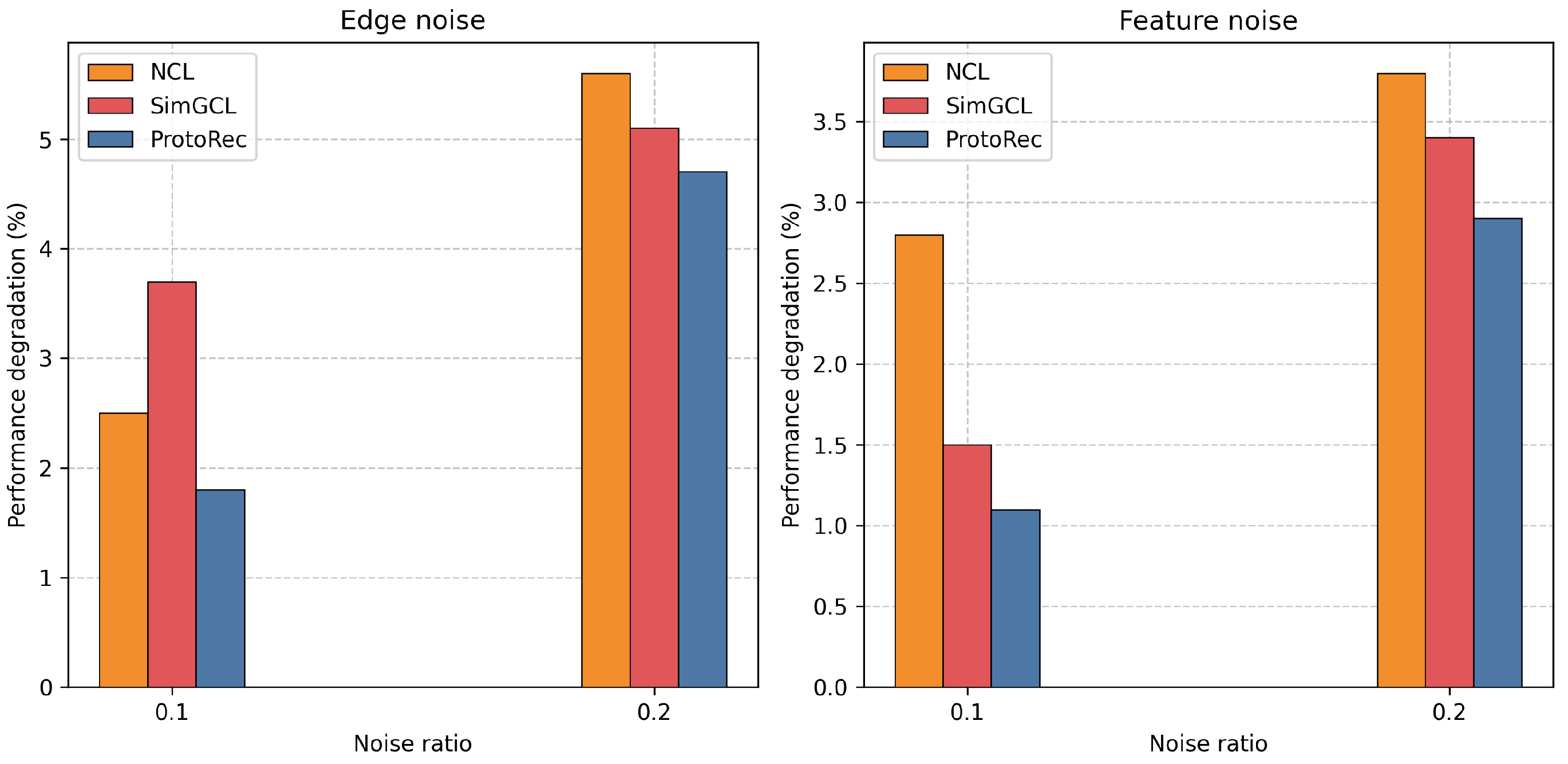
4.6. Robustness Study (RQ5)
5. Related Work
5.1. Graph-Based Collaborative Filtering
5.2. Graph Contrastive Learning for Recommendation
5.3. Prototype-Based Contrastive Learning
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, L.; He, X.; Wang, X.; Zhang, K.; Wang, M. A survey on accuracy-oriented neural recommendation: From collaborative filtering to information-rich recommendation. IEEE Trans. Knowl. Data Eng. 2022, 35, 4425–4445. [Google Scholar] [CrossRef]
- Lian, J.; Zhou, X.; Zhang, F.; Chen, Z.; Xie, X.; Sun, G. xdeepfm: Combining explicit and implicit feature interactions for recommender systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 1754–1763. [Google Scholar]
- He, X.; Liao, L.; Zhang, H.; Nie, L.; Hu, X.; Chua, T. Neural collaborative filtering. In Proceedings of the 26th International Conference on World Wide Web, Perth, Australia, 3–7 April 2017; pp. 173–182. [Google Scholar]
- He, X.; Deng, K.; Wang, X.; Li, Y.; Zhang, Y.; Wang, M. Lightgcn: Simplifying and powering graph convolution network for recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual, 25–30 July 2020; pp. 639–648. [Google Scholar]
- Wu, J.; Wang, X.; Feng, F.; He, X.; Chen, L.; Lian, J.; Xie, X. Self-supervised graph learning for recommendation. In Proceedings of the 44th international ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual, 11–15 July 2021; pp. 726–735. [Google Scholar]
- Yu, J.; Yin, H.; Xia, X.; Chen, T.; Li, J.; Huang, Z. Self-supervised learning for recommender systems: A survey. IEEE Trans. Knowl. Data Eng. 2023, 36, 335–355. [Google Scholar] [CrossRef]
- Ren, X.; Wei, W.; Xia, L.; Huang, C. A comprehensive survey on self-supervised learning for recommendation. arXiv 2024, arXiv:2404.03354. [Google Scholar]
- Ding, K.; Xu, Z.; Tong, H.; Liu, H. Data augmentation for deep graph learning: A survey. ACM SIGKDD Explor. Newsl. 2022, 24, 61–77. [Google Scholar] [CrossRef]
- Zhu, Y.; Xu, Y.; Yu, F.; Liu, Q.; Wu, S.; Wang, L. Deep graph contrastive representation learning. arXiv 2020, arXiv:2006.04131. [Google Scholar]
- Yu, J.; Yin, H.; Xia, X.; Chen, T.; Cui, L.; Nguyen, Q.V.H. Are graph augmentations necessary? Simple graph contrastive learning for recommendation. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval, Madrid, Spain, 11–15 July 2022; pp. 1294–1303. [Google Scholar]
- Xia, J.; Wu, L.; Chen, J.; Hu, B.; Li, S.Z. Simgrace: A simple framework for graph contrastive learning without data augmentation. In Proceedings of the ACM Web Conference 2022, Lyon, France, 25–29 April 2022; pp. 1070–1079. [Google Scholar]
- Cai, X.; Huang, C.; Xia, L.; Ren, X. LightGCL: Simple yet effective graph contrastive learning for recommendation. arXiv 2023, arXiv:2302.08191. [Google Scholar]
- Liu, F.; Zhao, S.; Cheng, Z.; Nie, L.; Kankanhalli, M. Cluster-based Graph Collaborative Filtering. ACM Trans. Inf. Syst. 2024, 42, 1–24. [Google Scholar] [CrossRef]
- Lin, S.; Liu, C.; Zhou, P.; Hu, Z.Y.; Wang, S.; Zhao, R.; Liang, X. Prototypical graph contrastive learning. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 2747–2758. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Wang, H.; Ni, B.; Guo, H.; Tang, J. Self-supervised graph-level representation learning with local and global structure. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 11548–11558. [Google Scholar]
- Wang, X.; Jin, H.; Zhang, A.; He, X.; Xu, T.; Chua, T.S. Disentangled graph collaborative filtering. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual, 25–30 July 2020; pp. 1001–1010. [Google Scholar]
- Wu, F.; Souza, A.; Zhang, T.; Fifty, C.; Yu, T.; Weinberger, K. Simplifying graph convolutional networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 6861–6871. [Google Scholar]
- Rendle, S.; Freudenthaler, C.; Gantner, Z.; Schmidt-Thieme, L. BPR: Bayesian personalized ranking from implicit feedback. In Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–21 June 2009; pp. 452–461. [Google Scholar]
- Kuo, C.; Ma, C.; Huang, J.; Kira, Z. Featmatch: Feature-based augmentation for semi-supervised learning. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; pp. 479–495. [Google Scholar]
- Lin, Z.; Tian, C.; Hou, Y.; Zhao, W. Improving graph collaborative filtering with neighborhood-enriched contrastive learning. In Proceedings of the ACM Web Conference 2022, Lyon, France, 25–29 April 2022; pp. 2320–2329. [Google Scholar]
- Ou, Y.; Chen, L.; Pan, F.; Wu, Y. Prototypical contrastive learning through alignment and uniformity for recommendation. arXiv 2024, arXiv:2402.02079. [Google Scholar]
- Oord, A.V.D.; Li, Y.; Vinyals, O. Representation learning with contrastive predictive coding. arXiv 2018, arXiv:1807.03748. [Google Scholar]
- Wang, C.; Yu, Y.; Ma, W.; Zhang, M.; Chen, C.; Liu, Y.; Ma, S. Towards representation alignment and uniformity in collaborative filtering. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 1816–1825. [Google Scholar]
- Wu, Y.; Zhang, L.; Mo, F.; Zhu, T.; Ma, W.; Nie, J.Y. Unifying graph convolution and contrastive learning in collaborative filtering. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Barcelona, Spain, 25–29 August 2024; pp. 425–3436. [Google Scholar]
- Zhang, D.; Geng, Y.; Gong, W.; Qi, Z.; Chen, Z.; Tang, X.; Tang, J. RecDCL: Dual Contrastive Learning for Recommendation. In Proceedings of the ACM on Web Conference 2024, Singapore, 13–17 May 2024; pp. 3655–3666. [Google Scholar]
- Jiang, Y.; Huang, C.; Huang, L. Adaptive graph contrastive learning for recommendation. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Long Beach, CA, USA, 6–10 August 2023; pp. 4252–4261. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Wang, X.; He, X.; Wang, M.; Feng, F.; Chua, T.S. Neural graph collaborative filtering. In Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval, Paris, France, 21–25 July 2019; pp. 165–174. [Google Scholar]
- Berg, R.V.D.; Kipf, T.N.; Welling, M. Graph convolutional matrix completion. arXiv 2017, arXiv:1706.02263. [Google Scholar]
- Li, G.; Muller, M.; Thabet, A.; Ghanem, B. Deepgcns: Can gcns go as deep as cnns? In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9267–9276. [Google Scholar]
- Xia, L.; Huang, C.; Xu, Y.; Zhao, J.; Yin, D.; Huang, J. Hypergraph contrastive collaborative filtering. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval, Madrid, Spain, 11–15 July 2022; pp. 70–79. [Google Scholar]
- Chen, M.; Huang, C.; Xia, L.; Wei, W.; Xu, Y.; Luo, R. Heterogeneous graph contrastive learning for recommendation. In Proceedings of the Sixteenth ACM International Conference on Web Search and Data Mining, Singapore, 27 February–3 March 2023; pp. 544–552. [Google Scholar]
- Jiang, Y.; Yang, Y.; Xia, L.; Huang, C. Diffkg: Knowledge graph diffusion model for recommendation. In Proceedings of the 17th ACM International Conference on Web Search and Data Mining, Mérida, Mexico, 4–8 March 2024; pp. 313–321. [Google Scholar]
- Zhu, Y.; Wang, C.; Zhang, Q.; Xiong, H. Graph Signal Diffusion Model for Collaborative Filtering. In Proceedings of the 47th International ACM SIGIR Conference on Research and Development in Information Retrieval, Washington, DC, USA, 14–18 July 2024; pp. 1380–1390. [Google Scholar]
- Wu, S.; Sun, F.; Zhang, W.; Xie, X.; Cui, B. Graph neural networks in recommender systems: A survey. ACM Comput. Surv. 2022, 55, 1–37. [Google Scholar] [CrossRef]
- Yu, J.; Yin, H.; Li, J.; Wang, Q.; Hung, N.Q.V.; Zhang, X. Self-supervised multi-channel hypergraph convolutional network for social recommendation. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 413–424. [Google Scholar]
- You, Y.; Chen, T.; Sui, Y.; Chen, T.; Wang, Z.; Shen, Y. Graph contrastive learning with augmentations. Adv. Neural Inf. Process. Syst. 2020, 33, 5812–5823. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International Conference on Machine Learning, Online, 13–18 July 2020; pp. 1597–1607. [Google Scholar]
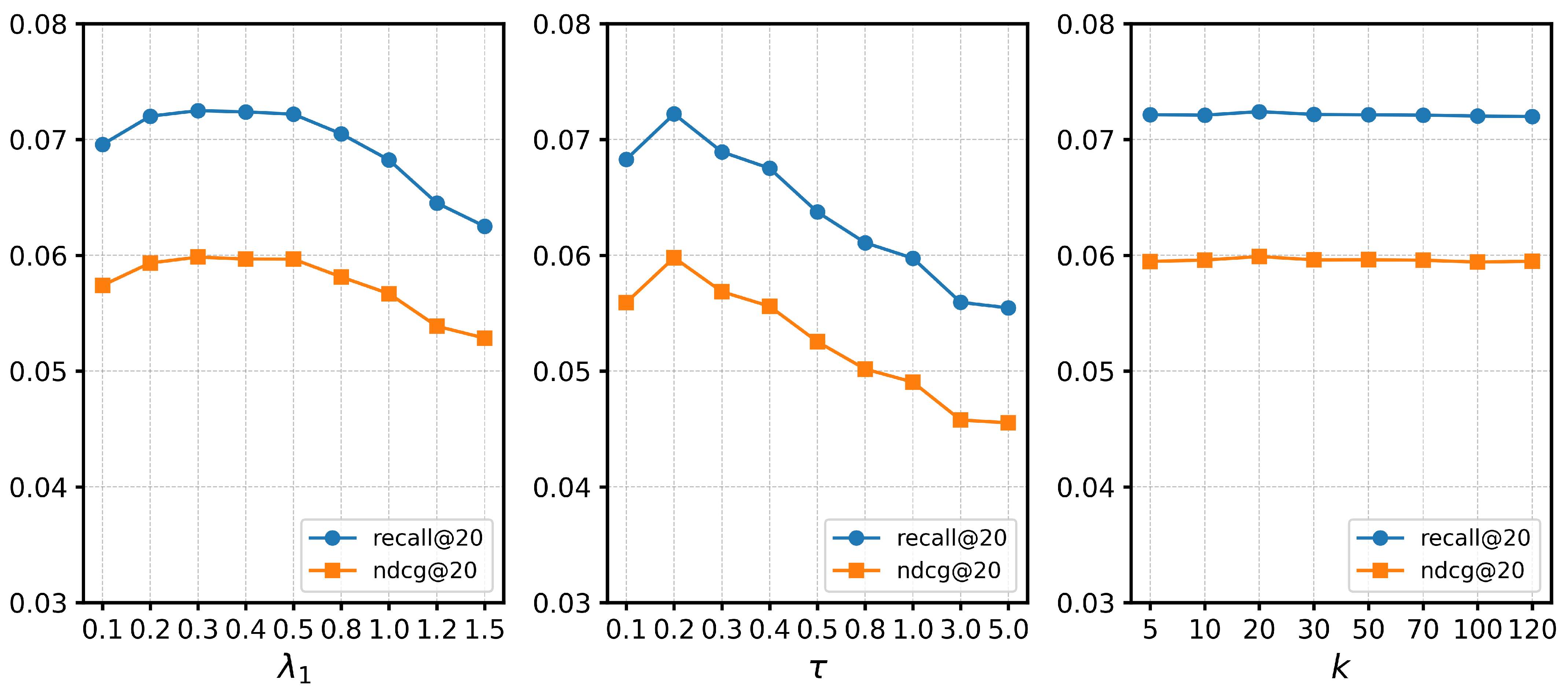
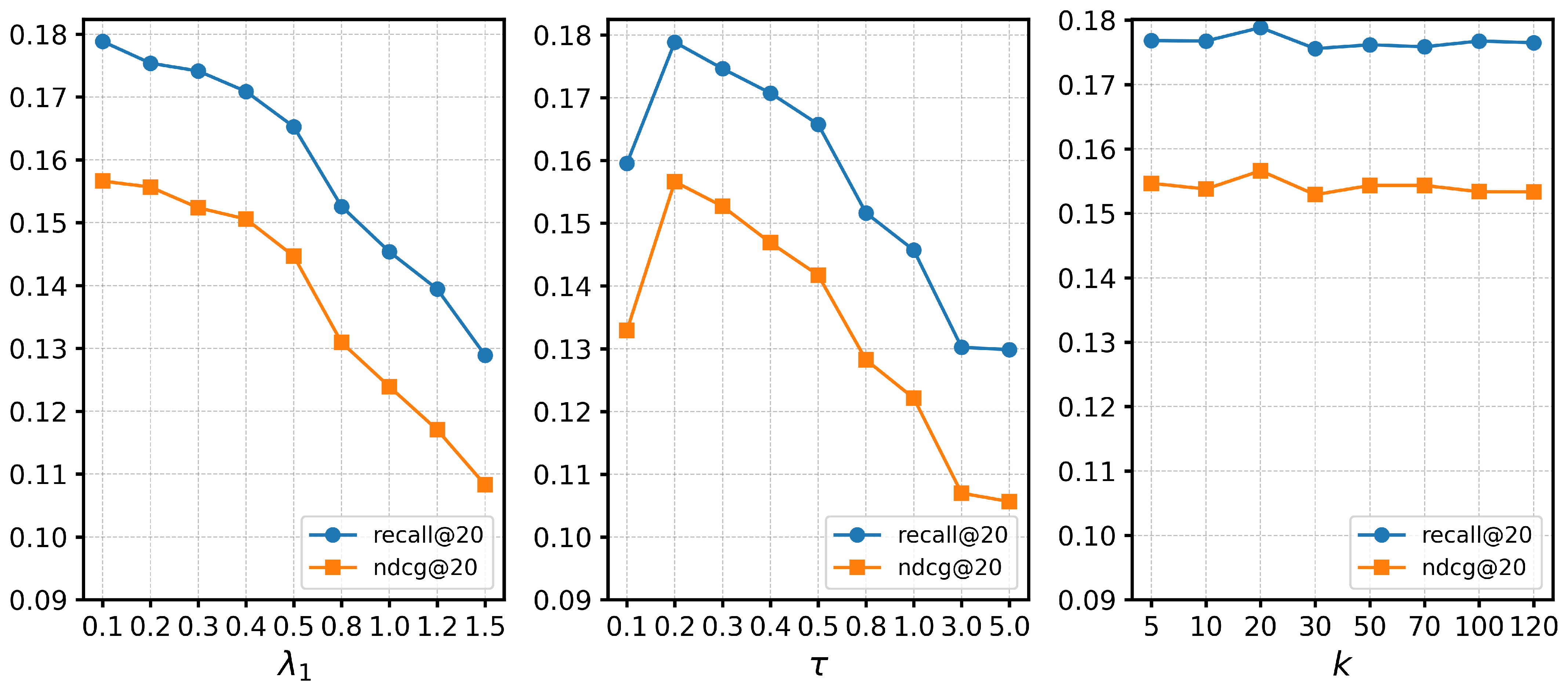

| Dataset | #Users | #Items | #Interactions | Density |
|---|---|---|---|---|
| Yelp2018 | 31,668 | 38,048 | 1,561,406 | 0.00130 |
| Douban-Book | 13,024 | 22,347 | 792,062 | 0.00272 |
| Amazon-Book | 52,463 | 91,599 | 2,984,108 | 0.00062 |
| Dataset | Metric | LightGCN | ProtoAU | NCL | SGL | LightGCL | DirectAU | RecDCL | SCCF | AdaGCL | SimGCL | ProtoRec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Yelp2018 | recall@20 | 0.0592 | 0.0611 | 0.0669 | 0.0676 | 0.0684 | 0.0704 | 0.0690 | 0.0701 | 0.0710 | 0.0721 | 0.0722 |
| ndcg@20 | 0.0482 | 0.0503 | 0.0547 | 0.0556 | 0.0561 | 0.0583 | 0.0560 | 0.0580 | 0.0585 | 0.0596 | 0.0598 | |
| recall@40 | 0.0981 | 0.1020 | 0.1097 | 0.1120 | 0.1110 | 0.1141 | 0.1122 | 0.1139 | 0.1152 | 0.1179 | 0.1188 | |
| ndcg@40 | 0.0630 | 0.0657 | 0.0709 | 0.0723 | 0.0721 | 0.0748 | 0.0733 | 0.0745 | 0.0752 | 0.0768 | 0.0773 | |
| Douban-Book | recall@20 | 0.1485 | 0.1500 | 0.1635 | 0.1740 | 0.1574 | 0.1640 | 0.1664 | 0.1711 | 0.1713 | 0.1774 | 0.1788 |
| ndcg@20 | 0.1248 | 0.1265 | 0.1387 | 0.1516 | 0.1371 | 0.1413 | 0.1526 | 0.1539 | 0.1542 | 0.1561 | 0.1566 | |
| recall@40 | 0.2101 | 0.2144 | 0.2264 | 0.2382 | 0.2075 | 0.2188 | 0.2183 | 0.2285 | 0.2312 | 0.2412 | 0.2431 | |
| ndcg@40 | 0.1431 | 0.1450 | 0.1571 | 0.1701 | 0.1512 | 0.1571 | 0.1578 | 0.1596 | 0.1617 | 0.1744 | 0.1750 | |
| Amazon-Book | recall@20 | 0.0381 | 0.0391 | 0.0444 | 0.0467 | 0.0497 | 0.0503 | 0.0491 | 0.0510 | 0.0504 | 0.0515 | 0.0519 |
| ndcg@20 | 0.0298 | 0.0309 | 0.0344 | 0.0367 | 0.0390 | 0.0401 | 0.0399 | 0.0405 | 0.0400 | 0.0411 | 0.0413 | |
| recall@40 | 0.0627 | 0.0655 | 0.0731 | 0.0761 | 0.0796 | 0.0805 | 0.0798 | 0.0807 | 0.0801 | 0.0808 | 0.0819 | |
| ndcg@40 | 0.0391 | 0.0408 | 0.0452 | 0.0478 | 0.0503 | 0.0505 | 0.0503 | 0.0506 | 0.0506 | 0.0521 | 0.0526 |
| Dataset | Yelp2018 | Douban-Book | Amazon-Book | |||
|---|---|---|---|---|---|---|
| Method | Recall@20 | NDCG@20 | Recall@20 | NDCG@20 | Recall@20 | NDCG@20 |
| ProtoRecdbscan | 0.0716 | 0.0591 | 0.1727 | 0.1482 | 0.0518 | 0.0412 |
| ProtoRechc | 0.0718 | 0.0592 | 0.1732 | 0.1492 | 0.0514 | 0.0409 |
| ProtoRecgmm | 0.0719 | 0.0593 | 0.1731 | 0.1486 | 0.0515 | 0.0413 |
| ProtoReca | 0.0689 | 0.0568 | 0.1706 | 0.1513 | 0.0472 | 0.0374 |
| ProtoRecl | 0.0723 | 0.0597 | 0.1783 | 0.1553 | 0.0516 | 0.0411 |
| ProtoRecc | 0.0722 | 0.0593 | 0.1774 | 0.1544 | 0.0511 | 0.0405 |
| w/o-SIG | 0.0721 | 0.0594 | 0.1754 | 0.1543 | 0.0513 | 0.0406 |
| w/o-PFN | 0.0643 | 0.0530 | 0.1473 | 0.1266 | 0.0427 | 0.0343 |
| ProtoRec | 0.0722 | 0.0598 | 0.1788 | 0.1566 | 0.0519 | 0.0413 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, T.; Yang, C.; Zheng, Y. Prototypical Graph Contrastive Learning for Recommendation. Appl. Sci. 2025, 15, 1961. https://doi.org/10.3390/app15041961
Wei T, Yang C, Zheng Y. Prototypical Graph Contrastive Learning for Recommendation. Applied Sciences. 2025; 15(4):1961. https://doi.org/10.3390/app15041961
Chicago/Turabian StyleWei, Tao, Changchun Yang, and Yanqi Zheng. 2025. "Prototypical Graph Contrastive Learning for Recommendation" Applied Sciences 15, no. 4: 1961. https://doi.org/10.3390/app15041961
APA StyleWei, T., Yang, C., & Zheng, Y. (2025). Prototypical Graph Contrastive Learning for Recommendation. Applied Sciences, 15(4), 1961. https://doi.org/10.3390/app15041961






