CFD Numerical Simulation of Slurry Flow Characteristics Under the Clogged Form of Coal Gangue Slurry Transportation Pipeline

Abstract

Slurry filling technology has been increasingly adopted in coal mines in the northwest region. However, due to the complexity of slurry transport pipelines, blockages remain a frequent issue. These blockages can reduce operational efficiency, with different blockage types causing varying levels of damage. Despite the significance of this issue, there is limited in-depth analysis in the literature, especially regarding the role of pressure in pipeline blockages. This study utilizes FLUENT 2020R2 (the fluid simulation software) for computational fluid dynamics simulations of slurry pipeline blockages, focusing on the impact of blockage morphology, location, and extent on slurry transport pressure distribution. The results indicate that the greater the blockage extent, the more pronounced the pressure loss along the pipeline. Furthermore, blockage morphology also has a varying effect on pressure drop. At lower blockage levels, the pressure drop variation across the three blockage types is relatively minor. However, when the blockage exceeds 50%, sedimentation-type blockages (B-blockage) cause the most significant harm. The study identifies the underlying causes of this and provides recommendations to mitigate sedimentation-type blockages. Within 1 m downstream of the blockage, the flow velocity rapidly decreases to near zero, creating a stagnant zone that accelerates the deposition of gangue particles, thereby worsening the blockage. After a sudden blockage, the location of the blockage has minimal impact on pressure drop. The influence on slurry pressure is ranked as follows: sedimentation-type blockage (B-blockage) > composite blockage (C-blockage) > attachment-type blockage (A-blockage).

1. Introduction

Pipeline blockage is a common issue in mining and slurry filling operations. Slurry filling technology, tailored to the unique characteristics of mines in the western regions—such as large volumes of gangue and significant underground void space—optimizes and integrates traditional techniques, including inter-layer grouting, coal mine fire prevention, and long-distance pipeline transport. This results in the development of a new, regionally adaptive, process-matching, and cost-effective slurry filling technology [1]. The technology has been successfully applied in several coal mines in the Northwestern region, such as Longwang Gou, Huang Ling No. 2, and Bulian Gou coal mines, for gangue slurry treatment. This demonstrates that the technology can effectively address the treatment needs of coal-based solid waste, yielding significant economic and social benefits [2]. However, this technology also faces the issue of pipeline blockages in the slurry transport system. The technology involves mixing coal-based solid waste with water in a specific ratio, and then preparing a slurry with the required concentration either on the surface or underground for transportation. The slurry is pumped through pipelines, with the remaining voids in the underground mined-out areas serving as the filling location, enabling in situ filling of solid waste and achieving zero discharge on the surface. Therefore, the slurry transport pipeline is the critical component of this filling technology. However, various factors can lead to pipeline blockages, which reduce the pipe diameter, increase the flow resistance, cause a significant rise in pumping pressure, and decrease the slurry flow rate. In severe cases, insufficient flow velocity may result in complete blockage, preventing continuous and timely filling of the mined-out spaces.

Foreign researchers [3,4,5] have conducted in-depth studies on the detection and localization of pipeline blockages. Zhao Lian and Xu Zhenliang [6] analyzed the causes of slurry pipeline blockages, focusing on the effects of factors such as flow velocity and slurry concentration on the blockage mechanism. Zhang Qinli et al. [7] used fault tree analysis to investigate various factors and their logical relationships contributing to filling pipeline blockages, identifying 16 key factors, including improper slurry mix and excessive bends, as the most significant contributors. Han Xuejing et al. [8] examined the causes of pipeline blockages due to excessive instantaneous slurry flow velocity. Liu Fuming [9] conducted a computational fluid dynamics (CFD) simulation to analyze the flow characteristics of slurry in a 90° elbow pipe, investigating the effects of varying velocity and particle size on the particle velocity distribution and volume fraction. The results indicated that at lower velocities, slurry tends to experience phase separation, whereas at higher velocities, the particle distribution becomes more uniform, which is in line with the requirements for long-distance pipeline transportation. Pipeline blockage not only increases operating costs and maintenance costs, leading to production delays, but may also cause slurry leakage; pollute groundwater and soil; and further cause environmental problems, such as soil erosion and ecological damage. In addition, blockage accidents may reduce the efficiency of filling operations, lead to waste of resources, and affect the economic benefits of enterprises [10,11]. In slurry injection pipelines, blockage is inevitable, and there are different ways of blockage, and each blockage has different hazards to slurry transportation. In this regard, few studies have been conducted. Blockage will cause changes in flow rate, pressure, and other factors [12,13,14,15], which will cause vibrations on the pipe wall. We use Distributed Acoustic Sensing (DAS) to be sensitive to phase, thereby achieving vibration testing [16]. Existing CFD simulation studies primarily focus on conventional slurry transportation processes, often overlooking the influence of different blockage types on flow behavior. In contrast, this study concentrates on the transportation of gangue slurry under various blockage conditions. Compared to traditional slurries, gangue slurry exhibits distinct rheological properties, making it particularly susceptible to significant impacts from factors such as blockage and deposition during transport. Our research provides an in-depth analysis of the transportation characteristics of gangue slurry under different blockage types, thus filling a critical gap in this field. To assess the impact of the internal fluid flow on pipe wall vibrations, CFD simulations using FLUENT software were employed to analyze the pressure and velocity distribution characteristics of the slurry in the pipeline under different blockage scenarios. This approach aims to alleviate the blockage issues encountered in slurry transportation.

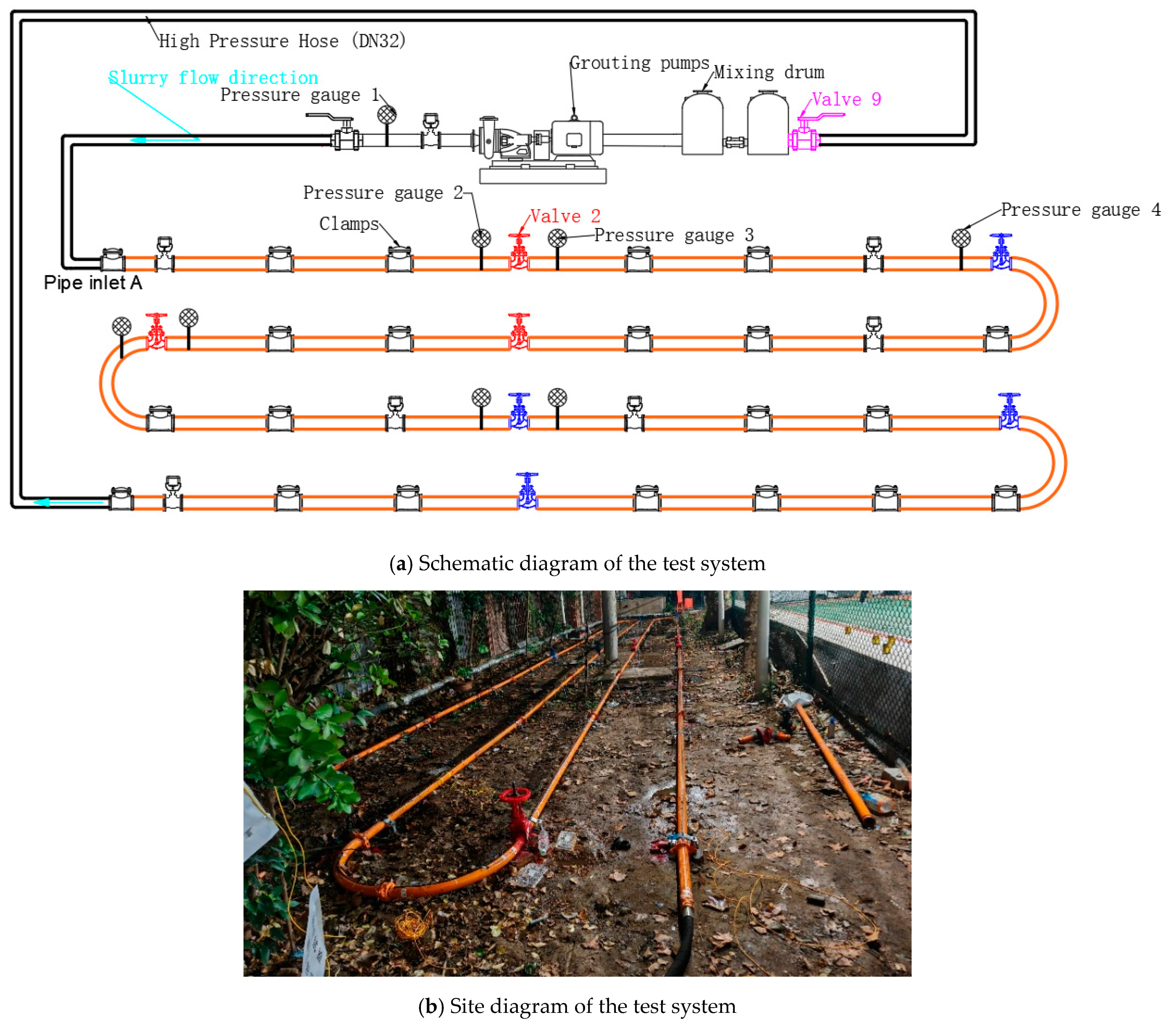
2. Long-Distance Gangue Slurry Ring Tube Experiment

2.1. Test System

This experiment simulates the straight pipe section of the underground slurry filling and transport system, using adjacent and low-position grouting techniques. A tailings slurry transport system was built using the existing grouting pump and pipeline setup. The system includes a slurry storage tank, grouting tank, pump, flow meter, pressure gauge, valves, and pipeline.

The experimental system spans 130.71 m, comprising 89.71 m of grouting pipeline and 40 m of high-pressure rubber hose. The grouting pipeline consists of 28 straight pipes (3 m in length), 3 elbow pipes (1 m in length), and 2 connecting pipes (0.5 m in length). These components are arranged into 4 rows, each containing 7 straight pipes, as shown in Figure 1.

The grouting pump is essential for tailings slurry transport, providing the energy needed to maintain continuous flow. This experiment uses a pressure-based transport method, with pump selection being a key factor. Common pump types include reciprocating, centrifugal, and diaphragm pumps. Considering the short pipeline and low lifting height, and based on hydraulic calculations, the 2ZBY120/15-18.5-type mining hydraulic grouting pump was selected. This pump has a flow rate range of 30–120 L/min and a grouting pressure range of 0–15 MPa.

Pressure gauges monitor the pipeline pressure. Pressure gauge 1 measures the initial pressure, while pressure gauges 2 and 3 monitor variations downstream of the blockage. The YK-100B digital pressure gauge was chosen for this purpose (see Figure 2).

2.2. Introduction to Distribution

Based on the experimental site, FLUENT numerical simulations were conducted, modeling the first row of pipes on-site, which is 43 m long. The average pressure value from pressure gauge 4 was used as the boundary condition for the pressure outlet. The pressures measured by pressure gauges 1, 2, and 3 were compared with corresponding points in the simulation. The results of this comparison are illustrated in Figure 3.

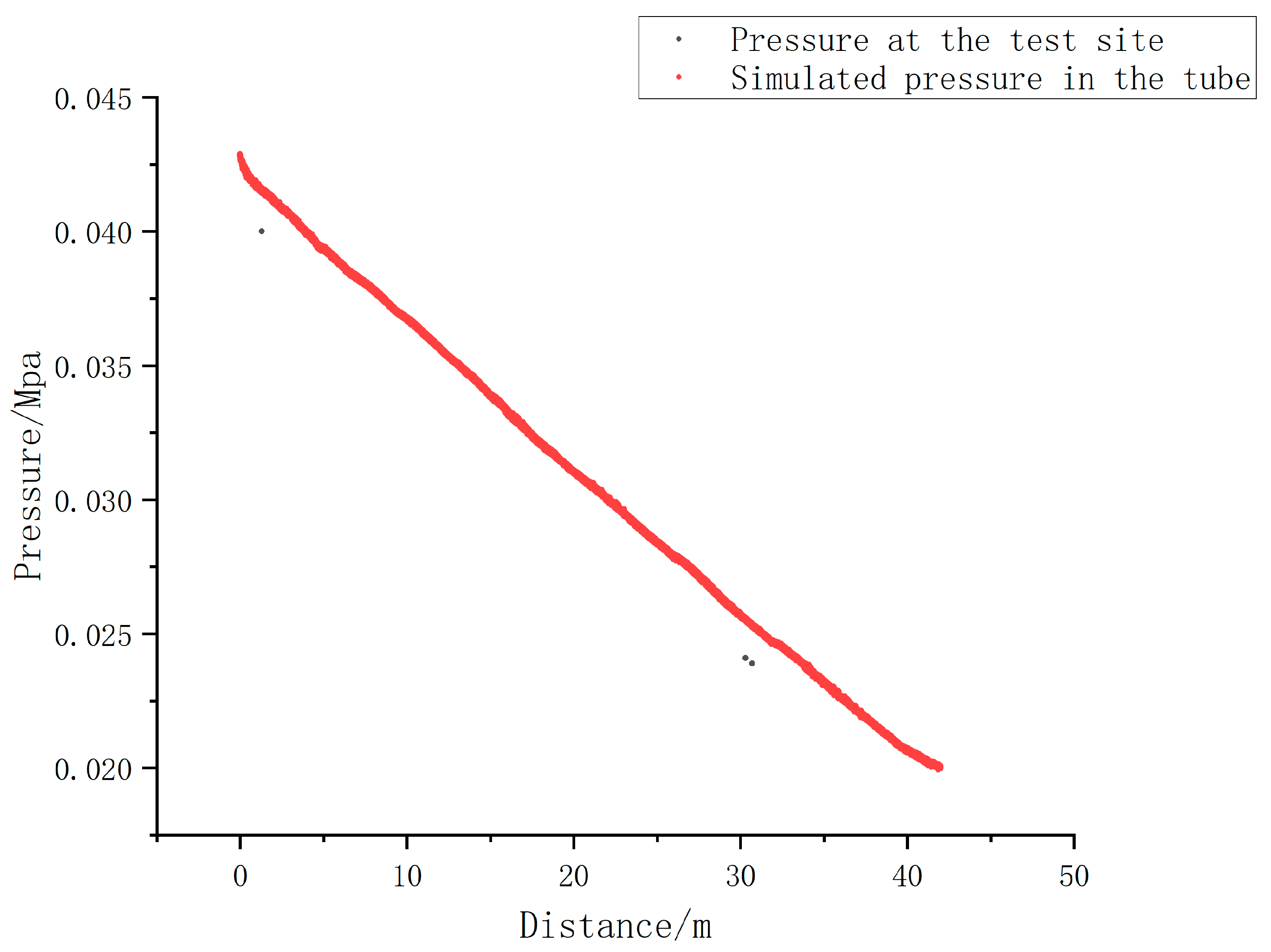
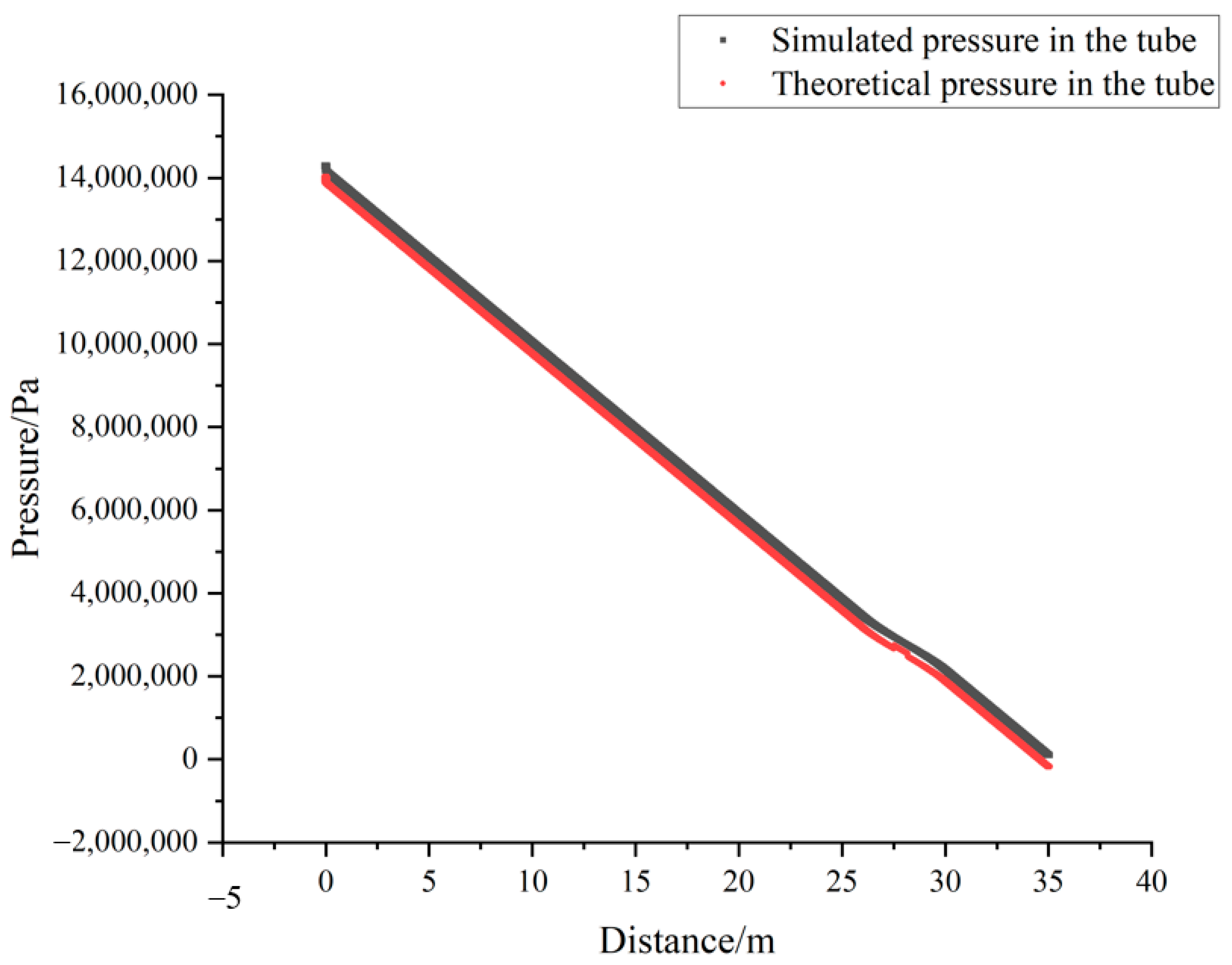
2.3. Comparative Analysis of Simulations and Experiments

To validate the fluid characteristics of this experiment, FLUENT numerical simulations were conducted to analyze the fluid properties of the gangue slurry transport experiment, and a comparison was made.

As shown in Figure 3, the pressure distribution obtained from the software simulation is generally consistent with the results from the experimental site. Comparing the pressure values from pressure gauges 1, 2, and 3 with the simulation data, the agreement is satisfactory, with the error remaining within 6%. This indicates that the on-site experimental measurements are relatively accurate.

3. Establishment of a Grouting Pipeline Blockage Model

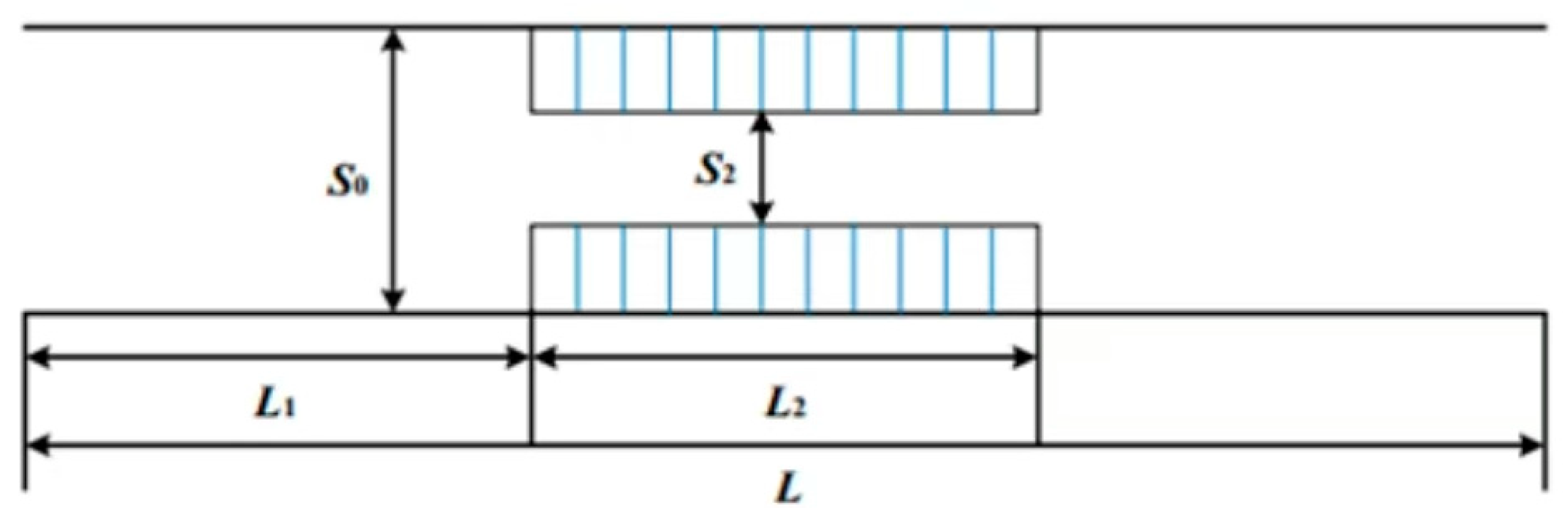
3.1. Establishment of Gangue Pipeline Blockage Form

The length of the pipeline in the grout filling system varies, and during numerical simulations, a buffer zone is commonly included to ensure adequate grout flow. In the experiment, an extra horizontal section of 3 m to 5 m is chosen as the buffer zone. In this study, a 5 m long straight pipe is selected as the buffer zone. Based on the field conditions, this study simulates a 21 m long horizontal straight pipe and a 90° elbow with a 2 m bending radius, using 16 Mn wear-resistant seamless steel pipes. And based on the process of blockage formation in the on-site grouting pipeline, blockages can be classified into attachment-type blockages (A-blockage), deposition-type blockages (B-blockage), and composite blockages (C-blockage), as shown in Figure 4 [17]. Furthermore, according to the cause and nature of the blockage, they can be categorized into partial blockages and complete blockages. Partial blockages can be further divided into single blockages and multiple blockages [18].

In actual grouting pipeline blockages, most blockages are partial rather than complete. The shape and distribution of the blocking material are irregular and unpredictable. In this study, the simulations focus on three specific types of blockages: attachment-type, deposition-type, and composite blockages. To preserve the integrity of characteristic parameters and minimize the complexity of subsequent model calculations, the irregular shape of the blocking material within the pipeline is simplified and approximated to a regular shape, as shown in Figure 5.

In the Figure 5, S0 represents the cross-sectional area of the grout pipeline, in square meters (m²); S2 represents the cross-sectional area of the pipeline segment affected by blockage, also in square meters (m²); L₁ is the distance from the start of the pipeline to the beginning of the blocked section, in meters (m); L₂ is the length of the blocked segment in the pipeline, in meters (m); and L is the total simulated length of the grout pipeline, in meters (m).

To thoroughly investigate the flow characteristics of the grout in the injection pipeline, a 1:1 scale three-dimensional model of the grout pipeline and blockage scenario was established using ANSYS. The three-dimensional physical model of the grout pipeline, with different blockage locations and degrees of blockage, is established as shown in Figure 6. The cross-sectional view of the pipeline is shown in Figure 7. The experiment primarily utilizes SolidWorks to create the 3D geometric model, with the fluid inside the pipe being filled using the Volume Extraction command. The ANSYS-mess module is then employed to generate the mesh for the fluid inside the pipeline, ensuring accurate simulation of the fluid flow. Due to the relatively simple pipeline structure, the mesh generation prioritizes the use of hexahedral elements for accuracy and computational efficiency. In areas with irregular shapes, such as blockage locations, tetrahedral elements are used. This choice is made because hexahedral meshes offer better quality, faster convergence, and lower computational costs, while tetrahedral meshes are more adaptable, efficiently filling complex geometric shapes. Additionally, mesh refinement is applied near the pipe wall, the blockage region, and the inlet and outlet areas. The use of hexahedral meshes yielded good results, with the total number of mesh elements ranging from 1.29 million to 1.4 million. Finally, mesh quality was evaluated using the Skewness criterion, which indicated that the element quality was classified as excellent and good.

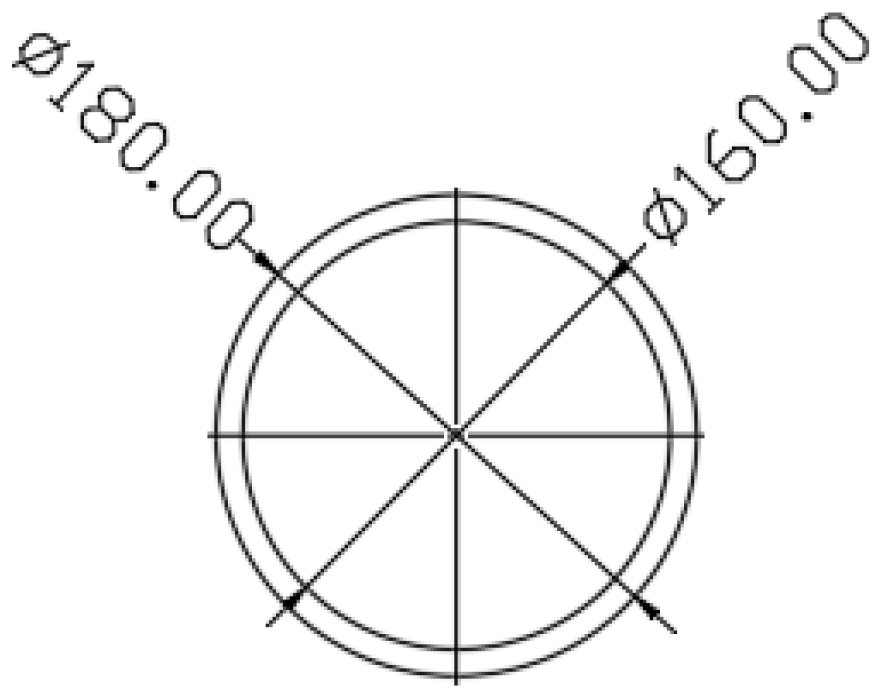
3.2. Establishment of Computational Models

The slurry used in the grouting system has a density of 1700 kg/m³, yield stress of 368.3 Pa, and viscosity of 0.5 Pa·s. The flow regime in the pipeline (laminar, turbulent, or transitional) is determined using the Reynolds number. The Reynolds number is calculated using the following equation [19]:

$$R_e={\displaystyle \frac{v\rho d}{\mu }},$$

(1)

In the equation, ρ represents the fluid density, v is the average velocity at the cross-section, μ denotes the dynamic viscosity of the fluid, and d refers to the inner diameter of the filling pipeline.

Given that the density of the filling slurry is 1700 kg/m³, the pipeline transport velocity is selected as 2 m/s, and the diameter of the transport pipeline is 0.16 m.

$$R_e={\displaystyle \frac{\nu \rho d}{\eta }}={\displaystyle \frac{2\times 1700\times 0.16}{0.5}}=1088$$

The critical Reynolds number for a Newtonian fluid is 2100. For non-Newtonian Bingham slurry in engineering applications, the critical Reynolds number is variable and generally exceeds 2100. Therefore, the flow within the slurry pipeline remains in a laminar state. The motion of any substance must satisfy the mass conservation equation, which, in a Cartesian coordinate system, is expressed as follows:

Equation for conservation of fluid mass:

$${\displaystyle \frac{\partial \rho }{\partial t}}+{\displaystyle \frac{\partial \rho u_i}{\partial x_i}}=0$$

(2)

Particle mass conservation equation:

$${\displaystyle \frac{\partial {\rho }_p}{\partial t}}+{\displaystyle \frac{\partial {\rho }_p{U}_{pj}}{\partial x_j}}={\displaystyle \frac{\partial }{\partial x_j}}\left({\displaystyle \frac{{\nu }_p}{{\sigma }_p}}{\displaystyle \frac{\partial {\rho }_p}{\partial x_j}}\right),$$

(3)

In the equation, ρ represents the fluid density, xi is the coordinate component in the i-direction, and u_i denotes the velocity in the i-direction. Moreover, x_i refers to the Eulerian coordinates, with i = 1, 2, and 3; ρ represents the liquid phase density; ${\rho }_p$ represents the solid phase density; $u_i$ is the velocity vector of the liquid phase; $U_{pj}$ denotes the velocity vector of the solid phase; and ${\nu }_p$ is the turbulent diffusion coefficient.

During the motion of the fluid, the momentum conservation equation also applies. Essentially, the momentum equation follows Newto n’s second law, which states that the rate of change in momentum at a fluid node is equal to the sum of all external forces acting on that node. The equation is expressed as follows:

$${\displaystyle \frac{\partial }{\partial t}}({\alpha }_i{\rho }_i{\upsilon }_i)+\nabla ·({\alpha }_i{\rho }_i{\upsilon }_i{\upsilon }_i)={\alpha }_i{\rho }_{i}g+M_i-{\alpha }_i\nabla p+\nabla ·{\tau }_i,$$

(4)

$${\tau }_l={\alpha }_l{\mu }_l(\nabla {\upsilon }_l+\nabla {\upsilon }_l^T),$$

(5)

$${\tau }_s={\alpha }_s{\mu }_s\left(\nabla {\upsilon }_s+\nabla {\upsilon }_s^T\right)+{\alpha }_s\left({\lambda }_s-{\displaystyle \frac{2}{3}}{\mu }_s\right)\nabla ·{\upsilon }_s,$$

(6)

where

• ${\tau }_i$ represents the shear stress tensor;
• μ denotes the shear viscosity;
• $M_i$ indicates the momentum exchange between the solid and liquid phases;
• ${\lambda }_s$ represents the overall viscosity of the solid phase.

3.3. FLUENT Software Settings

FLUENT 2020R2 is a commonly used CFD [20,21,22] software for simulating fluid flows, heat transfer, and chemical reactions. It can provide results that closely approximate experimental findings and reflect the overall characteristics of fluid motion, such as flow velocity, pressure, and other dynamic parameters. This study investigates the flow behavior of slurry in injection pipelines, where the pipeline temperature is approximately 20 °C. Since the filling slurry is a multiphase complex fluid containing gas, liquid, and solid phases, and it behaves as a non-Newtonian Bingham plastic [23,24], the slurry maintains its homogeneity and uniformity during pipeline transport without segregation or layering. As a simplification, the slurry flow is assumed to be single-phase. The semi-implicit method for pressure-coupling equations is selected. The inlet is set as a velocity inlet with an inflow velocity of 2 m/s, and the outlet is set as a pressure outlet with a static pressure of 10,100 Pa (relative pressure under atmospheric conditions). To verify the accuracy of the simulation model and computational precision, a residual monitoring window is set, and the residual curve is shown in Figure 8. After fluid initialization, the iteration step is set to 600 steps for computation. During the iterations, the residual curves for each condition converge, and the flux conservation at the inlet and outlet approaches zero, as shown in Figure 9. This indicates that the simulation model closely represents the actual slurry blockage scenarios. The slurry is modeled as a non-Newtonian Bingham fluid, specifically using the H-B model. The slurry density is set to 1700 kg/m³, and the H-B model parameters are configured as follows: the exponent is set to 1, the critical shear stress is 100 r/s, the apparent viscosity is 165.6 Pa·s, and the slurry yield stress is 8.277 Pa.

The rheological model for the slurry is recommended to be the Herschel–Bulkley model, abbreviated as H-B model, with the general equation as follows:

$$\tau ={\tau }_0+\mu {\gamma }^n,$$

(7)

where

• $\tau$ is the shear stress, in Pa;
• $\gamma$ is the shear rate, in s⁻¹;
• μ is the apparent viscosity, in Pa·s;
• τ₀ is the initial yield stress, in Pa;
• n is the flow behavior index. When n = 1 and τ₀ = 0, it is a Newtonian fluid;
• when n = 1 and, τ₀ > 0, it is a Bingham plastic;
• when n > 1, it is a dilatant fluid;
• when n < 1, it is a pseudoplastic fluid.

3.4. Simulated Condition Settings

In this study, slurry flow characteristics under pipeline blockage conditions were investigated for a slurry concentration of 70% and density of 1.7 t/m³, with a filling capacity of 130 m³/h at the Buliangou Coal Mine. The analysis focuses on three variables: blockage degree, position, and morphology. The aim is to explore the relationship between these variables and the changes in pipeline pressure along the length of the pipeline, as well as the pressure drop between the pipeline inlet and outlet. The blockage degree is categorized into three levels; the blockage morphology is also classified into three levels; and the blockage position is set at two levels—straight pipe and bent pipe. Additionally, a no-blockage condition is included as a control. In total, 19 experimental conditions were designed, as shown in

Table 1. Slurry pipeline simulation scheme.

Case Number	The Degree of Blockage	Blockage Pattern	Blockage Location/m
1	0%	not	0
2–7	25%	A, B, and C blockages	13.0 The center of the elbow
8–13	50%	A, B, and C blockages	13.0 The center of the elbow
14–19	75%	A, B, and C blockages	13.0 The center of the elbow

.

4. Analysis of CFD Simulation Results

4.1. Analysis of Simulation Results of Non-Clogging Conditions

According to the Bernoulli equation for fluid transport in pipelines, the energy equation for slurry transport in filling systems is given by the following:

$$P+\rho gH={\displaystyle \frac{\rho {\nu }^2}{2}}+I,$$

(8)

In the equation, P represents the pressure provided by the filling pump at the pipeline inlet (Pa); $P$ denotes the slurry density (kg/m³); g is the gravitational acceleration (9.81 m/s²); H refers to the height difference between the pipeline inlet and outlet (m); v is the slurry flow velocity at the outlet (m/s); and I is the total resistance loss in the pipeline (Pa).

Generally, the pipeline resistance loss consists of two parts [25,26]: the frictional loss along the straight pipe section, i_s, and the local resistance loss, i_b, which is primarily associated with 90° elbows [27,28,29].

The frictional resistance loss, i_s, along the straight pipe section can be expressed as the product of the total length of the straight section, Ls, and the unit length frictional resistance loss, i_s, as shown in the following equation:

$$i_s={\displaystyle \frac{16}{3D}}{\tau }_0+\eta {\displaystyle \frac{32\nu }{D^2}},$$

(9)

where τ₀ is the initial yield stress of the fluid, D is the pipeline diameter, η is the fluid viscosity, and ν is the fluid’s kinematic viscosity (dynamic viscosity divided by density).

The flow behavior of slurry in pipe bends is more complex, and in the literature, the local losses in the pipe-bend section are generally considered in conjunction with the overall frictional resistance losses along the pipe. The local resistance is typically estimated as 10% to 20% of the total resistance loss in the pipeline. As part of the pipeline system, the pipe bend shares the same inner diameter and slurry parameters as the straight sections, and its resistance loss can also be calculated based on the unit length. The unit length local resistance loss, i_b, of the pipe bend is typically expressed as a multiple of the unit length frictional resistance loss, $i_s$, as follows:

$$i_b=k{s}_i=k({\displaystyle \frac{16}{3D}}{\tau }_0+\eta {\displaystyle \frac{32\nu }{D^2}}),$$

(10)

Under the condition of no blockage, the pressure distribution of the pipeline during normal operation is shown in Figure 10, which includes both the simulation results and theoretical calculations. As shown in Figure 10, the pressure distribution obtained from the software simulation aligns closely with the theoretical calculation results, and the pressure decreases linearly with increasing pipeline length. Overall, the calculated pressure values and the simulation results are in good agreement, with a deviation of 9.12%. This error primarily arises from the selection of the coefficient k at the pipe bend. Due to the complex flow conditions at the bend, it is difficult to accurately determine the k value. Nevertheless, it can be concluded that this model design closely reflects the actual operating conditions of the pipeline.

4.2. Analysis of Simulation Results of Blockage Conditions

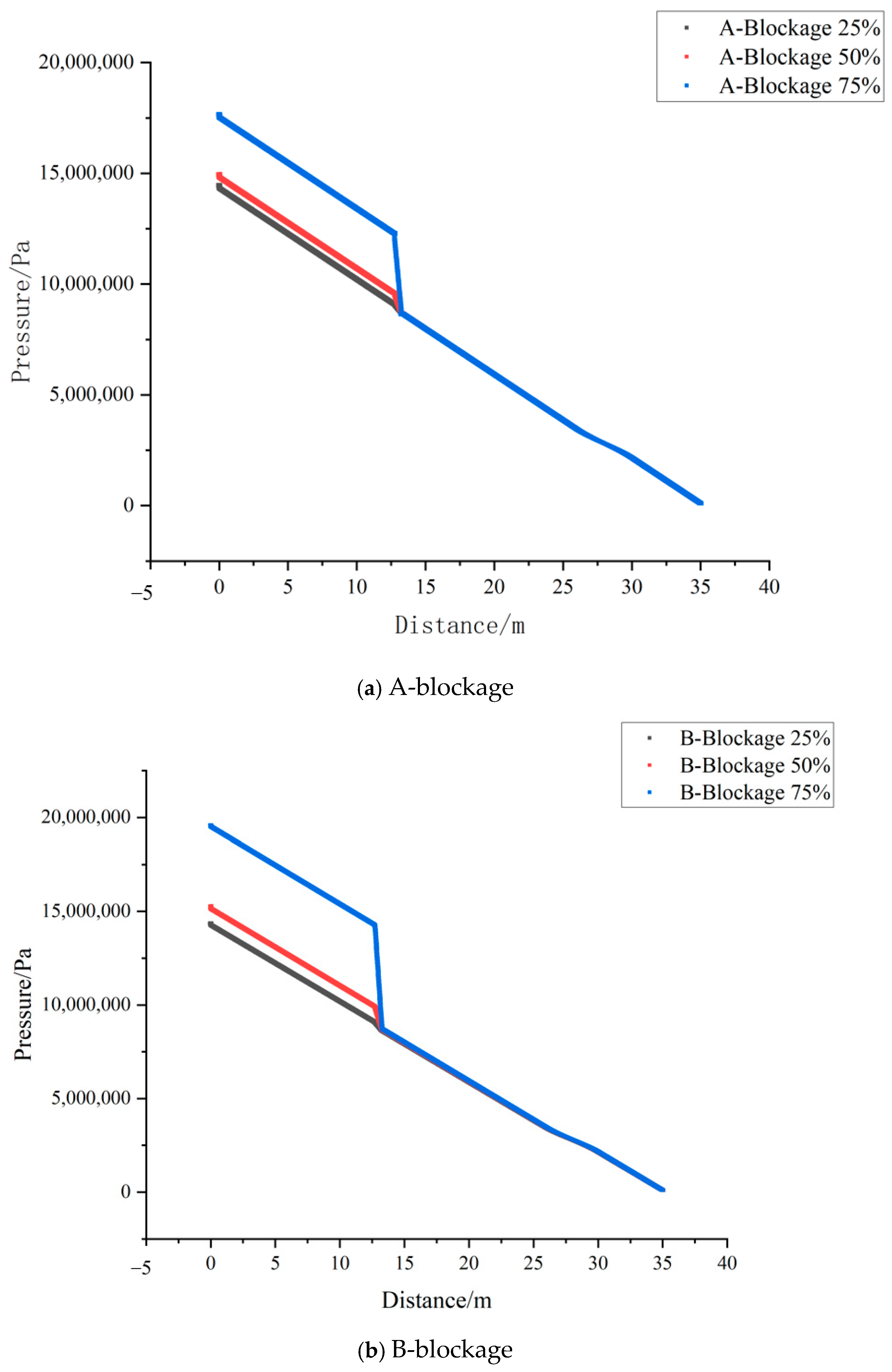
4.2.1. The Influence of the Degree of Blockage on the Distribution of Pipeline Characteristics

To investigate the relationship between blockage degree and pipeline pressure drop, experimental data under three different blockage shapes were selected. Each set of data corresponds to three levels of blockage: 25%, 50%, and 75%. The pressure along the pipeline for each condition was recorded and compared, as shown in Figure 11.

As observed in Figure 11, under the three types of blockage, blockage will cause the overall pressure in the pipe to increase. It is obvious that after the blockage of type B, the pressure is too high, but overall, the pressure-drop values under different blockage degrees increase with the increase in the blockage degree. On the other hand, when the blockage degree is relatively low (i.e., less than 50%), the variation in pressure along the pipeline is minimal, with the maximum pressure drop being only about 3% of the maximum pressure. However, when the blockage degree exceeds 75%, the pressure drop along the pipeline increases sharply, with the minimum pressure drop being over 17% of the maximum pressure. This indicates that the degree of blockage is a significant factor influencing the water flow pressure in the pipeline.

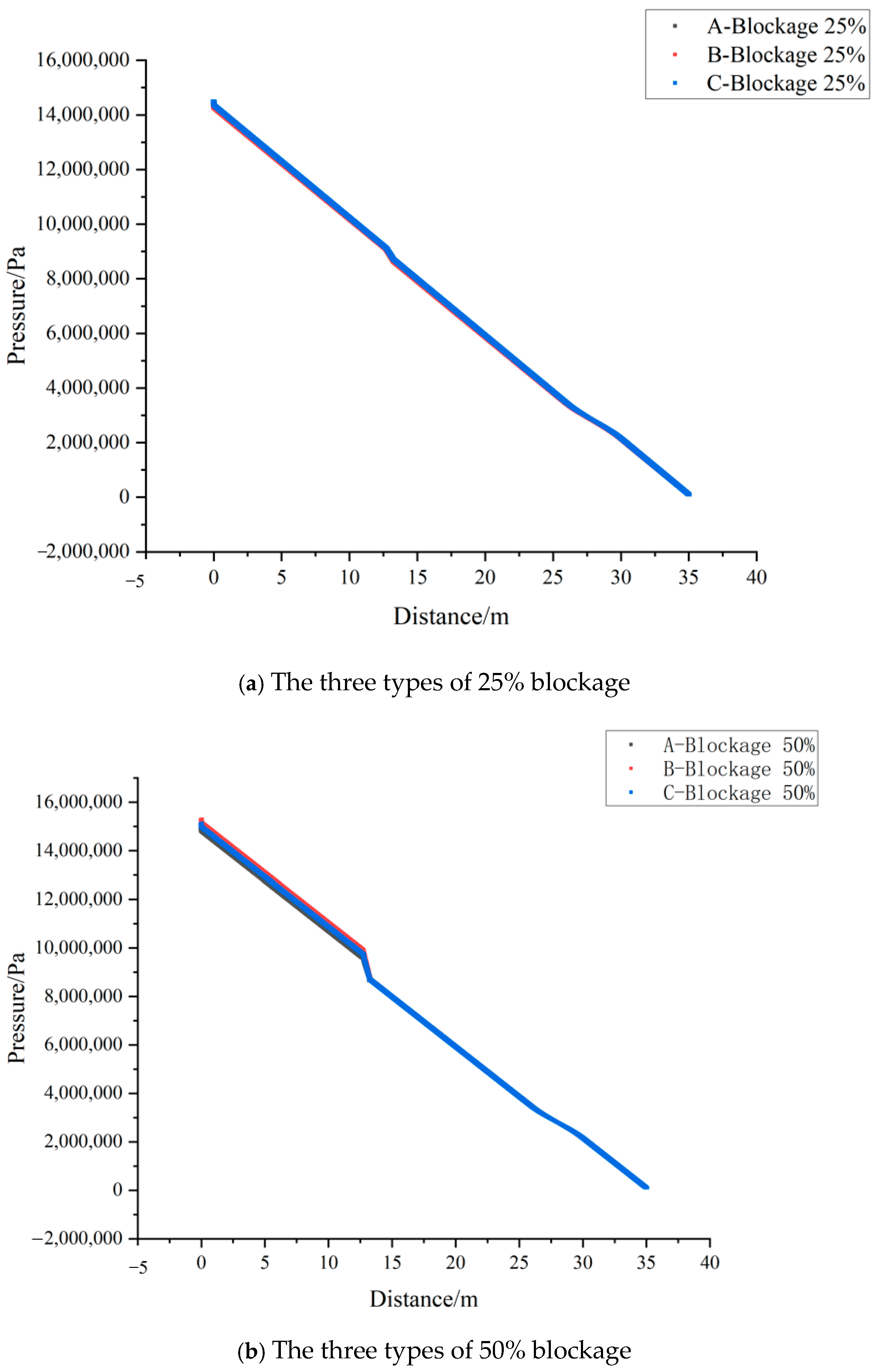
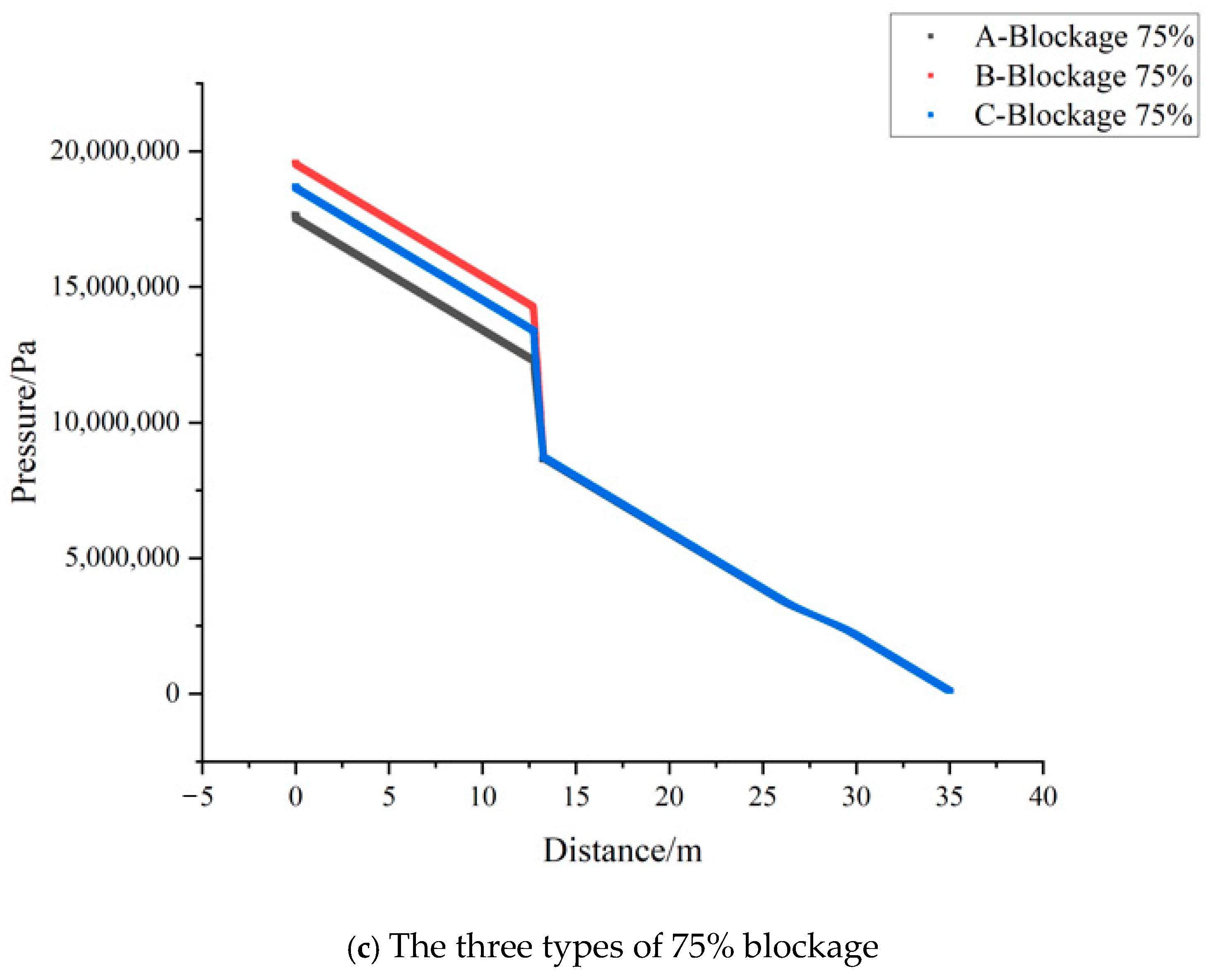
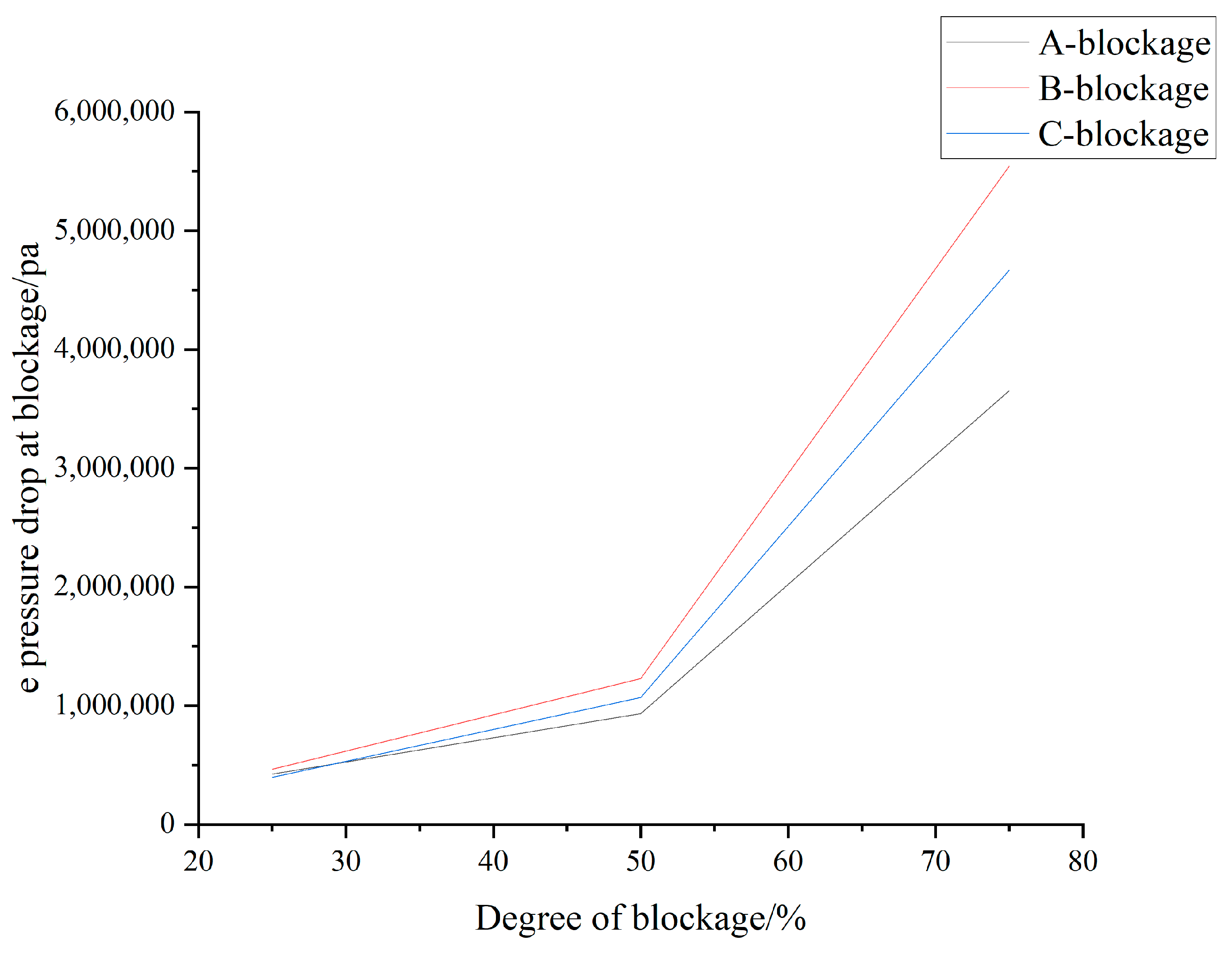
4.2.2. The Influence of Blockage Pattern on the Distribution of Pipeline Characteristics

To study the effect of blockage shape on pressure distribution, three common shapes were simulated under identical conditions. The resulting pressure variations for each shape are compared in Figure 12.

Under a 25% blockage condition, the pressure drop along the pipeline for all three shapes is nearly identical. When the blockage is 50%, the three types of blockages have different changes in the pressure drop along the way. As the blockage degree increases, the pressure drop increases, and the three types of blockages become more and more obvious. As the blockage degree increases, the pressure drop becomes more pronounced. Notably, the pressure drop for B-blockage type is greater than that for C- and A-blockage types, with the C type being larger than the A type. Especially when the blockage is 75%, it is obvious that the b-blockage type, that is, sedimentation-type blockage, is the most harmful. Therefore, the B-blockage type, which corresponds to deposition-type blockage, presents the most severe hazard. The primary cause of B-blockage lies in the behavior of the slurry particles inside the pipeline. These particles lose their original balance and, under the influence of gravity, gradually settle to the bottom of the pipeline, forming a deposition-type blockage. As the particles settle, their velocity decreases, eventually coming to a stop due to the frictional resistance at the rough surface of the pipeline. The greater the roughness of the pipe wall, the larger the frictional resistance, and the more likely the particles are to stop, accelerating the formation of deposition-type blockage. To prevent deposition-type blockage, it is recommended to select pipes with smooth inner walls and low roughness when designing slurry injection pipelines.

4.2.3. The Influence of Blockage Location on Pipeline Pressure Distribution

Simulations were conducted to examine the effect of blockage location on pressure distribution, focusing on straight and bent sections under a 75% blockage condition. The pressure drop along the pipeline was compared for three blockage shapes. Results are presented in Figure 13.

Based on the analysis of Figure 13, it can be concluded that the variation in blockage location has minimal impact on the pressure distribution. The pressure drop along the straight section of the pipeline decreases approximately linearly, while in the bent section, the pressure follows an arcuate reduction in accordance with the theoretical model. When the blockage occurs at the bend, the pressure first decreases linearly along the arc at the blockage point and then continues to drop along the original curvature of the bend.

Overall, the differences in pressure distribution due to blockage location are insignificant. Whether in straight or bent sections, the pressure-drop variations show little distinction. Therefore, compared to blockage degree and blockage shape, the location of the blockage has a smaller effect on the water flow pressure inside the pipeline.

According to

Table 2. Pressure-drop statistics for different blockage types.

Blockage Type	Pressure Drop at 25% Blockage (pa)	Pressure Drop at 25% Blockage (pa)	Pressure Drop at 25% Blockage (pa)
A-blockage	424,500	932,270	3,652,260
B-blockage	464,150	1,229,830	5,542,770
C-blockage	397,240	1,069,050	4,669,570

, Figure 14 and Figure 15, the data reveal a clear trend: as the degree of blockage increases, the pressure drop (Pa) induced by all three types of blockages (A-blockage, B-blockage, and C-blockage) rises significantly. Notably, B-blockage results in the highest pressure drop across all levels of blockage, while A-blockage causes the lowest pressure drop. At a 25% blockage degree, B-blockage leads to the greatest pressure drop of 464,150 Pa, whereas A-blockage results in the lowest pressure drop of 424,500 Pa, and C-blockage induces a pressure drop of 397,240 Pa. As the blockage degree increases to 50%, the pressure drop for B-blockage rises further to 1,229,830 Pa, significantly exceeding that of A-blockage (932,270 Pa) and C-blockage (1,069,050 Pa). At a 75% blockage degree, B-blockage causes the highest pressure drop, reaching 5,542,770 Pa, compared to 3,652,260 Pa for A-blockage and 4,669,570 Pa for C-blockage. B-blockage generates the greatest flow resistance within the pipeline, leading to the most substantial pressure drop. Therefore, timely removal of B-blockage is essential for maintaining the normal operation of the pipeline. Furthermore, as the degree of blockage increases, the pressure-drop variation becomes more pronounced, indicating a nonlinear impact of the blockage on flow behavior.

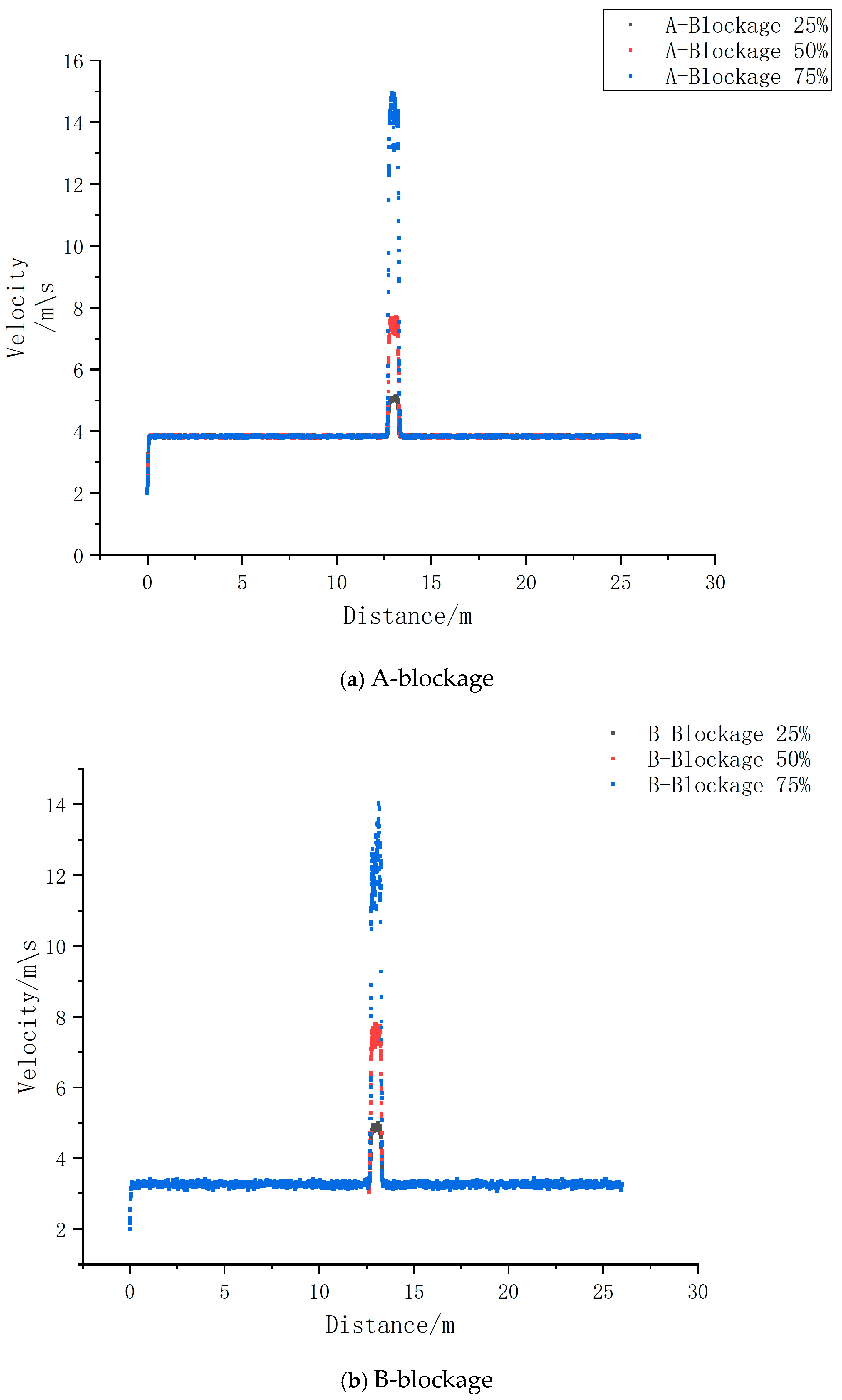
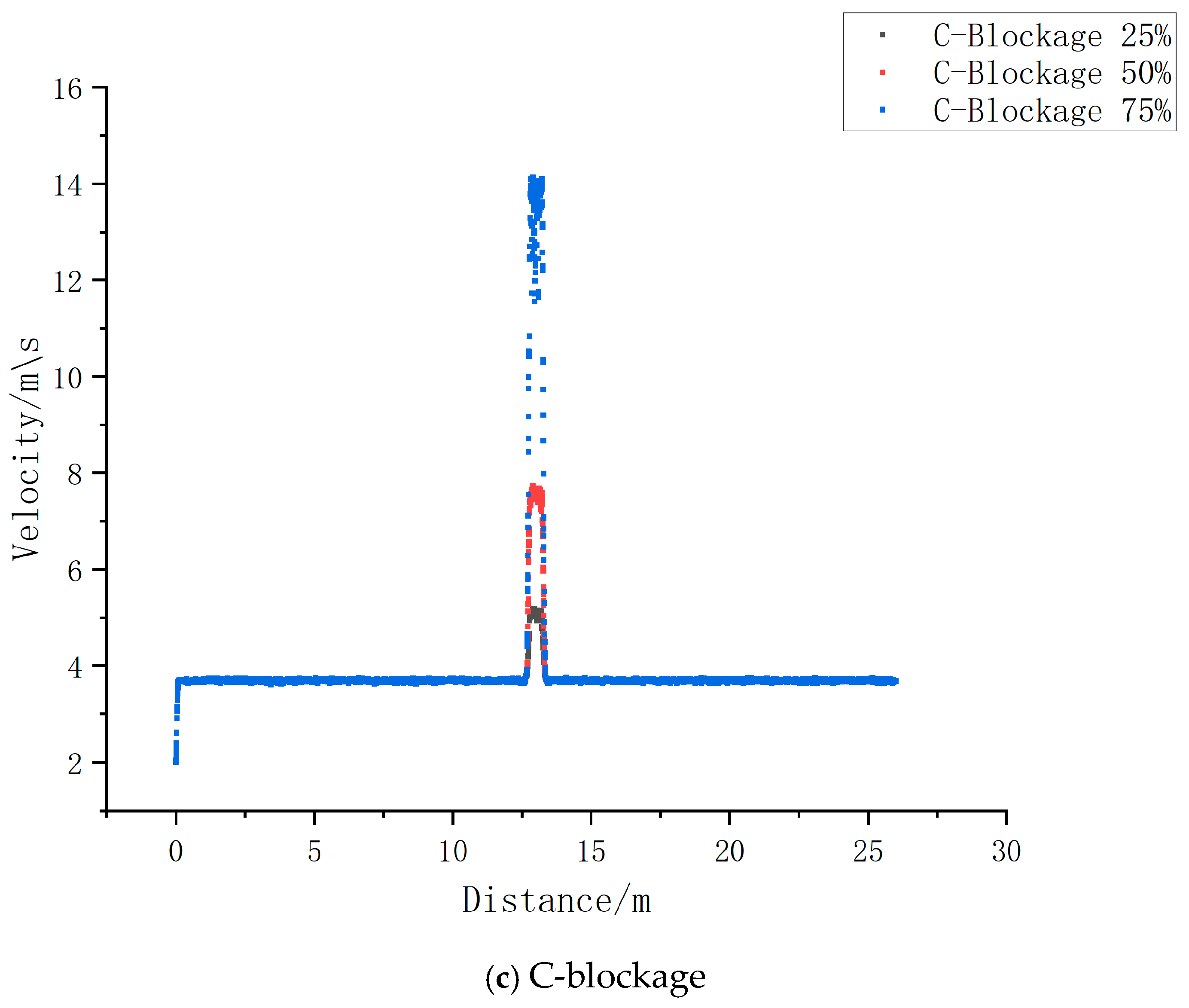
4.2.4. Analysis of the Influence of Flow Velocity Under Blockage Conditions

The effect of flow velocity on pipeline fluid flow was analyzed under three blockage shapes (25%, 50%, and 75% blockage levels).

From Figure 16, it can be observed that all three blockage shapes lead to a significant increase in flow velocity. Excessively high flow velocities can cause pipe erosion and corrosion, threatening the safe operation of the pipeline. Below the blockage and in the short section downstream, the flow velocity quickly decreases to near zero, forming a stagnation zone. This condition exacerbates the deposition of solids, thereby worsening the blockage. Notably, in the case of blockage B and C, the stagnation zone area is much larger than that of blockage shape A, indicating that different blockage shapes cause varying levels of disturbance in the subsequent section of the pipeline. Therefore, timely removal of blockages is crucial for the maintenance and management of the grout injection pipeline. To avoid the formation of B- and C-blockages, it is advisable to select pipes with smooth inner walls and low roughness during pipeline construction.

As shown in Figure 17, this study analyzes the cross-sections S1, S2, and S3 located at distances of 800 mm, 13,000 mm, and 18,000 mm from the pipeline’s inlet and outlet, respectively, as the sections for the analysis.

As seen in Figure 18, the slurry transport inside the pipeline exhibits distinct laminar flow behavior for all three blockage shapes. During slurry transport, the maximum slurry velocity consistently occurs at the center of the pipeline, forming a “flow core” where the velocity remains high. In contrast, the flow velocity at the top and bottom of the pipeline is slower. This phenomenon results from friction between the slurry and the pipeline’s top and bottom surfaces, thus creating resistance and causing the slurry’s velocity to remain highest in the center of the pipe, while the flow at the bottom and top is relatively slower.

From Figure 19, it can be observed that the flow velocity in the pipeline dramatically increases at the blockage location, reaching its maximum value within a short time. As the blockage degree increases, the velocity in the blocked region rises sharply, with the maximum flow velocity located at the center of the blockage. When the blockage degree exceeds 25%, the flow velocity in the blocked section is several times greater than that in the unblocked portion of the pipeline.

5. Conclusions

(1)

The presence of blockage results in significant pressure and velocity gradients near the blockage point. As the blockage increases, so does the pressure gradient, particularly beyond 50%, where a strong correlation with blockage characteristics is observed. Similarly, the velocity gradient increases with the blockage degree, and the relationship between the velocity gradient and the blockage characteristics is also positively correlated. Therefore, by detecting the pressure drop at the pipeline’s starting point, initial velocity, and the sharp changes in the pressure and velocity distribution curves, it is possible to detect and locate the blockage.

(2)

The effects of the three blockage shapes on the internal pressure of the pipeline are ranked as follows: B-blockage has the greatest impact, followed by C-blockage, and A-blockage has the least impact. When the blockage degree is less than 50%, the changes in the pressure drop along the pipeline caused by the three blockage types are not significantly different. However, as the blockage degree increases, the pressure variations, particularly in B- and C-blockages, become more pronounced, with a larger fluctuation in the pressure along the pipeline. Among these, the B-blockage results in the most dramatic pressure changes. The formation of such blockages was analyzed in detail, and corresponding suggestions were proposed to address them.

(3)

In all three blockage types, the flow of slurry in the pipeline is characterized by distinct laminar flow, with the maximum flow velocity occurring at the center of the pipeline, forming a “flow core”. The velocity at the top and bottom is lower due to friction with the pipeline surface. Moreover, the blockage shape significantly affects the flow velocity and pipeline safety. The stagnant flow region (dead zone) area for B- and C-blockages is larger than that for A-blockage, underscoring the importance of timely blockage removal. To prevent blockages, it is recommended to use pipeline materials with smooth inner surfaces and low roughness.