Abstract
In order to realize effective attitude-predictive control during large-diameter shield tunneling, this study established an intelligent framework for attitude prediction. Specifically, a principal component analysis–support vector regression (PCA-SVR) hybrid model was constructed, based on principal component analysis. The principal component analysis method was used to mine the relevant input parameters and reduce the accompanying data noise. SVR used statistical learning and structural risk minimization to overcome data overfitting. Taking a large-diameter shield tunnel, the Zhuhai Xingye Express Tunnel, as an example, the proposed PCA-SVR model was validated by considering tunnel excavation parameters, geometric parameters, and geological parameters. At the same time, the correlation coefficient was used to analyze the relationship between input parameters and attitude parameters. The results show that the propulsion cylinder pressure is an important factor affecting the trajectory of attitude motion. The geometrical and geological parameters of the shield have a strong correlation with the attitude parameters. The attitude parameters predicted by the model are within the range of the corresponding monitoring data. The high prediction accuracy verifies that the proposed PCA-SVR hybrid model can accurately predict the attitude parameters during shield tunneling. The prediction framework can be used for reference for the attitude-prediction control of shields in similar projects.
1. Introduction
With the continuous development of urbanization, urban traffic has become increasingly tense, and urban rail transit is the main method for alleviating traffic problems. Shield construction technology has continuously developed, and shield tunneling is characterized by high cost efficiency and low disturbance to the surrounding soil. Thus, it is widely used in the construction of urban highway tunnels [1,2]. Owing to the lack of certain mature guiding theories and prediction methods, the attitude deviation of shields is severe, frequently exceeding the limit. This affects the safety and efficiency of shield construction, leading to problems, such as surface subsidence, shield axis deviation, and segment floating, which constitute hidden dangers for normal tunnel operations [3,4,5]. The machine learning method can combine various monitoring data, such as excavation, geological, and geometric parameters. In addition, it has a self-updating mechanism and dynamic prediction ability [6,7,8,9]. Thus, machine learning can intelligently regulate and optimize the excavation process, solving the randomness and nonlinear problems of the excavation process [10,11]. Owing to the concealability of shield construction and the lack of clarity regarding the attitude migration mechanism of shields, attitude control mainly depends on the experience of shield operators [12]. Thus, it is necessary to study machine learning algorithms for the large-diameter shield-posture prediction effect.
Presently, the research status of machine learning in shield tunneling is focused on four challenges of shield-tunneling sites, such as the tunneling parameters, stratum category and bad geology, surface deformation, and the attitude deviation of shield tunneling [13]. The machine learning methods currently used in shield-tunnel engineering mainly include support vector machines (SVMs), neural networks, and random forests (RFs). Support vector regression (SVR) is a commonly used machine learning method in shield-tunnel construction [14,15,16].
To prevent the shield attitude deviation from exceeding the limit, it is important to adjust the driving path in time. By predicting the shield-tunneling attitude deviation, the relationship between the tunneling, geological, and geometric parameters and the attitude deviation parameters can be investigated, which can significantly guide the operator to adjust the attitude in time and prevent the attitude deviation of shield tunneling [6,17,18,19]. Shen et al. [20] considered the database of shield tunneling, geological conditions, and operation parameters. They used the wavelet threshold (WT) to eliminate irrelevant noise in time- and frequency-domain data. Adam was employed to improve the reliability of long short-term memory (LSTM) neural networks and optimize the gradient training process, and a deep learning model for the real-time prediction of the attitude trajectory in the tunneling process was proposed. Sun et al. [21] extended geological data using the interpolation method and combined geological and operational data according to the position of each operational datum. They employed a data-driven RF method and proposed a dynamic load-forecasting method based on data-driven technology and in situ data. Huang et al. [22] considered shield attitude, construction parameters, and stratum characteristics. They improved the multilayer perception, SVM, a gradient-enhanced regression machine learning algorithm, and a genetic algorithm based on principal component analysis (PCA) to forecast the shield posture. By analyzing the kinematics of the thrust mechanism, Wang et al. [23] developed a mathematical method for calculating the target movement of the thrust cylinder. They studied the target movement of the thrust cylinder when the shield was excavated along an arbitrary curve, to predict the shield-tunneling attitude in real time. Wu et al. [24] focused on the shield-tunneling parameters as input values and constructed a set of intelligent methods for optimizing the shield-tunneling parameters and predicting the shield-tunneling attitude. Zhang et al. [25] employed PCA to analyze the correlated parameters and implemented the rolling window mode in the gated cycle unit. Thereafter, they established an intelligent framework for trajectory deviation prediction in the shield-tunneling process to predict the attitude deviation in real time.
However, although studies have been conducted on shield-trajectory deviation prediction, two challenges (interrelated high-dimensional data and data noise processing) remain. Data in shield-acquisition systems are not independent of each other. Their quality is frequently affected by measurement sensor failures, and using these raw data can lead to the over-fitting of machine learning models.
To solve these problems, a hybrid model of attitude trajectory deviation prediction for shield machines based on PCA and SVR is proposed herein. PCA was employed to reduce the dimension of input parameters and filter the raw data noise by preserving the principal components. Statistical learning and structural risk minimization were applied in SVR to forecast the target parameters [26]. Thereafter, the proposed method was employed in a super-large-diameter shield-tunnel project in Zhuhai, China. The results were compared with those of the classical SVR model, and the relationship between the tunneling, geometric, and geological parameters and the attitude trajectory parameters is discussed. The proposed attitude-prediction model provides a reference for similar projects in the future.
2. Methodology
During tunneling, there are many factors affecting the attitude of the shield, and there are complicated relations among them, which means that the conventional mathematical model can not accurately predict the attitude of the shield tunneling. By using the support vector regression (SVR) algorithm in machine learning, a mathematical model can be built to accurately predict the attitude of shield tunneling. Figure 1 shows the flow of the shield-attitude-prediction method based on principal component analysis (PCA) and support vector regression algorithm. In our method, the initial stage focuses on data preparation, where the site data are systematically categorized into geological parameters, operational parameters, and geometric parameters. These parameters, combined with the geological exploration report, shield-machine driving system details, and the shield design specifications, provide a comprehensive description of the shield-machine state. The selection of these parameters was rigorously based on their direct impact on tunneling efficiency, stability, and safety, especially under complex geological conditions. The second stage is data preprocessing and feature extraction, which mainly includes eliminating stopping data and filtering noise to improve the accuracy of prediction model, and using principal component analysis to reduce the dimension of data. The third stage is model establishment and execution; that is, a support vector regression (PCA-SVR) hybrid model based on principal component analysis is established, and the model data is divided into training sets and test sets. After model training, the trajectory of the shield’s driving attitude is predicted based on the input parameters after noise reduction.
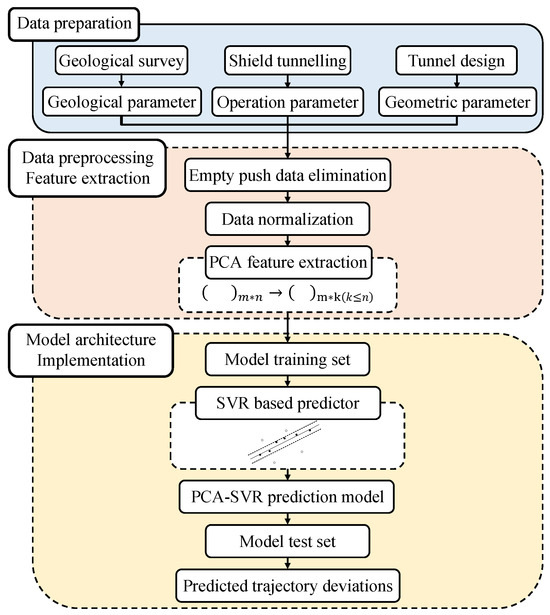
Figure 1.
Attitude-prediction process.
2.1. Support Vector Regression Model
Support vector regression (SVR) is a kind of machine learning algorithm based on the structural risk minimization theory and the statistical learning theory, which has good generalization ability when solving small sample problems [27]. The basic principle is to find an optimal classification surface in the high dimensional space by mapping the nonlinear relation of input variables in the low dimensional space to the high dimensional space through the kernel function, so that the data can be linearly separable in the high dimensional space. When constructing the support vector regression model, it is necessary to introduce the insensitive loss function ε to find an optimal classification surface, so that the error of all training samples from this classification surface is minimized. When the deviation between the output value (predicted value) of the model algorithm and the corresponding true value is [−ε, ε], the loss is ignored; otherwise, it is included in the loss, as shown in Figure 2.
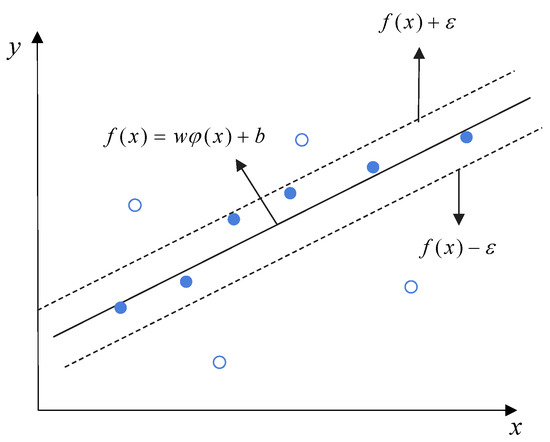
Figure 2.
Support vector regression schematic.
Let there be n training samples {xi, yi}(i = 1, 2, 3, …, m, xi ∈ Rd, yi ∈ R) for regression fitting, where xi is the input variable of the i-th sample and yi is the corresponding output parameter. The linear regression function is established in the high-dimensional space, and the sample is projected into the high-dimensional linear space through the nonlinear mapping relationship:
where w and b are the parameters to be solved.
In order to find the optimal w and b, the relaxation variables ξi and ζi are introduced to construct a minimal objective function, namely:
where is the penalty factor—the larger the is, the larger the penalty is for the sample whose training error is greater than ε; ε reflects the error requirement of the regression function, and a smaller ε means a smaller error of the regression function.
According to the optimization theory, it is transformed into a dual problem, and a Lagrange function and kernel function k(xi, xj) = φ(xi)·φ(xj) are introduced to solve it:
Suppose the optimal solution obtained by solving the above formula is α and α*, then:
where Nnsv is the number of support vectors.
Finally, the support vector regression function is as follows:
In the construction of regression models, relevant kernel functions are provided in Python Sklearn 0.24.2, including the linear, polynomial, Gaussian, and Sigmoid kernel functions (Table 1).

Table 1.
Support vector regression kernel function classification.
2.2. Principal Component Analysis
Principal component analysis (PCA) is a method that reduces unimportant dimensions by analyzing the covariance structure of the original dataset and describes the dataset using a few irrelevant comprehensive indicators [20]. By converting the data from one coordinate system to another coordinate system, this ensures the first coordinate after conversion contains the largest variance in the dataset, the second coordinate contains the second largest variance, and so on, to achieve the purpose of dimensionality reduction. In this process, principal component analysis retains the main information of the dataset, ignores the dimensions that contribute little to the variance of the dataset, and simplifies the data.
Assuming that the original dataset c contains m observed samples and each sample has n features, that is, matrix c ∈ Rm×n, the main steps of the principal component analysis based on matrix c are as follows:
Step 1: Normalize matrix c and calculate the normalized matrix Sij:
where σj and μj denote the standard deviation and mean of the j-th variable, respectively.
Step 2: The covariance matrix C of matrix X is determined by singular value decomposition
Step 3: Calculate the eigenvalues λ1 ≥ λ2 ≥ λ3... ≥ λn of the covariance matrix C and the corresponding eigenvectors P1, P2, P3,…, Pl.
Step 4: Select the principal component with a higher cumulative variance contribution to preserve the main information of the data.
where denotes the contribution rate of the first k principal components, and Tc denotes the contribution threshold.
Step 5: Construct the dataset after dimensionality reduction:
The PCA-SVR approach distinguishes itself from existing hybrid methods in tunneling engineering by offering enhanced predictive accuracy and interpretability. Specifically, it integrates PCA for dimensionality reduction with the robust regression of SVR, resulting in a streamlined and efficient model that captures complex tunneling data relationships with fewer parameters. This unique combination not only delivers a superior generalization performance compared to traditional hybrid models, but also provides deeper insights into the underlying factors influencing tunneling processes, ultimately facilitating more informed decision making in engineering practice.
2.3. Evaluation Index
To evaluate the validity and reliability of PCA–SVR, we conducted a comparison with the SVR machine learning model. Specifically, we employed the average absolute error (MAE), coefficient of determination (R2), and root-mean-square error (RMSE) as metrics to assess the prediction error of the model. These three indicators, commonly used to evaluate the performance of prediction models, are defined as follows: RMSE provides a measure of the average magnitude of the errors in a set of predictions, MAE gives the average absolute difference between the predicted and actual values, and R2 quantifies the proportion of the variance in the dependent variable that is predictable from the independent variables. These three indicators were defined as follows:
where denotes the predicted value, denotes the measured value, and denotes the average value of the measured value.
3. Case Study
3.1. Project Background
The Xingye Express (southern section), situated in Xiangzhou District, Zhuhai, China, is a project managed by CCCC Tunnel Engineering Co., Ltd. (Beijing, China). Table 2 presents the primary shield parameters, which have been estimated based on comprehensive project data and detailed design information furnished by the aforementioned company. The main shield begins from the working shaft of Yinhua road and ends at the working shaft of Banzhang mountain (Figure 3). The length of the line is approximately 4.77 km, and the length of the main shield section is 1739 m. The outer and inner diameters of the main-line shield tunnel are 15.2 and 13.9 m, respectively. The segment thickness is 650 mm, and the ring width is 2.0 m. The minimum and maximum buried depths of the tunnel are 9.8 and 41.3 m, respectively. The minimum horizontal curve radius is 599.5 m, and the section is V-shaped. The minimum vertical curve radius is 1500 m, and the maximum vertical curve radius is 2500.0 m.

Table 2.
Mud–water equilibrium shield parameters.
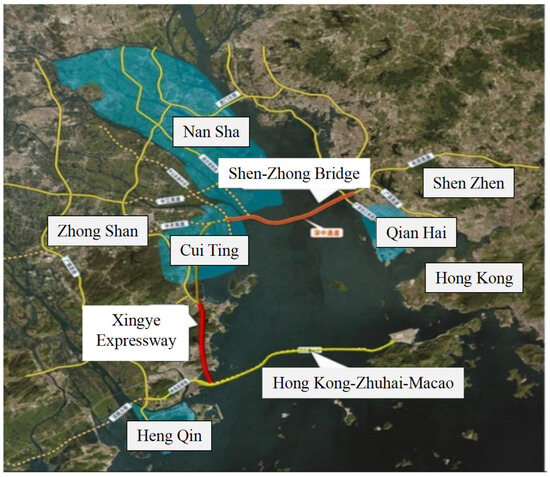
Figure 3.
Tunnel engineering diagram.
The propulsion system of the shield machine comprised 56 sets of built-in travel sensors, which were arranged according to the segments. The jack cylinder was divided into six zones (Figure 4). The propulsion cylinders in each section of the propulsion system can be individually controlled and selected and were fitted with a set of built-in stroke and pressure measurement sensors. The oil pressure was manually adjusted on the control console, and the stroke and pressure of each cylinder and each zone were displayed in real time on the display screen in the control room.
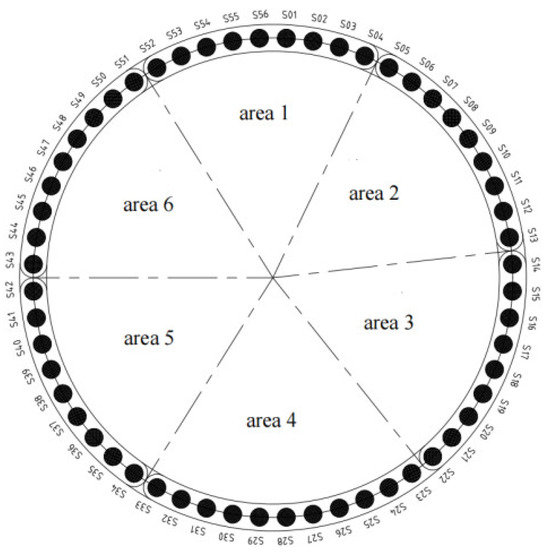
Figure 4.
Jack cylinder partition of propulsion system.
The main strata through which the main-line shield passes are silty clay, silty soil, gravel sand, gravel clay, fully weathered granite, and moderately weathered granite. The main shield section traverses the main strata as follows: The livable gravel sand layer (approximately 256 m long); a clay and fully weathered rock section (approximately 550 m long); a downslope section with soft and hard strata on the upper part (strongly weathered) and a lower part (breezy rock—the lowest part of the main-line shield was the entire section of breezy rock) (approximately 100 m long); and the lower part (breezy rock, approximately 460 m long). The end section is a full-section breezy rock formation (approximately 100 m long). The physical characteristics of the main soil layers are shown in Table 3 [28].

Table 3.
Physical characteristics of major soil layers.
3.2. Data Preprocessing
The automatic acquisition system of the shield machine collects field data every one minute, including the working time of the shield machine and the time when each ring stops installing segments. Therefore, the dataset contains empty data collected during shutdown and abnormal data of the tunneling state. When any one of the parameters such as cutter torque (CT), total thrust (TH), and cutter speed (CS) is zero, the shield machine is regarded as in a non-shutdown state. In data preprocessing, define the functions:
If the value of the variable is zero, then the value of the function is zero, and the function Q is also zero, and this part of the data is deleted. In addition, in order to accelerate the computational convergence of the model, the following formula is used to normalize the data:
where is the normalized data of the i-th variable at time t, and represent the minimum and maximum values of the i-th variable, respectively, and represents the data of the i-th variable at time t.
3.3. Input and Output Variable Selection
The original field data were collected from the left line (130–300 rings). During the tunneling, the shield machine was oriented by the navigation system. The measurement accuracy was high, and the front horizontal deviation (FHD), front vertical deviation (FVD), back horizontal deviation (BHD), back vertical deviation (BVD), rolling angle (RA), pitch angle (PA), and other parameters were measured (Figure 5). Here, four attitude parameters (FHD, FVD, BHD, and BVD) of the shield machine measured by the system were used to quantify the driving attitude trajectory. Figure 6 shows the path projection view and attitude position parameters of the shield machine. When the shield head or tail was on the right side of the designed tunnel axis (DTA) along the driving direction, the horizontal deviation was positive. When the shield head or tail was higher than the DTA, the vertical deviation was positive. The four attitude parameters were continuously monitored to provide a reference for the adjustment of the attitude trajectory. Thus, they were selected as the output parameters of the predictive model.
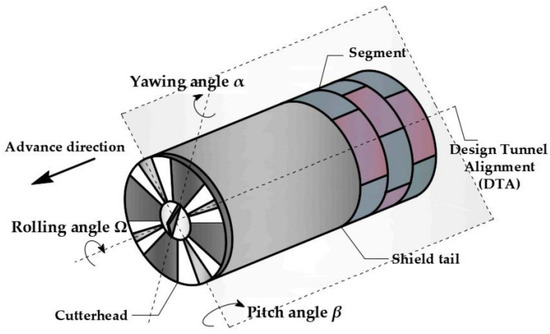
Figure 5.
Shield machine and attitude angle.
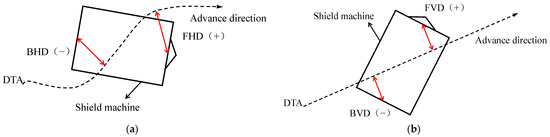
Figure 6.
Projection of the shield-tunneling route and deviation diagram of the track. (a) Top view; (b) side view.
The input parameters of the model comprised shield tunneling, geometric, and geological parameters. Operational parameters were obtained from the shield-machine equipment, such as the propulsion and guide systems. These parameters included the CS, CT, pressure in each pushing interval, TH of the propulsion cylinder, upper and lower stroke difference (SD), penetration (P), cutting face pressure (FP), deflection moment in the y-direction (MY), cut water pressure, and No.01–No.56 propulsion cylinder pressure (S01–S56). The geometric parameters included the pitch angle (PA), rolling angle (RA), hinged horizontal deviation (HHD), hinged vertical deviation (HVD), and cover depth (CD). Other geometric parameters, such as the tunnel diameter, shape, and slope, were unchanged. Geological parameters were obtained from the geological exploration data of the project, including soil weight (SW), cohesion (C), internal friction angle (IFA), and compression modulus (CM).
Summarily, 170 sets of data from 130 to 300 rings of the Zhuhai Xingye Express Tunnel project were used as the database. Considering the influence of the shield tunneling, geological, and geometric parameters, 82 input parameters were selected. Four groups (FHD, FVD, BHD, and BVD) of characteristic shield-attitude trajectory parameters were predicted (Table 4).

Table 4.
Statistics for input and output parameters.
4. Analysis of Attitude-Prediction Results
4.1. Model Implementation and Parameter Processing
Sklearn in the Python programming software was employed to construct a prediction model [29]. To ensure the optimal performance of SVR model, we systematically utilized Random Search to adjust the kernel functions, regularization parameter, and epsilon values to fine-tune the model parameters. A total of 16518 data samples were obtained after preprocessing; 13214 data samples from 130 to 266 rings were used as training datasets, and 3304 data samples from 267 to 300 rings were used as test datasets. The training and test sets accounted for 80% and 20% of the total data sample, respectively. The input and output parameters of the model are shown in Table 4.
After completing the data preprocessing stage, we employed PCA to discern the fundamental attributes of the initial 82 input parameters listed in Table 4. Subsequently, we determined the contribution rates for each principal component, as illustrated in Figure 7. Adopting a rigorous standard, we opted for a cumulative contribution rate threshold of 90% to select the most significant principal components, in alignment with established practices [27]. Table 5 presents the cumulative contributions of the k-th principal components. Notably, the first 13 principal components achieved a cumulative contribution rate of 90%, thereby encapsulating the primary information contained within the raw data. This meticulous approach ensures that our analysis focuses on the most informative and representative features of the dataset.
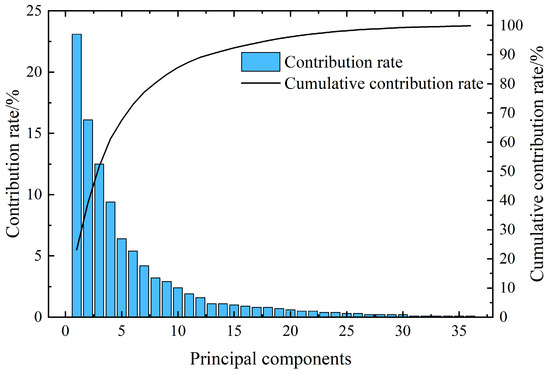
Figure 7.
Principal component analysis of input parameters.

Table 5.
Principal component contribution of input parameters.
4.2. Model Evaluation
Table 6 shows the error results of the two prediction models (PCA–SVR and SVR). The proposed PCA–SVR model exhibited better prediction accuracy than the SVR model. Its R2 exceeded 90%, its RMSE was below 6.0, and its MAE was below 3.5. In addition, the running time of the PCA–SVR model was 22.8 s, which reduced the unimportant dimensions by analyzing the covariance structure of the original dataset, thereby reducing the model computation cost. Thus, this model can be used to predict the attitude trajectory parameters and guide the operators to optimize parameter settings and obtain a better attitude trajectory of the shield tunneling.

Table 6.
Absolute prediction accuracy of different attitude parameters.
4.3. Prediction Model Validation
Figure 8 shows the relationship curves between the four selected attitude trajectory parameters and the monitoring date. As shown in Figure 8, the data of the four attitude deviation parameters significantly changed, and the data of the FVD and BVD parameters abruptly changed on 23 April 2022. This was because the selected parameter of the shield section through the strata was variable. Furthermore, there were different slope or curve sections of the tunnel, and the problem of tunnel segment floating caused by the improper control of the grouting pressure or slurry mix ratio occurred on site.
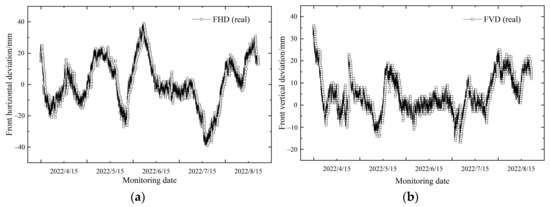
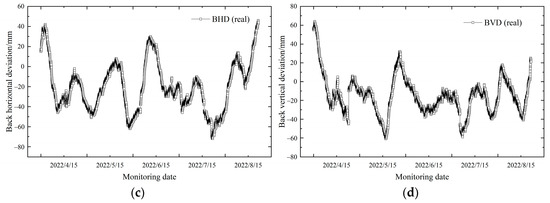
Figure 8.
The relationship between attitude parameters and monitoring date. (a) FHD; (b) FVD; (c) BHD; (d) BVD.
The PCA–SVR model divided the parameter dataset into 80% training and 20% test sets. Considering that the original monitoring dataset sampling was automatically ordered, the attitude parameter data had abrupt sections with a large degree of change over time (Figure 8). This could lead to a poor training effect in the verification or test set, thereby deteriorating the overall performance of the prediction model. Thus, this study randomly shuffled the dataset, which solved the problem of abrupt sections and a large degree of change in the attitude parameter data. In addition, a randomly divided dataset may be more representative of the entire data (including uncollected data).
Figure 9 presents the correlation prediction and monitoring results for the four attitude trajectory parameters in the test set. The hybrid model predicted ranges of −36 to 36 m for FHD, −11 to 32 mm for FVD, −68 to 43 mm for BHD, and −58 to 60 mm for BVD, all of which fell within the corresponding monitoring data ranges. Furthermore, the model’s performance was evaluated with R2 values of 0.938, 0.917, 0.929, and 0.950, along with RMSE values of 3.79, 5.88, 5.53, and 4.61, and MAE values of 2.68, 1.73, 3.36, and 3.22, respectively.
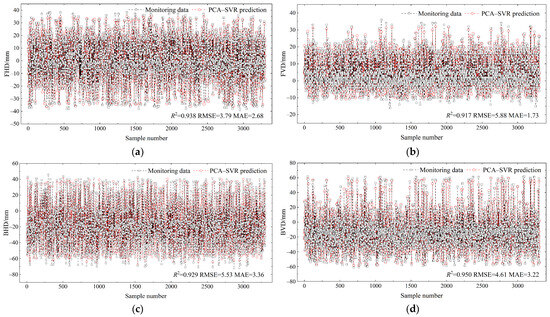
Figure 9.
Prediction and monitoring results of attitude parameters. (a) FHD; (b) FVD; (c) BHD; (d) BVD.
The coefficients of determination, R2, for the attitude parameter prediction of the FHD, FVD, BHD, and BVD were 0.938, 0.917, 0.929, and 0.950, respectively. They all exceeded 0.9, and other error evaluation indexes were small, indicating that the attitude parameter prediction effect was good (Figure 9). An engineering example confirmed that the proposed model and method based on machine learning were reliable and could accurately predict the trajectory of attitude motion during shield tunneling.
The Pearson correlation coefficient (P value) was employed to study the sensitivity and analyze the importance of input parameters in the posture correction process. The correlation degree of vectors is typically determined by the following value ranges: P = 0.8–1.0 highly correlated, P = 0.6–0.8 strongly correlated, P = 0.4–0.6 moderately correlated, P = 0.2–0.4 weakly correlated, and P = 0.0–0.2 weakly correlated or not correlated. The P value was defined as shown in (13).
where xi denotes the i-th input variable, yi denotes the i-th output variable, and n denotes the total number of samples.
Figure 10 shows the Pearson correlation analysis results of the input parameters listed in Table 4, including the tunneling, geometric, and geological parameters. The correlation between the geometric and geological parameters of the shield was generally strong (P = 0.2–0.8). RA and C were positively correlated with the attitude parameters, whereas SW, IFA, and CM were negatively correlated with the attitude parameters. Figure 10a shows that the HHD and HVD were strongly correlated with the horizontal and vertical deviation, respectively (P = 0.6–0.8).
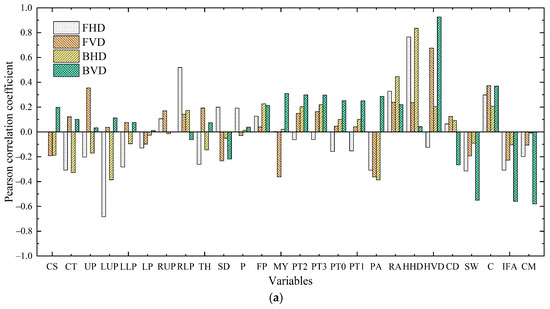
In addition, Figure 10a shows that the propulsion system pressure in area 1 (UP) was weakly correlated with the FHD and FVD (P = 0.2–0.4), whereas the propulsion system pressure in area 6 (LUP) was negatively correlated with the FHD and BHD (P = 0.4–0.8). The propulsion system in area 5 (LLP) was negatively correlated with the FHD (P = 0.4–0.6), whereas the propulsion system in area 2 (RLP) was positively correlated with the FHD (P = 0.4–0.6). CT was weakly correlated with the FHD and BHD; TH was weakly correlated with the FVD and FVD; the upper and lower SD was weakly correlated with the FHD, FVD, and BVD; and the cut water pressure was weakly correlated with the BVD (P = 0.2–0.4). MY was negatively and positively correlated with the FVD and BVD, respectively. A poor linear relationship existed between the other driving parameters and the output parameters (most p values < 0.2).
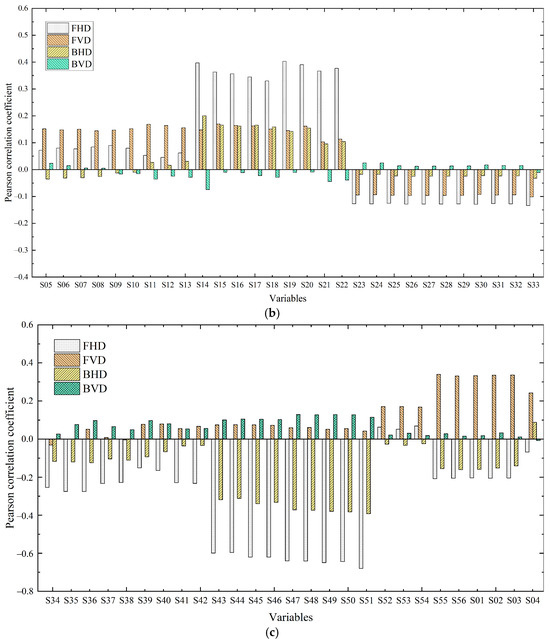
The trajectory deviation of shield attitude motion was continuously monitored to avoid exceeding the warning deviation. The shield operator generally controlled the attitude of the shield by adjusting the angle between the shield head and tail (Figure 4). This was achieved by adjusting the pressure of the propulsion cylinder in different areas, which frequently had SDs. Figure 4 shows the layout of jack cylinders in the propulsion system of the shield machine. Thrust cylinders S01–S56 were divided into six areas and distributed clockwise. Figure 10b,c show that the pressure of the propulsion cylinder in different regions had different correlations with the attitude deviation parameters. The correlation between the pressure of the propulsion cylinder and the attitude deviation parameters in each area was more consistent. The pressure of each thrust cylinder was generally more correlated with the attitude deviation of the shield head than the attitude deviation of the shield tail. The pressure of propulsion cylinders SP05–SP13 (area 2) and SP14–SP22 (area 3) was positively correlated with the FHD. The pressure of propulsion cylinders SP34–SP42 (area 5) and SP43–SP51 (area 6) was negatively correlated with the FHD and BHD. SP14–SP22 was weakly correlated with the FHD (P = 0.2–0.4), and SP43–SP51 was moderately correlated with the FHD and BHD (P = 0.4–0.6). The pressure of propulsion cylinders SP52–SP56 and SP01–SP04 (area 1) was positively correlated with the FVD, whereas the pressure of propulsion cylinder SP23–SP33 (area 4) was negatively correlated with the FVD and BVD. SP52–SP56 and SP01–SP04 exhibited a weak correlation with FVD (P = 0.2–0.4). This shows that the shield propulsion system was an important factor that affected the attitude motion trajectory, and the deviation between the attitude and DTA can be adjusted by controlling the corresponding position of the propulsion cylinder pressure.
In addition, the attitude motion trajectory of the shield-tunneling machine can be adjusted by controlling the deflection MY, the difference in up and down stroke, and the cut water pressure. The correlation between other driving parameters and output parameters was weak. In particular, the geometric and geological parameters of the shield were also strongly correlated with the attitude parameters. The shield attitude was mainly controlled by the field adjustment of the propulsion cylinder pressure and was considerably affected by its geometric and geological parameters.
5. Discussion
Qualitative results indicate that the PCA–SVR model not only improves prediction accuracy but also reduces computational complexity. The model’s ability to capture the underlying patterns in the data, despite the presence of noise, demonstrates its robustness. Furthermore, the engineering example showcases the practical application of the model in real-world scenarios, highlighting its potential for guiding shield-tunneling operations.
While the PCA–SVR model performs well, there are still areas for improvement. For instance, the model’s sensitivity to certain driving parameters could be enhanced by incorporating more comprehensive datasets. Additionally, exploring advanced machine learning techniques, such as deep learning, could further improve prediction accuracy and computational efficiency. Future research should also focus on validating the model across different shield-tunneling projects to ensure its generalizability and reliability.
6. Conclusions
This study proposed a hybrid PCA–SVR to predict the attitude motion trajectory of a shield-tunneling machine. The model was validated using the in situ data of the shield tunnel project of the Xingye Express line in Zhuhai, China. The conclusions are as follows:
- (1)
- An intelligent model combining principal component analysis (PCA) and support vector regression (SVR) was employed to predict the trajectory of the shield’s driving attitude. PCA effectively reduced the data dimension and accompanying data noise, while the SVR model adopted the principle of structural risk minimization and statistical learning theory to predict the attitude parameters of the shield machine. The PCA–SVR model was validated using in situ data from the shield-tunnel project of the Xingye Express line in Zhuhai, China, and accurately foresaw the trajectory deviations of tunneling.
- (2)
- An engineering example confirmed that the proposed hybrid PCA–SVR model accurately predicted the attitude motion trajectory. Compared with the standalone SVR model, PCA–SVR reduced the calculation time cost and exhibited a high prediction accuracy. The proposed prediction model has the potential to guide shield operators in adjusting tunneling parameters, thereby improving the attitude motion trajectory.
- (3)
- The sensitivity analysis revealed that the propeller cylinder pressure significantly affected the attitude trajectory of the shield machine. Additionally, the correlation between the geometric and geological parameters of the shield and the output parameters was generally strong. However, the correlation between certain driving parameters and the output parameters was weak. Deviations from the desired tunneling attitude (DTA) were regulated by the thrust of the push cylinders in the corresponding positions. Future work should refine the model with more parameters and advanced machine learning, and test it at various geological sites, including those with complex rocks, to enhance its accuracy and general applicability. Additionally, research will focus on real-time prediction, with the proposal of a program embeddable in the shield computer for real-time data export and training.
Author Contributions
Conceptualization, H.L., D.Z. and D.S.; methodology, Y.T., S.Q. and D.S.; data curation, H.L. and H.L.; data analysis, D.Z. and Y.T.; writing—original draft preparation, Y.T.; writing—review and editing, D.S.; supervision, H.L.; project administration, D.Z.; funding acquisition, D.S. and H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Shenzhen Science and Technology Program (Grant No. 20220808143139001), Key Research and Development Project of Guangdong Province (Grant No. 2019B111105001), and Shenzhen University 2035 Program for Excellent Research (2022B007).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data included in this study are available upon request by contact with the corresponding author.
Acknowledgments
We are grateful for the guidance and support provided by our supervisor. We also appreciate the assistance received from our colleagues during this study. Thank you to the reviewers for their constructive comments.
Conflicts of Interest
Authors Hui Li, Decheng Zeng and Shiye Qiao were employed by the company CCCC Tunnel Engineering Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Stavropoulou, M.; Xiroudakis, G.; Exadaktylos, G. Spatial estimation of geotechnical parameters for numerical tunneling simulations and TBM performance models. Acta Geotech. 2010, 5, 139–150. [Google Scholar] [CrossRef]
- Lorenzo, S.G. Design guidelines for concrete segmental linings in transverse interaction with the TBM. Tunn. Undergr. Space Technol. 2022, 122, 104388. [Google Scholar] [CrossRef]
- Jia, G.P.; Huo, J.Z.; Yang, B.W.; Wu, Z. The real-time optimal attitude control of tunnel boring machine based on reinforcement learning. Appl. Sci. 2023, 13, 10026. [Google Scholar] [CrossRef]
- Li, X.; Di, X.H.; Zhou, S.X.; Huo, P.; Huang, Q. Effective method for adjusting the uplifting of shield machine tunneling in upper-soft lower-hard strata. Tunn. Undergr. Space Technol. 2021, 115, 104040. [Google Scholar] [CrossRef]
- Kong, X.X.; Ling, X.Z.; Tang, L.; Tang, W.C.; Zhang, Y.F. Random forest-based predictors for driving forces of earth pressure balance (EPB) shield tunnel boring machine (TBM). Tunn. Undergr. Space Technol. 2022, 122, 104373. [Google Scholar] [CrossRef]
- Xiao, H.H.; Xing, B.; Wang, Y.J.; Yu, P.; Liu, L.P.; Cao, R.L. Prediction of Shield Machine Attitude Based on Various Artificial Intelligence Technologies. Appl. Sci. 2021, 11, 10264. [Google Scholar] [CrossRef]
- Zhang, W.G.; Phoon, K.K. Editorial for advances and applications of deep learning and soft computing in geotechnical underground engineering. J. Rock Mech. Geotech. Eng. 2022, 14, 671–673. [Google Scholar] [CrossRef]
- Chwała, M. Undrained bearing capacity of spatially random soil for rectangular footings. Soils Found. 2019, 59, 1508–1521. [Google Scholar] [CrossRef]
- Savvides, A.A.; Papadopoulos, L. A neural network model for estimation of failure stresses and strains in cohesive soils. Geotechnics 2022, 2, 1084–1108. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Guo, D.; Li, J.H.; Jiang, S.H.; Li, X.; Chen, Z.Y. Intelligent assistant driving method for tunnel boring machine based on big data. Acta Geotech. 2022, 17, 1019–1030. [Google Scholar] [CrossRef]
- Zhang, W.G.; Li, H.R.; Li, Y.Q.; Liu, H.L.; Chen, Y.M.; Ding, X.M. Application of deep learning algorithms in geotechnical engineering a short critical review. Artif. Intell. Rev. 2021, 54, 5633–5673. [Google Scholar] [CrossRef]
- Pan, Q.J.; Li, X.Z.; Huang, S.; Wang, L.; Wang, S.Y.; Fang, G.G. Application of machine learning to intelligent shield tunnelling: Review and prospects. Hazard Control Tunn. Undergr. Eng. 2022, 4, 10–30. (In Chinese) [Google Scholar]
- Mahdevari, S.; Shahriar, K.; Yagiz, S.; Shirazi, M.A. A support vector regression model for predicting tunnel boring machine penetration rates. Int. J. Rock Mech. Min. 2014, 72, 214–229. [Google Scholar] [CrossRef]
- Lin, S.S.; Shen, S.L.; Zhang, N.; Zhou, A.N. Modelling the performance of EPB shield tunnelling using machine and deep learning algorithms. Geosci. Front. 2021, 12, 101177. [Google Scholar] [CrossRef]
- Shen, S.L.; Njock, P.G.A.; Zhou, A.N.; Lyu, H.M. Dynamic prediction of jet grouted column diameter in soft soil using Bi-LSTM deep learning. Acta Geotech. 2021, 16, 303–315. [Google Scholar] [CrossRef]
- Fu, X.L.; Wu, M.Z.; Ponnarasu, S.; Zhang, L.M. A hybrid deep learning approach for dynamic attitude and position prediction in tunnel construction considering spatio-temporal patterns. Expert Syst. Appl. 2023, 212, 118721. [Google Scholar] [CrossRef]
- Zhou, C.; Xu, H.C.; Ding, L.Y.; Wei, L.C.; Zhou, Y. Dynamic prediction for attitude and position in shield tunneling: A deep learning method. Automat. Constr. 2019, 105, 102840. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Gong, G.F.; Yang, H.Y.; Li, W.J.; Liu, J. Precision versus intelligence: Autonomous supporting pressure balance control for slurry shield tunnel boring machines. Automat. Constr. 2020, 114, 103173. [Google Scholar] [CrossRef]
- Shen, S.L.; Elbaz, K.; Shaban, W.M.; Zhou, A.N. Real-time prediction of shield moving trajectory during tunnelling. Acta Geotech. 2022, 17, 1533–1549. [Google Scholar] [CrossRef]
- Sun, W.; Shi, M.L.; Zhang, C.; Zhao, J.H.; Song, X.G. Dynamic load prediction of tunnel boring machine (TBM) based on heterogeneous in-situ data. Automat. Constr. 2018, 92, 23–34. [Google Scholar] [CrossRef]
- Huang, H.W.; Chang, J.Q.; Zhang, D.M.; Zhang, J.; Wu, H.M.; Li, G. Machine learning-based automatic control of tunneling posture of shield machine. J. Rock Mech. Geotech. Eng. 2022, 14, 1153–1164. [Google Scholar] [CrossRef]
- Wang, L.T.; Yang, X.; Gong, G.F.; Du, J.N. Pose and trajectory control of shield tunneling machine in complicated stratum. Automat. Constr. 2018, 93, 192–199. [Google Scholar] [CrossRef]
- Wu, H.M.; Chang, J.Q.; Li, G.; Zhang, D.M.; Huang, H.W. Prediction of driving posture and optimization of construction parameters for shield based on support vector machine. Tunn. Constr. 2021, 41, 11–18. (In Chinese) [Google Scholar]
- Zhang, N.; Zhang, N.; Zheng, Q.; Xu, Y.S. Real-time prediction of shield moving trajectory during tunnelling using GRU deep neural network. Acta Geotech. 2021, 17, 1167–1182. [Google Scholar] [CrossRef]
- Zhao, S.; Liao, S.M.; Yang, Y.F.; Tang, L.H. Prediction of shield tunneling attitudes: A muti-dimensional feature synthesizing and screening method. J. Rock Mech. Geotech. Eng. 2024. [Google Scholar] [CrossRef]
- Ayawah, P.E.A.; Sebbeh-Newton, S.; Azure, J.W.A.; Kaba, A.G.A.; Anani, A.; Bansah, S.; Zabidi, H. A review and case study of artificial intelligence and machine learning methods used for ground condition prediction ahead of tunnel boring machines. J. Rock Mech. Geotech. Eng. 2022, 125, 104497. [Google Scholar] [CrossRef]
- Yang, W.H.; Su, D.; Lin, X.T.; Lv, Z.J.; Yao, Z.H.; Li, H.; Zhang, Y.Z.; Chen, X.S. Super-large diameter slurry shield tunnel encountering boulder formation: Detection, treatment and data analysis. Transp. Geotech. 2024, 49, 101408. [Google Scholar] [CrossRef]
- Gajjar, S.; Palazoglu, A. A data-driven multidimensional visualization technique for process fault detection and diagnosis. Chemom. Intell. Lab. Syst. 2016, 154, 122–136. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).