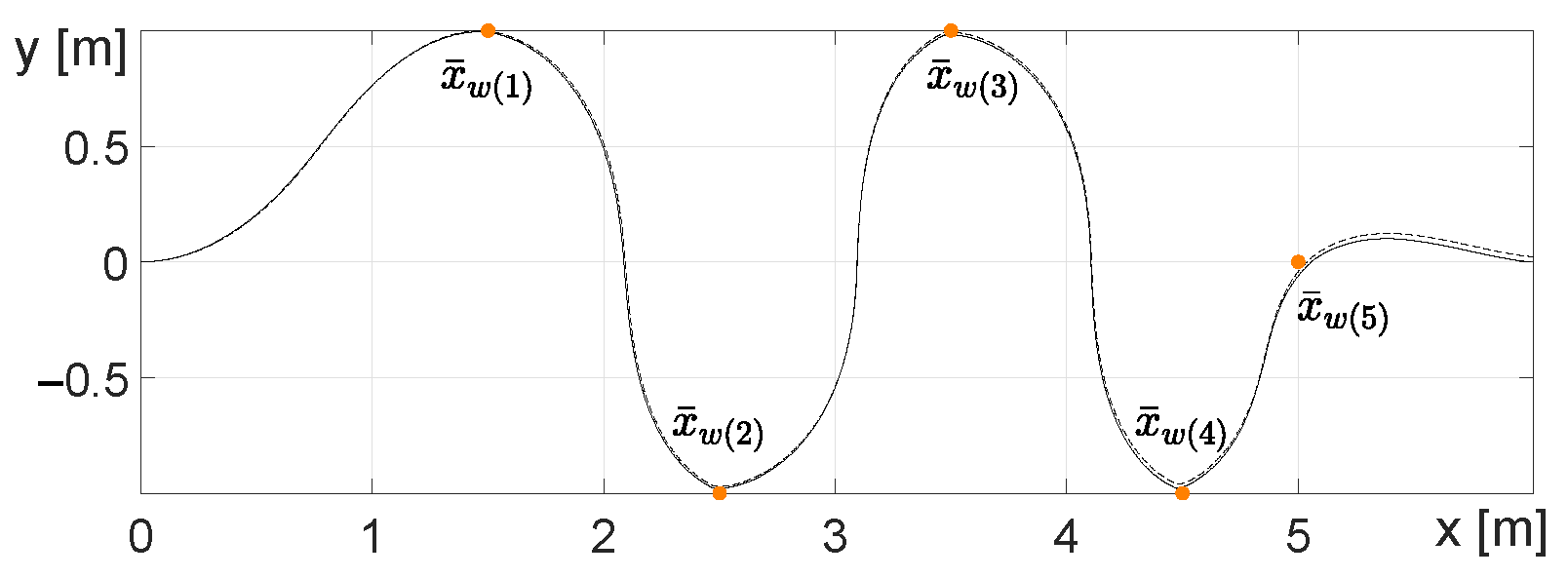Redesign of a Towing Mobile Robot Control Architecture and Implementation of Outdoor Experiments Using the Transverse Function Approach

Abstract

This article discusses the redesign of a towing mobile robot to obtain a modern system for implementing mobile robot control research. Controller architecture issues are presented, and a selected control algorithm is considered in detail. The reconstruction of the robot is also intended to ensure that the current standards for the electronic architecture controlling the robot are met and that this architecture can be easily developed to include components related to the safety of the robot’s operation. The discussion of the control architecture is divided into a description of the high-level controller responsible for the position stabilization algorithm and a description of the low-level controller responsible for the drive motor control and robot safety. The high-level control algorithm is responsible for a trajectory tracking task realized with use of a transverse function approach algorithm. A time elastic band algorithm was also used to generate a reference trajectory, allowing the robot to be guided through waypoints. The low-level controller is comprehensively described with details on the industrial controller architecture used, the communication between the controller modules, and the interaction of these modules with the on-board computer. The redesign of the towing mobile robot was summarized by the implementation of outdoor experiments where the task of driving through reference points was completed.

1. Introduction

The research results presented in this article are part of an ongoing project related to the rebuilding of a Towing Mobile Robot (TMR). This robot is a prototype device designed for various transportation tasks and can also serve as a platform for service robots. It was fully designed and built by the Institute of Automation and Robotics (IAR) of Poznan University of Technology as part of the project entitled “Construction of a service mobile robot with modular structure” led by Krzysztof Kozłowski in collaboration with with Jarosław Majchrzak [1]. It is one of the projects carried out by the IAR in the field of designing specialized robots [2,3], especially mobile robots [4,5,6]. The project we mentioned above was then continued under another project entitled “Intelligent Mobile Robot Control System”, supervised by Bartłomiej Krysiak, involving the reconstruction of the TMR robot. The primary goal of this project was the robot’s redesign to achieve current standards in autonomous mobile robots in terms of control, operation safety in an environment with humans, and flexibility of software implementation. In addition, an important goal of rebuilding the architecture of the robot’s control system was to obtain such a controller architecture to ensure the possibility of convenient and efficient research and testing of new control/navigation methods in mobile robotics.

The design and development of mobile robots requires a broad knowledge of not only robotics but also mechanics, electronics, and IT tools. The way in which components are designed and selected depends on the type of locomotion and the intended use of the mobile robot vehicle. The design of the mechanical structure is usually the first stage, depending on the tasks set for the robot and the working environment. There are different requirements for indoor applications, for example, cleaning robots [7] or mobile construction robots [8]. The development of mobile robots for outdoor tasks is usually more demanding in terms of the design of the mobile platform and the equipping of it with a set of sensors [9,10] allowing robustness and mobility in different terrain conditions [11]. Sometimes, such platforms are designed to be versatile with a choice of configuration or adaptation of the type of drive from wheeled to crawler depending on the task and terrain [12,13].

In any robotic system, a key issue is the control architecture. On the one hand, the control system architecture can be thought of as a system that acquires and processes sensory information, determining actions and control signals to achieve set goals. In the classical view, the control architecture can be centralized or distributed, and the reasoning could be reactive or deliberative. In this context, one can consider how input signals should be processed, by sensor fusion or command arbitration [14]. More recent works propose combining different assumptions to create hybrid architectures [15] and behavior-based approaches [16,17]. A more complex issue is the control architectures for the formation of multiple mobile robots [6,18].

When considering the control architecture, a distinction can also be made between a low-level and a high-level control layer. The low-level layer is mainly related to the hardware part of the system, which is responsible for executing movement through the robot drives and collecting and processing measurements from internal sensors. This layer can also be tasked for the safety and proper behavior if the high-level controller fails. The high-level controller is the main computing unit responsible for sensor acquisitions for environment perception, localization, planning and navigation, general diagnostics, and communication with the low-level controller. Currently, a commonly used software tool for high-level software preparation is the Robot Operating System (ROS), which provides system modularity and easy data exchange between different devices and software modules [17,19,20].

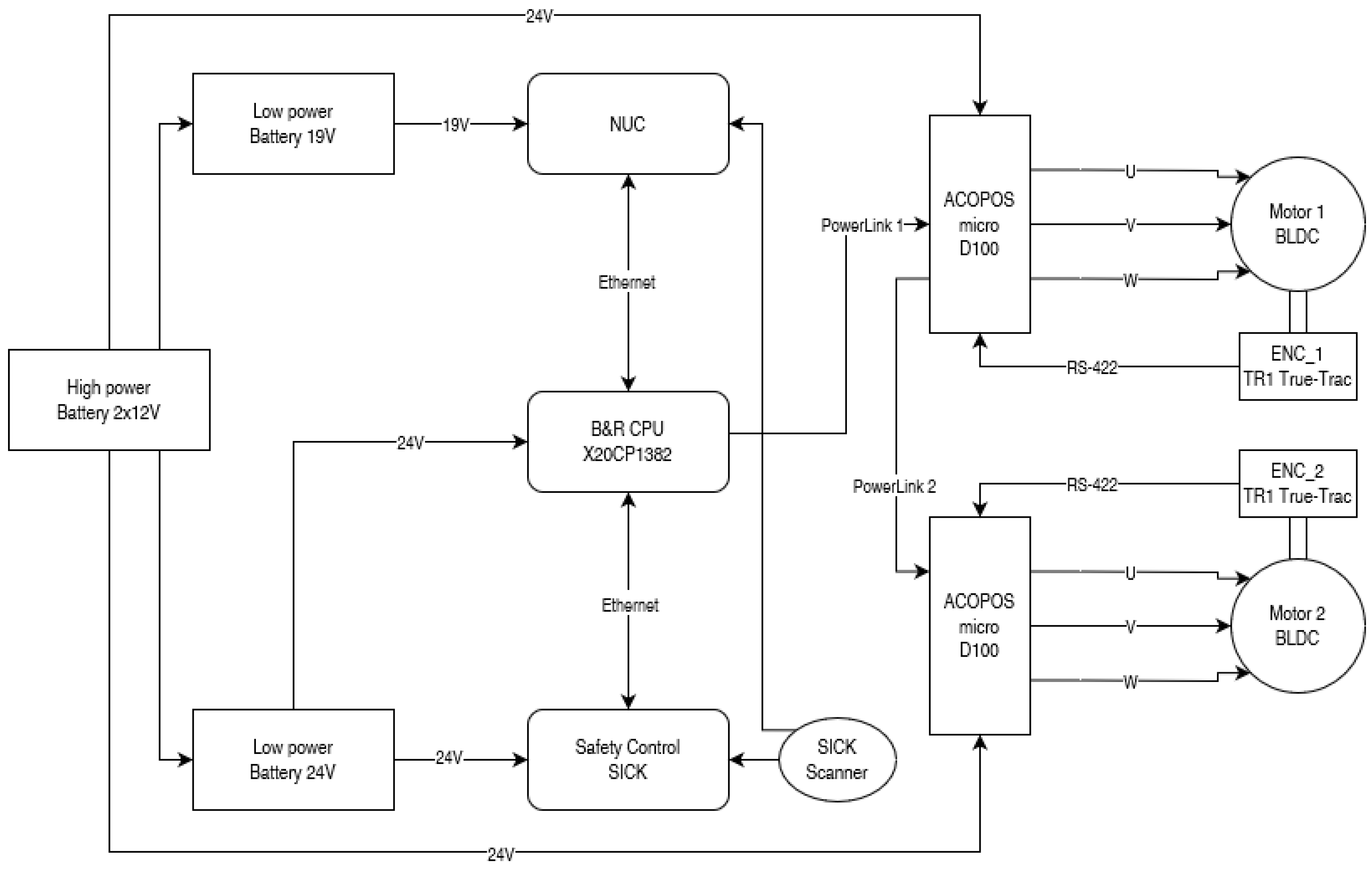
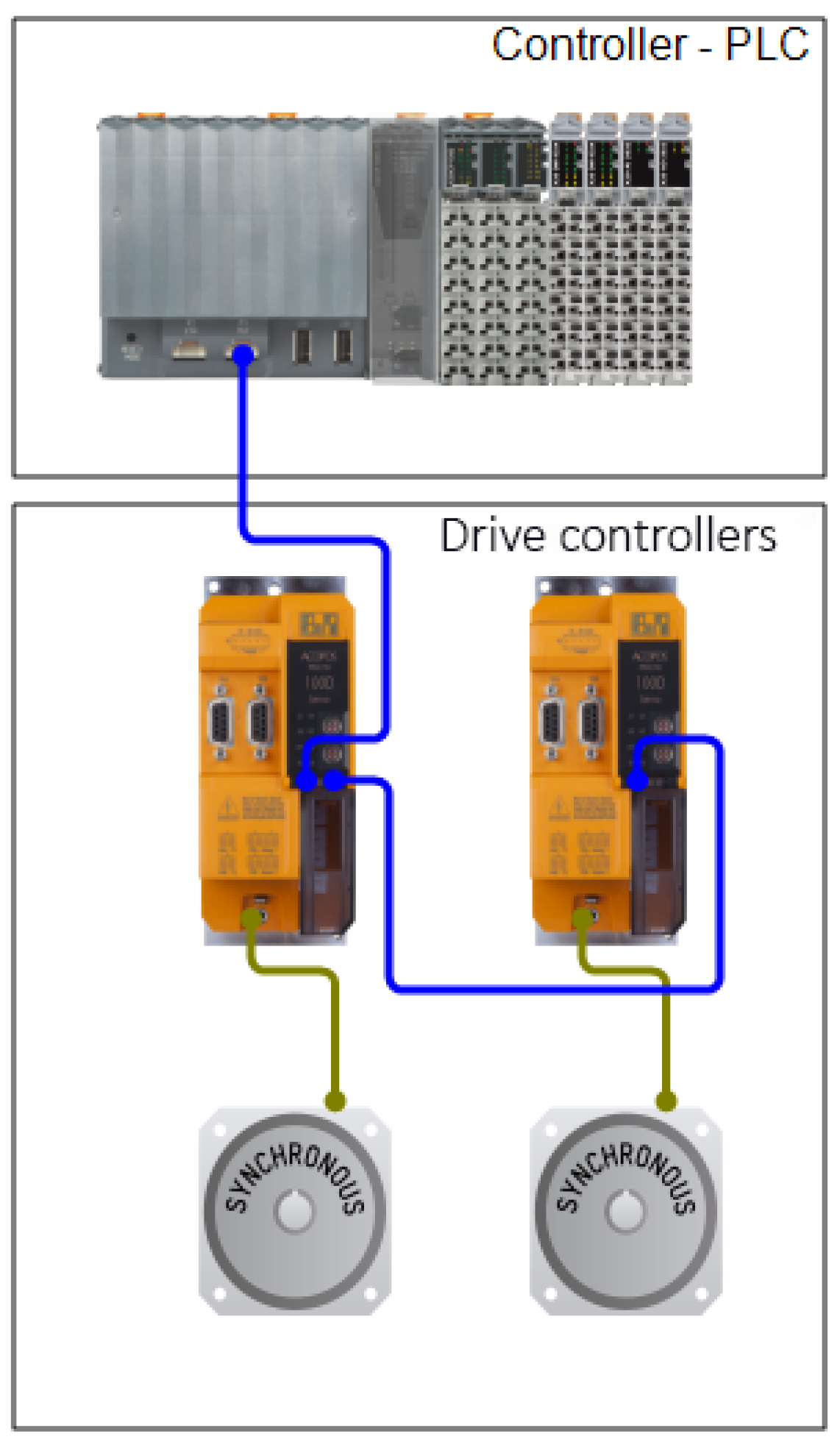
As a result of the modifications employed, the mechanical structure of the TMR chassis was enlarged, and its electrical and electronic components were replaced, including wheel rotation sensors and the laser scanner. In preparation for testing the robot in an outdoor environment, the implementation of control algorithms was realized. A high-level controller responsible for generating a reference trajectory and stabilizing the robot’s position along this trajectory and a low-level controller responsible for executing set speeds through the drive motors were considered. The specific type of algorithm was selected for high-level controller taking into account a number of methods proposed in the literature. In this case, an advanced method derived from geometric non-linear control techniques was chosen, using the so-called transverse functions (TFs) [21]. It should be noted that it is a universal smooth stabilizer that enables practical stabilization along any bounded trajectory including a fixed point. Although there are applications of this approach to mobile robot control, i.e., [22,23], not many papers deal with the experimental validation of this approach. Works such as [24,25] show experiments with a mobile robot in an indoor environment. The motion control algorithm considered in this article was developed with a modified method of tuning the transverse function parameters; this method was introduced in [3], where a nonholonomic manipulator control was considered. The TF algorithm performs stabilization of the robot’s position on a trajectory that was generated using the time elastic band algorithm [26]. This provided a practical and fast way to prototype different trajectories of the robot’s traversal using the passage points, which significantly facilitates the implementation of field tests. The high-level control algorithm involving transverse functions and time elastic band methods was implemented on the robot’s on-board computer, and integration with the low-level controller responsible for stabilizing electric motors operation was carried out. The low-level controller was implemented using an industrial PLC, which is also responsible for the safety of the robot’s operation. Consequently, the paper also presents basic issues related to the implementation of a low-level controller. In addition, basic information on the robot’s design is presented.

This paper is focused both on theoretical and practical aspects of motion control in mobile robotics. In particular, the design of a novel control architecture that enables the operational deployment of the rebuilt towing mobile robot in outdoor tests is discussed. In this paper, the architecture is understood as the specific solution that integrates a non-standard motion controller with the TEB planner, using modern industrial automation components, rather than as a new paradigm for how different system blocks are interconnected. The publication presents the application of modern techniques for implementing robot control architecture using industrial PLCs. Few publications in the field of mobile robot control cover these issues in detail. In many cases, this is due to the use of mobile robots produced by the robotics industry for research, which do not provide such data. An important contribution of the publication is also the presentation of the details of the implementation of the control algorithm at the level of servo drives and at the level of the responsible high-level algorithm. To implement the high-level control algorithm, the transverse function algorithm is used together with the time elastic band method. This solution allows a unified approach for tracking trajectories generated through transit points to be achieved. To the best of the authors’ knowledge, this represents the first synthesis of the transverse function algorithm together with the time elastic band method. The results of the outdoor experimental research presented here confirm the effectiveness and stability of the proposed control architecture using a continuous smooth feedback controller along with a time-optimized controller generating the robot’s motion trajectory.

In summary, the key contributions can be described as follows:

• Implementation of a nonlinear controller using transverse functions using a novel tuning scheme: Despite prior theoretical works available in the literature, this method has not been widely adopted or applied in practical robotics, particularly in user-level robots;
• Integration of modern industrial automation components in mobile robotics: Industrial automation elements are incorporated into the control architecture of a nonholonomic robot, enhancing its functionality and bridging the gap between advanced control theory and practical applications in robotics;
• Development of a universal robotic testing platform using the ROS environment: The robot is designed as a versatile platform within the ROS ecosystem, enabling experimentation and validation of advanced control strategies and automation technologies in real-world transport applications.

2. Theoretical Background

We consider the planar motion of a two-wheeled robot. Its position is described by the coordinates $(x_c,y_c)$ of a point fixed at the center of the axis of the wheels in the inertial frame, and its orientation relative to this frame is given by $\theta$. Assuming a non-skid condition for both wheels, the kinematics of the robot can be represented by the following unicycle model:

$$\begin{array}{c}\dot{x}=X_1\left(x\right)u_1+X_2\left(x\right)u_2,\end{array}$$

(1)

where $x={\left[x_1{x}_2{x}_3\right]}^T={\left[x_c{y}_c{\theta }_c\right]}^T\in \mathcal{X}\subseteq {\mathbb{R}}^3$ is the configuration (state) and $u={\left[u_1{u}_2\right]}^T\in \mathcal{U}\subseteq {\mathbb{R}}^2$ is the control input, representing linear and angular velocity controls, and

$$X_1\left(x\right)={\left[cos{x}_{3}sin{x}_{3}0\right]}^T\in {\mathbb{R}}^3,X_2\left(x\right)={\left[001\right]}^T\in {\mathbb{R}}^3$$

(2)

are control vector fields. The kinematic structure (1) allows it to be defined on a Lie group isomorphic to the Special Euclidean Group $SE\left(2\right)$ [27]. This property can be used efficiently for control design.

To facilitate the notation used in this paper, let us briefly recall the basic designations associated with representation on the Lie group.

• G—a Lie group;
• g—a group element;
• $g_1{g}_2$—a group operation of the elements $g_1$ and $g_2$, i.e., $g_3=g_1{g}_2$ creates a new group element $g_3$;
• $L_{g_1}$—the left translation on G, where $g_1\in G$, i.e., $L_{g_1}{g}_2=g_1{g}_2$;
• $X\left(g\right)$—a vector field (vf) $X\in \mathcal{X}$ evaluated at the point $g\in G$, where $\mathcal{X}$ is a set of all smooth vfs;
• $X_{i\_j}$—a matrix consisting of $j-i+1$ vfs, i.e., $X_{i\_j}=\left[X_i{X}_{i+1}\dots X_{j-1}{X}_j\right]$, where $0<i<j$;
• e—the neutral element, i.e., $ge=eg=g$, where $e\in G$;
• $g^{-1}$—the inverse element of g, i.e., $g{g}^{-1}=g^{-1}g=e$;
• Ad—the group adjoint representation, where ${\mathrm{Ad}}_g:T_{e}G\to T_{e}G$, i.e., ${\mathrm{Ad}}_g=\mathrm{d}{c}_g\left(e\right)$, d is a symbol of a differential, $c_g\left(e\right)=ge{g}^{-1}$; additionally Ad can be defined with use of the derivative of left translation as ${\mathrm{Ad}}_g=\mathrm{d}{L}_g\left(g^{-1}\right)\mathrm{d}{L}_e\left(g^{-1}\right)$, where $g\in G$;
• ${\mathrm{Ad}}_g^X$—the adjoint representation projected on $X\left(e\right)$, i.e., ${\mathrm{Ad}}_{g}X\left(e\right)=X\left(e\right){\mathrm{Ad}}_g^X$; by extension of this definition, we allow for the usage of ${\mathrm{Ad}}_g^X$ when considering the adjoint representation projected on a matrix $X_{a\_b}\left(e\right)$, i.e., ${\mathrm{Ad}}_g{X}_{a\_b}\left(e\right)={\mathrm{Ad}}_g\left[X_a\left(e\right)\dots X_b\left(e\right)\right]=\left[{\mathrm{Ad}}_g{X}_a\left(e\right)\dots {\mathrm{Ad}}_g{X}_b\left(e\right)\right]$$=\left[X_a{\mathrm{Ad}}_g^X\dots X_b{\mathrm{Ad}}_g^X\right]$
  $=X_{a\_b}\left(e\right){\mathrm{Ad}}_g^X$.

For a broader introduction to representation on the Lie group, the reader is referred to [28]. Following the methodology used in this paper, we consider control vfs in (1) as generators of a Lie algebra $\mathfrak{g}$ and assume that the following set of vfs ${\mathcal{X}}_{1\_3}=\{X_1,X_2,X_3\}\subseteq \mathfrak{g}$, with $X_3=[X_1,X_2]$ being the Lie bracket, constitutes the algebra basis. This choice of algebra basis is rather standard, and a broader discussion of this topic can be found in [27]. Taking advantage of matrix vector notation, we define the matrix $X_{1\_3}\left(x\right)=\left[X_1\left(x\right)X_2\left(x\right)X_3\left(x\right)\right]$ that uses vfs from ${\mathcal{X}}_{1\_3}$. Using this basis, it is possible to represent system (1) as

$$\dot{x}=X_{1\_3}\left(x\right)C\widehat{u},$$

(3)

where $C:=\left[C_1{\mathbb{0}}_{3\times 1}\right]\in {\mathbb{R}}^{3\times 3}$, $C_1:={\left[{\mathbb{I}}_{2\times 2}{\mathbb{0}}_{1\times 2}\right]}^T\in {\mathbb{R}}^{3\times 2}$, ${\mathbb{I}}_{2\times 2}\in {\mathbb{R}}^{2\times 2}$ is an identity matrix, and ${\mathbb{0}}_{3\times 1}\in {\mathbb{R}}^{3\times 1}$ and ${\mathbb{0}}_{1\times 2}\in {\mathbb{R}}^{1\times 2}$ are zero matrices. $\widehat{u}={\left[u_1{u}_2{u}_3\right]}^T\in \widehat{\mathcal{U}}\subseteq {\mathbb{R}}^3$ is an extended input, where $u_1$ and $u_2$ are from (1) and $u_3$ is a new element, which is currently not used and will be useful later when expanding the control vector with a new variable.

Since kinematics (1) is a system defined in the Lie group G, it implies that $x\in G$ is an element of the group and vfs in the Lie algebra $\mathfrak{g}$ are left invariant with respect to an operation of a Lie group. Lie group G is a smooth manifold with the group operation stated above. In general, it means that the mapping is associative, the group has e elements, there exists the inverse of g denoted as $g^{-1}$, and the mapping is smooth. In the case of the unicycle robot, the following group operation can be considered [21]:

$$\forall g_1,g_2\in G,g_1{g}_2=g_3\in G,$$

(4)

$$\begin{array}{cc}\hfill g_{31}& =g_{11}+cos\left(g_{13}\right)g_{21}-sin\left(g_{13}\right)g_{22},\hfill \\ \hfill g_{32}& =g_{12}+sin\left(g_{13}\right)g_{21}+cos\left(g_{13}\right)g_{22},\hfill \\ \hfill g_{33}& =g_{13}+g_{23},\hfill \end{array}$$

where $g_i={\left[g_{i1}{g}_{i2}{g}_{i3}\right]}^T$ and $i\in \{1,2,3\}$. In this case, the neutral element is $e={\left[000\right]}^T$, and using the group operation shown above, the inverse element is calculated, which is [21]:

$$g_1^{-1}=g_4,$$

(5)

$$\begin{array}{cc}\hfill g_{41}& =-cos(-g_{13})g_{11}+sin(-g_{13})g_{12},\hfill \\ \hfill g_{42}& =sin(-g_{13})g_{11}-cos(-g_{13})g_{12},\hfill \\ \hfill g_{43}& =-g_{13},\hfill \end{array}$$

where $g_4={\left[g_{41}{g}_{42}{g}_{43}\right]}^T$. Later in this paper, the above operators are used to compose group elements and to calculate the inverse of group elements. A broader discussion on the calculation of the group operation and the neutral element with respect to systems evolving on $SE\left(2\right)$ group can be found in [27].

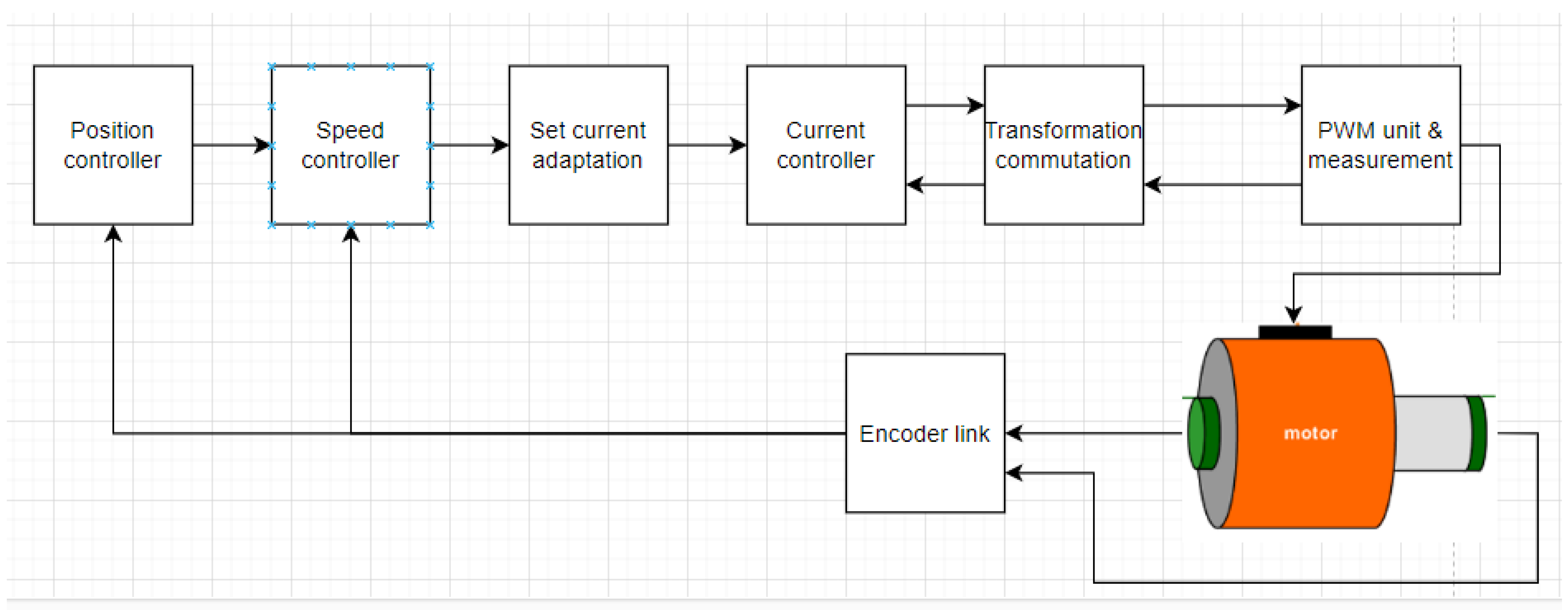
3. Overview of the Controller Architecture

The fundamental component of the proposed control architecture for a nonholonomic robot is a universal motion controller based on the transverse function (TF) approach [21]. One of the most significant control challenges encountered in nonholonomic kinematics is that a smooth feedback cannot achieve asymptotic point stabilization or asymptotic tracking for any feasible reference trajectory. The TF approach is particularly well-suited for such systems due to its ability to achieve practical stabilization for any reference trajectory—whether feasible or not—persistently excited or reduced to a fixed point. By introducing an additional dynamic system to govern the evolution of the so-called transverse function and relaxing the requirement for asymptotic convergence of posture errors, it becomes possible to overcome the challenges in stabilizing nonholonomic systems, as highlighted by Brockett [29].

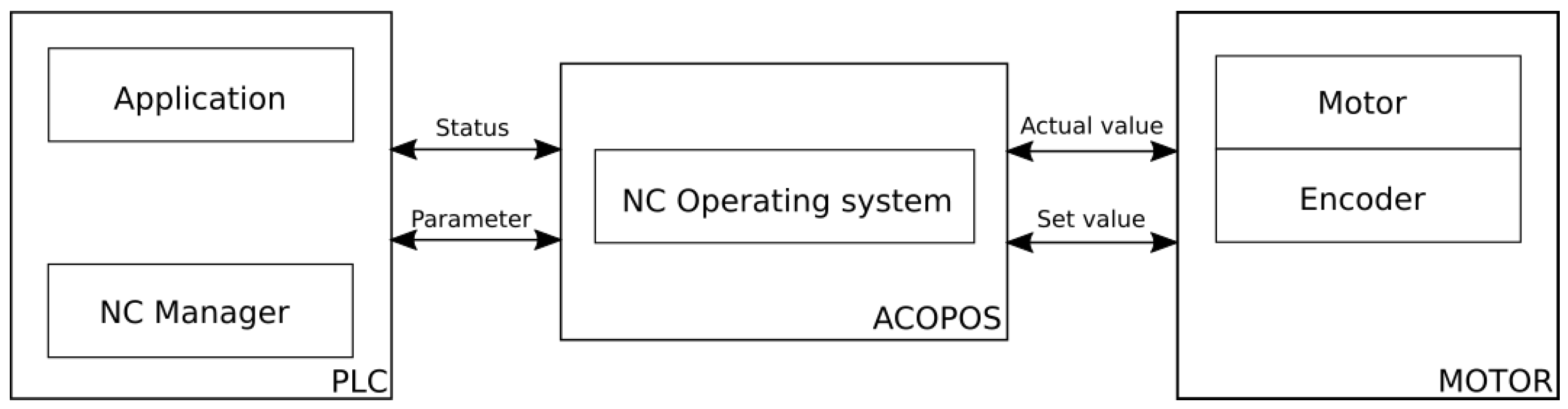
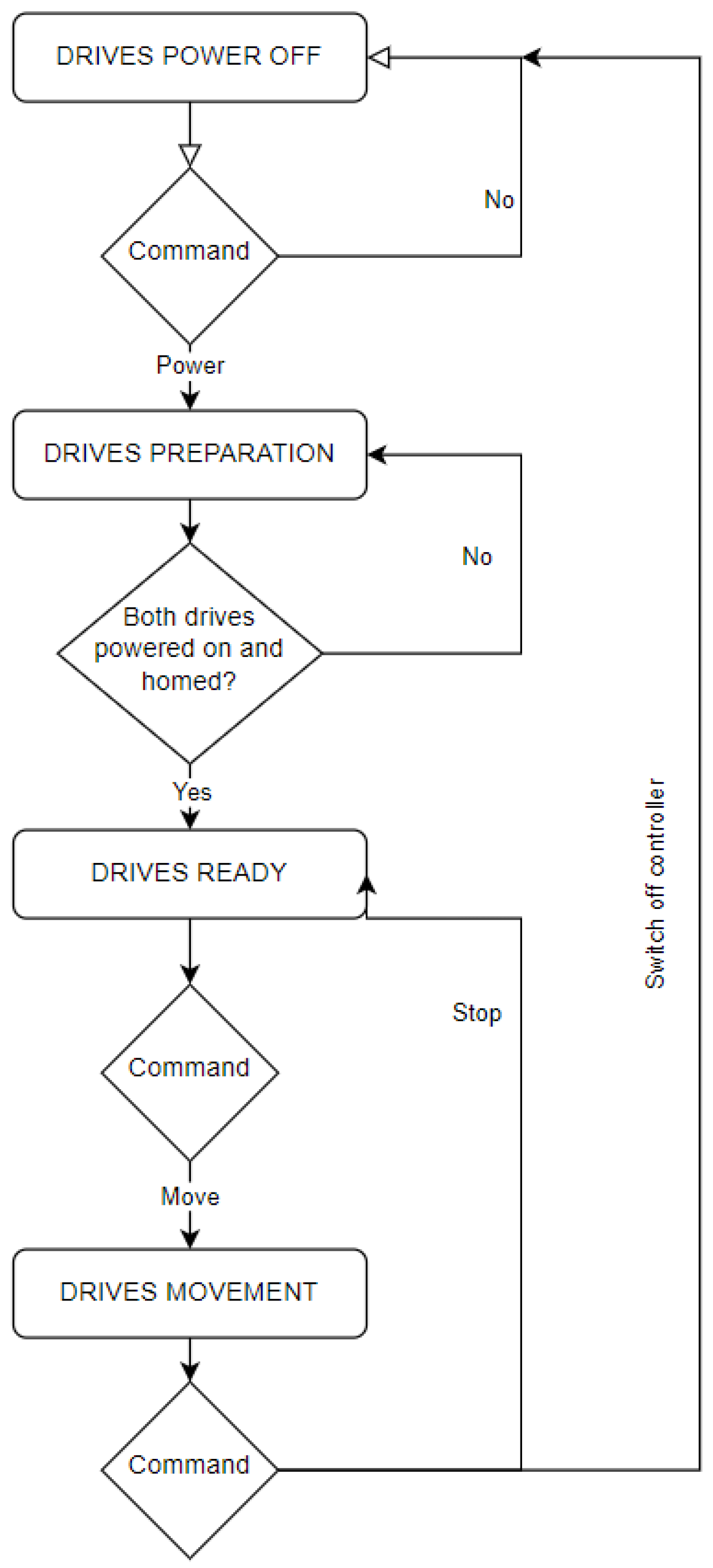
Essentially, the controller is designed at the kinematic level, meaning it generates the nominal control input $u={\left[u_1{u}_2\right]}^T$ for kinematics (1) based on the current reference posture specified by the trajectory $x_r={\left[x_{r1}{x}_{r2}{x}_{r3}\right]}^T\in {\mathcal{X}}_r\subseteq {\mathbb{R}}^3$, which is assumed to be sufficiently smooth. In this case, since the control strategy is smooth, the nominal signals are also smooth, which facilitates the extension of the control strategy to the dynamic level by incorporating an additional control loop. This can be implemented in a cascade manner such that the nominal kinematic inputs become the desired velocity trajectory, which is assumed to be tracked by the robot’s actual velocity. In practice, the velocity of the two-wheeled robot platform considered in this paper is measured and controlled based on the velocities of the left and right wheels. This approach is feasible, however, under operating conditions where wheel slip is negligible, specifically when the assumed velocity constraints are maintained. In such conditions, drive controllers stabilizing velocities of wheels can be employed. Assuming that these controllers ensure velocity tracking with sufficiently small errors, the perturbations affecting the kinematic control law specified for the robot platform become insignificant.

A motion controller based purely on feedback is usually insufficient to solve more complex tasks in mobile robotics. As a result, it is required to take advantage of planning-based strategies to efficiently shape the reference trajectory $x_r$ in order to ensure the proper operation of the robotic platform. This make it possible to include additional constraints, such as the presence of obstacles and limitations on acceleration and velocity. In the designed architecture, such a trajectory is generated with use of a time elastic band algorithm, which was first presented in [26] and later extended in [30]. The time elastic band algorithm was developed using the solution of a sparse scalar multi-objective optimization problem realized in an open loop. In Figure 1, the architecture responsible for realization of motion tasks is presented. The main blocks can be distinguished, such as the planner generating the reference trajectory based on a preliminary set of waypoints. This trajectory is followed by the feedback-based controller augmented by internal dynamics governing the transverse functions. Next, the drive controller is responsible for the realization of the kinematic control strategy by ensuring that velocity error is reduced significantly.

4. Motion Controller

The considered controller is defined on the Lie group G to take advantage of the symmetry of $SE\left(2\right)$ configuration space. Consequently, the difference between any two configurations can be understood in terms of the Lie group. In particular, to quantify the tracking error on the Lie group G, we define:

$$x_e=x_r^{-1}x,$$

(6)

where the group operation (4) and inverse (5) are used, and $x_e={\left[x_{e1}{x}_{e2}{x}_{e3}\right]}^T\in {\mathcal{X}}_e\subseteq {\mathbb{R}}^3$. Analyzing the Formula (6), we find that it has a straightforward geometric interpretation; namely, it represents the robot coordinates x with respect to the reference trajectory coordinate system $x_r$.

4.1. Transverse Function

With use of TF, we designed a bounded kinematic control law u for (1) which provides ${sup}_{t\ge 0}∥x_e\left(t\right)∥<\infty$ and ${lim}_{t\to \infty }{x}_e\left(t\right)\in V_0$, where $V_0$ it is a set of numbers representing the surroundings of a selected point, i.e., a hyperball with the center in the origin and an arbitrary small radius $r_{V_0}>0$. Thus, it is theoretically possible to arbitrarily choose the radius $r_{V_0}$ to select the size of the neighborhood to which the error $x_e$ converges. Stating control problems in this way means that we expect to obtain stabilization of $x_e$ in a practical sense, as opposed to the often postulated asymptotic stabilization. Thus, the trajectory $x_e\left(t\right)$ converges to a small vicinity of e, which is a reasonable result in practical control problems involving a wide range of reference trajectories.

The transverse function can be proposed for a driftless system in form of (1) to satisfy the so-called transversality condition. One of the possibilities is to apply the exponential map of control vector fields [21]. Using this map for the kinematics (1) and employing the parameterization shown in [3], one can obtain the transverse function as:

$$f(\alpha ,\epsilon )=exp\left(\epsilon {\beta }_{1}sin\left(\alpha \right)X_1\left(f_3\right)+\epsilon {\beta }_{2}cos\left(\alpha \right)X_2\left(f_3\right)\right),$$

(7)

where $f(\alpha ,\epsilon )={\left[f_1(\alpha ,\epsilon )f_2(\alpha ,\epsilon )f_3(\alpha ,\epsilon )\right]}^T\subseteq {\mathbb{R}}^3$, $\alpha \in {\mathbb{S}}^1$ is a new control variable, and where for the sake of simplicity, we adopt a designation $f_3\equiv f_3(\alpha ,\epsilon )$, and ${\beta }_1,{\beta }_2\ne 0$ are constants. The meaning of $\epsilon$ will be discussed in the next section.

In this paper, we chose a simpler form of TF that approximates the solution of (1) in a vicinity of e without losing the transversality condition. Taking advantage of the parameterization used in (7), we consider the following formula

$$f(\alpha ,\epsilon )={\left[\epsilon {\beta }_{1}sin\left(\alpha \right)\epsilon {\beta }_{2}cos\left(\alpha \right){\displaystyle \frac{{\epsilon }^2{\beta }_1{\beta }_2}{4}}sin\left(2\alpha \right)\right]}^T.$$

(8)

4.2. Tuning the Transverse Function

In [27], it is shown that $f(\alpha ,\epsilon )$ is maintained in the neighborhood of e, where the radius of this neighborhood can be arbitrarily reduced by choosing a sufficiently small value of $\epsilon$. As a result, the value of $\epsilon$ is responsible adjusting the size of f. However, it is preferable that the value of $\epsilon$ is not too small initially, avoiding highly oscillatory state trajectories and controls. This phenomenon appears especially when implementing trajectory tracking violating the non-holonomic constraints imposed on the system (1). As proposed in [3], in the discussed robot controller, $\epsilon$ is not constant but gradually decreases according to the following formula:

$$\epsilon :={\epsilon }_{min}+{\gamma }_{1}exp(-{\gamma }_{2}t),$$

(9)

where t is time, and the variables ${\gamma }_1,{\gamma }_2,{\epsilon }_{min}\in {\mathbb{R}}_{+}$ are constant positive coefficients. Such a tuning scheme allows for narrowing the convergence tunnel of f to the neighborhood of e, with the radius of ${\epsilon }_{min}$ as time progresses.

4.3. Auxiliary Tracking Error

The transverse function f provides an auxiliary trajectory that remains in the vicinity of e. This trajectory is then tracked by a feedback control law to ensure that the difference between this trajectory and the error $x_e$ converges to e, which simultaneously implies that x approaches a neighborhood of $x_r$. To facilitate control design, the following auxiliary error in the Lie group G is considered

$${\widehat{x}}_e:=x_e{f}^{-1}(\alpha ,\epsilon ),$$

(10)

where ${\widehat{x}}_e\in {\widehat{\mathcal{X}}}_e\subseteq {\mathbb{R}}^3$. The inverse of $f(\alpha ,\epsilon )$ given as $f^{-1}(\alpha ,\epsilon )$ utilizes (5). The composition of $x_e$ and $f^{-1}(\alpha ,\epsilon )$ is achieved with use of the group operation (4).

4.4. Practical Stabilization Controller

The control aim is to design a feedback to ensure that ${lim}_{t\to \infty }{\widehat{x}}_e\left(t\right)=e$. For this purpose, we determine the dynamics of ${\widehat{x}}_e$:

$${\dot{\widehat{x}}}_e=X_{1\_3}\left({\widehat{x}}_e\right){\mathrm{Ad}}_f^X\left(\widehat{C}\left(\alpha ,\epsilon \right)\widehat{u}-A_{\epsilon }\left(\alpha ,\epsilon \right)\dot{\epsilon }-{\mathrm{Ad}}_{x_e^{-1}}^X{v}_r\right),$$

(11)

where $\widehat{C}(\alpha ,\epsilon ):=\left[C-A_{\alpha }(\alpha ,\epsilon )\right]$, $A_{\alpha }\left(\alpha ,\epsilon \right)=X_{1\_3}^{-1}\left(f\right){\displaystyle \frac{\partial f}{\partial \alpha }}$, $A_{\epsilon }\left(\alpha ,\epsilon \right)=X_{1\_3}^{-1}\left(f\right){\displaystyle \frac{\partial f}{\partial \epsilon }}$, $f\equiv f(\alpha ,\epsilon )$. As stated in the section on notation, $X_{1\_3}$ is a matrix composed of vf $X_1$, $X_2$, and $X_3$ from (1). In addition, $X_{1\_3}^{-1}$ is the inverse of the matrix $X_{1\_3}\equiv X_{1\_3}\left({\widehat{x}}_e\right)$. The adjoin operator ${\mathrm{Ad}}_f^X$ is calculated as a combination of operations with the matrix $X_{1\_3}$ as in $X_{1\_3}{\mathrm{Ad}}_f^X={\mathrm{Ad}}_f{X}_{1\_3}$; the adjoin operator ${\mathrm{Ad}}_f$ acting on matrix $X_{1\_3}$ was introduced earlier. The second adjoin operator ${\mathrm{Ad}}_{x_e^{-1}}^X$ is calculated similarly, that is, $X_{1\_3}{\mathrm{Ad}}_{x_e^{-1}}^X={\mathrm{Ad}}_{x_e^{-1}}{X}_{1\_3}$. The element $x_e^{-1}$ is the inverse of $x_e$ given by (6). In addition, here, we introduce the substitution of the input $u_3$ with a time derivative of the variable $\alpha$, which defines the dynamics of changes in $f(\alpha ,\epsilon )$. So, the input is $\widehat{u}={\left[u_1{u}_2{u}_3\right]}^T={\left[u_1{u}_2\dot{\alpha }\right]}^T\in \widehat{\mathcal{U}}\subseteq {\mathbb{R}}^3$. Thus, it is obvious that $u_1$ and $u_2$ are the same as in (1). In (11), there is also an additional control input $v_r={\left[v_{r1}{v}_{r2}{v}_{r3}\right]}^T\in {\mathcal{V}}_r\subseteq {\mathbb{R}}^3$, which is a reference input bounded with $x_r$ (6) by the reference dynamics

$${\dot{x}}_r=X_{1\_3}\left(x_r\right)v_r,$$

(12)

which is equivalent to (3).

Taking into account that the operator $X_{1\_3}\left({\widehat{x}}_e\right){\mathrm{Ad}}_f^X$ is globally invertible and that $\overline{C}(\alpha ,\epsilon )$ is invertible for all $\alpha \in {\mathbb{S}}^1$ due to the properties of the transverse function, we can easily decouple the dynamics (11). As a result, we can propose the following control law:

$$\widehat{u}:={\widehat{C}}^{-1}\left(\alpha ,\epsilon \right)\left({\mathrm{Ad}}_{f^{-1}}^X{X}_{1\_3}^{-1}\left({\widehat{x}}_e\right)K{\widehat{x}}_e+A_{\epsilon }\left(\alpha ,\epsilon \right)\dot{\epsilon }\right),$$

(13)

where $K\in {\mathbb{R}}^{3\times 3}$ is a stable Hurwitz matrix. Substitution of (13) to system (11) yields a linear system ${\dot{\widehat{x}}}_e=K{\widehat{x}}_e$. This controller provides the exponential stability of ${\widehat{x}}_e$ and practical stability at the same time of $x_e$. This, in turn, leads to the state x converging to the vicinity of the reference state $x_r$, ensuring that the robot approximately follows the reference trajectory in practice. The properties of the controller given by (13) are discussed in detail in [27].

5. Motion Planner

In the research under consideration, a planner based on the elastic band approach is used to generate the reference trajectory from waypoints. It is worth mentioning that this algorithm offers much broader capabilities, such as path planning in the presence of obstacles. In the following, we describe the method for optimizing the trajectory within the overall planning task. Certain dependencies will be rewritten in a form that corresponds to the representation of the system (1). As the time elastic band algorithm is presented in the discrete domain in paper [30], this section follows the same approach.

Let us define the reference state in discrete time $x_r\left(k\right)={\left[x_{r1}\left(k\right)x_{r2}\left(k\right)x_{r3}\left(k\right)\right]}^T={\left[x_{rc}\left(k\right)y_{rc}\left(k\right){\theta }_{rc}\left(k\right)\right]}^T\in {\mathcal{X}}_r\subseteq {\mathbb{R}}^3$, where the corresponding elements denote the desired position and orientation with respect to the inertial coordinate frame. Hence, $x_r\left(k\right)$ is a discrete trajectory that determines the pose of the reference robot for $k=1,2,\cdots ,j$. Simultaneously, to represent the process in real time, we introduce the time interval for a given k sample in the form $\mathrm{\Delta }T\left(\overline{k}\right)\in {\mathbb{R}}^{+}$ where $\overline{k}=1,2,\cdots ,j-1$. Each sample $\mathrm{\Delta }T\left(\overline{k}\right)$ specifies the time to move from $x_r\left(k\right)$ to $x_r(k+1)$. Consequently, these values form pairs, which can be organized as a vector of transitions:

$$\begin{array}{cc}\hfill b:=& {[x_r\left(1\right)\mathrm{\Delta }T\left(1\right)x_r\left(2\right)\mathrm{\Delta }T\left(2\right)\cdots x_r(j-1)\mathrm{\Delta }T(j-1)x_r\left(j\right)]}^T.\hfill \end{array}$$

(14)

Consider auxiliary reference state values in the form of reference initial state $x_{r0}$ and final state $x_{rf}$. The goal is to determine reference controls that enable a transition from $x_{r0}$ to $x_{rf}$ in a minimum amount of time while ensuring that the constraints imposed by the robot’s kinematics are maintained. It is also necessary to define a function related to the kinematics constraints of the robot (1). Since it was previously assumed that the evolution of the reference trajectory $x_r$ must correspond to the solution of the dynamics (12), it must also correspond to these requirements. However, for simplicity, we will assume that the evolution of the reference trajectory will be restricted by vfs $X_1$ and $X_2$ without using vf $X_3$. This is a narrowing of the requirement for $x_r$ evolution, which is due to the practicalities involved in determining a convenient trajectory for the movement of mobile robots. There are many well-known ways to achieve this goal. In the paper [30], it was proposed that the constraints associated with robot kinematics would be introduced by a function that relates the local angle of the robot’s orientation with respect to the vector connecting the two selected consecutive states of robot $x_r\left(k\right)$ and $x_r(k+1)$. We define the vector connecting these points as the reduced increment of $x_r\left(k\right)$ in the form:

$$\mathrm{\Delta }{x}_r\left(k\right)={\left[x_{r1}(k+1)-x_{r1}\left(k\right)x_{r2}(k+1)-x_{r2}\left(k\right)0\right]}^T.$$

(15)

The points $x_r\left(k\right)$ and $x_r(k+1)$ are assumed to be in a common arc. Following [30], we define the constraint equation associated with the robot’s kinematics as follows:

$$h(x_r(k+1),x_r\left(k\right)):=\left[X_1\left(x_{r3}\left(k\right)\right)+X_1\left(x_{r3}\left(k\right)\right)\right]\times \Delta {\check{x}}_r\left(k\right),$$

(16)

where $X_1$ is defined by (2) and ’×’ denotes the cross product in ${\mathbb{R}}^3$.

According to [30], the optimization task can be specified by:

$$V^{*}\left(b\right):=\underset{b}{min}\sum _{\overline{k}=1}^{n-1}{(\Delta T\left(\overline{k}\right))}^2,$$

(17)

subject to initial and final constraints

$$x_r\left(1\right)=x_{r0},x_r\left(j\right)=x_{rf},$$

and subject to the following algebraic constraints

$$\begin{array}{cc}\hfill & h(x_r(k+1),x_r\left(k\right))=0,\hfill \\ \hfill & r(x_r(k+1),x_r\left(k\right))\ge 0,\hfill \\ \hfill & v(x_r(k+1),x_r\left(k\right),\Delta T\left(\overline{k}\right))\ge 0,\hfill \\ \hfill & a(x_r(k+2),x_r(k+1),x_r\left(k\right),\Delta T(\widehat{k}+1),\Delta T\left(\widehat{k}\right))\ge 0,\hfill \\ \hfill & a(x_r\left(2\right),x_r\left(1\right),\Delta T\left(1\right))\ge 0,\hfill \\ \hfill & a(x_r\left(j\right),x_r(j-1),\Delta T(j-1))\ge 0,\hfill \end{array}$$

where b is given by (14) and $\Delta T\left(k\right)>0$, $\widehat{k}=2,3,\cdots ,j-2$. The inequality $r(·)\ge 0$ relates to the steering angle constraint, which is of a strong practical importance for real-world implementations of this algorithm. In addition, $v(·)\ge 0$ and $a(·)\ge 0$ describe the constraints imposed on the robot speed and acceleration, respectively, which are important in real-time operations. Detailed considerations of these constraint functions are not presented here, and the reader interested in the details is referred to the articles [26,30].

6. Mobile Robot TMR

6.1. Basic Information About the Mobile Robot

The design of the TMR is based on a classical differential traction structure, equipped with two opposing main wheels and two supporting wheels. The TMR robot without the outer casing is presented in Figure 2. The two main wheels are driven by built-in BLDC electric motors fitted in the wheels with unique running rims. In addition, the robot is equipped with two self-adjustable support wheels. On top of the robot is a system for automatically docking the robot to a towed trailer. Since the robot control research presented in this article is concerned with controlling the movement of the robot without a trailer, the details of the trailer are omitted here. The support frame of the robot was enlarged due to the expansion of the robot’s components, such as development of the power battery system and control electronic systems. Basic dimension and mass data are given in

Table 1. Basic design information of the mobile robot.

Dimensions (Width, Length, Height)	600, 850, 480 [mm]
Net weight	50 kg
Payload	20 kg
Permissible trailer weight	50 kg
Drive wheel diameter	280 mm
Track width	482.5 mm
Max. speed	2 m/s

. The robot’s chassis structure is equipped with a suspension system that is adapted to the robot’s operation in outdoor spaces.

6.2. Robot Electronic Architecture

As a part of the robot’s design development, it was equipped with new electrical and electronic modules. The control system is based on the PLC made by B&R described in Section 6.3 and an Intel NUC Mini PC with the ROS environment implemented, which is discussed in Section 6.4. The position sensors for both wheels have been upgraded with TR1 TrueTrac encoders. A new modern safety controller was employed based on SICK’s Flexi Soft, SICK AG, Waldkirch, Germany. In addition, the robot was equipped with a new power supply system with charge control, an emergency power supply system, and the ability to flexibly connect electronic devices with different supply voltages. The motors are powered by 24 V high-power Pb batteries, while the electronics are powered by 24 V and 19 V low-power Li-Ion batteries. The block diagram of the connections between the individual modules is shown in Figure 3.

The implementation of new electrical and electronic modules forced the replacement of entire wiring, relays, switches, and transducers. New modules have been developed to enable flexible expansion of the robot’s electrical infrastructure, by adding, for example, new measurement devices.

6.3. Low-Level Drive Controller

The low-level control system consists of Programmable Logic Control (PLC) designed by B&R Industrial Automation GmbH, Eggelsberg, Austria with X20 series input and output cards and ACOPOSmicro servo drives (ACOPOS) which control 400-Series BLDC motors by Crystalyte; see Figure 4. The chosen PLC is equipped with 400 MHz and can work with a minimum cycle time of 1 ms. The ACOPOS server drive can work with nominal current of 8 A and voltage of 24 to 64 VDC. The used BLDC motor has a nominal voltage of 36 VDC and current of 2.42 A.

The PLC is a core part of the low-level controller. It receives a command from a high-level PC and processes an algorithm accordingly and controls physical inputs and outputs, such as analog signals and digital buttons from a joystick, enable signals from an emergency stop button, and battery status.

The communication architecture between the PLC and the servo drivers is shown in Figure 5. Motion control is the main part of the control process. According to the commands from a high-level PC, the PLC sends a command to servo drives (the ACOPOS in Figure 5), mostly in order to start the controller, to drive motors (marked as MOTOR in Figure 5) with proper parameters, i.e., set speed, acceleration, and jerk. Closed-loop control is covered by servo drives and is realized on the basis of the wheel rotation measurement, the actual value. The servo drives return status information to the PLC.

The algorithms implemented work in cycles depending on the demand for a fast reaction. The motion control module works with a 2 ms cycle, slower I/O with 100 ms, and TCP/IP communication with 200 ms. The motion control algorithm is shown in Figure 6.

The PLC sends parameters, such as speed and acceleration, to the ACOPOS servos and receives the status, e.g., an actual position, velocity, and the state, of each ACOPOS driver. The ACOPOS driver plans the setpoints and performs the control loop according to the control structure shown in Figure 7. The ACOPOS works in a loop—the cycle time of the position controller is 400 $\mathsf{\mu }$s, while that of the speed controller is 200 $\mathsf{\mu }$s and current controller is 200 $\mathsf{\mu }$s. The ACOPOS supplies motor with voltage and receives information about the actual motor current, shaft position, and velocity.

The ACOPOS controller uses PI-type regulators for both position and speed control of the motor in the cascade controller. Gain values for both regulators were determined using the built-in autotune procedure of the ACOPOS. This procedure was carried out on the basis of the guidelines from the ACOPOS documentation [31]. Subsequently, manual tuning of the controllers’ parameters was carried out. For this purpose, a positional override was set on the controller to achieve a trapezoidal profile of the set velocity. Then, the proportional gains of the controllers increased until the maximum dynamic responses were obtained and the speed overshoot was 5%. Subsequently, adjustment of the gain of the I component of the controller was made to increase the dynamics of the processes involved in leveling the steady-state deviation. Figure 8 shows the graphs recorded during the ACOPOS controller parameter tuning procedure, where the response was recorded using the final adjusted parameters. The overall goal of the tuning procedure was to find the smallest possible lag error for given velocity, acceleration, and deceleration values. The second graph in the series of charts shows the set constant speed value with a linear ramp up and down. The fourth graph shows the position value, and the first graph shows the position error. In the position error graph, it can be seen that in the period of 0–0.2 s, a deviation value of $\pm 0.3^{\circ }$ was obtained, so the stabilization time $0.2$ s was achieved. During constant velocity movement, in the period 0.2–1.0 s, the lag error is smaller and lies in the range of 0–0.1°.

6.4. High-Level Control

The high-level controller was implemented on an Intel NUC Mini PC running the Ubuntu with ROS operating system. The crucial role in the high-level software module is related to the main controller unit. This unit is responsible for calculations related to the velocity stabilization algorithm using transverse functions and the algorithm responsible for generating the reference trajectory of the robot’s movement. In addition, it aggregates measurement data from external sensors and collects diagnostic data from the low-level subsystem. Data exchange between the high-level control module and the low-level control module is carried out via the TCP/IP protocol. The communications software operates in two regimes, where the first concerns crucial data exchange, i.e., robot status management data of low-level control system and desired values for low-level controllers, where the exchanged is performed continuously in a loop of frequency up to 20 Hz. The second regime concerns communication on demand in a request–response manner to exchange less frequently updated data like configuration parameters.

7. Outdoor Experiments

The experiment illustrates the passage of a mobile robot in open space through a given point using an algorithm with transverse functions and a time elastic band algorithm to determine the reference trajectory. The time elastic band algorithm was implemented using the teb_local_planner plugin [32] for ROS.

The robot’s task is to pass through a set of waypoints ${\overline{x}}_w={\left[x_c{y}_c\right]}^T\in {\overline{\mathcal{X}}}_w\subseteq {\mathbb{R}}^2$, that is, points that define only the position without orientation: ${\overline{x}}_{w\left(1\right)}={\left[1.51\right]}^T$, ${\overline{x}}_{w\left(2\right)}={[2.5-1]}^T$, ${\overline{x}}_{w\left(3\right)}={\left[3.51\right]}^T$, ${\overline{x}}_{w\left(4\right)}={[4.5-1]}^T$ and ${\overline{x}}_{w\left(5\right)}={\left[05\right]}^T$. The starting point and goal point are denoted as $x_{w\left(0\right)}={\left[x_c{y}_c{\theta }_c\right]}^T$ and $x_{w\left(f\right)}={\left[x_c{y}_c{\theta }_c\right]}^T$ belonging to ${\mathcal{X}}_w\subseteq {\mathbb{R}}^3$ and are defined as $x_{w\left(0\right)}={\left[000\right]}^T$ and $x_{w\left(f\right)}={\left[060\right]}^T$. Most of the teb_local_planner plugin parameters were left at the default, with only a few changes. The parameters that were changed were maximum longitudinal speed $\mathit{max}\_\mathit{vel}\_\mathit{x}=0.5$ m/s, maximum angular speed $\mathit{max}\_\mathit{vel}\_\mathit{theta}=0.5$ m/s, forward movement preference parameter $\mathit{weight}\_\mathit{kinematics}\_\mathit{forward}\_\mathit{drive}=1000$, and minimization of the distance from the passage points $\mathit{weight}\_\mathit{viapoint}=300$. The parameters of the TF controller were as follows: the feedback gain matrix K was the identity matrix, the parameters responsible for the proportional gain of the individual members of the transverse function ${\beta }_1=1.2$, ${\beta }_2=1.7$ and the parameters of dynamics of convergence of functions $\epsilon$ ware ${\epsilon }_{min}=0.25$, ${\gamma }_1=2.5$, ${\gamma }_2=0.1$.

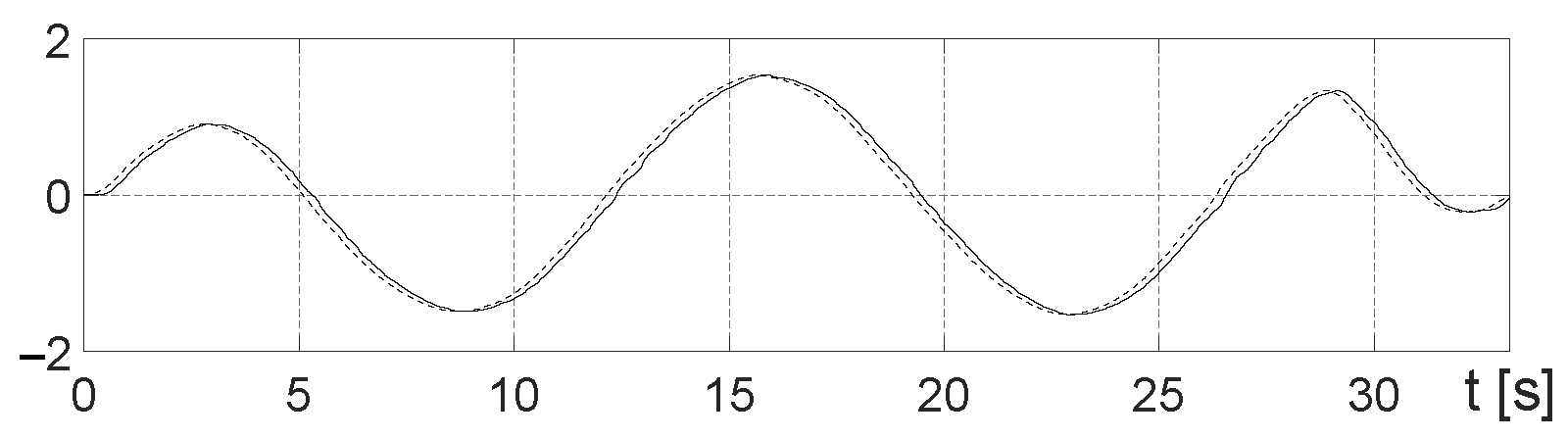
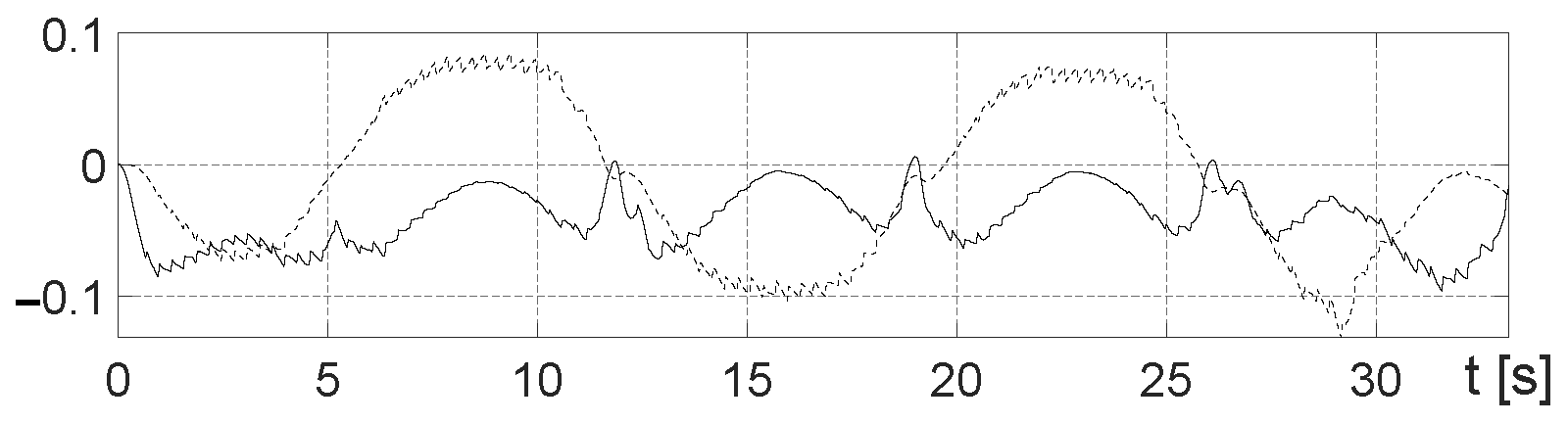
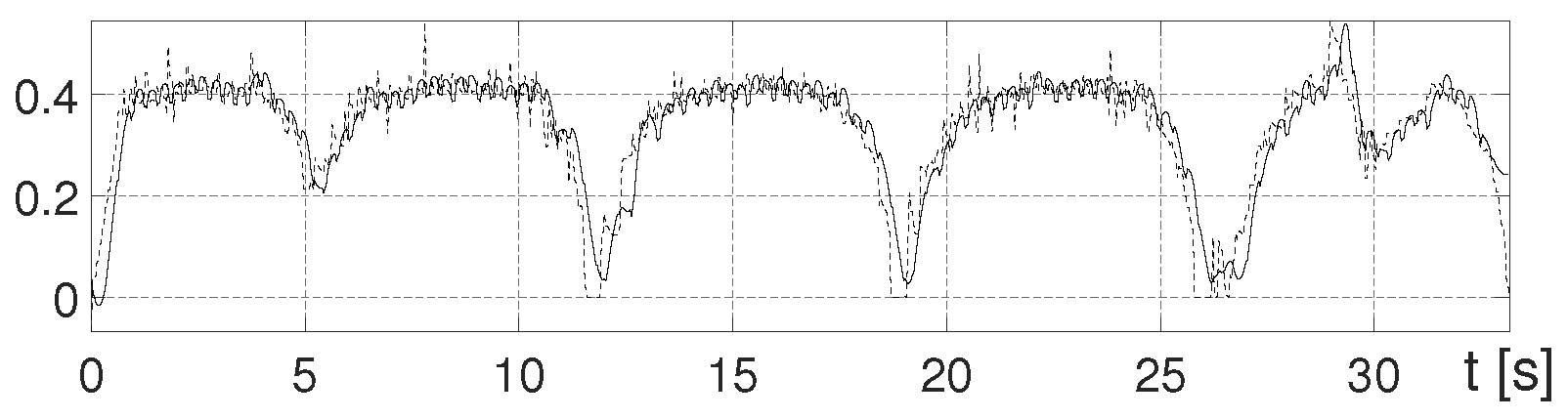
Figure 9 shows the trajectory of the robot’s movement along with the passage points. Analyzing the position of the passage points and the trajectory, it can be seen that it was generated correctly. At the same time, it can be observed that the continuity of the trajectory at the passage points is preserved, which is due to the limiting function $h\left(x_r\right)$ implemented in (16). Figure 10 and Figure 11 show the TMR position and orientation of the TMR along with the reference position and orientation, while Figure 12 and Figure 13 show the errors of these values. From Figure 12, it can be seen that the position error does not exceed $\pm 0.1$ m with $x_{e1}$ three times smaller than $x_{e2}$. From Figure 13, it can be noticed that the misalignment of orientation does not exceed $\pm 0.2$ rad. This is mainly due to the less aggressively adjusted gains of the proportional controller in the low-level controller. 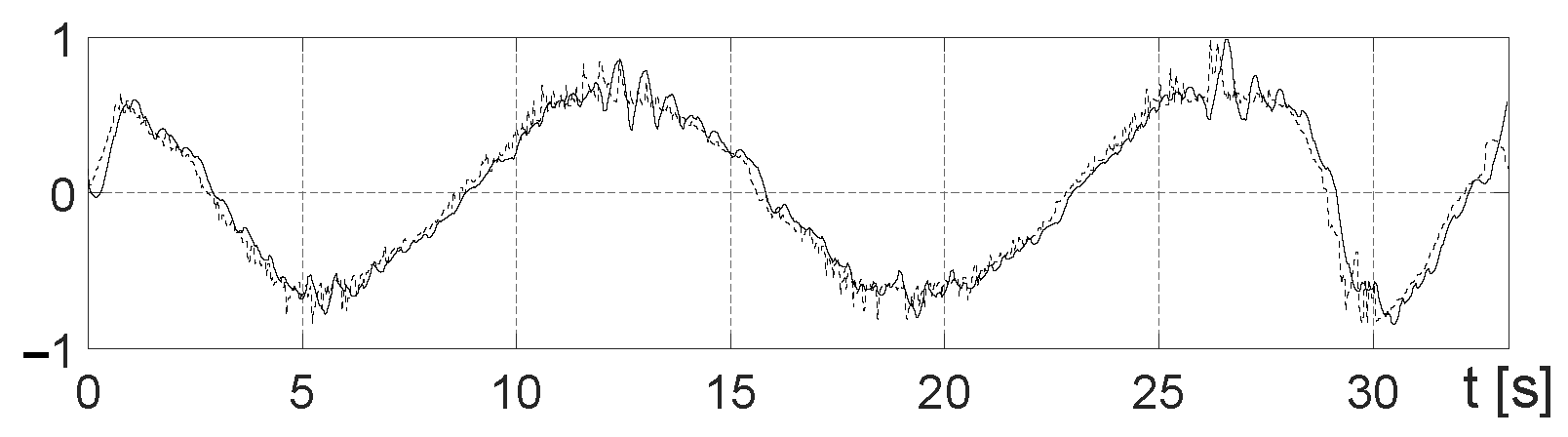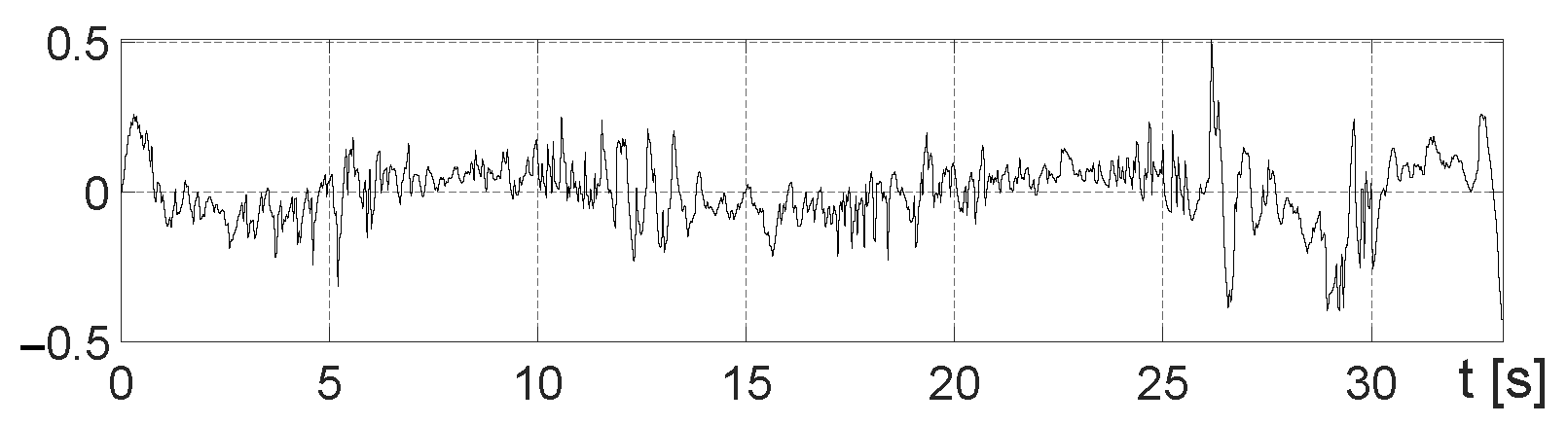Figure 14 and Figure 15 show the input control u and the reference control $v_r$, and Figure 16 and Figure 17 show the differences of these values. It can be observed that there are relatively large pulses in the control process, which most likely have the same cause as mentioned above.

The experiment confirms that the TMR stably performed the passage through the given points. The robot passed through the passage points with a precision of less than $0.08$ m. Figure 18 shows the robot during the execution of the experiment.

8. Conclusions

This paper covers the redevelopment of the TMR robot, focusing on the implementation of both high-level and low-level controllers. The high-level controller includes an algorithm for trajectory tracking, with the trajectory determined based on waypoints points for practical reasons. We have provided details of the control algorithm design, along with the architecture and structure of the low-level controller. Our research and experiments show that the proposed control architecture works well for the task at hand. This work marks the first presentation of the TMR robot after a complete redesign of its control systems and the first field tests. In particular, it is demonstrated that a kinematic controller based on the transverse function approach, combined with an elastic-band-based planner, can effectively support motion tasks for a class of service robots, including the TMR robot.

The paper also includes the first outdoor implementation of the transverse function synthesis algorithm. In the future, the TMR robot will be used for more in-depth research on mobile robot control, particularly for tasks such as pulling a trailer in environments that require obstacle avoidance. The platform and its architecture are open and modular, making it a well-suited tool to test advanced motion control methods for nonholonomic robots, with applications in both academic research and real-world use.