SCS-JPGD: Single-Channel-Signal Joint Projected Gradient Descent
Abstract
1. Introduction
- 1.
- A novel and effective adversarial sample generation method based on the Projected Gradient Descent attack is proposed, which can introduce sufficient interference to the model.
- 2.
- A joint training approach under gradient-based adversarial attacks is introduced, which allows the model to undergo adversarial training and regain high diagnostic accuracy under minor perturbations.
- 3.
- Comprehensive experiments were conducted on the CWRU dataset under four different operating conditions, achieving a classification accuracy of 90% and improving the model’s robustness.
2. Related Works
2.1. Application of Deep Learning in Fault Diagnosis
2.2. Adversarial Samples and Adversarial Training
2.3. One-Dimensional Convolutional Neural Network
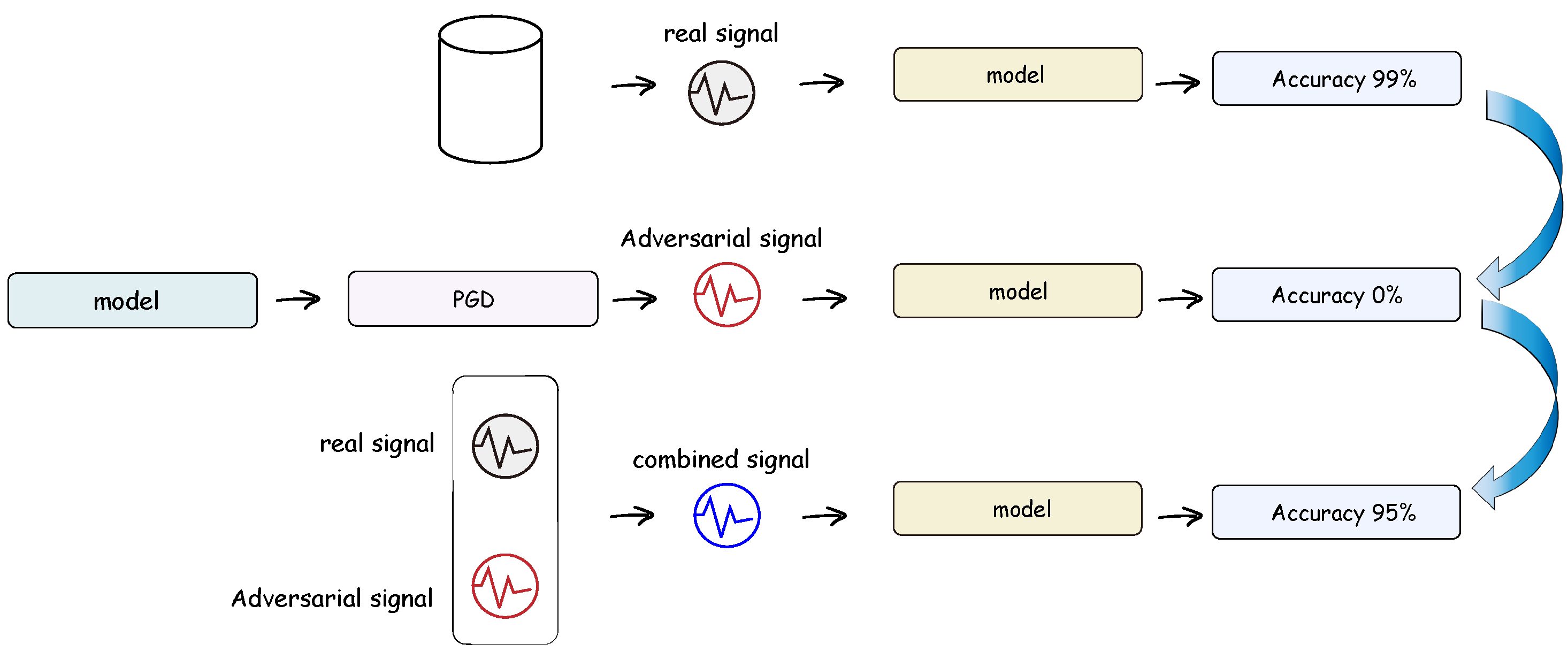
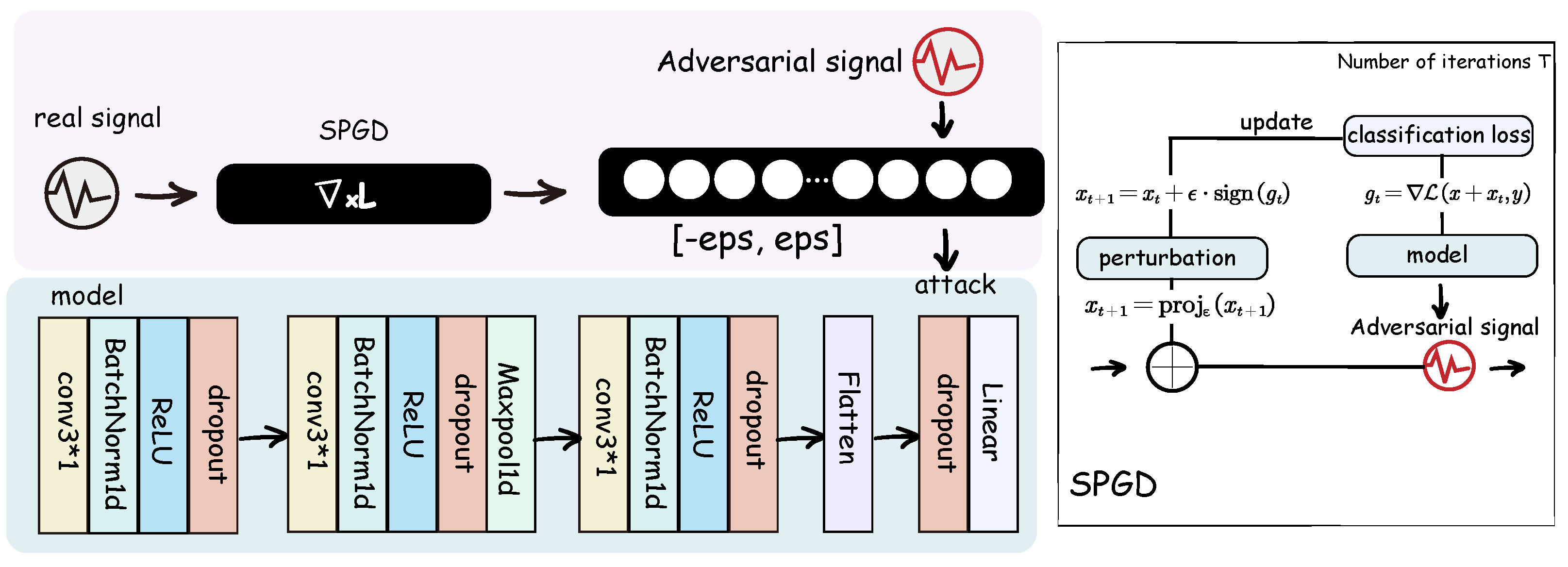
3. Methods
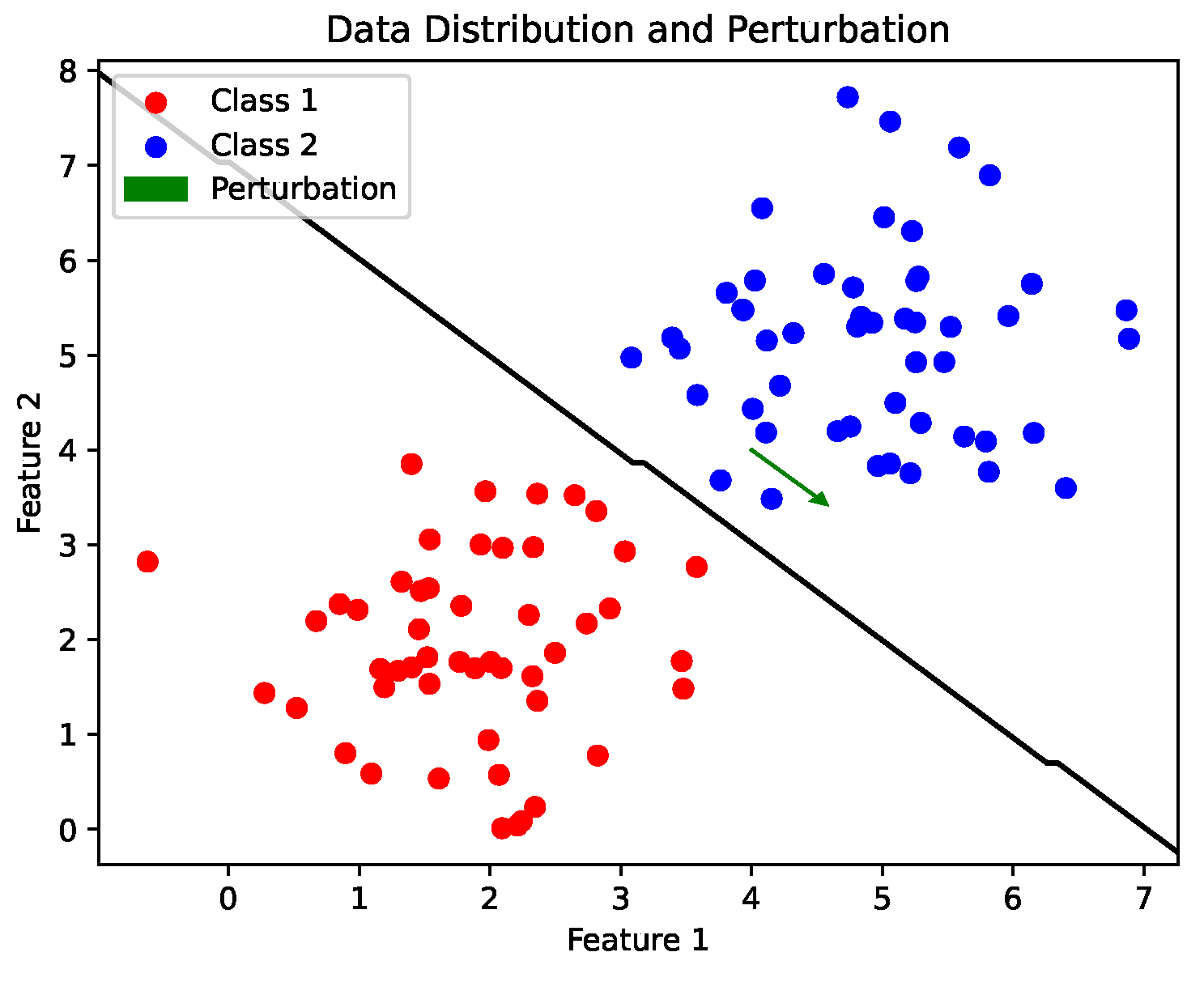
3.1. Signal Projected Gradient Descent
3.2. Adversarial Training
| Algorithm 1: Adversarial Training Algorithm |
|
4. Experiments and Results
4.1. Experimental Setup
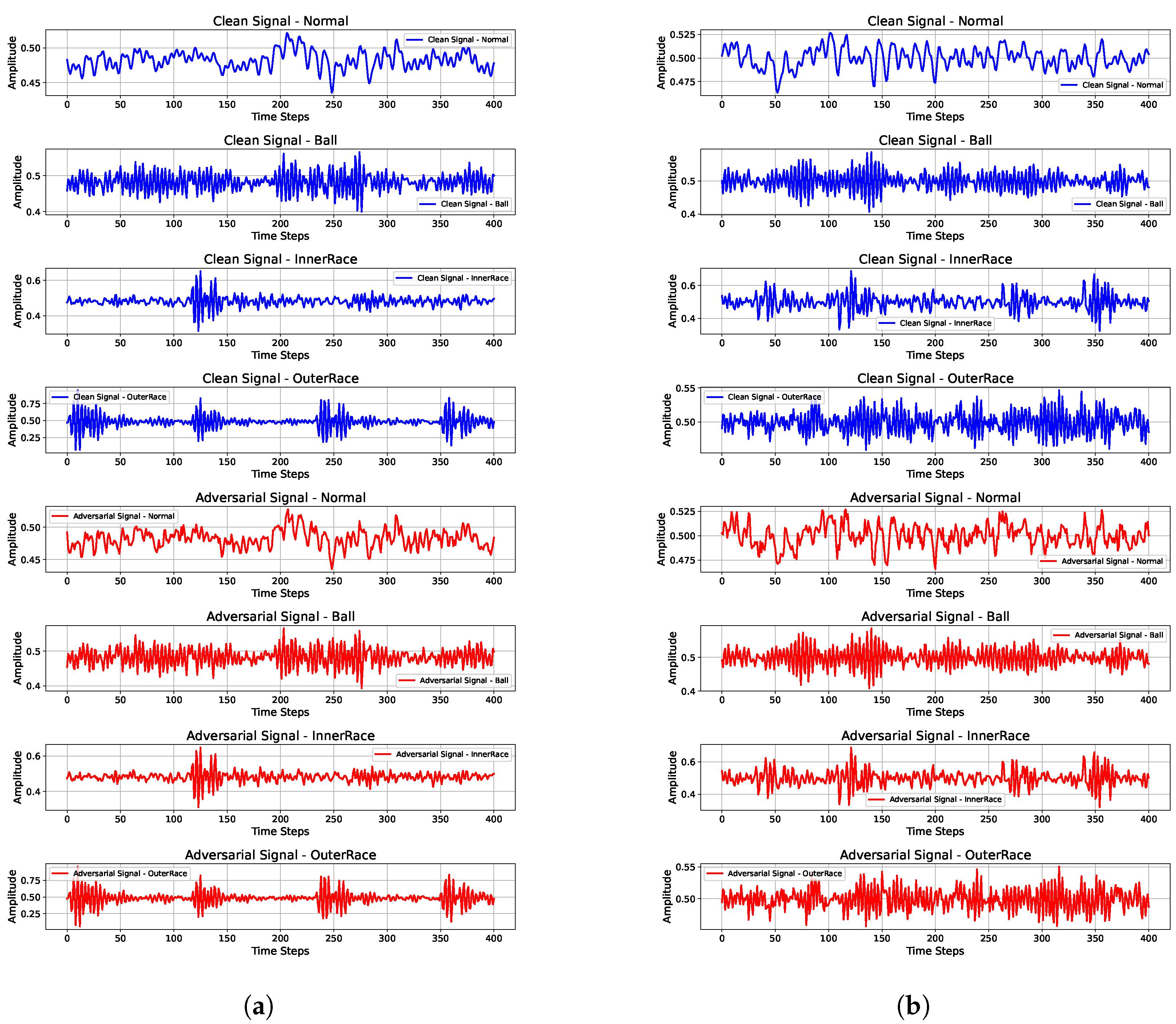
4.1.1. Data Description
4.1.2. Data Preprocessing
4.1.3. Model Hyperparameters
4.2. Experimental Results
| Model Type | Accuracy | Adversarial Test Accuracy |
|---|---|---|
| Baseline Model (1730) | 79.34% | 4.43% |
| SCS-JPGD (1730) | 90.34% | 66.72% |
| Baseline Model (1750) | 70.07% | 8.06% |
| SCS-JPGD (1750) | 93.42% | 60.36% |
| Baseline Model (1772) | 77.47% | 39.80% |
| SCS-JPGD (1772) | 94.24% | 74.01% |
| Baseline Model (1797) | 91.39% | 1.84% |
| SCS-JPGD (1797) | 99.80% | 69.47% |
| CNN [25] (FGSM) | 97.94% | 45.24% |
| CNN [25] (BIM) | 97.94% | 43.46% |
| CNN [25] (PGD) | 97.94% | 41.15% |
| CNN [25] (C&W) | 97.94% | 43.87% |
| LeNet [26] (FGSM) | 95.96% | 57.98% |
| LeNet [26] (BIM) | 95.96% | 58.09% |
| LeNet [26] (PGD) | 95.96% | 58.91% |
| LeNet [26] (C&W) | 95.96% | 58.36% |
| AlexNet [27] (FGSM) | 93.01% | 52.27% |
| AlexNet [27] (BIM) | 93.01% | 56.72% |
| AlexNet [27] (PGD) | 93.01% | 53.42% |
| AlexNet [27] (C&W) | 93.01% | 54.06% |
| ResNet-18 [28] (FGSM) | 96.45% | 60.08% |
| ResNet-18 [28] (BIM) | 96.45% | 61.14% |
| ResNet-18 [28] (PGD) | 96.45% | 60.78% |
| ResNet-18 [28] (C&W) | 96.45% | 59.98% |
4.3. Analysis of Results
4.4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ruan, D.; Wang, J.; Yan, J.; Gühmann, C. CNN parameter design based on fault signal analysis and its application in bearing fault diagnosis. Adv. Eng. Inform. 2023, 55, 101877. [Google Scholar] [CrossRef]
- Liang, Y.P.; Hsu, Y.S.; Chung, C.C. A Low-Power Hierarchical CNN Hardware Accelerator for Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2024, 73, 1–11. [Google Scholar] [CrossRef]
- Dao, F.; Zeng, Y.; Qian, J. Fault diagnosis of hydro-turbine via the incorporation of bayesian algorithm optimized CNN-LSTM neural network. Energy 2024, 290, 130326. [Google Scholar] [CrossRef]
- Choudhary, A.; Mishra, R.K.; Fatima, S.; Panigrahi, B.K. Multi-input CNN based vibro-acoustic fusion for accurate fault diagnosis of induction motor. Eng. Appl. Artif. Intell. 2023, 120, 105872. [Google Scholar] [CrossRef]
- Kim, H.; Lee, S.; Lee, J.; Lee, W.; Son, Y. Evaluating practical adversarial robustness of fault diagnosis systems via spectrogram-aware ensemble method. Eng. Appl. Artif. Intell. 2024, 130, 107980. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Chang, X.; Wang, J.; Rodríguez, R.J. AB-FGSM: AdaBelief optimizer and FGSM-based approach to generate adversarial examples. J. Inf. Secur. Appl. 2022, 68, 103227. [Google Scholar] [CrossRef]
- Ali, M.N.; Amer, M.; Elsisi, M. Reliable IoT paradigm with ensemble machine learning for faults diagnosis of power transformers considering adversarial attacks. IEEE Trans. Instrum. Meas. 2023, 72, 3525413. [Google Scholar] [CrossRef]
- Tripathi, A.M.; Behera, S.R.; Paul, K. Adv-IFD: Adversarial Attack Datasets for An Intelligent Fault Diagnosis. In Proceedings of the 2022 IEEE International Joint Conference on Neural Networks (IJCNN), Padua, Italy, 18–23 July 2022; pp. 1–8. [Google Scholar]
- Gao, D.; Zhu, Y.; Ren, Z.; Yan, K.; Kang, W. A novel weak fault diagnosis method for rolling bearings based on LSTM considering quasi-periodicity. Knowl.-Based Syst. 2021, 231, 107413. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, B.; Gao, D. Bearing fault diagnosis base on multi-scale CNN and LSTM model. J. Intell. Manuf. 2021, 32, 971–987. [Google Scholar] [CrossRef]
- Yu, P.; Ping, M.; Cao, J. An Interpretable Deep Learning Approach for Bearing Remaining Useful Life. In Proceedings of the 2023 IEEE China Automation Congress (CAC), Chongqing, China, 17–19 November 2023; pp. 6199–6204. [Google Scholar]
- An, Z.; Li, S.; Wang, J.; Jiang, X. A novel bearing intelligent fault diagnosis framework under time-varying working conditions using Recurrent Neural Network. ISA Trans. 2020, 100, 155–170. [Google Scholar] [CrossRef]
- Chen, M.; Shao, H.; Dou, H.; Li, W.; Liu, B. Data augmentation and intelligent fault diagnosis of planetary gearbox using ILoFGAN under extremely limited samples. IEEE Trans. Reliab. 2022, 72, 1029–1037. [Google Scholar] [CrossRef]
- Li, W.; Zhong, X.; Shao, H.; Cai, B.; Yang, X. Multi-mode data augmentation and fault diagnosis of rotating machinery using modified ACGAN designed with new framework. Adv. Eng. Inform. 2022, 52, 101552. [Google Scholar] [CrossRef]
- Li, Y.; Song, Y.; Jia, L.; Gao, S.; Li, Q.; Qiu, M. Intelligent fault diagnosis by fusing domain adversarial training and maximum mean discrepancy via ensemble learning. IEEE Trans. Ind. Inform. 2020, 17, 2833–2841. [Google Scholar] [CrossRef]
- Chen, Z.; He, G.; Li, J.; Liao, Y.; Gryllias, K.; Li, W. Domain adversarial transfer network for cross-domain fault diagnosis of rotary machinery. IEEE Trans. Instrum. Meas. 2020, 69, 8702–8712. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, W.; Liao, Y.; Song, Z.; Shi, J.; Jiang, X.; Shen, C.; Zhu, Z. Bearing fault diagnosis via generalized logarithm sparse regularization. Mech. Syst. Signal Process. 2022, 167, 108576. [Google Scholar] [CrossRef]
- Ma, Y.; Shi, H.; Tan, S.; Tao, Y.; Song, B. Consistency regularization auto-encoder network for semi-supervised process fault diagnosis. IEEE Trans. Instrum. Meas. 2022, 71, 1–15. [Google Scholar] [CrossRef]
- Shojaeinasab, A.; Jalayer, M.; Baniasadi, A.; Najjaran, H. Unveiling the black box: A unified XAI framework for signal-based deep learning models. Machines 2024, 12, 121. [Google Scholar] [CrossRef]
- Rojas-Dueñas, G.; Riba, J.R.; Moreno-Eguilaz, M. Black-box modeling of DC–DC converters based on wavelet Convolutional Neural Networks. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Kuok, S.C.; Yuen, K.V. Broad Bayesian learning (BBL) for nonparametric probabilistic modeling with optimized architecture configuration. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 1270–1287. [Google Scholar] [CrossRef]
- Cao, K.; Liu, M.; Su, H.; Wu, J.; Zhu, J.; Liu, S. Analyzing the noise robustness of deep neural networks. IEEE Trans. Vis. Comput. Graph. 2020, 27, 3289–3304. [Google Scholar] [CrossRef]
- Amini, S.; Ghaemmaghami, S. Towards improving robustness of deep neural networks to adversarial perturbations. IEEE Trans. Multimed. 2020, 22, 1889–1903. [Google Scholar] [CrossRef]
- Ayas, M.S.; Ayas, S.; Djouadi, S.M. Projected Gradient Descent adversarial attack and its defense on a fault diagnosis system. In Proceedings of the 2022 45th IEEE International Conference on Telecommunications and Signal Processing (TSP), Virtual, 13–15 July 2022; pp. 36–39. [Google Scholar]
- Forsyth, D.A.; Mundy, J.L.; di Gesú, V.; Cipolla, R.; LeCun, Y.; Haffner, P.; Bottou, L.; Bengio, Y. Object recognition with gradient-based learning. In Shape, Contour and Grouping in Computer Vision; Springer: Berlin/Heidelberg, Germany, 1999; pp. 319–345. [Google Scholar]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 2012, 25, 84–90. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]



| Hyperparameter | Value |
|---|---|
| Learning Rate | 0.003 |
| Training Epochs | 200 |
| Batch Size | 32 |
| Adversarial Training hyperparameters | 0.009 |
| Adversarial Training hyperparameters | 0.001 |
| Adversarial Training Iterations | 20 |
| Learning Rate | Accuracy | Adversarial Test Accuracy | ||
|---|---|---|---|---|
| 0.001 | 0.01 | 0.001 | 0.9201 | 0.5922 |
| 0.001 | 0.01 | 0.005 | 0.9939 | 0.5697 |
| 0.001 | 0.05 | 0.001 | 0.9857 | 0.0779 |
| 0.001 | 0.05 | 0.005 | 0.9590 | 0.0000 |
| 0.005 | 0.01 | 0.001 | 0.8320 | 0.5143 |
| 0.005 | 0.01 | 0.005 | 0.9898 | 0.6434 |
| 0.005 | 0.05 | 0.001 | 0.9898 | 0.1352 |
| 0.005 | 0.05 | 0.005 | 0.8320 | 0.0000 |
| 0.003 | 0.01 | 0.001 | 0.9959 | 0.6660 |
| 0.003 | 0.009 | 0.001 | 0.9980 | 0.6947 |
| Model | Accuracy | Adversarial Test Accuracy |
|---|---|---|
| LeNet | 95.96% | 60.20% |
| AlexNet | 93.01% | 56.76% |
| ResNet-18 | 96.45% | 64.36% |
| CNN (ours) | 99.80% | 69.47% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Cheng, S.; Du, X. SCS-JPGD: Single-Channel-Signal Joint Projected Gradient Descent. Appl. Sci. 2025, 15, 1564. https://doi.org/10.3390/app15031564
Wang Y, Cheng S, Du X. SCS-JPGD: Single-Channel-Signal Joint Projected Gradient Descent. Applied Sciences. 2025; 15(3):1564. https://doi.org/10.3390/app15031564
Chicago/Turabian StyleWang, Yulin, Shengyi Cheng, and Xianjun Du. 2025. "SCS-JPGD: Single-Channel-Signal Joint Projected Gradient Descent" Applied Sciences 15, no. 3: 1564. https://doi.org/10.3390/app15031564
APA StyleWang, Y., Cheng, S., & Du, X. (2025). SCS-JPGD: Single-Channel-Signal Joint Projected Gradient Descent. Applied Sciences, 15(3), 1564. https://doi.org/10.3390/app15031564





