Spectrum Attention Mechanism-Based Acoustic Vector DOA Estimation Method in the Presence of Colored Noise

Abstract

In the field of direction of arrival (DOA) estimation, a common assumption is that array noise follows a uniform Gaussian white noise model. However, practical systems often encounter non-ideal noise conditions, such as non-uniform or colored noise, due to sensor characteristics and external environmental factors. Traditional DOA estimation techniques experience significant performance degradation in the presence of colored noise, necessitating the exploration of specialized DOA estimation methods for such environments. This study introduces a DOA estimation method for acoustic vector arrays based on a spectrum attention mechanism (SAM). By employing SAM as an adaptive filter and constructing a double-branch model combining a convolutional neural network (CNN) and long short-term memory (LSTM), the method extracts the spatial and temporal features of signals, and effectively reduces the frequency components of colored noise, enhancing DOA estimation accuracy in colored noise scenarios. At an SNR of −5 dB, it achieves an accuracy rate of 85% while maintaining a low RMSE of only 2.03°.

1. Introduction

Direction of arrival (DOA) estimation has been widely used in radar [1], sonar [2], wireless communication [3] and other systems. Typically, a fundamental premise in the domain of DOA estimation is that the array noise conforms to uniform Gaussian white noise. However, this premise may not always hold true, as non-ideal noise conditions (non-uniform or colored noise [4]) often occur in practical systems due to factors related to the sensor itself and external environmental influences. In the presence of colored noise, the performance of traditional DOA estimation techniques is significantly compromised, to a considerable extent. Unlike white noise, colored noise exhibits a non-uniform power spectral density across different frequencies, possessing specific frequency characteristics. This non-uniformity alters the statistical properties of the signal and noise, thereby interfering with the normal operation of DOA estimation algorithms. Specifically, colored noise may introduce additional interference terms, causing the received signal model to deviate from the ideal state, which increases the difficulty and error in parameter estimation. In extreme cases, if the spectral characteristics of colored noise overlap severely with the spectrum of the target signal, traditional DOA estimation algorithms may completely fail, unable to accurately identify the direction of the signal origin. Therefore, in the context of colored noise, the degradation in DOA estimation performance not only manifests in a loss of accuracy but also poses serious threats to the stability and reliability of the algorithms.

Unlike the spatially uniform white noise model referenced in prior works [5,6,7,8,9,10,11,12], practical applications often encounter varying noise covariance among sensors [13]. Consequently, classical subspace-based DOA estimation techniques, such as the MUSIC method [11], which rely on the eigen-decomposition of the array covariance matrix, experience significant performance degradation. Furthermore, DOA methods independent of eigendecomposition, like maximum-likelihood estimation [14], are also heavily impacted. Additionally, some recently proposed sparse representation methods [6,12] share a dependence on the uniform white noise model. Given this, the challenge of DOA estimation in non-uniform noise environments has garnered increasing attention [7,15,16,17,18,19,20,21]. Deterministic and stochastic non-uniform maximum likelihood (ML) estimators have been developed to address noise non-uniformity [7,15], albeit involving computationally intensive nonlinear optimization problems. A power domain approach [16] simplifies complexity by bypassing sensor noise variance estimation, yet it still entails solving highly nonlinear optimization issues. Another strategy [17] estimates the noise covariance matrix using the interrelationships within the array covariance matrix blocks, but necessitates a sensor count exceeding three times the source number. The iterative ML subspace estimation (IMLSE) and iterative least-squares subspace estimation (ILSSE) algorithms [18] iteratively estimate the signal subspace and noise covariance matrix, subsequently determining DOAs with traditional direction-finding methods. A method presented in [19] estimates DOA by vectorizing the covariance matrix (excluding diagonal elements) and applying sparse representation techniques. While this approach mitigates the impact of noise non-uniformity, the deletion of diagonal elements may lead to information loss. The augmented subspace MUSIC (ASMUSIC) method [20] demonstrates that the discrepancy in noise power between the acoustic pressure and velocity components of an AVS (Acoustic Vector Sensor) significantly impairs the DOA estimation performance of the MUSIC method, yet it does not resolve the issue of DOA estimation in arrays with unequal noise power among elements. An alternating iterative weighted least squares (AIWLS) DOA estimation method [21] constructs the objective function for sparse signals and employs an iterative process to estimate source DOAs, achieving high accuracy in non-uniform noise environments.

In recent years, deep neural networks (DNNs) have been employed in the field of direction of arrival (DOA) estimation, yielding numerous research advancements [22,23,24,25]. Reference [22] addressed the challenge of underwater acoustic DOA estimation by framing it as an image classification task, leveraging the significant variations in covariance matrix characteristics across different directions. Reference [23] innovatively framed the problem as a multi-label classification task, leveraging convolutional neural networks (CNNs) to predict signal DOAs. Reference [24] presented the Deep-MUSIC approach, which employed multiple CNNs to model the intricate nonlinear relationship between received data and the MUSIC spatial spectrum, thereby facilitating multi-source DOA estimation. Reference [25] addressed the challenge of non-uniform noise by implementing a deep learning-based filter, effectively restoring the array covariance information. Despite these advancements, several limitations persist within the current methodologies. Firstly, existing research has overlooked effective DOA estimation methods in the presence of colored noise. Secondly, most existing methods only focused on the array covariance and its further improvement without considering the raw signal. Thirdly, traditional filtering algorithms cannot dynamically adjust weights, thus lacking the ability to process complex noise.

In this paper, we propose an acoustic vector DOA estimation method based on the spectrum attention mechanism (SAM) [26]. Specifically, SAM is used to neglect the insignificant frequency components and highlight the important ones, which is similar to an adaptive filter for colored noise. Then, the filtered signal is sent to a double-branch neural network consisting of a convolutional neural network (CNN) and long short-term memory (LSTM). Thus, the spatial and temporal features of the array signal are extracted to achieve high-accuracy DOA estimation.

The rest of the paper is organized as follows: Colored noise and DOA estimation tasks are described in Section 2. Section 3 presents the proposed method. Section 4 describes the experimental setup and discusses the results. Finally, conclusions are drawn in Section 5.

2. Problem Description

2.1. Colored Noise

Colored noise represents a class of random signals that deviate from the uniform power spectral density of white noise. This term encompasses noise signals whose power spectral density (PSD) varies as a function of frequency, leading to a non-flat spectral profile when plotted on a logarithmic scale.

Colored noise can be subclassified based on the specific pattern of its PSD variation across frequencies. Pink noise exhibits a power spectrum that decreases linearly with frequency, adhering to a $-{\displaystyle \frac{1}{f}}$ power law, resulting in equal power per octave. Brown noise, also referred to as red noise, demonstrates a PSD that decreases quadratically with frequency, conforming to a $-{\displaystyle \frac{2}{f}}$ power law, thus emphasizing the lower frequencies more prominently. Blue noise, distinguished by its increasing PSD with frequency, often following a steeper power law compared to pink noise, concentrates its energy in higher frequencies. Violet noise, the most steeply increasing in PSD with frequency among the colored noises, is concentrated in the very-high-frequency range.

In this paper, the signal captured by the array is significantly disrupted by colored noise. We show the vector components of the disrupted signal matrix and the frequency spectrum of corresponding noise for analysis. As depicted in Figure 1, all visualized values are linearly represented. The four subplots on the left show the results of signal components being disturbed by red, blue, pink, and purple noise, respectively. The horizontal axis represents the number of snapshots, i.e., time variation, and the vertical axis represents the amplitude values of complex signals at different snapshots. The four corresponding subgraphs on the right show the spectra of red, blue, pink, and purple noise, respectively. Due to the application of Fourier transform for frequency domain transformation, the curves exhibit symmetry. The horizontal axis represents frequency in hertz (Hz), and the vertical axis represents the amplitude distribution of the signal at different frequencies in decibels (dB). Colored noise presents different spectra, which means that different filtering algorithms need to be applied to different types of noise. Therefore, our goal is to apply an adaptive filter to preprocess the signal.

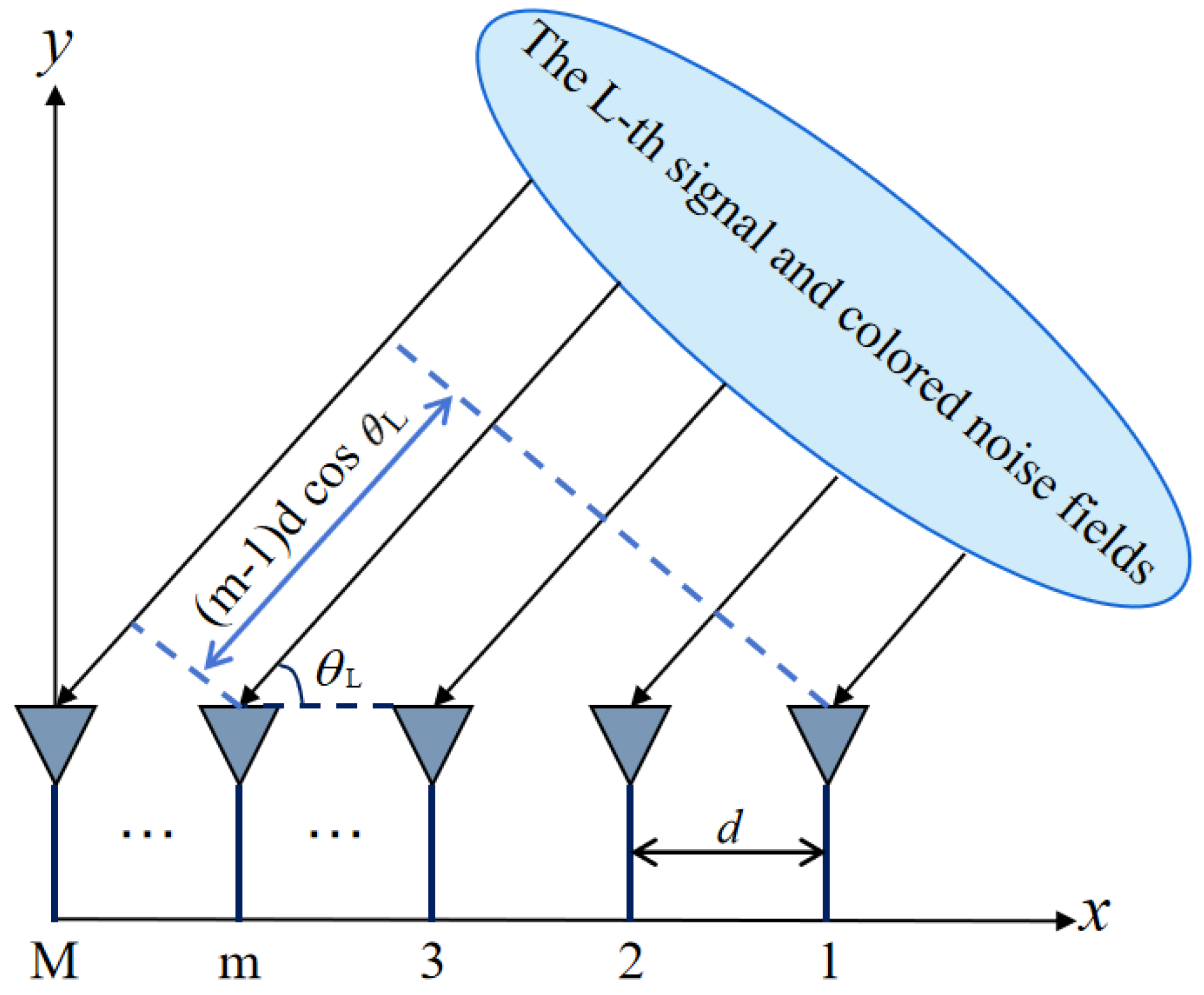
2.2. Array Signal Model

The uniform linear vector hydrophone model studied in this paper consists of a series of vector hydrophones arranged in a straight line at equal intervals. Each vector hydrophone is capable of simultaneously measuring both the pressure component and the particle velocity components of the acoustic field, thus providing rich information about the acoustic environment. This model boasts advantages such as a simple structure, ease of deployment and maintenance. Through signal processing techniques such as beamforming and noise suppression, it enables precise detection, localization, and tracking of underwater targets. Furthermore, the uniform linear vector hydrophone model has broad application prospects in marine environment monitoring, seabed terrain exploration, and marine ecological research, providing powerful technical support for research and applications in the field of underwater acoustics.

In this paper, we use the uniform linear array (ULA) as shown in Figure 2 to simulate hydrophone array signal reception under far-field narrowband conditions. There are M elements in a ULA and each element corresponds to an individual channel. The array element spacing d is half of the signal wavelength. Assuming that the signal source and array are in the same plane, the incident signal can be simulated as a plane wave. This assumption is grounded in the principles of wave propagation. When the distance between the signal source and the receiver array is considerably larger than the physical dimensions of the array, the curvature of the wavefront that emanates from the source becomes negligible as it approaches the array. Under these conditions, the wavefront can be approximated as a plane, or more specifically, as a plane wave. Simulating the incident signal as a plane wave in the context of signal processing and array signal analysis is a valid and widely adopted assumption. This assumption simplifies the mathematical modeling and enables the extraction of critical information from the received signals.

We take the first array element as the reference, so the signals reaching different antennas will have wave path difference $D_m$; it can be formulated as follows:

$$D_m=(m-1)dsin\theta ,m=1,2,\dots ,M$$

(1)

The difference of the wave path leads to the time difference of the received signal. Assuming the speed of signal propagation is v, the time difference of the signal received by the m-th array element can be expressed as ${\tau }_m={\displaystyle \frac{(m-1)dsin\theta }{v}}$. The frequency domain phase difference of the signal received by the array element can be expressed as $\beta =e^{-j\ast 2\pi {\displaystyle \frac{(m-1)dsin\theta }{\lambda }}}$ with $\lambda ={\displaystyle \frac{v}{f}}$, where $\lambda$ is the wavelength and f is the frequency of signal. So, we obtain the flow pattern matrix of the array A; it can be formulated as follows:

$$A\left(\theta \right)=\left[\begin{array}{cccc}1& 1& \cdots & 1\\ e^{-j^{*}2\pi {\displaystyle \frac{dsin{\theta }_1}{\lambda }}}& e^{-j^{*}2\pi {\displaystyle \frac{dsin{\theta }_2}{\lambda }}}& \cdots & e^{-j^{*}2\pi {\displaystyle \frac{dsin{\theta }_L}{\lambda }}}\\ ⋮& ⋮& ⋮& ⋮\\ e^{-j^{*}2\pi {\displaystyle \frac{(M-1)dsin{\theta }_1}{\lambda }}}& e^{-j^{*}2\pi {\displaystyle \frac{(M-1)dsin{\theta }_2}{\lambda }}}& \cdots & e^{-j^{*}2\pi {\displaystyle \frac{(M-1)dsin{\theta }_L}{\lambda }}}\end{array}\right]$$

(2)

where L is the number of narrowband far-field sources and j is $\sqrt{-1}$.

In this paper, colored noise is used to simulate the actual noise environment. The original signal vector and noise vector at the t-th snapshot can be expressed as:

$$S\left(t\right)=\left[\begin{array}{c}{s}_1\left(t\right)\\ s_2\left(t\right)\\ ⋮\\ s_L\left(t\right)\end{array}\right],N\left(t\right)=\left[\begin{array}{c}{n}_1\left(t\right)\\ n_2\left(t\right)\\ ⋮\\ n_M\left(t\right)\end{array}\right]$$

(3)

Assuming that each array element has no directionality and coupling between the arrays, the final received signal vector of the array at the tth snapshot is mathematically expressed as:

$$X\left(t\right)=A\left(\theta \right)S\left(t\right)+N\left(t\right)$$

(4)

and the final array signal matrix is described as:

$$X=[X\left(t_1\right),X\left(t_2\right),\cdots ,X\left(t_n\right)]$$

(5)

where n denotes the number of snapshots. The goal of DOA estimation is to extract the direction angles of the sources from X.

3. Methodology

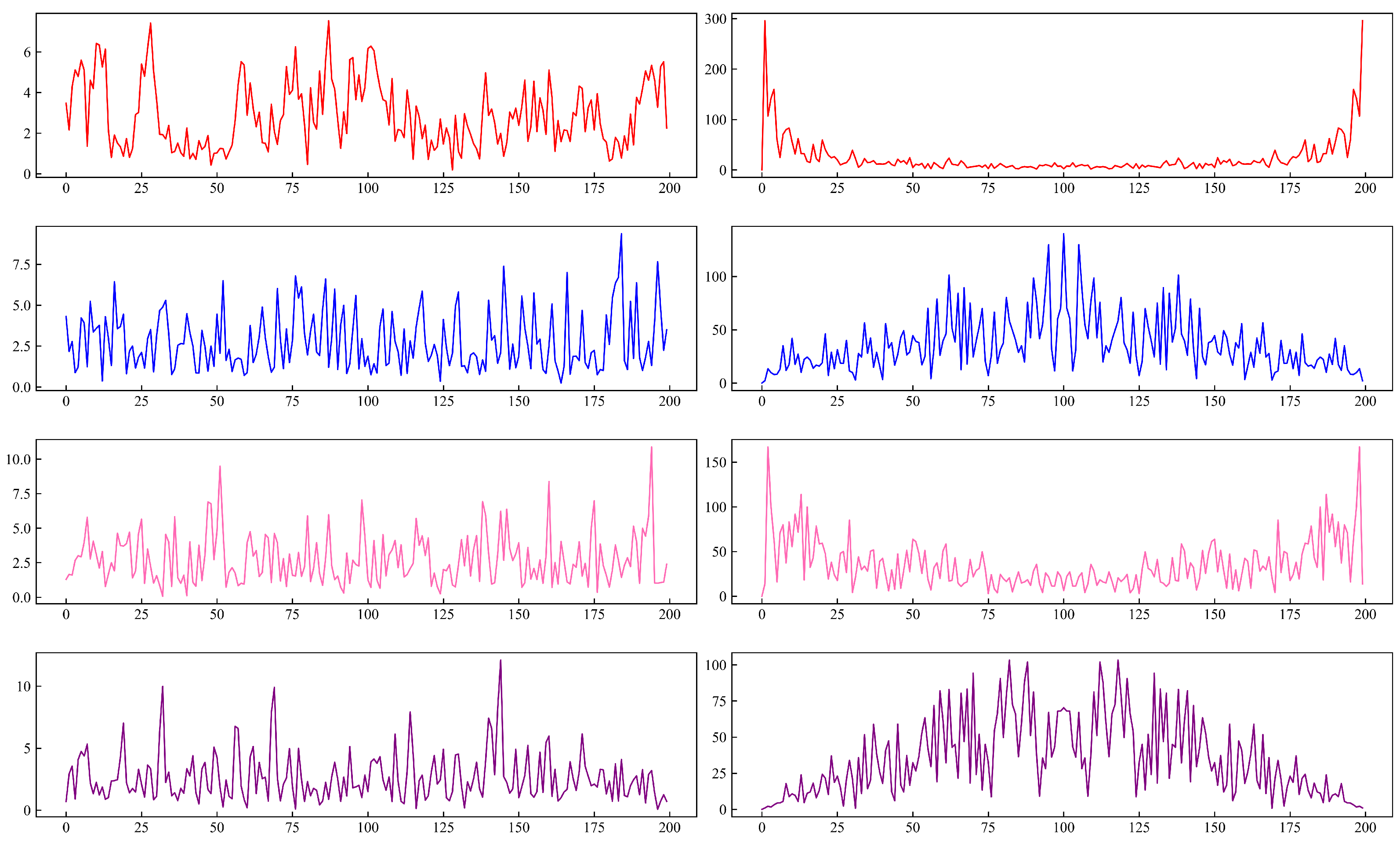
3.1. SAM

Frequency domain filtering involves eliminating unimportant frequency components while preserving or enhancing the significant ones, which aligns with the concept of the attention mechanism. SAM is an attention mechanism that acts on the spectrum. Its workflow is shown in Figure 3. Specifically, it incorporates a trainable parameter mask that matches the dimension of the input signal. This mask signifies the weight assigned to each frequency component, initially set to 1. During the training process, these weights are adjusted to achieve adaptive filtering and enhance feature extraction. In addition, SAM uses DCT instead of traditional DFT to implement frequency domain transformation, which has the following main benefits: (1) The coefficients of DCT are real numbers, while the coefficients of DFT are complex numbers. This feature makes DCT more suitable for the optimization algorithm based on gradient descent. (2) DCT performs better when processing signals with trends. In practical applications, time series often contain trend components, and DFT may be troubled by the problem of “frequency leakage” when representing simple trends. (3) When the adjacent values are highly correlated, DCT can achieve better energy concentration than DFT. In time series, adjacent data points usually have a certain correlation, which makes DCT more advantageous in extracting key features. The forward propagation of this layer is outlined in Algorithm 1.

Algorithm 1 Spectrum Attention Mechanism (SAM)

Input: Captured signal sequence $x^n$ Output: $x_{filtered}^n$ 1: Initialize: All-ones learnable array $mas{k}^n$ 2: # Transform the input series into frequency domain $s{p}^n\leftarrow DCT\left(x^n\right)$ 3: # Element-wise multiply $spectrum$ by $mask$ $masked\_s{p}^n\leftarrow s{p}^n·mas{k}^n$ 4: # Transform the $spectrum$ back into the time domain $x_{filtered}^n\leftarrow IDCT(masked\_s{p}^n)$

SAM is a simple attention mechanism, but it has an inherent defect. It relies on the entire signal spectrum, failing to capture the phase information inherent in the original signal. To preserve some of this crucial phase data, we employ segmented SAM (SSAM). SSAM works by utilizing a sliding window to split the original sequence into K equal-length segments, subsequently applying SAM to each segment individually. The resulting SAM outputs from these segments are then concatenated along the channel dimension to form the output features. The core algorithm is outlined in Algorithm 2.

Algorithm 2 Segmented SAM (SSAM)

Input: $x^n$, number of segments K Output: generated features $x_{out}^{T\times K}$ 1: Initialize: Length of each segment $T\leftarrow n//K$ 2: $x_{out}\leftarrow zeros(T,K)$ # Initialize $x_{out}$ 3: for $i=1$ to K do 4:     # Get the $i^{th}$ segment $cur\leftarrow x\left[\right(i-1)\ast T:i\ast T]$ 5:     # Apply SAM to the $i^{th}$ segment $cu{r}_{out}\leftarrow SAM\left(cur\right)$ 6:     # Update output $x_{out}[:,i]\leftarrow cu{r}_{out}$ 7: end for

Compared to existing filters, the SAM filter has the following advantages: (1) SAM achieves adaptive filtering by assigning appropriate weights to each frequency component. This mechanism can be dynamically adjusted based on the characteristics of the data, which helps reduce the impact of noise and improve the robustness of the model. (2) Traditional attention mechanisms may overlook temporal information. The SAM filter introduces SSAM to segment raw data using a rolling window and apply SAM on each segment, thereby preserving temporal information and improving classification accuracy.

3.2. CNN

The architecture of a CNN layer is primarily comprised of a convolutional layer and a pooling layer, as shown in Figure 4. The convolutional layer is responsible for extracting features from the input data, while the pooling layer serves to reduce the spatial dimensions of the feature maps, thus enhancing computational efficiency and controlling overfitting. Together, these layers form the foundational building blocks of CNNs, enabling them to learn hierarchical patterns from the input data.

(1)

Convolutional layer

The process of extracting features from input data using convolutional kernels in convolutional layers can be expressed as:

$$\begin{array}{cc}\hfill Z^{l+1}(i,j)& =\left[Z^l\otimes w^{l+1}\right](i,j)+b\hfill \\ \hfill & =\sum _{k=1}^{K_l}\sum _{x=1}^f\sum _{y=1}^f\left[Z_k^l(s_{0}i+x,s_{0}j+y)w_k^{l+1}(x,y)\right]\hfill \\ \hfill & +b(i,j)\in \{0,1,...,L_{l+1}\},\hfill \\ \hfill L_{l+1}& ={\displaystyle \frac{L_l+2p-f}{s_0}}+1\hfill \end{array}$$

(6)

where $Z^{l+1}$ and $Z^l$ represent the output and input of the layer $l+1$, respectively, K is the number of channels, $Z(i,j)$ is the pixel at the point $(i,j)$, b is the weight bias term, $w^{l+1}$ is the weight of the convolution kernel in the layer $l+1$, $L_{l+1}$ is the size of $Z^{l+1}$, $s_0$ and f are the size of the convolution step and convolution kernel, respectively, and p is the number of filling layers.

(2)

Pooling layer

The pooling layer functions between consecutive convolutional layers to choose the feature mappings, efficiently decreasing the dimensionality of the feature mappings while preserving crucial global information. In this research, the pooling procedure can be formulated as:

$$A_k^l(i,j)={\left[\sum _{x=1}^f\sum _{y=1}^f{A}_k^l{(s_{0}i+x,s_{0}j+y)}^p\right]}^{{\displaystyle \frac{1}{p}}}$$

(7)

Pooling layers can be categorized into various types based on the setting of the default parameter p. Commonly utilized in CNN designs are mean pooling $(p=1)$ and maximum pooling $(p\to \infty )$, which serve to maintain the background and texture details of an image, albeit at the cost of reducing the spatial dimensions of the information or feature map.

3.3. LSTM

The sophisticated design and functionality of recurrent neural networks (RNNs) have significantly advanced with the introduction of various modifications, among which the LSTM unit stands out prominently. The internal structure of the LSTM unit consists of a forgetting gate ${\mathit{f}}_t$, equipped with weight parameters ${\mathit{W}}_{xf}$, ${\mathit{W}}_{hf}$, ${\mathit{W}}_{cf}$, and ${\mathit{b}}_f$. Additionally, it includes an update gate ${\mathit{i}}_t$, which possesses weight parameters ${\mathit{W}}_{xi}$, ${\mathit{W}}_{hi}$, ${\mathit{W}}_{ci}$, and ${\mathit{b}}_i$. There is also an output gate ${\mathit{o}}_t$, characterized by weight parameters ${\mathit{W}}_{xo}$, ${\mathit{W}}_{ho}$, ${\mathit{W}}_{co}$, and ${\mathit{b}}_o$. Furthermore, a data combination component ${\mathit{g}}_t$ with weight parameters ${\mathit{W}}_{xc}$, ${\mathit{W}}_{hc}$, ${\mathit{W}}_{cc}$, and ${\mathit{b}}_c$, is integrated. Thus, the structure of LSTM is shown in Figure 5.

The received input, unit state, and unit output of the current neuron are set as ${\mathit{x}}_t$, ${\mathit{c}}_t$, and ${\mathit{h}}_t$, respectively. The unit output and unit state of the previous neuron are set as ${\mathit{h}}_{t-1}$ and ${\mathit{c}}_{t-1}$, respectively.

The forget gate ${\mathit{f}}_t$, update gate ${\mathit{i}}_t$, selected signal information ${\mathit{g}}_t$, cell state ${\mathit{c}}_t$, output gate ${\mathit{o}}_t$, and hidden state ${\mathit{h}}_t$ at moment t can be formulated as:

$$\left\{\begin{array}{cc}& {\mathit{f}}_t=\sigma ({\mathit{W}}_{xf}·{\mathit{x}}_t+{\mathit{W}}_{hf}·{\mathit{h}}_{t-1}+{\mathit{W}}_{cf}·{\mathit{c}}_{t-1}+{\mathit{b}}_f)\hfill \\ & {\mathit{i}}_t=\sigma ({\mathit{W}}_{xi}·{\mathit{x}}_t+{\mathit{W}}_{hi}·{\mathit{h}}_{t-1}+{\mathit{W}}_{di}·{\mathit{c}}_{t-1}+{\mathit{b}}_i)\hfill \\ & {\mathit{g}}_t=tanh({\mathit{W}}_{xc}·{\mathit{x}}_t+{\mathit{W}}_{hc}·{\mathit{h}}_{t-1}+{\mathit{W}}_{cc}·{\mathit{c}}_{t-1}+{\mathit{b}}_{\mathrm{c}})\hfill \\ & {\mathit{c}}_t={\mathit{i}}_t{\mathit{g}}_t+{\mathit{f}}_t{\mathit{c}}_{t-1}\hfill \\ & {\mathit{o}}_t=\sigma ({\mathit{W}}_{xo}·{\mathit{x}}_t+{\mathit{W}}_{ho}·{\mathit{h}}_{t-1}+{\mathit{W}}_{co}·{\mathit{c}}_{t-1}+{\mathit{b}}_{\mathrm{o}})\hfill \\ & {\mathit{h}}_t={\mathit{o}}_t\tanh \left({\mathit{c}}_t\right)\hfill \end{array}\right.$$

(8)

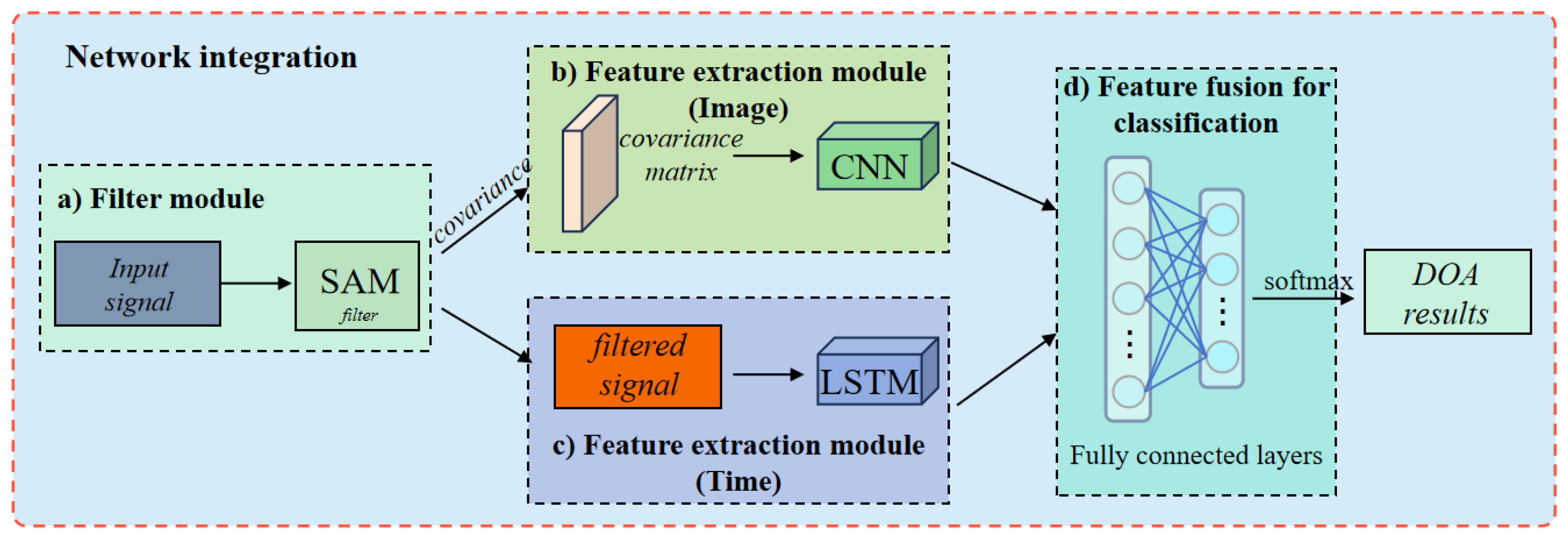
3.4. Network Integration

The DOA estimation model proposed in this study consists of the SAM adaptive filter, and LSTM and CNN networks. Specifically, SAM is used to adaptively filter the frequency components of colored noise, which can be seen as a preprocessing module of the signal. Then, LSTM and CNN construct a double-branch model to learn the spatial and temporal features, and a fully connected module is applied to fuse the output of LSTM and CNN. Finally, the DOA results are output by softmax. The key benefits of this model encompass the following: (1) The SAM filter module can adaptively learn features of colored noise, and filter unimportant frequency components, which improves the noise suppression ability of the model. (2) Acoustic vector arrays capture data with temporal attributes, and by leveraging LSTM, which excels in processing time series data, the accuracy of the DOA estimation model can be bolstered. (3) The input for CNN consists of the covariance matrix of the received signal, with the data dimension solely determined by the number of array elements, enabling DOA estimation irrespective of the snapshot count. (4) Integrating LSTM with CNN and concurrently extracting both temporal and spatial information from the signal data can further improve the performance of the model. The overall framework diagram of the model is shown in Figure 6.

4. Experimental Results

4.1. Training Data

In our experiments, AVSs, as a novel sensing approach, offer substantial performance advantages over traditional scalar sound pressure sensors by enabling the synchronous and co-located measurement of sound pressure and acoustic velocity vector information along three orthogonal directions. Consequently, they have garnered significant attention in the fields of acoustic detection and signal processing. When employed as array elements in ULAs to receive acoustic signals from diverse directions, acoustic vector sensors provide a richer and more accurate array of signal characteristics by capturing both sound pressure and acoustic velocity vector data, ultimately enhancing the precision of DOA estimation.

We adopt the ULA model introduced in Section 2 for acquiring the training dataset. The signal type is a monoharmonic acoustic signal and the noise type is set to red noise. The speed of the sound wave v is set to 1500 m/s and the frequency f is set to 1500 Hz; then, according to the description in Section 2, the wavelength $\lambda$ is 1 m. The array configuration consists of 10 sensors spaced at ${\displaystyle \frac{\lambda }{2}}$. In this scenario, two sources impinge a ULA with a $1^{\circ }$ angular separation, spanning a DOA range of [−90°, 90°]. Then, 200 samples are created for each angle, resulting in a comprehensive dataset of D = 36,000 entries. Half of this dataset is randomly designated as the training subset, while the remaining half serves as the testing subset. To enhance data randomness, we vary the number of snapshots across 50, 80, 100, 200, and 500, and adjust the signal-to-noise ratio (SNR) from −20 dB to 20 dB in increments of 5 dB. For model parameter updates, we select the Adam optimizer with an initial learning rate of 0.0001. The batch size is configured to 180, and the training process spans 800 epochs. The program is developed using PyTorch and executed on a hardware platform featuring an Intel (R) Core (TM) i9-14900K CPU @ 3.20 GHz, RTX 4090 GPU.

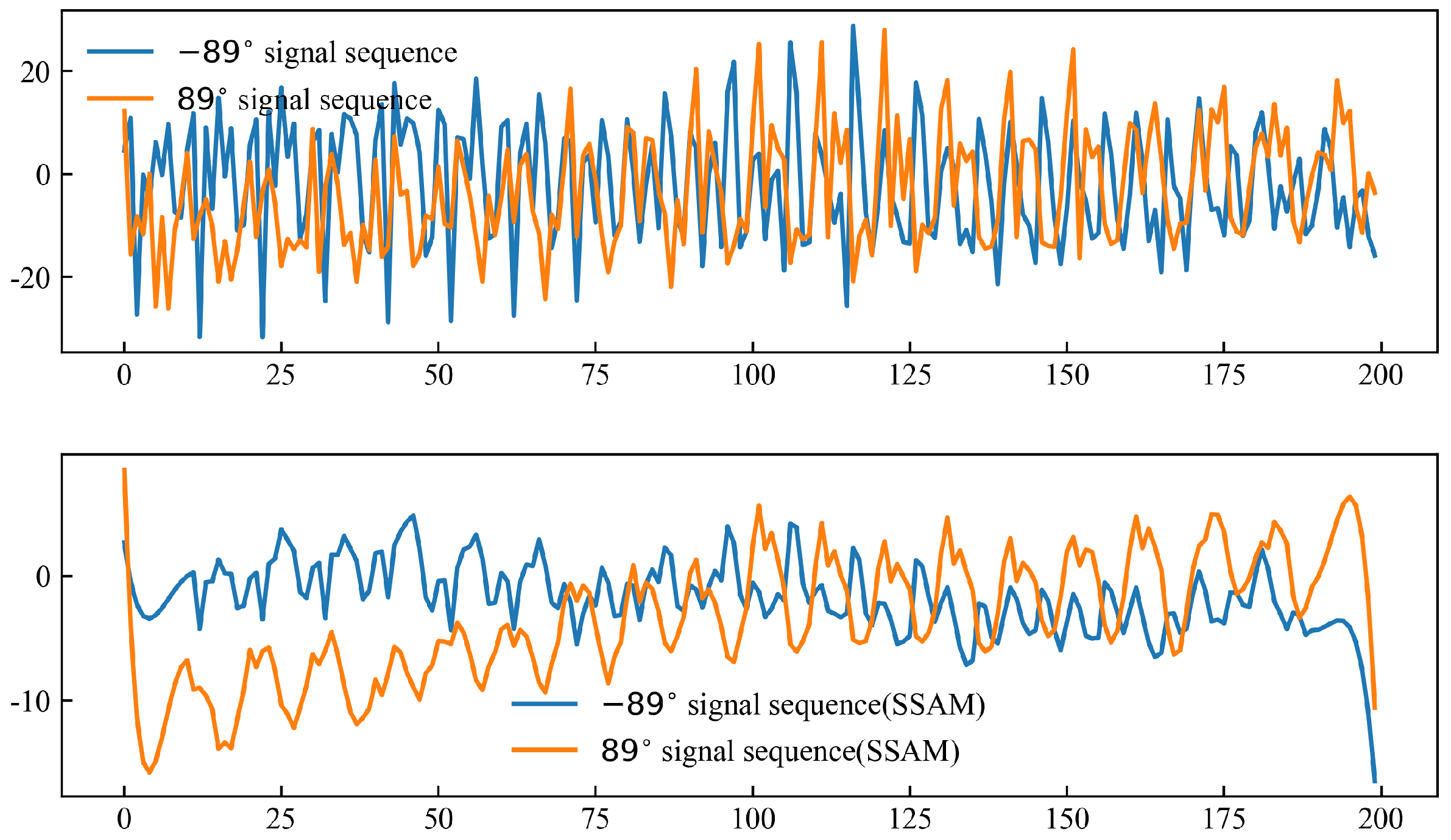
4.2. Filter Results

To verify the performance of our adaptive filter, we used a trained mask to filter the noise of the two captured signal components separately, as shown in Figure 7.

The angles of the two sources are $-{89}^{\circ }$ and ${89}^{\circ }$, respectively. The SNR is set to −10 dB and the number of snapshots is 200. Due to the influence of colored noise, which exhibits a non-uniform power distribution across the frequency spectrum, the original time series lose the characteristics of monoharmonic signals, leading to a remarkable similarity between them. This similarity can weaken the differentiation ability of neural networks, thereby potentially compromising their performance in signal processing tasks. However, more discriminative features are generated by SSAM, making the network easier to train. Therefore, SSAM can indeed filter unimportant frequency components, and improve the ability of neural networks to distinguish between two sources.

4.3. Performance of DOA Estimation Model

In this segment, we evaluate the proposed model against algorithms such as MUSIC, ASMUSIC, DeepMUSIC, ILSSE, CNN, LSTM, and CNN-LSTM to demonstrate its superiority and efficacy. Assume that the signal is of the same power p. The SNR is used to indicate the influence degree of environmental noise, and the expression is given as follow:

$$\mathrm{SNR}={\displaystyle \frac{1}{M}}\sum _{m=1}^M{\displaystyle \frac{p}{q_m}}$$

(9)

where M is the number of sensors, and $q_m$ is the mth diagonal element of the covariance matrix.

To verify the performance of each algorithm, the root mean square error (RMSE) is expressed as:

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{IQ}}\sum _{i=1}^I\sum _{q=1}^Q{\left(\widehat{{\theta }_q^i}-{\theta }_q\right)}^2}$$

(10)

where I represents the total number of Monte Carlo simulations conducted, while Q denotes the quantity of signal sources requiring estimation. For each source q in the ith Monte Carlo experiment, $\widehat{{\theta }_q^i}$ stands for the estimated DOA, and ${\theta }_q$ corresponds to its true DOA.

The accuracy metric is subsequently defined as:

$$Acc={\displaystyle \frac{K_c}{K}}\times 100\%$$

(11)

where K and $K_c$ are the total number of samples and the number of correctly estimated samples.

Experiment 1: Assessment of RMSE performance as SNR increases.

During this experimental setup, predictions were made for all test set samples. We set the number of snapshots to $T=500$ and computed the average RMSEs for DOA estimates. As SNR increases, the RMSEs for MUSIC, ASMUSIC, DeepMUSIC, ILSSE, CNN, LSTM, CNN-LSTM, and our model are depicted in Figure 8a and summarized in

Table 1. RMSEs of DOA estimates, considering a fixed number of snapshots at 500 and SNR ranging from −20 dB to 20 dB.

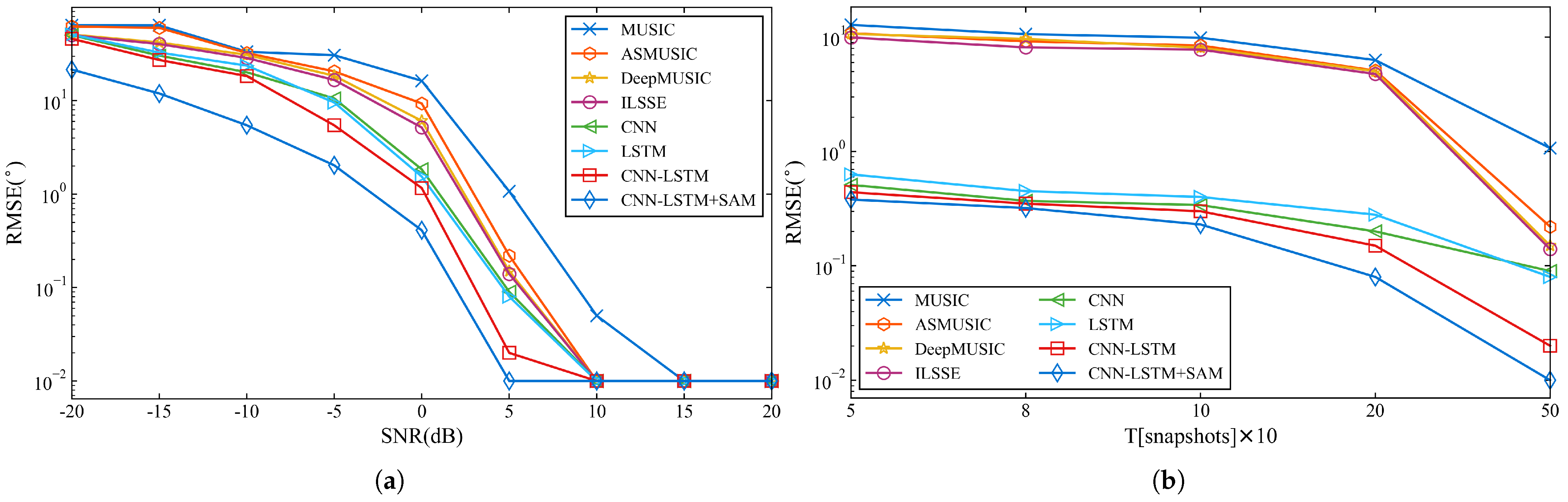
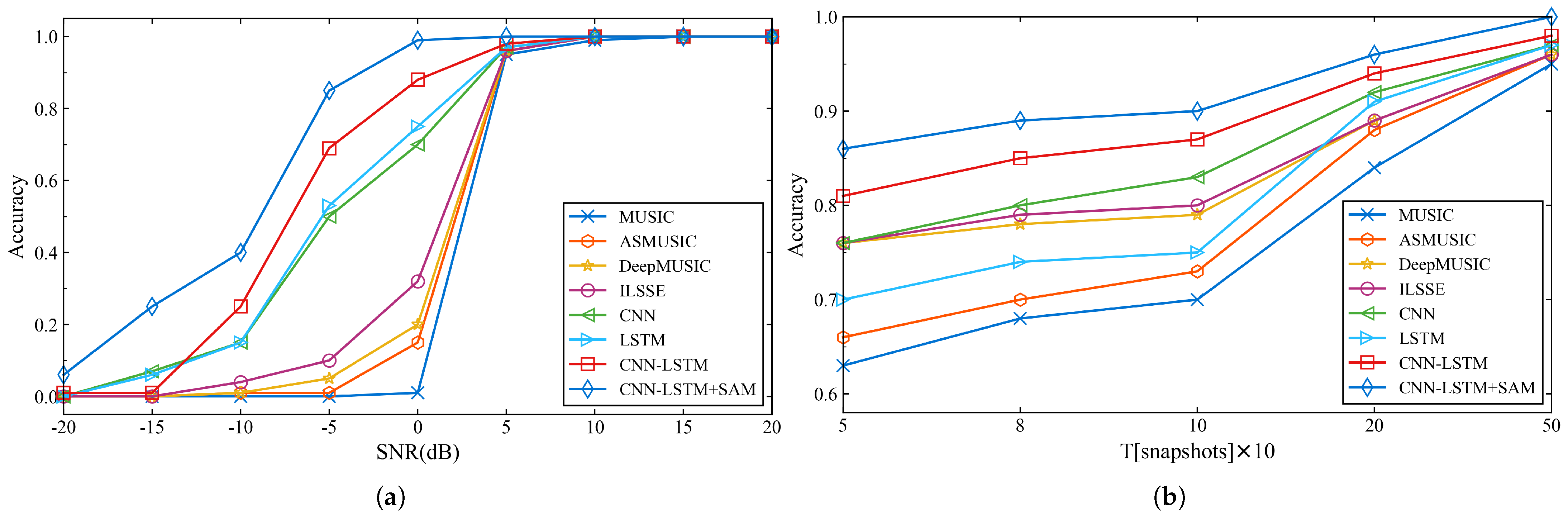
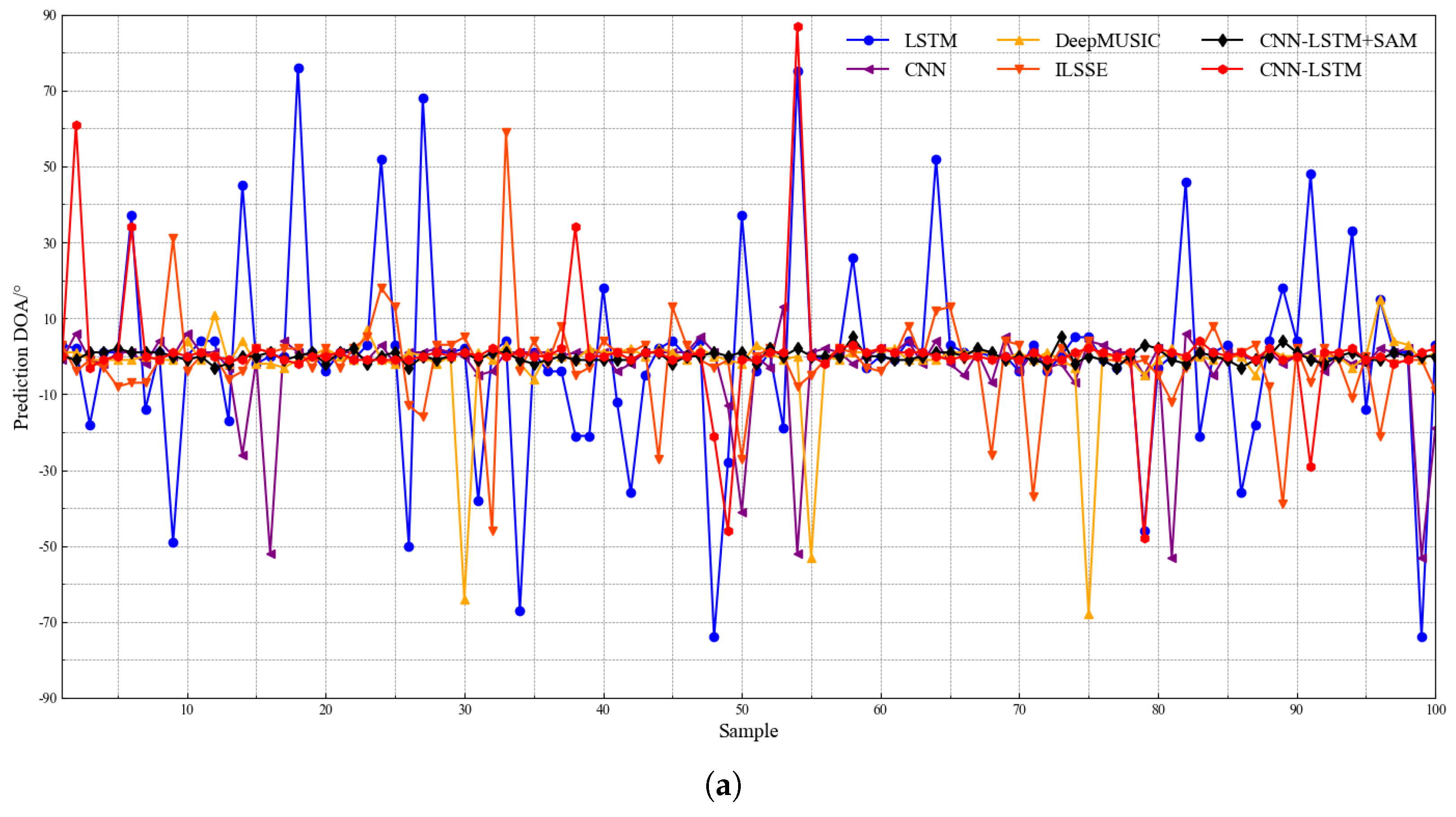
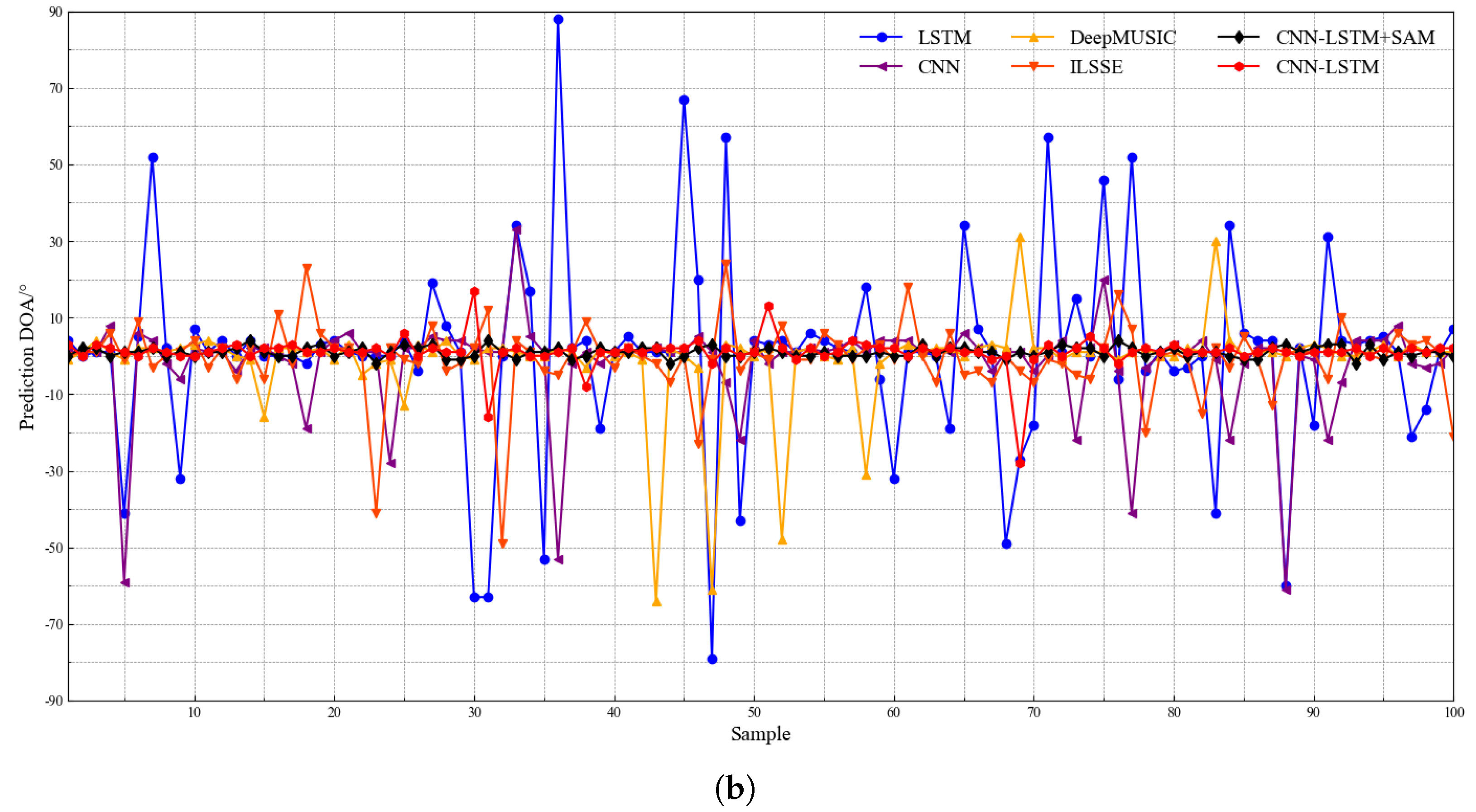
Methods	−20 dB	−15 dB	−10 dB	−5 dB	0 dB	5 dB	10 dB	15 dB	20 dB
MUSIC	64.03	63.89	33.29	30.63	16.31	1.07	0.05	0.01	0.01
ASMUSIC	62.11	60.08	32.35	20.55	9.33	0.22	0.01	0.01	0.01
DeepMUSIC	50.91	41.92	30.88	18.43	6.08	0.15	0.01	0.01	0.01
ILSSE	50.12	40.32	28.59	16.65	5.16	0.14	0.01	0.01	0.01
CNN	50.09	30.31	20.11	10.56	1.84	0.09	0.01	0.01	0.01
LSTM	50.80	32.71	23.68	9.55	1.54	0.08	0.01	0.01	0.01
CNN-LSTM	45.92	27.22	18.32	5.44	1.16	0.02	0.01	0.01	0.01
CNN-LSTM+SAM	21.51	11.93	5.45	2.03	0.41	0.01	0.01	0.01	0.01

. Observations from Figure 8a and Table 1 reveal that DL-based approaches (i.e., those utilizing deep learning) exhibit superior performance in low-SNR conditions. Conversely, MUSIC shows poor performance within the SNR range of −20 dB to 0 dB. The high power of colored noise significantly impairs the predictive capabilities of the traditional algorithm. On the whole, the deep learning-based methods, i.e., CNN, LSTM, CNN-LSTM, CNN-LSTM+SAM are superior to MUSIC, ASMUSIC, DeepMUSIC, and ILSSE, mainly because the performance of the traditional algorithms will be degraded severely due to the colored noise field. Furthermore, in a low-SNR environment, specifically at −20 dB SNR, the RMSE of CNN-LSTM+SAM is notably lower than that of CNN-LSTM by a significant margin of 24.41°, as it reduces the noise weight of the received signal in the frequency domain. Specifically, this enhanced neural network incorporates more distinguishing information. In summary, our proposed model demonstrates comparable performance to other algorithms in high-SNR environments, with RMSEs for all algorithms converging to approximately 0.01°. However, it exhibits a notable advantage in low-SNR conditions. Traditional algorithms are more prone to being affected by colored noise compared to deep learning-based algorithms.

Experiment 2: Evaluation of RMSE performance with varying numbers of snapshots.

For Experiment 2, the parameters remain consistent with those utilized in Experiment 1. At a constant SNR of 5 dB, the number of snapshots is varied, ranging from 50 to 500 (specifically, 50, 80, 100, 200, and 500). In Figure 8b and

Table 2. RMSEs of DOA estimates, considering a fixed SNR of 5dB and with snapshots ranging from 50 to 500.

Methods	50 Snapshots	80 Snapshots	100 Snapshots	200 Snapshots	500 Snapshots
MUSIC	12.78	10.61	9.87	6.29	1.07
ASMUSIC	10.79	9.18	8.44	5.10	0.22
DeepMUSIC	10.65	9.63	8.08	5.02	0.15
ILSSE	9.92	8.12	7.77	4.75	0.14
CNN	0.51	0.37	0.34	0.20	0.09
LSTM	0.63	0.45	0.40	0.28	0.08
CNN-LSTM	0.44	0.35	0.30	0.15	0.02
CNN-LSTM+SAM	0.38	0.32	0.23	0.08	0.01

, we present the RMSEs of our proposed method and its competitors as the number of snapshots increases.

Observing Figure 8b and Table 2, it is evident that as the number of snapshots increases, the RMSEs of all methods decline. However, MUSIC and ASMUSIC exhibit relatively large errors, whereas the other algorithms show improved performance. The proposed model extracts spatial, time domain information from the signal array, and the noise weight is reduced through the spectrum attention mechanism. At a snapshot count of 50, the RMSE of the proposed model is 0.38°. When the snapshot count reaches 500, the RMSE decreases to 0.01°, thus achieving better results. This experiment shows that the model proposed by us retains its advantage even at low snapshot numbers, indicating that the filtering effectiveness of the SAM module remains unimpaired by a limited number of snapshots.

Experiment 3: Assessment of prediction accuracy as SNR increases.

The simulated conditions for Experiment 3 mirror those of Experiment 1. Figure 9a and

Table 3. Prediction accuracy of DOA estimates with a fixed number of snapshots at 500 and SNR ranging from −20 dB to 20 dB.

Methods	−20 dB	−15 dB	−10 dB	−5 dB	0 dB	5 dB	10 dB	15 dB	20 dB
MUSIC	0%	0%	0%	0%	1%	95%	99%	100%	100%
ASMUSIC	0%	0%	1%	1%	15%	96%	100%	100%	100%
DeepMUSIC	0%	0%	1%	5%	20%	96%	100%	100%	100%
ILSSE	0%	0%	4%	10%	32%	96%	100%	100%	100%
CNN	0%	7%	15%	50%	70%	97%	100%	100%	100%
LSTM	0%	6%	15%	53%	75%	97%	100%	100%	100%
CNN-LSTM	1%	14%	25%	69%	88%	98%	100%	100%	100%
CNN-LSTM+SAM	6%	25%	40%	85%	99%	100%	100%	100%	100%

depict the prediction accuracy of the proposed network alongside the compared methods as the SNR varies.

The data presented in Figure 9a and Table 3 reveal that the prediction accuracy of the MUSIC, ASMUSIC, DeepMUSIC, ILSSE, CNN, LSTM, CNN-LSTM hybrid models, and our proposed model all improve as SNR increases. Among these, our proposed model exhibits the highest level of performance, achieving an accuracy rate of 85% at −5 dB SNR and reaching a perfect accuracy of 100% at 5 dB SNR.

Experiment 4: Evaluation of prediction accuracy as snapshots increase.

The experimental setup for Experiment 4 mirrors that of Experiment 2, while the criteria for assessing DOA prediction accuracy align with those used in Experiment 3. Figure 9b and

Table 4. Prediction accuracy of DOA estimates as snapshots increase and with SNR being 5 dB.

Methods	50 Snapshots	80 Snapshots	100 Snapshots	200 Snapshots	500 Snapshots
MUSIC	63%	68%	70%	84%	95%
ASMUSIC	66%	70%	73%	88%	96%
DeepMUSIC	76%	78%	79%	89%	96%
ILSSE	76%	79%	80%	89%	96%
CNN	76%	80%	83%	92%	97%
LSTM	70%	74%	75%	91%	97%
CNN-LSTM	81%	85%	87%	94%	98%
CNN-LSTM+SAM	86%	89%	90%	96%	100%

present a comparative analysis of prediction accuracy between the proposed networks and other methods, highlighting the impact of varying the number of snapshots.

Both the graphical illustration in Figure 9b and the numerical results in Table 4 reveal that with an increasing number of snapshots, the accuracy rates of all methods undergo different levels of enhancement. Notably, the proposed network surpasses its competitors, achieving a full accuracy rate of 100% at 500 snapshot counts, marking an improvement of roughly 3% in comparison to other algorithms. This superior performance can be attributed to the trainable mask, which functions akin to a filter, effectively suppressing noise and enhancing the performance.

Experiment 5: Performance of DOA estimation under random angle.

In the scenario of DOA estimation involving randomly chosen angles, the angular separation between the two sources is fixed at $\Delta \theta =1^{\circ }$, and SNR is maintained at 0 dB. The DOA of the first source varies from $-{90}^{\circ }$ to ${89}^{\circ }$, with each step increasing by $1^{\circ }$. The DOA of the second source ranges from $-{89}^{\circ }$ to ${90}^{\circ }$ with a step increment of $1^{\circ }$. All the samples used for this analysis belong to the test set, aimed at validating the efficacy of the proposed method.

The number of snapshots is fixed at $T=500$. Experiment 5 demonstrates the performance of MUSIC, ASMUSIC, DeepMUSIC, ILSSE, CNN, LSTM, CNN-LSTM, and CNN-LSTM+SAM in terms of DOA estimation. The solid line indicates the actual DOA, while the estimated DOA is illustrated by the colored blocks. Figure 10a–h exhibit the DOA estimation abilities of the proposed networks in contrast to other methods. Upon examining Figure 10, it is evident that MUSIC, ASMUSIC, DeepMUSIC, ILSSE, CNN, LSTM, and CNN-LSTM exhibit significant DOA estimation errors. Conversely, the proposed model demonstrates the lowest estimation errors, suggesting superior DOA performance.

Experiment 6: Performance of DOA estimation under specific angle.

In this experiment, 100 samples are taken from the test set. The first DOA source of each sample is $0^{\circ }$, and the second DOA source is $1^{\circ }$. The SNR is set to −5 dB and the number of snapshots is 200, and CNN, LSTM, DeepMUSIC, ILSSE, CNN-LSTM, and our proposed model are selected to predict these 100 samples; the prediction results are shown in Figure 11. From Figure 11a,b, it can be seen that except for the proposed model, the predictions of other algorithms show varying degrees of significant errors, indicating the accurate prediction ability of our model at low SNR. The success of our model can be attributed to several factors. Firstly, it leverages the strengths of both CNN and LSTM architectures, combining convolutional layers for feature extraction and recurrent layers for temporal dependency modeling. This hybrid approach allows the model to capture both the spatial and temporal characteristics of the signals, enhancing its ability to distinguish between closely spaced DOA sources. Secondly, our model uses an effective filter for colored noise. This filter operates as a preprocessing step, cleaning the input data before they are fed into the neural network. By reducing the noise level, it helps to improve the SNR effectively, even though the initial SNR is set to −5 dB. This preprocessing step, combined with the advanced features and techniques of our proposed model, enables it to outperform other algorithms under low-SNR conditions.

5. Conclusions

In this paper, a double-branch neural network with SAM adaptive filter modules is proposed to estimate DOA in the presence of colored noise. Specifically, the filter module is used to adaptively filter the frequency components of colored noise while retaining useful information. In addition, CNN and LSTM are integrated to simultaneously mine the temporal and spatial information of the signal data. Simulation experiments showcased the remarkable performance of the proposed model. At an SNR of −5 dB, our network achieves an accuracy rate of 85%, with an RMSE of only 2.03°. These results demonstrate a significant improvement over existing algorithms, particularly in challenging scenarios characterized by low SNR and limited snapshot counts. The proposed network exhibits superior capabilities in suppressing colored noise and enhancing DOA estimation performance.