Discrete Cartesian Coordinate Transformations: Using Algebraic Extension Methods
Abstract
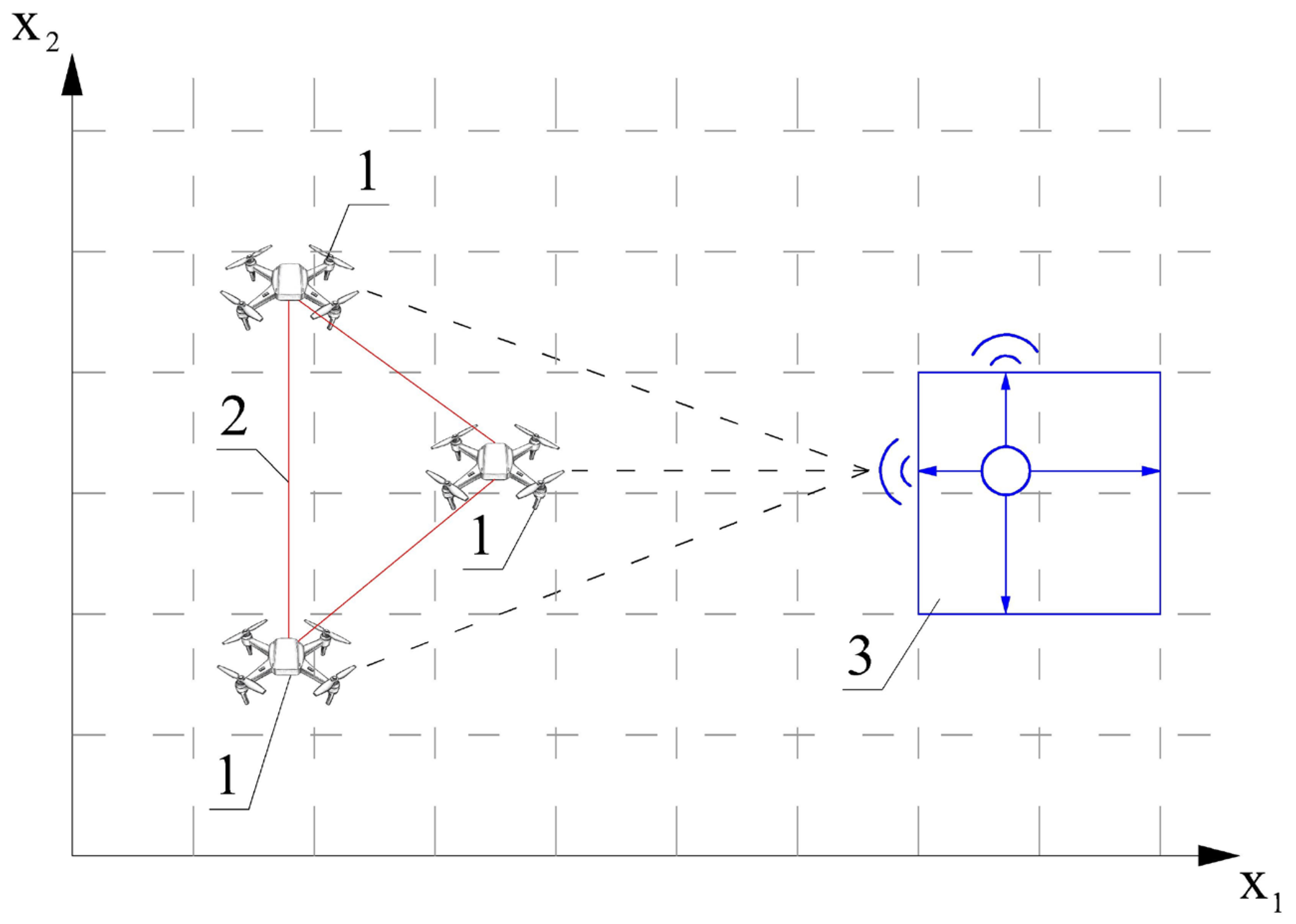
1. Introduction
2. Background: Technical Aspect
3. Background: Theoretical Aspect
4. Results
4.1. Nonstandard Method of Algebraic Extensions
4.2. Construction of Algebraic Rings via Nonstandard Algebraic Extensions of Galois Fields
4.3. Representation of Operators Through Algebraic Extensions
4.4. Advantages of Representations of Linear Operators Using Idempotent Elements
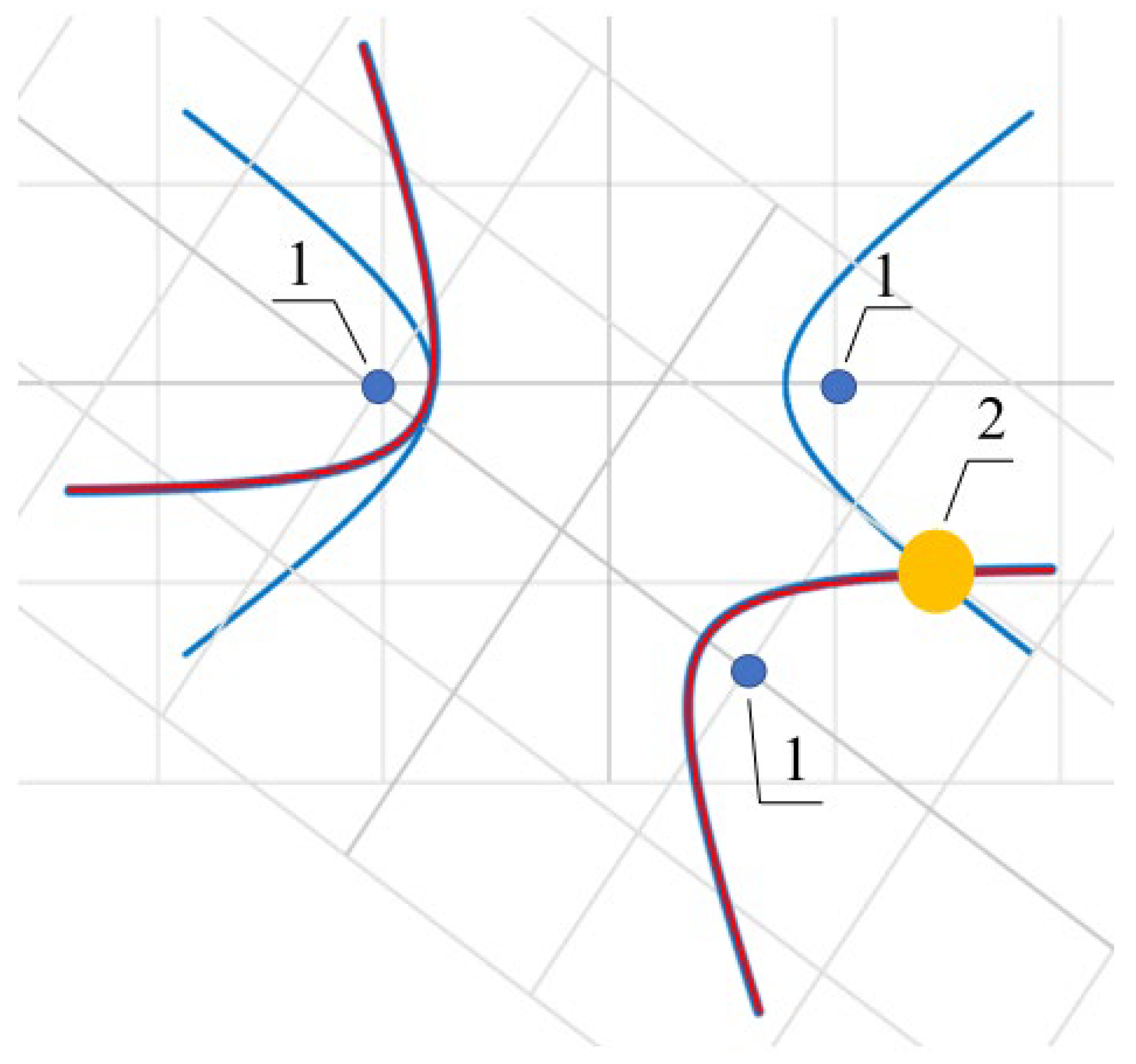
5. Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, W.; Yang, D. Analysis and comparison of automatic image focusing algorithms in digital image processing. J. Radiat. Res. Appl. Sci. 2023, 16, 100672. [Google Scholar] [CrossRef]
- Costarelli, D.; Seracini, M.; Vinti, G. A comparison between the sampling Kantorovich algorithm for digital image processing with some interpolation and quasi-interpolation methods. Appl. Math. Comput. 2020, 374, 125046. [Google Scholar] [CrossRef]
- Rohhila, S.; Singh, A.K. Deep learning-based encryption for secure transmission of digital images: A survey. Comput. Electr. Eng. 2024, 116, 109236. [Google Scholar] [CrossRef]
- Cheng, X.; Ma, Q.; Zhou, S.; Guo, L.; Ma, S. Using unsupervised learning based convolutional neural networks to solve Digital Image Correlation. Opt. Laser Technol. 2025, 180, 111414. [Google Scholar] [CrossRef]
- Dzhanashia, K.; Evsutin, O. Neural networks-based data hiding in digital images: Overview. Neurocomputing 2024, 581, 127499. [Google Scholar] [CrossRef]
- Duan, X.; Xu, H.; Dong, R.; Lin, F.; Huang, J. Digital image correlation based on convolutional neural networks. Opt. Laser Eng. 2023, 160, 107234. [Google Scholar] [CrossRef]
- Mukhamediev, R.I. State-of-the-Art Results with the Fashion-MNIST Dataset. Mathematics 2024, 12, 3174. [Google Scholar] [CrossRef]
- Sun, Y.; Li, D.; Xiang, Q.; Yuan, Y.; Hu, Z.; Hua, X.; Jiang, Y.; Zhu, Y.; Fu, Y. Scalable quantum convolutional neural network for image classification. Physica A 2024, 657, 130226. [Google Scholar] [CrossRef]
- Guler, N.; Hazem, Z.B. Semantic Communication-based Convolutional Neural Network for Enhanced Image Classification. Franklin Open 2024, 9, 100192. [Google Scholar] [CrossRef]
- Carletti, M.; Sinigaglia, A.; Terzi, M.; Susto, G.A. On the limitations of adversarial training for robust image classification with convolutional neural networks. Inf. Sci. 2024, 675, 120703. [Google Scholar] [CrossRef]
- Lemoine, D. The discrete Bessel transform algorithm. J. Chem. Phys. 1994, 101, 3936–3944. [Google Scholar] [CrossRef]
- Lee, G.; Kim, W. Image Processing in L1-Norm-Based Discrete Cartesian and Polar Coordinates. Electronics 2024, 13, 1088. [Google Scholar] [CrossRef]
- Tang, W.; Argyropoulos, C.; Kallos, E.; Song, W.; Hao, Y. Discrete Coordinate Transformation for Designing All-Dielectric Flat Antennas. IEEE Trans. Antennas Propag. 2010, 58, 3795–3804. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Kyriakidis, P.C. Forward and Inverse Transformations between Cartesian and Channel-fitted Coordinate Systems for Meandering Rivers. Math. Geol. 2006, 38, 927–958. [Google Scholar] [CrossRef]
- Smith, H.; Norato, J.A. Topology optimization with discrete geometric components made of composite materials. Comput. Methods Appl. Mech. Eng. 2021, 376, 113582. [Google Scholar] [CrossRef]
- Laghari, A.A.; Jumani, A.K.; Laghari, R.A.; Nawaz, H. Unmanned aerial vehicles: A review. Cognit. Robot. 2023, 3, 8–22. [Google Scholar] [CrossRef]
- Ma’Sum, M.A.; Arrofi, M.K.; Jati, G.; Arifin, F.; Kurniawan, M.N.; Mursanto, P.; Jatmiko, W. Simulation of intelligent Unmanned Aerial Vehicle (UAV) For military surveillance. In Proceedings of the 2013 International Conference on Advanced Computer Science and Information Systems (ICACSIS), Jakarta, Indonesia, 28–29 September 2013. [Google Scholar] [CrossRef]
- Udeanu, G.; Dobrescu, A.; Oltean, M. Unmanned Aerial Vehicle in Military Operations. Sci. Res. Educ. Air Force 2016, 18, 199–206. [Google Scholar] [CrossRef]
- Wang, D.; Bai, B.; Zhao, W.; Han, Z. A Survey of Optimization Approaches for Wireless Physical Layer Security. IEEE Commun. Surv. Tutor. 2018, 21, 1878–1911. [Google Scholar] [CrossRef]
- Zoli, M.; Mitev, M.; Barreto, A.N.; Fettweis, G. Estimation of the secret key rate in wideband wireless physical-layer-security. In Proceedings of the 2021 International Symposium on Wireless Communication Systems (ISWCS), Berlin, Germany, 6–9 September 2021. [Google Scholar] [CrossRef]
- Hamamreh, J.M.; Furqan, H.M.; Arslan, H. Classifications and Applications of Physical Layer Security Techniques for Confidentiality: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2019, 21, 1773–1828. [Google Scholar] [CrossRef]
- Shindo, N.; Kobatake, T.; Masson, D.; Fafard, S.; Matsuura, M. Optically Powered and Controlled Drones Using Optical Fibers for Airborne Base Stations. Photonics 2022, 9, 882. [Google Scholar] [CrossRef]
- Sawa, T.; Sato, K.; Watari, K. Remote Control of Underwater Drone by Fiber-Coupled Underwater Optical Wireless Communication. In Proceedings of the 2022 IEEE/OES China Ocean Acoustics Symposium (COA), Wuhan, China, 21–24 February 2022. [Google Scholar]
- Isaac, S.; Conrad, A.; Schroeder, A.J.; Javid, T.; Sanchez-Rosales, D.; Cochran, R.; Gutha, A.; Gauthier, D.; Kwiat, P. Drone-Based Quantum Key Distribution. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 15–20 May 2022. [Google Scholar] [CrossRef]
- Ermukhambetova, B.; Mun, G.; Kabdushev, S.; Kadyrzhan, A.; Kadyrzhan, K.; Vitulyova, Y.; Suleimenov, I.E. New approaches to the development of information security systems for unmanned vehicles. Indones. J. Electr. Eng. Comput. Sci. 2023, 31, 810. [Google Scholar] [CrossRef]
- Pavlov, V.V.; Krasnova, N.K. Synthesis of electrostatic fields for transportation of charged particle beams. St. Petersburg Polytech. Univ. J. Phys. Math. 2016, 2, 103–110. [Google Scholar] [CrossRef][Green Version]
- Liu, M.; He, M.; Sun, P. Mixed finite element analysis for a modified Poisson-Fermi interface problem accounting for electrostatic correlations. Commun. Nonlinear Sci. Numer. Simul. 2025, 140, 108385. [Google Scholar] [CrossRef]
- Fuchs, J.; Schweigert, C.; Wood, S.; Yang, Y. Algebraic Structures in Two-Dimensional Conformal Field Theory. Encyc. Math. Phys. 2025, 3, 604–617. [Google Scholar]
- Needham, T. Visual Complex Analysis; Oxford University Press: Oxford, UK, 2023. [Google Scholar]
- Van Der Waerden, B.L. Algebra; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Jetzek, U. Applications of Galois Fields and Linear Feedback Shift Registers. In Galois Fields, Linear Feedback Shift Registers and Their Applications; Springer: Berlin/Heidelberg, Germany, 2018; pp. 97–158. [Google Scholar] [CrossRef]
- Chowla, S. A note on the construction of finite Galois fields GF(pn). J. Math. Anal. Appl. 1966, 15, 53–54. [Google Scholar] [CrossRef]
- Lloris Ruiz, A.; Castillo Morales, E.; Parrilla Roure, L.; García Ríos, A.; Lloris Meseguer, M.J. Galois Fields GF(p^n). In Arithmetic and Algebraic Circuits; Springer: Cham, Switzerland, 2021; Volume 201. [Google Scholar] [CrossRef]
- Vitulyova, E.S.; Matrassulova, D.K.; Suleimenov, I.E. Construction of generalized Rademacher functions in terms of ternary logic: Solving the problem of visibility of using Galois fields for digital signal processing. Int. J. Electron. Telecommun. 2022, 68, 237–244. [Google Scholar] [CrossRef]
- Azimov, O.; Schevchuk, O.; Azimova, K.; Dorofey, Y.; Tomchenko, O. Integration of GIS and RSE aiming to the effective monitoring of the surroundings of landfills. Ukr. J. Remote Sens. 2020, 27, 4–12. [Google Scholar] [CrossRef]
- Bennett, M.M.; Gleason, C.J.; Tellman, B.; Alvarez Leon, L.F.; Friedrich, H.K.; Ovienmhada, U.; Mathews, A.J. Bringing satellites down to Earth: Six steps to more ethical remote sensing. Glob. Environ. Change Adv. 2024, 2, 100003. [Google Scholar] [CrossRef]
- Wei, H.; Jia, K.; Wang, Q.; Cao, B.; Qi, J.; Zhao, W.; Yang, J. Real-time remote sensing detection framework of the earth’s surface anomalies based on a priori knowledge base. Int. J. Appl. Earth Obs. Geoinf. 2023, 122, 103429. [Google Scholar] [CrossRef]
- Joshi, P.; Sandhu, K.S.; Dhillon, G.S.; Chen, J.; Bohara, K. Detection and monitoring wheat diseases using unmanned aerial vehicles (UAVs). Comput. Electron. Agric. 2024, 224, 109158. [Google Scholar] [CrossRef]
- Han, J.Y.; Hsu, C.R.; Huang, C.J. Automated progress monitoring of land development projects using unmanned aerial vehicles and machine learning. Autom. Constr. 2024, 168, 105827. [Google Scholar] [CrossRef]
- Mollick, T.; Azam, M.G.; Karim, S. Geospatial-based machine learning techniques for land use and land cover mapping using a high-resolution unmanned aerial vehicle image. Remote Sens. Appl. Soc. Environ. 2023, 29, 100859. [Google Scholar] [CrossRef]
- Mukhamediev, R.I.; Symagulov, A.; Kuchin, Y.; Zaitseva, E.; Bekbotayeva, A.; Yakunin, K.; Assanov, I.; Levashenko, V.; Popova, Y.; Akzhalova, A.; et al. Review of Some Applications of Unmanned Aerial Vehicles Technology in the Resource-Rich Country. Appl. Sci. 2021, 11, 10171. [Google Scholar] [CrossRef]
- Xu, X.; Baydur, C.; Feng, J.; Wu, C. Integrating spatial-temporal soundscape mapping with landscape indicators for effective conservation management and planning of a protected area. J. Environ. Manag. 2024, 356, 120555. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Zhang, Y.; Chang, X.; Wang, Y.; Xu, J. Cloud-aware generative network: Removing cloud from optical remote sensing images. IEEE Geosci. Remote Sens. Lett. 2019, 17, 691–695. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.; Cheng, Q.; Wu, P.; Gan, W.; Fang, L. Cloud removal in remote sensing images using nonnegative matrix factorization and error correction. ISPRS J. Photogramm. Remote Sens. 2019, 148, 103–113. [Google Scholar] [CrossRef]
- Mukhamediev, R.; Amirgaliyev, Y.; Kuchin, Y.; Aubakirov, M.; Terekhov, A.; Merembayev, T.; Yelis, M.; Zaitseva, E.; Levashenko, V.; Popova, Y.; et al. Operational Mapping of Salinization Areas in Agricultural Fields Using Machine Learning Models Based on Low-Altitude Multispectral Images. Drones 2023, 7, 357. [Google Scholar] [CrossRef]
- Lu, R.; Zhang, Y.; Huang, Q.; Zeng, P.; Shi, Z.; Ye, S. A refined edge-aware convolutional neural networks for agricultural parcel delineation. Int. J. Appl. Earth Obs. Geoinf. 2024, 133, 104084. [Google Scholar] [CrossRef]
- Mendoza-Bernal, J.; González-Vidal, A.; Skarmeta, A.F. A Convolutional Neural Network approach for image-based anomaly detection in smart agriculture. Expert Syst. Appl. 2024, 247, 123210. [Google Scholar] [CrossRef]
- Sharma, B.L.; Khatri, N.; Sharma, A. An analytical review on FPGA based autonomous flight control system for small UAVs. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 1369–1372. [Google Scholar] [CrossRef]
- Fuller, B.; Kok, J.; Kelson, N.; Gonzalez, F. Hardware design and implementation of a MAVLink interface for an FPGA-based autonomous UAV flight control system. In Proceedings of the 16th Australasian Conference on Robotics and Automation, Melbourne, Australia, 2–4 December 2014; pp. 1–6. [Google Scholar]
- Dorigo, M.; Theraulaz, G.; Trianni, V. Swarm Robotics: Past, Present, and Future. Proc. IEEE 2021, 109, 1152–1165. [Google Scholar] [CrossRef]
- Chung, S.-J.; Paranjape, A.A.; Dames, P.; Shen, S.; Kumar, V. A Survey on Aerial Swarm Robotics. IEEE Trans. Robot. 2018, 34, 837–855. [Google Scholar] [CrossRef]
- Tosato, P.; Facinelli, D.; Prada, M.; Gemma, L.; Rossi, M.; Brunelli, D. An Autonomous Swarm of Drones for Industrial Gas Sensing Applications. In Proceedings of the 2019 IEEE 20th International Symposium on “A World of Wireless, Mobile and Multimedia Networks” (WoWMoM), Washington, DC, USA, 10–12 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Raj, A.; Ahuja, K.; Busnel, Y. AI algorithm for predicting and optimizing trajectory of massive UAV swarm. Robot. Auton. Syst. 2025, 186, 104910. [Google Scholar] [CrossRef]
- Poghosyan, S.; Poghosyan, V.; Abrahamyan, S.; Lazyan, A.; Astsatryan, H.; Alaverdyan, Y.; Eguiazarian, K. Cloud-based mathematical models for self-organizing swarms of UAVs: Design and analysis. Drone Syst. Appl. 2024, 12, 1–12. [Google Scholar] [CrossRef]
- Zhao, B.; Huo, M.; Li, Z.; Yu, Z.; Qi, N. Graph-based multi-agent reinforcement learning for large-scale UAVs swarm system control. Aerosp. Sci. Technol. 2024, 150, 109166. [Google Scholar] [CrossRef]
- Feng, S.; Chen, Y.; Huang, M.; Shu, F. Optimization of Resource Allocation in Unmanned Aerial Vehicles Based on Swarm Intelligence Algorithms. Comput. Mater. Contin. 2023, 75, 4341–4355. [Google Scholar] [CrossRef]
- Asaamoning, G.; Mendes, P.; Rosário, D.; Cerqueira, E. Drone Swarms as Networked Control Systems by Integration of Networking and Computing. Sensors 2021, 21, 2642. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.-C.; Lin, K.-H.; Wu, J.-C. Analysis of hyperbolic and circular positioning algorithms using stationary signal-strength-difference measurements in wireless communications. IEEE Trans. Veh. Technol. 2006, 55, 499–509. [Google Scholar] [CrossRef]
- Kuptsov, V.; Badenko, V.; Ivanov, S.; Fedotov, A. Method for Remote Determination of Object Coordinates in Space Based on Exact Analytical Solution of Hyperbolic Equations. Sensors 2020, 20, 5472. [Google Scholar] [CrossRef]
- Barvinok, A.; Rudelson, M. When a system of real quadratic equations has a solution. Adv. Math. 2022, 403, 108391. [Google Scholar] [CrossRef]
- Chi, Y.; Lu, Y.M. Kaczmarz method for solving quadratic equations. IEEE Signal Process. Lett. 2016, 23, 1183–1187. [Google Scholar] [CrossRef]
- Huang, M.; Xu, Z. Solving systems of quadratic equations via exponential-type gradient descent algorithm. arXiv 2018, arXiv:1806.00904. [Google Scholar] [CrossRef]
- Madhu, K. Two-point iterative methods for solving quadratic equations and its applications. Math. Sci. Appl. E-Notes 2018, 6, 66–80. [Google Scholar] [CrossRef][Green Version]
- Schinianakis, D.; Stouraitis, T. Residue Number Systems in Cryptography: Design, Challenges, Robustness. In Secure System Design and Trustable Computing; Chang, C.-H., Potkonjak, M., Eds.; Springer: Cham, Switzerland, 2016; pp. 115–161. [Google Scholar] [CrossRef]
- Givaki, K.; Hojabr, R.; Najafi, M.H.; Khonsari, A.; Gholamrezayi, M.H.; Gorgin, S.; Rahmati, D. Using Residue Number Systems to Accelerate Deterministic Bit-Stream Multiplication. In Proceedings of the 2019 IEEE 30th International Conference on Application-specific Systems, Architectures and Processors (ASAP), New York, NY, USA, 15–17 July 2019; p. 40. [Google Scholar] [CrossRef]
- Valueva, M.V.; Nagornov, N.N.; Lyakhov, P.A.; Valuev, G.V.; Chervyakov, N.I. Application of the Residue Number System to Reduce Hardware Costs of the Convolutional Neural Network Implementation. Math. Comput. Simul. 2020, 177, 232–243. [Google Scholar] [CrossRef]
- Zhuang, H.; Lin, Z.; Yang, Y.; Toh, K.-A. An analytic formulation of convolutional neural network learning for pattern recognition. Inf. Sci. 2025, 686, 121317. [Google Scholar] [CrossRef]
- Patil, A.; Rane, M. Convolutional Neural Networks: An Overview and Its Applications in Pattern Recognition. Inf. Commun. Technol. Intell. Syst. 2021, 195, 21–30. [Google Scholar]
- Wei, S. Reconfigurable computing: A promising microchip architecture for artificial intelligence. J. Semicond. 2020, 41, 020301. [Google Scholar] [CrossRef]
- Luo, S.; Song, M.; Li, X.; Zhang, Y.; Hong, J.; Yang, X.; You, L. Reconfigurable skyrmion logic gates. Nano Lett. 2018, 18, 1180–1184. [Google Scholar] [CrossRef]
- Torres, F.; Basaran, A.C.; Schuller, I.K. Thermal management in neuromorphic materials, devices, and networks. Adv. Mater. 2023, 35, 2205098. [Google Scholar] [CrossRef]
- Suleimenov, I.; Gabrielyan, O.; Kopishev, E.; Kadyrzhan, A.; Bakirov, A.; Vitulyova, Y. Advanced Applications of Polymer Hydrogels in Electronics and Signal Processing. Gels 2024, 10, 715. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.H.; Zou, J.; Zhang, H.; Shi, Y.Z.; Luo, S.B.; Wang, N.; Liu, A.Q. Space-efficient optical computing with an integrated chip diffractive neural network. Nat. Commun. 2022, 13, 1044. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Butt, M.A.; Khonina, S.N. Optical computing: Status and perspectives. Nanomaterials 2022, 12, 2171. [Google Scholar] [CrossRef] [PubMed]
- Giovannitti, A.; Sbircea, D.-T.; Inal, S.; Nielsen, C.B.; Bandiello, E.; Hanifi, D.A.; Sessolo, M.; Malliaras, G.G.; McCulloch, I.; Rivnay, J. Controlling the Mode of Operation of Organic Transistors through Side-Chain Engineering. Proc. Natl. Acad. Sci. USA 2016, 113, 12017–12022. [Google Scholar] [CrossRef]
- Wu, X.; Wang, S.; Huang, W.; Dong, Y.; Wang, Z.; Huang, W. Wearable In-Sensor Reservoir Computing Using Optoelectronic Polymers with through-Space Charge-Transport Characteristics for Multi-Task Learning. Nat. Commun. 2023, 14, 468. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, W.; Zeng, J.; Fan, F.; Gu, J.; Chen, X.; Yan, L.; Xie, G.; Liu, S.; Yan, Q.; et al. 90% Yield Production of Polymer Nano-Memristor for in-Memory Computing. Nat. Commun. 2021, 12, 1984. [Google Scholar] [CrossRef]
- Gärisch, F.; Schröder, V.; List-Kratochvil, E.J.W.; Ligorio, G. Scalable Fabrication of Neuromorphic Devices Using Inkjet Printing for the Deposition of Organic Mixed Ionic-Electronic Conductor. Adv. Electron. Mater. 2024, 10, 2400479. [Google Scholar] [CrossRef]
- Zhang, Y.; Van Doremaele, E.R.W.; Ye, G.; Stevens, T.; Song, J.; Chiechi, R.C.; Van De Burgt, Y. Adaptive Biosensing and Neuromorphic Classification Based on an Ambipolar Organic Mixed Ionic–Electronic Conductor. Adv. Mater. 2022, 34, 2200393. [Google Scholar] [CrossRef] [PubMed]
- Oh, S.; Hwang, H.; Yoo, I.K. Ferroelectric materials for neuromorphic computing. APL Mater. 2019, 7, 091109. [Google Scholar] [CrossRef]
- Vitulyova, E.S.; Matrassulova, D.K.; Suleimenov, I.E. New application of non-binary Galois fields Fourier transform: Digital analog of convolution theorem. Indones. J. Electr. Eng. Comput. Sci. 2021, 23, 1718–1726. [Google Scholar] [CrossRef]
- Matrassulova, D.K.; Vitulyova, Y.S.; Konshin, S.V.; Suleimenov, I.E. Algebraic fields and rings as a digital signal processing tool. Indones. J. Electr. Eng. Comput. Sci. 2023, 29, 206–216. [Google Scholar] [CrossRef]
- Suleimenov, I.; Bakirov, A.; Moldakhan, I. Formalization of ternary logic for application to digital signal processing. In Energy Management of Municipal Transportation Facilities and Transport; Springer: Cham, Switzerland, 2019; pp. 26–35. [Google Scholar] [CrossRef]
- Zahoor, F.; Jaber, R.A.; Isyaku, U.B.; Sharma, T.; Bashir, F.; Abbas, H.; Alzahrani, A.S.; Gupta, S.; Hanif, M. Design implementations of ternary logic systems: A critical review. Results Eng. 2024, 23, 102761. [Google Scholar] [CrossRef]
- Suleimenov, I.E.; Bakirov, A.S.; Matrassulova, D.K. A technique for analyzing neural networks in terms of ternary logic. J. Theor. Appl. Inf. Technol. 2021, 99, 2537–2553. [Google Scholar]
- Wang, X.-Y.; Dong, C.-T.; Wu, Z.-R.; Cheng, Z.-Q. A review on the design of ternary logic circuits. Chin. Phys. B 2021, 30, 12601. [Google Scholar] [CrossRef]
- Efstathiou, C.; Kouretas, I.; Kitsos, P. On the modulo 2n+1 addition and subtraction for weighted operands. Microprocess. Microsyst. 2023, 101, 104897. [Google Scholar] [CrossRef]
- Patel, B.K.; Kanungo, J. Efficient Tree Multiplier Design by using Modulo 2n+1 Adder. In Proceedings of the 2021 Emerging Trends in Industry 4.0 (ETI 4.0), Raigarh, India, 19–21 May 2021; pp. 1–6. [Google Scholar]
- Ahmadifar, H.; Torabi, Z. Adder-Only Reverse Converters for 5-Moduli Set {2q, 2q-1, 2q+1±1, 2q+2-1}. IETE J. Res. 2024, 70, 7346–7353. [Google Scholar] [CrossRef]
- Suleimenov, I.E.; Vitulyova, Y.S.; Kabdushev, S.B.; Bakirov, A.S. Improving the efficiency of using multivalued logic tools. Sci. Rep. 2023, 13, 1108. [Google Scholar] [CrossRef] [PubMed]
- Suleimenov, I.E.; Vitulyova, Y.S.; Kabdushev, S.B.; Bakirov, A.S. Improving the efficiency of using multivalued logic tools: Application of algebraic rings. Sci. Rep. 2023, 13, 22021. [Google Scholar] [CrossRef]
- Capineri, L.; Falorni, P.; Ivashov, S.; Zhuravlev, A.; Vasiliev, I.; Razevig, V.; Bechtel, T.; Stankiewicz, G. Combined Holographic Subsurface Radar and Infrared Thermography for Diagnosis of the Conditions of Historical Structures and Artworks. Near Surf. Geophys. 2009, 8, 355–364. [Google Scholar] [CrossRef]
- Pryshchenko, O.; Dumin, O.; Plakhtii, V. Discrete Tomography Approach for Subsurface Object Detection by Artificial Neural Network. In Proceedings of the 2022 IEEE 2nd Ukrainian Microwave Week (UkrMW), Kharkiv, Ukraine, 14–18 November 2022; pp. 701–706. [Google Scholar] [CrossRef]
- Fortuny-Guasch, J. A novel 3-D subsurface radar imaging technique. IEEE Trans. Geosci. Remote Sens. 2002, 40, 443–452. [Google Scholar] [CrossRef]
- Pumplün, S. Factoring skew polynomials over Hamilton’s quaternion algebra and the complex numbers. J. Algebra 2015, 427, 20–29. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kadyrzhan, A.; Matrassulova, D.; Vitulyova, Y.; Suleimenov, I. Discrete Cartesian Coordinate Transformations: Using Algebraic Extension Methods. Appl. Sci. 2025, 15, 1464. https://doi.org/10.3390/app15031464
Kadyrzhan A, Matrassulova D, Vitulyova Y, Suleimenov I. Discrete Cartesian Coordinate Transformations: Using Algebraic Extension Methods. Applied Sciences. 2025; 15(3):1464. https://doi.org/10.3390/app15031464
Chicago/Turabian StyleKadyrzhan, Aruzhan, Dinara Matrassulova, Yelizaveta Vitulyova, and Ibragim Suleimenov. 2025. "Discrete Cartesian Coordinate Transformations: Using Algebraic Extension Methods" Applied Sciences 15, no. 3: 1464. https://doi.org/10.3390/app15031464
APA StyleKadyrzhan, A., Matrassulova, D., Vitulyova, Y., & Suleimenov, I. (2025). Discrete Cartesian Coordinate Transformations: Using Algebraic Extension Methods. Applied Sciences, 15(3), 1464. https://doi.org/10.3390/app15031464





