Wavelength Selection for Satellite Quantum Key Distribution
Abstract
1. Introduction
2. Transmittance and Spectral Radiance
2.1. Key Assumptions and Limitations of MODTRAN Simulations
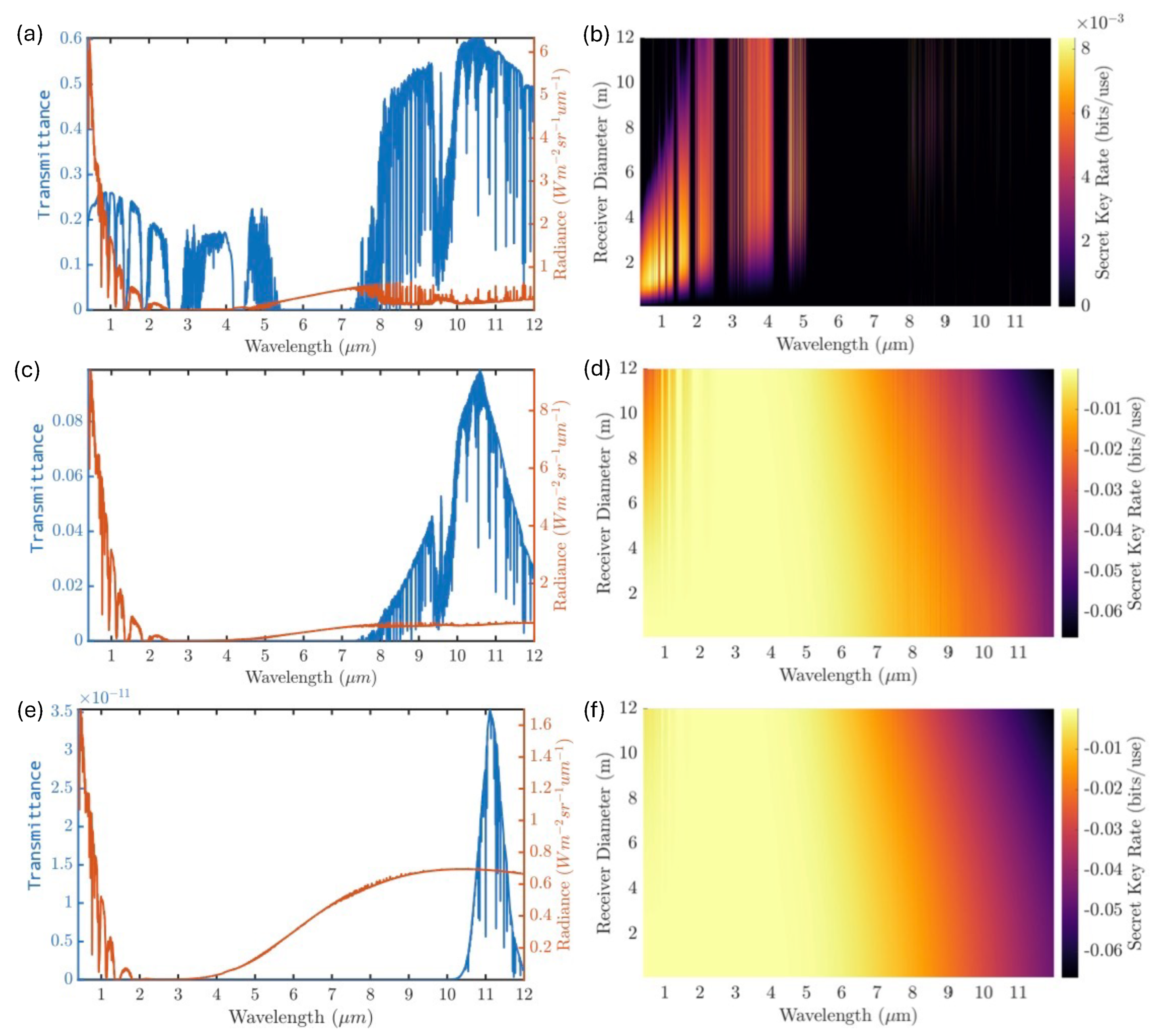
2.1.1. Scenario 1: Tucson, Arizona
2.1.2. Scenario 2: Waterford, Ireland
2.2. Atmospheric Windows
3. Channel Model
3.1. Free-Space Diffraction
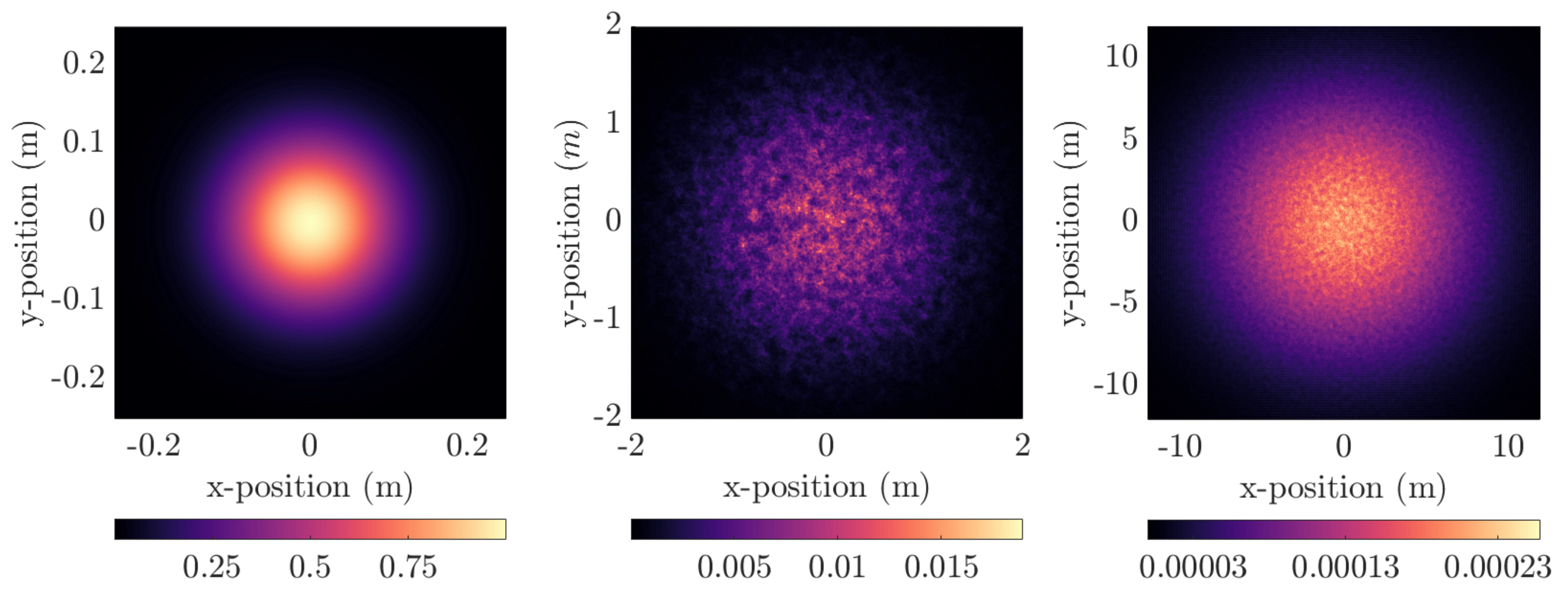
3.2. Turbulence
3.3. Background Noise
4. QKD Performance
4.1. QKD Protocol
4.2. Adaptive Optics
4.3. Filtering Techniques
5. Results and Discussion
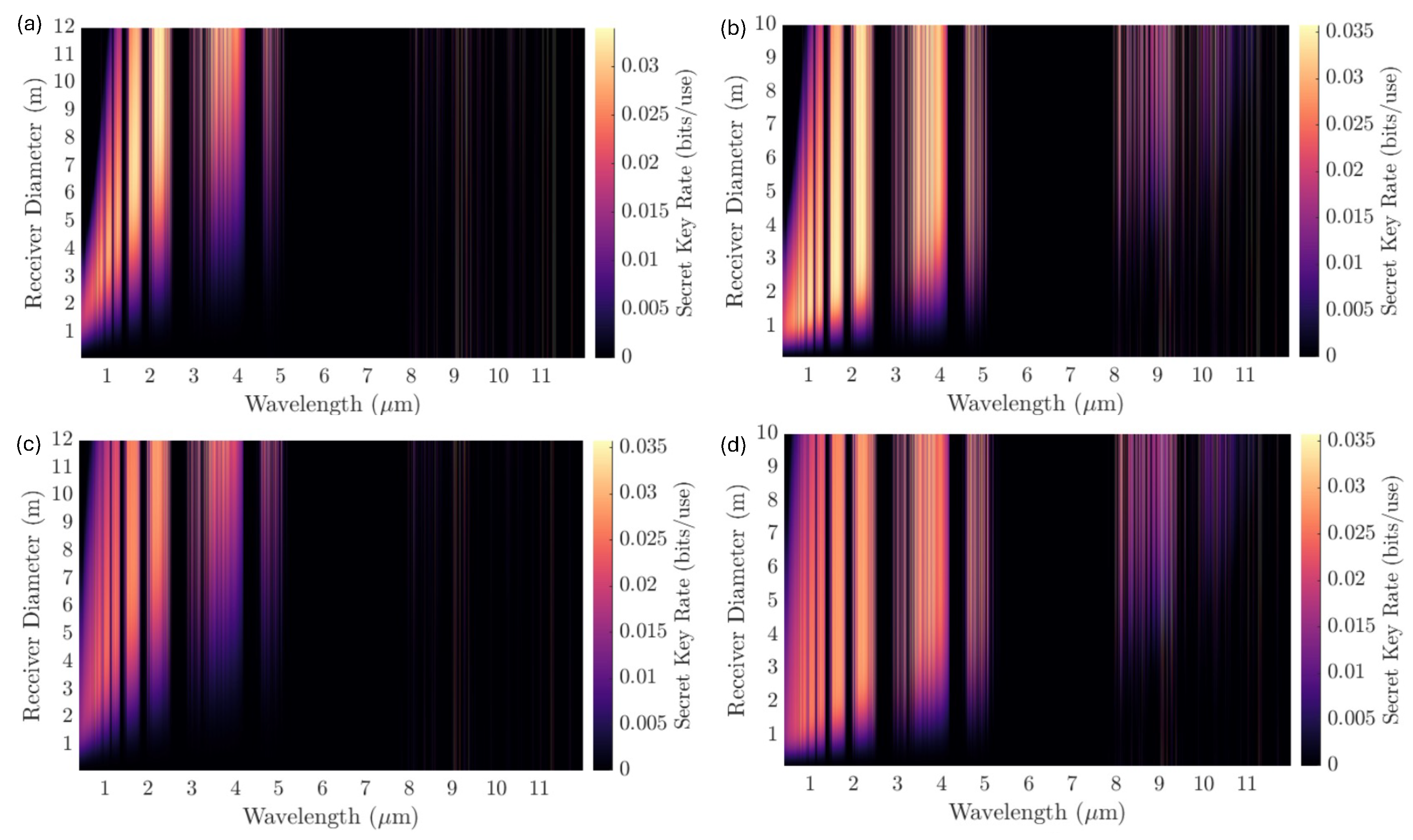
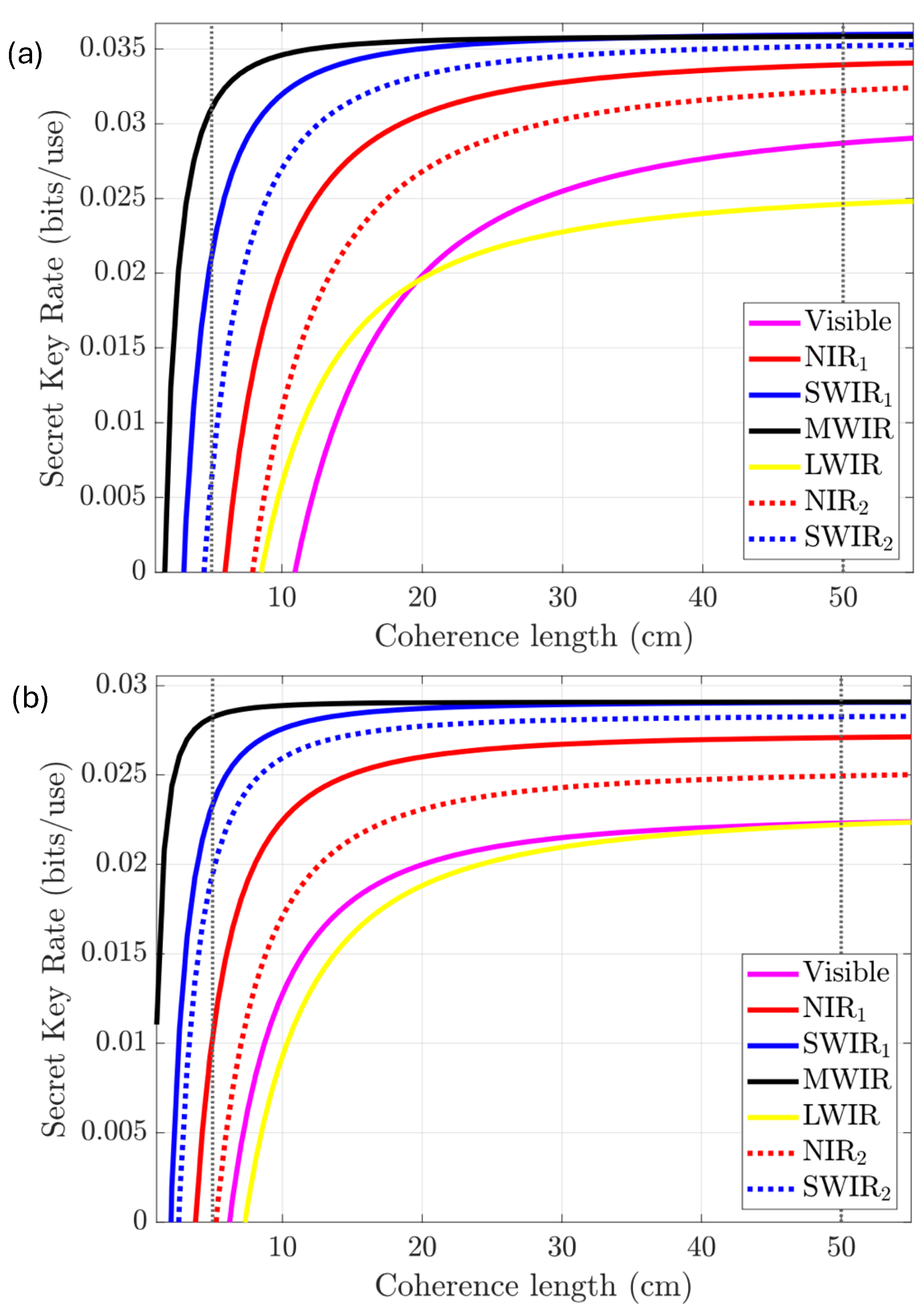
5.1. Wavelength Selection
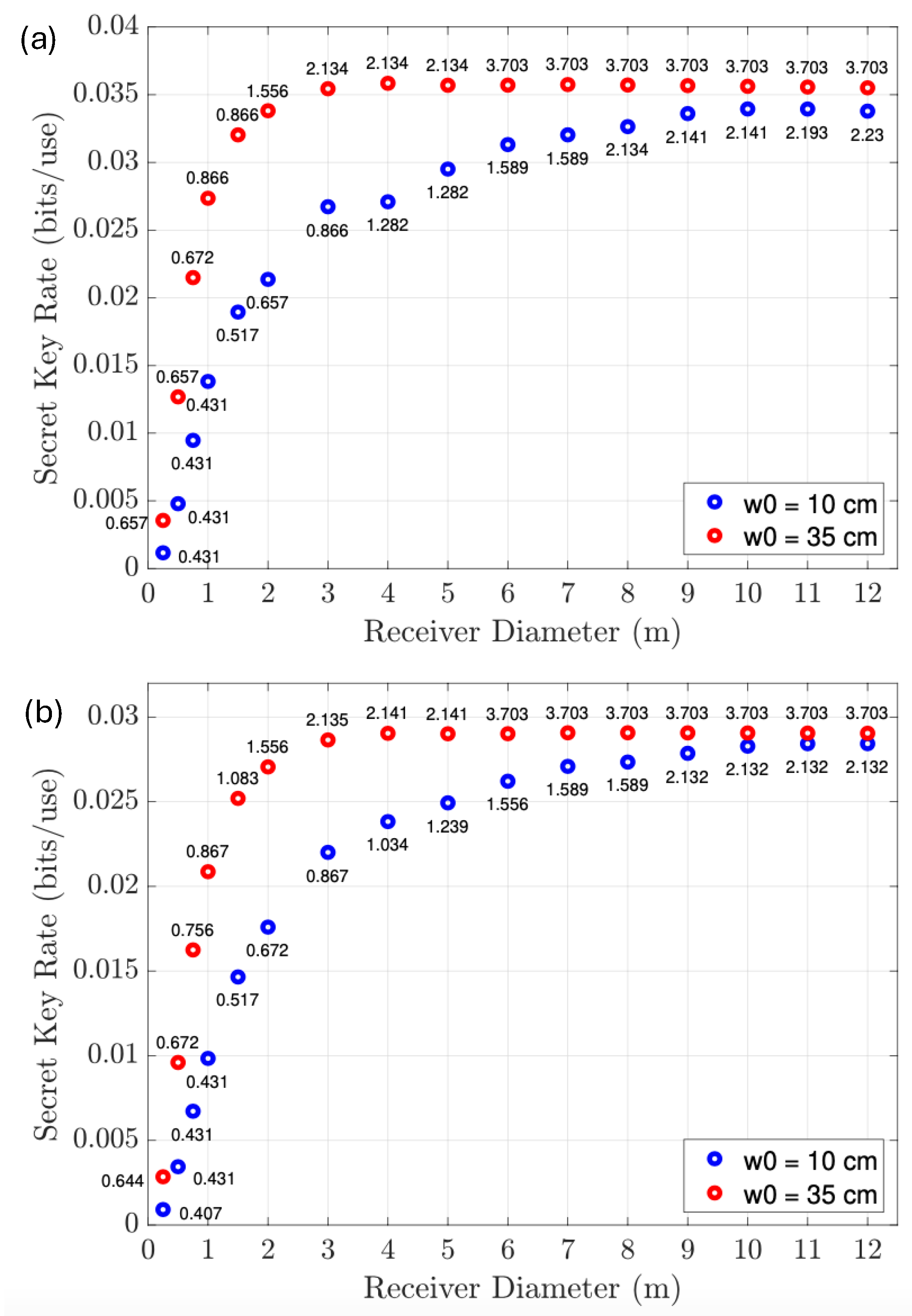
5.2. Component Size Optimization
5.3. Wavelength Selection Through Atmospheric Turbulence
5.4. Adverse Atmospheric Conditions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Phase Screen Model
References
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Mermin, N.D. Quantum cryptography without Bell’s theorem. Phys. Rev. Lett. 1992, 68, 557. [Google Scholar] [CrossRef] [PubMed]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Ralph, T.C. Security of continuous-variable quantum cryptography. Phys. Rev. A 2000, 62, 062306. [Google Scholar] [CrossRef]
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Briegel, H.J.; Dür, W.; Cirac, J.I.; Zoller, P. Quantum Repeaters: The Role of Imperfect Local Operations in Quantum Communication. Phys. Rev. Lett. 1998, 81, 5932–5935. [Google Scholar] [CrossRef]
- Ruihong, Q.; Ying, M. Research Progress Of Quantum Repeaters. J. Phys. Conf. Ser. 2019, 1237, 052032. [Google Scholar] [CrossRef]
- Kong, W.; Sun, Y.; Dou, T.; Xie, Y.; Li, Z.; Gao, Y.; Zhao, Q.; Chen, N.; Gao, W.; Hao, Y.; et al. Enhanced Coexistence of Quantum Key Distribution and Classical Communication over Hollow-Core and Multi-Core Fibers. Entropy 2024, 26, 601. [Google Scholar] [CrossRef]
- Jasion, G.T.; Sakr, H.; Hayes, J.R.; Sandoghchi, S.R.; Hooper, L.; Fokoua, E.N.; Saljoghei, A.; Mulvad, H.C.; Alonso, M.; Taranta, A. 0.174 dB/km hollow core double nested antiresonant nodeless fiber (DNANF). In Proceedings of the 2022 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 6–10 March 2022. [Google Scholar]
- Chen, Y.; Petrovich, M.; Fokoua, E.N.; Adamu, A.; Hassan, M.; Sakr, H.; Slavík, R.; Gorajoobi, S.; Alonso1, M.; Ando, R. Hollow Core DNANF Optical Fiber with <0.11 dB/km Loss. In Proceedings of the 2024 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 24–28 March 2024. [Google Scholar]
- Liao, S.K.; Cai, W.Q.; Liu, W.Y.; Zhang, L.; Li, Y.; Ren, J.G.; Yin, J.; Shen, Q.; Cao, Y.; Li, Z.P.; et al. Satellite-to-ground quantum key distribution. Nature 2017, 549, 43–47. [Google Scholar] [CrossRef]
- Yin, J.; Cao, Y.; Li, Y.H.; Liao, S.K.; Zhang, L.; Ren, J.G.; Cai, W.Q.; Liu, W.Y.; Li, B.; Dai, H.; et al. Satellite-based entanglement distribution over 1200 kilometers. Science 2017, 356, 1140–1144. [Google Scholar] [CrossRef]
- Sidhu, J.S.; Joshi, S.K.; Gündoğan, M.; Brougham, T.; Lowndes, D.; Mazzarella, L.; Krutzik, M.; Mohapatra, S.; Dequal, D.; Vallone, G.; et al. Advances in space quantum communications. IET Quantum Commun. 2021, 2, 182–217. [Google Scholar] [CrossRef]
- Pirandola, S. Satellite quantum communications: Fundamental bounds and practical security. Phys. Rev. Res. 2021, 3, 023130. [Google Scholar] [CrossRef]
- Belenchia, A.; Carlesso, M.; Bayraktar, Ö.; Dequal, D.; Derkach, I.; Gasbarri, G.; Herr, W.; Li, Y.L.; Rademacher, M.; Sidhu, J.; et al. Quantum physics in space. Phys. Rep. 2022, 951, 1–70. [Google Scholar] [CrossRef]
- Dequal, D.; Trigo Vidarte, L.; Roman Rodriguez, V.; Vallone, G.; Villoresi, P.; Leverrier, A.; Diamanti, E. Feasibility of satellite-to-ground continuous-variable quantum key distribution. Npj Quantum Inf. 2021, 7, 3. [Google Scholar] [CrossRef]
- Ghalaii, M.; Pirandola, S. Quantum communications in a moderate-to-strong turbulent space. Commun. Phys. 2022, 5, 38. [Google Scholar] [CrossRef]
- Pirandola, S. Limits and security of free-space quantum communications. Phys. Rev. Res. 2021, 3, 013279. [Google Scholar] [CrossRef]
- Bedington, R.; Arrazola, J.M.; Ling, A. Progress in satellite quantum key distribution. NPJ Quantum Inf. 2017, 3, 30. [Google Scholar] [CrossRef]
- Er-long, M.; Zheng-fu, H.; Shun-sheng, G.; Tao, Z.; Da-Sheng, D.; Guang-Can, G. Background noise of satellite-to-ground quantum key distribution. New J. Phys. 2005, 7, 215. [Google Scholar] [CrossRef]
- Tomaello, A.; Bonato, C.; Da Deppo, V.; Naletto, G.; Villoresi, P. Link budget and background noise for satellite quantum key distribution. Adv. Space Res. 2011, 47, 802–810. [Google Scholar] [CrossRef]
- Gruneisen, M.T.; Sickmiller, B.A.; Flanagan, M.B.; Black, J.P.; Stoltenberg, K.E.; Duchane, A.W. Adaptive spatial filtering of daytime sky noise in a satellite quantum key distribution downlink receiver. Opt. Eng. 2016, 55, 026104. [Google Scholar] [CrossRef]
- Gruneisen, M.T.; Eickhoff, M.L.; Newey, S.C.; Stoltenberg, K.E.; Morris, J.F.; Bareian, M.; Harris, M.A.; Oesch, D.W.; Oliker, M.D.; Flanagan, M.B.; et al. Adaptive-Optics-Enabled Quantum Communication: A Technique for Daytime Space-To-Earth Links. Phys. Rev. Appl. 2021, 16, 014067. [Google Scholar] [CrossRef]
- Plank, T.; Leitgeb, E.; Pezzei, P.; Ghassemlooy, Z. Wavelength-selection for high data rate Free Space Optics (FSO) in next generation wireless communications. In Proceedings of the 2012 17th European Conference on Networks and Optical Communications, Geltru, Spain, 20–22 June 2012; IEEE: New York, NY, USA, 2012; pp. 1–5. [Google Scholar]
- Vasylyev, D.; Semenov, A.; Vogel, W. Atmospheric quantum channels with weak and strong turbulence. Phys. Rev. Lett. 2016, 117, 090501. [Google Scholar] [CrossRef] [PubMed]
- Aellen, T.; Giovannini, M.; Faist, J.; Von der Weid, J.P. Feasibility study of free-space quantum key distribution in the mid-infrared. Quantum Inf. Comput. 2008, 8, 0001–0011. [Google Scholar]
- Wang, Z.; Malaney, R.; Green, J. Inter-satellite quantum key distribution at terahertz frequencies. In Proceedings of the ICC 2019–2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; IEEE: New York, NY, USA, 2019; pp. 1–7. [Google Scholar]
- Pavelchek, A.; Trissel, R.G.; Plante, J.; Umbrasas, S. Long-wave infrared (10-micron) free-space optical communication system. In Proceedings of the Free-Space Laser Communication and Active Laser Illumination III. International Society for Optics and Photonics, San Diego, CA, USA, 4–6 August 2003; Volume 5160, pp. 247–252. [Google Scholar]
- Achour, M. Free-space optics wavelength selection: 10 μm versus shorter wavelengths. J. Opt. Netw. 2003, 2, 127–143. [Google Scholar] [CrossRef]
- Colvero, C.; Cordeiro, M.; De Faria, G.; Von der Weid, J. Experimental comparison between far-and near-infrared wavelengths in free-space optical systems. Microw. Opt. Technol. Lett. 2005, 46, 319–323. [Google Scholar] [CrossRef]
- Pang, X.; Ozolins, O.; Zhang, L.; Schatz, R.; Udalcovs, A.; Yu, X.; Jacobsen, G.; Popov, S.; Chen, J.; Lourdudoss, S. Free-Space Communications Enabled by Quantum Cascade Lasers. Phys. Status Solidi (A) 2021, 218, 2000407. [Google Scholar] [CrossRef]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in quantum cryptography. Adv. Opt. Photon. 2020, 12, 1012–1236. [Google Scholar] [CrossRef]
- Xu, F.; Ma, X.; Zhang, Q.; Lo, H.K.; Pan, J.W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002. [Google Scholar] [CrossRef]
- Marulanda Acosta, V.; Dequal, D.; Schiavon, M.; Montmerle-Bonnefois, A.; Lim, C.B.; Conan, J.M.; Diamanti, E. Analysis of satellite-to-ground quantum key distribution with adaptive optics. New J. Phys. 2024, 26, 023039. [Google Scholar] [CrossRef]
- Lu, C.Y.; Cao, Y.; Peng, C.Z.; Pan, J.W. Micius quantum experiments in space. Rev. Mod. Phys. 2022, 94, 035001. [Google Scholar] [CrossRef]
- Sidhu, J.S.; Brougham, T.; McArthur, D.; Pousa, R.G.; Oi, D. Finite key effects in satellite quantum key distribution. NPJ Quantum Inf. 2022, 8, 18. [Google Scholar] [CrossRef]
- Sidhu, J.S.; Brougham, T.; McArthur, D.; Pousa, R.G.; Oi, D. Finite key performance of satellite quantum key distribution under practical constraints. NPJ Quantum Inf. 2023, 6, 210. [Google Scholar] [CrossRef]
- Li, Y.; Liao, S.K.; Cao, Y.; Ren, J.G.; Liu, W.Y.; Yin, J.; Shen, Q.; Qiang, J.; Zhang, L.; Yong, H.L.; et al. Space-ground QKD network based on a compact payload and medium-inclination orbit. Optica 2022, 9, 933–938. [Google Scholar] [CrossRef]
- Zheng, Y.; Deng, Y.; Shi, Z.; Fan, Y.; Wang, Z.; Lei, D.; Zhou, Z.K.; Wang, X.H. Enriching Metasurface Functionalities by Fully Employing the Inter-Meta-Atom Degrees of Freedom for Double-Key- Secured Encryption. Adv. Mater. Technol. 2023, 8, 2201468. [Google Scholar] [CrossRef]
- Luo, W.; Cao, L.; Shi, Y.; Wan, L.; Zhang, H.; Li, S.; Chen, G.; Li, Y.; Li, S.; Wang, Y.; et al. Recent progress in quantum photonic chips for quantum communication and internet. Light. Sci. Appl. 2023, 12, 175. [Google Scholar] [CrossRef] [PubMed]
- Hwang, W.Y. Quantum key distribution with high loss: Toward global secure communication. Phys. Rev. Lett. 2003, 91, 057901. [Google Scholar] [CrossRef] [PubMed]
- Kneizys, F.X.; Shettle, E.P.; Anderson, G.P.; Gallery, W.O.; Abreu, L.W.; Selby, J.E.A.; Chetwynd, J.H.; Clough, S.A. The Modtran 2/3 and Lowtran 7 Model; MODTRAN Report; Spectral Sciences Inc.: Burlington, MA, USA, 1995. [Google Scholar]
- Anderson, G.P.; Clough, S.A.; Kneizys, F.X.; Shettle, E.P.; Abreu, L.W.; Chetwynd, J.H.; Hall, L.A. FASCOD3: Spectral simulation. In Proceedings of the I.R.S.1988 International Symposium, Lille, France, 18–24 August 1988; Volume 4. [Google Scholar]
- Henniger, H.; Wilfert, O. An introduction to free-space optical communications. Radioengineering 2010, 19, 203. [Google Scholar]
- Chen, X.; Wei, H. A combined atmospheric radiative transfer model (CART): A review and applications. J. Opt. Soc. Korea 2010, 14, 190–198. [Google Scholar] [CrossRef]
- Nilsson, B.A. Analysis of the Atmospheric Aerosol Extinction in the 0.5–14 μm region. In FOA Report C 30396-E1,E3; Defence Research Establishment, Department 3, FOA3: Linköping, Sweden, 1986. [Google Scholar]
- Hågård, A.; R., P. Infrared transmission measurement in the atmosphere. In Proceedings of the SPIE-Proceedings, Bellingham, WA, USA, 21–22 July 1992; Volume 1762. [Google Scholar]
- Berk, A.; Conforti, P.; Kennett, R.; Perkins, T.; Hawes, F.; Van Den Bosch, J. MODTRAN® 6: A major upgrade of the MODTRAN® radiative transfer code. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014; IEEE: New York, NY, USA, 2014; pp. 1–4. [Google Scholar]
- Berk, A.; Conforti, P.; Hawes, F. An accelerated line-by-line option for MODTRAN combining on-the-fly generation of line center absorption within 0.1 cm–1 bins and pre-computed line tails. In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XXI, Baltimore, MD, USA, 21–23 April 2015; International Society for Optics and Photonics: Bellingham, DC, USA, 2015; Volume 9472, p. 947217. [Google Scholar]
- Kaushal, H.; Jain, V.; Kar, S. Free Space Optical Communication; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Svelto, O.; Hanna, D.C. Principles of Lasers; Springer: Berlin/Heidelberg, Germany, 1998; Volume 4. [Google Scholar]
- Schmidt, J.D. Numerical Simulation of Optical Wave Propagation with Examples in MATLAB; SPIE: Bellingham, DC, USA, 2010. [Google Scholar]
- Hufnagel, R.E.; Stanley, N.R. Modulation transfer function associated with image transmission through turbulent media. J. Opt. Soc. Am. A 1964, 54, 52–61. [Google Scholar] [CrossRef]
- Villaseñor, E.; Malaney, R.; Mudge, K.A.; Grant, K.J. Atmospheric Effects on Satellite-to-Ground Quantum Key Distribution using Coherent States. In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Martin, J.; Flatté, S.M. Intensity images and statistics from numerical simulation of wave propagation in 3-d random media. Appl. Opt. 1988, 27, 2111–2126. [Google Scholar] [CrossRef]
- Frehlich, R. Simulation of laser propagation in a turbulent atmosphere. Appl. Opt. 2000, 39, 393–397. [Google Scholar] [CrossRef] [PubMed]
- Andrews, L.; Phillips, R.; Yu, P. Optical scintillations and fade statistics for a satellite-communication system. Appl. Opt. 1995, 34, 7742–7751. [Google Scholar] [CrossRef]
- Lanning, R.N.; Harris, M.A.; Oesch, D.W.; Oliker, M.D.; Gruneisen, M.T. Quantum Communication over Atmospheric Channels: A Framework for Optimizing Wavelength and Filtering. Phys. Rev. Appl. 2021, 16, 044027. [Google Scholar] [CrossRef]
- Ma, X.; Qi, B.; Zhao, Y.; Lo, H.K. Practical decoy state for quantum key distribution. Phys. Rev. A 2005, 72, 012326. [Google Scholar] [CrossRef]
- Gruneisen, M.T.; Flanagan, M.B.; Sickmiller, B.A. Modeling satellite-Earth quantum channel downlinks with adaptive-optics coupling to single-mode fibers. Opt. Eng. 2017, 56, 126111. [Google Scholar]
- Liao, S.K.; Yong, H.L.; Liu, C.; Shentu, G.L.; Li, D.D.; Lin, J.; Dai, H.; Zhao, S.Q.; Li, B.; Guan, J.Y.; et al. Long-distance free-space quantum key distribution in daylight towards inter-satellite communication. Nat. Photonics 2017, 11, 509. [Google Scholar] [CrossRef]
- Zhu, L.; Sun, P.C.; Bartsch, D.U.; Freeman, W.R.; Fainman, Y. Wave-front generation of Zernike polynomial modes with a micromachined membrane deformable mirror. Appl. Opt. 1999, 38, 6019–6026. [Google Scholar] [CrossRef] [PubMed]
- Morgan, R.E.; Vlahakis, S.; Douglas, E.; Allan, G.; do Vale Pereira, P.; Egan, M.; Furesz, G.; Gubner, J.; Haughwout, C.; Holden, B.; et al. On-orbit operations summary for the Deformable Mirror Demonstration Mission (DeMi) CubeSat. In Adaptive Optics Systems VIII; Proceedings of the SPIE Astronomical Telescopes + Instrumentation, Montréal, QC, Canada, 17–22 July 2022; SPIE: Bellingham, DC, USA, 2022; Volume 12185. [Google Scholar]
- You, L. Superconducting nanowire single-photon detectors for quantum information. Nanophotonics 2020, 9, 2673–2692. [Google Scholar] [CrossRef]
- Verma, V.B.; Korzh, B.; Walter, A.B.; Lita, A.E.; Briggs, R.M.; Colangelo, M.; Zhai, Y.; Wollman, E.E.; Beyer, A.D.; Allmaras, J.P.; et al. Single-photon detection in the mid-infrared up to 10 μm wavelength using tungsten silicide superconducting nanowire detectors. APL Photonics 2021, 6, 056101. [Google Scholar] [CrossRef]
- Rockwell, D.A.; Mecherle, G.S. Wavelength selection for optical wireless communications systems. In Proceedings of the Optical Wireless Communications IV, Denver, CO, USA, 19–24 August 2001; International Society for Optics and Photonics: Bellingham, DC, USA, 2001; Volume 4530, pp. 27–35. [Google Scholar]
- Avesani, M.; Calderaro, L.; Schiavon, M.; Stanco, A.; Agnesi, C.; Santamato, A.; Zahidy, M.; Scriminich, A.; Foletto, G.; Contestabile, G.; et al. Full daylight quantum-key-distribution at 1550 nm enabled by integrated silicon photonics. NPJ Quantum Inf. 2021, 7, 93. [Google Scholar] [CrossRef]
- Pudelko, J.; Bayraktar, ö.; Khan, I.; Boxleitner, W.; Petscharnig, S.; Pacher, C.; Leuchs, G.; Marquardt, C. Integrated Photonics for Quantum Communication on a Cubesat. In Proceedings of the 2023 Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference (CLEO/Europe-EQEC), Munich, Germany, 26–30 June 2023; p. 1. [Google Scholar]
- Waterford. WeatherSpark.com. Available online: https://weatherspark.com/d/33020/12/21/Average-Weather-on-December-21-in-Waterford-Ireland#Figures-Temperature (accessed on 15 January 2022).
- Manor, H.; Arnon, S. Performance of an optical wireless communication system as a function of wavelength. Appl. Opt. 2003, 42, 4285–4294. [Google Scholar] [CrossRef] [PubMed]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation Through Random Media; SPIE: Bellingham, DC, USA, 2005. [Google Scholar]
- Coulman, C.; Vernin, J.; Coqueugniot, Y.; Caccia, J. Outer scale of turbulence appropriate to modeling refractive-index structure profiles. Appl. Opt. 1988, 27, 155–160. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhang, Q.; Xin, X.; Tian, Q.; Tao, Y.; Tian, F.; Shen, Y.; Cao, G.; Chen, D.; Wang, Y.; et al. Numerical Simulation of Ground-to-Satellite Laser Transmission based on Unequal Spacing Phase Screen. In Proceedings of the 2019 18th International Conference on Optical Communications and Networks (ICOCN), Huangshan, China, 5–8 August 2019; pp. 1–3. [Google Scholar]


| Scenario 1: Tucson | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | Visible | NIR | SWIR | MWIR | LWIR | NIR2 | SWIR2 |
| Wavelength (m) | 0.69739 | 1.2857 | 2.1344 | 3.7026 | 8.3031 | 0.867 | 1.556 |
| Secret key rate (bits/use) | 0.0287 | 0.0339 | 0.036 | 0.0358 | 0.0246 | 0.0322 | 0.0352 |
| Receiver diameter (m) | 1.3784 | 2.1613 | 3.1423 | 4.5 | 5.1342 | 1.6757 | 2.5477 |
| Initial beam waist (m) | 0.3261 | 0.4465 | 0.5819 | 0.7625 | 1.1538 | 0.3712 | 0.5067 |
| Scenario 2: Waterford | |||||||
| Parameter | Visible | NIR | SWIR | MWIR | LWIR | NIR2 | SWIR2 |
| Wavelength (m) | 0.69739 | 1.2988 | 2.1407 | 3.7026 | 8.303 | 0.867 | 1.556 |
| Secret key rate (bits/use) | 0.0223 | 0.0271 | 0.029 | 0.0291 | 0.0222 | 0.0249 | 0.0282 |
| Receiver diameter (m) | 1.5865 | 2.3694 | 3.3405 | 4.936 | 5.273 | 1.8541 | 2.7856 |
| Initial beam waist (m) | 0.3261 | 0.4615 | 0.5819 | 0.7625 | 1.1538 | 0.3712 | 0.5067 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hearne, S.; Horgan, J.; Boujnah, N.; Kilbane, D. Wavelength Selection for Satellite Quantum Key Distribution. Appl. Sci. 2025, 15, 1308. https://doi.org/10.3390/app15031308
Hearne S, Horgan J, Boujnah N, Kilbane D. Wavelength Selection for Satellite Quantum Key Distribution. Applied Sciences. 2025; 15(3):1308. https://doi.org/10.3390/app15031308
Chicago/Turabian StyleHearne, Shane, Jerry Horgan, Noureddine Boujnah, and Deirdre Kilbane. 2025. "Wavelength Selection for Satellite Quantum Key Distribution" Applied Sciences 15, no. 3: 1308. https://doi.org/10.3390/app15031308
APA StyleHearne, S., Horgan, J., Boujnah, N., & Kilbane, D. (2025). Wavelength Selection for Satellite Quantum Key Distribution. Applied Sciences, 15(3), 1308. https://doi.org/10.3390/app15031308





