Abstract
This study investigates the classification of damage modes in adhesively bonded carbon fiber-reinforced plastic (CFRP) composites, a critical factor in advancing lightweight automotive design. Adhesive bonding, replacing traditional riveting, improves structural integrity while reducing weight and CO2 emissions. Mechanical testing on CFRP composites was performed, and acoustic emission (AE) signals were collected to evaluate damage mechanisms. A deep autoencoder (DAE) framework was developed to automate damage characterization by reducing AE signal dimensionality through singular value decomposition (SVD) and classifying features using the k-means algorithm. This approach effectively identified three primary damage modes: matrix cracking, interfacial debonding, and fiber breakage. Traditional AE features, such as entropy and amplitude were also classified and validated using spectral analysis. The DAE-based strategy demonstrated superior capability in real-time damage mode differentiation. Fractographic analysis confirmed crack growth in the adhesive layer, leading to interfacial debonding, fiber-matrix separation, and eventual fiber rupture. These findings highlight the DAE framework’s effectiveness in enhancing damage mode characterization, offering valuable insights for optimizing the structural performance of bonded CFRP composites in automotive applications.
1. Introduction
The 21st century has intensified the global energy crisis, driving the automotive industry towards reducing fuel consumption and CO2 emissions [1,2]. Lightweight materials have emerged as a critical solution, with several studies highlighting their potential to reduce vehicle weight, thereby enhancing fuel efficiency and minimizing environmental impact [3,4,5,6].
Among these materials, carbon fiber-reinforced plastic (CFRP) composites have gained widespread acclaim for their exceptional strength-to-weight ratio and design flexibility compared to traditional materials such as steel and aluminum [7]. CFRP composites also offer superior corrosion resistance, thermal and electrical insulation, and wear resistance, making them integral to large structural components, including aircraft parts and high-pressure cylinders [8].
In addition to material selection, assembly techniques significantly impact vehicle performance [9,10]. Traditional joining methods like riveting, while ensuring assembly strength, can increase weight and complicate repairs [11]. Adhesive bonding offers substantial advantages, such as weight reduction, improved stress distribution, and enhanced damage tolerance [12]. Unlike riveting, it reduces the stress concentration and enhances the overall durability of joints without significantly affecting the mechanical properties of the adherends [13].
Given these benefits, adhesive bonding has emerged as a crucial joining technology in modern vehicle manufacturing. It is particularly valuable for lightweight vehicle design, allowing for the effective joining of various materials, including light metals, steel, plastics, and fiber-reinforced composites [14,15]. This adaptability enables manufacturers to meet weight reduction targets while preserving essential vehicle characteristics like structural rigidity, crash performance, and noise-vibration-handling properties [16].
The choice of appropriate adhesives, such as epoxy or polyurethane, along with precise control of bond thickness, is vital for optimizing joint performance [17]. Moreover, the process demands meticulous attention to surface preparation, interfacial coatings, and joint design to ensure long-term reliability [16].
As the automotive industry increasingly focuses on lightweight and energy-efficient structures, adhesive bonding has become integral to multimaterial vehicle construction. It not only facilitates weight reduction but also improves assembly efficiency, thereby contributing to the overall sustainability and performance of modern automotive design [17].
Despite the benefits of adhesive bonding, the detailed analysis of damage evolution in bonded composites remains relatively underexplored. Studies like those conducted by Li et al. have shown that adhesive joints dissipate energy under stress, resulting in various damage mechanisms such as matrix cracking, fiber/matrix debonding, and fiber breakage [18]. Traditionally, assessing the reliability of these joints has relied on both destructive and nondestructive testing (NDT) methods across different environmental and loading scenarios. The primary goal of these methods is to monitor assembly quality and predict the progression of damage [19].
Among NDT methods, the acoustic emission (AE) technique has demonstrated exceptional effectiveness for real-time monitoring of complex composite structures [20,21,22,23]. AE captures stress wave energy, offering valuable insights into internal structural changes [24]. Additionally, the AE technique can be broadly interpreted to include applications such as counting events or locating them through spatial triangulation. However, the inherent complexity of CFRP composites often leads to internal damage that accumulates without visible surface signs, making assessment challenging [25]. While other methods such as X-ray, ultrasonic, and infrared thermography are employed, AE is distinguished by its capability to monitor damage in real time, providing a critical advantage for ongoing structural health evaluation [26].
Recent studies have advanced the understanding of damage progression in adhesively bonded composite joints using AE techniques. Li et al. demonstrated the effectiveness of AE in the real-time monitoring of CFRP joints, employing wavelet decomposition and hierarchical clustering to categorize damage mechanisms [27]. Rubio-González et al. combined AE with self-sensing carbon nanotube networks to monitor glass fiber/epoxy composites, using k-means and principal component analysis to identify various failure modes [28]. Zhou et al. applied AE to study single-lap composite joints with adhesive defects, revealing correlations between AE parameters and damage processes [29]. Mishra et al. utilized AE to assess pre- and post-damage growth in single adhesive lap joints, evaluating strain energy release rates and sound amplitude dissipation [30]. These studies collectively highlight AE’s capability to provide real-time insights into damage initiation, propagation, and classification in composite structures, offering valuable tools for structural health monitoring.
AE descriptor-based methods still require significant human intervention, complicating damage characterization in CFRP composites [31,32]. Various AE descriptors, including peak amplitude, frequency, cumulative acoustic energy, and counts, have been employed to assess damage modes [33]. However, the effectiveness of these descriptors can be limited by factors such as material properties, sample dimensions, and sensor characteristics, as highlighted by Godin et al. in their study, where they demonstrated how these variables influence the accuracy of damage assessment using AE signals [34].
Recent advancements have focused on enhancing damage characterization through innovative techniques like Laplacian scores for feature selection and k-means clustering, which help establish relationships between AE parameters [35]. Additionally, approaches such as principal component analysis (PCA) combined with frequency response function (FRF) have demonstrated potential for improving damage sensitivity and clustering outcomes in plate-like structures [36].
However, a clear research gap exists in automating the extraction of damage-sensitive features from AE signals. Automating this process would enhance the efficiency and accuracy of differentiating damage modes, enabling more precise damage detection with minimal human intervention. These advancements emphasize the need for refined methods that can fully leverage AE signals for real-time, efficient monitoring of structural integrity in complex composite materials.
This study introduces a framework that combines a deep autoencoder with AE techniques to automate the differentiation of damage modes in bonded CFRP composites. The proposed approach integrates deep learning with conventional AE methods, enhancing the monitoring of damage evolution. Mechanical tests on CFRP specimens in a joggled lap shear configuration are analyzed using this framework, which includes k-means clustering, Hilbert spectrum analysis (HHT), and Fast Fourier Transform (FFT). A comparative analysis highlights the limitations of the conventional descriptor-based approach versus the new framework.
2. Materials and Methods
2.1. Materials
2.1.1. Material Properties
The CFRP laminates were fabricated using an epoxy-carbon fiber prepreg, ER450 epoxy (SAATI CIT CC206 ER450 43%). The carbon fibers are arranged in a woven configuration, with layers of fibers overlapping one another. The adherends were cured using the autoclave method. The composite laminates for both JLS specimens (Figure 1) were cured using the autoclave method. Figure 1 illustrates the nominal dimensions of the specimens, including side and top views. Table 1 summarizes the geometric properties and material characteristics of the specimens, covering the dimensions (length, width, and thickness), number of plies, and stacking sequence for both flat and curved adherends, as well as the geometry of the overlapping adhesive region. Specifically, the flat and curved adherends have nominal lengths of 101.6 mm, widths of 26.09 mm, and thicknesses of 2.0 mm, while the overlapping adhesive region has a width of 2.0 mm and a thickness of 3.67 mm. The stacking sequences for the adherends are [+45/−45]3/−45/+45, and the nominal ply thickness is 0.244 mm.
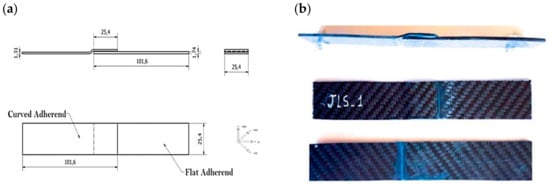
Figure 1.
(a) Nominal dimensions of the specimens and (b) side and top views of the specimen.

Table 1.
Description of geometry and properties for joggled lap shear (JLS) specimens.
The adhesive used to join the laminates is a high-strength structural adhesive characterized by a shear strength of 25 MPa and a peel strength of 65 MPa.
2.1.2. Preparation Methods
The adherends were bonded using a joggled lap shear (JLS) configuration. The adhesive was applied in accordance with the supplier’s recommendations, ensuring a uniform bondline thickness of 0.76 mm using appropriate fixtures. The adhesive was cured at a temperature of 65 °C for 1 h, followed by a post-curing interval of 5 days prior to testing. Figure 1 illustrates the JLS bonded laminates, providing both top and side views of the specimens, along with a geometrical sketch of the sample.
2.1.3. Experimental Procedures
The testing procedures adhered to ASTM D5868, which specifies methods for lap shear adhesion testing of fiber-reinforced plastics (FRP) bonded with adhesives. Dimensions of the test specimens were prepared according to the standard, with adherends cut into flat coupons of 25.4 mm × 101.6 mm (1 inch × 4 inches) and bonded with a 25.4 mm × 25.4 mm (1 inch × 1 inch) lap joint. The bondline thickness was controlled using glass beads to maintain a uniform 0.76 mm (0.03 inch) gap.
Three specimens, designated JLS1, JLS2, and JLS3, were tested under identical conditions. All specimens were subjected to tensile loading in an INSTRON servo-hydraulic testing machine with a load capacity of 100 kN. To monitor damage evolution, acoustic emission signals were collected during testing. Two R30a AE sensors (Physical Acoustics, MISTRAS Group, Princeton Junction NJ, USA), with a sensitivity range of 150 kHz to 450 kHz and a resonant frequency of 300 kHz, were affixed to the bonded adherends at a distance of 40 mm from the specimen midpoint (see Figure 2 for the testing rig setup). The AE signals were preamplified by 40 dB using an AST 2/4/6 preamplifier. Waveform data were sampled at 1 MHz to satisfy the Nyquist criterion while minimizing data volume.

Figure 2.
Testing rig with acoustic emission sensors mounted on the specimen.
2.2. Methods
2.2.1. Overall Framework
The method proposed in this work for damage mode classification is illustrated in Figure 3. Firstly, the AE signals collected from the tensile tests of the JLS specimens are used to train a deep autoencoder (DAE) model. The training process is structured into two main stages: encoding and decoding. During the encoding process, the AE signals are processed to condense their dimensions and to extract the essential features that reflect the state or changes in the signal data. This step transforms the raw data into a more compact format called latent features. Decoding, meanwhile, involves interpreting and reconstructing a representation of the original data from the condensed features obtained during encoding. In this work, the latent features obtained during encoding are extracted using singular value decomposition. These latent features are then analyzed using the k-means algorithm, and each cluster is assigned to different damage modes in the tested composite specimens. The procedure is further expanded for data validation using time-frequency analysis. The AE data reconstructed by the decoder is analyzed using Hilbert Spectrum Analysis. The architecture and hyperparameters of the DAE model are optimized for reconstruction errors and k-means loss. The details of the proposed algorithms are presented in the following sections.
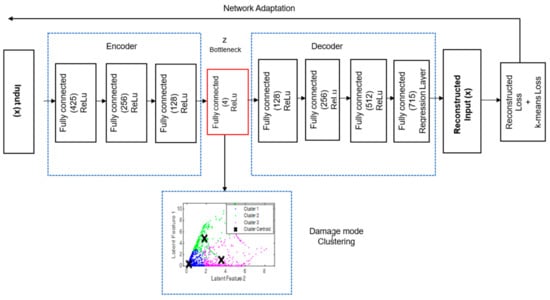
Figure 3.
An overview of the damage mode characterization framework based on deep autoencoder, k-means clustering.
2.2.2. Deep Autoencoder (DAE)
The architecture is composed of an encoder and a decoder block. The autoencoder is a specialized form of artificial neural network used to learn efficient features of unlabeled data, enabling it to estimate input variables (reconstruction) [37]. This is achieved by capturing the inherent relationships and statistical patterns between the input variables in the data [38,39]. A schematic representation of the DAE is presented in Figure 3. The graphs in the lower part of Figure 4 highly illustrate the transformation process of complex input data by a deep autoencoder. Initially, the encoder reduces the dimensionality of this data, effectively transforming it from a high-dimensional space to a more compact, lower-dimensional representation in the latent space [40]. This is achieved by extracting the most significant attributes inherent to the data. Subsequently, the data are reconstructed into a simplified output by the decoder through the learned low-dimensional information in the feature space [41]. For the autoencoder, different types of neural network architectures can be used, depending on the specific data type. For instance, the convolutional neural networks (CNNs) are suitable for extracting features from spatial data, such as images. The long short-term memory networks (LSTMs) are used for sequential data such as time-series forecasting or speech recognition because of their ability to store long-term dependencies. The dense networks, known for their simplicity, are versatile in general pattern recognition, as they are able to encode data in a compact form and reconstruct it. The architecture chosen for this study is based on fully connected (dense) neural networks, which demonstrate an exceptional ability to encode data in a reduced-dimensional space and reconstruct it with high fidelity.
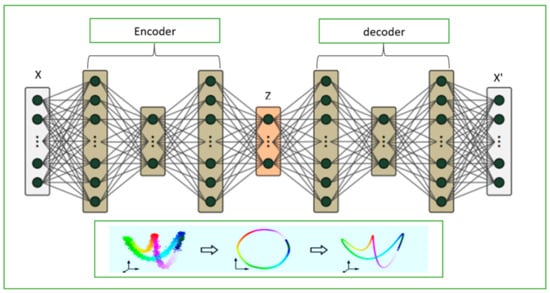
Figure 4.
Schematic of deep autoencoder model architecture.
The overview of the training parameters of the deep autoencoder model used in this study is presented in Table 2. The model architecture consists of eight layers organized into four stages: input, encoding, bottleneck, and decoding, leading to the regression output. The input dimensions of 5120 × 715 correspond to the data, where 5120 is the signal length and 715 represents the number of samples collected from AE signals measured during a tensile test. The network undergoes a compression process, reducing the number of neurons from 425 to 256, and then to 128, with ReLU activations applied at each layer to enhance feature extraction. At the core, the bottleneck layer, composed of only four neurons and a ReLU activation, captures the essential features of the data.

Table 2.
Configuration of the deep autoencoder model.
The choice of four bottleneck neurons was based on the need to strike a balance between dimensionality reduction and feature retention, ensuring the model effectively captures the most important latent features while avoiding overfitting. This configuration was optimized through experimental trials and cross-validation. Architectures with fewer than four neurons failed to capture enough variance, resulting in poor clustering, while those with more neurons introduced redundant information, with minimal additional variance (below 5%) and reduced interpretability. A key design aspect involved evaluating the reconstruction error between the input and the output reconstructed by the decoder. Since the decoder reconstructs the signal based on the compressed representation generated by the encoder, the reconstruction quality directly measures the adequacy of the bottleneck. The goal was to reduce dimensionality while preserving data quality, which was verified by minimizing the difference between the input and output signals. The selected architecture with four bottleneck neurons achieved an optimal balance, minimizing reconstruction error while maintaining interpretability and efficient data compression [42].
This approach aligns with prior research. Hinton and Salakhutdinov showed that the reconstruction quality of an autoencoder can help determine the optimal bottleneck size [42]. Kramer emphasized the importance of maintaining data quality during dimensionality reduction [43], and Rifai et al. demonstrated how compact bottleneck representations improve feature robustness and interpretation [44].
The model then transitions into an expansion phase, where neuron counts increase from 128 to 425 across three layers, each with a ReLU activation, reconstructing the data around the compressed features from the bottleneck. The final layer, with 715 neurons, produces the regression output. The output dimensions match the input, illustrating the network’s ability to handle complex regression tasks, including compression and expansion.
Hyperparameters such as the number of layers, activation functions, and learning rates were fine-tuned using grid search to optimize reconstruction accuracy and clustering performance, further validating the chosen architecture.
The encoding process effectively transforms the input, denoted as , into a compact hidden representation , and this process can be expressed as follows:
In Equation (1), is the activation function of the rectified linear unit (ReLu) that represents the nonlinear mapping between the input and the output , from the input layer to the fourth layer, with as the weight matrix and as the bias vector, respectively. The dimensionality of inputs decreases in proportion to the number of neurons in the bottleneck hidden layer, where the dominant features that represent information content in the input data are automatically extracted [45]. Subsequently, the decoder utilizes the bottleneck hidden layer to reconstruct the initial input through mapping by the activation function Relu .
where and are the output and input from the fourth layer to the eighth layer in the decoder network, and its parameters include the weight matrix and offset vector . Consider a scenario in which we have raw data , where each row represents an individual sample within a collection of samples. In the training process, the root mean squared error (RMSE) metric is used for a given collection containing data points. The primary objective of the loss function is to minimize the discrepancy between the reconstructed output and the original input .
With is the i-th reconstructed sample.
The latent feature from the bottleneck layer is used for classifying the damage modes. This process is explained in detail in the subsequent sections.
2.2.3. Latent Feature Clustering Using K-Means
In this research, k-means clustering is used to group latent features of the AE signals generated by the composites tested. As mentioned earlier, these latent features are taken from the bottleneck layer of the DAE. The main objective is to assign the latent features to the different damage modes in the tested JLS specimens. K-means clustering is based on assigning each datapoint in the dataset to each cluster by calculating the minimum distance between the datapoint and the cluster centroid. The objective of the k-means clustering in Equation (4). serves as the representative of the cluster , and forms the set of representatives. The functions define distance metrics within .
In Equation (4), . quantifies the distance between an object and its latent feature representation ; it is the function that assigns the closest feature to the cluster. To update the autoencoder for k-means compatibility, meaning to ensure that data points are evenly distributed around cluster centers, Yan et al. [36] proposed the following cost function:
where is the total clustering loss for the latent features, is the number of data points, represents a set of latent features, is a cluster center and is a Boolean variable that assigns with . Minimizing this loss with respect to the network parameters ensures that the distance between each data point and its assigned cluster center is small, improving the clustering quality when applying k-means.
In addition to this, the unsupervised k-means clustering is also used to analyze the AE descriptors for the damage characterization of the JLS specimens [46,47,48,49,50].
3. Results and Discussions
3.1. Mechanical Test Results
The mechanical characterization of the damage modes of JLS specimens was carried out through a series of tensile tests, following the recommendations of the ASTM D5868 standard [51]. Two critical points can be identified from the mechanical results presented in Figure 5: the maximum load at initial failure, which indicates the onset of damage, and the maximum load at final failure, which represents the complete failure of the specimen. Although the three specimens share similar material characteristics, their peak load values differ significantly. This finding has been observed by several authors on the bonded specimen, such as Avila et al., Liu et al., Adin et al., and Kadioglu et al. [52,53,54,55]. This variation can be attributed to a series of factors such as overlap length, adhesive thickness, and scarf angle.
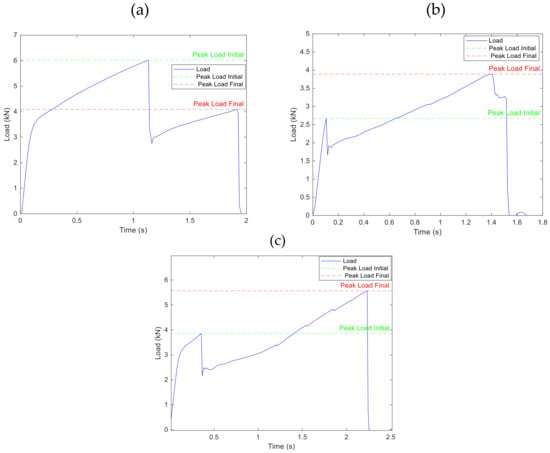
Figure 5.
(a) Mechanical properties of JLS1 specimen, (b) Mechanical properties of JLS2 specimen, (c) Mechanical properties of JLS3 specimen.
These researchers unanimously recognized the significant impact of these factors on the performance of joined composites under static stress. Adin et al. revealed that modifying joint dimensions could reduce maximum stress [54]. Meanwhile, Silva et al. observed that the use of hand-mixed adhesives in CFRP composites could introduce geometric variations in the bonded areas, affecting their load-bearing capacity. They also noted the importance of surface treatment, temperature, and exposure to hostile environments, highlighting their effect on load performance [56]. Manohar et al. highlighted that the choice of adhesive and bonding agent, overlap length, and pretreatment methods influence joint strength [57]. Kowatz et al. discussed that the reduced shear strength in composite structures is attributed to the uneven shear stress distribution and found less resilience to fatigue under repeated loading [58]. Lu et al. explored the effect of the number of CFRP layers and bonding mode on the mechanical properties of composites [59,60]. One of their works reported an improvement in load-bearing capacity and stiffness with an increase in the number of layers [60], while the other found that the double-sided reinforcement was effective [59]. Karachalios et al. found that the adhesive thickness strongly affects joint strength, with thicker adhesives giving stronger joints [61]. Martínez et al. concluded that the shear stress in single-lap joints is mainly affected by the thickness of the adhesive [61], while the deformation, elastic modulus, and absorbed energy are influenced by the overlap length [62]. In summary, these studies demonstrate that variation in the mechanical properties in bonded composites can be attributed to the following factors: interface strength, adhesive thickness, presence of defects, and bonding method. In addition, they collectively highlight the complex interplay of these factors that could lead to the variations in the failure loads. The JLS 1 specimen withstood a considerably higher initial load than the JLS 2 and JLS 3 specimens. In particular, specimen JLS 2 showed low resistance to initial and final fracture (see Figure 5a–c).
3.2. Results of Deep Autoencoder Training
The AE signals acquired from the mechanical testing of the bonded composites are used to train the modeled DAE. During the training phase, the DAE is engaged in accurately reconstructing the AE’s input signals. AE signals collected from JLS1, JLS2, and JLS3, each containing waveforms of length 5120 samples, were used to train and evaluate the model. The dataset contains 715 waveforms from JLS1, 393 waveforms from JLS2, and 827 waveforms from JLS3. The variation in the number of extracted waveforms across samples can be attributed to the manual bonding process of the adhesive, which introduces variability in adhesive thickness, void distribution, and bond uniformity. During the training process, the DAE reduced the dimension of the waveform into a low-dimensional space of four latent features at the bottleneck layer through the encoder. Then, it is decoded using the trained weights in the decoder layers to restore it to its original state. The k-fold cross-validation is used to improve training and validation by dividing the dataset into k = 10 subsets (or “folds”). At each training iteration, k − 1 datasets are used for training, while one remaining dataset is reserved for validation. This approach aims to reduce bias by using the majority of data for training in all k iterations. This process is performed on a PC with a speed of 2.92 GHz and a RAM of 16.0 GB.
The hyperparameters for this DAE training were designed to optimize the model’s performance. To achieve a balance between model convergence and the prevention of overfitting, training is continued for 250 epochs. The mini-batch size of 128 improves the efficiency of the computation and the stability of the gradient. Data shuffling is included at the start of each epoch, which maintains diversity within the mini-batches. Validation is repeated for every 15 mini-batches. A learning rate of 0.001 is used to ensure smooth convergence. To enhance the learning process, a piecewise learning rate schedule is implemented, which reduces the learning rate by a factor of 0.7 every 20 epochs (refer to Table 3). Figure 6a, Figure 6b, and Figure 6c each illustrate an example of an original signal and its reconstructed signal from specimens JSL1, JSL2, and JSL3, respectively. These plots provide a visual comparison between the input signals and their corresponding reconstructed signals, demonstrating the effectiveness of the reconstruction process. The signals are presented in both the time and amplitude domains, allowing for a clear assessment of the reconstruction quality. The reconstruction error for each parametric study case was measured by root-mean-square error (RMSE) to assess the respective performance (see Figure 7). For JLS1, the average RMSE is approximately 0.170045. For JLS2, the average RMSE error is approximately 1.107225. Finally, for JLS3, the mean RMSE error is approximately 0.671855. The RMSE values reflect the reconstruction quality of the signals for each sample. A lower RMSE indicates better reconstruction quality, while a higher RMSE suggests larger discrepancies between the original and reconstructed signals. These values provide insight into how accurately the signal reconstruction process performs for each specimen. The main objective was to extract latent features that represent high-dimensional input data containing information about the damage mechanism of specimens under load and reduce them to low-dimensional features retaining the same information. To ensure efficiency, it is essential that the RMSE error is low, indicating that the model can reconstruct the data accurately, closely reflecting the original input. It should be noted that, in some cases, DAE is also used to reduce noise in the data [63].

Table 3.
Training parameters of the deep autoencoder model.
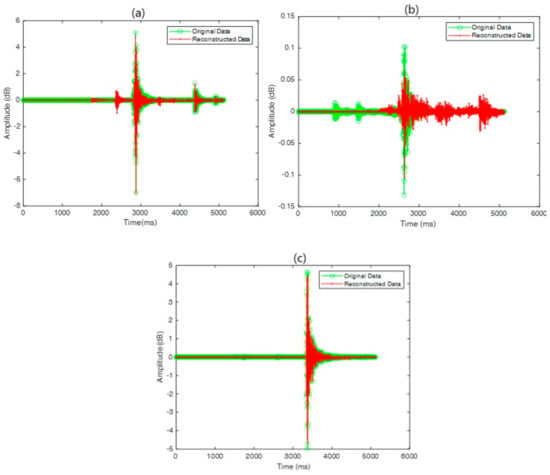
Figure 6.
Original and reconstructed signal based on deep autoencoder for (a) JLS 1; (b) JLS 2; and (c) JLS3.
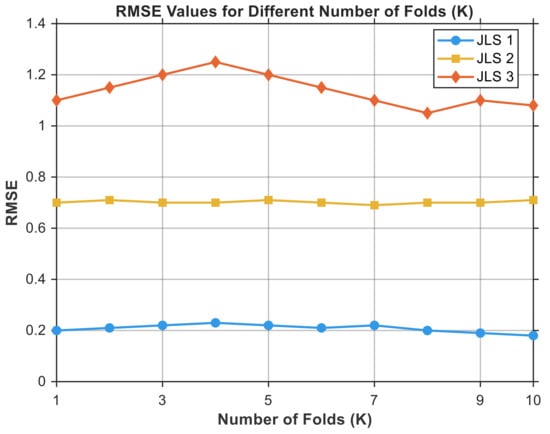
Figure 7.
Effect of cross-validation folds (K) on RMSE values for different specimen types.
Damage Characterization Using Latent Features
The latent features from the bottleneck layer are used for damage clustering. Singular value decomposition (SVD) is employed to select the most significant latent features that best reflect the original signal data. In this study, the threshold is set at 80% of the cumulative variance to identify the dominant latent features. Figure 8a shows that the dominant singular value for the JLS1 specimens is two, explaining 95.8% of the variance. Similarly, for JLS2, 81.1% of the variance is explained by the dominant singular value (Figure 8b), and for JLS3, the dominant value explains 80% of the variance (Figure 8c).
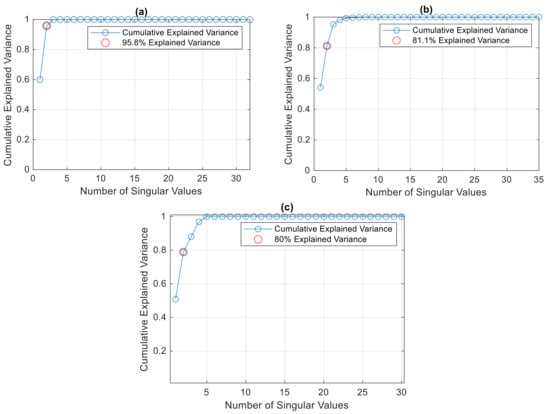
Figure 8.
Selection of dominant features from the bottleneck layer by SVD: (a) JLS1; (b) JLS 2; and (c) JLS3.
The dominance of these singular values is critical, as it demonstrates that a small number of latent features can explain a significant proportion of the total variance in the data. This indicates that these features effectively capture the essential characteristics of the original AE signals, allowing for efficient clustering and damage mode classification. The high variance explained by the selected singular values confirms the effectiveness of the SVD approach in reducing the dimensionality of the data, while preserving the most important information for subsequent damage analysis.
The unsupervised k-means pattern recognition algorithm was used to examine the selected latent features. In this context, the Silhouette criterion is used to assess cluster quality by comparing the similarity of an object within its own cluster against its similarity to the objects in other clusters. A higher Silhouette score is indicative of a model characterized by well-delineated clusters. The Silhouette criterion returns k = 3 as the optimal number of clusters (see Figure 9a–c). This finding implies that the three-cluster model contains significant intracluster homogeneity and distinct intercluster separation and, therefore, is capable of elucidating the inherent structure of the dataset.
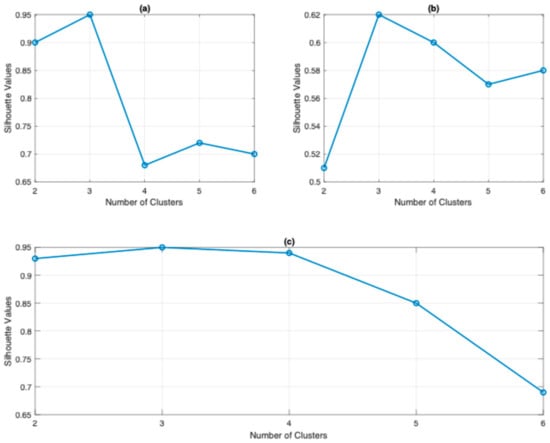
Figure 9.
Silhouette values of clusters for latent features of (a) JSL1; (b) JLS 2; and (c) JLS3.
Figure 10a–c illustrate each latent feature clustered from specimens JLS1, JLS2, and JLS3, respectively. The three distinct clusters of latent features reflect different damage modes observed during mechanical testing.
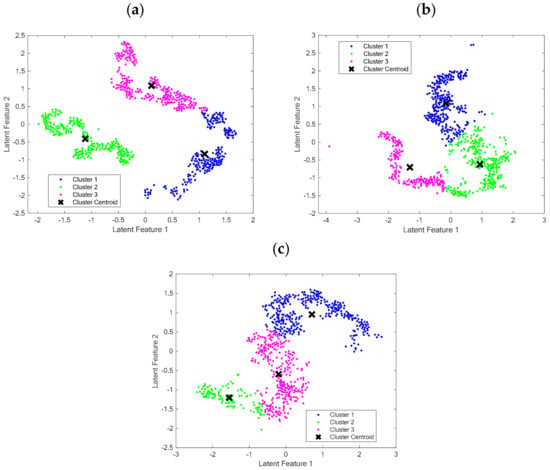
Figure 10.
Latent features clustered by the k-means algorithm for (a) JLS 1, (b) 2, and (c) 3.
Recent studies have applied various forms of autoencoders, including deep convolutional, variational, and stacked autoencoders, for damage detection in different materials [64,65]. The methods have demonstrated improvements in the automated detection and classification of damage mechanisms. Despite these advances, the relationship between latent features and specific damage modes remains unexplored. This represents a significant gap that limits our understanding of damage mechanisms. To address this limitation, the model proposes analyzing the AE waveforms corresponding to the clustered data points. These analyses are carried out on the corresponding signals reconstructed by the decoder. Therefore, a frequency-domain analysis of the waveforms is performed using a fast Fourier transform. The objective is to accurately identify the frequency characteristics responsible for damage modes in bonded composite specimens.
All waveforms analyzed were randomly selected to ensure a balanced representation of the data for analysis. The examination of the JLS 1 specimen is illustrated in Figure 11. The spectrum for Cluster 1 shows a prominent peak near 100 kHz, with other lower peaks up to about 300 kHz. The highest peak is slightly above 4 × 10−4 dB. The frequency spectrum of Cluster 2 has a peak at approximately 250 kHz, with other minor peaks extending up to 300 kHz. The peak amplitude is slightly above 3 × 10−4 dB. Cluster 3 shows multiple high peaks, especially at approximately 300 kHz and extending beyond, up to 500 kHz. The amplitude in this spectrum is significantly higher, reaching approximately 0.5 dB.
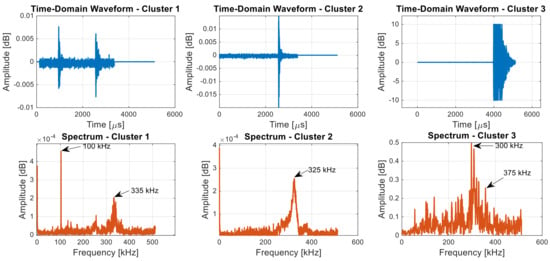
Figure 11.
Typical AE frequency domain waveforms from JLS 1: Cluster 1; Cluster 2; and Cluster 3 based on latent feature.
The frequency analysis of the AE signals from the JLS 2 is shown in Figure 12. The spectrum of the cluster 1 shows a dominant peak at approximately 170 kHz, with other smaller peaks spreading up to approximately 300 kHz. The peak amplitude reaches approximately 3.5 × 10−4 dB. The spectrum of Cluster 2 shows a peak around 250 kHz, with additional marks distributed between 335 and 350 kHz. The peak amplitude is approximately 1.2 × 10−3 dB, which is significantly higher than Cluster 1. Cluster 3 shows significant activity in the frequency range of 100 to 500 kHz, with several high peaks, particularly approximately 300–450 kHz. The amplitude reaches approximately 0.2 dB, indicating a strong and energetic waveform.
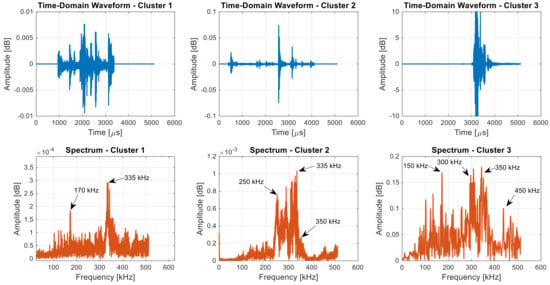
Figure 12.
Typical AE frequency domain waveforms from JLS 2: Cluster 1; Cluster 2; and Cluster 3 based on latent feature.
In the case of specimen JLS3, as shown in Figure 13, the frequency spectrum for Cluster 1 reveals multiple peaks, with the most prominent ones occurring below 135 kHz and several smaller peaks extending up to 315 kHz. The maximum amplitude observed is approximately 3 × 10−4 dB, indicative of relatively low-intensity acoustic emissions. Cluster 2 exhibits a distinct peak at approximately 325 kHz, with a dominant frequency band spanning from 300 to 375 kHz and an amplitude reaching approximately 1 × 10−3 dB. This increase in frequency and amplitude suggests more significant damage, such as interfacial debonding, which tends to produce acoustic emissions within this frequency range due to the dynamic separation at the interface, releasing more energy compared to matrix cracking.
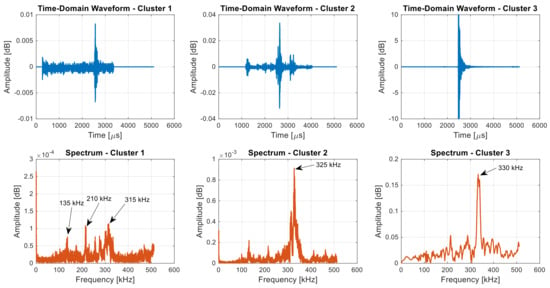
Figure 13.
Typical AE frequency domain waveforms form JLS 3: Cluster 1; Cluster 2; and Cluster 3 based on latent features.
The frequency spectrum for Cluster 3 is characterized by a prominent peak at approximately 330 kHz, with other significant frequencies up to 500 kHz. The amplitude reaches approximately 0.2 dB, reflecting more intense acoustic emissions. This behavior is typical of fiber breakage, involving a higher release of strain energy due to the brittle nature of carbon fibers and the high energy release during a rupture. These observations indicate that higher frequency and amplitude signals are characteristic of severe damage modes, such as fiber breakage.
The AE frequency analysis of specimens JLS 1, JLS 2, and JLS 3 provides insights into the progression of damage mode mechanisms in CFRP bonded by adhesive under tensile loading conditions. Each specimen demonstrates a distinct pattern of AE signal frequencies and amplitudes across three damage clusters, revealing the different stages of structural damage.
Three primary frequency ranges correspond to matrix cracking, fiber-matrix debonding, and fiber breakage. Cluster 1 in each specimen, with lower frequencies, is associated with matrix cracking and initial adhesive peeling, marking the onset of structural degradation. This is consistent with observations by De Groot et al., who identified low-frequency AE signals as indicative of matrix cracking due to the brittle nature of matrix microcracks [66]. Other studies, including our previous work, also confirm that matrix cracking typically produces low-frequency emissions within this range [67].
Cluster 2, observed within the 250–375 kHz range across specimens, corresponds to fiber-matrix debonding or interfacial debonding, representing intermediate damage as the adhesive layer’s integrity deteriorates under stress. This frequency range aligns with reports in the literature that associate 250–350 kHz and 250–375 kHz frequency bands with matrix/fiber debonding [68]. The predominant frequency band for a large number of signals in each JLS specimen was centered at approximately 250–375 kHz, suggesting that the load was transmitted through the adhesive layer, thereby initiating interlaminar crack growth and generating acoustic events.
Cluster 3, characterized by high frequencies between 300 and 500 kHz, is associated with fiber breakage, indicating catastrophic failure and the final stage of damage in the bonded CFRP specimens. This observation correlates with established findings in CFRP literature, where frequencies in the 400–500 kHz range are linked to fiber breakage and interlaminar cracking [68,69]. Studies using supplementary techniques such as Digital Image Correlation (DIC) have validated that fiber rupture or pull-out events typically generate high-frequency AE signals within this range. For example, recent work by Andraju and Raju has categorized delamination and fiber pullout within 400–600 kHz, while fiber failure is observed above 600 kHz [35]. Similarly, Mahesh et al. identified interface failure within the 270–400 kHz range, with fiber breakage occurring at higher frequencies in open-hole CFRP laminates under tension-shear loading [32].
Our findings are further supported by studies on different CFRP configurations and adhesive applications. For instance, Ali et al. associated matrix cracking (50–180 kHz), interface failure (180–400 kHz), and fiber breakage (400–670 kHz) in woven carbon fabric laminates under flexural loading [70]. Zarouchas and Hemelrijck’s work on thick adhesives in wind turbine blades revealed microcracks between 80 and 110 kHz, matrix macrocracks between 210 and 280 kHz, and fiber breakage in the 410–480 kHz range [71]. These comparisons underline a consistent correlation between specific AE frequency bands and particular damage modes in CFRP structures, reinforcing the validity of the AE analysis performed on JLS specimens in this study. Although this new approach has been developed, the old method will also be included. Therefore, a complementary study based on damage mode characterization using AE features will be discussed.
3.3. Damage Characterization Using AE Feature
The second part of the damage characterization uses AE descriptors, the amplitude and entropy. The amplitude and entropy of the AE signals from the JLS specimens are clustered using the k-means algorithm. These features are often used to effectively characterize materials, including CFRP composites subjected to mechanical loading [72]. In the context of our study, the choice of amplitude and entropy descriptors for AE signal analysis is dictated by their ability to provide distinct and complementary insights into the dynamics of failure events [67]. The entropy characterizes the uncertainty or disorder of the signal data, thereby enabling a qualitative analysis of failure structures. Recently, several key studies have demonstrated the effectiveness of entropy in AE analysis. For example, Burud et al. have demonstrated that wavelet entropy can effectively estimate spectral disorder in the AE signals, providing valuable information on fracture processes in concrete [73]. The use of entropy and amplitude thus enriches our understanding of failure mechanisms. The integration of these two measures significantly enhances the ability to distinguish between different types of damage, facilitating the characterization and classification of failure modes in CFRP composites. However, it is important to note that this method may not be universally applicable in all situations, and there are certain limitations when applying it to the current analysis. As explained in the previous subsection, the Silhouette criterion is applied to determine the optimal number of clusters. Figure 14a–c illustrate the Silhouette coefficient analysis, a widely used metric for evaluating cluster quality and determining the optimal number of clusters in partitional clustering algorithms like k-means [74]. The Silhouette coefficient assesses both cohesion within clusters and separation between clusters, with values ranging from −1 to 1. Higher scores indicate better-defined clusters [75]. These figures show that three clusters provide the highest Silhouette scores, suggesting that this configuration yields the most coherent and well-separated clusters.
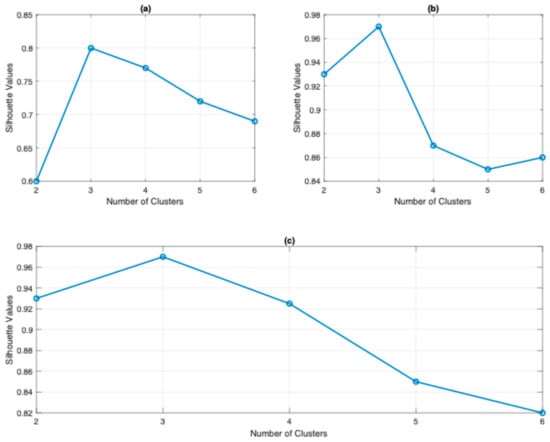
Figure 14.
Silhouette values of AE features of (a) JSL1; (b) JLS 2; and (c) JLS3.
In Figure 15 and Table 4, cluster assignments for specimens JLS1, JLS2, and JLS3 are presented. For specimen JLS1, the first cluster exhibits a low amplitude range of 40–48 dB and an entropy distribution from 0.01 to 1.54, indicating initial damage, such as microcracks. Cluster 2, with an amplitude range of 49–65 dB and entropy from 0.02 to 1.01, suggests damage progression, with signs of interlaminar cracks. The third cluster, spanning 67–99 dB in amplitude and 0.03–0.8 in entropy, reveals severe damage, possibly indicating critical failure. The specimen JLS2 exhibits damage beginning with a first cluster ranging from 40 to 58 dB in amplitude and 0.03–2.10 in entropy, suggesting a more varied initiation of damage, potentially due to debonding or microcracking. The second cluster, displaying an amplitude of 59–78 dB and an entropy of 0.02–1.35, indicates a progression towards moderate damage. The third cluster, from 79 to 100 dB in amplitude and 0.07–1.03 in entropy, denotes critical damage, with a strong indication of fiber breakages, signaling an advanced stage of structural degradation. For JLS3, the first cluster reveals an amplitude of 40–53 dB and an entropy distribution of 0.01–2.59, highlighting a wide range of initial damages, from minor debonding to various microcracks. The second cluster, with an amplitude of 54–75 dB and an entropy of 0.02–1.88, shows signs of more serious damage, likely more complex and extensive matrix cracking. Finally, the third cluster, with amplitudes of 76–100 dB and entropy of 0.04–1.52, signals very severe damage, such as fiber ruptures, indicating the most critical phase of degradation. The initial observation is that there are three modes of damage for each specimen, each with a slightly different distribution. This variation can be attributed to the fact that the adhesive used for these specimens was applied manually. Liu et al. identified acoustic emission amplitudes for matrix cracking as 50–60 dB, delamination, 60–80 dB, interface failure, 50–70 dB, and fiber breakage, 80–90 dB in fiber-reinforced composites [76]. Zhuang and Yan’s study on polyethylene composites reported similar amplitudes: matrix cracking below 60 dB, delamination 60–85 dB, interface failure 30–45 dB, and fiber breakage 80–97 dB [77]. Barre and Benzeggagh found in glass/polypropylene composites amplitudes of 40–55 dB for matrix cracking, 65–85 dB for delamination, 60–65 dB for interface failure, and 85–95 dB for fiber breakage [78]. Based on these observations, a hypothesis can be formulated. In Table 4, the clustered AE feature entropy versus amplitude may indicate different damage processes. Cluster 1 represents AE signals generated by matrix cracking; Cluster 2 represents signals from delamination events; and Cluster 3 represents signals from fiber breakage.
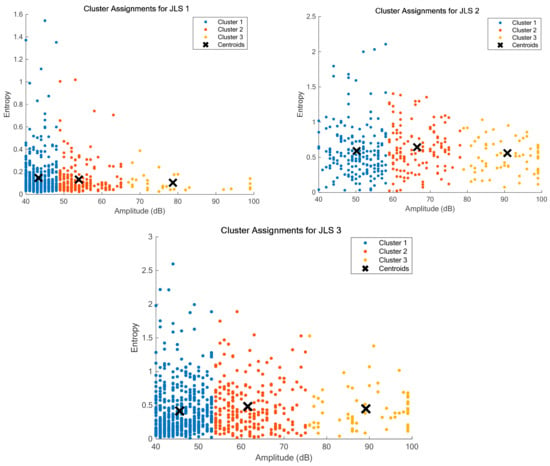
Figure 15.
Cluster assignments between amplitude and entropy for specimens: JLS1; JLS2; and JLS3.

Table 4.
Entropy and amplitude cluster ranges across all specimens.
In this study, time-frequency analysis based on HSA is used to support this hypothesis. Previous research has identified CFRP specimen damage modes based on frequency range and the instantaneous energy of AE waveforms [79].
In the literature, many authors have investigated structural damage using frequency and time-frequency analyses [80]. In this subsection, the analysis relies on Hilbert spectral analysis for further exploration. At random, AE signals are extracted for each cluster and specimen for detailed analysis. The observed spectrum naturally exhibits distinct frequency distributions, complementing previously identified AE features by providing additional insights from the complete frequency-time distribution. This approach offers a more comprehensive understanding of the AE signals and their correlation with various damage modes. As mentioned earlier, HSA is used as a signal-processing technique to extract relevant characteristics from AE waveforms [81]. In Figure 16, instantaneous energy is concentrated between 250 and 375 kHz at 2 ms (Figure 16a). This concentration indicates that the initial stages of damage in this specimen begin in the frequency range of 250 to 375 kHz, which is typical for interfacial debonding and crack growth, as discussed earlier in the section. In the second HSA, the energy is focused between 300 and 350 kHz at 2 ms (Figure 16b). This narrower concentration compared to the first HSA suggests a more localized damage evolution within a tighter frequency band, which may be associated with matrix cracking or delamination. The third has, the spectrum shows higher instantaneous energy, with concentration from 250 to 390 kHz at 2 ms (Figure 16c). The fact that this range exceeds the 375 kHz range from the first and second HSAs indicates an intensification of the energy and more severe degradation. This could suggest that damage has progressed further, affecting the adhesive and fibers more significantly.
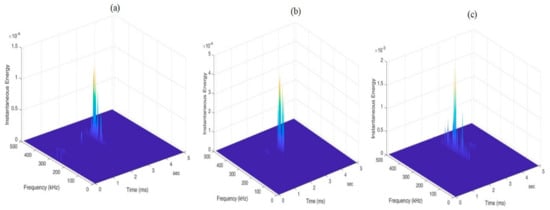
Figure 16.
Typical AE frequency domain waveforms from JLS 1: (a) Cluster 1; (b) Cluster 2; and (c) Cluster 3.
A progressive increase in instantaneous energy from the first to the third HSA is observed, confirming that the damage intensifies across similar frequency ranges, but with variations in energy levels depending on the progression of damage.
Figure 17 presents the HSA of specimen JLS2. The first HSA: At 2.5 ms, energy is concentrated between 275 and 375 kHz, with spectral lines at 1.5 ms and 3.4 ms showing low energy (Figure 17a). This suggests that, while the damage starts in a frequency range similar to that in JLS1, it is in an earlier or more moderate phase, with lower energy transfer. The second HSA: Energy is concentrated between 300 and 350 kHz at 2.2 ms, with a spectral line of approximately 3 ms exhibiting medium energy (Figure 17b). This narrower concentration and moderate energy level suggest an amplification of damage at a later stage, possibly linked to delamination or cracking mechanisms becoming more pronounced at this stage. The third HSA: The spectrum extends from 250 to 375 kHz at 4.8 ms, showing greater energy concentration (Figure 17c). This indicates that the damage has progressed to a more advanced stage, where the interaction between different failure modes (crack growth and delamination) is more prominent.
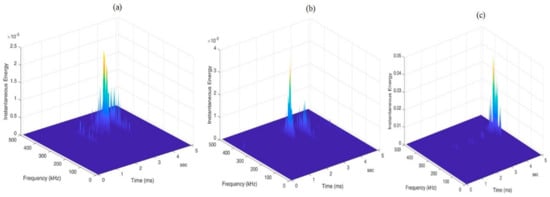
Figure 17.
Typical AE frequency domain waveforms from JLS 2: (a) Cluster 1; (b) Cluster 2; and (c) Cluster 3.
Figure 18 shows the HSA for the signals from specimen JLS3. The first HSA: The frequency range is from 275 to 375 kHz at 2 ms, as shown in Figure 18a. This behavior is similar to the first cluster from the other specimens, indicating a general trend of damage initiation in this frequency range. The second HSA: The spectrum narrows to the range of 300–350 kHz at 2 ms (Figure 18b). A more concentrated focus in this band suggests a more targeted and localized damage at this stage of material behavior. The third HSA: Similar to the first cluster, this HSA shows a frequency range of 250–375 kHz at 2 ms (Figure 18c). This indicates that, despite the variations in instantaneous energy observed, the spectral shape remains relatively constant over time. This similarity to other specimens for the first cluster reinforces the idea that the initial damage follows a similar pattern between specimens.
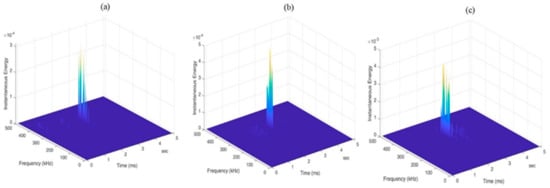
Figure 18.
Typical AE frequency domain waveforms from JLS 3: (a) Cluster 1; (b) Cluster 2; and (c) Cluster 3.
Through these figures, it can be observed that a concentration of instantaneous energy in the range of 250–375 kHz for all specimens confirms that the dominant damage modes in the JLS specimens are primarily related to interfacial debonding and crack growth. The increase in instantaneous energy and the time shift of peaks in the different figures indicate that damage progresses with more intensity over time, with variations in frequency concentration and energy levels.
This also suggests that the load transmission mechanism through the adhesive layer is the main factor driving damage progression, with a strong likelihood of delamination, matrix cracking, and fiber breakage, which are the most common failure modes observed in these specimens.
3.4. Fractographic Analysis
The damage mechanisms identified through AE signal analysis matrix cracking, fiber-matrix debonding (or interfacial debonding), and fiber breakage were confirmed through fractographic analysis, providing a comprehensive view of failure progression in the JLS specimens. Fractographic examination post-failure corroborated these mechanisms, revealing specific structural features associated with each damage mode.
Matrix cracking, initially detected as lower-frequency AE signals, was identified as the first stage of damage. This mechanism typically involves the formation of microcracks within the matrix material, marking localized stress concentrations that set the stage for further damage progression. Fractographic analysis showed that initial adhesive peeling occurred at the knee of the bend in the overlap region (see Figure 19a), suggesting that mechanical stress concentrates in this area, leading to early adhesive debonding under tensile load. This peeling and microcracking weaken the bond between the adhesive layer and CFRP laminates, initiating interfacial crack growth, a critical damage mode highlighted by acoustic emissions in the 250–375 kHz frequency range.

Figure 19.
Fractographic analysis of CFRP bonded in JLS (a) peeling at the knee of adhesive; (b) delamination along the boundary of the adhesive layer interface; (c) fiber breakage; (d) fiber/matrix debonding.
As matrix cracking and adhesive peeling progress, the bond between the matrix and fibers deteriorates, resulting in fiber-matrix debonding or interfacial debonding (see Figure 19d). Fractographic evidence supported this observation, showing compromised integrity of the adhesive layer and leading to laminate debonding, as illustrated in Figure 18b. This interfacial separation detected by AE signals in the mid-frequency range corresponds to a stage where the laminates are no longer fully bonded, creating a higher risk of delamination. The fractographic analysis confirmed this delamination, revealing that, as peeling and debonding advance, individual fibers become exposed to irregular forces. These forces are not fully supported by the matrix, increasing susceptibility to rupture.
The Delamination along the boundary of the adhesive layer interface is observed in Figure 19b. The adhesive not only detached from the lamina but also triggered fiber/matrix debonding within the same layer. Figure 19c provides a magnified view of the circled region in Figure 19b.
The final stage of damage, fiber breakage, is marked by high-frequency AE signals. Fractographic evidence in Figure 19c shows fiber breakage at the end of the lamina, where exposed fibers fail under unbalanced forces as matrix support diminishes. The combination of fiber-matrix separation and initial fiber breakage exacerbates the problem of fiber-matrix adhesion, leading to a complete breakdown in the load-bearing capability of the composite. These findings confirm that fiber breakage is the ultimate mode of failure in the JLS specimens, coinciding with the highest recorded AE frequencies and corresponding to catastrophic structural failure. The AE results, confirmed by fractographic analysis, establish interfacial debonding and interlaminar crack growth as the primary failure mechanisms in the JLS specimens. The majority of AE signals, centered in the 250–375 kHz band, indicate that load transmission primarily occurs through the adhesive layer, with interfacial crack growth responsible for most acoustic activity. The convergence of acoustic and visual data underscores the significant role of adhesive integrity in load transmission, with interfacial cracking emerging as a key indicator of structural damage in adhesively bonded CFRP composites.
4. Conclusions
This study focused on characterizing damage modes in adhesively bonded CFRP composites under mechanical loading through the analysis of acoustic emission (AE) signals. A deep autoencoder (DAE)-based framework was introduced to automate the damage characterization process, significantly improving the precision of AE signal analysis. The DAE reduced the dimensionality of the AE signals, extracting latent features via singular value decomposition (SVD). These features were analyzed using the k-means clustering algorithm, which successfully identified three primary damage modes: matrix cracking, interfacial debonding, and fiber breakage. The accuracy of these findings was validated using Hilbert Spectral Analysis (HSA) and Fast Fourier Transform (FFT), further corroborating the effectiveness of the DAE approach.
A predominant frequency band between 250 kHz and 375 kHz was observed across all specimens. This frequency range reflects the role of the adhesive layer in transmitting the load, with AE signals primarily originating from interfacial crack growth within this layer. The identified damage modes were consistent with fractographic analysis, which revealed crack initiation and growth at the adhesive interface, leading to fiber-matrix separation and adhesive peeling.
While the study highlighted the effectiveness of both traditional and innovative methods in damage detection, it also underscored the complexity of characterizing CFRP damage. Variations in the frequency content within each damage mode suggest that current methodologies may not fully capture all the damage signatures. This indicates the need for a more integrated approach, combining conventional AE features with advanced analytical techniques to improve damage mode identification.
The integration of deep learning-based techniques like DAE with traditional acoustic emission methods holds significant potential for enhancing damage characterization in CFRP composites. This hybrid approach will refine the understanding of complex damage modes and improve the accuracy of predictive models, contributing to the optimization of CFRP composites in automotive and other high-performance applications.
Author Contributions
Conceptualization D.K.M.; methodology, C.B., D.K.M. and G.P.; software, D.K.M.; validation, C.B., D.K.M. and G.P.; formal analysis, C.B., D.K.M. and G.P.; investigation, C.B., D.K.M. and G.P; resources, C.B. and G.P.; data curation, C.B. and D.K.M.; writing—original draft preparation, D.K.M.; writing—review and editing, C.B., D.K.M. and G.P.; visualization, D.K.M.; supervision, G.P. and C.B.; project administration, CC.; funding acquisition, C.C. All authors have read and agreed to the published version of the manuscript.
Funding
C.B., G.P. and D.K.M. would like to acknowledge the following funding. The project is funded under the National Recovery and Resilience Plan (PNRR), Mission 4 Component C2 Investment 1.1—Call for Proposals for the development of “Projects of Significant National Interest” (PRIN)—2 February 2022—D.D. No. 104/2022 PRIN 2022. Award number: 2022JFMPSC—INnovative damage MOnitoring Of Self-HEAling Composites by acoustic emissions in civil and aerospace Applications—IN MOOSHEAC—Grant n. CUP: D53D23003600006—Politecnico di BARI. C.C. would like to acknowledge the following funding. The project is funded under the National Recovery and Resilience Plan (PNRR), Mission 4 Component C2 Investment 1.3—Italian Ministry of University and Research funded by the European Union—NextGenerationEU. Award Number: CNMS named MOST, Concession Decree No. 1033 of 17 June 2022 adopted by the Italian Ministry of University and Research, CUP: D93C22000410001, Spoke 11 “Innovative materials and lightweighting”.
Data Availability Statement
The data used in the research work is available upon request to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chou, C.W.; Liao, W.C.; Wu, S.; Wee, H.M. The Role of Technical Innovation and Sustainability on Energy Consumption: A Case Study on the Taiwanese Automobile Industry. Energies 2015, 8, 6627–6640. [Google Scholar] [CrossRef]
- Jobson, E. Future Challenges in Automotive Emission Control. Top. Catal. 2004, 28, 191–199. [Google Scholar] [CrossRef]
- Mayyas, A.T.; Mayyas, A.R.; Omar, M. Sustainable Lightweight Vehicle Design: A Case Study in Eco-Material Selection for Body-in-White. In Lightweight Composite Structures in Transport: Design, Manufacturing, Analysis and Performance; Woodhead Publishing: Sawston, UK, 2016; pp. 267–302. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, J. Advanced Lightweight Materials for Automobiles: A Review. Mater. Des. 2022, 221, 110994. [Google Scholar] [CrossRef]
- Ahmad, H.; Markina, A.A.; Porotnikov, M.V.; Ahmad, F. A Review of Carbon Fiber Materials in Automotive Industry. IOP Conf. Ser. Mater. Sci. Eng. 2020, 971, 032011. [Google Scholar] [CrossRef]
- Alaneme, K.K.; Fajemisin, A.V.; Maledi, N.B. Development of Aluminium-Based Composites Reinforced with Steel and Graphite Particles: Structural, Mechanical and Wear Characterization. J. Mater. Res. Technol. 2019, 8, 670–682. [Google Scholar] [CrossRef]
- Liu, X.; Tian, S.; Tao, F.; Yu, W. A Review of Artificial Neural Networks in the Constitutive Modeling of Composite Materials. Compos. B Eng. 2021, 224, 109152. [Google Scholar] [CrossRef]
- Sugita, Y.; Winkelmann, C.; La Saponara, V. Environmental and Chemical Degradation of Carbon/Epoxy Lap Joints for Aerospace Applications, and Effects on Their Mechanical Performance. Compos. Sci. Technol. 2010, 70, 829–839. [Google Scholar] [CrossRef]
- Ballo, F.M.; Gobbi, M.; Mastinu, G.; Previati, G. Structural Optimisation in Road Vehicle Components Design. Optim. Lightweight Constr. Princ. 2021, 233–270. [Google Scholar] [CrossRef]
- Romero, C.A.; Correa, A.; Echeverri, E.A.; Vergara, D.; Romero, C.A.; Correa, P.; Anderson, E.; Echeverri, A.; Vergara, D. Strategies for Reducing Automobile Fuel Consumption. Appl. Sci. 2024, 14, 910. [Google Scholar] [CrossRef]
- Kim, K.Y.; Sim, J.; Jannat, N.E.; Ahmed, F.; Ameri, S. Challenges in Riveting Quality Prediction: A Literature Survey. Procedia Manuf. 2019, 38, 1143–1150. [Google Scholar] [CrossRef]
- Yu, Q.Q.; Gao, R.X.; Gu, X.L.; Zhao, X.L.; Chen, T. Bond Behavior of CFRP-Steel Double-Lap Joints Exposed to Marine Atmosphere and Fatigue Loading. Eng. Struct. 2018, 175, 76–85. [Google Scholar] [CrossRef]
- De Araujo, R.; Lima, A.; Bernasconi, A.; Carboni, M. Acoustic Emission Applied to Mode I Fatigue Damage Monitoring of Adhesively Bonded Joints. e-J. Nondestruct. Test. 2023, 28, 1–9. [Google Scholar] [CrossRef]
- Dilger, K. Selecting the Right Joint Design and Fabrication Techniques. In Advances in Structural Adhesive Bonding; Elsevier: Amsterdam, The Netherlands, 2010; pp. 295–315. [Google Scholar] [CrossRef]
- Mallick, P.K. Joining for Lightweight Vehicles. In Materials, Design and Manufacturing for Lightweight Vehicles; Elsevier: Amsterdam, The Netherlands, 2010; pp. 275–308. [Google Scholar] [CrossRef]
- Burt, V. Adhesive Bonding. In Aluminum Science and Technology; Springer Science\& Business Media: Berlin/Heidelberg, Germany, 2018; pp. 783–789. [Google Scholar] [CrossRef]
- Liu, Y.; Carnegie, C.; Ascroft, H.; Li, W.; Han, X.; Guo, H.; Hughes, D.J. Investigation of Adhesive Joining Strategies for the Application of a Multi-Material Light Rail Vehicle. Materials 2021, 14, 6991. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Pang, S.S.; Woldesenbet, E.; Stubblefield, M.A.; Mensah, P.F.; Ibekwe, S.I. Investigation of Prepreg Bonded Composite Single Lap Joint. Compos. B Eng. 2001, 32, 651–658. [Google Scholar] [CrossRef]
- Zhao, W.; Pei, N.; Xu, C. Experimental Study of Carbon/Glass Fiber-Reinforced Hybrid Laminate Composites with Torsional Loads by Using Acoustic Emission and Micro-CT. Compos. Struct. 2022, 290, 115541. [Google Scholar] [CrossRef]
- Taib, A.A.; Boukhili, R.; Achiou, S.; Boukehili, H. Bonded Joints with Composite Adherends. Part II. Finite element analysis of joggle lap joints. Int. J. Adhes. Adhes. 2006, 26, 237–248. [Google Scholar] [CrossRef]
- Gresil, M.; Revol, V.; Kitsianos, K.; Kanderakis, G.; Koulalis, I.; Sauer, M.O.; Trétout, H.; Madrigal, A.M. EVITA Project: Comparison Between Traditional Non-Destructive Techniques and Phase Contrast X-Ray Imaging Applied to Aerospace Carbon Fibre Reinforced Polymer. Appl. Compos. Mater. 2017, 24, 513–524. [Google Scholar] [CrossRef]
- Cawley, P. The Rapid Non-Destructive Inspection of Large Composite Structures. Composites 1994, 25, 351–357. [Google Scholar] [CrossRef]
- Cheng, L.; Tian, G.Y. Surface Crack Detection for Carbon Fiber Reinforced Plastic (CFRP) Materials Using Pulsed Eddy Current Thermography. IEEE Sens. J. 2011, 11, 3261–3268. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Guided Waves in Structural Health Monitoring. Key Eng. Mater. 2004, 270–273, 14–21. [Google Scholar] [CrossRef]
- Nsengiyumva, W.; Zhong, S.; Lin, J.; Zhang, Q.; Zhong, J.; Huang, Y. Advances, Limitations and Prospects of Nondestructive Testing and Evaluation of Thick Composites and Sandwich Structures: A State-of-the-Art Review. Compos. Struct. 2021, 256, 112951. [Google Scholar] [CrossRef]
- Chandarana, N.; Sanchez, D.M.; Soutis, C.; Gresil, M. Early Damage Detection in Composites during Fabrication and Mechanical Testing. Materials 2017, 10, 685. [Google Scholar] [CrossRef]
- Li, W.; Liu, Z.; Ji, D.; Liu, Y. Damage Detection in CFRP Composite Joints Using Acoustic Emission Analysis. Int. Conf. Comput. Exp. Eng. Sci. 2024, 31, 1. [Google Scholar] [CrossRef]
- Rubio-González, C.; de Urquijo-Ventura, M.d.P.; Rodríguez-González, J.A. Damage Progression Monitoring Using Self-Sensing Capability and Acoustic Emission on Glass Fiber/Epoxy Composites and Damage Classification through Principal Component Analysis. Compos. B Eng. 2023, 254, 110608. [Google Scholar] [CrossRef]
- Zhou, W.; Liu, R.; Lv, Z.H.; Chen, W.Y.; Li, X.T. Acoustic Emission Behaviors and Damage Mechanisms of Adhesively Bonded Single-Lap Composite Joints with Adhesive Defects. J. Reinf. Plast. Compos. 2014, 34, 84–92. [Google Scholar] [CrossRef]
- Mishra, N.K.; Dash, P.K.; Yashwanth, N. Damage Monitoring of Single Lap Bonded Composite Using Acoustic Emission Technique. IOP Conf. Ser. Mater. Sci. Eng. 2018, 455, 012026. [Google Scholar] [CrossRef]
- Balázs, G.L.; Grosse, C.U.; Koch, R.; Reinhardt, H.W. Damage Accumulation on Deformed Steel Bar to Concrete Interaction Detected by Acoustic Emission Technique. Mag. Concr. Res. 2015, 48, 311–320. [Google Scholar] [CrossRef]
- Andraju, L.B.; Raju, G. Damage Characterization of CFRP Laminates Using Acoustic Emission and Digital Image Correlation: Clustering, Damage Identification and Classification. Eng. Fract. Mech. 2023, 277, 108993. [Google Scholar] [CrossRef]
- Barile, C.; Casavola, C.; Pappalettera, G.; Kannan, V.P. Application of Different Acoustic Emission Descriptors in Damage Assessment of Fiber Reinforced Plastics: A Comprehensive Review. Eng. Fract. Mech. 2020, 235, 107083. [Google Scholar] [CrossRef]
- Godin, N.; Reynaud, P.; Fantozzi, G. Challenges and Limitations in the Identification of Acoustic Emission Signature of Damage Mechanisms in Composites Materials. Appl. Sci. 2018, 8, 1267. [Google Scholar] [CrossRef]
- Barile, C.; Casavola, C.; Pappalettera, G.; Paramsamy Kannan, V. Laplacian Score and K-Means Data Clustering for Damage Characterization of Adhesively Bonded CFRP Composites by Means of Acoustic Emission Technique. Appl. Acoust. 2022, 185, 108425. [Google Scholar] [CrossRef]
- Siow, P.Y.; Ong, Z.C.; Khoo, S.Y.; Lim, K.S. Damage Sensitive PCA-FRF Feature in Unsupervised Machine Learning for Damage Detection of Plate-Like Structures. Int. J. Struct. Stab. Dyn. 2020, 21, 2150028. [Google Scholar] [CrossRef]
- Arumugam, V.; Suresh Kumar, C.; Santulli, C.; Sarasini, F.; Stanley, A.J. Identification of Failure Modes in Composites from Clustered Acoustic Emission Data Using Pattern Recognition and Wavelet Transformation. Arab. J. Sci. Eng. 2013, 38, 1087–1102. [Google Scholar] [CrossRef]
- Ca, P.V.; Edu, L.T.; Lajoie, I.; Ca, Y.B.; Ca, P.-A.M. Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion Pascal Vincent Hugo Larochelle Yoshua Bengio Pierre-Antoine Manzagol. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Lee, H.; Lim, H.J.; Skinner, T.; Chattopadhyay, A.; Hall, A. Automated Fatigue Damage Detection and Classification Technique for Composite Structures Using Lamb Waves and Deep Autoencoder. Mech. Syst. Signal Process 2022, 163, 108148. [Google Scholar] [CrossRef]
- Tornyeviadzi, H.M.; Seidu, R. Leakage Detection in Water Distribution Networks via 1D CNN Deep Autoencoder for Multivariate SCADA Data. Eng. Appl. Artif. Intell. 2023, 122, 106062. [Google Scholar] [CrossRef]
- Wen, H.; Guo, W.; Li, X. A Novel Deep Clustering Network Using Multi-Representation Autoencoder and Adversarial Learning for Large Cross-Domain Fault Diagnosis of Rolling Bearings. Expert. Syst. Appl. 2023, 225, 120066. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Kramer, M.A. Nonlinear principal component analysis using autoassociative neural networks. AIChE J. 1991, 37, 233–243. [Google Scholar] [CrossRef]
- Rifai, S.; Vincent, P.; Muller, X.; Glorot, X.; Bengio, Y. Contractive auto-encoders: Explicit invariance during feature extraction. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Bellevue, WA, USA, 28 June–2 July 2011; pp. 833–840. [Google Scholar]
- Zhao, K.; Jiang, H.; Liu, C.; Wang, Y.; Zhu, K. A New Data Generation Approach with Modified Wasserstein Auto-Encoder for Rotating Machinery Fault Diagnosis with Limited Fault Data. Knowl. Based Syst. 2022, 238, 107892. [Google Scholar] [CrossRef]
- Yan, J.; Jin, D.; Lee, C.W.; Liu, P. A Comparative Study of Off-Line Deep Learning Based Network Intrusion Detection. In Proceedings of the 2018 Tenth International Conference on Ubiquitous and Future Networks (ICUFN), Prague, Czech Republic, 3–6 July 2018; pp. 299–304. [Google Scholar] [CrossRef]
- Zabalza, J.; Ren, J.; Zheng, J.; Zhao, H.; Qing, C.; Yang, Z.; Du, P.; Marshall, S. Novel Segmented Stacked Autoencoder for Effective Dimensionality Reduction and Feature Extraction in Hyperspectral Imaging. Neurocomputing 2016, 185, 1–10. [Google Scholar] [CrossRef]
- Li, L.; Lomov, S.V.; Yan, X.; Carvelli, V. Cluster Analysis of Acoustic Emission Signals for 2D and 3D Woven Glass/Epoxy Composites. Compos. Struct. 2014, 116, 286–299. [Google Scholar] [CrossRef]
- Cheng, X.; Ying, J.; Wu, Z.; Shi, L.; Hu, X. Mode I Interlaminar Fracture Characteristics of CNTs Doped Woven and Unidirectional CFRP via Acoustic Emission. Theor. Appl. Fract. Mech. 2023, 124, 103812. [Google Scholar] [CrossRef]
- Yang, B.; Fu, X.; Sidiropoulos, N.D.; Hong, M. Towards K-Means-Friendly Spaces: Simultaneous Deep Learning and Clustering. In Proceedings of the 34th International Conference on Machine Learning, ICML 2017, Sydney, NSW, Australia, 6–11 August 2017; Volume 8, pp. 5888–5901. [Google Scholar]
- ASTM D 5868-01; Standard Test Method for Lap Shear Adhesion for Fiber Reinforced Plastic (FRP) Bonding. ASTM International: West Conshohocken, PA, USA, 2001. Available online: https://www.astm.org/d5868-01r14.html (accessed on 28 April 2024).
- Ávila, A.F.; de O. Bueno, P. An experimental and numerical study on adhesive joints for composites. Compos. Struct. 2004, 64, 531–537. [Google Scholar] [CrossRef]
- Liu, X.; Shao, X.; Li, Q.; Sun, G. Experimental Study on Residual Properties of Carbon Fibre Reinforced Plastic (CFRP) and Aluminum Single-Lap Adhesive Joints at Different Strain Rates after Transverse Pre-Impact. Compos. Part A Appl. Sci. Manuf. 2019, 124, 105372. [Google Scholar] [CrossRef]
- Adin, H. Effect of Overlap Length and Scarf Angle on the Mechanical Properties of Different Adhesive Joints Subjected to Tensile Loads. Mater. Test. 2017, 59, 536–546. [Google Scholar] [CrossRef]
- Kadioglu, F.; Demiral, M.; El Zaroug, M. Effects of Overlap Length on the Strength of Bolted, Bonded and Hybrid Single Lap Joints with Different Adherend Materials and Thicknesses. J. Adhes. Sci. Technol. 2019, 33, 2191–2206. [Google Scholar] [CrossRef]
- Silva, M.A.G.; Biscaia, H.; Ribeiro, P. On Factors Affecting CFRP-Steel Bonded Joints. Constr. Build. Mater. 2019, 226, 360–375. [Google Scholar] [CrossRef]
- Manohar, K.R.; Raghunadh, Y.M.K.; Kumar, B.K.; Ranganath, L.; Koteswararao, B. Experiment Analysis to Examine the Effects of Adhesive and Adherent Type of Geometrical Configuration on Joint Failure Loads. Mater. Today Proc. 2019, 18, 4665–4674. [Google Scholar] [CrossRef]
- Kowatz, J.; Teutenberg, D.; Meschut, G. Experimental Failure Analysis of Adhesively Bonded Steel/CFRP Joints under Quasi-Static and Cyclic Tensile-Shear and Peel Loading. Int. J. Adhes. Adhes. 2021, 107, 102851. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, H.; Liu, S. Experimental Study on Tensile Properties of Steel Plate Bonded by CFRP. J. Wuhan. Univ. Technol. Mater. Sci. Ed. 2008, 23, 727–732. [Google Scholar] [CrossRef]
- Lu, Y.; Li, W.; Li, S.; Li, X.; Zhu, T. Study of the Tensile Properties of CFRP Strengthened Steel Plates. Polymers 2015, 7, 2595–2610. [Google Scholar] [CrossRef]
- Karachalios, E.F.; Adams, R.D.; da Silva, L.F.M. Single Lap Joints Loaded in Tension with High Strength Steel Adherends. Int. J. Adhes. Adhes. 2013, 43, 81–95. [Google Scholar] [CrossRef]
- Martínez, M.A.; López de Armentia, S.; Abenojar, J. Influence of Sample Dimensions on Single Lap Joints: Effect of Interactions between Parameters. J. Adhes. 2021, 97, 1358–1369. [Google Scholar] [CrossRef]
- Bhowick, D.; Gupta, D.K.; Maiti, S.; Shankar, U. Stacked Autoencoders Based Machine Learning for Noise Reduction and Signal Reconstruction in Geophysical Data. arXiv 2019, arXiv:1907.03278. [Google Scholar]
- Pathirage, C.S.N.; Li, J.; Li, L.; Hao, H.; Liu, W. Application of Deep Autoencoder Model for Structural Condition Monitoring. J. Syst. Eng. Electron. 2018, 29, 873–880. [Google Scholar] [CrossRef]
- Lee, K.; Jeong, S.; Sim, S.H.; Shin, D.H. Field Experiment on a PSC-I Bridge for Convolutional Autoencoder-Based Damage Detection. Struct. Health Monit. 2020, 20, 1627–1643. [Google Scholar] [CrossRef]
- De Groot, P.J.; Wijnen, P.A.M.; Janssen, R.B.F. Real-Time Frequency Determination of Acoustic Emission for Different Fracture Mechanisms in Carbon/Epoxy Composites. Compos. Sci. Technol. 1995, 55, 405–412. [Google Scholar] [CrossRef]
- Barile, C.; Casavola, C.; Pappalettera, G.; Vimalathithan, P.K. Damage Characterization in Composite Materials Using Acoustic Emission Signal-Based and Parameter-Based Data. Compos. B Eng. 2019, 178, 107469. [Google Scholar] [CrossRef]
- Saeedifar, M.; Zarouchas, D. Damage Characterization of Laminated Composites Using Acoustic Emission: A Review. Compos. B Eng. 2020, 195, 108039. [Google Scholar] [CrossRef]
- Mahesh, P.; Chinthapenta, V.; Raju, G.; Ramji, M. Experimental Investigation on Open-Hole CFRP Laminate under Combined Loading Using Acoustic Emission and Digital Image Correlation. Theor. Appl. Fract. Mech. 2024, 130, 104300. [Google Scholar] [CrossRef]
- Ali, H.Q.; Emami Tabrizi, I.; Khan, R.M.A.; Tufani, A.; Yildiz, M. Microscopic Analysis of Failure in Woven Carbon Fabric Laminates Coupled with Digital Image Correlation and Acoustic Emission. Compos. Struct. 2019, 230, 111515. [Google Scholar] [CrossRef]
- Zarouchas, D.; Van Hemelrijck, D. Mechanical Characterization and Damage Assessment of Thick Adhesives for Wind Turbine Blades Using Acoustic Emission and Digital Image Correlation Techniques. J. Adhes. Sci. Technol. 2014, 28, 1500–1516. [Google Scholar] [CrossRef]
- Karimian, S.F.; Modarres, M. Acoustic Emission Signal Clustering in CFRP Laminates Using a New Feature Set Based on Waveform Analysis and Information Entropy Analysis. Compos. Struct. 2021, 268, 113987. [Google Scholar] [CrossRef]
- Burud, N.B.; Kishen, J.M.C. Non-Extensive Statistical Mechanics for Acoustic Emission in Disordered Media: Entropy, Size Effect, and Self-Organization. Int. J. Mech. Sci. 2021, 202–203, 106514. [Google Scholar] [CrossRef]
- Shahapure, K.R.; Nicholas, C. Cluster quality analysis using silhouette score. In Proceedings of the 2020 IEEE 7th International Conference on Data Science and Advanced Analytics (DSAA), Sydney, NSW, Australia, 6–9 October 2020; pp. 747–748. [Google Scholar] [CrossRef]
- Nitya Sai, L.; Sai Shreya, M.; Anjan Subudhi, A.; Jaya Lakshmi, B.; Madhuri, K.B. Optimal K-means clustering method using silhouette coefficient. J. Adv. Manuf. Technol. 2017, 33, 335–344. [Google Scholar] [CrossRef]
- Liu, P.F.; Chu, J.K.; Liu, Y.L.; Zheng, J.Y. A Study on the Failure Mechanisms of Carbon Fiber/Epoxy Composite Laminates Using Acoustic Emission. Mater. Des. 2012, 37, 228–235. [Google Scholar] [CrossRef]
- Zhuang, X.; Yan, X. Investigation of Damage Mechanisms in Self-Reinforced Polyethylene Composites by Acoustic Emission. Compos. Sci. Technol. 2006, 66, 444–449. [Google Scholar] [CrossRef]
- Barré, S.; Benzeggagh, M.L. On the Use of Acoustic Emission to Investigate Damage Mechanisms in Glass-Fibre-Reinforced Polypropylene. Compos. Sci. Technol. 1994, 52, 369–376. [Google Scholar] [CrossRef]
- Wenqin, H.; Ying, L.; Aijun, G.; Yuan, F.G. Damage Modes Recognition and Hilbert-Huang Transform Analyses of CFRP Laminates Utilizing Acoustic Emission Technique. Appl. Compos. Mater. 2016, 23, 155–178. [Google Scholar] [CrossRef]
- Wirtz, S.F.; Beganovic, N.; Söffker, D. Investigation of Damage Detectability in Composites Using Frequency-Based Classification of Acoustic Emission Measurements. Struct. Health Monit. 2018, 18, 1207–1218. [Google Scholar] [CrossRef]
- Han, W.Q.; Gu, A.J.; Zhou, J. A Damage Modes Extraction Method from AE Signal in Composite Laminates Based on DEEMD. J. Nondestruct. Eval. 2019, 38, 70. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).