GeoSAE: A 3D Stratigraphic Modeling Method Driven by Geological Constraint
Abstract
1. Introduction
- (1)
- Geological and geophysical knowledge is relied upon in traditional explicit modeling methods to construct geological interfaces, with data from geological maps, boreholes, and geological cross-sections being utilized [3]. The quality of the model is significantly influenced by the accuracy of the interpreted data. Each stratigraphic surface is explicitly modeled, and constrained grid interpolation is employed to refine the model and generate more detailed surfaces [4]. Additionally, semi-automated, interactive methods are employed to enable the manual addition of geological constraints [5,6,7], ensuring better alignment with geological knowledge. Various interpolation methods, including Bézier curve interpolation [8], non-uniform rational B-Spline (NURBS) interpolation [9], and the discrete smoothing interpretation (DSI) method introduced by J. Mallet in 2002 [10,11], have been proposed to better fit geological observations and adapt to different geological structures.
- (2)
- Isosurfaces traced from a 3D potential field are used in implicit modeling to represent geological interfaces [12], and discrete geological data—such as interface points and structural observations—are interpolated using implicit functions [13]. Various implicit modeling methods have been proposed, with different mathematical frameworks being employed, including Kriging-based implicit modeling [14,15], discrete smoothing interpolation (DSI) [16], and radial basis function (RBF) methods [17,18].
- (3)
- Intrinsic geological features are mined from large geological data samples through training with different learning paradigms in deep learning methods. Geological prior knowledge is incorporated to explore geological expressions that align with geological laws, observations, and structural anisotropy. Various 3D geological modeling methods based on deep learning are being continuously explored. Classification algorithm-based networks, such as support vector machines and BP neural networks, are employed to automate the construction of 3D geological models from borehole data [22]. Semantic mining is performed using recurrent neural networks (RNNs), where the prediction of stratum types and layer thicknesses is simulated [23]. Three-dimensional geological model parameters are inverted from geophysical data using convolutional neural networks (CNNs), and geological datasets are synthesized [24]. Generative adversarial networks (GANs), including variants such as deep convolutional generative adversarial networks (DCGAN) and Monte Carlo simulation-based GANs (MC-GAN), have been proposed to improve 3D geological modeling [25,26,27]. Reliable 3D geological models are constructed by combining drill holes, outcrops, and 2D geological cross-sections as strong constraints in these methods. Stochastic processes are modeled, and scale conversion is facilitated in these methods, while geological observations are integrated into graph structures using graph neural networks (GNNs), thereby extending the range of constraints [28]. Geological constraints are often added to the inversion function or applied during post-processing of the inversion model after each inversion step to align it with geological characteristics in the construction of 3D geological models with geological constraints [29]. For specific geological formations, seismic voxels are used to estimate relative geologic time (RGT) for stratigraphy interpretation and fault detection, and fault models consistent with geological structures are generated [30]. However, the modeling of non-integrated structures is still considered difficult. A framework combining deep learning with implicit modeling has recently been proposed to improve the application of implicit methods in structural geology, with a multilayer perceptron (MLP) architecture being utilized [31].
2. Methods
2.1. Geologically Constrained Loss Function Construction
2.1.1. Consistency Constraints on Sampling Points of Stratigraphic Surfaces
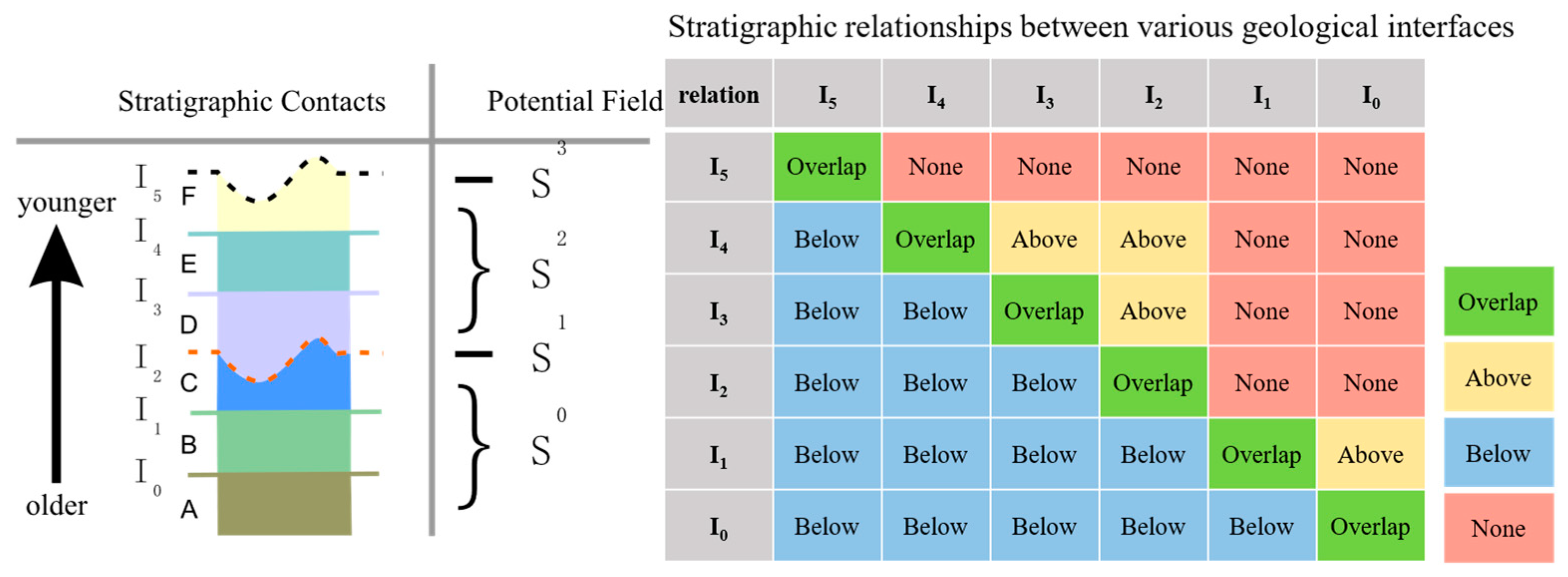
2.1.2. Stratigraphic Sequence Constraints
2.1.3. Attitude Constraints on Attitude Points
2.1.4. Stratigraphic Interface Smoothness Constraints
2.1.5. Total Loss Function
2.2. Stacked Autoencoder Network Framework
2.2.1. Stacked Autoencoder Network Construction
2.2.2. Stacked Autoencoder Network Training Framework
2.3. Overall Modeling Workflow Architecture
3. Experimental Verification and Results
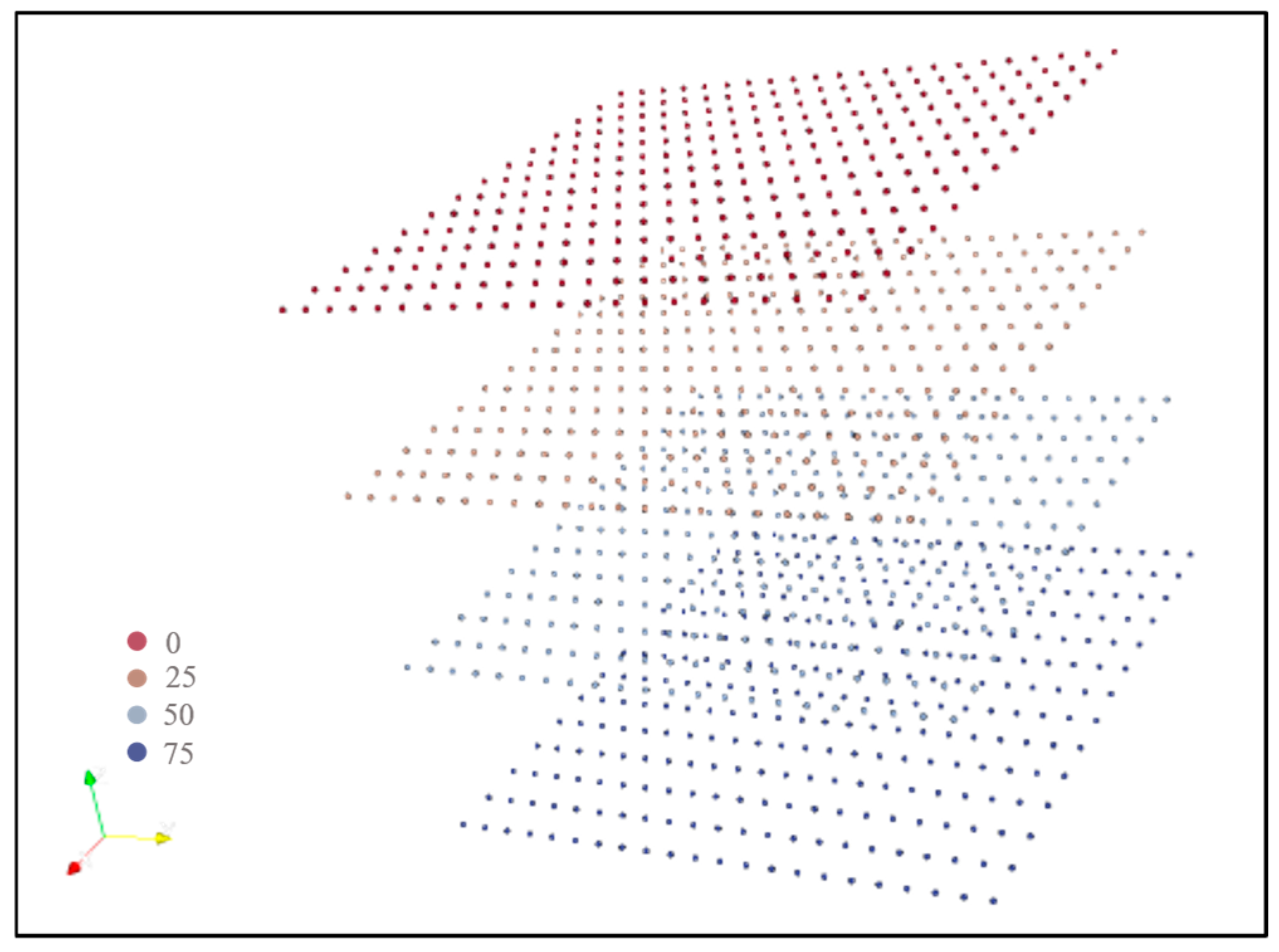
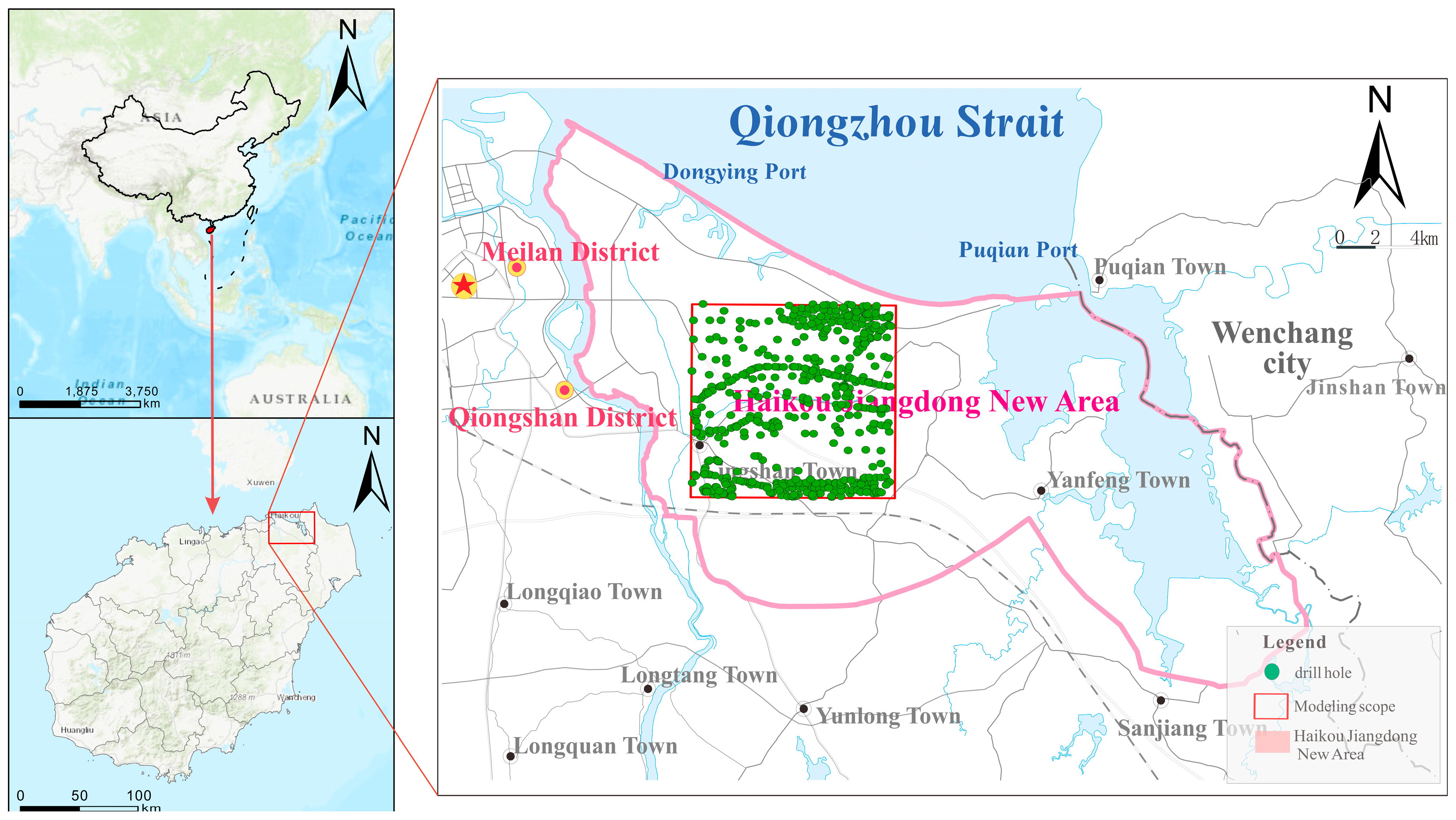
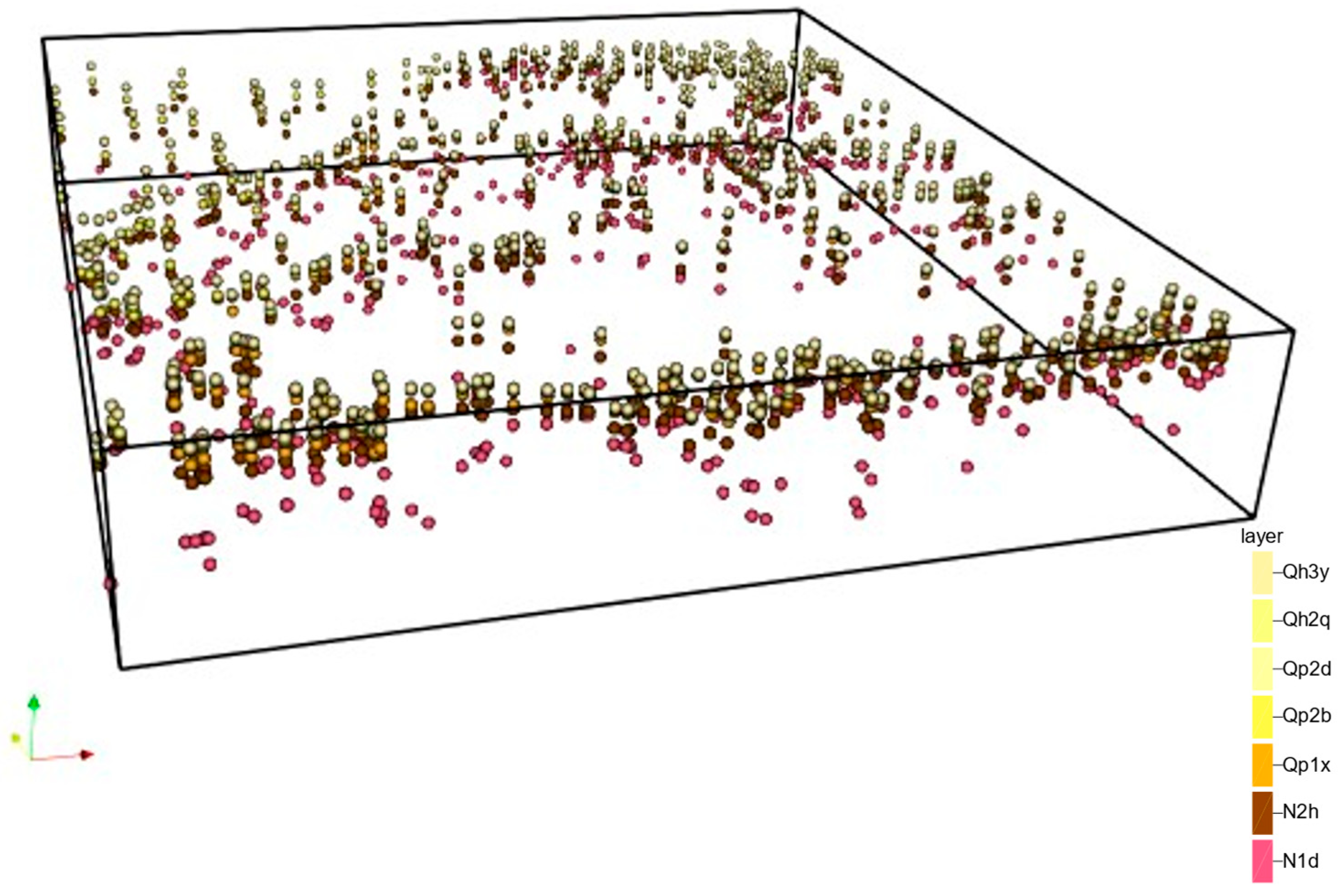
3.1. Data Preparation and Analysis
3.2. Construction of Three-Dimensional Geological Models
3.3. Comparison and Control of Stratigraphic Smoothness
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Birch, C. New Systems for Geological Modelling-Black Box or Best Practice? J. S. Afr. Inst. Min. Metall. 2014, 114, 993–1000. [Google Scholar]
- McInerney, P.; Goldberg, A.; Calcagno, P.; Courrioux, G.; Guillen, A.; Seikel, R. Improved 3D Geology Modelling Using an Implicit Function Interpolator and Forward Modelling of Potential Field Data. In Proceedings of the Exploration 07: Fifth Decennial International Conference on Mineral Exploration, Toronto, ON, Canada, 9–12 September 2007; Volume 7, pp. 919–922. [Google Scholar]
- Wellmann, F.; Caumon, G. 3-D Structural Geological Models: Concepts, Methods, and Uncertainties. In Advances in Geophysics; Elsevier: Amsterdam, The Netherlands, 2018; Volume 59, pp. 1–121. [Google Scholar]
- Si, H. Constrained Delaunay Tetrahedral Mesh Generation and Refinement. Finite Elem. Anal. Des. 2010, 46, 33–46. [Google Scholar] [CrossRef]
- Wang, B.; Wu, L.; Li, W.; Qiu, Q.; Xie, Z.; Liu, H.; Zhou, Y. A Semi-Automatic Approach for Generating Geological Profiles by Integrating Multi-Source Data. Ore Geol. Rev. 2021, 134, 104190. [Google Scholar] [CrossRef]
- Lyu, M.; Ren, B.; Wu, B.; Tong, D.; Ge, S.; Han, S. A Parametric 3D Geological Modeling Method Considering Stratigraphic Interface Topology Optimization and Coding Expert Knowledge. Eng. Geol. 2021, 293, 106300. [Google Scholar] [CrossRef]
- Gonçalves, Í.G.; Kumaira, S.; Guadagnin, F. A Machine Learning Approach to the Potential-Field Method for Implicit Modeling of Geological Structures. Comput. Geosci. 2017, 103, 173–182. [Google Scholar] [CrossRef]
- González-Garcia, J.; Jessell, M. A 3D Geological Model for the Ruiz-Tolima Volcanic Massif (Colombia): Assessment of Geological Uncertainty Using a Stochastic AResearch on 3D Geological Modelingpproach Based on Bézier Curve Design. Tectonophysics 2016, 687, 139–157. [Google Scholar] [CrossRef]
- De Kemp, E.A.; Sprague, K.B. Interpretive Tools for 3-D Structural Geological Modeling Part I: Bezier-Based Curves, Ribbons and Grip Frames. GeoInformatica 2003, 7, 55–71. [Google Scholar] [CrossRef]
- Mallet, J.-L. Discrete Smooth Interpolation in Geometric Modelling. Comput.-Aided Des. 1992, 24, 178–191. [Google Scholar] [CrossRef]
- Mallet, J.-L. Discrete Smooth Interpolation. ACM Trans. Graph. 1989, 8, 121–144. [Google Scholar] [CrossRef]
- Collon, P.; Steckiewicz-Laurent, W.; Pellerin, J.; Laurent, G.; Caumon, G.; Reichart, G.; Vaute, L. 3D Geomodelling Combining Implicit Surfaces and Voronoi-Based Remeshing: A Case Study in the Lorraine Coal Basin (France). Comput. Geosci. 2015, 77, 29–43. [Google Scholar] [CrossRef]
- Zhong, D.; Wang, L.; Lin, B.I.; Jia, M. Implicit Modeling of Complex Orebody with Constraints of Geological Rules. Trans. Nonferrous Met. Soc. China 2019, 29, 2392–2399. [Google Scholar] [CrossRef]
- de la Varga, M.; Schaaf, A.; Wellmann, F. GemPy 1.0: Open-Source Stochastic Geological Modeling and Inversion. Geosci. Model Dev. 2019, 12, 1–32. [Google Scholar] [CrossRef]
- Marinoni, O. Improving Geological Models Using a Combined Ordinary–Indicator Kriging Approach. Eng. Geol. 2003, 69, 37–45. [Google Scholar] [CrossRef]
- Frank, T.; Tertois, A.-L.; Mallet, J.-L. 3D-Reconstruction of Complex Geological Interfaces from Irregularly Distributed and Noisy Point Data. Comput. Geosci. 2007, 33, 932–943. [Google Scholar] [CrossRef]
- Cuomo, S.; Galletti, A.; Giunta, G.; Marcellino, L. Reconstruction of Implicit Curves and Surfaces via RBF Interpolation. Appl. Numer. Math. 2017, 116, 157–171. [Google Scholar] [CrossRef]
- Skala, V. RBF Interpolation with CSRBF of Large Data Sets. Procedia Comput. Sci. 2017, 108, 2433–2437. [Google Scholar] [CrossRef]
- Wellmann, J.F.; Lindsay, M.; Poh, J.; Jessell, M. Validating 3-D Structural Models with Geological Knowledge for Improved Uncertainty Evaluations. Energy Procedia 2014, 59, 374–381. [Google Scholar] [CrossRef]
- Guo, J.; Wang, J.; Wu, L.; Liu, C.; Li, C.; Li, F.; Lin, M.; Jessell, M.W.; Li, P.; Dai, X. Explicit-Implicit-Integrated 3-D Geological Modelling Approach: A Case Study of the Xianyan Demolition Volcano (Fujian, China). Tectonophysics 2020, 795, 228648. [Google Scholar] [CrossRef]
- Ross, M.; Taylor, A.; Kelley, S.; Lopez, S.; Allanic, C.; Courrioux, G.; Bourgine, B.; Calcagno, P.; Carit, S.; Gabalda, S. Integrated Rule-Based Geomodeling—Explicit and Implicit Approaches. In Applied Multidimensional Geological Modeling; Keith Turner, A., Kessler, H., Van Der Meulen, M.J., Eds.; Wiley: Hoboken, NJ, USA, 2021; pp. 273–294. ISBN 978-1-119-16312-1. [Google Scholar]
- Liu, L.; Li, T.; Ma, C. Research on 3D Geological Modeling Method Based on Deep Neural Networks for Drilling Data. Appl. Sci. 2024, 14, 423. [Google Scholar] [CrossRef]
- Zhou, C.; Ouyang, J.; Ming, W.; Zhang, G.; Du, Z.; Liu, Z. A Stratigraphic Prediction Method Based on Machine Learning. Appl. Sci. 2019, 9, 3553. [Google Scholar] [CrossRef]
- Guo, J.; Li, Y.; Jessell, M.W.; Giraud, J.; Li, C.; Wu, L.; Li, F.; Liu, S. 3D Geological Structure Inversion from Noddy-Generated Magnetic Data Using Deep Learning Methods. Comput. Geosci. 2021, 149, 104701. [Google Scholar] [CrossRef]
- Cui, Z.; Chen, Q.; Liu, G.; Xun, L. SA-RelayGANs: A Novel Framework for the Characterization of Complex Hydrological Structures Based on GANs and Self-Attention Mechanism. Water Resour. Res. 2024, 60, e2023WR035932. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, Q.; Cui, Z.; Liu, G.; Dong, S.; Tian, Y. Automatic Reconstruction Method of 3D Geological Models Based on Deep Convolutional Generative Adversarial Networks. Comput. Geosci. 2022, 26, 1135–1150. [Google Scholar] [CrossRef]
- Chen, Q.; Cui, Z.; Liu, G.; Yang, Z.; Ma, X. Deep Convolutional Generative Adversarial Networks for Modeling Complex Hydrological Structures in Monte-Carlo Simulation. J. Hydrol. 2022, 610, 127970. [Google Scholar] [CrossRef]
- Hillier, M.; Wellmann, F.; Brodaric, B.; De Kemp, E.; Schetselaar, E. Three-Dimensional Structural Geological Modeling Using Graph Neural Networks. Math. Geosci. 2021, 53, 1725–1749. [Google Scholar] [CrossRef]
- Giraud, J.; Caumon, G.; Grose, L.; Ogarko, V.; Cupillard, P. Integration of Automatic Implicit Geological Modelling in Deterministic Geophysical Inversion. Solid Earth 2024, 15, 63–89. [Google Scholar] [CrossRef]
- Bi, Z.; Wu, X.; Geng, Z.; Li, H. Deep Relative Geologic Time: A Deep Learning Method for Simultaneously Interpreting 3-D Seismic Horizons and Faults. J. Geophys. Res. Solid Earth 2021, 126, e2021JB021882. [Google Scholar] [CrossRef]
- Hillier, M.; Wellmann, F.; de Kemp, E.A.; Brodaric, B.; Schetselaar, E.; Bédard, K. GeoINR 1.0: An Implicit Neural Network Approach to Three-Dimensional Geological Modelling. Geosci. Model Dev. 2023, 16, 6987–7012. [Google Scholar] [CrossRef]
- Pan, D.; Xu, Z.; Lu, X.; Zhou, L.; Li, H. 3D Scene and Geological Modeling Using Integrated Multi-Source Spatial Data: Methodology, Challenges, and Suggestions. Tunn. Undergr. Space Technol. 2020, 100, 103393. [Google Scholar] [CrossRef]
- Charte, D.; Charte, F.; del Jesus, M.J.; Herrera, F. An Analysis on the Use of Autoencoders for Representation Learning: Fundamentals, Learning Task Case Studies, Explainability and Challenges. Neurocomputing 2020, 404, 93–107. [Google Scholar] [CrossRef]
- Aster, R.C.; Thurber, C.H.; Borchers, B. Parameter Estimation and Inverse Problems; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Gropp, A.; Yariv, L.; Haim, N.; Atzmon, M.; Lipman, Y. Implicit Geometric Regularization for Learning Shapes. arXiv 2020, arXiv:2002.10099. [Google Scholar]
- Liu, L.; Zhou, J.; Jiang, D.; Zhuang, D.; Mansaray, L.R. Lithological Discrimination of the Mafic-Ultramafic Complex, Huitongshan, Beishan, China: Using ASTER Data. J. Earth Sci. 2014, 25, 529–536. [Google Scholar] [CrossRef]
- Su, Q.; Li, Z.; Li, G.; Zhu, D.; Hu, P. Coastal Erosion Risk Assessment of Hainan Island, China. Acta Oceanol. Sin. 2023, 42, 79–90. [Google Scholar] [CrossRef]
- Dilek, Y.; Tang, L. Magmatic Record of the Mesozoic Geology of Hainan Island and Its Implications for the Mesozoic Tectonomagmatic Evolution of SE China: Effects of Slab Geometry and Dynamics in Continental Tectonics. Geol. Mag. 2021, 158, 118–142. [Google Scholar] [CrossRef]
- Yao, W.; Li, Z.X.; Li, W.X.; Li, X.H. Proterozoic Tectonics of Hainan Island in Supercontinent Cycles: New Insights from Geochronological and Isotopic Results. Precambrian Res. 2017, 290, 86–100. [Google Scholar] [CrossRef]
- Sullivan, C.; Kaszynski, A. PyVista: 3D Plotting and Mesh Analysis through a Streamlined Interface for the Visualization Toolkit (VTK). J. Open Source Softw. 2019, 4, 1450. [Google Scholar] [CrossRef]
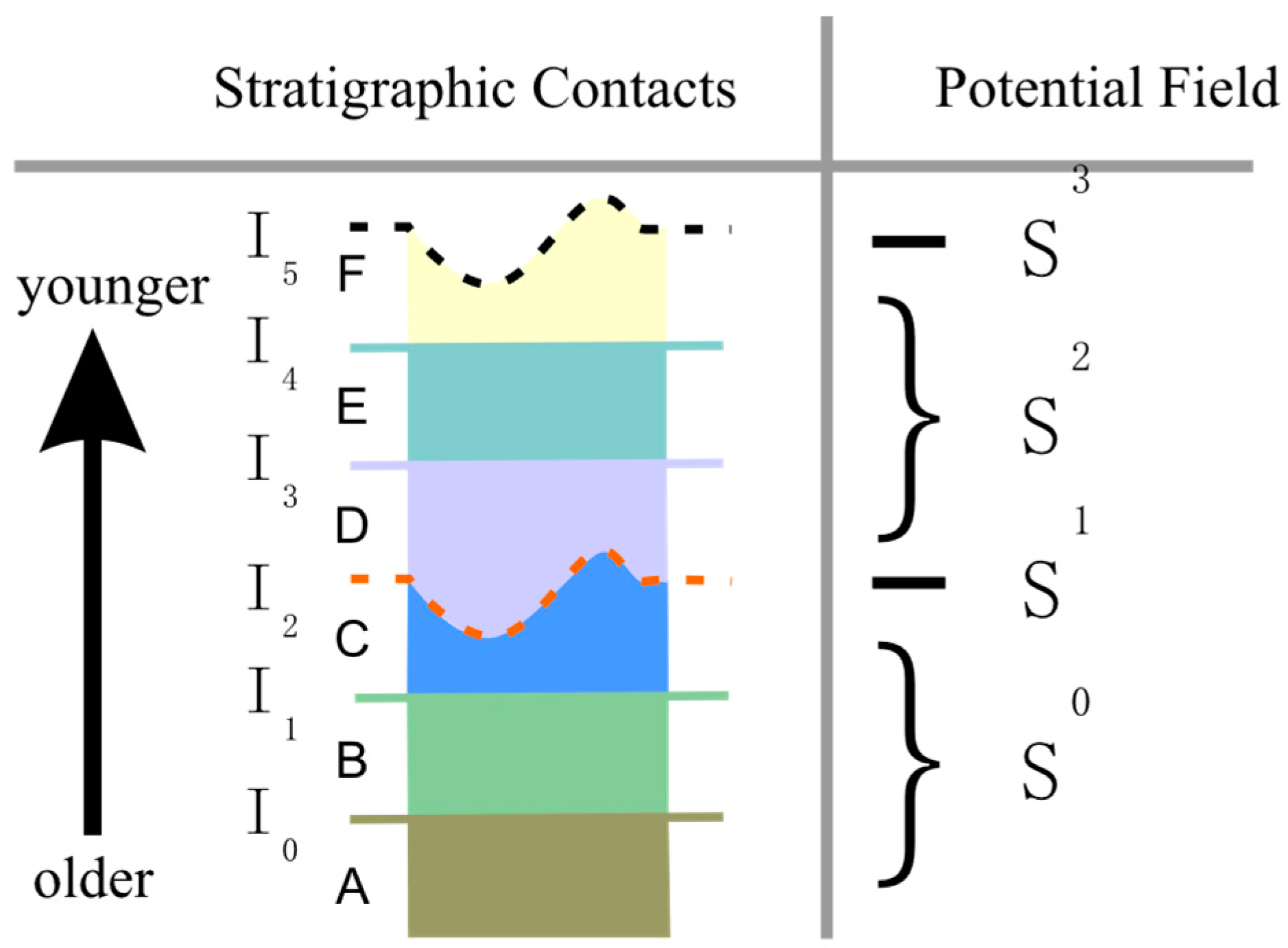

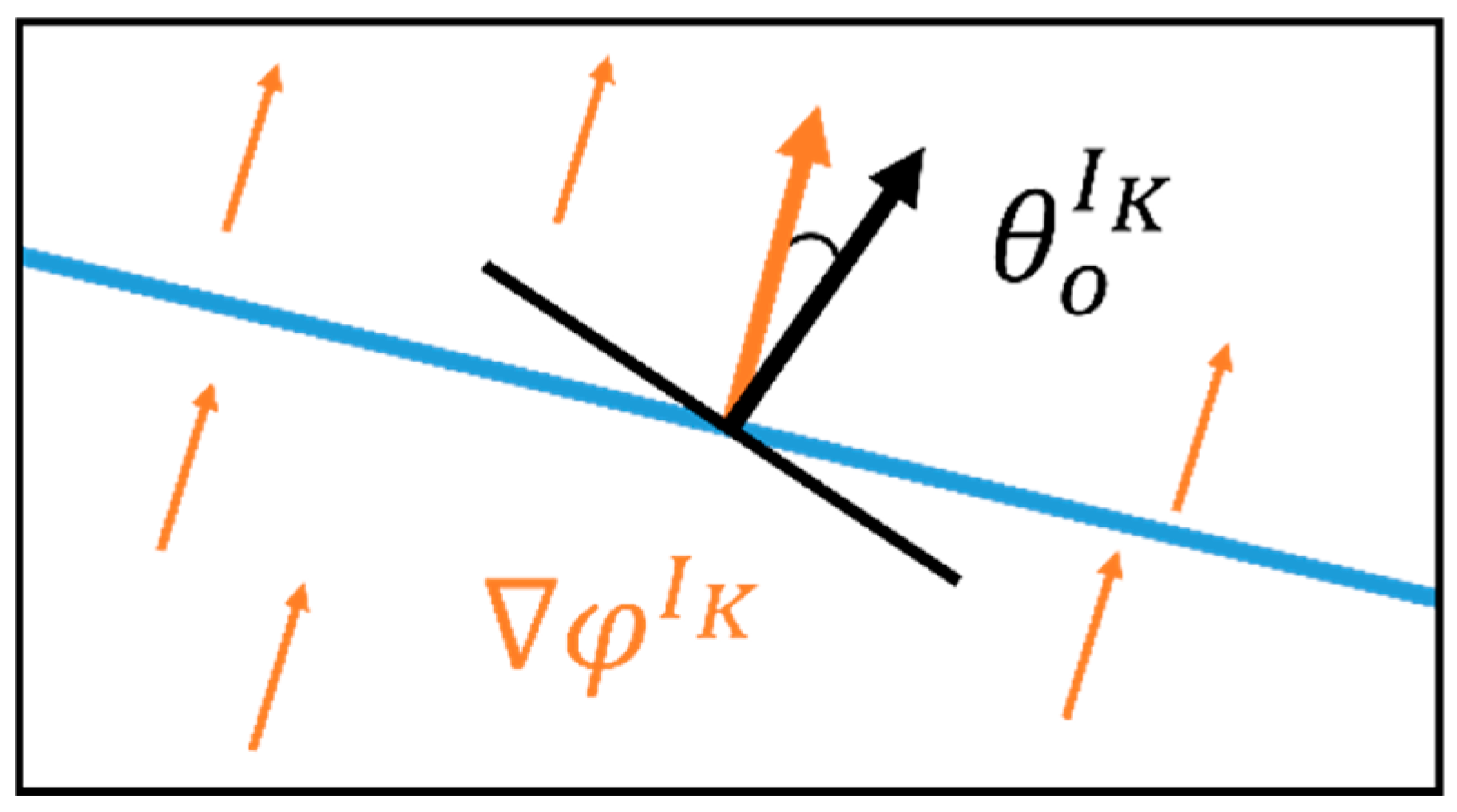
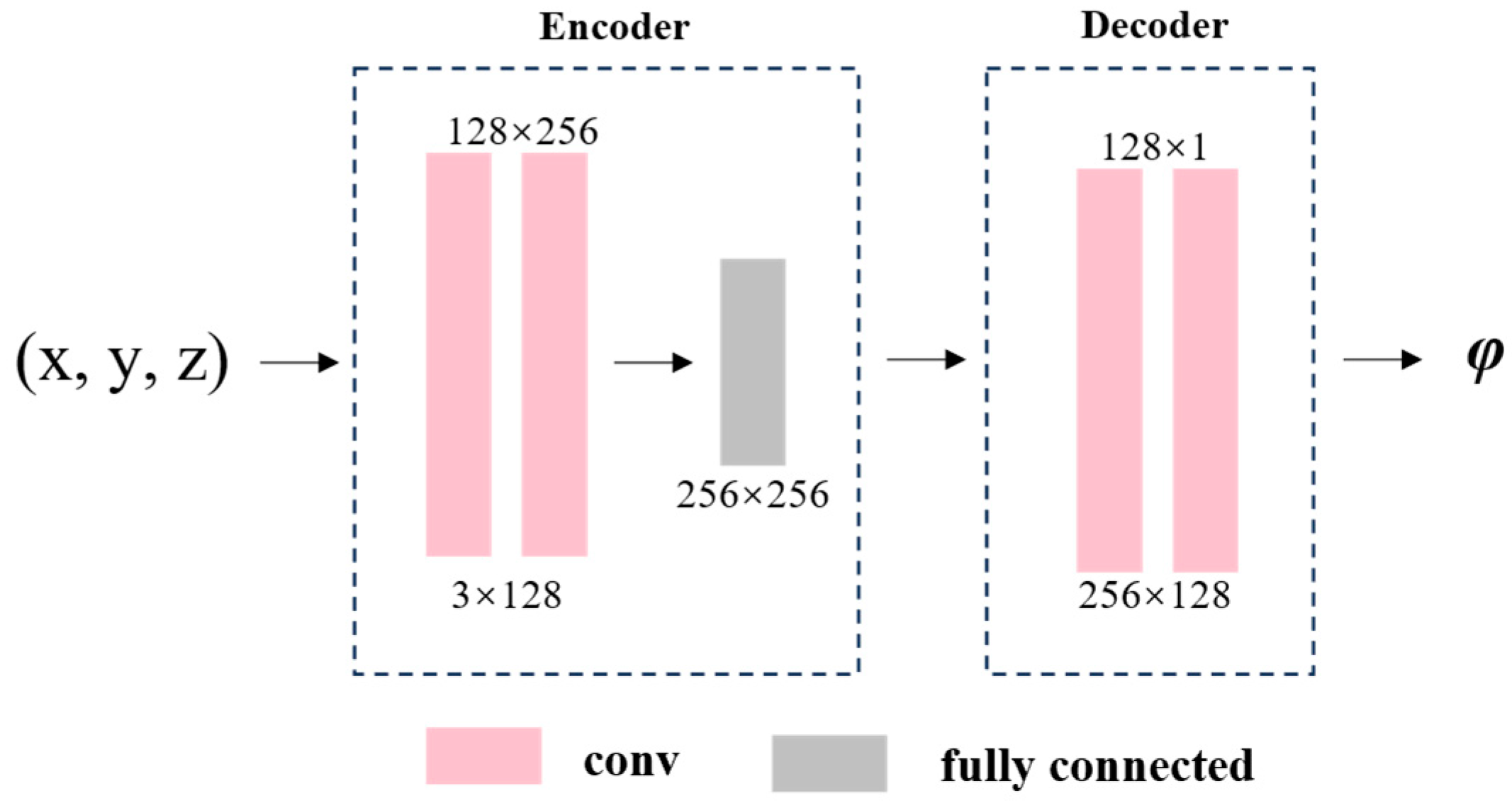





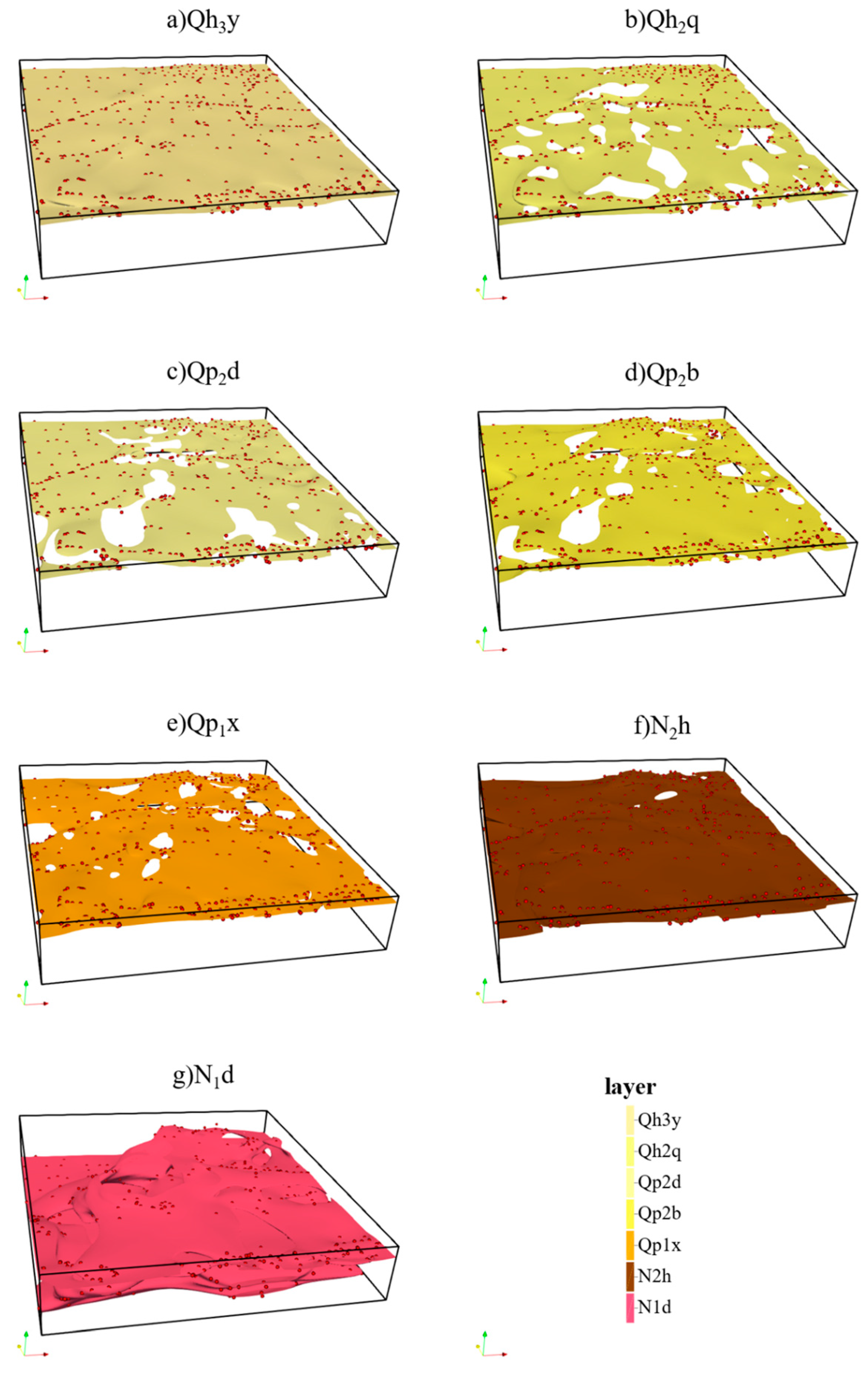
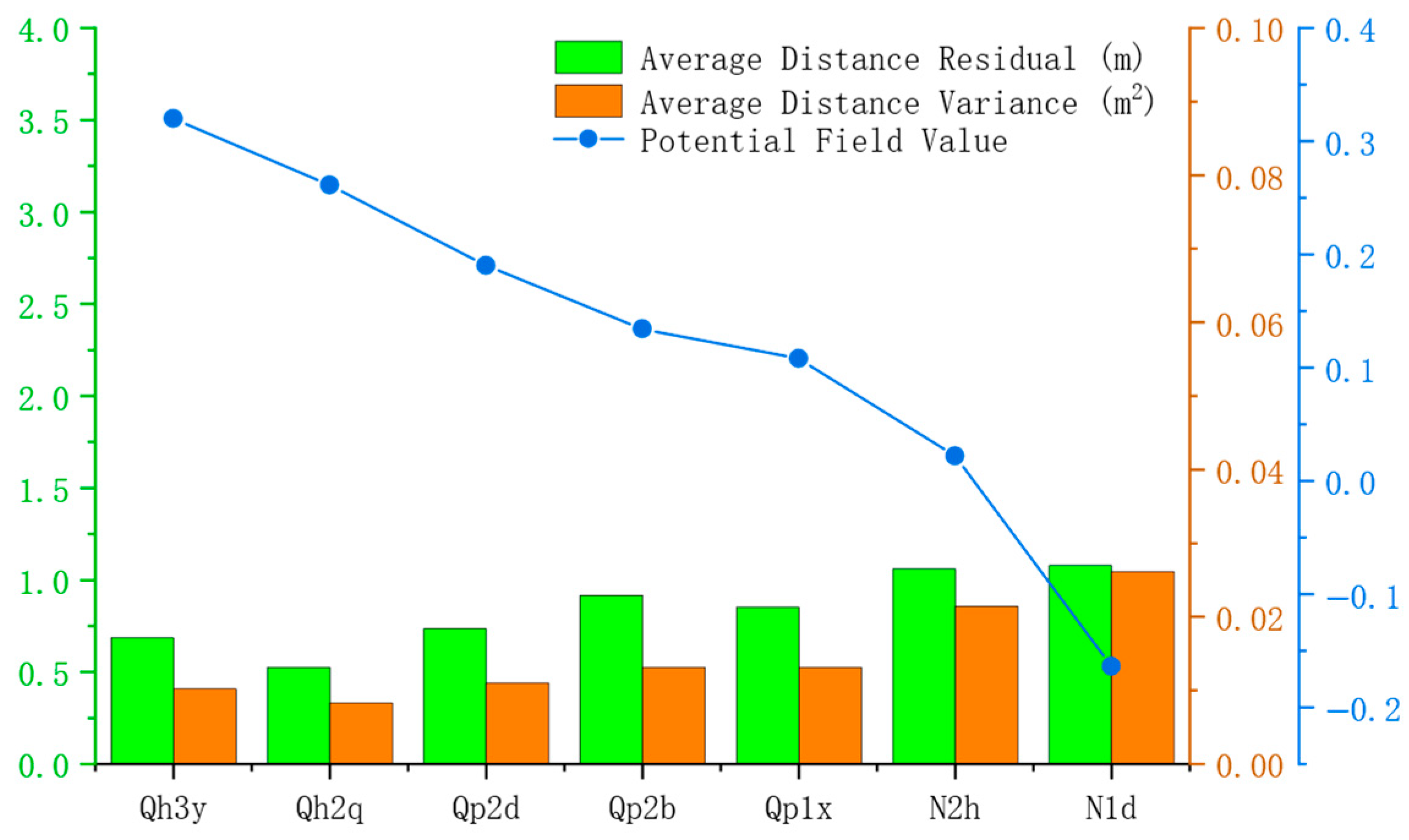
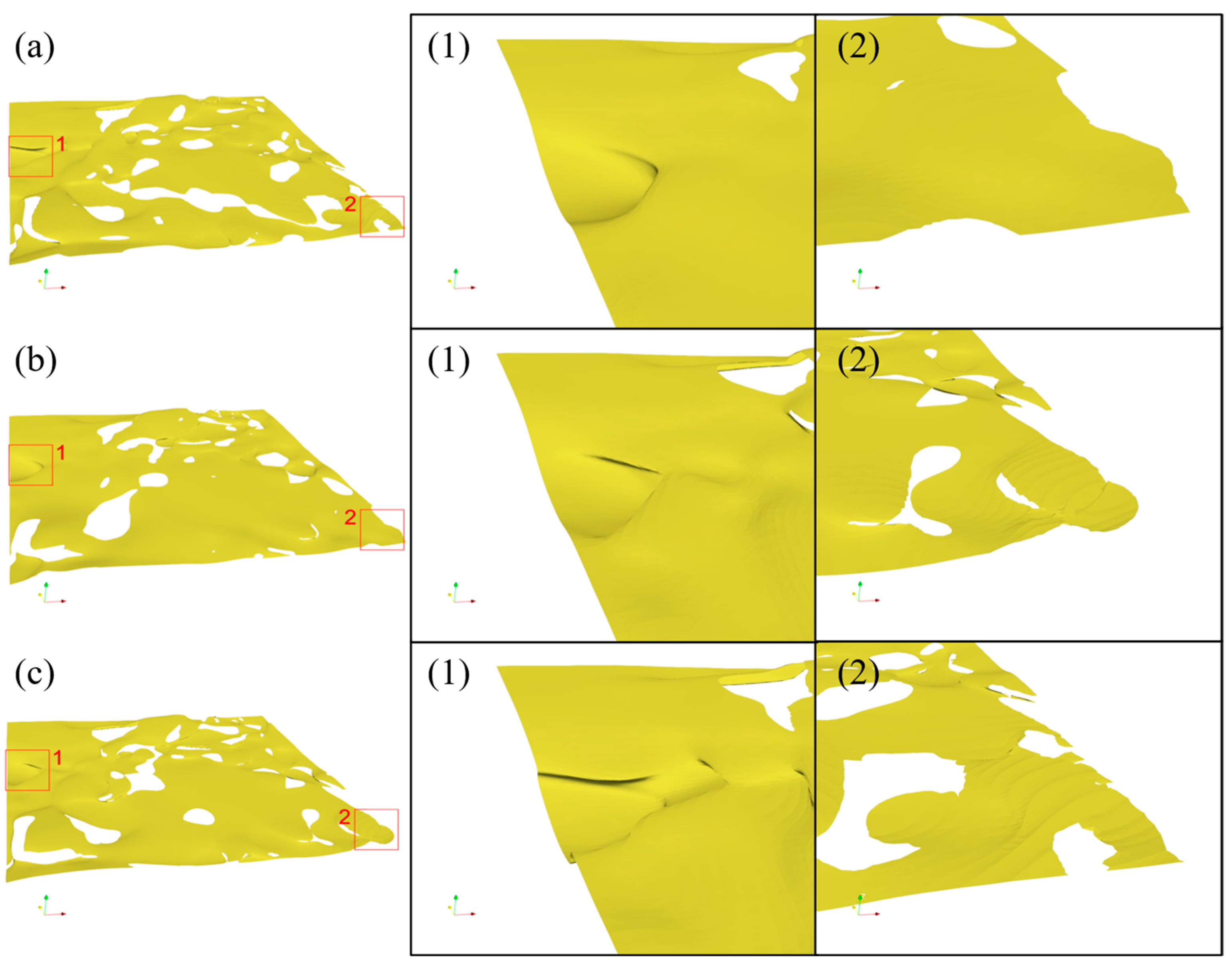
| Network | Use Stage | Loss Function | Network Structure | Description |
|---|---|---|---|---|
| Auto-Encoder (AE) Model | Pre-training Stage | L1, L2 loss function | Encoder: Conv(3 × 128) → Conv(128 × 256) → FC(256 × 256) Decoder: Conv(256 × 128) → Conv(128 × 1) | Construct the Basic Model Structures of SAE and GeoSAE |
| Stacked Auto-Encoder (SAE) Model | / | / | AEF°AEF−1°⋯°AE2°AE1, “°” represents the stacking operation between model | Stack AE for a specified number of times to obtain the result |
| GeoSAE Method | Training and Prediction Stage | Loss Function with Geological Constraints Proposed in Section 2.1 | Stack SAE for the number of specified scalar fields | The loss function is modified based on SAE to the geological constraint loss function proposed in Section 2.1, thus obtaining the GeoSAE method |
| Geological Age System | Formation Group | Sedimentary Environment | Stratigraphic Code | Contact (to Upper Strata) | |||
|---|---|---|---|---|---|---|---|
| Era | Period | Epoch | Age | ||||
| Cenozoic | Quaternary system | Holocene epoch | undivided | Alluvial deposits Qh | fluvial facies | 1-1-1 | / |
| upper | Yandun group Qh3y | coastal-lagoon facies | 1-1-2 | parallel unconformable | |||
| middle | Qiongshan group Qh2q | deltaic facies | 1-1-3 | conformable | |||
| Pleistocene epoch | middle | Duowen Group Qp2d | volcanic facies | 1-2-1 | parallel unconformable | ||
| Beihai group Qp2b | alluvial fan facies | 1-2-2 | parallel unconformable | ||||
| lower | Xiuying group Qp1x | lacustrine facies | 1-2-3 | parallel unconformable | |||
| Neogene series | Pliocene epoch | Haikou groupN2h | shallow marine shelf/barrier island facies | 2-1-1 | parallel unconformable | ||
| Miocene epoch | Dengjiaolou Group N1d | shallow marine shelf facies | 2-2-1 | conformable | |||
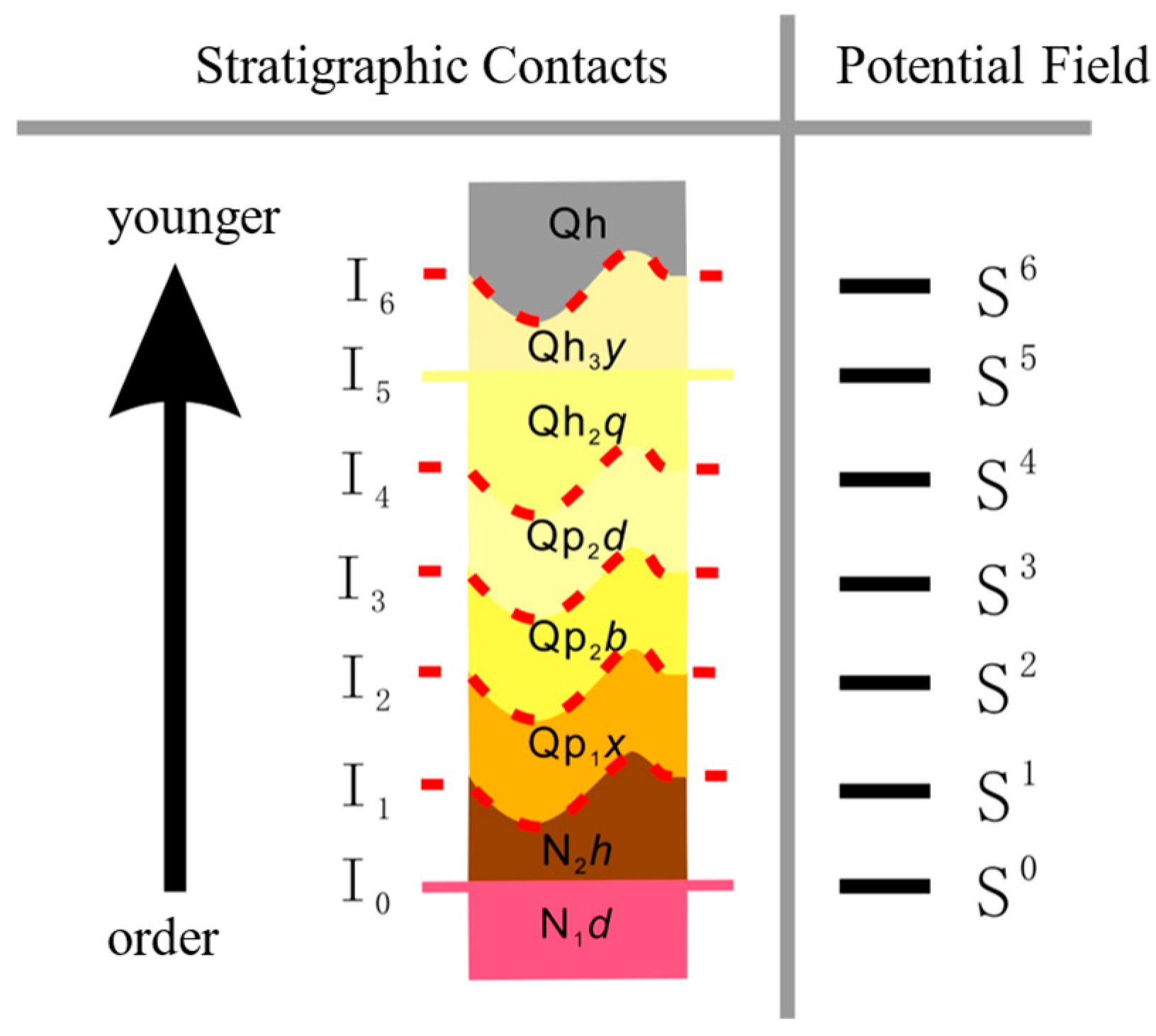
| Stratigraphic Surfaces | Formation Group | Stratigraphic Code | Potential Field Code | Upper Geological Interface | Lower Geological Interface |
|---|---|---|---|---|---|
| I0 | N1d | 2-2-1 | S0 | None | None |
| I1 | N2h | 2-1-1 | S1 | None | I0 |
| I2 | Qp1x | 1-2-3 | S2 | None | I0, I1 |
| I3 | Qp2b | 1-2-2 | S3 | None | I0, I1, I2 |
| I4 | Qp2d | 1-2-1 | S4 | None | I0, I1, I2, I3 |
| I5 | Qh2q | 1-1-3 | S5 | None | I0, I1, I2, I3, I4 |
| I6 | Qh3y | 1-1-2 | S6 | None | I0, I1, I2, I3, I4, I5 |
| Model Loss Metrics | Worth |
|---|---|
| Loss of stratigraphic consistency | 0.00336 |
| Global smoothing loss | 0.02705 |
| Potential field bias loss | 0.05635 |
| Potential field variance loss | 0.00114 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Zhou, J.; Ruan, M.; Xiao, H.; Hua, W.; Wei, W. GeoSAE: A 3D Stratigraphic Modeling Method Driven by Geological Constraint. Appl. Sci. 2025, 15, 1185. https://doi.org/10.3390/app15031185
Yang Y, Zhou J, Ruan M, Xiao H, Hua W, Wei W. GeoSAE: A 3D Stratigraphic Modeling Method Driven by Geological Constraint. Applied Sciences. 2025; 15(3):1185. https://doi.org/10.3390/app15031185
Chicago/Turabian StyleYang, Yongpeng, Jinbo Zhou, Ming Ruan, Haiqing Xiao, Weihua Hua, and Wencheng Wei. 2025. "GeoSAE: A 3D Stratigraphic Modeling Method Driven by Geological Constraint" Applied Sciences 15, no. 3: 1185. https://doi.org/10.3390/app15031185
APA StyleYang, Y., Zhou, J., Ruan, M., Xiao, H., Hua, W., & Wei, W. (2025). GeoSAE: A 3D Stratigraphic Modeling Method Driven by Geological Constraint. Applied Sciences, 15(3), 1185. https://doi.org/10.3390/app15031185






