Finite-Element Simulations of the Static Behavior and Explosive-Rupture Dynamics of 500 kV SF₆ Porcelain Hollow Bushings

Abstract

We investigate the explosive-rupture behavior of porcelain hollow bushings using a representative 500 kV SF₆ incident as the reference case. Finite-element simulations are performed for both the static response and the rupture process. Results show that internal SF₆ pressure drives the maximum equivalent (von Mises) stress to the flange, while strain localizes near the bushing mid-span. These findings highlight the cement–grout potting between the porcelain shell and flange, the waterproofing treatment, and the mid-span bonded joint as key manufacturing control points. Dynamic simulations further indicate that comparing the explosive-equivalent energy of the SF₆ pressure impulse with the gas expansion (burst) energy enables diagnosis of the failure mode. From the viewpoint of fragment kinetic energy, the analysis indirectly verifies that rupture is initiated by intrinsic porcelain defects and subsequent crack propagation. The simulated fragment morphology and ground dispersion agree with field observations from the actual event, underscoring the critical role of microcracks in brittle fracture. Accordingly, optimizing firing processes to reduce internal cracks and voids—via raw-material control and firing-temperature optimization—is essential for reliability improvement and life extension. The results provide a practical reference for the design and long-term operation of porcelain bushings.

1. Introduction

Electric power is indispensable to modern society, and the stability and safety of its supply are critical to socioeconomic development. As a key component of ultra-high-voltage (UHV) grids, 500 kV high-voltage circuit breakers play an essential role; their reliability directly affects supply continuity, system stability, and grid operating safety. The 500 kV bushing—serving as both a primary insulation and mechanical support element for the breaker—is therefore vital to secure power transmission. Failure statistics for power transformers show that bushing-related defects are a major cause of outages [1], and on-line partial-discharge monitoring studies further emphasize the need to ensure bushing insulation integrity [2].

SF₆-filled 500 kV porcelain hollow bushings are widely deployed because of their excellent dielectric performance and mechanical strength. However, analyses of bushing failures and fragment trajectories [3,4], investigations of porcelain failure mechanisms [5], and recent seismic failure case studies of 500 kV transformer–bushing systems [6] indicate that explosive rupture of porcelain bushings can occur in service and that the resulting fragments may scatter widely, posing serious risks to personnel and grid assets. For example, on 28 August 2015, the busbar-side bushing on phase A of a 500 kV breaker at Substation A suffered a burst failure; on 16 December 2016, the busbar-side bushing on phase B of a 500 kV breaker at Substation B failed in a similar manner. In both cases, porcelain fragments were dispersed within an ~80 m radius, and surrounding equipment sustained various degrees of damage—including fractured grounding flat bars and punctures in the casings of adjacent breakers—as illustrated in Figure 1. Fortunately, no personnel were in the vicinity at the time, and no injuries occurred.

Extensive research has been conducted worldwide on the causes of porcelain bushing rupture and on measures to enhance in-service reliability. These efforts have not only traced the root causes of explosive rupture but also proposed practical prevention strategies.

International work has focused mainly on improving porcelain formulations and processing, optimizing bushing design, and deploying on-line monitoring. For example, Jonsson, Lundborg and colleagues at ABB (Sweden) combined porcelain bushings with composite insulators to enhance dielectric performance and ageing resistance [7] and applied on-line diagnostics to detect incipient hazards in service [8]. Naito and co-workers at NGK Insulators (Japan) experimentally investigated the rupture process and proposed measures to mitigate risks to nearby equipment and maintenance personnel, such as reducing SF₆ pressure and adding an interposed fiberglass-reinforced plastic (FRP) sleeve to decrease the gas volume acting on the porcelain [9]. At Cranfield University, C. Knock et al. first developed Monte Carlo models for the initial attributes and flight trajectories of porcelain fragments and predicted fragment paths and impact forces [10]; in a follow-up study, they performed complementary experiments and simulations by varying the size of the nylon core to modify the internal gas volume, and found that volume reduction does not necessarily lessen fragment risk [11].

Despite these advances, bushing-rupture incidents have not been fully eliminated. SF₆ internal pressure exerts complex effects on the bushing, and the intrinsic properties of porcelain mean that bushings in service are subjected to multiple mechanical loads—internal pressure, self-weight, temperature variations, mechanical shocks, and vibration. Consequently, long-term reliability assessment under coupled, real-world conditions remains at an early stage.

To address these gaps, this study undertakes a detailed analysis of the rupture causes in 500 kV SF₆ porcelain hollow bushings and employs finite-element simulations of both statics and dynamics to elucidate their in-service mechanical behavior and rupture mechanisms. In the broader context of computational fracture mechanics, enriched finite-element formulations have been developed to improve the representation of discontinuities and singular fields by embedding problem-specific enrichment functions into the standard interpolation [12]. Such approaches can efficiently capture crack initiation and propagation without excessive mesh refinement when crack paths are highly curved or not known a priori. In the present work, however, the failure plane is largely constrained by the porcelain bushing geometry and the interface configuration, so that the dominant rupture path can be anticipated in advance. We therefore adopt a conventional finite-element formulation with locally refined meshes around critical regions, which provides a suitable balance between accuracy and computational efficiency for the large-scale parametric simulations required in this study.

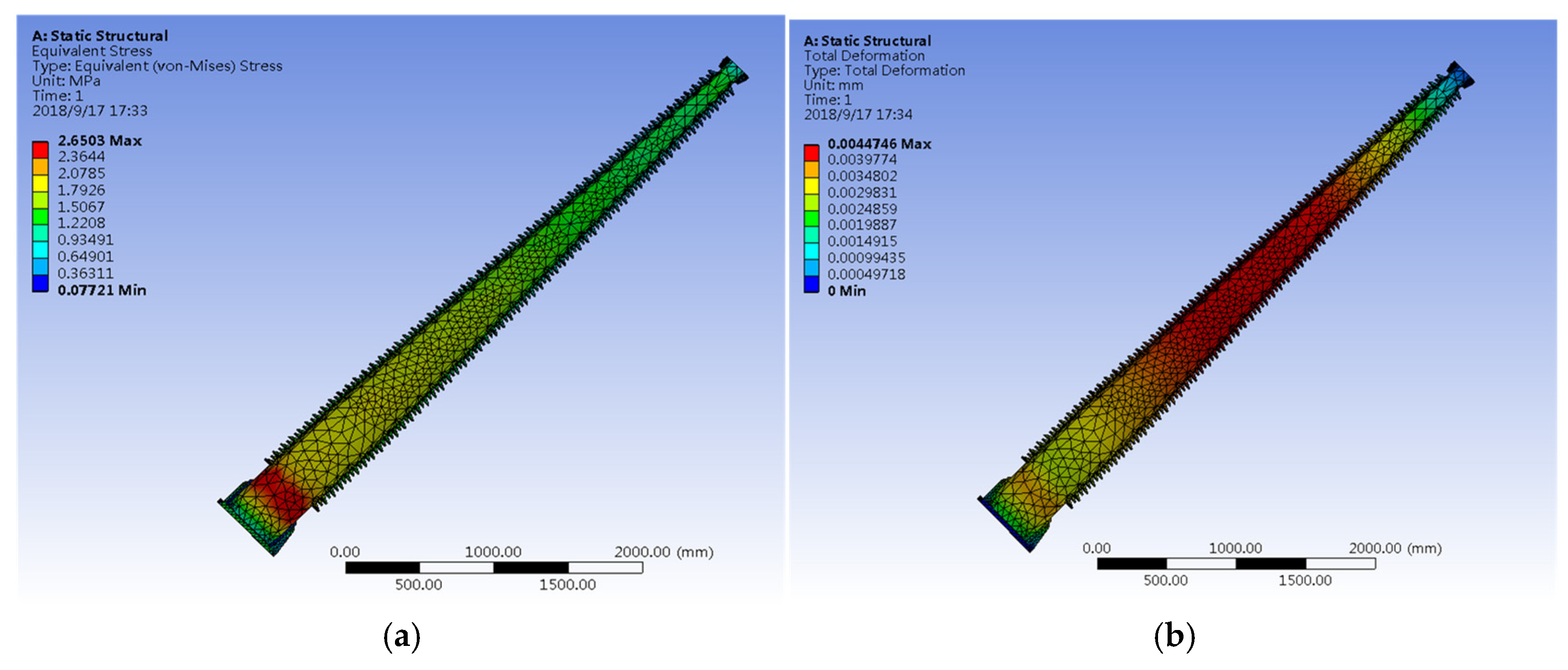
2. Stress Analysis of the Bushing

During service, the inner surface of the bushing is subjected to the steady internal pressure of SF₆ gas. Static structural finite-element analysis is used to evaluate stresses, displacements, and strains under stable loading, and to verify the product’s strength, stiffness, and stability. Following the methodology outlined in the previous section, a full-scale (1:1) numerical model of the manufacturer’s porcelain bushing was constructed in ANSYS STUDENT 2025 R2, as shown in Figure 2. The porcelain shell is discretized using three-dimensional quadratic tetrahedral solid elements. A locally refined mesh is employed in the flange and metal–porcelain junction region, where the characteristic element size is about 15–20 mm, while a coarser mesh with an element size of about 30–40 mm is used along the mid-span. In total, the model contains roughly 4 × 10⁴ solid elements and 7 × 10⁴ nodes, with the highest element density concentrated in the critical flange zone where rupture is most likely to initiate.

Material parameters were set according to

Table 1. Material properties used in the simulation model.

Component	Elastic Modulus, E (GPa)	Poisson’s Ratio, ν	Density, ρ (kg·m−3)
Porcelain	110	0.35	2800
Cement (grout)	35	0.33	2600
Cast iron	200	0.30	7800

. based on reported properties of porcelain insulators [13], cementitious grout [14] and cast-iron components [15] in similar high-voltage equipment. The internal SF₆ gas applies a pressure of 0.6 MPa on the bushing’s inner surface, while mutual constraints within the ceramic produce the corresponding internal stress field. Excessive stress may trigger brittle fracture. A quarter-symmetry model (1/4 model) was used for the structural analysis. The bottom flange that connects the bushing to the transformer tank was fully fixed in all translational degrees of freedom (U_x = U_y = U_z = 0), representing the clamped support. Symmetry boundary conditions were imposed on the two orthogonal mid-planes of the 1/4 model, constraining the normal displacement while allowing in-plane displacements to remain free. The porcelain body, cementitious grout and metallic fittings were tied to each other to ensure compatible displacements across their interfaces. The resulting equivalent (von Mises) stress contour is shown in Figure 3a, and the total strain map in Figure 3b.

As shown in Figure 3a, under an internal SF₆ pressure of 0.6 MPa, the porcelain–flange transition exhibits the peak equivalent (von Mises) stress (≈2.65 MPa). This hotspot arises from the geometric and stiffness discontinuity combined with end restraint, which concentrates load paths and superposes tensile principal and circumferential stresses at the flange root. Along the axial direction, the equivalent stress rapidly decays and approaches a more uniform state in the tubular body. The length and quality of the cement–grout potting between the porcelain and the flange directly affect this concentration: a potting length that is too short, or modulus/CTE incompatibility, shifts additional hoop tension into the flange region and reduces safety margins. Waterproofing of the potting zone is also essential. Cement is hygroscopic; without waterproofing, its volume and apparent hardness increase with moisture uptake, thereby raising constraint stresses on the porcelain. Since cured cement is porous and may contain cracks, freeze–thaw cycling in cold climates propagates those cracks and induces frost heave, imposing abnormal additional stresses on the porcelain [16,17]. These simulation-based inferences are consistent with field observations: Figure 4a (Substation C, manufacturer A) shows a through-crack at the flange produced by long-term stress concentration, and Figure 4b (Substation B, manufacturer B) shows a burst in which the lack of waterproofing at the potting region is among the most plausible causes. Consequently, engineering measures should aim to mitigate flange-region stress concentration and improve reliability by adopting appropriate potting length and smooth geometric transitions, ensuring modulus/CTE compatibility of the potting compound, and implementing robust waterproof sealing and quality control.

As shown in Figure 3b, the deformation field (Total Deformation) is axisymmetric with outward radial bulging. End restraints suppress local displacement, whereas the mid-span exhibits larger strain than the two ends, with a peak total displacement of ~0.0045 mm. Although the absolute displacement is small and the global stiffness is adequate, failure in brittle porcelain is governed by the coupling of local tensile stress with pre-existing microdefects. The elevated circumferential tensile strain at mid-span is particularly detrimental to surface/subsurface pores and microcracks and tends to promote their growth. This distribution is critical for multi-section assembled bushings, in which the mid-span typically coincides with an adhesive/bonded joint; the joint’s strength and uniformity directly bound the safety margin under combined internal pressure and thermal differentials. This understanding is consistent with the conclusions of [18]. Similar domestic failures have been reported: Figure 5a (Substation A, manufacturer C) shows joint separation under internal hydrostatic pressure due to deficient adhesive quality at the splice, while Figure 5b (Substation C, manufacturer C) shows that elevated SF₆ pressure produced large mid-span strain, leading to debonding and eventual rupture. Taken together, the simulations and cases identify the mid-span adhesive joint and the flange potting/waterproofing system as primary manufacturing and O&M control points. We recommend tighter process control and nondestructive evaluation of the joint (e.g., ultrasonics or infrared thermography), along with design refinements in wall-thickness uniformity and transition radii, and tighter control of geometric tolerances and residual stress, so as to reduce the mid-span strain peak and the risk of interfacial separation.

3. Dynamic Simulation of the Bushing Rupture Process

This Section is divided into three parts. Section 3.1 presents the methods for estimating the rupture energy based on fragment statistics and fragment flight kinematics. Section 3.2 develops the TNT-equivalent blast model of porcelain bushing rupture using the JWL equation of state. Section 3.3 compares the numerical predictions with the measured fragment distribution and damage radius.

3.1. Mechanism of Bushing Rupture

Porcelain is widely used for hollow bushings because of its high hardness, excellent electrical insulation, and chemical stability [19]. However, several intrinsic shortcomings must be considered. First, the selection of raw constituents and control of the sintering schedule have a decisive influence on the formation of internal defects and microcracks during manufacturing [20]. Second, porcelain is highly brittle and thus prone to fracture under impact or bending, especially in the absence of sufficient plastic deformation to absorb and redistribute stress [21]. Third, porcelain is sensitive to rapid temperature changes; its poor thermal-shock resistance facilitates crack initiation during fast heating or cooling [22]. In addition, even within a single production batch, material strength may exhibit notable statistical scatter (e.g., Weibull-type dispersion), which increases the risk of occasional in-service failures [23,24].

Accordingly, we hypothesize that rupture is triggered by pre-existing internal cracks in the porcelain. During an internal arc, the associated shock wave and transient thermal stresses drive rapid crack extension, culminating in burst failure. The following dynamic simulations of the explosive-rupture process are used to test and substantiate this hypothesis.

3.1.1. Energy of Rupture Due to Crack Growth and Gas Expansion

Crack-driven failure in a pressurized porcelain bushing derives most of its burst energy from the expansion of the enclosed gas. For the SF₆ bushing, the pressure drop from the pre-burst value to atmospheric pressure is commonly approximated as an adiabatic expansion with negligible heat exchange. The gas-release (burst) energy can therefore be estimated by [25]:

$$E_g={\displaystyle \frac{PV}{k-1}}\left[1-{\left({\displaystyle \frac{0.1013}{P}}\right)}^{{\displaystyle \frac{k-1}{k}}}\right]\times {10}^3,$$

(1)

where E_g is the burst energy of the SF₆ gas (kJ), P is the absolute gas pressure before rupture (MPa), V is the internal volume of the bushing (m³), and k is the adiabatic index of SF₆. Unless otherwise stated, the internal SF₆ pressure is taken as P = 0.6 MPa, corresponding to the rated filling pressure of the 500 kV porcelain hollow bushing under normal service conditions, and is used as the baseline for estimating the gas-release energy. V ≈ 0.34 m³, and k = 1.13, we obtain E_g ≈ 292.8 kJ.

3.1.2. Energy Associated with Internal Discharge

An alternative (and often coupled) cause of explosive-rupture in pressurized porcelain bushings is internal discharge [26]. The arc’s high temperature produces rapid gas expansion and a steep pressure rise; the resulting shock loading can drive the porcelain past its fracture threshold. Following a post-event site survey at Substation B, we analyzed 14 sampling locations in accordance with explosion-mechanics principles. The dataset (

Table 2. Sampling data for major ceramic fragments at the blast site.

Fragment ID	Azimuth (°)	Distance (m)	Mass (kg)
1	10	18.0	8.0
2	20	17.8	27.0
3	45	18.0	5.5
4	60	17.9	1.0
5	90	28.2	48.9
6	140	29.4	8.5
7	170	57.9	3.3
8	195	35.7	7.5
9	200	32.7	3.0
10	225	42.0	6.0
11	250	19.5	9.8
12	270	28.2	23.6
13	300	21.3	16.0
14	315	18.5	35.3

Azimuth is defined with 0° at due east from the blast center, increasing counterclockwise.

) includes azimuth, standoff distance, and fragment mass for each location, which are subsequently used to infer fragment kinetic energy and to back-estimate the discharge-induced energy release during the event.

The flight of the porcelain fragments is shown in Figure 6. In this schematic, u_f denotes the magnitude of the initial fragment velocity, φ is the initial launch angle measured from the horizontal, and Y_min is the minimum vertical distance between the fragment trajectory and the ground. Field observations indicate that most fragments travelled close to horizontally (small φ), so when evaluating the throw distance, the motion is approximated by its horizontal projection (φ ≈ 0), while Figure 6 is retained as a general kinematic diagram to define these parameters. Neglecting aerodynamic drag, the launch can be approximated as a horizontal projection. Using the measured horizontal stand-off distances from the blast center, the initial horizontal velocity of each fragment was back-calculated. The mass-weighted mean fragment velocity is 22.36 m/s.

Explosions involve coupled electrical and chemical processes, making post-event energy diagnosis challenging. Here, we adopt a simplified approach [27,28] by converting the event energy to an equivalent TNT mass and estimating it with the Gurney formula for hollow cylindrical charges. The Gurney relation [29,30] empirically links the explosive energy to the initial fragment velocity for hollow cylindrical charges, and is given by:

$$V_0=\sqrt{2E}{\left({\displaystyle \frac{M}{C}}+{\displaystyle \frac{1}{2}}\right)}^{-1/2},$$

(2)

where V₀ is the mass-weighted initial velocity of the porcelain bushing fragments (m/s), M is the bushing (shell) mass (kg)—preliminarily estimated as 650–850 kg, C is the equivalent TNT mass, and is a constant taken as 2400 m/s from tabulated values [27]. In applying the Gurney method, the strength of the shell and energy losses associated with rupture are neglected. Back-calculating from (2) yields an equivalent TNT mass of 55–75 g, corresponding to 250.8–342 kJ. This TNT equivalence is used as an engineering surrogate to obtain the correct order of magnitude of the released energy, rather than as a fully calibrated description of the specific arc–gas–porcelain system.

Combining the above results, the rupture energy estimated from gas expansion and crack growth in the SF₆-filled bushing is E_g ≈ 292.8 kJ, whereas the fragment-flight analysis based on the Gurney approach yields an equivalent TNT mass of 55–75 g, corresponding to 250.8–342 kJ. These two independent methods thus give rupture energies of the same order of magnitude, and their mid-range values differ by only about 1–2%. This agreement, within the expected uncertainty of the simplified models, supports the energy level adopted for the subsequent dynamic simulations of the porcelain bushing rupture.

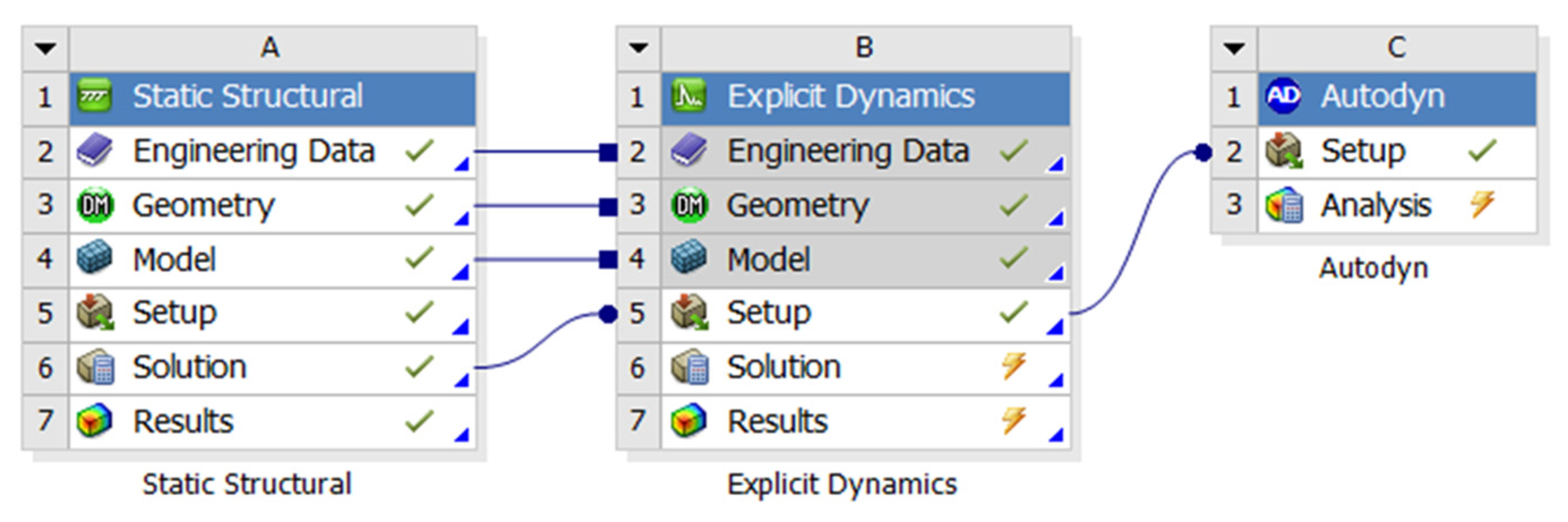
3.2. Principle of Dynamic Simulation for the Bushing Rupture Process

The rupture process is treated as the explosive-rupture of a pressurized vessel. The blast overpressure is computed using the ideal-gas equation of state:

$$P=\left(\gamma -1\right)\rho e+P_{shift},$$

(3)

where γ is the ratio of specific heats (adiabatic index), ρ is the density, e is the specific internal energy, and P_shift denotes the initial pressure offset.

The arc generated by gas discharge—and the resulting thermo-expansion force—is modeled by an equivalent explosive. The explosive products are described by the Jones–Wilkins–Lee (JWL) equation of state [31], an empirical pressure–volume–energy relationship widely used for high explosives, and the detonation is characterized by the Chapman–Jouguet (C–J) isentrope, given by:

$$P_s=A{e}^{-R_{1}V}+B{e}^{-R_{2}V}+{\displaystyle \frac{C}{V^{w+1}}},$$

(4)

Along an isentrope,

$$e_s=-{\displaystyle \int P_{s}dV},$$

(5)

which gives the isentropic specific internal energy as a function of the (dimensionless) relative volume V:

$$e_s={\displaystyle \frac{A}{R_1}}{e}^{-R_{1}V}+{\displaystyle \frac{B}{R_2}}{e}^{-R_{2}V}+{\displaystyle \frac{C}{w{V}^w}},$$

(6)

Substituting (5) and (6) into the Grüneisen equation of state,

$$P-P_s={\displaystyle \frac{\Gamma }{V}}\left(e-e_s\right),$$

(7)

and setting ω = Γ, one obtains,

$$P=A\left(1-{\displaystyle \frac{w}{R_{1}V}}\right)e^{-R_{1}V}+B\left(1-{\displaystyle \frac{w}{R_{2}V}}\right)e^{-R_{2}V}+{\displaystyle \frac{we}{V}},$$

(8)

In (8), P is the pressure; v = 1/ρ is the specific volume of the explosive and v₀ its initial specific volume; e is the specific internal energy of the explosive. The absolute internal energy is $e_a=m{c}_{v}T$ (J). The initial specific internal energy is

$$e_0={\displaystyle \frac{e_a}{v_0}}={\displaystyle \frac{m{c}_{v}T}{v_0}},$$

(9)

and the specific internal energy at relative volume is e = e₀/V.

On this basis, the dynamic rupture process is modeled in an energy-equivalent manner using a TNT charge. First, the rupture energy E_g obtained in Section 3.1 is converted into an equivalent TNT mass so that the specific energy release of the charge matches the internal energy available inside the bushing. The JWL equation of state and the C–J isentrope are then used to describe the pressure–volume–energy state of the TNT products, and the resulting pressure–time history is applied as the internal loading on the porcelain, grout and steel components. This TNT-equivalent framework is used as an engineering surrogate: similar to a TNT-filled cylindrical shell, a pressurized porcelain bushing fails by the rapid release of internal energy in a confined volume and the fragmentation of a brittle shell, so global quantities such as peak overpressure and fragment velocity are governed mainly by energy and geometry. At the same time, the present event differs from a true detonation because the energy originates from compressed SF₆ and arc heating and the pressure rise is slower; the TNT model is therefore intended to approximate the intensity and spatial distribution of the impulsive loading, rather than to reproduce the detailed chemistry of an explosive.

3.3. Dynamic Simulation of the Rupture Process

To represent the impulsive loading on the porcelain bushing produced by an internal (arc) discharge, we model the discharge as an equivalent explosive. The blast dynamics simulations are performed with the nonlinear transient dynamics code AUTODYN, which is widely used in aerospace and defense applications for analyzing blast and shock effects. AUTODYN can extract fragment-related outputs during a run—including the number of fragments, individual masses, kinetic energies, and spatial coordinates—and is well suited for structural dynamics, impact, and blast/shock-wave response problems. It is broadly recognized as an effective tool for simulating structures under short-duration loads and for capturing associated failure modes.

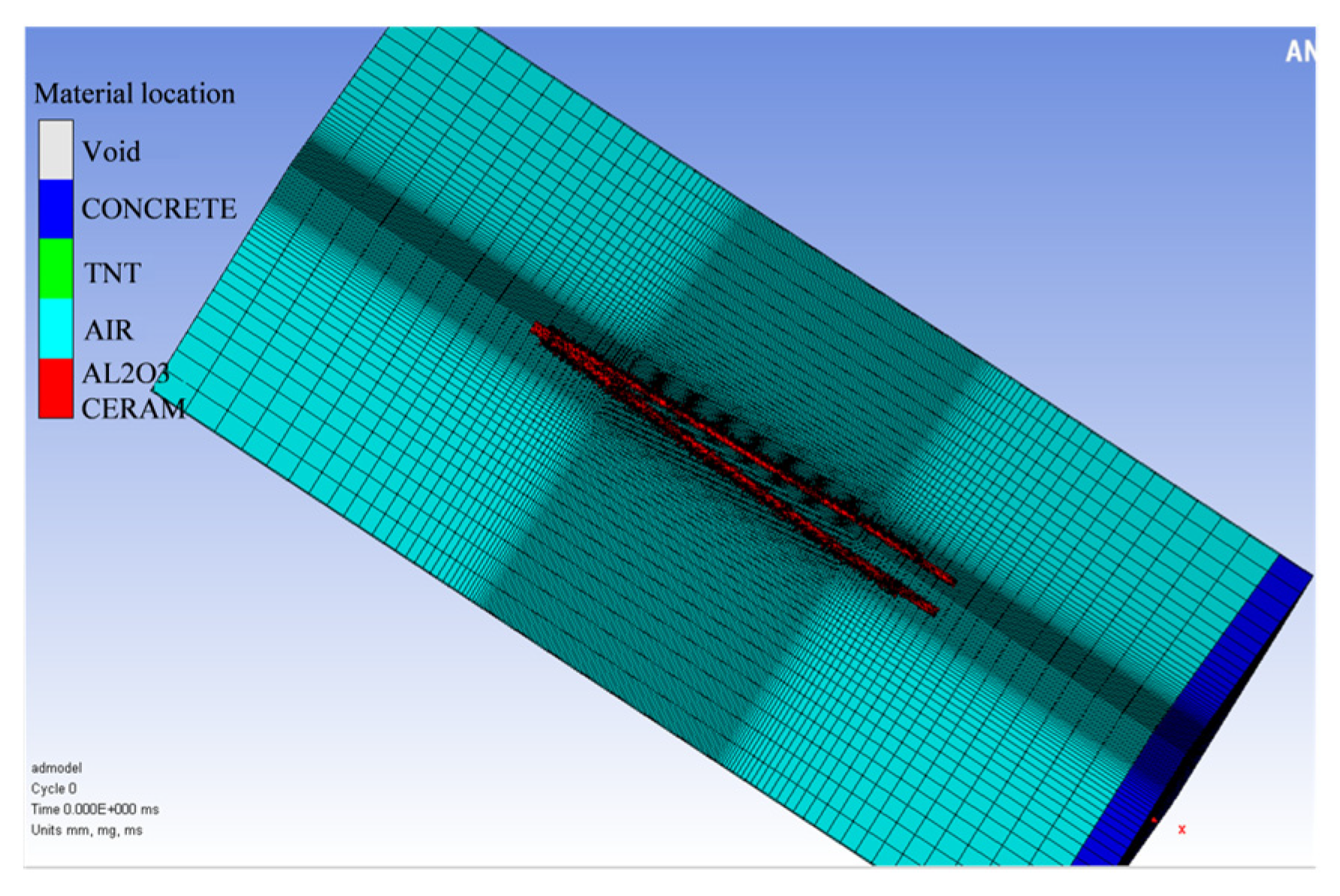
3.3.1. Construction of the Simulation Model

A geometric model of the porcelain bushing was first created in SolidWorks 2024. Pre-processing and model association were then carried out in ANSYS Workbench 2024 R2, as shown in Figure 7. The Static Structural system was used to generate the mesh, apply boundary conditions (initial pre-stress, gravity, and fixed supports), and pass the solution as initial conditions to the Explicit Dynamics system. Within ANSYS Workbench (Component Systems), AUTODYN was dragged onto the Setup cell of Explicit Dynamics (ANSYS) to configure and run the blast dynamics simulation of the bushing. To reduce the computational cost per run, only the porcelain shell was modeled and a quarter-symmetry (1/4) model was employed.

After completing the geometric model, a finite-element (FE) model with nodes and elements was generated by meshing. The porcelain bushing was discretized using tetrahedral elements. The mesh was created rapidly and automatically, with curvature- and size-based local refinement applied in critical regions. Inflation layers were introduced near solid boundaries to enhance resolution in the surface-normal direction. Once the model setup was finalized, the static solution was obtained and passed to AUTODYN.

After importing the preprocessed solution into AUTODYN, an air domain was constructed to simulate blast-wave propagation. The complete AUTODYN model therefore comprised the porcelain bushing, ambient air, ground (target) surface, and the TNT charge, as illustrated in Figure 8.

3.3.2. AUTODYN Parameter Settings

As schematized in Figure 8, the computational domain comprises the explosive charge, the porcelain bushing, and a surrounding air region of sufficient extent. A fluid–structure interaction (FSI) scheme is adopted [32], in which the bushing is discretized with a Lagrangian mesh embedded within a Eulerian air domain via the built-in coupling algorithm. Using LOAD, the AUTODYN material library is accessed to assign models for Air, the Explosive, and the Ground/target [33]. Air is represented by the ideal-gas equation of state (EOS); the explosive is described by the JWL EOS; and the porcelain bushing is modeled as Al₂O₃ ceramic (AL2O3 CERA in the library) with a Linear EOS [34]. The strength behavior follows the Johnson–Holmquist ceramic model, suitable for brittle materials at large strain, high strain rate, and high pressure, while failure is captured using Mott statistical fragmentation (strain-based failure). This configuration enables the simulation to resolve shock loading, structural response, and fragmentation under blast conditions with appropriate fidelity.

3.3.3. Executing the AUTODYN Solution

Within AUTODYN, the materials, solver algorithms, contacts, coupling, and boundary conditions are configured to represent the equivalent TNT energy release associated with the bushing burst. The burst origin is used to emulate the initial fault location on the porcelain; in this study the charge (burst point) is positioned at the upper one-third of the porcelain insulator above the mounting flange (i.e., the upper one-third of the ceramic body, excluding the flange), as indicated by the red dot in Figure 9. To reduce computational cost, only the porcelain shell is modeled and quarter-symmetry (1/4) is applied. The simulation is advanced in time, and four representative output instants are selected to visualize the progression of rupture and fragment development, yielding the states shown in Figure 9a–d.

To establish a defect baseline, we first performed single-initiation blast simulations with a crack-free porcelain shell. In this case, the fragments of the porcelain bushing exhibited nearly identical masses (≈1 kg each), reflecting material and geometric homogeneity and quasi-periodic circumferential segmentation governed by the JH–Mott failure law in a uniform field. In contrast, field evidence shows a broad, multi-modal fragment-mass distribution (‘few large slabs + many fines’), indicating that pre-existing microcracks and material heterogeneity are decisive. Accordingly, the follow-up simulations explicitly seed multiple microcracks with sizes of 50 μm–5 mm and random orientations in the porcelain body and glaze. The crack centres are randomly positioned within the high-stress band near the flange identified by the static analysis, and their lengths are sampled from a truncated distribution in this size range. The crack population is chosen such that the mean spacing between neighbouring crack tips is on the order of one to two local element sizes, thereby representing a moderate defect density. No deterministic crack network or spatially correlated random field is imposed; instead, a purely stochastic seeding is adopted to reflect the uncertain defect layout in the actual bushing. Model calibration targets the fragment-mass histogram and the mass-weighted initial velocity (≈22.36 m·s⁻¹) and ground-dispersion radius/azimuth inferred from the Gurney analysis: the microcrack density and distribution are adjusted within realistic bounds until the simulated mass distribution and dispersion envelope qualitatively match the field data. In parallel, energy calibration uses explosion mechanics together with the azimuth–distance–mass data from 14 field fragments to back-calculate an equivalent TNT mass of 55–75 g (250.8–342 kJ), while the SF₆ gas burst energy computed under an adiabatic-expansion assumption is 292.833 kJ. The comparable magnitude and overlap between these ranges are used to select the TNT-equivalent charge for AUTODYN, ensuring that the imposed blast loading is consistent with both the stored gas energy and the observed fragment kinematics.

Using the ANSYS Workbench pre-processor, multiple microcracks were explicitly seeded into the simulation model; the crack locations are indicated in Figure 10a, where regions of mesh densification mark the inserted flaws. A subsequent blast simulation produced the fragment set shown in Figure 10b. With microcracks introduced, the porcelain bushing yielded several large-mass fragments, with representative masses of 77 kg, 30 kg, 19 kg, 18 kg, and 10 kg.

Figure 10a shows the porcelain-bushing microcrack model in the ANSYS Workbench pre-processing stage. The bushing is a long cylindrical shell with sheds, discretized by a tetrahedral volume mesh. Multiple microcracks are randomly seeded at several axial locations; the surrounding zones exhibit local mesh densification to enhance numerical resolution of crack-tip stress/strain gradients and to mitigate element-size locking in erosion/strain-based failure. Under this initial defect field, internal-pressure/blast loading generates hoop (circumferential) principal tension that first concentrates at the crack tips; subsequent reflections across the wall thickness—caused by impedance mismatch—produce secondary tensile waves that promote coalescence and branching of neighboring microcracks. Cracks propagate circumferentially with near-regular spacing, while their axial evolution is modulated by the asymmetric boundary conditions imposed by the initiation site, thereby seeding the non-uniform fragmentation that follows [35,36].

Figure 10b presents the post-blast fragmentation morphology and fragment statistics from AUTODYN 2024 R2. For clarity, only the porcelain material is shown (red, Material Location: AL₂O₃ CERA), with air/explosive/ground suppressed. A through-opening first forms in the upper segment near the burst point and then spreads bilaterally, with fragments being ejected predominantly along the shell normal; the lower segment remains comparatively intact, indicating that initiation location and boundary constraints dominate the flexural–torsional coupled response. The fragment list on the right reports several large-mass primary fragments—approximately 77.6 kg, 30.2 kg, 19.3 kg, 18.3 kg, and 13.0 kg—together with numerous smaller pieces, yielding a broad, multi-modal mass spectrum characterized by “a few large slabs plus a fines tail.” This distribution is consistent with classical Mott/Grady–Kipp dynamic fragmentation and with the Weibull statistical dispersion of brittle strength: tensile-dominated fracture at high strain rate produces slab-like fragments alongside wide size scatter, while the statistical distribution of intrinsic defects further broadens the spectrum [37]. Employing AUTODYN for explicit blast–fragmentation dynamics together with the JWL products equation of state effectively reproduces the short-duration wave propagation and failure morphology observed in such events [38,39].

To facilitate a direct comparison between field observations and numerical predictions, the main fragment-mass statistics are summarised in

Table 3. Comparison of fragment-mass statistics between field data and numerical simulation.

Quantity	Field Data (14 Major Fragments, Table 2)	Numerical Simulation (10 Main Fragments, Figure 10b)
Number of fragments considered, N	14	10
Minimum fragment mass/kg	1.0	5.4
Maximum fragment mass/kg	48.9	77.6
Mean fragment mass/kg	14.5	18.6
Standard deviation of mass/kg	14.1	22.3

. For the field case, the statistics are computed from the 14 major fragments listed in Table 2, whereas for the numerical case they are evaluated from the 10 main porcelain fragments identified in the AUTODYN simulation (Fragment Nos. 1–10 in Figure 10b). Overall, the numerical model reproduces the order of magnitude and broad spread of fragment masses observed in service, although it predicts a heavier largest fragment and a slightly larger mean mass, which is reasonable in view of the simplified representation of microcracks and material heterogeneity.

For energy calibration, we used explosion mechanics together with field data from 14 major fragments (azimuth–distance–mass) and, via the Gurney formula for hollow-cylindrical charges, back-estimated an equivalent TNT mass of 55–75 g (corresponding to ≈250.8–342 kJ). In parallel, the SF6 gas burst energy computed under an adiabatic-expansion assumption is 292.833 kJ. The comparable magnitude and strong overlap between these ranges indicate a self-consistent energy setting and rupture-mechanism diagnosis, providing reliable energy boundary conditions for subsequent simulations. Furthermore, after explicitly seeding multiple microcracks in the model, the resulting fragment mass spectrum and spatial dispersion more closely matched the actual bushing failure; in contrast to the crack-free baseline that produced near-uniform fragments (≈1 kg each), the microcrack model exhibits a broad, multi-modal distribution characterized by a few large slabs with a fines tail. Given that porcelain bushings are fabricated by sintering and thus unavoidably contain pores and microcracks, their nominal strength depends not only on intrinsic material properties but is also strongly governed by the statistical distribution of defects (e.g., Weibull behavior). Consequently, initial microcracks and material heterogeneity are the key factors that trigger and shape the real fragmentation pattern. This understanding both reconciles the discrepancy between field observations and the crack-free simulations and highlights that reliability improvements should focus on manufacturing and quality-control measures aimed at suppressing and screening microdefects.

4. Conclusions

(1)

Static finite-element analysis indicates that the porcelain–flange transition experiences the maximum equivalent (von Mises) stress. When the potting length at the flange is insufficient or assembly interference is present, the local strength margin diminishes and cracking/rupture is more likely. Waterproofing of the potted region is required to suppress moisture uptake and freeze–thaw-induced constraint and degradation.

(2)

Under internal SF₆ pressure, strain concentrates near the mid-span of the bushing. For multi-section (segmented) designs, the material quality and process consistency of the adhesive joint directly govern resistance to debonding. Improving adhesive formulation and bonding procedures is therefore critical to preventing joint separation and subsequent burst of segmented bushings.

(3)

Using azimuth–distance–mass data from 14 field fragments and the Gurney formula for hollow-cylindrical charges, the back-estimated equivalent TNT is 55–75 g (≈250.8–342 kJ), while the SF₆ gas burst energy computed via an adiabatic-expansion approximation is 292.833 kJ. The comparable magnitudes and overlapping ranges support the consistency of the energy setting and mechanism assessment, and indirectly suggest the plausibility of a failure sequence in which gas-driven rupture precedes secondary discharge.

(4)

After explicitly seeding multiple microcracks in the model, the simulated fragment mass spectrum and spatial dispersion agree with field observations, indicating that pores and microcracks exert a decisive influence on fracture strength and fragmentation mode. Brittle failure driven by internal crack extension is likely one of the principal causes of explosive-rupture. Process improvements—raw-material control and optimization of firing temperature/soak—can reduce internal defects and enhance in-service reliability.

(5)

The results provide quantitative guidance for manufacturing and O&M, helping to reduce explosive-rupture incidents and safeguard power-transmission safety. Future work should refine long-term reliability assessment under coupled environmental loads, develop higher-sensitivity methods for detecting and quantitatively inferring internal microcracks, and explore materials and process routes that improve anti-burst capability.