GNSS Vector Networks in a Local Conventional Reference Frame

Abstract

The paper presents a proposal for a simple method of transforming initial GNSS vectors into a spatial local conventional reference frame. This transformation can serve as an alternative to the complex traditional procedure, which involves projecting coordinates onto a reference ellipsoid, mapping them onto a plane of an official local reference frame, and converting ellipsoidal heights into a system of orthometric heights. Local vectors (increments in horizontal coordinates and height differences) are often used in land surveying to analyse relative ground displacement, for example. The article offers a detailed definition of a local conventional reference frame and discusses its potential value for surveying practice. The proposed computation procedure was verified using a control network established to monitor displacement in a mining area. The calculated values of vector components in the local conventional reference frame were compared with the results of the traditional method for transforming GNSS vectors into official local reference frames (the PL-2000 coordinate system and the PL-EVRF2007-NH vertical reference frame). The results of both methods were verified against reference values from typical terrestrial surveys (electronic distance measurement and high-precision geometric levelling). The analysis demonstrates that the proposed numerical procedure is appropriate for control networks with certain areal limitations (up to about 300 m).

1. Introduction

Methods involving GNSS (Global Navigation Satellite Systems) have gained a solid footing in many surveying disciplines. Their popularity is amplified by the availability and improving accuracy of the technology. Other drivers include the ease of use and automated computations. It is particularly true for kinematic surveys, such as RTK (Real-Time Kinematic) or RTN (Real-Time Network) [1,2,3], where the measured point is positioned almost immediately using a selected reference frame. Additionally, the paradigm is supported by many different systems of active reference stations (such as ASG-EUPOS) [1,4,5,6], which facilitate measurements even without georeferencing to a traditional control network.

Still, kinematic techniques may be inadequate for some survey problems, such as ground displacement [7,8,9,10,11,12,13,14,15], given the accuracy and reliability of their results (coordinates). In this case, static GNSS can be used. Its downsides include longer survey times (typically 30–60 min) and a dedicated post-processing step after the measurements are completed [5,16,17]. As reported in easily available literature [18,19,20,21], satellite surveys generate results in the form of 3D vectors (ΔX, ΔY, ΔZ). The operator can easily convert them into XYZ coordinates in a geocentric, Cartesian reference frame linked to ellipsoid GRS80/WGS84 (Geodetic Reference System 80/World Geodetic System 84; both reference ellipsoids are virtually the same and are used interchangeably in geodesy [22]). For displacement surveys, periodic survey results are usually analysed in local reference frames [6,23,24,25,26] because they require information on changes in the relative positions of control points in the plane (horizontal distance) and in the vertical (height differences). In this case, the 3D coordinates (XYZ) are converted into local reference frames: xy (horizontal) and H (vertical). Regrettably, this ‘transition’ involves complicated multi-stage computations, such as the projection of coordinates onto the XYZ reference ellipsoid, map projection of the ellipsoidal coordinates (BLh) onto a local reference frame’s plane [22,25,27], and transformation of height coordinates from the ellipsoidal reference frame (h) into an orthometric reference frame [18] based on a local geoid model [28,29,30,31]. Such transformations from initial GNSS coordinates to local reference frames must involve errors (e.g., projection errors, geoid model errors, etc.).

Existing scientific studies on the processing of GNSS observations do not indicate any simple way of utilizing original vector measurement results in relation to a local reference frame. In many engineering surveying applications (e.g., when determining displacements in landslide areas), it is essential to perform analyses of changes in horizontal distances and heights (differences in height). Periodic measurements of GNSS vectors (ΔX, ΔY, ΔZ), after their transformation to a local planar coordinate system (Δx, Δy) and a local height system (ΔH), can be the source of necessary information about the changes in points’ position (horizontally and vertically).

This article presents a simplified method for converting initial GNSS vectors from a global (XYZ) reference frame to a so-called local conventional reference frame (xyH) [25,32]. This conventional reference frame is defined based on the assumption that heights H are calculated perpendicular to the 2D xy coordinate system’s plane, which is tangent to the reference ellipsoid at a point of tangency P (Figure 1, cf. [23]). This assumption holds for surveys of relatively small areas, where the impact of Earth’s curvature is negligible (considering the required accuracy, mainly for height H). Assuming the mean Earth radius of R = 6370 km, the height difference (ΔH) error can be easily estimated at below 1 mm for 100 m, about 7 mm for 300 m, and about 2 cm at 500 m, for example [33] (p. 234).

Are the accuracies given above sufficient, for example, for control network points used to determine displacements? The answer should consider both the expected (required) accuracy of the points’ location and the accuracy of the measurement technology. Another factor is the approximation for calculating height from a numerical geoid. An acclaimed scholar and expert in reference frame transformation, Łyszkowicz [23] provides the following accuracy estimates in his monograph: ellipsoidal height (h) error (from GNSS measurements) is about 2.5 cm, while the accuracy of geoid models used is about 1 cm (note that he describes the accuracies as ‘optimistic’). Therefore, the resultant mean error of orthometric height (in relation to the geoid) is about 2.7 cm.

In light of this accuracy estimate, it seems that it is fairly safe to propose a computation method in the conventional reference frame for vector networks up to 200–300 m as defined in the article (for such distances, the height error caused by disregarding Earth’s curvature does not exceed the geoid model error).

The proposed method for converting a GNSS vector network into a local conventional reference frame does not require map projection onto a plane or the use of a local geoid model when converting heights. The primary characteristic of the conversion should be the preservation of the geometry of the space figure composed of the measured GNSS vectors (see the example in Figure 2 and Figure 3). Kutoglu [24] proves that the slope (spatial) lengths based on the components of vectors of observation (ΔX, ΔY, ΔZ), when subjected to transformation between two systems of coordinates do not depend on the reference frame. Consequently, the components of the local vectors calculated in the conventional reference frame (Δx, Δy, ΔH) will also not depend on the terrain height difference. The ΔH component, however, may be affected by an error resulting from the very definition of the conventional frame (neglecting the effect of Earth’s curvature).

The numerical method has been verified with a real-life vector network established to monitor ground displacement. Its results have been compared with a conventional transformation (projection onto an ellipsoid, map projection of ellipsoidal coordinates onto a plane, and calculation of heights relative to the geoid). Both methods were verified for the consistency of the local vectors (Δx, Δy, ΔH) with results from typical terrestrial surveys (electronic distance measurement and an altimetric survey with high-precision geometric levelling).

2. Materials and Methods

This section first presents the traditional procedure for converting GNSS survey results into official local reference frames [34]. The objective is to demonstrate the complexity of the traditional procedure compared to the proposed method for transforming GNSS vectors into a 3D local conventional reference frame.

2.1. Traditional Procedure for GNSS Vector Conversion into Local Reference Frames

Static GNSS surveys produce a set of observations in the form of vectors (ΔX, ΔY, ΔZ) in a 3D space of a geocentric reference frame based on the WGS84 ellipsoid. Certain computations (conversions) are necessary to transform these observations into 2D vectors Δx, Δy (for example, on the projection plane of the official coordinate system PL-2000 for Poland, see [34]) and height difference ΔH. They can be divided into several stages.

• Adjust GNSS vectors in the geocentric reference frame based on the WGS84 ellipsoid

This step involves solving a set of linear equations of adjustments (with the least squares method [35,36]) for each vector ij [18,37,38], such as:

$$\left\{\begin{array}{l}{v}_{ij}^{\left(\Delta X\right)}=\delta X_j-\delta X_i+l_{ij}^{\left(\Delta X\right)}\\ v_{ij}^{\left(\Delta Y\right)}=\delta Y_j-\delta Y_i+l_{ij}^{\left(\Delta Y\right)}\\ v_{ij}^{\left(\Delta Z\right)}=\delta Z_j-\delta Z_i+l_{ij}^{\left(\Delta Z\right)}\end{array}\right.$$

(1)

where

$$l_{ij}^{\left(\Delta X\right)}=X_j^{\left(0\right)}-X_i^{\left(0\right)}-\Delta X_{ij}; l_{ij}^{\left(\Delta Y\right)}=Y_j^{\left(0\right)}-Y_i^{\left(0\right)}-\Delta Y_{ij}; l_{ij}^{\left(\Delta Z\right)}=Z_j^{\left(0\right)}-Z_i^{\left(0\right)}-\Delta Z_{ij}$$

(ΔX, ΔY, ΔZ) is the GNSS vector (its components); v^(ΔX), v^(ΔY), v^(ΔZ) are the adjustments for the GNSS vector components; X⁽⁰⁾, Y⁽⁰⁾, Z⁽⁰⁾ are the approximate coordinates; δX, δY, δZ are the estimated increments of the approximate coordinates; and l^(ΔX), l^(ΔY), l^(ΔZ) are absolute terms.

2.

Calculate adjusted Cartesian coordinates XYZ

Cartesian coordinates of each point j are calculated by adding the adjusted components of vector ij to the known coordinates of point i:

$$\left\{\begin{array}{l}{X}_j=X_i+\Delta X_{ij}+v_{ij}^{\left(\Delta X\right)}\\ Y_j=Y_i+\Delta Y_{ij}+v_{ij}^{\left(\Delta Z\right)}\\ Z_j=Z_i+\Delta Z_{ij}+v_{ij}^{\left(\Delta Z\right)}\end{array}\right.$$

(2)

3.

Project the points onto the surface of the WGS84 reference ellipsoid (convert Cartesian coordinates XYZ to ellipsoidal coordinates BLh)

This task requires basic geodetic equations [22,27]:

$$\left\{\begin{array}{l}X=\left(R_N+h\right)·\cos B·\cos L\\ Y=\left(R_N+h\right)·\cos B·\sin L\\ Z=\left(R_N·\left(1-e^2\right)+h\right)·\sin B\end{array}\right.$$

(3)

where

$$R_N={\displaystyle \frac{a}{\sqrt{1-e^2·{\sin }^{2}B}}}; e^2={\displaystyle \frac{a^2-b^2}{a^2}},$$

B, L are the latitude and longitude, respectively; h is the point’s height above the ellipsoid (calculated along the normal to the ellipsoid); R_N is the radius of curvature in the prime vertical; e is the first eccentric of the ellipsoid; and a, b are the WGS84 ellipsoid’s semi-axes (a = 6,378,137.0000; b = 6,356,752.31414 [34]).

Equations (3) are used to solve the problem directly: BLh → XYZ. For a ‘reversed’ problem (XYZ → BLh), they have to be transformed. The first step is to find the meridian radius (r) for the projection of a point onto the ellipsoid (one potential solution) with a function derived from relationship (3):

$$F\left(r\right)=\left(\left(R_N+h\right)·\cos B-e^2·r\right)·\sqrt{\left(a-r\right)·\left(a+r\right)}-{\displaystyle \frac{Z·r·b}{a}}=0$$

(4)

Radius r is calculated iteratively:

$$r_{i+1}=r_i-{\displaystyle \frac{F\left(r_i\right)}{F^{\prime }\left(r_i\right)}}$$

(5)

where

i = 0, 1, 2, … are the iteration indices and $F^{\prime }\left(r_i\right)$ is the value of the derivative of function $F\left(r_i\right)$ with respect to r.

A complete derivation of the presented Formulas (4) and (5) can be found in many literature references, e.g., [22,25,27,36].

The initial value of r is assumed as the distance between the point and the ellipsoid’s axis of rotation (assuming for the time being that h = 0):

$$r_0=\left(R_N+h\right)·\cos B=\sqrt{X^2+Y^2}$$

(6)

The iteration procedure (5) is terminated when r exhibits no significant numerical changes (at the level of significant figures). Finally, the ellipsoidal coordinates are determined from the following equations (cf. [22]):

$$\left\{\begin{array}{l}B={\displaystyle \frac{\pi }{2}}-\mathrm{arctg}\left({\displaystyle \frac{b·r}{a·\left(a-r\right)·\left(a+r\right)}}\right)\\ L=\arccos \left({\displaystyle \frac{X}{\sqrt{X^2+Y^2}}}\right)=\arcsin \left({\displaystyle \frac{Y}{\sqrt{X^2+Y^2}}}\right)\\ h=\sqrt{{\left(\sqrt{X^2+Y^2}-r\right)}^2+{\left(Z-{\displaystyle \frac{b·\left(a-r\right)·\left(a+r\right)}{a}}\right)}^2}\end{array}\right.$$

(7)

4.

Project the BL ellipsoidal coordinates onto the plane of a local reference frame (such as xy2000)

This task involves several steps (cf. [22]).

• (4.1). Transform the ellipsoid into a sphere (Lagrange projection): $\left(B,L\right)\to \left(\phi ,\lambda =L\right)$

The following equation represents the relationship between ellipsoidal latitude B and spherical latitude φ

$$\tan \left({\displaystyle \frac{\phi }{2}}+{\displaystyle \frac{\pi }{4}}\right)={\left({\displaystyle \frac{1-e·\sin B}{1+e·\sin B}}\right)}^{{\displaystyle \frac{e}{2}}}·\tan \left({\displaystyle \frac{B}{2}}+{\displaystyle \frac{\pi }{4}}\right)$$

(8)

To solve Equation (8), one has to employ the so-called approximation using power series or trigonometric series.

• (4.2). Apply transverse cylindrical Mercator projection: $\left(\phi ,\lambda \right)\to \left(x_{MERC},y_{MERC}\right)$

$$\left\{\begin{array}{l}{x}_{MERC}=R_0·\arctan \left({\displaystyle \frac{\sin \phi }{\cos \phi ·\cos \left(\lambda -{\lambda }_0\right)}}\right)\\ y_{MERC}=0.5·R_0·\ln \left({\displaystyle \frac{1+\cos \phi ·\sin \left(\lambda -{\lambda }_0\right)}{1-\cos \phi ·\sin \left(\lambda -{\lambda }_0\right)}}\right)\end{array}\right.$$

(9)

where λ₀ is the meridian of tangency for the sphere and cylinder, and R₀ is the sphere radius.

• (4.3). Project the Mercator plane onto the Gauss-Krüger (G-K) plane: $\left(x_{MERC},y_{MERC}\right)\to \left(x_{G\text{-}K},y_{G\text{-}K}\right)$

Typically, trigonometric polynomials are used as

$$\left\{\begin{array}{l}{x}_{G\text{-}K}=x_{MERC}+R_0·{\displaystyle \sum _{k=2,4,6\dots }{a}_k·\sin \left(k·\frac{x_{MERC}}{R_0}\right)}·\cosh \left(k·{\displaystyle \frac{y_{MERC}}{R_0}}\right)\\ y_{G\text{-}K}=y_{MERC}+R_0·{\displaystyle \sum _{k=2,4,6\dots }{a}_k·\cos \left(k·\frac{x_{MERC}}{R_0}\right)}·\sinh \left(k·{\displaystyle \frac{y_{MERC}}{R_0}}\right)\end{array}\right.$$

(10)

where a_k is the coefficient of the polynomial.

• (4.4). Convert G-K coordinates into a local projection system (such as PL-2000): $\left(x_{G\text{-}K},y_{G\text{-}K}\right)\to \left(x_{″2000″},y_{″2000″}\right)$

After introducing conventional displacement parameters (x₀ and y₀), scale parameter(m₀) (relative to the initial G-K projection), and projection zone number (c), it yields

$$\left\{\begin{array}{l}{x}_{″2000″}=m_0·x_{G\text{-}K}+x_0\\ y_{″2000″}=c·{10}^6+m_0·y_{G\text{-}K}+y_0\end{array}\right.$$

(11)

For the coordinate system used in Poland, PL-2000 (see [34]), the transformation parameters are: x₀ = 0; y₀ = 500,000 m; m₀ = 0.999923; c = (5, 6, 7, 8).

5.

Create a set of 2D vectors (for each vector ij)

$$\Delta x_{ij}=x_j-x_i; \Delta y_{ij}=y_j-y_i$$

(12)

where (x_i, y_i) and (x_j, y_j) are the coordinates after transformation (11).

6.

Convert ellipsoidal heights (h) (7) into orthometric heights (H_n)

This task is addressed using a numerical model of the geoid [31]:

$$H_n=h-N$$

(13)

where H_n are the normal heights with respect to the official quasi-geoid used in Poland; N is the geoid-ellipsoid separation [23,30,31].

7.

Create differences (increments) in normal heights (for each vector ij)

$${\left(\Delta H_n\right)}_{ij}={\left(H_n\right)}_j-{\left(H_n\right)}_i$$

(14)

The numerical stages listed above (1–14) are usually performed by computer software for survey network adjustments and coordinate conversion (for example, [16,39,40]).

2.2. Procedure for Transforming GNSS Vectors into a Local Conventional Reference Frame

The transformation method proposed here is much simpler than the traditional one (1–14). This is mainly because no map projection and conversion of geometric (ellipsoidal) heights into orthometric heights are necessary, as no numerical model of the local geoid is involved. However, the theoretical assumptions underlying the definition of the conventional reference frame (see the Introduction section) impose certain limitations on the method’s practicability.

At the heart of the method lies the mathematical relationship between components of an adjusted GNSS vector (ΔX, ΔY, ΔZ) (1) and the associated differences in relation to the coordinates in the conventional local reference frame (Δx, Δy, ΔH) [21,23,36]:

$$\left[\begin{array}{c}\Delta X\\ \Delta Y\\ \Delta Z\end{array}\right]=R·\left[\begin{array}{c}\Delta y\\ \Delta x\\ \Delta H\end{array}\right]$$

(15)

where R is the transformation matrix:

$$R=\left[\begin{array}{ccc}-\sin L& -\sin B·\cos L& \cos B·\cos L\\ \cos L& -\sin B·\sin L& \cos B·\sin L\\ 0& \cos B& \sin B\end{array}\right]$$

(16)

In this case, a reverse transformation is necessary:

$$\left[\begin{array}{c}\Delta y\\ \Delta x\\ \Delta H\end{array}\right]=R^{-1}·\left[\begin{array}{c}\Delta X\\ \Delta Y\\ \Delta Z\end{array}\right]$$

(17)

To use relationship (17), one must first calculate the ellipsoidal coordinates B and L (7). Increments in coordinates Δx, Δy (17) on the plane of the conventional reference frame are not identical to the respective values on a map plane in PL-2000 because of orientation differences in relation to the reference ellipsoid (Figure 1). The definition of the local conventional reference frame (see Section 1) must be complemented with the directions of reference frame’s axes (cf. [23]): The H axis is along the normal to the ellipsoid, the y axis (positive, eastward) is perpendicular to the plane of the meridian of point P (the origin of the 3D coordinate system), and the x axis (positive, northward) is on the meridian’s plane.

The elements of the R transformation matrix (16) obviously depend on the values of the ellipsoidal coordinates B and L, i.e., on the adopted point of tangency (P) between the plane and the ellipsoid (see Figure 1). A change in the point of tangency results in a change in the R matrix, and consequently, a change in the conventional reference frame. In order to preserve a single reference frame, one point of tangency P must be adopted as the initial point for all transformed vectors.

The results of the two methods, (12), (14) and (17), can be compared by aligning the reference frames after calculating the rotation angle (if the coordinates of at least two ij points in the PL-2000 system are known):

$$\gamma =A_{ij}^{\left(U\right)}-A_{ij}^{\left(K\right)}$$

(18)

where A_ij is the geodetic azimuth; (U) is the conventional reference frame; and (K) is the map coordinate system.

Next, simplified formulae for the Helmert transformation in the plane are used [22,40,41,42], without translation or scaling:

$$\left[\begin{array}{c}{x}^{\left(K\right)}\\ y^{\left(K\right)}\end{array}\right]=\left[\begin{array}{cc}\cos \gamma & \sin \gamma \\ -\sin \gamma & \cos \gamma \end{array}\right]·\left[\begin{array}{c}{x}^{\left(U\right)}\\ y^{\left(U\right)}\end{array}\right]$$

(19)

The final coordinate increments, determined in the conventional reference frame and reduced to the PL-2000 coordinate system, are calculated as shown below:

$$\Delta x_{ij}^{\left(K\right)}=x_j^{\left(K\right)}-x_i^{\left(K\right)}; \Delta y_{ij}^{\left(K\right)}=y_j^{\left(K\right)}-y_i^{\left(K\right)}$$

(20)

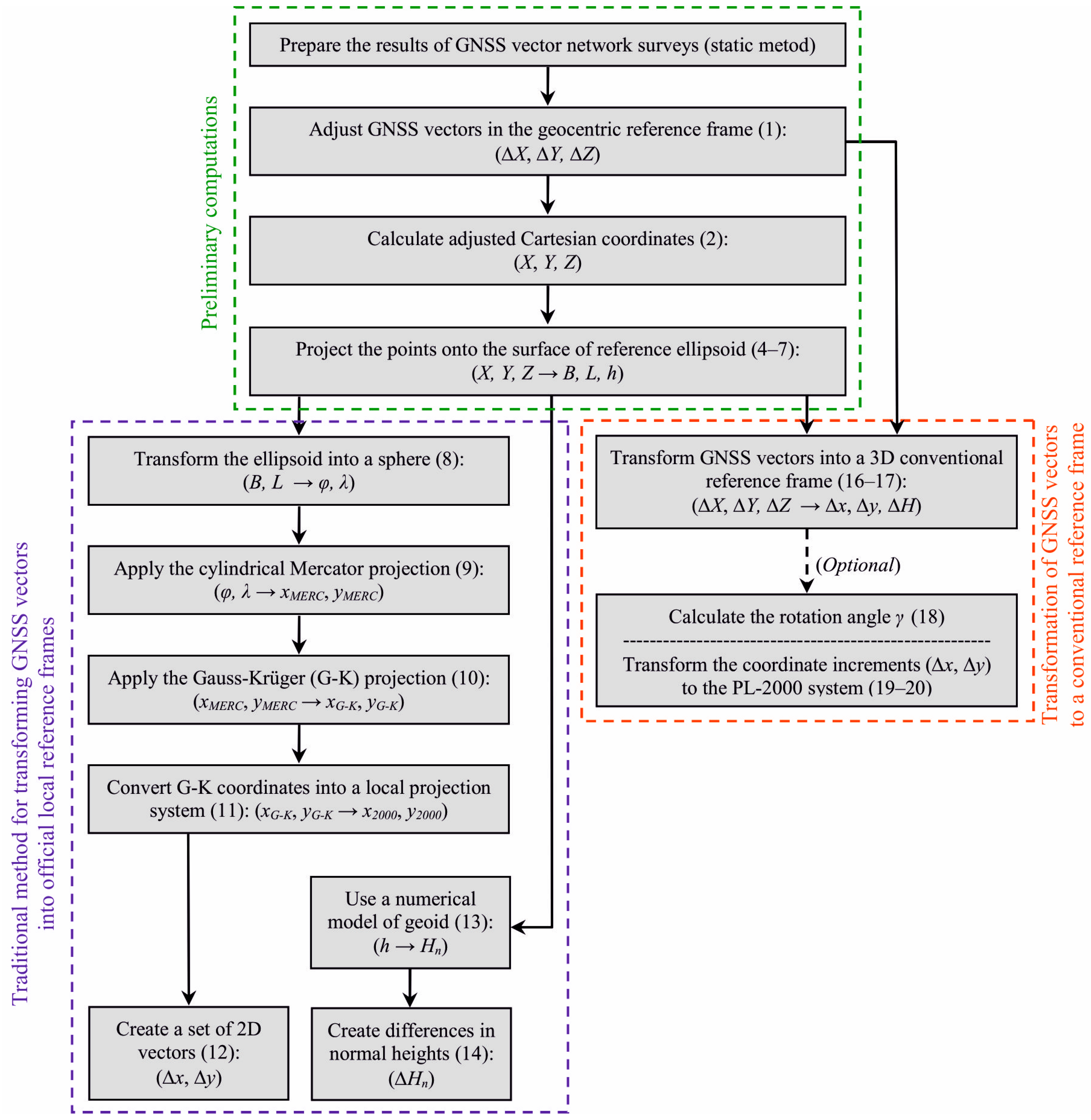
2.3. Diagram of the Computational Procedures

The entire computational procedures (see Section 2.1 and Section 2.2) are organised into a diagram (Figure 4), which involves three parts:

-

Preliminary computations (common to both methods);

-

Traditional procedure for converting GNSS vectors into official local reference frames;

-

Transforming GNSS vectors into the conventional reference frame (the method proposed in this paper).

The individual calculation steps are implemented using the corresponding equations, which are given in brackets.

3. Numerical Example (Results and Discussion)

The proposed procedure for transforming initial GNSS vectors into a 3D conventional reference frame has been verified with real-life data. The analysis involves the results of a periodic survey of a control network for determining displacement in a mining area (Figure 5). Control points 1–8 were measured with static GNSS, which yielded 16 local vectors (ΔX, ΔY, ΔZ) tied in to four ASG-EUPOS reference stations. The results are summarised in

Table 1. Results of static GNSS measurements of the vector network.

Vector Index		Observations (Components of GNSS Vectors) [m]			Mean Errors of Measurement [m]
from	to	ΔX	ΔY	ΔZ	mΔX	mΔY	mΔZ
1	3	18.8574	−46.1353	−2.5065	0.0062	0.0052	0.0061
1	4	26.0581	−69.9464	−1.6011	0.0068	0.0056	0.0066
2	1	−9.1227	23.2029	0.8991	0.0062	0.0051	0.0061
2	3	9.7354	−22.9314	−1.6057	0.0037	0.0032	0.0039
2	4	16.9362	−46.7425	−0.6996	0.0036	0.0031	0.0038
3	4	7.2020	−23.8102	0.9088	0.0041	0.0032	0.0032
5	3	−8.7924	47.6362	−6.0945	0.0075	0.0058	0.0056
5	4	−1.5898	23.8237	−5.1855	0.0066	0.0051	0.0052
5	7	−29.2102	−26.7750	29.6711	0.0056	0.0049	0.0059
5	8	−43.3054	−40.9754	44.7031	0.0056	0.0049	0.0058
6	3	5.3467	61.6613	−20.5954	0.0047	0.0036	0.0036
6	4	12.5497	37.8504	−19.6865	0.0048	0.0037	0.0038
6	5	14.1397	14.0259	−14.5022	0.0058	0.0051	0.0061
6	7	−15.0700	−12.7488	15.1701	0.0043	0.0038	0.0047
6	8	−29.1668	−26.9499	30.2007	0.0037	0.0032	0.0040
7	8	−14.0972	−14.2010	15.0301	0.0039	0.0034	0.0042

(the table does not include values for the 25 tie-in vectors between the control network points and the reference stations due to a large volume of data).

The vector network was adjusted using the standard least squares method (1)–(2). Values of the adjusted vectors are summarised in

Table 2. Adjusted vectors.

Vector Index		Adjusted GNSS Vectors [m]
from	to	ΔX	ΔY	ΔZ
1	2	9.1255	−23.1996	−0.9019
2	3	9.7368	−22.9292	−1.6060
3	4	7.2019	−23.8099	0.9069
4	5	1.5923	−23.8212	5.1854
5	6	−14.1382	−14.0270	14.5021
6	7	−15.0709	−12.7482	15.1687
7	8	−14.0965	−14.2012	15.0313

, while the final coordinates with tie-in points are in

Table 3. Coordinates adjusted (2) in the geocentric ETRF89 reference frame and their mean errors.

Point	X [m]	Y [m]	Z [m]	mX [m]	mY [m]	mZ [m]
1	3,871,848.0173	1,345,998.1564	4,870,464.0874	0.0073	0.0062	0.0073
2	3,871,857.1428	1,345,974.9568	4,870,463.1855	0.0054	0.0047	0.0054
3	3,871,866.8796	1,345,952.0276	4,870,461.5795	0.0050	0.0042	0.0046
4	3,871,874.0815	1,345,928.2177	4,870,462.4864	0.0051	0.0043	0.0046
5	3,871,875.6738	1,345,904.3965	4,870,467.6718	0.0072	0.0058	0.0062
6	3,871,861.5356	1,345,890.3695	4,870,482.1739	0.0062	0.0051	0.0054
7	3,871,846.4647	1,345,877.6213	4,870,497.3426	0.0088	0.0076	0.0085
8	3,871,832.3682	1,345,863.4201	4,870,512.3739	0.0088	0.0076	0.0085
KATO	3,862,992.3806	1,332,822.6741	4,881,105.4573	-	-	-
KRAW	3,856,936.1743	1,397,750.4815	4,867,719.4488	-	-	-
WODZ	3,896,698.7807	1,300,673.7066	4,863,029.3737	-	-	-
ZYWI	3,904,633.3207	1,360,191.8920	4,840,630.7894	-	-	-

(ETRF89 based on the WGS84 ellipsoid).

Next, the vectors were transformed into the 2D map coordinate system, PL-2000 and to the orthometric height reference frame, PL-EVRF2007-NH (the official height reference frame used in Poland, cf. [34]), as per the traditional numerical procedure (3)–(14). Selected intermediate results for the stages are reported in

Table 4. Ellipsoidal coordinates and orthometric heights (7, 13).

Point No.	Geographic Ellipsoidal Coordinates (WGS84)		Ellipsoidal Height h [m]	Orthometric Height (PL-EVRF2007-NH) Hn [m]
	Latitude B [º]	Longitude L [º]
1	50.1044577593	19.1693493783	279.8002	238.7604
2	50.1044456499	19.1690012024	279.7508	238.7105
3	50.1044248848	19.1686537911	279.5885	238.5477
4	50.1044371169	19.1683063863	279.6331	238.5918
5	50.1045105889	19.1679845766	279.5595	238.5179
6	50.1047180819	19.1678642683	279.1664	238.1252
7	50.1049325987	19.1677651230	278.9891	237.9482
8	50.1051432656	19.1676423213	278.9908	237.9503
Mean	50.1046337433	19.1683208809	-	-

,

Table 5. Horizontal coordinates in the map coordinate system (11).

Point No.	2D Coordinates (PL-2000)
	x [m]	y [m]
1	5,552,693.2722	6,583,648.1303
2	5,552,691.5354	6,583,623.2456
3	5,552,688.8370	6,583,598.4307
4	5,552,689.8085	6,583,573.5587
5	5,552,697.6198	6,583,550.4112
6	5,552,720.5623	6,583,541.4443
7	5,552,744.3096	6,583,533.9792
8	5,552,767.6023	6,583,524.8286

and

Table 6. Horizontal vectors (12) on the plane of PL-2000 and height differences (14) in PL-EVRF2007-NH.

Vector Index		Coordinate Differences [m]
from	to	Δx	Δy	ΔHn
1	2	−1.7368	−24.8847	−0.0499
2	3	−2.6984	−24.8149	−0.1628
3	4	0.9715	−24.8720	0.0441
4	5	7.8113	−23.1475	−0.0739
5	6	22.9425	−8.9669	−0.3927
6	7	23.7473	−7.4651	−0.1770
7	8	23.2927	−9.1506	0.0021

. Table 4 also provides an average of the ellipsoidal coordinates (B, L) to facilitate further comparisons.

Table 6 shows the end results of the traditional numerical procedure, the GNSS vectors transformed into the official local reference frame (Table 2). We expect to obtain a similar outcome using the proposed procedure for transforming vectors into a 3D conventional reference frame (17). Each point of the control network (Figure 5) has ellipsoidal coordinates (Table 4). Therefore, it is possible to calculate increments Δx, Δy, and ΔH in several conventional reference frames with different points of tangency (cf. Figure 1) and then evaluate changes in the increments for individual point pairs (vectors). The next comparison option is to calculate the increments for the averaged ellipsoidal coordinates of points 1–8 (the last row in Table 4). The results for this stage are summarised in

Table 7. Increments in the conventional reference frame depending on the point of tangency (B, L).

Vector Index		B, L–Point 1			B, L–Point 4			B, L–Point 8			B, L–Mean
from	to	Δx	Δy	ΔH	Δx	Δy	ΔH	Δx	Δy	ΔH	Δx	Δy	ΔH
1	2	−1.347	−24.910	−0.049	−1.347	−24.910	−0.049	−1.348	−24.910	−0.049	−1.347	−24.910	−0.049
2	3	−2.310	−24.855	−0.162	−2.310	−24.855	−0.162	−2.310	−24.855	−0.162	−2.310	−24.855	−0.162
3	4	1.361	−24.855	0.044	1.361	−24.855	0.045	1.360	−24.855	0.045	1.361	−24.855	0.045
4	5	8.173	−23.023	−0.074	8.173	−23.023	−0.074	8.173	−23.023	−0.073	8.173	−23.023	−0.074
5	6	23.081	−8.607	−0.393	23.081	−8.607	−0.393	23.081	−8.607	−0.393	23.081	−8.607	−0.393
6	7	23.862	−7.093	−0.178	23.862	−7.093	−0.177	23.862	−7.093	−0.177	23.862	−7.093	−0.177
7	8	23.434	−8.785	0.001	23.434	−8.785	0.001	23.434	−8.786	0.002	23.434	−8.785	0.002
8	1	−76.254	122.127	0.811	−76.253	122.128	0.810	−76.251	122.129	0.808	−76.253	122.128	0.809

(with an additional theoretical vector 8 → 1). For the purpose of the comparative analysis, the results are reported down to three decimal places. This seems sufficient considering the accuracy of GNSS measurements, the geoid model accuracy, etc.

A comparison of increments for individual points of tangency (Table 7) reveals minor differences (below 1 mm) only for some height differences ΔH; slightly larger discrepancies (2–3 mm) were found for the longest vector 8 → 1. This order of magnitude of the changes seems of little importance compared to the accuracy of GNSS measurements.

Horizontal increments (Δx, Δy, summarised in Table 7) cannot be consistent with values calculated in PL-2000 (Table 6). Still, after the angle of rotation is calculated (18) for the longest direction 8 → 1, for example, and a 2D transformation is applied (19), it is easy to calculate the corrected values of the increments (

Table 8. Increments corrected in the conventional reference frame and compared to the initial reference frame (Table 6): δ—deviation.

Azimuth of Direction 8 → 1 Angle of Rotation (19) [gon]		Vector Index		Conventional Reference Frame, Corrected [m]			Deviations from PL-2000 and PL-EVRF2007-NH [m]
		from	to	Δx	Δy	ΔH	δ(Δx)	δ(Δy)	δ(ΔH)
		1	2	−1.737	−24.886	−0.049	0.000	0.000	0.001
A(U) = 135.5325		2	3	−2.699	−24.816	−0.162	0.000	0.000	0.001
		3	4	0.972	−24.873	0.045	0.000	0.000	0.001
A(K) = 134.5365		4	5	7.812	−23.148	−0.074	0.000	0.000	0.000
		5	6	22.943	−8.967	−0.393	0.000	0.000	0.000
γ = 0.9960		6	7	23.748	−7.465	−0.177	0.000	0.000	0.000
		7	8	23.293	−9.151	0.002	0.000	0.000	−0.001
		8	1	−74.333	123.306	0.809	0.000	0.000	−0.001

).

Table 8 presents the final outcome of the transformation of the GNSS vectors into a 3D conventional reference frame (Δx, Δy, ΔH). It is clear that the values are nearly identical to those for the traditional procedure for transforming coordinates into a 2D map coordinate system (Δx, Δy) and an orthometric height system (ΔH_n). The only discrepancies of millimetres were found for height differences (ΔH) for some vectors, which seems a very good result. Errors of this magnitude are acceptable even for high-precision displacement measurements [13]. These minor discrepancies are most likely due to ignoring Earth’s curvature (for the conventional reference frame), leading to the plumb line deviating from the normal to the ellipsoid [18].

Because relevant positions of points are critical for ground displacement measurements (which was the primary objective of the control network used in the study, Figure 5), it is necessary to analyse the magnitudes of the vectors (distances between points) calculated using the increments in each reference frame (

Table 9. Spatial distances between control network points (see Table 2, Table 6 and Table 8).

Vector Index		Actual (Spatial) Distances [m]
		Initial GNSS Vectors	PL-2000; EVRF2007	Conventional System
from	to
1	2	24.946	24.945	24.946
2	3	24.963	24.962	24.963
3	4	24.892	24.891	24.892
4	5	24.431	24.430	24.431
5	6	24.636	24.636	24.636
6	7	24.895	24.894	24.895
7	8	25.026	25.026	25.026
8	1	143.980	143.975	143.980

and

Table 10. Horizontal distances and height differences (ΔH) juxtaposed with direct measurements: (T)—total station measurement, (U)—conventional reference frame, (K)—PL-2000, (G)—geometric levelling.

Vector Index		Horizontal Distance [m]					Height Difference [m]
		Measurement on Site	Map Coordinate System PL-2000		Conventional Reference Frame		Geometric Levelling	Height Deviation (See Table 6 and Table 8)
from	to	d(T)	d(K)	d(K) − d(T)	d(U)	d(U)− d(T)	ΔH(G)	ΔH(EVRF)− ΔH(G)	ΔH(U)− ΔH(G)
1	2	24.958	24.945	−0.013	24.946	−0.012	−0.058	0.008	0.009
2	3	24.964	24.961	−0.003	24.962	−0.002	−0.163	0.000	0.001
3	4	24.892	24.891	−0.001	24.892	0.000	0.042	0.002	0.003
4	5	24.442	24.430	−0.012	24.431	−0.011	−0.072	−0.002	−0.002
5	6	24.637	24.633	−0.004	24.633	−0.004	−0.399	0.006	0.006
6	7	24.898	24.893	−0.005	24.894	−0.004	−0.173	−0.004	−0.004
7	8	25.019	25.026	0.007	25.026	0.007	−0.002	0.004	0.004
8	1	143.992	143.973	−0.019	143.978	−0.014	0.825	−0.015	−0.016

).

Table 9 summarises the actual (spatial) distances calculated as resultants of three component increments, ΔX, ΔY, and ΔZ or Δx, Δy, and ΔH (as appropriate). The distances in the conventional reference frame are exactly consistent (to within 1 mm) with the lengths of the initial GNSS vectors (Table 2), indicating that the proposed transformation of their components (17) does not distort the relative positioning of the points. The minor differences in distances for the traditional transformation into PL-2000 and PL-EVRF2007-NH can be accounted for by the fact that the height increments (ΔH_n, Table 6) were calculated along the local plumb line instead of the normal to the ellipsoid.

Table 10 summarises 2D (horizontal) distances calculated as the resultants of increments Δx and Δy and their deviations from the distances as measured accurately with a total station. A similar list was compiled for vertical distances, that is, differences in heights (ΔH, right-hand part of Table 10) in relation to results of high-precision geometric levelling (results summarised with an accuracy down to 1 mm). In both cases (distances and heights), the direct on-site measurements can be considered a reference for the GNSS measurements.

Analysis of the horizontal distance deviations (Table 10) reveals that they are similar for both reference frames (PL-2000 and conventional), with a minor advantage of the conventional reference frame, where the deviations are slightly lower (by about 1 mm for short vectors and about 5 mm for the longest vector 8 → 1). In the case of height differences, the official reference frame (PL-EVRF2007-NH) fares slightly better than the conventional reference frame. Still, the differences are measured in millimetres.

It is also a good opportunity to comment on the magnitudes of deviations from the reference values, which are mostly several millimetres (for both distances and height differences). The deviations seem to originate from random errors of static GNSS measurement (linked to receiver centring or antenna height measurement), which is best evidenced in point 1 (the largest deviations for vectors 8 → 1 and 1 → 2 for both distances and height differences).

4. Summary and Conclusions

The article outlines a transformation method of initial GNSS vectors (ΔX, ΔY, ΔZ) into a certain local, 3D conventional reference frame. New increments in coordinates (Δx, Δy, ΔH) are, in this case, a function of ellipsoidal coordinates B, L (latitude and longitude) of the point of the local reference frame tangency to the reference ellipsoid. The increments of horizontal coordinates (Δx, Δy) are on the plane of the local conventional reference frame, while height increments (ΔH) are calculated along the normal to the ellipsoid at the point of tangency (which makes them perpendicular to the 2D coordinate system xy).

The proposed procedure can serve as an alternative to the traditional transformation of GNSS vectors into official local reference frames, which involves many stages of complex calculations. Increments in plane coordinates and local height differences are often used to determine so-called relative displacements [11,12,13,43] in potentially unstable sites, such as mining areas (replacing XYZ or xyH coordinates).

The advantages of the proposed method compared to the traditional approach include:

• Simple computation (no need to convert the ellipsoidal height into the orthometric height system using the geoid model or use map projection onto the plane of the official local reference frame);
• The local height difference (ΔH) is free from the impact of the geoid numerical model’s uncertainty;
• Increments of 2D coordinates (Δx, Δy) are free from map projection errors.

Its downsides include:

• Survey (control network) area limited to about 300 m;
• The calculated height difference (ΔH) does not account for Earth’s curvature (still, for a vector magnitude up to about 300 m, the impact is below the local geoid model error).

The verification of the method on results from a real-life control network (for displacement measurements) demonstrated complete consistency between the local increments in coordinates (Δx, Δy) calculated with the new method and those from traditional calculations. Only small discrepancies were found (±1 mm) for height differences (ΔH) and several vectors (including for the longest vector of about 144 m).

Horizontal distances between the control network points, calculated based on the local increments (Δx, Δy), were also analyzed. The discrepancies between the two methods were up to ±1 mm for shorter vectors (about 25 m) and 5 mm for the longest vector (about 144 m).

Therefore, the numerical analyses suggest that the errors involved in converting GNSS vectors into a conventional local reference frame are of negligible impact compared to the estimated accuracy of GNSS measurements. The error in the local height difference calculated with the proposed method also appears minuscule compared to the accuracy of the geoid models used to calculate orthometric heights. Hence, there seems to be no reason not to use the proposed numerical method in various survey engineering tasks (such as analysis of relative displacement of the ground), always assuming a limited size of the survey area (up to about 300 m).