Research on the Precise Positioning of Mining Working Faces and an Inversion Method for Characteristic Working Face Parameters Based on a Robust Genetic Algorithm
Abstract
1. Introduction
2. Methods
2.1. Underground Working Face Mining and Surface Deformation Response Mechanism
2.2. Method for Solving the Precise Position and Working Surface Characteristic Parameter System
- (1)
- Data preparation: Regarding the traditional measurement technology-derived surface deformation data of the surface, the parameters of the probability integration method are identified in light of the actual mining conditions and relevant observation information of the adjacent mining face. The position of the underground mining face and the value range of the working face characteristic parameter system G are also provided.
- (2)
- Genetic algorithm fitness function calculation: Based on the specific position of the underground mining face and the defined value range of its characteristic parameter system G, binary encoding is used to randomly generate an initial population, after which the parameters of the initial population are fed into the PIM model to acquire predicted deformation values. Utilizing the surface deformation monitoring results of the mining working face obtained through traditional measurement technology monitoring, the fitness function can be calculated as follows:
- (3)
- Robust genetic algorithm optimization: The optimization process of the robust genetic algorithm is similar to that of the traditional genetic algorithm. Firstly, the probability of individuals being selected is calculated. Secondly, the population is processed through selection, crossover, and mutation operations, which are used to produce a new population. Thereafter, the fitness function corresponding to the new generation of the population is recalculated by updating the weight Pi in Equation (7).
- (4)
- Parameter iteration calculation: Continuously execute steps (2) to (3); after meeting the iteration requirements, stop executing steps (2) to (3) and output the optimal underground mining face position and face characteristic parameter system G. Guided by the above ideas, the technical route of the precise positioning method for mining faces based on the robust GA is presented in Figure 1.
3. Simulated Experiment
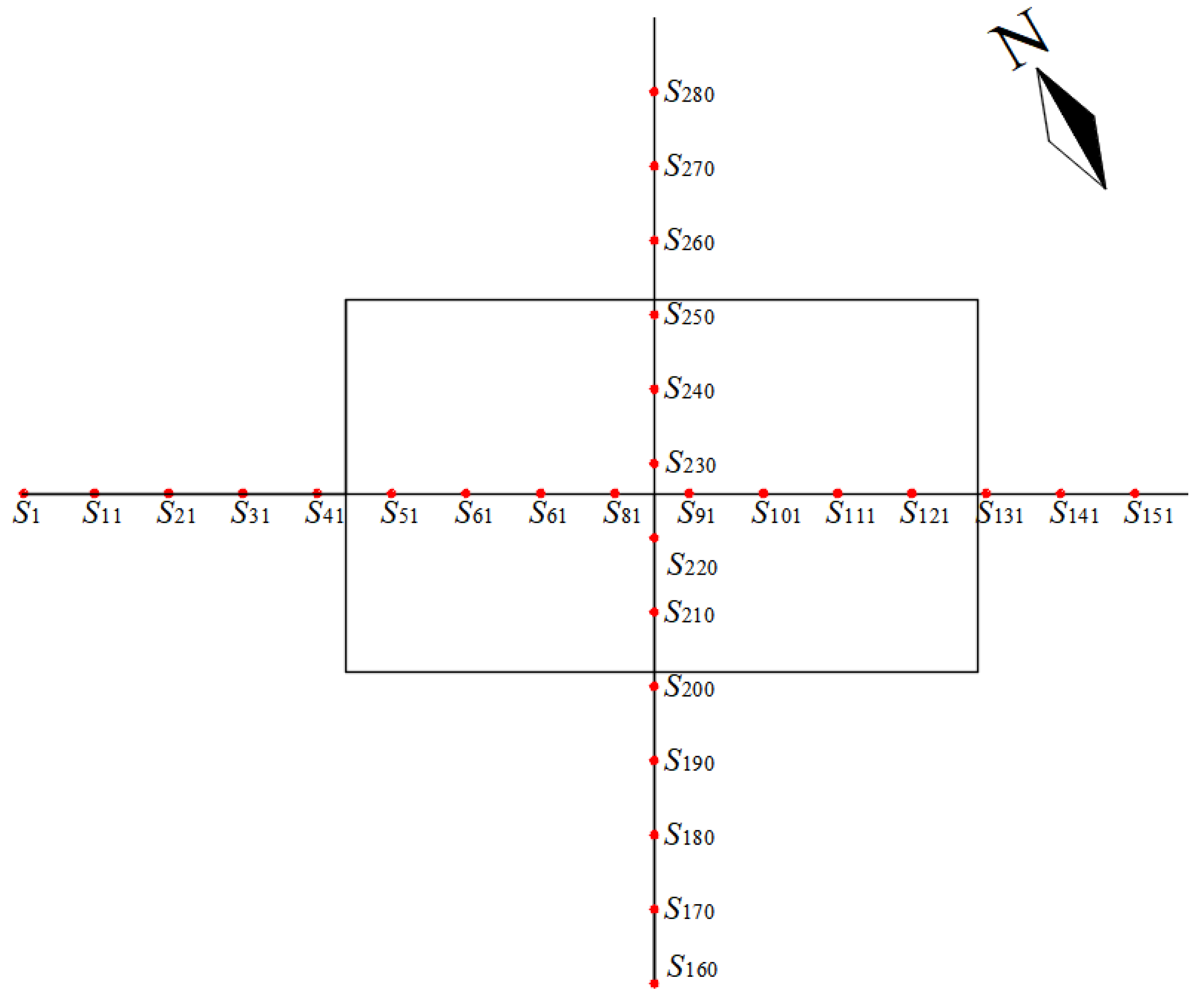
3.1. Surface Deformation Simulation and Experimental Plan Design for Underground Working Face Mining
- Simulation of surface deformation during underground working face mining
- 2.
- Experimental plan design
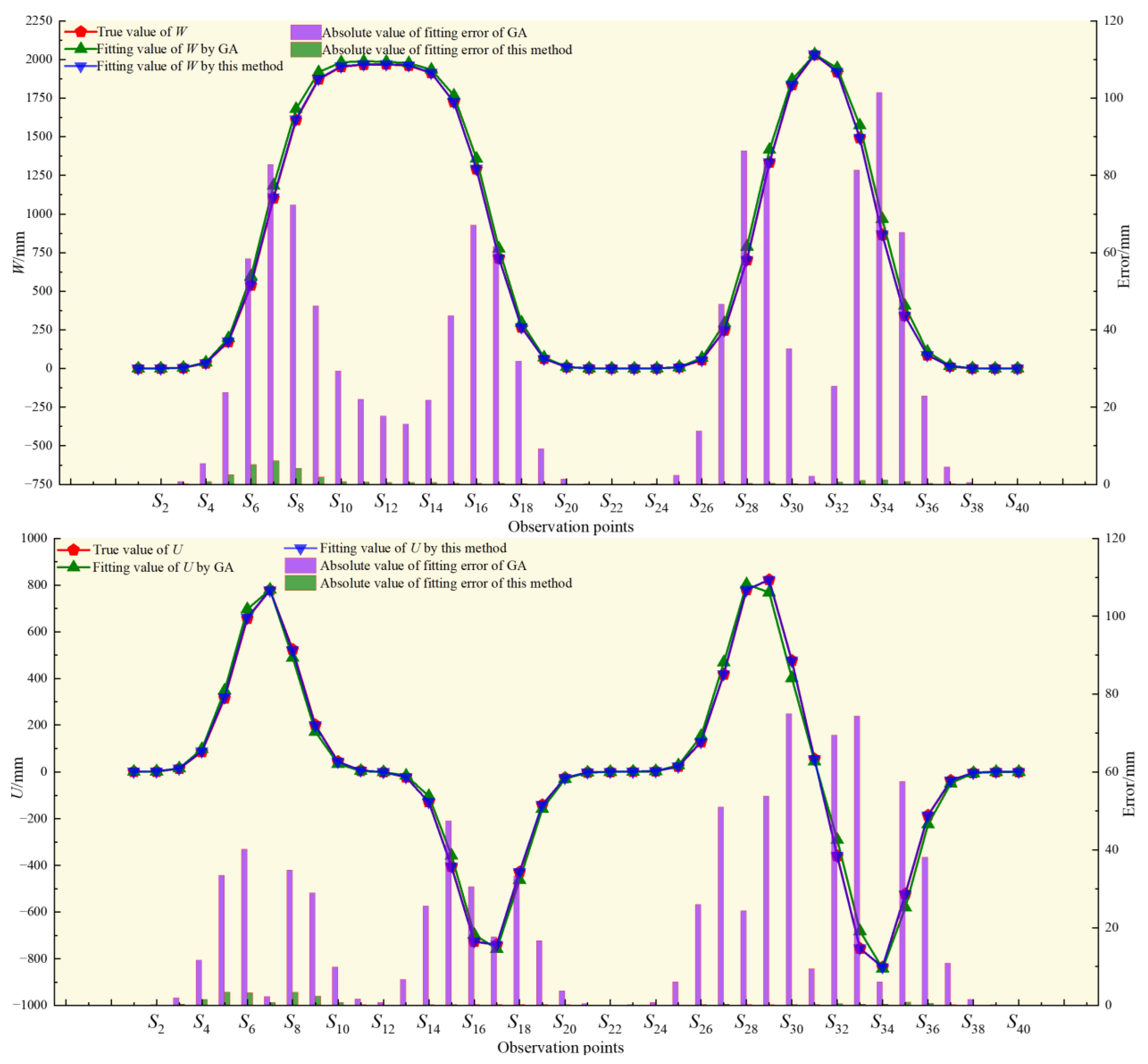
3.2. Working Surface Positioning and Spatial Characteristics Inversion
4. Real Data Experiment on the 1414 (1) Working Face
4.1. Data Overview
4.2. Experimental Results
5. Discussion
6. Conclusions
- (1)
- Based on the correlation between deformation and the mining-induced response of the underground working face, combined with a weighted iterative robust genetic algorithm, we constructed a precise positioning method for mining working faces based on a robust genetic algorithm. The results of simulation experiments and from engineering cases show that, in contrast to the traditional genetic algorithm, the fitting error yielded by this method is significantly smaller when inverting characteristic mining parameters, thereby indicating that the proposed method achieves better fitting accuracy. The construction method can be used to accurately locate the working face and invert characteristic mining parameters. It should be noted that the method presented in this paper is not applicable to non-rectangular working face mining. Studying inversion methods suitable for mining subsidence characteristics of arbitrarily shaped working faces constitutes our future plans.
- (2)
- Utilizing the simulated InSAR monitoring deformation data, the proposed method is further validated. As indicated by the presented results, the absolute error associated with the moving deformation values predicted from accurate positioning of the working face and the inverted characteristic mining parameters produced by the proposed method is notably smaller than that produced by the GA, suggesting that the method presented herein is highly robust. Based on the use of InSAR deformation values, this method can be used to accurately locate mining faces.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DIMDS | D-InSAR-based Illegal Mining Detection System |
| DInSAR | Differential Interferometric Synthetic Aperture Radar |
| InSAR | Interferometric Synthetic Aperture Radar |
| IGG | Institute of Geodesy and Geophysics |
| LOS | Line of Sight |
| GA | Genetic Algorithm |
| RMSE | Root Mean Squared Error |
| PIM | Probability Integral Method |
References
- Yuan, L.; Jiang, Y.-D.; Wang, K.; Wang, K.; Zhao, Y.-X.; Hao, X.-J.; Xu, C. Precision Exploitation and Utilization of Closed/Abandoned Mine Resources in China. J. China Coal Soc. 2018, 43, 14–20. [Google Scholar]
- Liu, Q.; Sun, Y.; Xu, Z.; Jiang, S.; Zhang, P.; Yang, B. Assessment of Abandoned Coal Mines as Urban Reservoirs. Mine Water Environ. 2019, 38, 215–225. [Google Scholar] [CrossRef]
- Xia, Y.P.; Wang, Y.J. InSAR- and PIM-based Inclined Goaf Determination for Illegal Mining Detection. Remote Sens. 2020, 12, 3884. [Google Scholar] [CrossRef]
- Bharti, A.K.; Pal, S.K.; Priyam, P.; Pathak, V.K.; Kumar, R.; Ranjan, S.K. Detection of Illegal Mine Voids Using Electrical Resistivity Tomography: The Case-Study of Raniganj Coalfield (India). Eng. Geol. 2016, 213, 120–132. [Google Scholar] [CrossRef]
- Thitimakorn, T.; Kampananon, N.; Jongjaiwanichkit, N.; Kupongsak, S. Subsurface Void Detection Under the Road Surface Using Ground Penetrating Radar (GPR): A Case Study in the Bangkok Metropolitan Area, Thailand. Int. J. Geo-Eng. 2016, 7, 2. [Google Scholar] [CrossRef]
- Xue, G.Q.; Yan, Y.J.; Cheng, J.L. Researches on Detection of 3-D Underground Cave Based on TEM Technique. Environ. Earth Sci. 2011, 64, 425–430. [Google Scholar] [CrossRef]
- Yuan, H.; Liu, J.; Yuan, Y. Using 4-D Seismic Data for Detecting Gob Areas of Coal Mines: A Case Study from the Zhangji Coal Mine. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5917810. [Google Scholar] [CrossRef]
- Yang, X.; Sasak, K.; Zhang, X.; Sugai, Y. Permeability Estimate of Underground Long-Wall Goaf from P-Wave Velocity and Attenuation by Lab-Scale Experiment on Crushed Rock Samples. J. Appl. Geophys. 2018, 159, 785–794. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, L.; Duan, G.; Chen, Z.; Yuan, X.; Zhao, S.; Zhang, D.; Tian, J. Seismic Response Characteristics of Coal Goaf Based on Forward Modeling. CT Theory Appl. 2021, 30, 291–300. [Google Scholar] [CrossRef]
- Martínez-Moreno, F.J.; Galindo-Zaldívar, J.; Pedrera, A.; Teixidó, T.; Peña, J.; González-Castillo, L. Regional and Residual Anomaly Separation in Microgravity Maps for Cave Detection: The Case Study of Gruta de las Maravillas (SW Spain). J. Appl. Geophys. 2015, 114, 1–11. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Yin, W.M.; Zhang, X.Z. Application of Comprehensive Geophysical Prospecting Method in Detecting Goaf of Thick Overburden Coal Mine. Geol. Rev. 2021, 67 (Suppl. S1), 51–53. [Google Scholar] [CrossRef]
- Wang, Q.; Tian, Y.; Liu, H.; Zhu, C.; Bai, C.; Hao, S. Application of Comprehensive Geophysical Prospecting in Investigation of Coal Mine Goaves. Geophys. Geochem. Explor. 2022, 46, 531–536. [Google Scholar] [CrossRef]
- He, G.Q. Mine Mining Subsidence; China University of Mining and Technology Press: Xuzhou, China, 1991. [Google Scholar]
- Guo, Z.Z.; Chai, H.B. Coal Mine Mining Subsidence; China Coal Industry Press: Beijing, China, 2013. [Google Scholar]
- Li, Z.W.; Xu, W.B.; Hu, J.; Feng, G.; Yang, Z.; Li, J.; Zhang, H.; Zhen, Q.; Zhu, J.; Wang, Q. InSAR Partial Geoscience Parameter Inversion. Acta Geod. Cartogr. Sin. 2022, 51, 1458–1475. [Google Scholar]
- Nguyen, L.; Le, T.; Nguyen, T.; Tran, D. Prediction of Underground Mining-Induced Subsidence: Artificial Neural Network Based Approach. Min. Miner. Depos. 2023, 17, 45–52. [Google Scholar] [CrossRef]
- Hu, Z.; Ge, L.; Li, X.; Rizos, C. Designing an illegal mining detection system based on DInSAR. In Proceedings of the International Geoscience and Remote Sensing Symposium 2010 (IGARSS), Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Hu, Z.; Ge, L.; Li, X.; Zhang, K.; Zhang, L. An underground-mining detection system based on DInSAR. IEEE Trans. Geosci. Remote Sens. 2013, 51, 615–625. [Google Scholar] [CrossRef]
- Du, S.; Wang, Y.J.; Zheng, M.N. Goaf Locating Based on InSAR and Probability Integration Method. Remote Sens. 2019, 11, 812. [Google Scholar] [CrossRef]
- Yang, Z.F.; Li, Z.W.; Zhu, J.J.; Yi, H.; Feng, G.; Hu, J.; Wu, L.; Preusse, A.; Wang, Y.; Papst, M. Locating and Defining Underground Goaf Caused by Coal Mining from Space-Borne SAR Interferometry. ISPRS J. Photogramm. Remote Sens. 2018, 135, 112–126. [Google Scholar] [CrossRef]
- Fan, H.; Li, T.; Gao, Y.; Deng, K.; Wu, H. Characteristics Inversion of Underground Goaf Based on InSAR Techniques and PIM. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102526. [Google Scholar] [CrossRef]
- Li, T.; Zhang, H.; Fan, H.; Zheng, C.; Liu, J. Position Inversion of Goafs in Deep Coal Seams Based on DS-InSAR Data and the Probability Integral Methods. Remote Sens. 2021, 13, 2898. [Google Scholar] [CrossRef]
- Zhang, W.; Shi, J.; Yi, H.; Zhu, Y.; Xu, B. Underground Goaf Parameters Estimation by Cross-Iteration with InSAR Measurements. Remote Sens. 2021, 13, 3204. [Google Scholar] [CrossRef]
- Bu, P.; Li, C.K.; Yang, W.T.; Liao, M. D-InSAR and Optimization Algorithm for Goaf Geometric Parameter Inversion. Sci. Surv. Mapp. 2021, 46, 143–152. [Google Scholar]
- Zhang, W.H. InSAR-Based Mine Goaf Geometric Parameter Inversion and Dynamic 3D Deformation Prediction. Master’s Thesis, Central South University, Changsha, China, 2022. [Google Scholar]
- Wei, T.; Guo, G.L.; Li, H.Z.; Wang, L.; Yang, X.S.; Wang, Y.Z. Fusing Minimal Unit Probability Integration Method and Optimized Quantum Annealing for Spatial Location of Coal Goafs. KSCE J. Civ. Eng. 2022, 26, 2381–2391. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, K.G.; Wei, T. Development of a New Inversion Method for Detecting Spatiotemporal Characteristics of Coal Mines Based on Earth Observation Technology. Int. J. Appl. Earth Obs. Geoinf. 2021, 100, 102346. [Google Scholar] [CrossRef]
- Zha, J.F.; Feng, W.K.; Zhu, X.J. Research on Parameters Inversion in Probability Integral Method by Genetic Algorithm. J. Min. Saf. Eng. 2011, 28, 655–659. [Google Scholar]
- Yang, J.; Liu, C.; Wang, B. BFGS Method Based Inversion of Parameters in Probability Integral Model. J. China Coal Soc. 2019, 44, 3058–3068. [Google Scholar]
- Jiang, C.; Liu, W.; Wang, L.; Zhu, X.; Tan, H. A Probability Integral Parameter Inversion Method Integrating a Selection-Weighted Iterative Robust Genetic Algorithm. Appl. Sci. 2025, 15, 8102. [Google Scholar] [CrossRef]
- Yang, Z.F.; Li, Z.W.; Zhu, J.J.; Hu, J.; Wang, Y.J.; Chen, G.L. InSAR-Based Model Parameter Estimation of Probability Integral Method and Its Application for Predicting Mining-Induced Horizontal and Vertical Displacements. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4818–4832. [Google Scholar] [CrossRef]
- Yang, Z.F.; Li, Z.W.; Zhu, J.J.; Preusse, A.; Yi, H.W.; Wang, Y.J.; Papst, M. An Extension of the InSAR-Based Probability Integral Method and Its Application for Predicting 3-D Mining-Induced Displacements Under Different Extraction Conditions. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3835–3845. [Google Scholar] [CrossRef]
- Baltiyeva, A.Y.; Orynbassarova, E.; Zharaspaev, M.; Akhmetov, R. Studying Sinkholes of the Earth’s Surface Involving Radar Satellite Interferometry in Terms of Zhezkazgan Field, Kazakhstan. Min. Miner. Depos. 2023, 17, 61–74. [Google Scholar] [CrossRef]
- Bazaluk, O.; Kuchyn, O.; Saik, P.; Soltabayeva, S.; Brui, H.; Lozynskyi, V.; Cherniaiev, O. Impact of Ground Surface Subsidence Caused by Underground Coal Mining on Natural Gas Pipeline. Sci. Rep. 2023, 13, 19327. [Google Scholar] [CrossRef]











| Name | X1/m | Y1/m | H/m | m/m | D3/m | D1/m | α/° | ϑ/° |
|---|---|---|---|---|---|---|---|---|
| Scope | 500–1100 | 0–600 | 200–600 | 2–5 | 600–1100 | 300–700 | 4–8 | 30–90 |
| Name | Iteration Count | Population Size | Mutation Rate | Crossover Rate | Binary Encoding Length |
|---|---|---|---|---|---|
| Value | 500 | 100 | 0.02 | 0.95 | 10 |
| Name | Data | ① | ② | |||
|---|---|---|---|---|---|---|
| GA | Our Method | GA | Our Method | |||
| X1/m | inverted value | 793.060 | 794.027 | 792.759 | 793.357 | 794.341 |
| relative error | 0.12% | 0.04% | 0.04% | 0.16% | ||
| Y1/m | inverted value | 304.006 | 303.948 | 304.235 | 309.412 | 303.639 |
| relative error | 0.02% | 0.08% | 1.78% | 0.12% | ||
| H/m | inverted value | 400 | 394.665 | 400.098 | 405.301 | 399.662 |
| relative error | 1.33% | 0.02% | 1.33% | 0.08% | ||
| m/m | inverted value | 3.5 | 3.436 | 3.501 | 3.641 | 3.503 |
| relative error | 1.83% | 0.01% | 4.04% | 0.11% | ||
| D3/m | inverted value | 850 | 866.262 | 850.749 | 843.208 | 850.847 |
| relative error | 1.91% | 0.09% | 0.80% | 0.10% | ||
| D1/m | inverted value | 500 | 527.072 | 500.130 | 489.250 | 497.875 |
| relative error | 5.41% | 0.03% | 2.15% | 0.42% | ||
| ɑ/° | inverted value | 6 | 6.012 | 5.999 | 5.791 | 6.1825 |
| relative error | 0.20% | 0.01% | 3.49% | 3.04% | ||
| ϑ/° | inverted value | 30 | 31.460 | 29.997 | 28.001 | 30.966 |
| relative error | 4.87% | 0.01% | 6.66% | 3.22% | ||
| RMSE/mm | WRMSE | 42.5 | 1.6 | 29.4 | 4.1 | |
| URMSE | 31.0 | 0.1 | 23.1 | 3.7 | ||
| Name | Data | ① | ② | |||
|---|---|---|---|---|---|---|
| GA | Our Method | GA | Our Method | |||
| X1/m | inverted value | 3,629,560.953 | 3,629,539.769 | 3,629,547.104 | 3,629,558.393 | 3,629,546.097 |
| relative error | 0.00% | 0.00% | 0.00% | 0.00% | ||
| Y1/m | inverted value | 459,088.510 | 459,083.251 | 459,096.225 | 459,103.591 | 459,099.081 |
| relative error | 0.00% | 0.00% | 0.00% | 0.00% | ||
| H/m | inverted value | 735 | 680.579 | 707.028 | 727.489 | 702.678 |
| relative error | 7.40% | 3.81% | 1.02% | 4.40% | ||
| m/m | inverted value | 3 | 3.157 | 3.256 | 3.458 | 3.212 |
| relative error | 5.22% | 8.52% | 15.26% | 7.05% | ||
| D1/m | inverted value | 241.1 | 220.132 | 220.215 | 220.132 | 220.188 |
| relative error | 8.70% | 8.66% | 8.70% | 8.67% | ||
| D3/m | inverted value | 2115.45 | 2125.637 | 2083.496 | 2059.904 | 2091.893 |
| relative error | 0.48% | 1.51% | 2.63% | 1.11% | ||
| ɑ/° | inverted value | 5 | 4.916 | 5.491 | 5.016 | 5.153 |
| relative error | 1.69% | 9.83% | 0.32% | 3.06% | ||
| ϑ/° | inverted value | 42 | 38.780 | 38.012 | 41.369 | 38.008 |
| relative error | 7.67% | 9.49% | 1.50% | 9.50% | ||
| RMSE/mm | 73.5 | 49.0 | 80.8 | 48.8 | ||
| Name | X1/m | Y1/m | H/m | m/m | D3/m | D1/m | ɑ/° | ϑ/° | RMSE/mm | |
|---|---|---|---|---|---|---|---|---|---|---|
| Data | 304.00 | 793.06 | 400 | 3.5 | 850 | 500 | 6 | 30 | ||
| GA | inverted value | 312.08 | 790.60 | 407.43 | 3.54 | 855.94 | 514.33 | 6.04 | 24.48 | 34.0 |
| relative error | 2.66% | 0.31% | 1.86% | 1.12% | 0.70% | 2.87% | 0.64% | 18.41% | ||
| Our method | inverted value | 304.06 | 793.08 | 399.97 | 3.50 | 849.97 | 500.11 | 6.17 | 29.99 | 0.2 |
| relative error | 0.02% | 0.00% | 0.01% | 0.04% | 0.00% | 0.02% | 2.88% | 0.03% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, C.; Liu, W.; Guo, Z.; Wang, L.; Zhu, X.; Tan, H. Research on the Precise Positioning of Mining Working Faces and an Inversion Method for Characteristic Working Face Parameters Based on a Robust Genetic Algorithm. Appl. Sci. 2025, 15, 12842. https://doi.org/10.3390/app152312842
Jiang C, Liu W, Guo Z, Wang L, Zhu X, Tan H. Research on the Precise Positioning of Mining Working Faces and an Inversion Method for Characteristic Working Face Parameters Based on a Robust Genetic Algorithm. Applied Sciences. 2025; 15(23):12842. https://doi.org/10.3390/app152312842
Chicago/Turabian StyleJiang, Chuang, Wei Liu, Zhongchen Guo, Lei Wang, Xu Zhu, and Hao Tan. 2025. "Research on the Precise Positioning of Mining Working Faces and an Inversion Method for Characteristic Working Face Parameters Based on a Robust Genetic Algorithm" Applied Sciences 15, no. 23: 12842. https://doi.org/10.3390/app152312842
APA StyleJiang, C., Liu, W., Guo, Z., Wang, L., Zhu, X., & Tan, H. (2025). Research on the Precise Positioning of Mining Working Faces and an Inversion Method for Characteristic Working Face Parameters Based on a Robust Genetic Algorithm. Applied Sciences, 15(23), 12842. https://doi.org/10.3390/app152312842





