Experimental Study of Micro/Macro Damage and Failure Mechanism of Granite Subjected to Different Impact Velocities and Numbers

Abstract

Rockfall typically involves repeated impacts that induce progressive damage and fragmentation in rock masses. To investigate the mechanism governing this process under different impact velocities, a series of controlled impact tests were conducted using a newly developed compressed gas-driven rock impact apparatus. This study systematically examined the effect of impact velocities and number on rock damage, distinguishing between internal damage (<10.0 m/s) and local failure (10.0 m/s–20.0 m/s). At the internal damage level, uniaxial compression tests with acoustic emission monitoring were employed to analyze the macro-mechanical properties and micro-failure processes of granite. At the local failure level, the repeated impact number required to transition from localized to complete failure was recorded, and polarizing microscopy was used to characterize microstructural evolution. The results show that damage and failure mechanisms are strongly influenced by both impact velocity and repeated impact number. Specifically, higher impact velocities and repeated impacts promote a shift toward brittle failure, with threshold behaviors observed at 5.0 m/s (fourth impact) and 7.5 m/s (third impact). A quantitative analysis further correlates impact conditions with mechanical degradation and energy evolution, providing insight into the underlying processes controlling rockfall fragmentation.

1. Introduction

Rockfalls, characterized by the abrupt detachment and movement of rock masses from steep slopes or cliffs, are common phenomena in mountainous areas and frequently occur on slopes that have been subjected to weathering and blast damage. These events can pose significant risks to human safety, engineering structures, infrastructure, and lifeline facilities worldwide [1,2,3,4]. To effectively mitigate the damage induced by rockfall, accurate prediction of falling rock trajectories is essential. In addition, the movement of a rockfall typically involves repeated impacts, leading to progressive damage and fragmentation [5,6,7,8,9], which significantly affect both the motion process and resulting hazard intensity. Therefore, it is crucial to investigate the mechanisms underlying repeated impact-induced damage and rock fragmentation characteristics under different impact velocities.

Over the past several decades, substantial research efforts have been made to investigate the dynamic response of rocks under complex dynamic loading conditions, particularly in terms of damage (micro-crack initiation and growth) and macro-fragmentation processes [9,10,11,12,13,14]. Studies indicated that dynamic damage in rock under impact loading is closely associated with the initiation and growth of micro-cracks at the grain scale [15,16,17,18]. Deng and Nemat-Nasser [19] developed a two-dimensional model incorporating frictional slip and rate-dependent and rate-independent plastic constitutive relations to describe the dynamic damage evolution in brittle materials. The results indicated that compressive loading causes micro-cracks to initiate from pre-existing micro-flaws and grow in the direction of compression. Based on laboratory tests and Particle Flow Code (PFC) simulations, Zhou et al. [20] investigated the micro-fracturing behavior and progressive damage process of granite under different loading rates. They proposed a damage model to interpret the degradation mechanism under impact loads and highlighted the essential role of micro-cracks in governing the dynamic behavior of rock. Cao et al. [13] experimentally investigated the influence of cyclic impact loading on the damage and fracture properties of marble and revealed that accumulating damage progressively degrades the rock’s strength and Mode II fracture toughness, leading to increasingly tortuous fracture surfaces with higher fractal dimensions. Lu et al. [21] studied the dynamic mechanical behavior and damage evolution of sandstone under hydrostatic pressure and found that increasing impact damage leads to a significant reduction in dynamic strength and dissipated energy ratio, with macro-microscopic analyses elucidating the underlying mechanisms. Jiang et al. [22] employed dynamic finite element simulations to investigate blasting-induced dynamic response and damage evolution in fractured rock masses, revealing that initial stress anisotropy accelerates stress wave propagation and localized damage, while identifying a critical influence range of four to five times the borehole diameters where rock damage transitions from complete to negligible. Utilizing a novel servo-controlled dynamic triaxial system, Li et al. [23] systematically investigated the intermediate strain rate (10⁻³–10⁰ s⁻¹) dependence of three rock types, revealing that increasing strain rates and confining pressures enhance dynamic strength and crack damage thresholds, whereas the dynamic stress intensity factor decreases, consequently elevating the axial stress required for crack initiation. Additionally, Zhou et al. [24] observed the energy conversion and damage evolution of nine rock materials under dynamic uniaxial compression, demonstrating that while strain energy density increases with strain rate, the relationship between damage and strain rate is highly complex and material-specific, leading to the proposal of a new energy-based damage variable.

For the macro-fragmentation process of rock subjected to impact loads, previous studies [25,26,27,28] have demonstrated that macro-fragmentation is mainly governed by the impact angle and impact velocity. Liu et al. [29] conducted rockslide simulations with varying slope angles and found that the impact angle plays an important role in rock block fragmentation. Wang and Tonon [30,31] investigated the effect of impact angle utilizing the DEM numerical method and showed that rock fragmentation was mainly affected by the magnitude of the normal velocity. Zhang et al. [32] systematically observed the dynamic degradation and wave propagation behaviors of deep tight sandstone under shock and impact disturbances. Based on dynamic impact tests and numerical simulations, Zuo et al. [33] studied the influence of natural joint angles on the fracture characteristics and energy evolution of rock, revealing that both the dynamic strength and energy dissipation exhibit a distinct “V”-shaped trend with increasing joint angles, accompanied by a transition in failure modes from tensile to shear-dominated mechanisms. Wang et al. [34] combined experimental tests and numerical simulations to study the dynamic response of marble under repeated impact loading. They found that both impact velocity and number significantly influence the stress–strain relationship, damage accumulation, and fracture progression, with a critical damage threshold identified at 120% of the static strength. Additionally, numerous scholars have employed the DEM method to investigate the fragmentation characteristics of rocks under impact loading [35,36,37].

As discussed above, while the damage and fragmentation mechanisms of rock under a single impact load have been extensively investigated, knowledge of the dynamic behavior of rock under repeated impact loading remains limited [38,39]. Through SHPB testing, Li et al. [40] demonstrated that repeated impacts induce progressive degradation in sandstone, characterized by a five-stage stress–strain response, a transition from volumetric compression to dilation, and a near-linear increase in crack population with cumulative energy absorption. Based on cyclic dynamic Brazilian and direct tension tests, Li et al. [41] studied the tensile fatigue behavior of granite and concluded that rock exhibits a lower fatigue threshold and distinct damage evolution under direct tension compared to indirect loading, with failure surface roughness showing opposite trends in these two testing configurations. Wang et al. [42] conducted coupled static–cyclic impact tests and investigated the dynamic response and energy evolution of confined granite. The results indicate that increasing confining pressure significantly enhances strength and energy dissipation capacity while altering crack propagation paths, whereas cyclic impacts lead to progressive stiffness degradation despite the stabilizing effect of confinement. Additionally, extensive studies on the damage and fragmentation characteristics of rocks under cyclic impact loading have been performed [14,43,44,45].

Although previous studies have advanced the understanding of rock behavior under repeated impacts, the micro-mechanisms governing damage accumulation and fragmentation under different impact numbers and velocities and their consequent influence on macroscopic dynamic properties remain inadequately characterized. Therefore, this study employs a self-developed compressed-gas-driven impact apparatus to systematically investigate the mechanical response of granite subjected to controlled impact conditions. By integrating macroscopic mechanical measurements with microscopic analysis, we quantitatively examine the effects of impact velocity and number on key mechanical parameters and energy evolution patterns. The findings provide critical insights into the progressive failure processes of rock under repeated dynamic loading, offering a scientific basis for enhanced stability assessment of rock engineering structures.

2. Experimental Design

2.1. Description of Rock Specimens

The granite specimens were selected from Changsha City, Hunan Province, China, which were processed into cylinders with a 50 mm diameter and 100 mm height. To re-duce the discretization of test results caused by the inhomogeneity of the specimens, all specimens were drilled from the same rock block, and specimens with similar wave velocity were selected for tests. Prior to conducting the impact tests, the basic mechanical properties of the specimens were first measured, where both the Young’s modulus and the uniaxial compressive strength were obtained from uniaxial compression tests. (shown in

Table 1. Basic mechanical parameters of selected granite sample.

Parameters	Density (g/cm3)	P-Wave Velocity (m/s)	Young’s Modulus (GPa)	Uniaxial Compressive Strength (MPa)
Value	2.63	4957	45.37	102.87

).

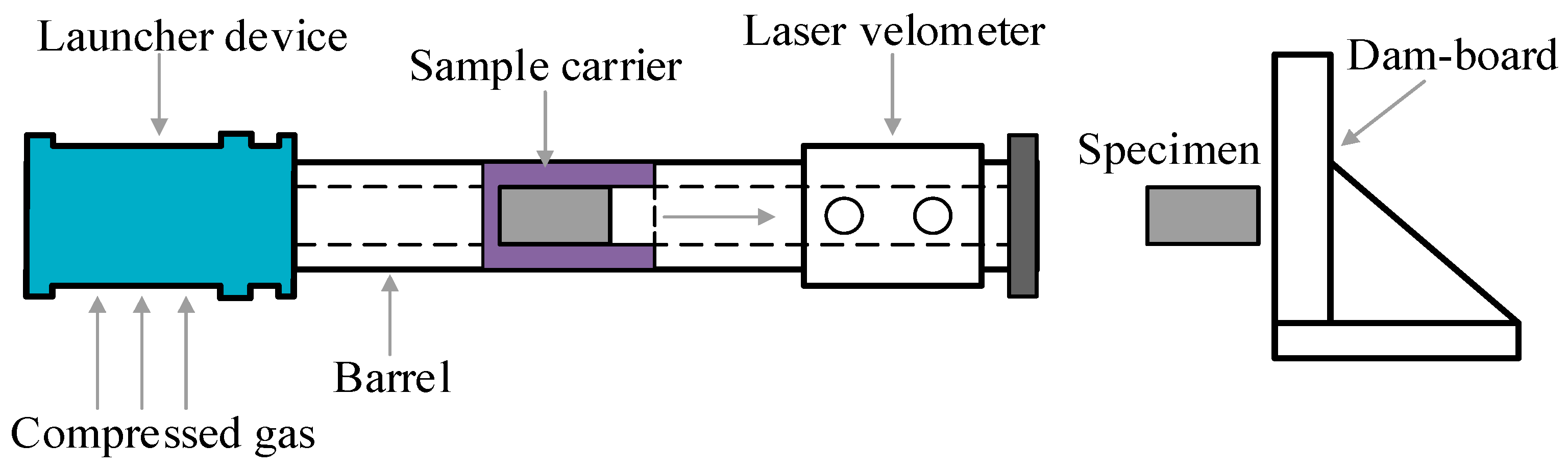
2.2. Test Equipment

A new compressed-gas-driven impact apparatus consisting of five main parts (launcher device, specimen carrier, laser velometer, dam-board, and high-speed shooting system), as shown in Figure 1, was developed for the impact test. Uniaxial compression tests were carried out using an RMT-301 hydraulic servo testing machine (see Figure 2). The AE pulse was collected via the AEWin-2 system (MISTRAS, Princeton, NJ, USA) during the uniaxial compression test. The thin sections of the rock specimens were observed using advanced orthogonal polarizing microscopy (see Figure 3).

2.3. Test Procedure

To investigate the influences of impact velocities and repeated impact numbers on the rock’s mechanical characteristics, impact tests with different impact velocities were conducted on rock specimens by controlling the compressed gas. In this experiment, to better analyze the micro/macro mechanism against the repeated impact-induced damage and fragmentation, the impact velocity is categorized into three typical levels based on the impact-induced damage degree, namely internal damage and local failure. In addition, during the impact tests, the error under different impact numbers of the same impact velocity was no more than 0.3 m/s. At the internal damage level (i.e., impact velocity smaller than 10.0 m/s), the maximum repeated impact number that changed rock specimens from internal damage to local failure was first recorded. Uniaxial compression tests were then carried out on the rock specimens treated with different impact velocities and repeated impact numbers, and the AE system was used to collect signals of the rock specimens’ micro-failure process. We also investigated the influences of internal damage on the macroscopic mechanical properties and micro-failure processes under different impact velocities and repeated impact numbers. At the local failure level (i.e., impact velocity ranging from 10.0 to 20.0 m/s), the impact velocity generated local fragmentation at the impacting face, which was different from the failure of a standard specimen being tested on a conventional mechanical testing machine. Therefore, the repeated impact number that changed the rock failure from local failure to the completely broken state should first be determined. In addition, to study the effects of different impact velocities and repeated impact numbers on the micro-structure of the rock specimen, sections about 30 μm thick were prepared from the end (near the impacting face) and middle parts of the broken specimen (see Figure 4). The micro-structure of the broken specimen was then obtained using orthogonal polarizing microscopy.

3. Experimental Results

3.1. Internal Damage Level

At the internal damage level, when the impact velocity increased from 5.0 to 10.0 m/s, the repeated impact number that changed the granite specimen from internal damage to local failure gradually decreased from 4 to 1. The variations in the macroscopic mechanical properties and micro-failure processes under different repeated impact numbers with velocities of 5.0, 7.5, and 10.0 m/s are discussed below.

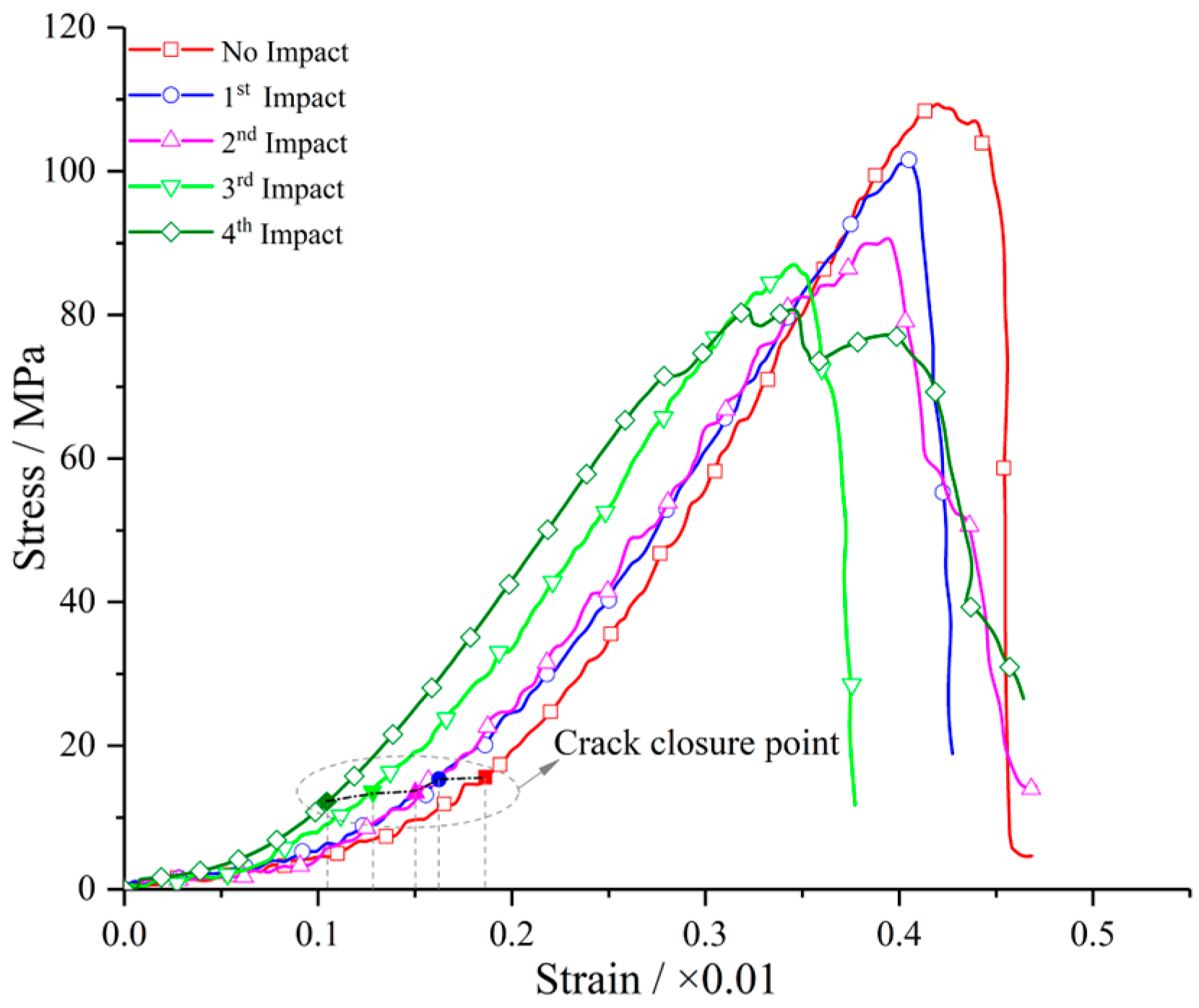
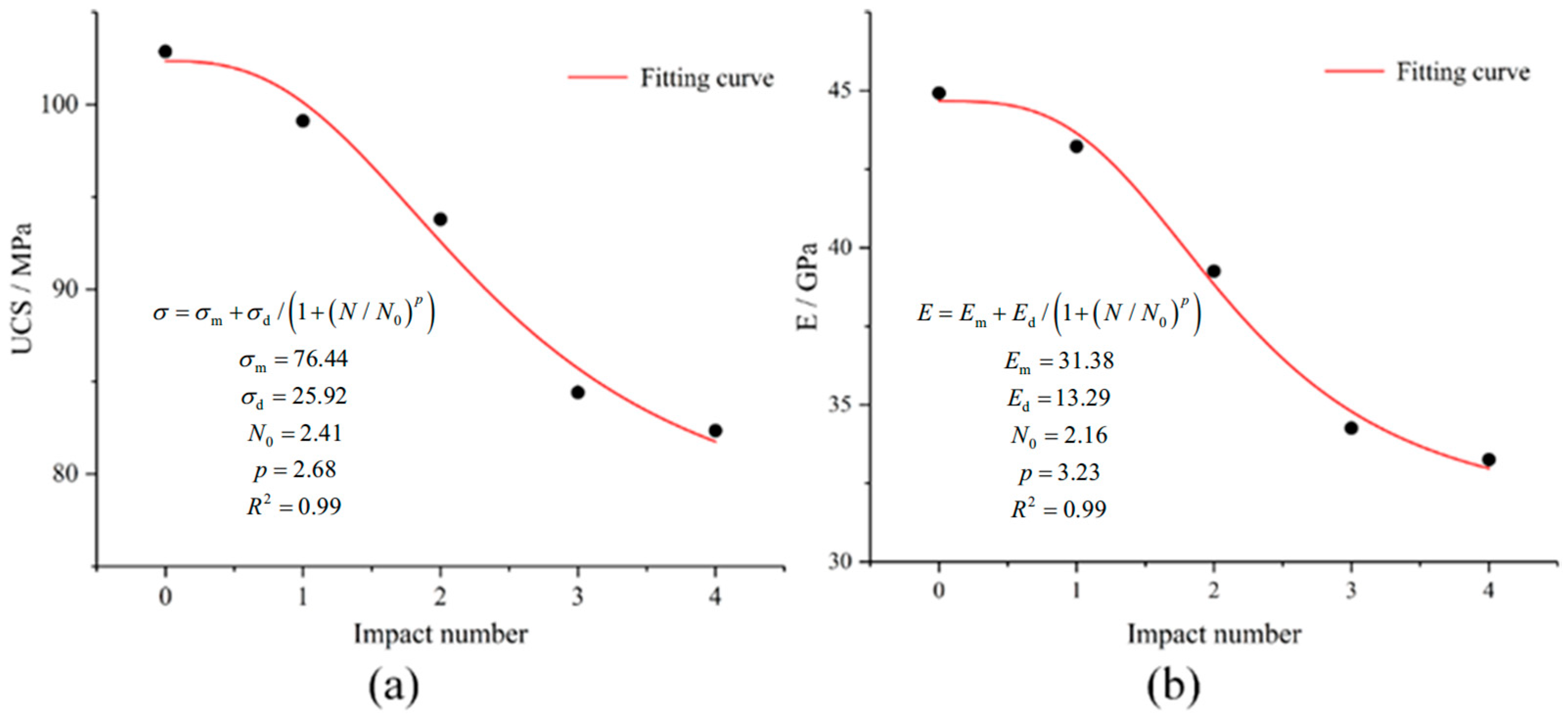
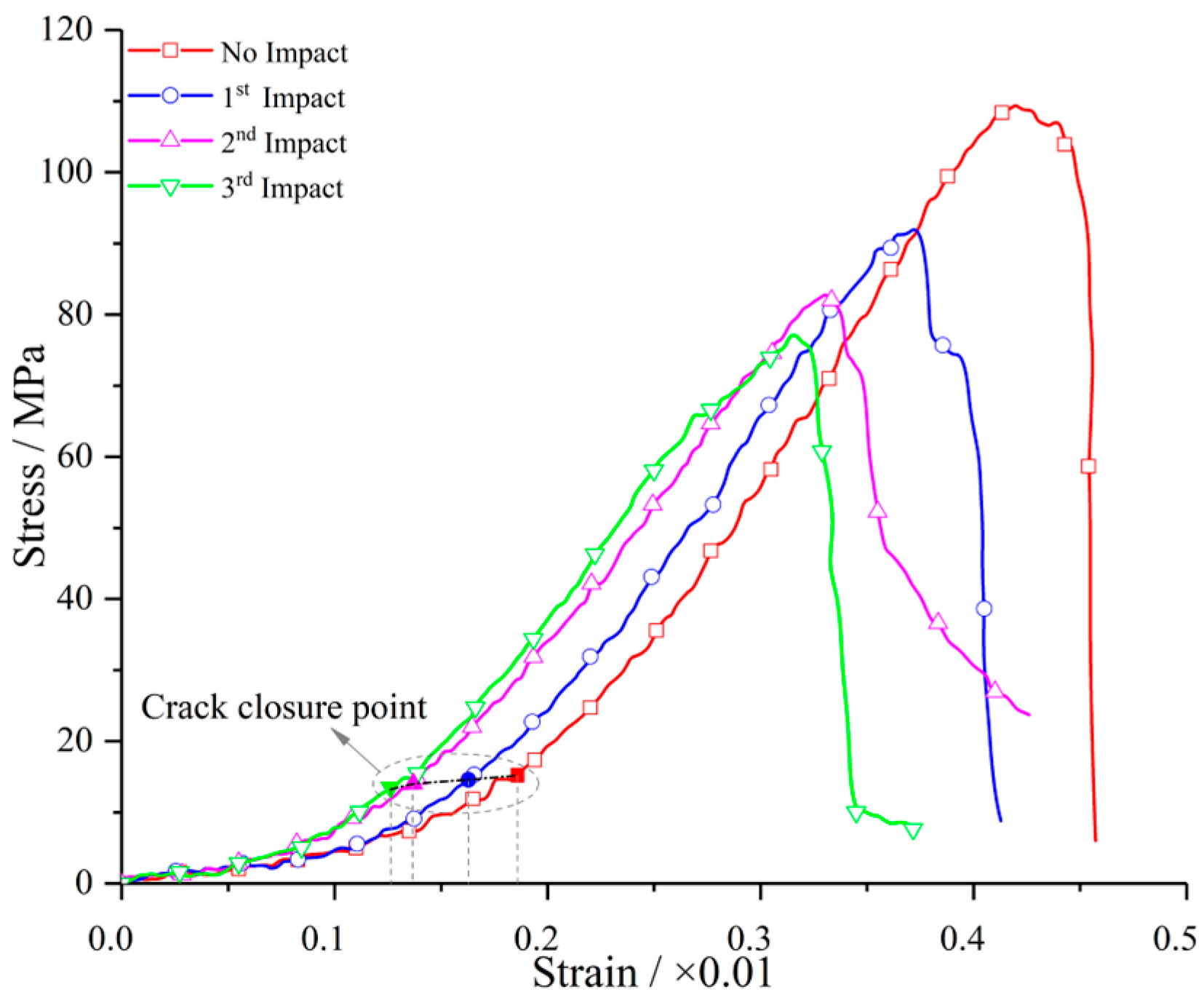
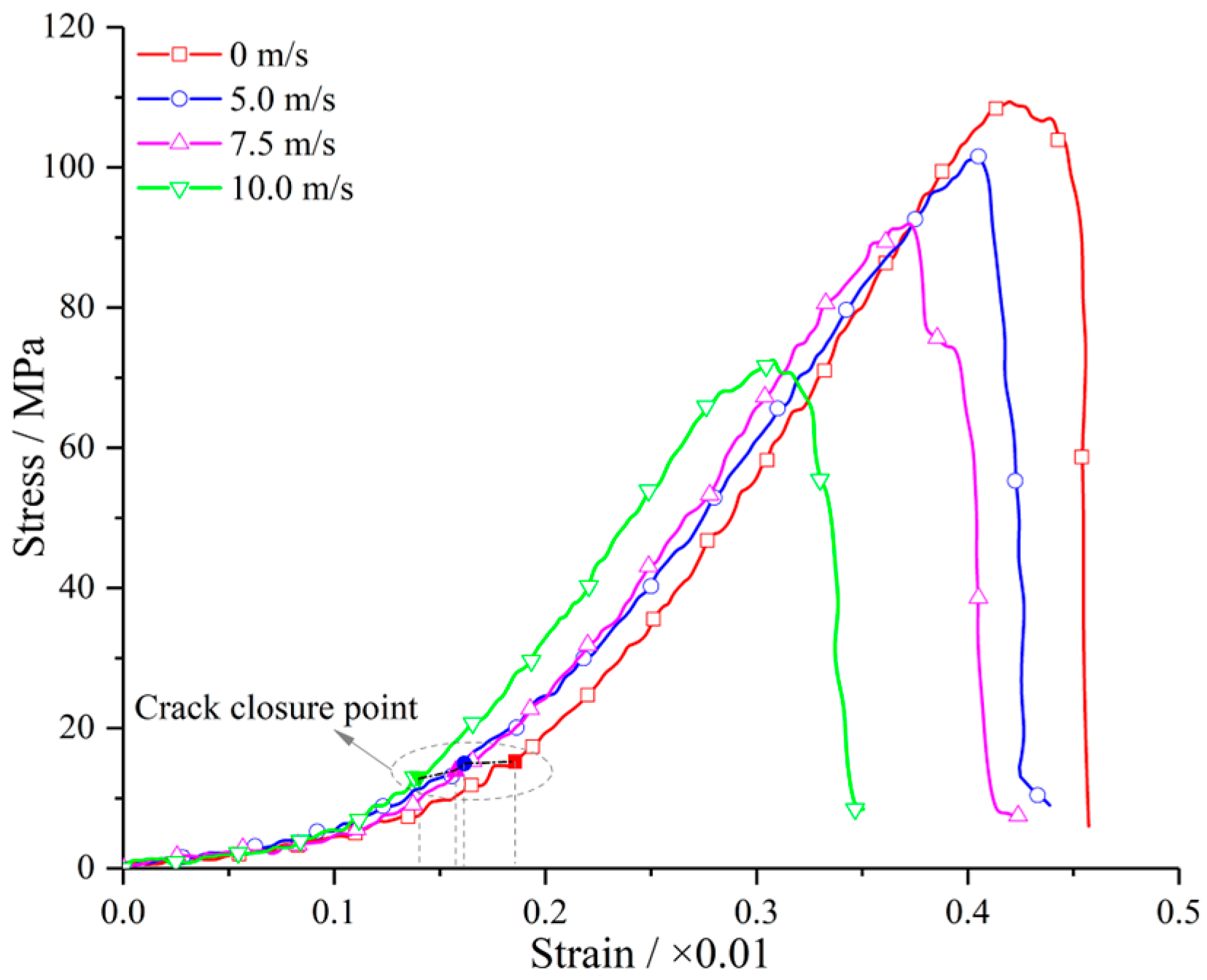
3.1.1. Mechanical Properties Under Different Impact Velocities and Repeated Impact Numbers

The stress–strain curves for specimens with different repeated impact numbers at a velocity of 5.0 m/s undergoing the quasi-static test are shown in Figure 5. The results show that these specimens experienced four typical stages; i.e., the crack/void compaction stage, elastic deformation and crack stable development stage, unsteady crack development stage, and post-failure stage. Figure 5 shows that the strain–stress curves of the granite specimens are significantly influenced by the repeated impact number. The crack/void compaction stage and the elastic deformation stage gradually shorten with an increasing repeated impact number, and the shortening phenomenon is more obvious for the last two impacts (impact only induces internal damage). This is mainly because the impact-induced crack closure and void compaction increase as the repeated impact number increases. In the unsteady crack development stage, both peak stress and the axial strain corresponding to peak stress gradually decrease with the increase in the repeated impact number, and the decrease is more obvious in the last impact (impact only induces internal damage). This phenomenon is probably due to the fact that as the repeated impact number increases, the internal damage to the granite specimen gradually increases, but the new damage induced by the last impact is significantly reduced.

The UCS and Young’s modulus of granite specimens subjected to repeated impact numbers at a velocity of 5.0 m/s were determined using uniaxial compression tests. Figure 6 illustrates the evolutions of the UCS and Young’s modulus (E) with an increasing repeated impact number under a velocity of 5.0 m/s. As the repeated impact number increases, both the UCS and Young’s modulus of the granite specimen decrease nonlinearly. Therefore, two empirical models based on the results of UCS and Young’s modulus are proposed:

$$\sigma ={\sigma }_{\mathrm{m}}+{\sigma }_{\mathrm{d}}/\left[1+{(N/N_0)}^p\right]$$

(1)

$$E=E_{\mathrm{m}}+E_{\mathrm{d}}/\left[1+{(N/N_0)}^p\right]$$

(2)

where σ and E are the predicted values of the UCS and Young’s modulus, respectively; σ_m and E_m represent the minimum values of the UCS and Young’s modulus, respectively; σ_d and E_d are the maximum decrements of the UCS and Young’s modulus, respectively; N is the repeated impact number of the granite specimen; and N₀ and p are the model parameters which control curvature.

The fitting results of the UCS and Young’s modulus obtained using the proposed models are presented in Figure 6. The high correlation coefficient (R²) indicates that the used models can well reflect the nonlinear relationship between the UCS, Young’s modulus, and the repeated impact number. The results show that both the UCS and Young’s modulus decrease with an increasing repeated impact number, and the rate of reduction gradually diminishes as the number of repeated impacts increases. This phenomenon is likely governed by the same mechanism as the previously discussed reduction in the new damage induced by the last impact with an increasing repeated impact number.

The stress–strain curves of granite specimens subjected to different repeated impact numbers at an impact velocity of 7.5 m/s are shown in Figure 7. Overall, their evolution characteristics are generally consistent with those at an impact velocity of 5.0 m/s, and therefore; only the main differences are briefly summarized here. At 7.5 m/s, the pre-peak portions of the stress–strain curves corresponding to the last two impacts (which only induce internal damage) almost coincide, indicating that the additional crack closure and void compaction in this stage are already very limited. Compared with the case of 5.0 m/s, both peak stress and the axial strain corresponding to peak stress at 7.5 m/s show a slight decrease under the same number of repeated impacts, suggesting that a higher impact velocity leads to more severe impact-induced damage. Based on the UCS and Young’s modulus obtained at 7.5 m/s, the empirical models given by Equations (1) and (2) are fitted, and the results are shown in Figure 8. It can be seen that these empirical models can also reasonably characterize the relationship among the UCS, Young’s modulus, and repeated impact number at an impact velocity of 7.5 m/s.

The stress–strain curves of granite specimens subjected to a single impact with different impact velocities are shown in Figure 9. The shortening of the crack/void compaction stage and the elastic deformation stage becomes more obvious as the impact velocity increases. In addition, the peak stress and axial strain corresponding to the peak strain decrease more obviously with increasing impact velocity. Furthermore, to quantitatively characterize the damage evolution of granite specimens under different impact velocities, two empirical models are proposed based on the results of the UCS and Young’s modulus. Considering that the two parameters change with the increasing impact velocity, as investigated in this study, a negative exponential function is adopted:

$$\sigma ={\sigma }_i+q\times \exp (-V/t)$$

(3)

where the σ is the predicted value of the UCS, σ_i is the initial value of the UCS, V is the impact velocity, and q and t are the model parameters.

$$E=E_i+q\times \exp (-V/t)$$

(4)

where the E is the predicted value of the Young’s modulus, and E_i is the initial value of the Young’s modulus.

The fitting results of the UCS and Young’s modulus obtained using the proposed models are shown in Figure 10. The correlation coefficient (R²) shows that the used negative exponential model can well capture the variation in the UCS and Young’s modulus in response to the change in impact velocity. It can be inferred from Figure 10 that when the impact velocity increases from 0 to 10.0 m/s, both the UCS and Young’s modulus of granite specimens decrease.

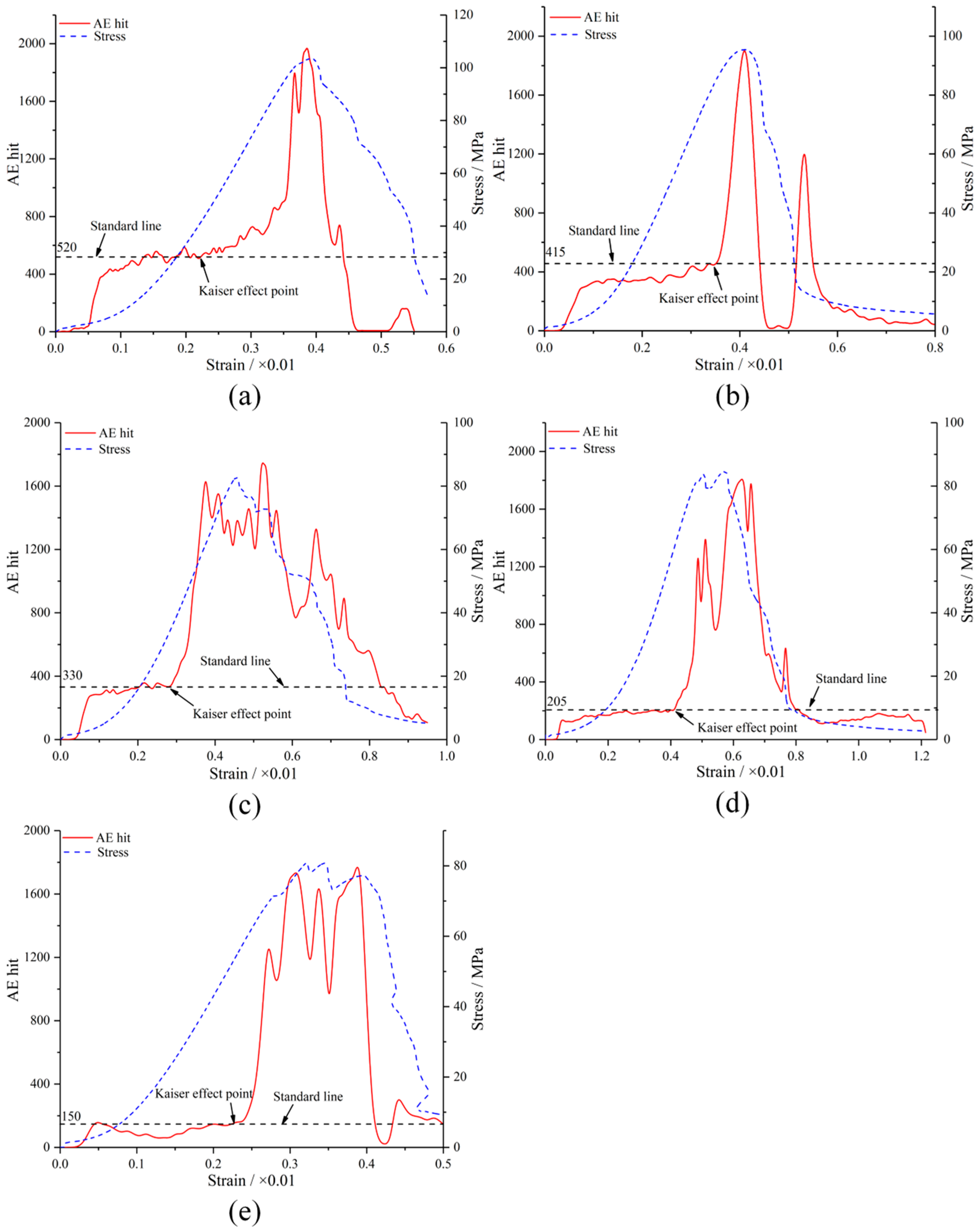
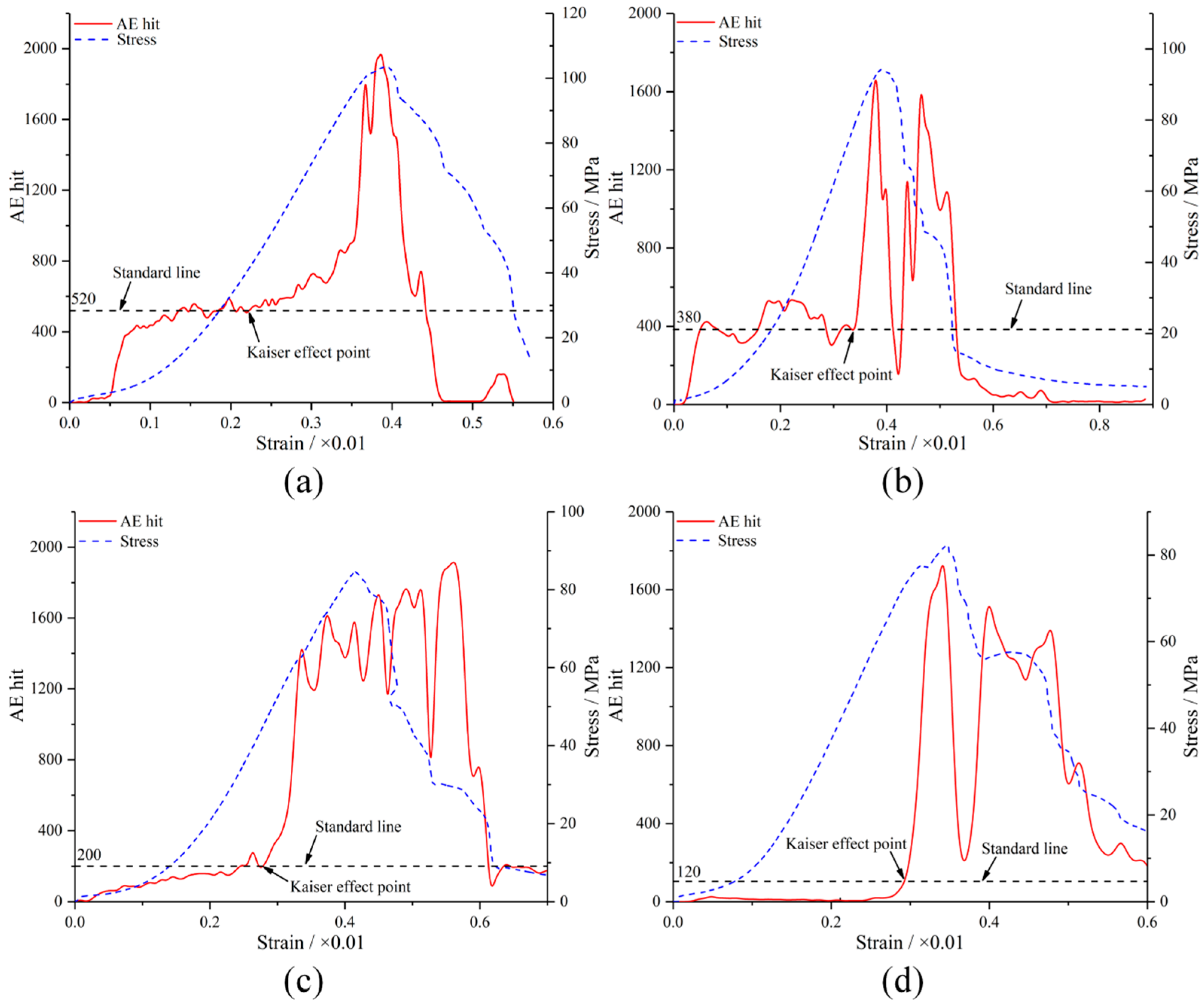
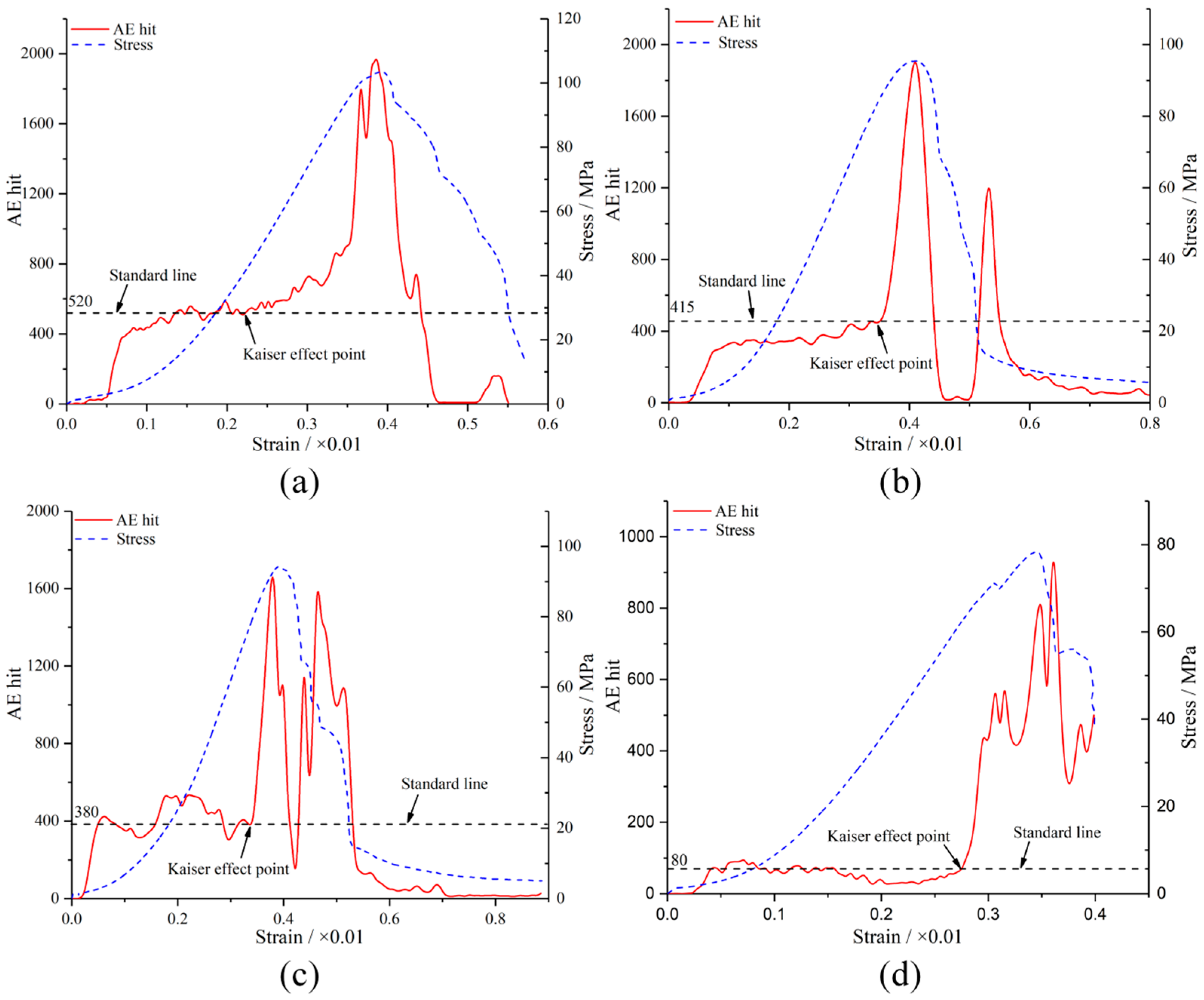
3.1.2. Micro-Failure Process Under Different Impact Velocities and Repeated Impact Numbers

The AE system is usually applied not only to monitor the micro-crack propagation but also to identify the failure mechanism of the rock micro-structure during rock mechanical tests [46,47,48,49]. The Kaiser effect is examined in this study [50]. The AE hit rate corresponding to the Kaiser effect point is defined as the AEK. The AE results for granite specimens under different repeated impact numbers at a velocity of 5.0 m/s are shown in Figure 11. In the sub-figures, the horizontal standard lines are drawn, and the intercepts of these standard lines with the AE axis are recognized as the AEK values. The AEK values for granite specimens under different repeated impact numbers at the velocity of 5.0 m/s are shown in Figure 12. The AEK value exhibits a monotonous decrease with an increasing repeated impact number. As the repeated impact number increases from 0 to 4, the AEK value decreases from 520 to 150. As proposed by Li and Nordlund [51], the Kaiser effect can be used to estimate the original damage within the rock specimen. Therefore, the AEK value of granite specimens under repeated impacts can be used as an indicator to describe their internal damage. Figure 12 shows that the AEK value gradually decreases with the increase in the repeated impact number, and the nonlinear relationship between the AEK and repeated impact number can be expressed as

$$N_{\mathrm{AEK}}=N_{\mathrm{m}}+N_{\mathrm{d}}/\left[1+{(N/N_0)}^p\right]$$

(5)

where N_AEK is the predicted value of AEK, N_M represents the minimum value of AEK, N_d is the maximum decrement of AEK, N is the repeated impact number of the rock specimen, and N₀ and p are the model parameters. Equation (5) is generally consistent with Equations (1) and (2) in Section 3.1.1. The same model with a high correlation coefficient (R²) indicates that the variation in the AEK value is similar to the results of the UCS and Young’s modulus. As the repeated impact number increases from 0 to 3, the AEK value gradually decreases from 520 to 205. However, when compared with the previous impact, the AEK value only decreases from 205 to 150 for the last impact (impact only induces internal damage) because as the repeated impact number gradually increases, the internal damage to the granite specimen continues to increase. Hence, when the granite specimen is loaded with a higher impact number, the micro-structure is more easily crushed, and the Kaiser effect easily occurs at a lower AE hit rate. It can be inferred that the cumulative micro-damage increases as the repeated impact number increases, but the new micro-damage induced by the last impact is greatly reduced.

The AE results for granite specimens under different repeated impact numbers at a velocity of 7.5 m/s are presented in Figure 13, while the AEK values are shown in Figure 14. The fitting result indicates that the variation in AEK value is similar to the results of the UCS and Young’s modulus, which is the same as the result for a velocity of 5.0 m/s.

The AE results for granite specimens subjected to a single impact at different impact velocities are shown in Figure 15, while Figure 16 shows that the AEK value constantly decreases with an increasing impact velocity. The nonlinear relationship between the AEK value and the impact velocity can be expressed as

$$N_{\mathrm{AEK}}=N_i+q\times \exp (-V/t)$$

(6)

where the N_AEK is the predicted value of AEK, N_i is the initial value of AEK, V is the impact velocity, and q and t are the model parameters. The fitting results with a high correlation coefficient (R²) obtained using the proposed model indicate that the variation in the AEK value with the impact velocity is similar to the results of the UCS and Young’s modulus. When the impact velocity increases from 0 to 7.5 m/s, the AEK value of the granite specimen only decreases by 26.92% (i.e., from 520 to 380). However, as the impact velocity increases from 7.5 to 10.0 m/s, the AEK value decreases by 78.95% (i.e., from 380 to 80). This indicates that the cumulative micro-damage of the granite specimen continuously increases with an increasing impact velocity, and the increase becomes more obvious as the impact velocity exceeds 7.5 m/s.

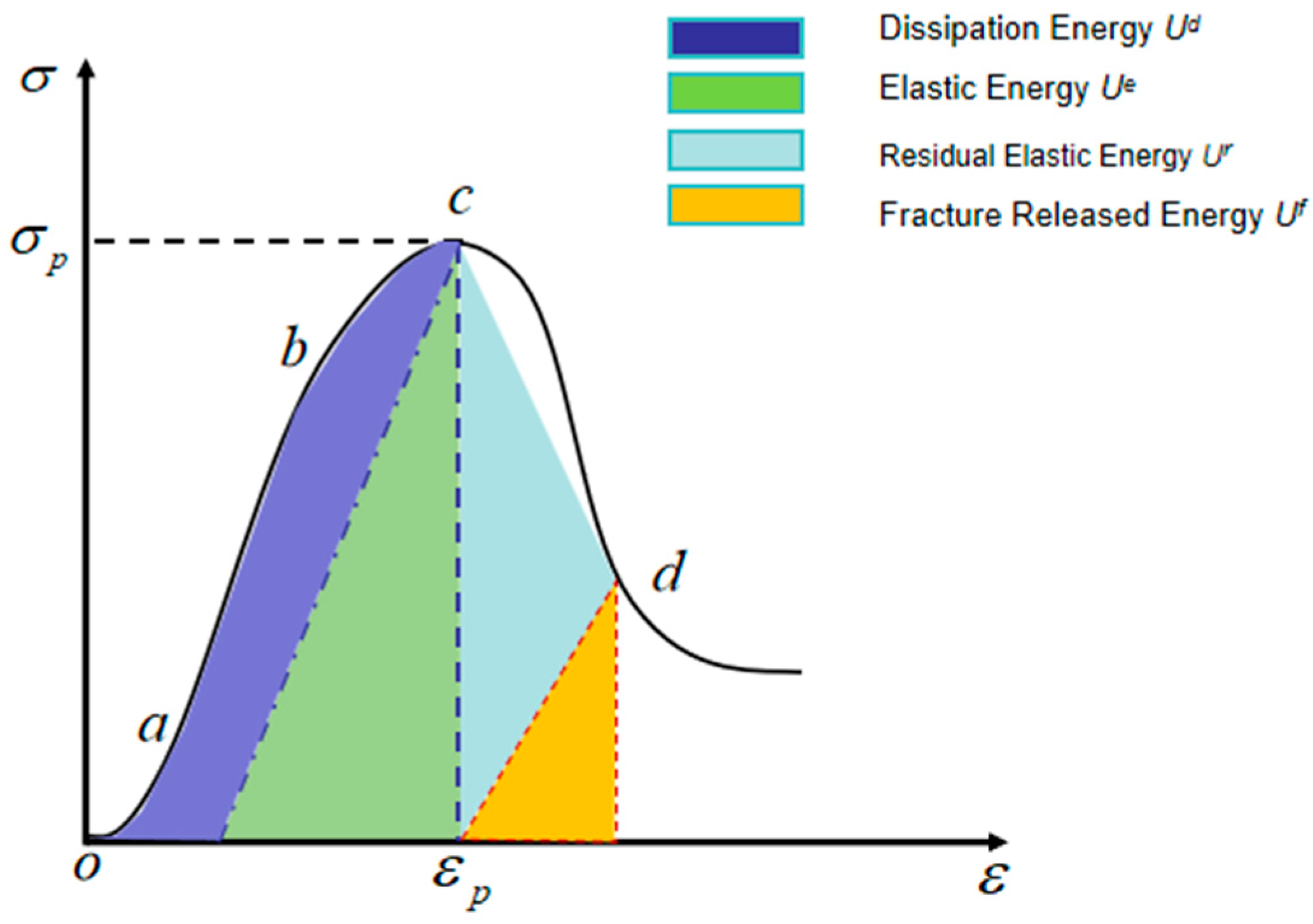
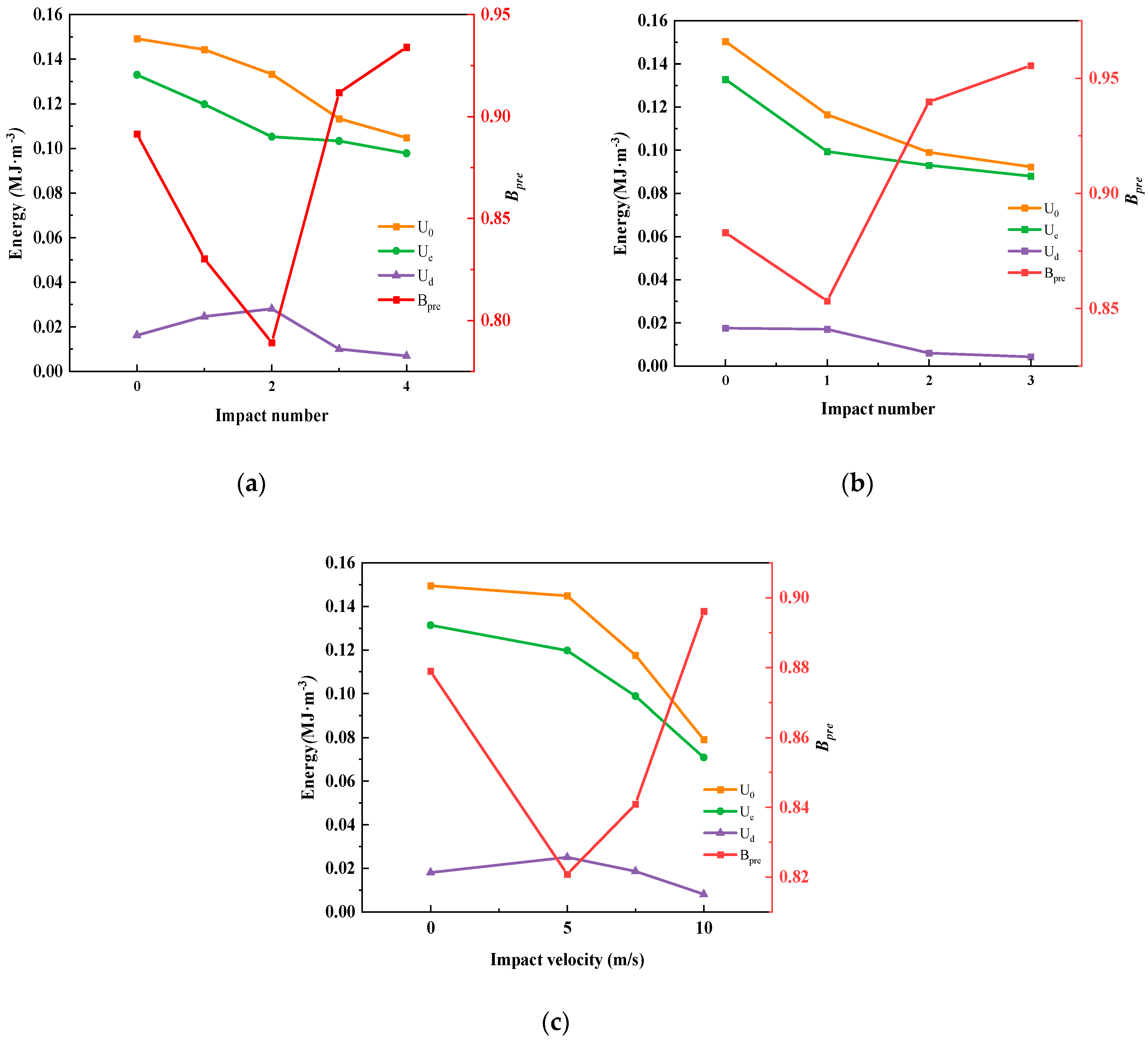
3.1.3. Energy Evolution

Under uniaxial compression conditions, rock samples undergo the processes of energy input, accumulation, release, and dissipation. The input energy was converted into elastic energy and dissipated energy during the compaction stage (stage a in Figure 17) and the linear elastic deformation stage (stage b in Figure 17). Subsequently, during the unstable fracture development stage (stage c in Figure 17) and the final failure stage (stage d in Figure 17), these energies gradually dissipated were released. Figure 17 shows that based on the conservation of energy, the energy evolution process during uniaxial compression can be represented by the following equations:

$$U_0=U_{\mathrm{e}}+U_{\mathrm{d}}$$

(7)

$$U_0={\displaystyle {\int }_0^{\epsilon }{\sigma }_{\mathrm{p}}}\mathrm{d}{\epsilon }_{\mathrm{p}}$$

(8)

$$U_{\mathrm{e}}={\displaystyle \frac{{\sigma }_{\mathrm{p}}^2}{2E}}$$

(9)

$$U_{\mathrm{d}}={\displaystyle {\int }_0^{\epsilon }{\sigma }_{\mathrm{p}}}d{\epsilon }_{\mathrm{p}}-{\displaystyle \frac{{\sigma }_{\mathrm{p}}^2}{2E}}$$

(10)

where U₀, U_e, and U_d represent the total energy absorbed before the peak, the stored elastic strain energy, and the dissipated energy released, respectively; ${\epsilon }_{\mathrm{p}}$ and ${ \sigma }_{\mathrm{p}}$ are the peak strain and peak stress, respectively; and E is the elastic modulus.

The ratio of the elastic strain energy stored before the peak to the total energy expended before the peak is defined as the peak brittleness index (B_pre), which can be expressed as

$$B_{\mathrm{pre}}={\displaystyle \frac{U_{\mathrm{e}}}{U_0}}$$

(11)

The higher the peak brittleness index of the rock, the greater the rate of elastic strain energy stored before the peak, providing more energy for the post-peak failure of the rock, increasing the degree of crack propagation after the peak, and thereby exhibiting greater brittleness.

The energy and peak brittleness index curves of granite specimens, depicted in Figure 18, illustrate a decrease in the total energy and elastic strain energy absorbed by the rock prior to the peak with increasing impact velocity and frequency. Conversely, the dissipated energy tends to increase initially and then decrease. Additionally, the peak brittleness index exhibits a biphasic trend, initially decreasing and then increasing with the augmentation of impact frequency and velocity, suggesting an initial increase in hardness followed by an increase in brittleness. This behavior may be attributed to the closure of micro-fractures and compaction of the rock under low-energy impacts, which results in a hardening effect. However, as the frequency and velocity of impacts escalate, the accumulation of damage alters the rock’s failure mode, culminating in a more brittle fracture.

3.2. Local Failure Level

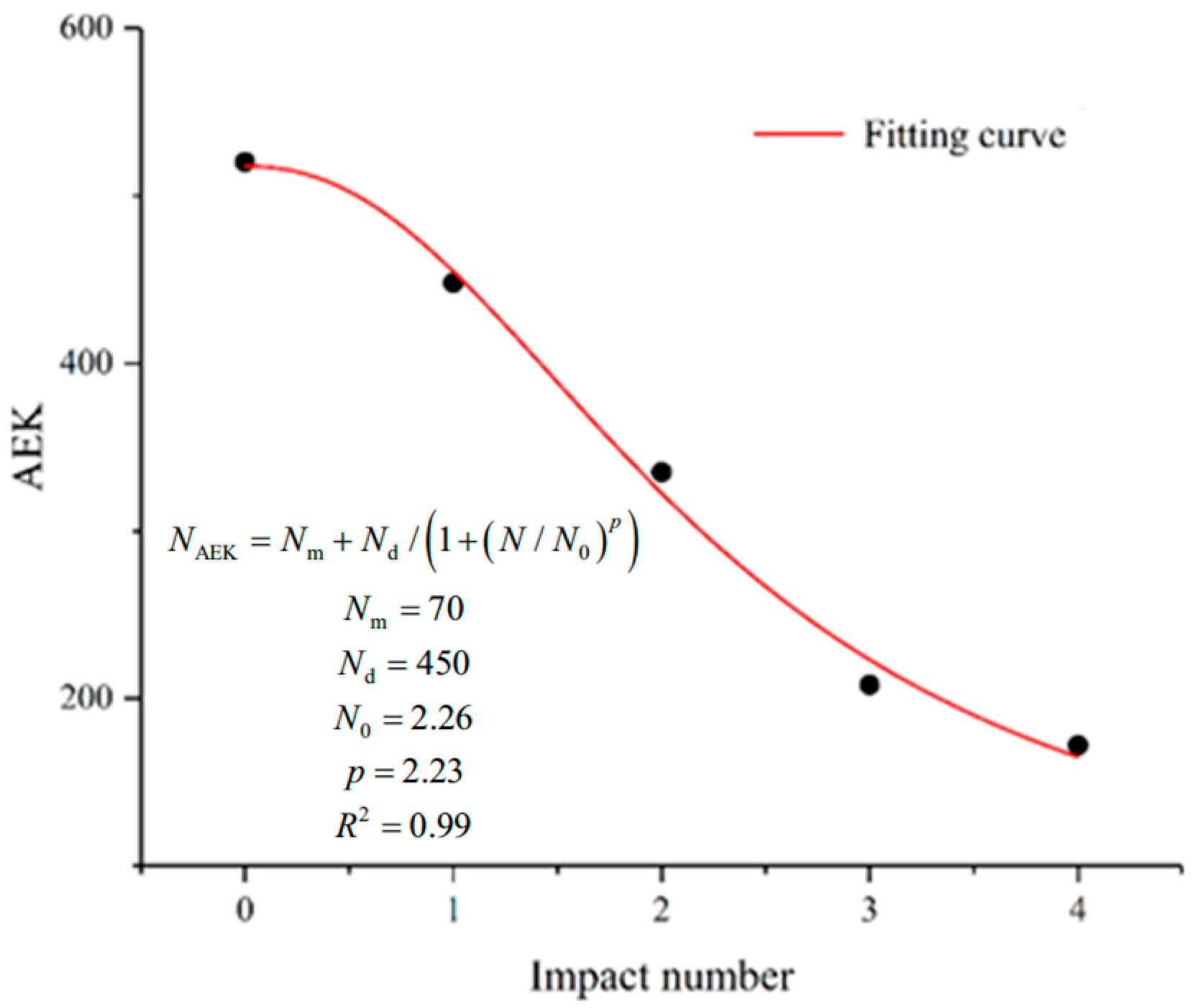
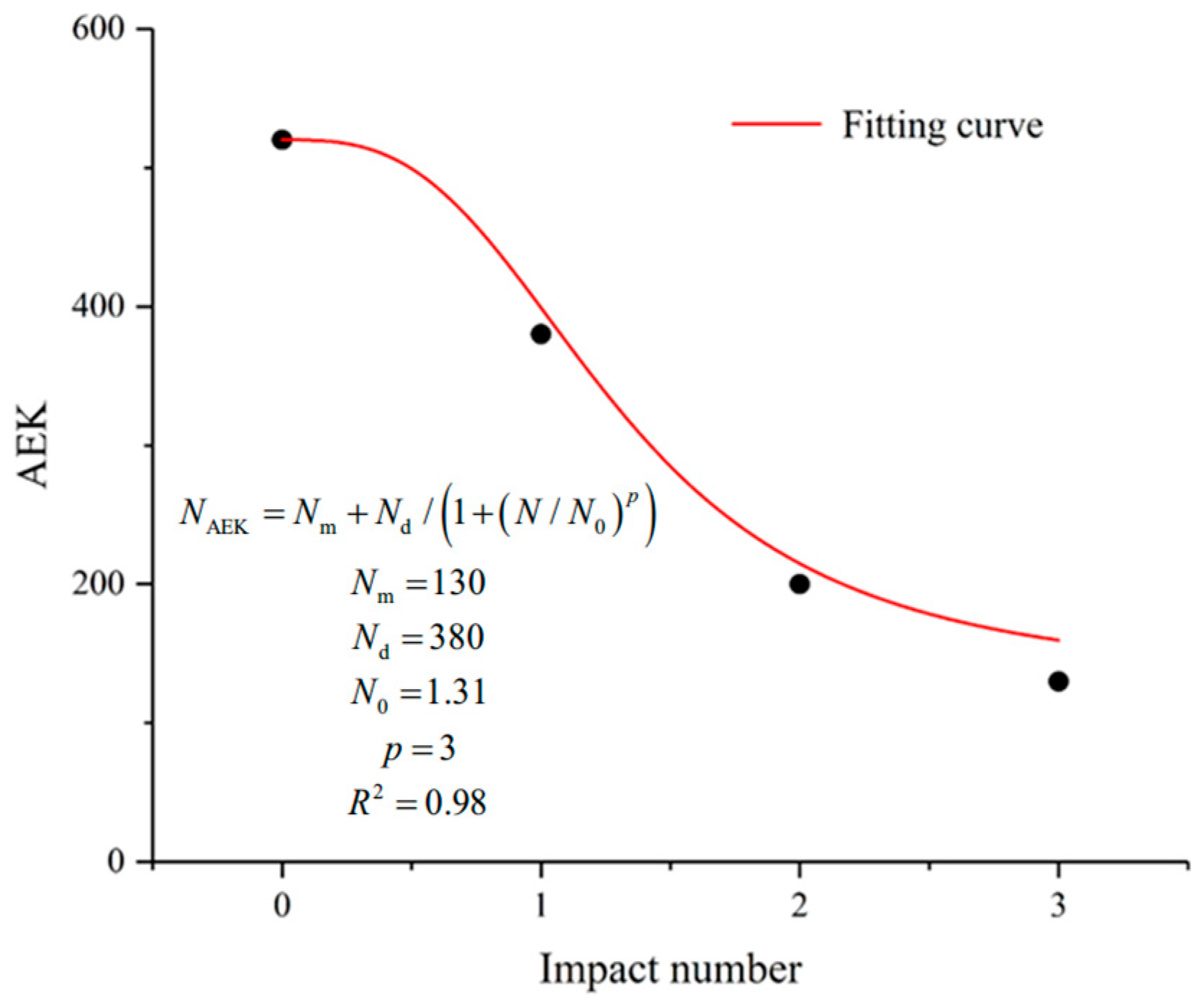
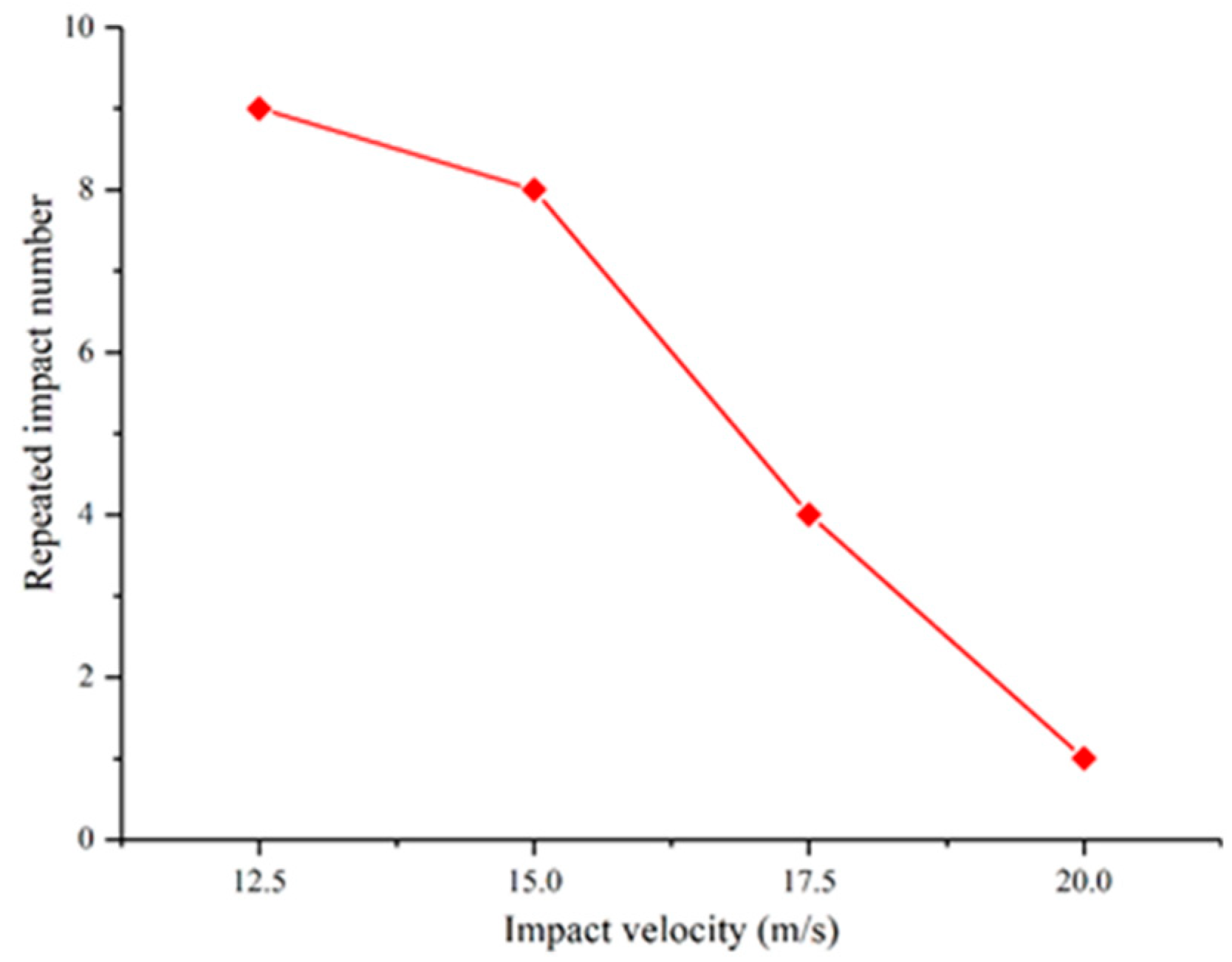
3.2.1. Repeated Impact Number That Causes the Specimen to Break Completely

At the local failure level, a medium impact velocity generates local fragmentation at the impact face, which is different from the failure of a standard specimen being tested on a conventional mechanical testing machine. Therefore, to account for the influence of the impact velocities at this level, we should determine the repeated impact number that changes a granite specimen from local failure to a completely broken state under different impact velocities. The variation in transition impact number with the impact velocity is presented in Figure 19. The results show that as the impact velocity increases from 12.5 to 20.0 m/s, the transition impact number corresponding to a completely broken granite specimen gradually decreases from 9 to 1. When the impact velocity increases from 12.5 to 15.0 m/s, the transition impact number only decreases from 9 to 8. However, when the impact velocity further increases to 17.5 m/s, the transition impact number decreases greatly from 8 to 4. Moreover, as the impact velocity continues to increase to 20.0 m/s, the granite specimen is completely broken under a single impact. This indicates that an impact velocity lower than 15.0 m/s has little influence on the transition impact number. An impact velocity exceeding 15.0 m/s has a significantly increased influence on the transition impact number.

3.2.2. Microscopic Observations

With the aid of polarizing microscopy, the micro-structure of the granite specimens under different impact velocities and repeated impact numbers can be directly observed and analyzed. This method is widely used to investigate the micro-crack distributions inside the granite specimen. In the present study, the micro-structure of prepared thin sections is enlarged by factors of 50 and 100, and the optical microscopy observations served as supplementary qualitative evidence to support the macroscopic test results, as shown in Figure 20. Two types of micro-cracks are analyzed in this study, i.e., intergranular cracks, which grow along grain boundaries, and transgranular cracks, which grow across a grain.

The micro-structural characteristics of each impact velocity are analyzed. Figure 20 shows that the micro-structural failure of the completely broken granite specimens after repeated impacts can be divided into three patterns: micro-cracks that penetrate multiple grains, micro-cracks in a single grain, and the complete breakage of small grains. When the impact velocity increases from 12.5 to 15.0 m/s, the micro-crack density (i.e., micro-crack number and length) of the broken granite specimen and the complete breakage of small grains all slightly increase. This is probably because as the impact velocity increases, the repeated impact number that induces complete breakage of the granite specimen only decreases from 9 to 8. As the impact velocity further increases to 17.5 m/s, the micro-crack density of the broken granite specimen decreases slightly with a notable increase in the complete breakage of small grains. This is because with a further increase in the impact velocity, the repeated impact number that induces complete breakage of the granite specimen decreases greatly from 8 to 4. Furthermore, there are multiple secondary cracks on the main micro-crack, which may be because secondary cracks gradually developed with the increase in repeated impact numbers. When the impact velocity continues to increase to 20.0 m/s, the granite specimen is completely broken under a single impact. In this case, both the micro-crack density and the complete breakage of small grains of the broken granite specimen have a certain reduction compared with those at 17.5 m/s. The results reveal that when the impact velocity is lower than 15.0 m/s, it has little influence on the repeated impact number that induces a completely broken granite specimen, resulting in little influence on the micro-crack density. When the impact velocity exceeds 15.0 m/s, it has a significantly increased influence on the repeated impact number, causing the micro-crack density of the granite specimen to gradually decrease with a decreasing repeated impact number. This may be because the impact-induced damage is small at the low velocity, resulting in a large repeated impact number. Moreover, the impact-induced damage increases slightly with the increase in the impact velocity, which results in a small decrease in the repeated impact number. However, impact-induced damage increases significantly with a larger impact velocity, which greatly reduces the repeated impact number. In addition, for all impact velocities, both the micro-crack density and the complete breakage of small grains developed in the end part (near the impact face) of the completely broken granite specimen are more obvious than those developed in the middle part. The results generally show that the impact-induced damage decreases with the increasing distance from the impact face.

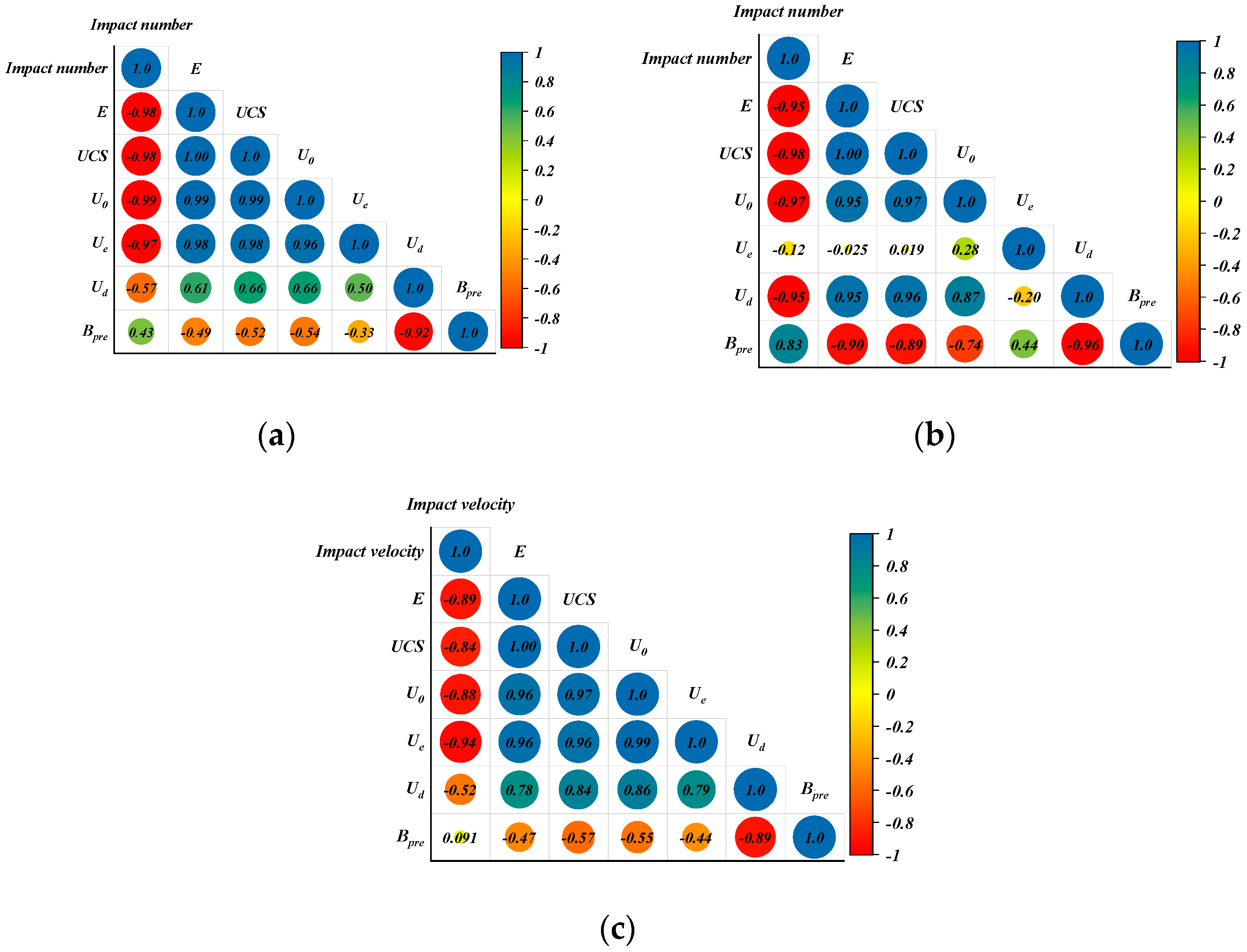
4. Discussions

To quantitatively study the influence of the repeated impact number and impact velocity on the mechanical property parameters (E, UCS and B_pre) and energy evolution characteristics (U₀, U_e and U_d) of rocks, the correlation coefficients between these variables were calculated using the Pearson algorithm, and the results are presented in Figure 21. It can be concluded that the repeated impact numbers and velocities are positively correlated with the pre-peak brittleness index (B_pre) and negatively correlated with other parameters. For different impact velocities and numbers, the elastic modulus is strongly positively correlated with the uniaxial compressive strength, reaching a value of 1.0. The dissipated energy (U_d) is highly negatively correlated with the pre-peak brittleness index (B_pre), exceeding −0.86. Compared to Figure 21a, Figure 21b shows a significant change in the correlation values between the elastic strain energy (U_e) and repeated impact number (E, UCS and U₀). Among these, the negative correlation value between U_e and the repeated impact number significantly decreased from −0.97 to −0.12. Additionally, the positive correlation values between U_e and E, UCS and U₀ also significantly decreased from 0.98 to −0.025 and 0.019, and from 0.96 to 0.28, respectively. In the three subfigures, some parameters have a strong positive relationship (close to 1.0), such as U₀ with E and UCS, while some parameters have a strong negative relationship (close to −1.0), such as impact velocity and repeated impact number with E, UCS, and U₀.

From an engineering perspective, the present results are relevant not only to rockfall impact analysis on slopes and protective structures [52,53,54], but also to impact-induced rock failure in application such as aggregate production, coal mining and drilling operations [55,56,57]. The established quantitative relationships among impact velocity, impact number, and the degradation of strength, stiffness and energy dissipation provide valuable references for estimating the damage degree and residual stability of rock blocks under repeated impacts, selecting appropriate impact energy levels and optimizing equipment parameters in crushing systems, as well as assessing damage accumulation and failure risk in rocks subjected to multiple impacts during mining and drilling.

This study has several limitations that should be addressed in future work. First, in terms of model applicability, all empirical models (Equations (1)–(6)) were calibrated using test results from Changsha granite with specific specimen dimensions and loading boundary conditions. As a result, these models exhibit a strong dependence on both rock type and loading conditions. Currently, they are applicable only to the rock type and experimental range considered in this study. Extending these relationships to other lithologies or different stress states will require additional dedicated experiments and recalibration of the model parameters. Second, regarding experimental design and statistical analysis, each combination of impact velocity and impact number was generally represented by only one large, relatively homogeneous specimen. Therefore, the tests are oriented toward an exploratory characterization of damage and failure mechanisms rather than large-sample statistical analysis. Under such conditions, it is difficult to derive statistically meaningful standard deviations, confidence intervals, or to perform rigorous significance tests for each condition. Consequently, the related conclusions are mainly based on trend and comparative analysis of the current dataset. Future work should involve systematic statistical analyses based on larger sample sizes and repeated tests to enhance the generality and reliability of the findings. Finally, with respect to microstructural characterization, the polarizing microscopy observations only allow qualitative comparisons of microcrack development under different impact velocities and impact numbers. Systematic quantitative statistics or stereological analyses, such as crack density, aperture, orientation distribution, and damaged zone dimensions, have yet to be performed for parameters.

5. Conclusions

In this study, impact tests on granite specimens with different impact velocities and repeated impact numbers were conducted on a rock impact apparatus driven by compressed gas. The micro/macro-mechanism against the repeated impact-induced damage and fragmentation under different impact velocities and repeated impact numbers was investigated. The following conclusions can be drawn:

(1)

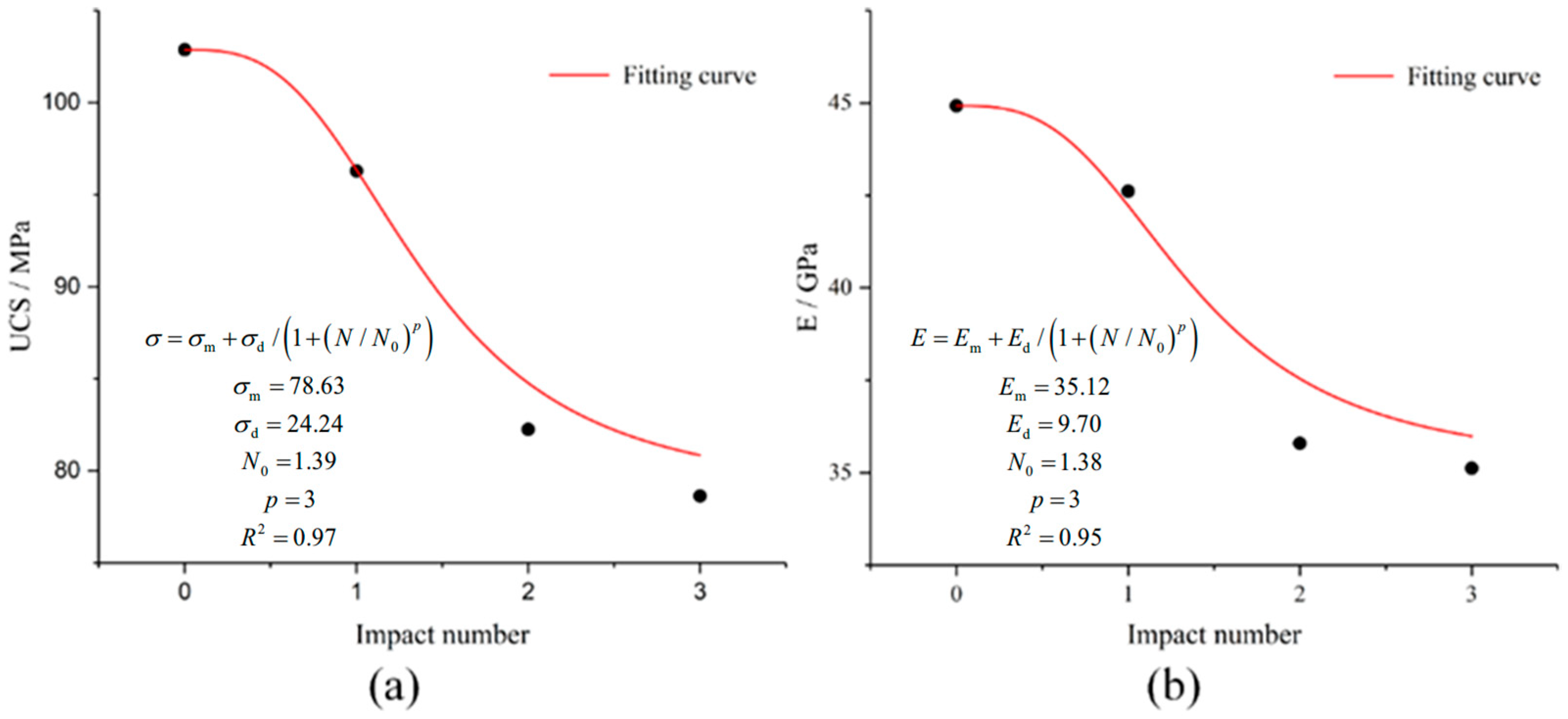
At the internal damage level, when the impact velocity increases from 5.0 to 10.0 m/s, the repeated impact number that changes a granite specimen from internal damage to local failure decreases from 4 to 1. The UCS and Young’s modulus monotonously decrease with an increasing number of repeated impacts, and the decrease is significantly weakened for the last impact (impact only induces internal damage).

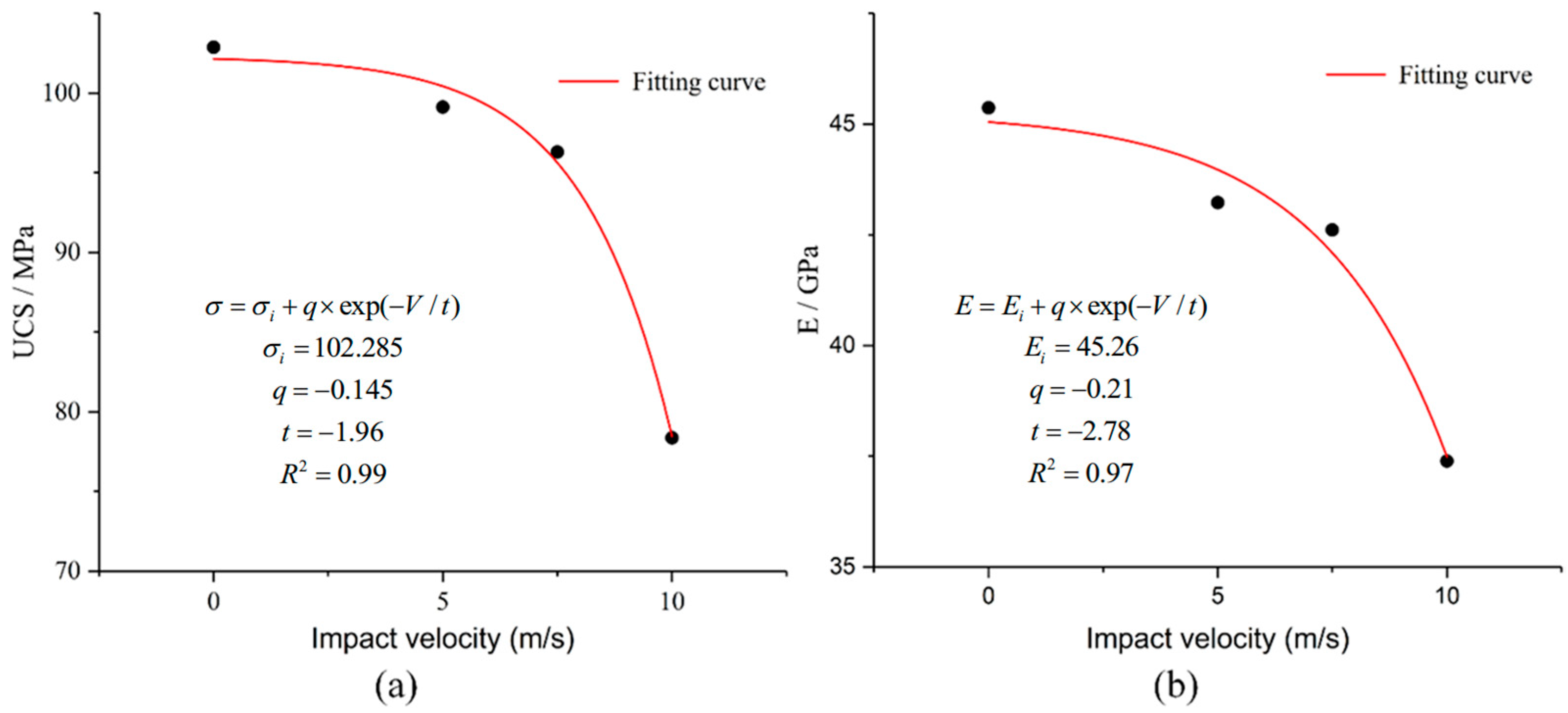
(2)

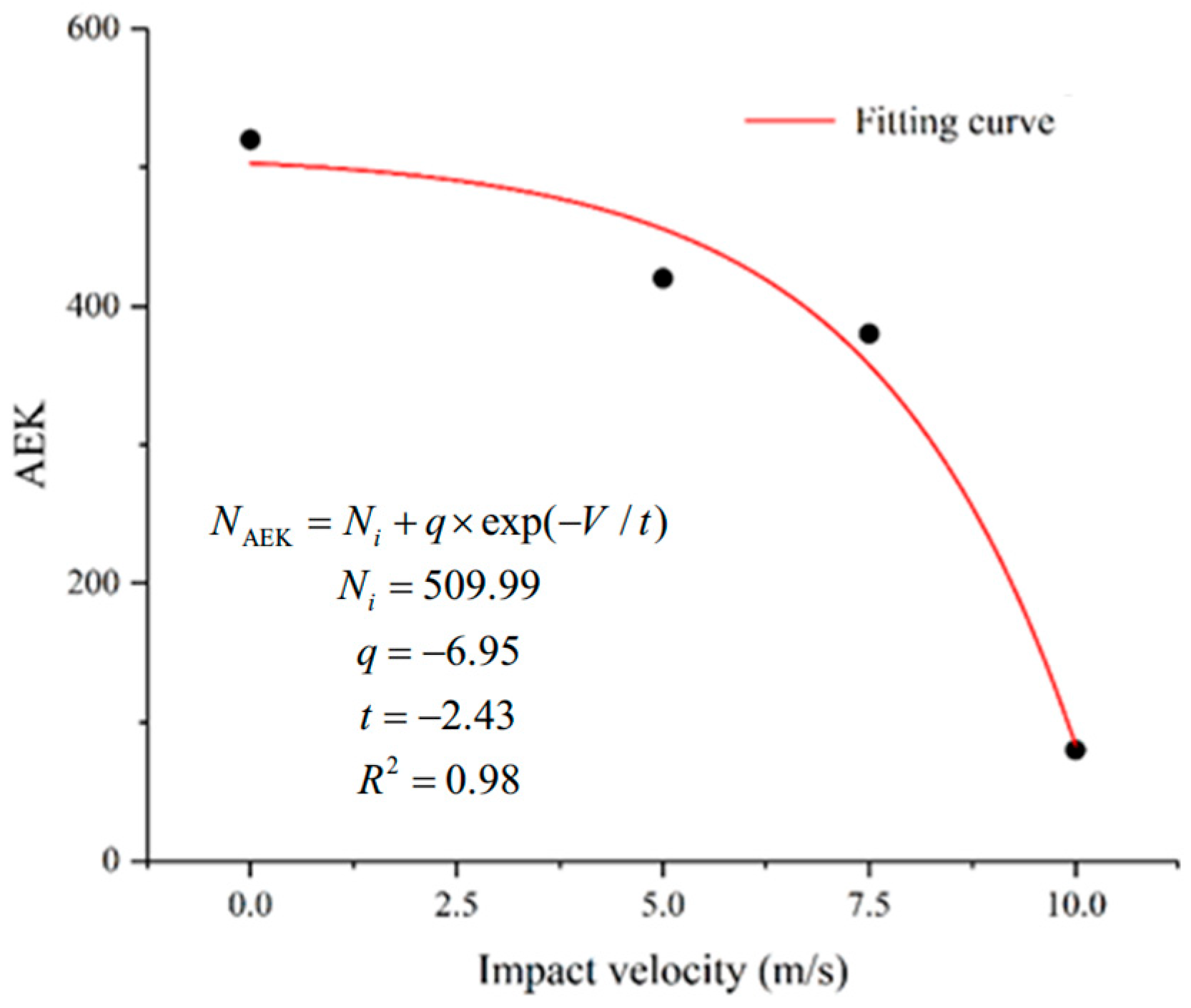
At the internal damage level, regarding the behavior of a granite specimen after a single impact, the proposed negative exponential models can well capture the variation in UCS and Young’s modulus with the impact velocity. When the impact velocity increases from 5.0 to 10.0 m/s, both the UCS and Young’s modulus of the granite specimen gradually decrease, experiencing a more obvious reduction when the impact velocity exceeds 7.5 m/s.

(3)

At the local failure level, when the impact velocity increases from 12.5 to 20.0 m/s, the repeated impact number that changes a granite specimen from local failure to a completely broken state decreases from 9 to 1. As the impact velocity increases from 12.5 to 15.0 m/s, the micro-crack density of the broken granite specimen increases slightly, while the complete breakage of small grains increases significantly. When the impact velocity further increases to 17.5 m/s, the micro-crack density of the broken granite specimen decreases as the complete breakage of small grains obviously increases. When the impact velocity continues to increase to 20.0 m/s, the granite specimen is completely broken under a single impact.

(4)

Different repeated impact numbers and velocities have significant effects on the brittle failure of granite, and there is an obvious negative correlation with granite’s mechanical property parameters (E and UCS) and the total energy absorbed before the peak (U₀). This indicates that the more often and the faster the granite is impacted, the more likely it is to fail in a brittle manner. Additionally, the higher the impact velocity and frequency, the greater the negative impact on the mechanical properties and the total energy it can absorb before peak stress is reached.