Analysis of Factors Influencing Skin Factor in Conventional Perforation Completion and Prediction Model Research
Abstract
1. Introduction
2. Establishment of Fluid Flow Model for Conventional Perforated Completion
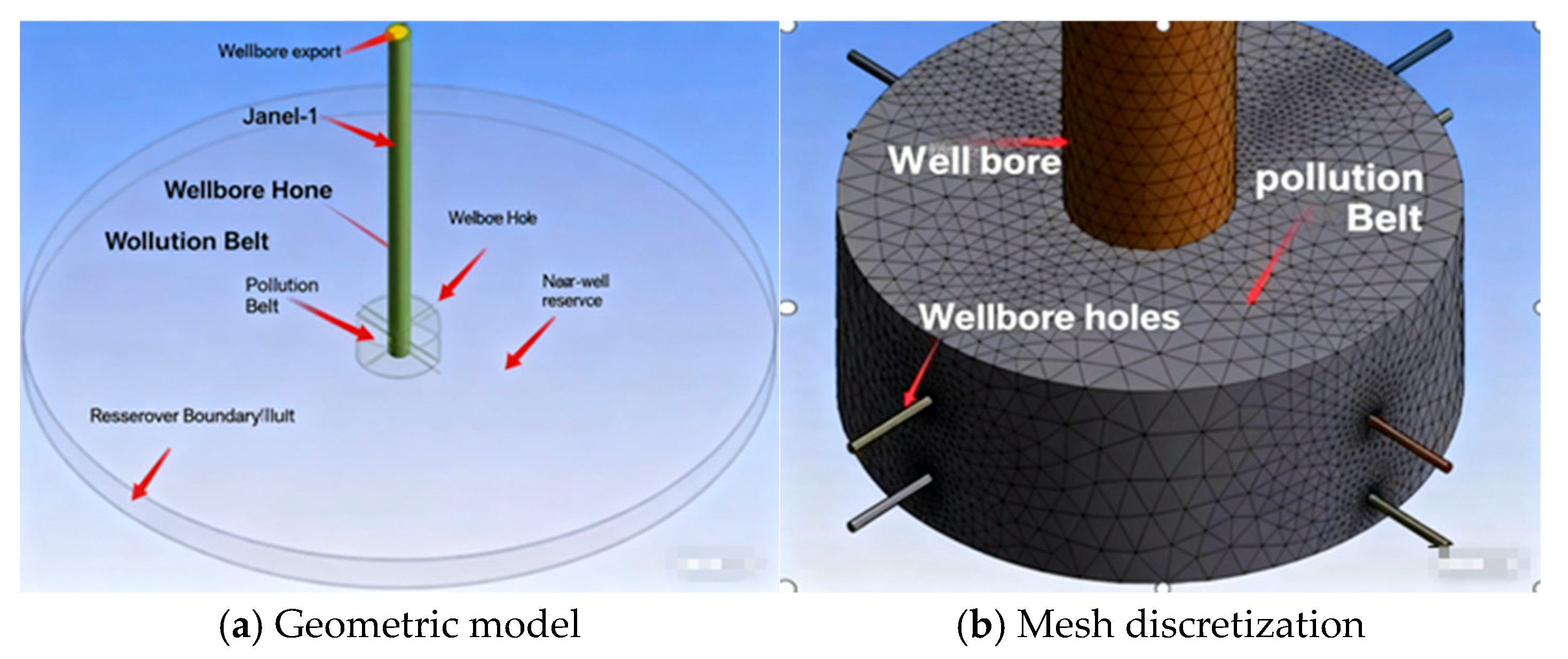
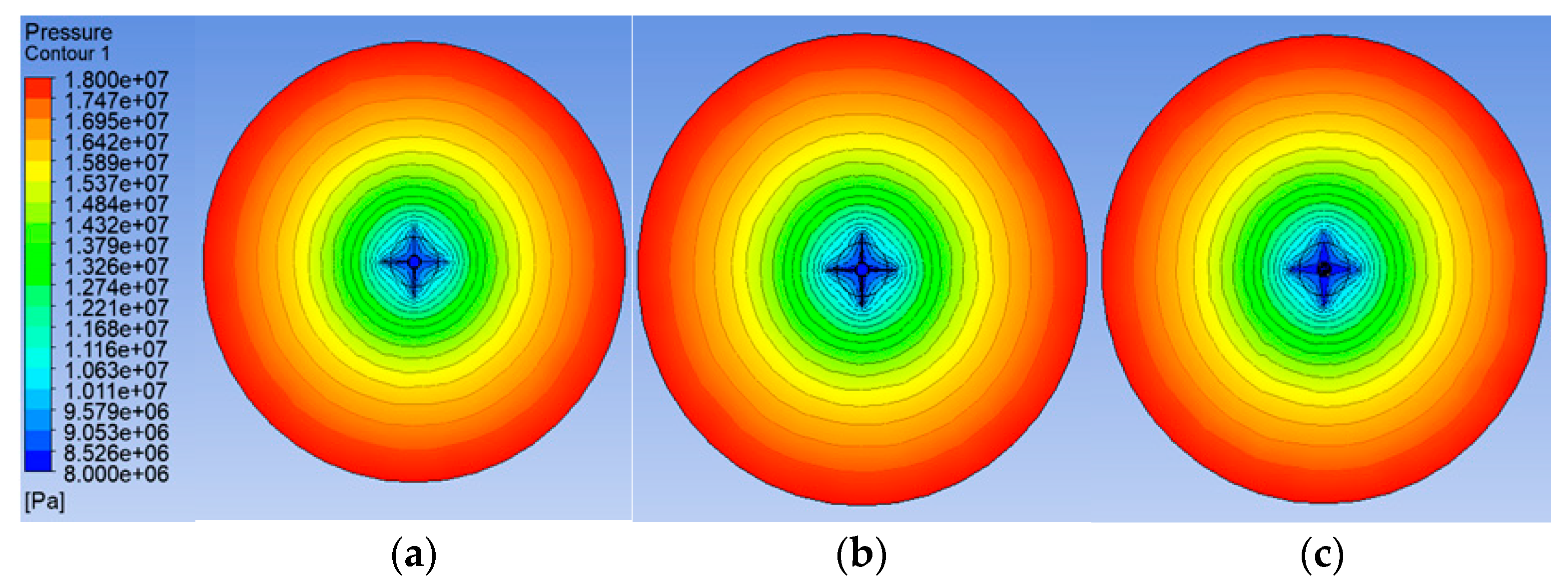
2.1. Physical Model of Conventional Perforated Completion
2.2. Establishment of Mathematical Model for Fluid Flow in Conventional Perforated Completion
- The near-wellbore zone is a homogeneous reservoir with uniform thickness, and the flow in the formation follows porous media.
- The perforation tunnels have equal diameters, and the influence of the compacted zone is not considered.
- The fluid flow is assumed to be steady-state seepage, and the flow in the perforation tunnels is regarded as laminar due to low velocity.
3. Analysis of Single Factors in Conventional Perforated Completions Under Different Reservoir Conditions
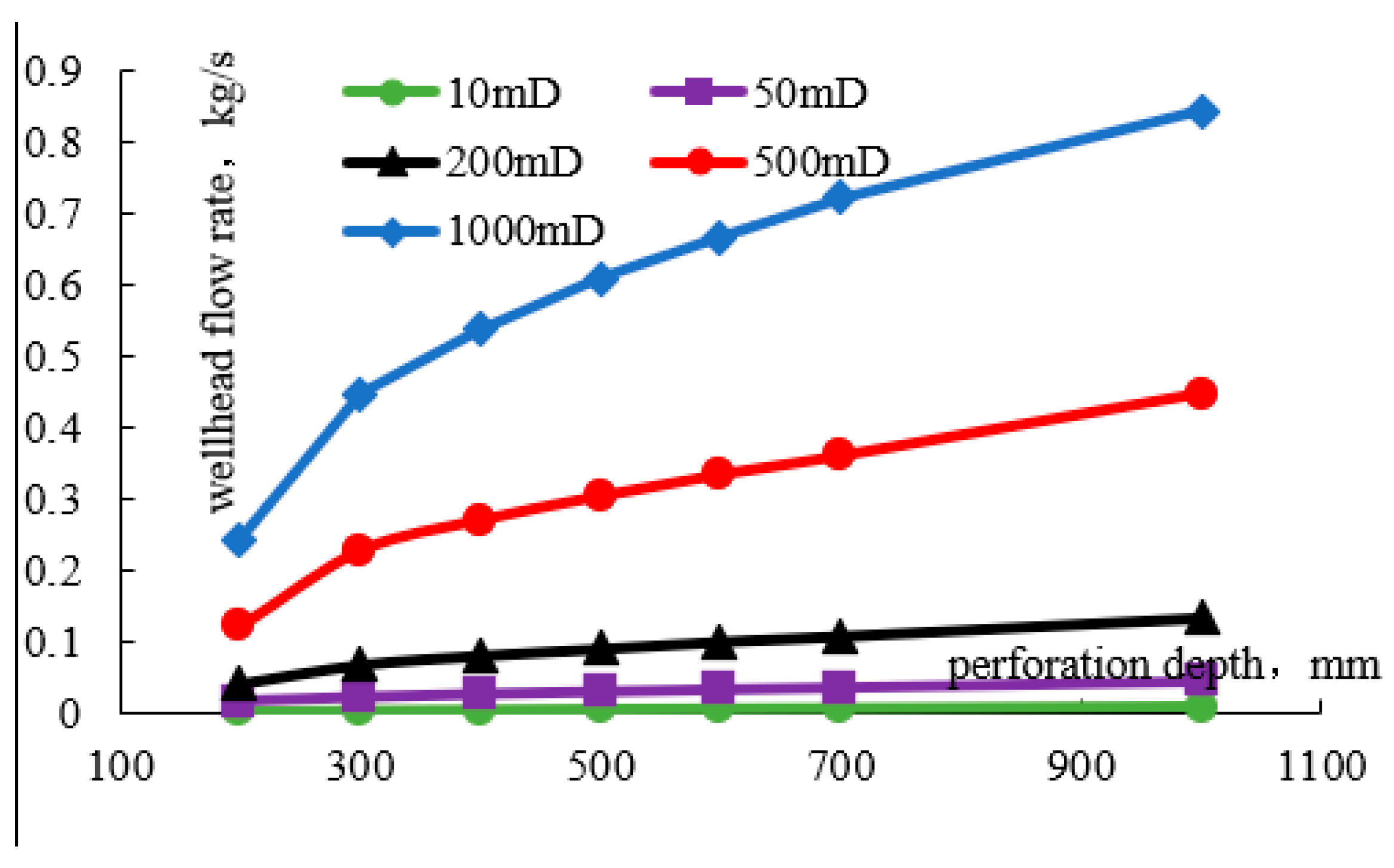
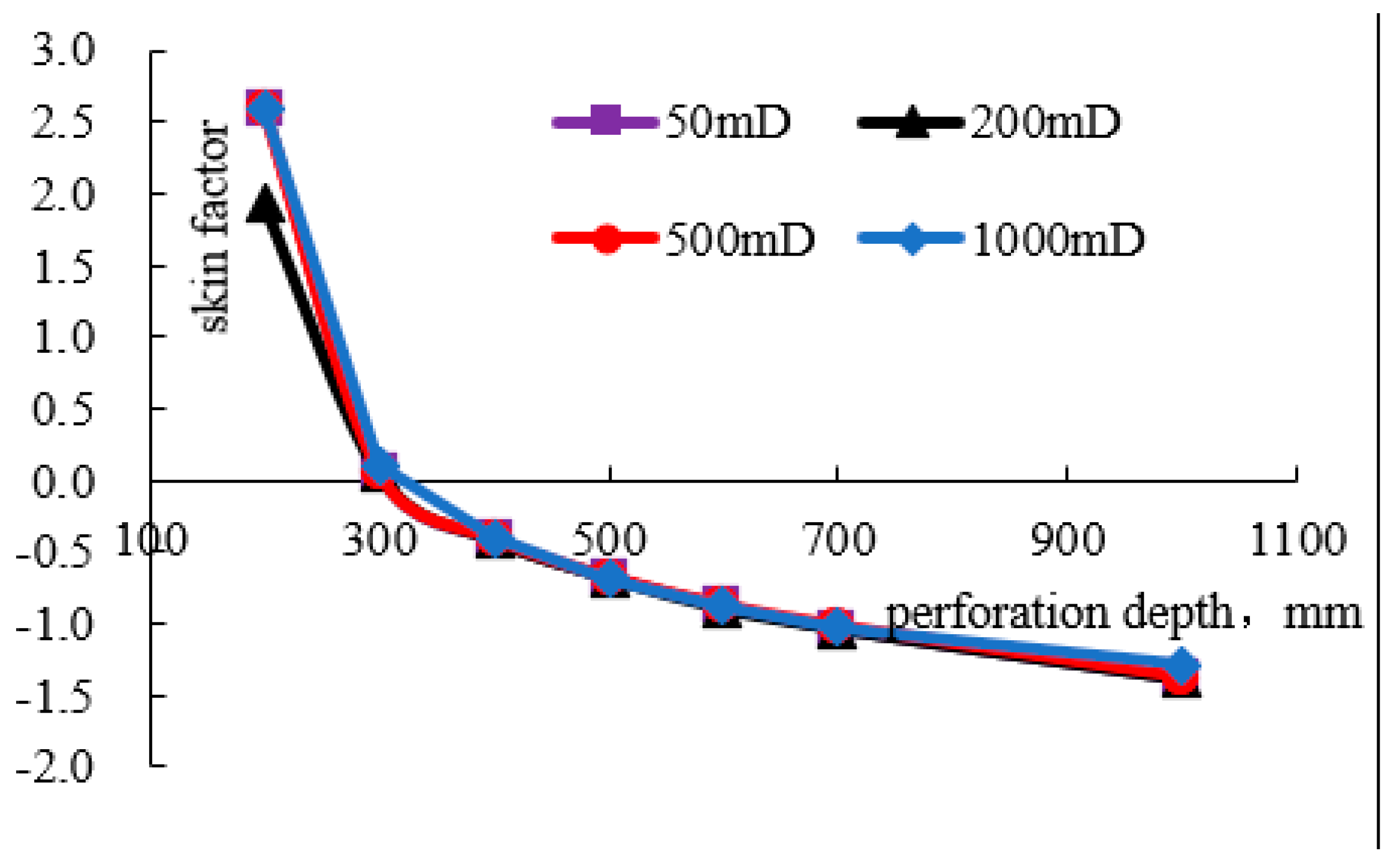
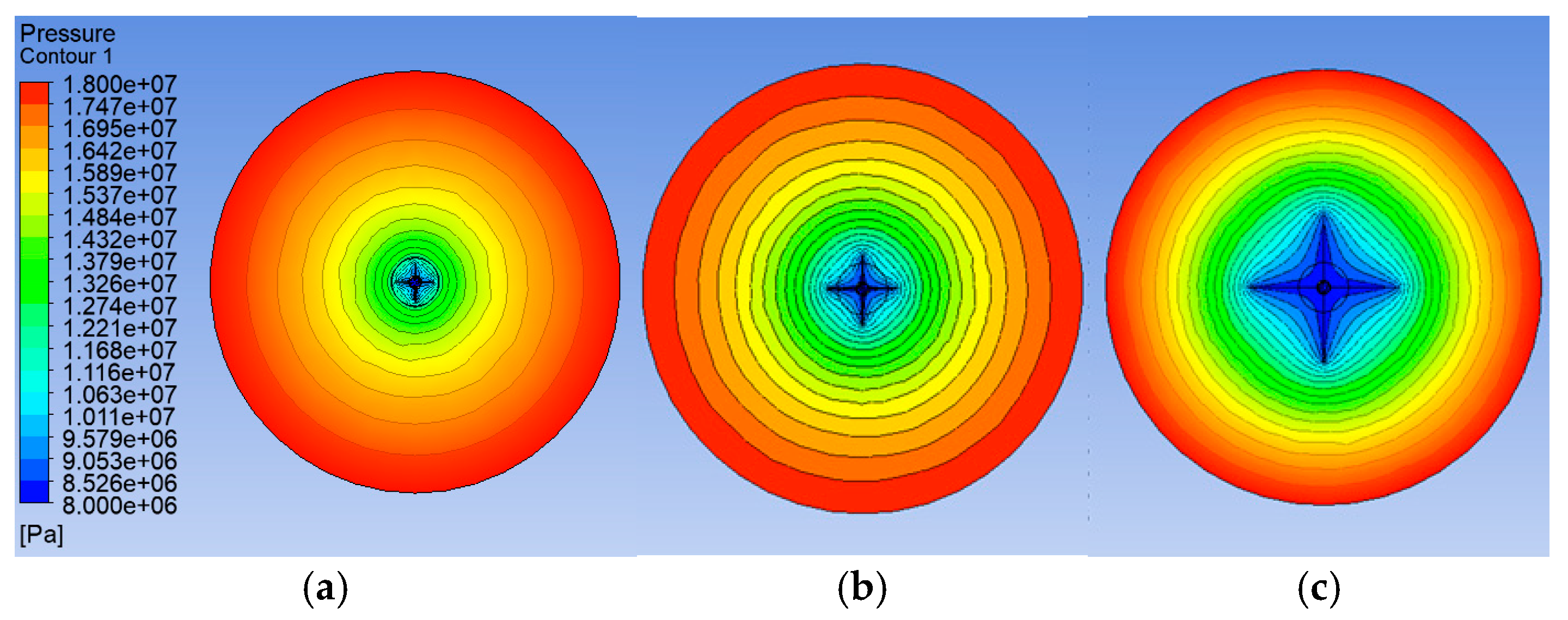
3.1. Perforation Depth Sensitivity Analysis
3.2. Shot Density Sensitivity Analysis
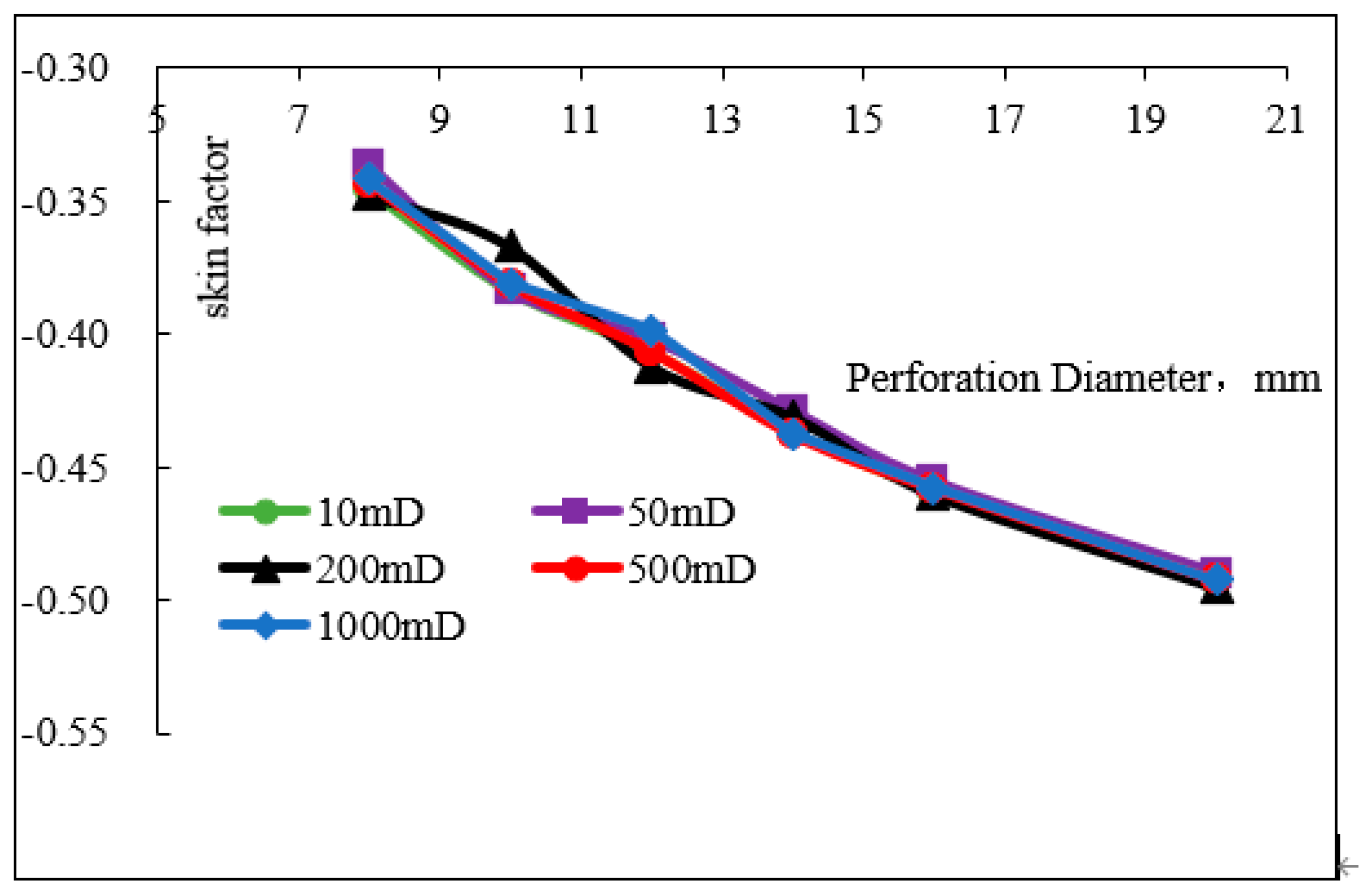
3.3. Perforation Diameter Sensitivity Analysis
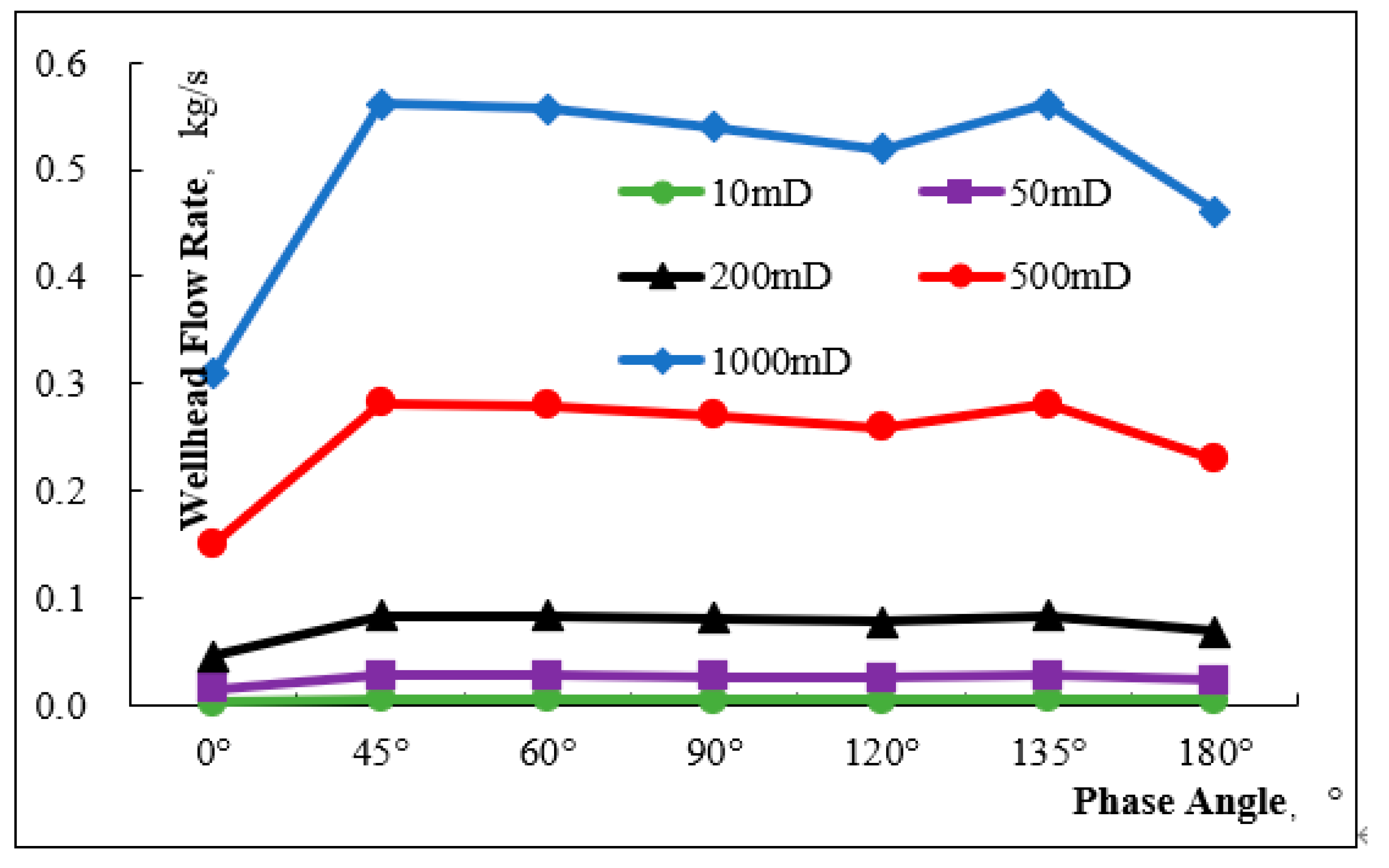
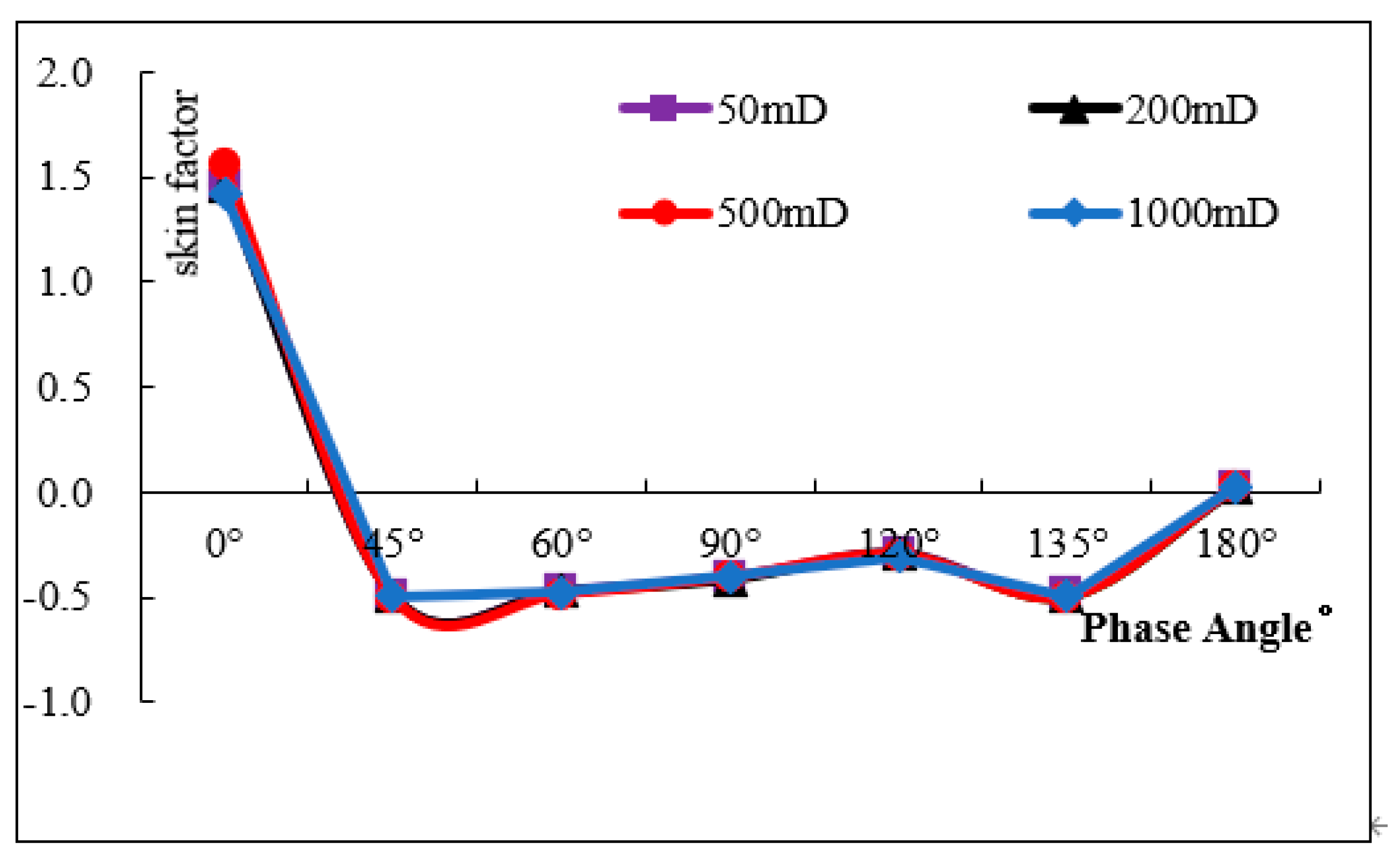
3.4. Phase Angle Sensitivity Analysis
4. Multi-Factor Analysis of Skin Factor in Conventional Perforation Completion Under Different Reservoir Conditions
4.1. Orthogonal Experiment and Gray Relational Analysis
4.2. Regression Model of Skin Factor for Conventional Perforation Completion
5. Conclusions and Insights
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Muskat, M. The Effect of Casing Perforations on Well Productivity. Pet. Technol. 1942, 151, 175–187. [Google Scholar] [CrossRef]
- McDowell, J.M.; Muskat, M. The Effect on Well Productivity of Formation Penetration Beyond Perforated Casing. Pet. Trans. AIME 1950, 189, 309–312. [Google Scholar] [CrossRef]
- Harris, M.H. The Effect of Perforating on Well Productivity. J. Pet. Technol. 1966, 18, 518–528. [Google Scholar] [CrossRef]
- Tariq, S.M. Evaluation of Flow Characteristics of Perforations Including Nonlinear Effects with the Finite-Element Method. SPE Prod. Eng. 1987, 2, 104–112. [Google Scholar] [CrossRef]
- Tariq, S.M.; Ichara, M.J.; Ayestaran, L. Performance of Perforated Completions in the Presence of Anisotropy, Laminations, or Natural Fractures. SPE Prod. Eng. 1989, 4, 376–384. [Google Scholar] [CrossRef]
- Karakas, M.; Tariq, S.M. Semianalytical Productivity Models for Perforated Completions. SPE Prod. Eng. 1991, 6, 73–82. [Google Scholar] [CrossRef]
- Lang, Z.; Zhang, L.; Gao, H. Numerical simulation study on CO2 huff and puff development of heavy oil reservoirs. J. Pet. Univ. Nat. Sci. Ed. 2000, 24, 37–40. [Google Scholar]
- Tang, Y.; Pan, Y.; Zhu, J. Finite Element Numerical Simulation Study on Perforation Completion of Gas Wells with Non-Darcy Flow. J. Southwest Pet. Inst. 2006, 2–140. [Google Scholar]
- Yildiz, T. Assessment of Total Skin Factor in Perforated Wells. SPE Reserv. Eval. Eng. 2006, 9, 61–76. [Google Scholar] [CrossRef]
- Yildiz, T.; Langlinais, J.P. Calculation of Pressure Losses Across Gravel Packs. In Proceedings of the SPE Formation Damage Control Symposium, Bakersfield, CA, USA, 8–9 February 1988; [SPE 17167]. Society of Petroleum Engineers: Richardson, TX, USA, 1988. [Google Scholar]
- Sun, D.; Li, B.; Gladkikh, M.; Satti, R.; Evans, R. Comparison of Skin Factors for Perforated Completions Calculated with Computational-Fluid-Dynamics Software and the Karakas-Tariq Semianalytical Model. SPE Drill. Complet. 2013, 28, 21–33. [Google Scholar] [CrossRef]
- Sun, D.; Li, B.; Gladkikh, M.; Satti, R.; Evans, R. Comparison of Skin Factors for Perforated Completions Calculated with Computational Fluid Dynamics Software and a Semi-Analytical Model. In Proceedings of the SPE European Formation Damage Conference, Noordwijk, The Netherlands, 7–10 June 2011; SPE 143663. Society of Petroleum Engineers: Richardson, TX, USA, 2011. [Google Scholar]
- Sun, D.; Satti, R.; Ochsner, D.; Sampson, T.; Li, B.; Gladkikh, M. Experimental and Computational Study of Flow Characteristics in a Drilled Perforated Core. In Proceedings of the SPE International Symposium and Exhibition on Formation Damage Control, Lafayette, LA, USA, 15–17 February 2012; SPE 151113. Society of Petroleum Engineers: Richardson, TX, USA, 2012. [Google Scholar]
- Li, B.; Sun, D.; Satti, R. Statistical Analysis of Significant Factors Affecting Perforation Flow at Well Scale. In Proceedings of the SPE International Symposium and Exhibition on Formation Damage Control, Lafayette, LA, USA, 15–17 February 2012; [SPE 150122]. Society of Petroleum Engineers: Richardson, TX, USA, 2012. [Google Scholar]
- Velayati, A.; Roostaei, M.; Fattahpour, V.; Mahmoudi, M.; Nouri, A.; Alkouh, A.; Fermaniuk, B.; Kyanpour, M. Design Optimization of Slotted Liner Completions in Cased and Perforated Wells: A Numerical Skin Model. In Proceedings of the SPE International Heavy Oil Conference and Exhibition (SPE-193670-MS), Kuwait City, Kuwait, 10–12 December 2018; Society of Petroleum Engineers: Richardson, TX, USA, 2018. [Google Scholar]
- API SPEC 5CT-2021; Specification for Casing and Tubing. American Petroleum Institute: Washington, DC, USA, 2021; pp. 2–5.
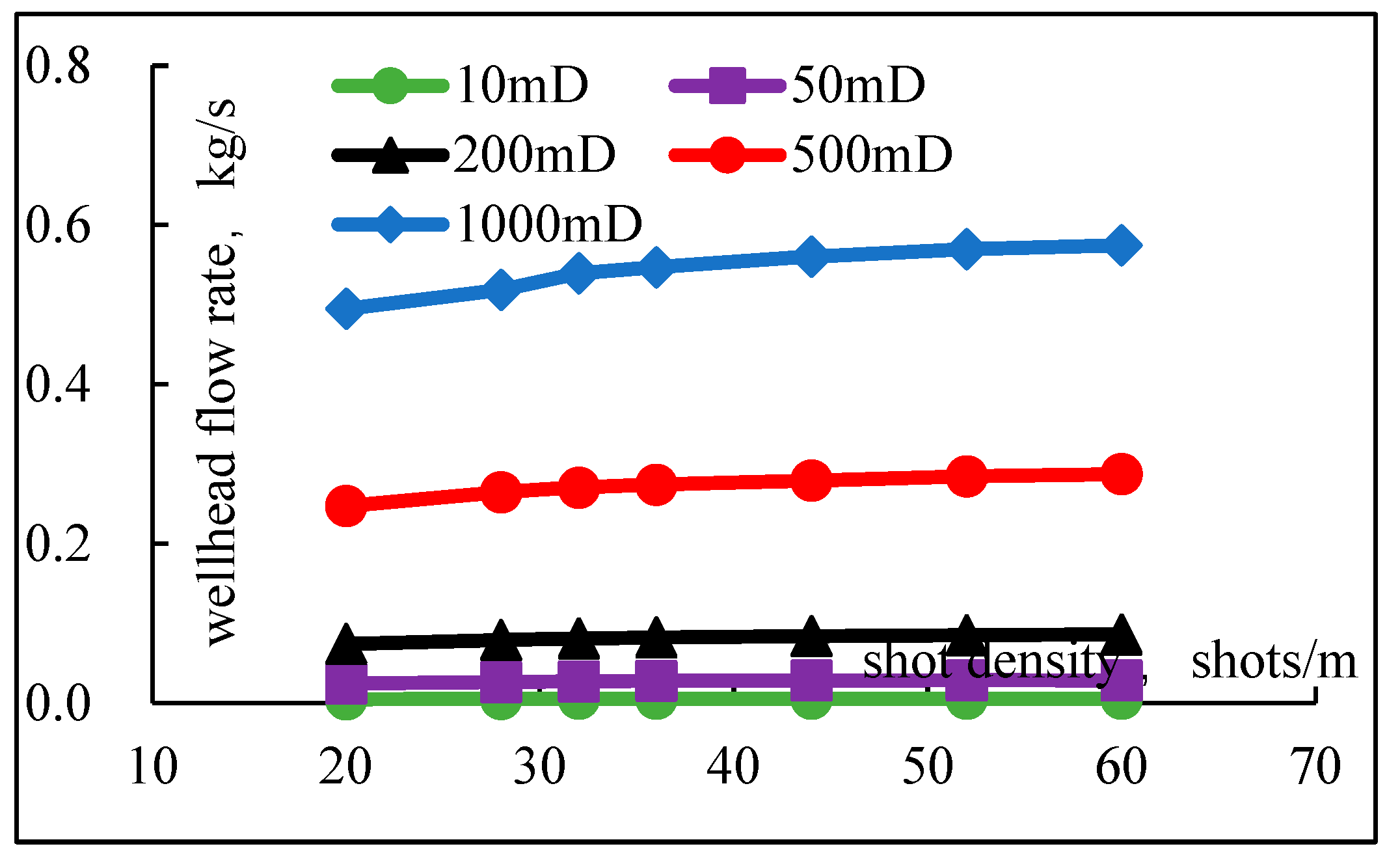
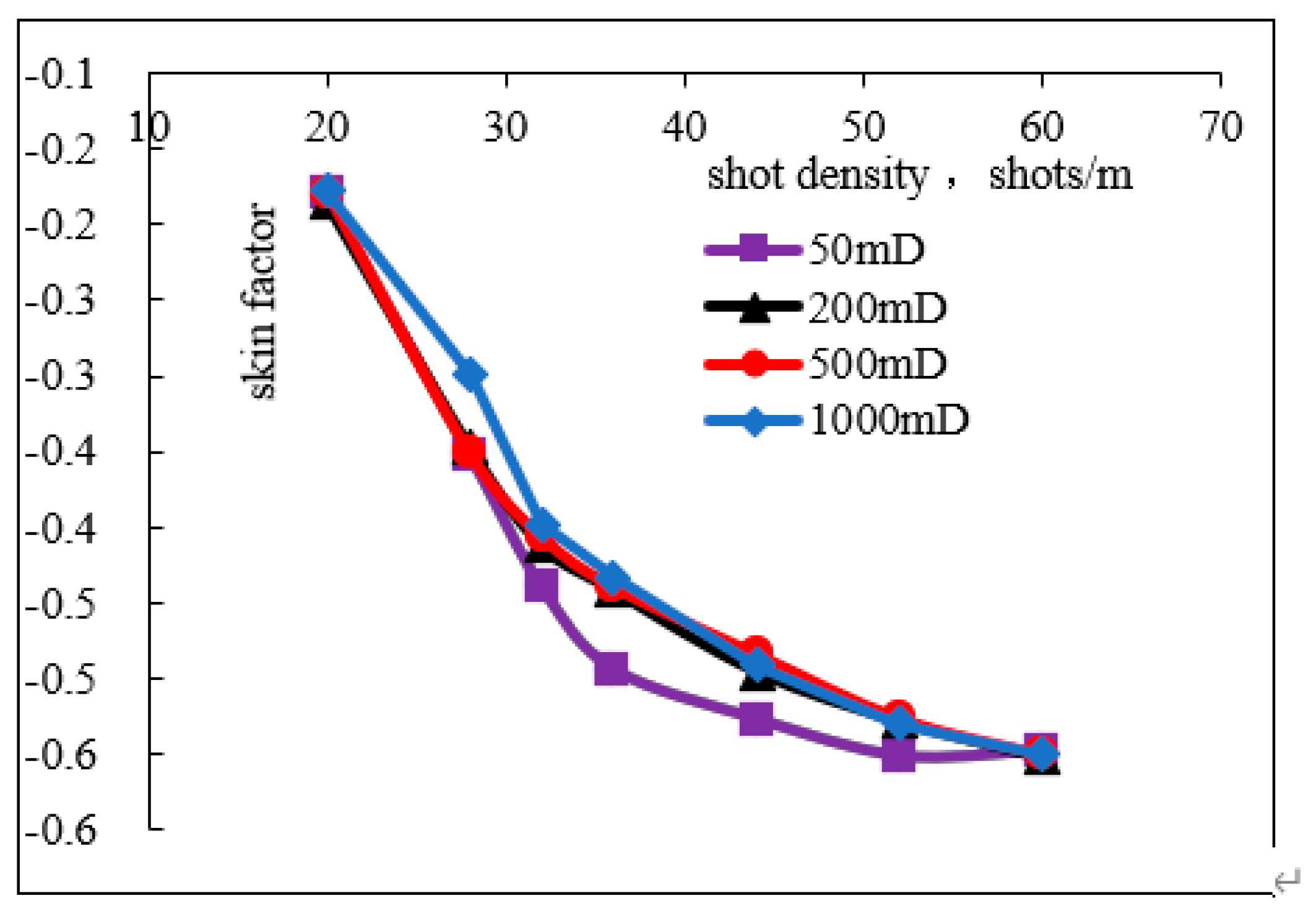
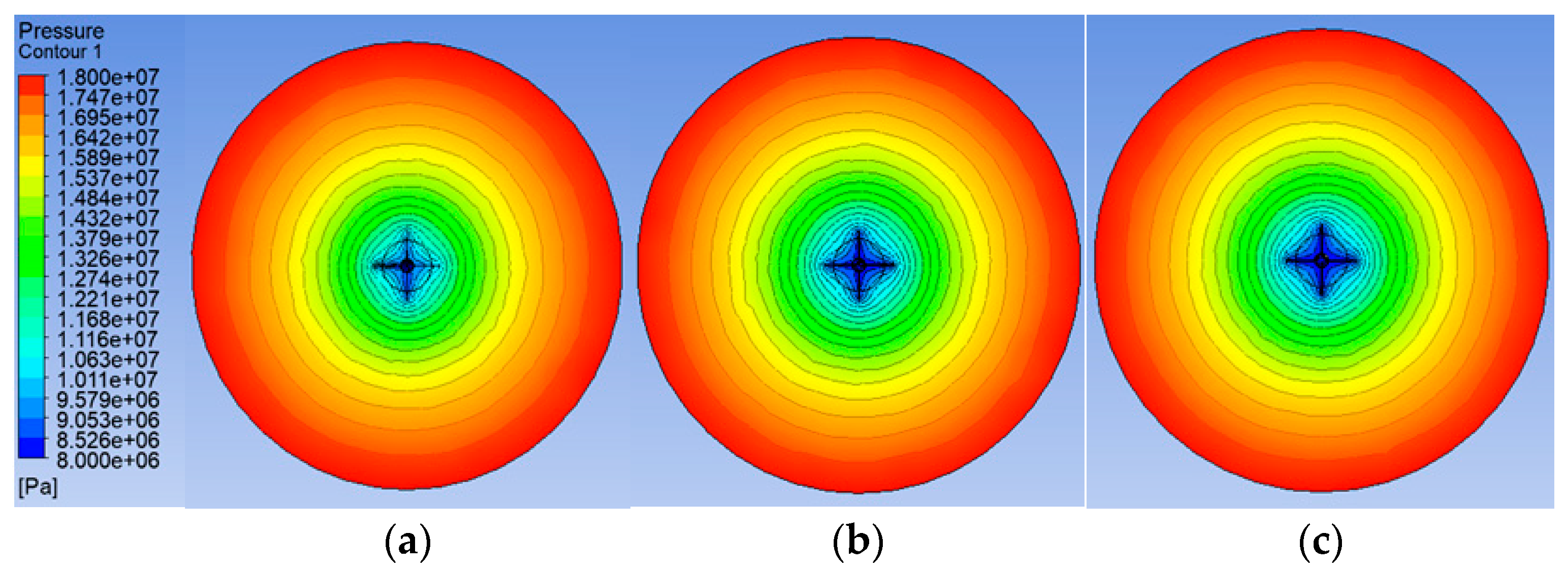
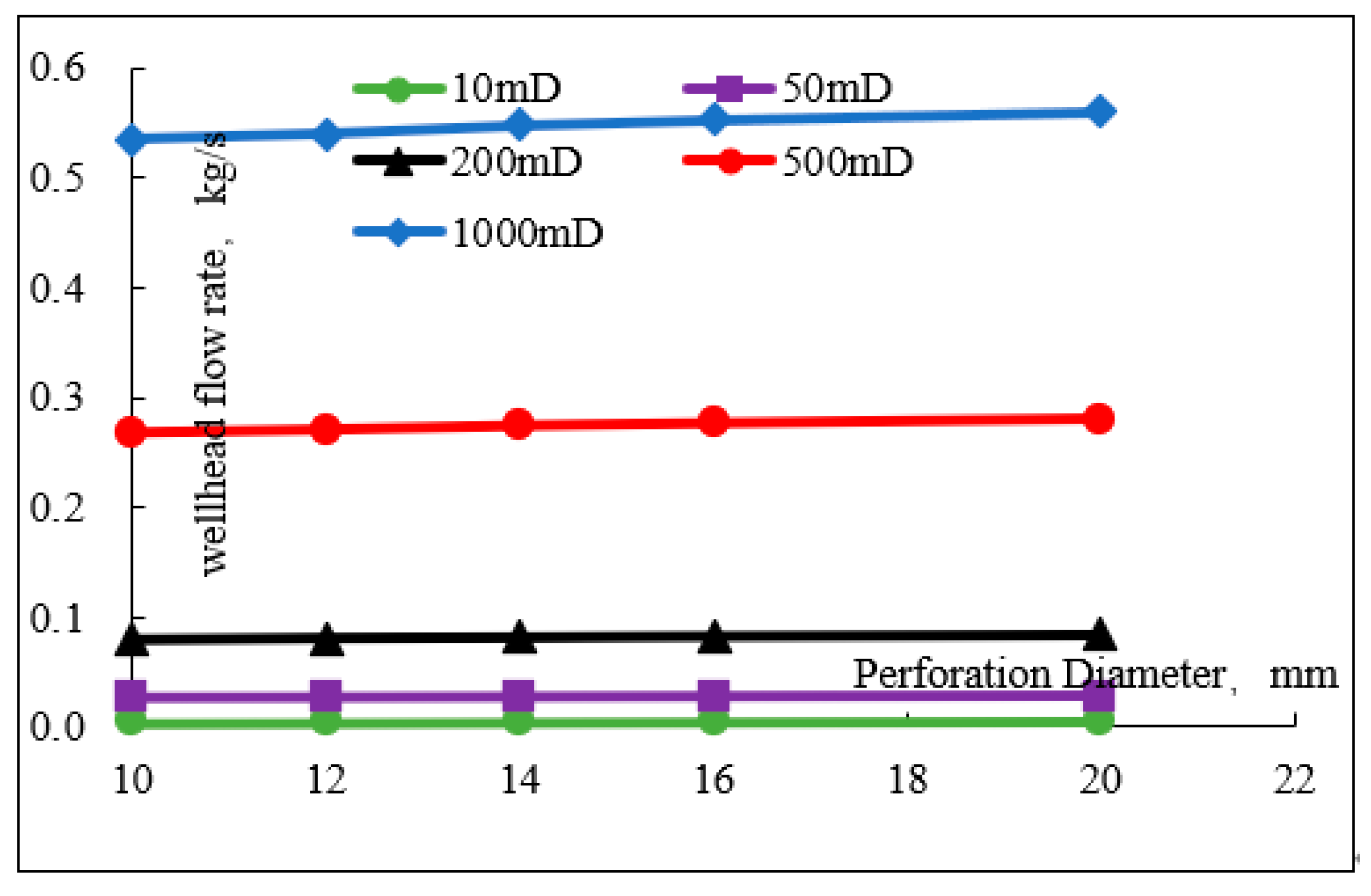
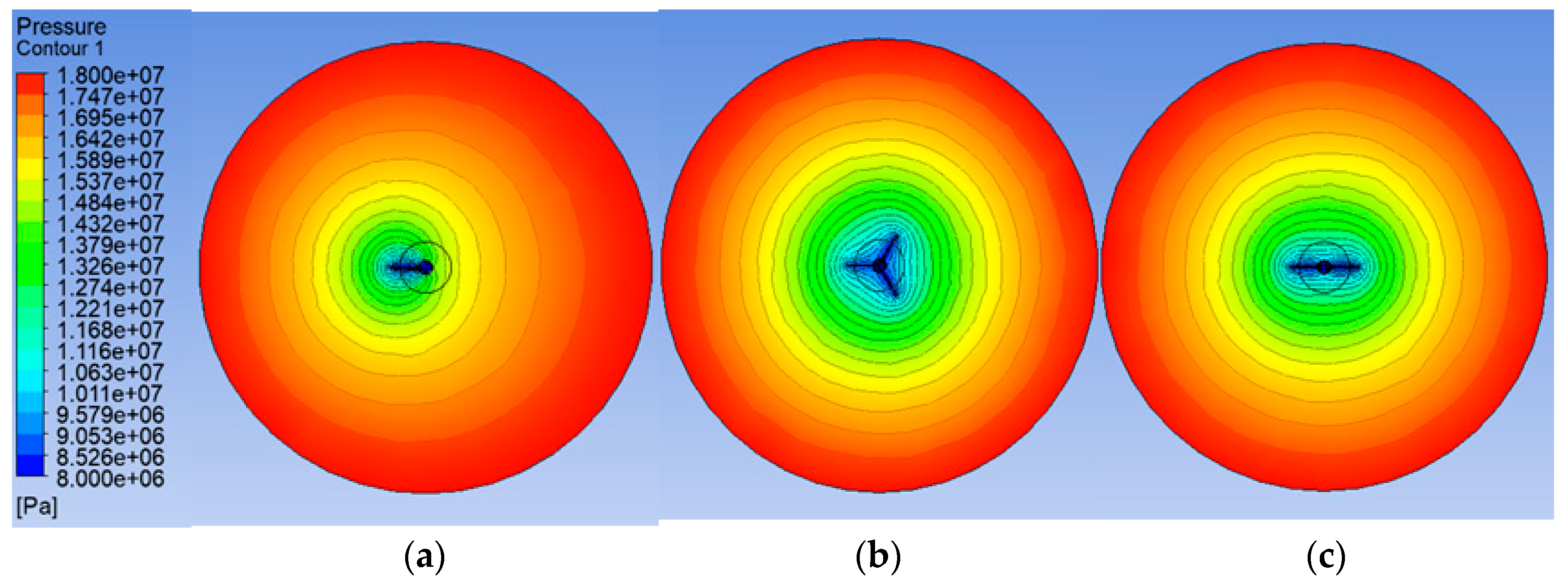
| Reservoir Classification | High-Permeability Reservoir | Medium-Permeability Reservoir | Low-Permeability Reservoir | ||
|---|---|---|---|---|---|
| Conventional Low-Permeability | Extra-Low Permeability | Ultra-Low Permeability | |||
| Permeability 10−3 um2 | >500 | 50–500 | 10–50 | 1–10 | 0.1–1 |
| Perforation Depth/mm | Shot Density Shots/m | Perforation Diameter/mm | Phasing Angle/° | Formation Thickness/m | Damage Radius/mm | Damage Radius/mpas | Crude Density kg/m3 | Wellbore Radius/mm | Near-Well Outer Radius/ mm |
|---|---|---|---|---|---|---|---|---|---|
| 500 | 40 | 10 | 90 | 1 | 280 | 10 | 880 | 85 | 3000 |
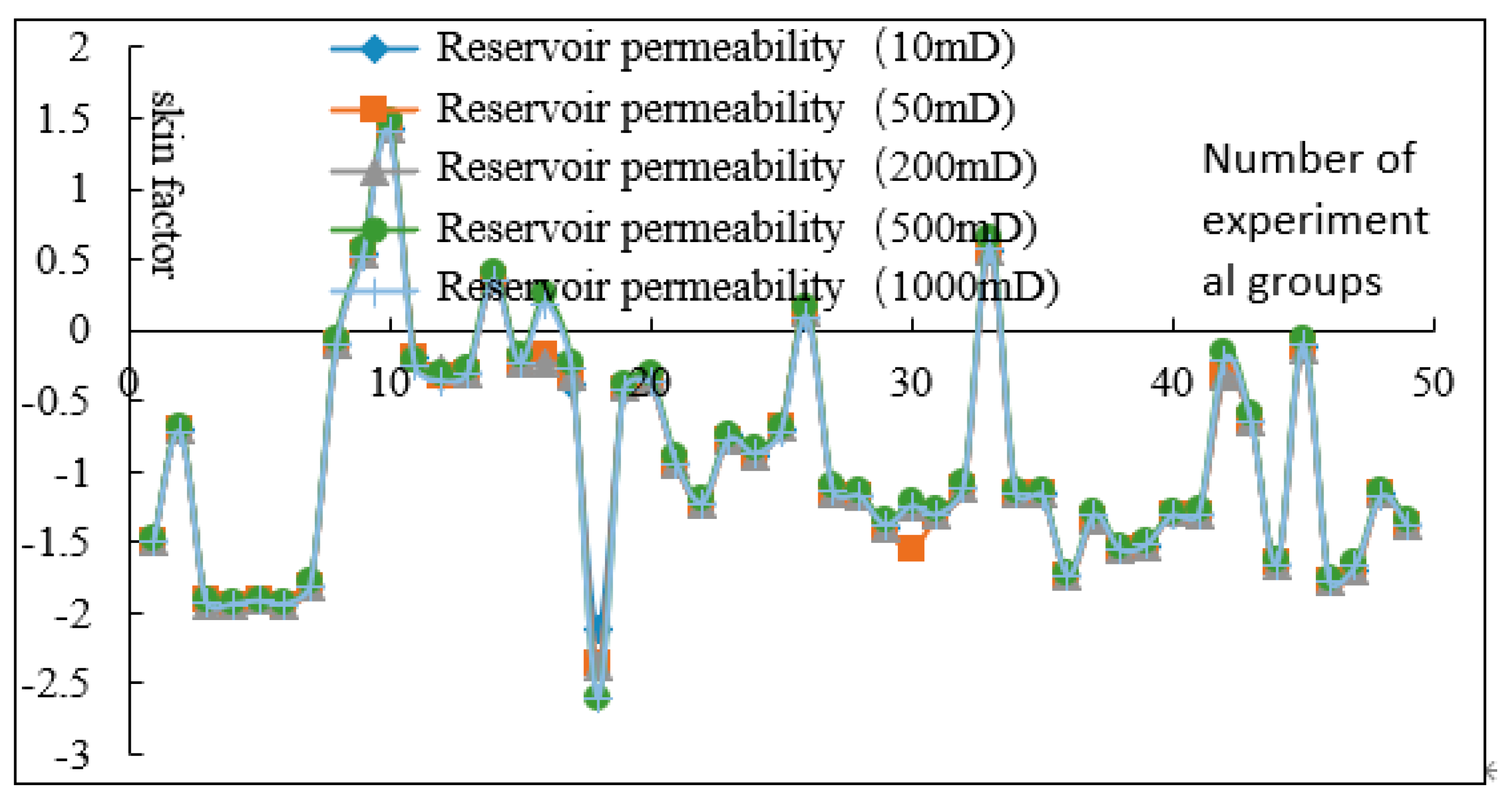
| No. | Perforation Depth/mm | Perforation Density/Holes/m | Perforation Diameter/mm | Damage Zone Depth/mm | Damage Degree of Damage Zone | Phase Angle/ Degree | Reservoir Permeability Is 1000 mD | |
|---|---|---|---|---|---|---|---|---|
| Wellhead Flow Rate/kg/s | Skin Factor | |||||||
| 1 | 1600 | 60 | 16 | 500 | 1 | 180 | 0.97 | −1.498 |
| 2 | 1600 | 20 | 14 | 330 | 0.9 | 0 | 0.62 | −0.728 |
| 3 | 1600 | 28 | 8 | 190 | 0.74 | 45 | 1.41 | −1.921 |
| 4 | 1600 | 32 | 6 | 50 | 0.58 | 60 | 1.44 | −1.941 |
| 5 | 1600 | 36 | 10 | 400 | 0.42 | 135 | 1.40 | −1.917 |
| 6 | 1600 | 52 | 16 | 260 | 0.26 | 90 | 1.44 | −1.939 |
| 7 | 1600 | 44 | 12 | 120 | 0.1 | 120 | 1.25 | −1.805 |
| 8 | 300 | 60 | 14 | 190 | 0.26 | 120 | 0.48 | −0.110 |
| 9 | 300 | 20 | 8 | 50 | 0.1 | 180 | 0.39 | 0.517 |
| 10 | 300 | 28 | 6 | 400 | 1 | 0 | 0.31 | 1.400 |
| 11 | 300 | 32 | 10 | 260 | 0.9 | 45 | 0.51 | −0.260 |
| 12 | 300 | 36 | 16 | 120 | 0.74 | 60 | 0.53 | −0.362 |
| 13 | 300 | 52 | 12 | 500 | 0.58 | 135 | 0.52 | −0.312 |
| 14 | 300 | 44 | 20 | 330 | 0.42 | 90 | 0.41 | 0.351 |
| 15 | 500 | 60 | 8 | 400 | 0.58 | 90 | 0.51 | −0.231 |
| 16 | 500 | 20 | 6 | 260 | 0.42 | 120 | 0.44 | 0.189 |
| 17 | 500 | 28 | 10 | 120 | 0.26 | 180 | 0.51 | −0.276 |
| 18 | 500 | 32 | 16 | 500 | 0.1 | 0 | 5.06 | −2.603 |
| 19 | 500 | 36 | 12 | 330 | 1 | 45 | 0.55 | −0.424 |
| 20 | 500 | 52 | 16 | 190 | 0.9 | 60 | 0.53 | −0.365 |
| 21 | 500 | 44 | 14 | 50 | 0.74 | 135 | 0.69 | −0.939 |
| 22 | 700 | 60 | 6 | 120 | 0.9 | 135 | 0.81 | −1.221 |
| 23 | 700 | 20 | 10 | 500 | 0.74 | 90 | 0.64 | −0.776 |
| 24 | 700 | 28 | 16 | 330 | 0.58 | 120 | 0.67 | −0.876 |
| 25 | 700 | 32 | 12 | 190 | 0.42 | 180 | 0.62 | −0.726 |
| 26 | 700 | 36 | 20 | 50 | 0.26 | 0 | 0.45 | 0.094 |
| 27 | 700 | 52 | 14 | 400 | 0.1 | 45 | 0.77 | −1.140 |
| 28 | 700 | 44 | 8 | 260 | 1 | 60 | 0.79 | −1.173 |
| 29 | 900 | 60 | 10 | 330 | 0.1 | 60 | 0.90 | −1.380 |
| 30 | 900 | 20 | 16 | 190 | 1 | 135 | 0.82 | −1.250 |
| 31 | 900 | 28 | 12 | 50 | 0.9 | 90 | 0.85 | −1.306 |
| 32 | 900 | 32 | 20 | 400 | 0.74 | 120 | 0.76 | −1.113 |
| 33 | 900 | 36 | 14 | 260 | 0.58 | 180 | 0.39 | 0.586 |
| 34 | 900 | 52 | 8 | 120 | 0.42 | 0 | 0.78 | −1.162 |
| 35 | 900 | 44 | 6 | 500 | 0.26 | 45 | 0.78 | −1.165 |
| 36 | 1100 | 60 | 16 | 50 | 0.42 | 45 | 1.18 | −1.737 |
| 37 | 1100 | 20 | 12 | 400 | 0.26 | 60 | 0.86 | −1.311 |
| 38 | 1100 | 28 | 20 | 260 | 0.1 | 135 | 1.02 | −1.557 |
| 39 | 1100 | 32 | 14 | 120 | 1 | 90 | 0.99 | −1.519 |
| 40 | 1100 | 36 | 8 | 500 | 0.9 | 120 | 0.86 | −1.313 |
| 41 | 1100 | 52 | 6 | 330 | 0.74 | 180 | 0.85 | −1.305 |
| 42 | 1100 | 44 | 10 | 190 | 0.58 | 0 | 0.50 | −0.209 |
| 43 | 1400 | 60 | 12 | 260 | 0.74 | 0 | 0.60 | −0.642 |
| 44 | 1400 | 20 | 20 | 120 | 0.58 | 45 | 1.10 | −1.655 |
| 45 | 1400 | 28 | 14 | 500 | 0.42 | 45 | 0.48 | −0.109 |
| 46 | 1400 | 32 | 8 | 330 | 0.26 | 135 | 1.23 | −1.782 |
| 47 | 1400 | 36 | 6 | 190 | 0.1 | 90 | 1.11 | −1.672 |
| 48 | 1400 | 52 | 10 | 50 | 1 | 120 | 0.79 | −1.179 |
| 49 | 1400 | 44 | 16 | 400 | 0.9 | 180 | 0.90 | −1.382 |
| Parameters | Perforation Depth/mm | Phase Angle/° | Perforation Density/Holes/m | Perforation Diameter/mm | Contamination Degree of the Damaged Zone | Depth of the Damaged Zone/mm |
|---|---|---|---|---|---|---|
| Correlation coefficient | 0.890 | 0.812 | 0.760 | 0.723 | 0.705 | 0.700 |
| Ranking | 1 | 2 | 3 | 4 | 5 | 6 |
| Parameters | Perforation Depth/mm | Phase Angle/° | Perforation Density/Holes/m | Perforation Diameter/mm |
|---|---|---|---|---|
| Reasonable range | Deep penetration | 45/135 | More than 36 holes/m | Have little impact |
| a1–10 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| −0.004 | −0.212 | 0.4241 | 0.0115 | −3.261 | −0.025 | 1 × 10−6 | −2 × 10−5 | 6 × 10−5 | −5 × 10−6 | |
| a11–20 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 0.0013 | 1 × 10−5 | 0.0019 | −0.006 | 7 × 10−6 | 0.2772 | 0.0002 | −0.011 | 0.0001 | −0.014 | |
| a21–30 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| −0.001 | −3 × 10−6 | 0.0033 | −7 × 10−5 | −3.220 | 0.0205 | 0.0001 | — | — | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Z.; Chen, M.; Yang, S.; Lei, J.; Liu, G.; Li, Y.; Zhang, S.; Ren, Z.; Zhang, C. Analysis of Factors Influencing Skin Factor in Conventional Perforation Completion and Prediction Model Research. Appl. Sci. 2025, 15, 12616. https://doi.org/10.3390/app152312616
Ma Z, Chen M, Yang S, Lei J, Liu G, Li Y, Zhang S, Ren Z, Zhang C. Analysis of Factors Influencing Skin Factor in Conventional Perforation Completion and Prediction Model Research. Applied Sciences. 2025; 15(23):12616. https://doi.org/10.3390/app152312616
Chicago/Turabian StyleMa, Zhongguo, Minjing Chen, Sen Yang, Jiacheng Lei, Gang Liu, Yuqi Li, Shixiong Zhang, Zongxiao Ren, and Chao Zhang. 2025. "Analysis of Factors Influencing Skin Factor in Conventional Perforation Completion and Prediction Model Research" Applied Sciences 15, no. 23: 12616. https://doi.org/10.3390/app152312616
APA StyleMa, Z., Chen, M., Yang, S., Lei, J., Liu, G., Li, Y., Zhang, S., Ren, Z., & Zhang, C. (2025). Analysis of Factors Influencing Skin Factor in Conventional Perforation Completion and Prediction Model Research. Applied Sciences, 15(23), 12616. https://doi.org/10.3390/app152312616





