Recreation of Gap Test with Damaged Plasticity Model

Abstract

A gap test is a relatively new experimental and numerical test proposed by Bažant and co-workers. The test is designed to show that the effective mode I (opening mode) fracture energy depends strongly on the crack-parallel normal stress. Other typical tests (for instance three-point bending) are not able to capture this influence. The gap test is therefore considered as a breakthrough in fracture mechanics. The authors of this paper tried to recreate numerically the gap test in a concrete specimen using a plasticity-based damage model for concrete, the so-called concrete damaged plasticity in Abaqus software. A specimen in the gap test is in the form of a concrete beam with a notch. At the first stage of the test the specimen is supported with poly-propylene pads. A static scheme of the specimen changes when the gap between the specimen and roller supports vanishes, exactly when the full yield of pads occurs. The gap test revealed the fact that the initial fracture energy varies its value depending on normal stress parallel to a crack propagating from the notch. To calculate the initial fracture energy, the authors of this paper used the size effect law. The results obtained by the authors are comparable with the laboratory and numerical results presented by Nguyen and co-workers.

1. Introduction

One of the most important assumptions in fracture mechanics of concrete is constancy of the fracture energy of material. This assumption is the basis of linear elastic fracture mechanics (LEFM) and the cohesive crack model (CCM). However, in 2020 Nguyen et al. [1] proved that the initial fracture energy (defined as the area under the initial tangent of the traction–separation curve) varies depending on the crack-parallel normal stress (also called the T-stress [1]). They proposed a new fracture test called a gap test, which revealed that the crack-parallel stress can almost double the fracture energy or reduce it to zero. This effect could not be captured earlier in the standard fracture test (for instance three-point bending, single-edge notch tension, double cantilever beam, etc.) because in all these tests the crack-parallel stress was negligible. Constancy of the fracture energy was also disputed earlier [2], but only the gap test revealed how the fracture energy changes under particular conditions.

The specimen in the gap test is a single-notched beam with a varying static scheme (see Figure 1). In the first stages of the test, the specimen is supported by poly-propylene pads placed near the notch. There is also a gap (hence the name of the test) between the end supports and the specimen. When full yielding of pads appears, the gap vanishes and the static scheme of the beam changes. This time the scheme is similar to a three-point bending test, but with additional yield force coming from the pads. During the whole test the scheme remains statically determinate. Nguyen et al. [3] reported that statically determinate systems make evaluation simple and unambiguous, and combined with the constancy of crack-parallel normal stress, they also make the size effect method possible to use. As a result of the test, a force–displacement diagram and a crack pattern are reported, and the initial fracture energy G_f is calculated. Details of this computation are presented later on in Section 3.1. To use the size effect method, usually three different sizes of the specimen (with a constant thickness) are investigated.

The gap test can be performed numerically or in a laboratory. A critical comparison of a few material models of concrete (in light of the gap test and classical fracture tests) was presented by Bažant et al. [4,5]. These models were the phase field model (PF), the peridynamics model (PD), and the crack band model with microplane damage model M7 (CBM). Nguyen et al. [3] presented their view on isotropic tensorial plastic failure models, including the Druker–Prager model and Mohr–Coulomb concrete model with a cap model from Abaqus. These authors reported that the CBM model reproduces the gap test very well, while

• The Drucker-Prager model returns no weakening phase in the diagram of evolution of the fracture energy G_f vs. T-stress;
• The CDPM2 model, described by Grassl et al. [6], shows some significant discrepancies in the G_f–T-stress diagram compared with experimental results;
• The Mohr–Coulomb model produces an artificial stiffening effect at the crack tip;
• The cohesive crack model (CCM) is a line crack model; so it cannot capture any effect of the T-stress.

In the next article, Bažant et al. [7] once again expressed their doubts concerning not only the line crack model, but also the classical plasticity models (Drucker–Prager and Coulomb–Mohr). They claimed that the failure criteria based on tensor invariants cannot capture real phenomena during the gap test, for instance the slip on planes of distinct orientations. The following models, phase field, crack cohesive, and the linear elastic fracture mechanics (LEFM), were also assessed as inapplicable to model the gap test. However, Lyu et al. [8] recognized the CDPM2 model as one that might be able to capture the T-stress effect thanks to its tensorial nature, which is contradictory to [7].

2. Research Significance

The authors of this paper recreated the gap test with the damaged plasticity model and showed that this recreation is possible only if damage conditions are applied. This was the main motivation of the authors, but not the only one. The gap test is a relatively new test related to the size effect method and fracture mechanics and has not yet been widely discussed. There are still too few works devoted to this test. It is worth mentioning the following papers: Brockmann & Salviato [9] recreated the test numerically and in a laboratory in carbon fiber composites while fiber-reinforced concrete was taken into consideration by Li et al. [10]. The authors of this paper want to fill this gap and develop numerical simulations of the gap test. No less important is another reason, namely that the gap test is connected with a very crucial issue called the size effect. The size effect law was applied to establish how the initial fracture energy depends on the T-stress.

The issue of the size effect has been investigated and discussed for many years till now; one can find an extensive description of the size effect in concrete and quasi-brittle materials in a classical handbook of Bažant [11]. A series of FraMCoS conferences has been faced with this issue for over thirty years, starting with the state-of-art report [12], followed by many papers, among which one can mention several of the most important ones. Bažant [13] presented a review of basic scaling theories and a universal size effect law and assessed a Weibull-type size effect theory as not relevant to concrete. Van Mier & van Vliet [14] presented results of laboratory investigations of the size effect in dog-bone specimens under uniaxial tension. They estimated the fracture energy in a very wide range of specimen proportions (from 1:1 to 1:32). Cedolin & Cusatis [15] and showed that the size effect law is equivalent to the asymptotic behavior given by the cohesive crack model. Another approach to the size effect was combined with fractals, used to model fracture surfaces, as presented by Saouma and co-workers [16,17].

3. Materials and Methods

3.1. Methodology

Generally the size effect appears when mechanical properties and bearing capacity of a structure depends on its geometric size. Analysis of the effect is very important, mainly for the reason that specimens investigated in laboratories are scaled in comparison with real structures. In case of the gap test, the analysis focuses on the initial fracture energy of the loading mode-I (the opening mode). According to the size effect law [18], the relation between the nominal stress σ_N and the specimen depth D can be written as:

$${\displaystyle \frac{1}{{\sigma }_N^2}}={\displaystyle \frac{g\left({\alpha }_0\right)}{E{G}_f}}D+{\displaystyle \frac{g^{\prime }\left({\alpha }_0\right)}{E{G}_f}}{c}_f,$$

(1)

where E is the elastic modulus, G_f is the fracture energy, g(α₀) is the energy release rate as a function of α₀ (a ratio of notch depth and specimen depth), g’(α₀) is the derivative of this function, and c_f stands for the critical effective crack extension. The nominal stress can be calculated according to the formula:

$${\sigma }_N={\displaystyle \frac{P}{bD}},$$

(2)

where P is the peak force (extracted from the force–displacement diagram obtained in an experiment or finite element calculations), and b denotes the thickness of the specimen. The energy release rate can be written as:

$$g\left({\alpha }_0\right)={\left(1.1682(2h-s){\displaystyle \frac{\sqrt{\pi \alpha }}{8{\beta }^{1.5}}}\left(5-{\displaystyle \frac{10\alpha }{3}}+{\alpha }^2+40{\alpha }^2{\left(1-\alpha \right)}^6+3e^{{\displaystyle \frac{-6.134\alpha }{1-\alpha }}}\right)\right)}^2,$$

(3)

where

$$h={\displaystyle \frac{L}{D}},$$

(4)

$$s={\displaystyle \frac{S}{D}},$$

(5)

$$\beta =1-{\alpha }_0,$$

(6)

where L denotes the half-span of the specimen (measured between the supports), and S is the distance between the two center span loads (see Figure 1). The parameters h, s, and β are dimensionless values which depend on the dimensions of the specimen.

Formula (1) can be expressed in the form of a linear function:

$$y=Ax+C,$$

(7)

where the proper substitutions are as follows:

$$y={\displaystyle \frac{1}{{\sigma }_N^2}},$$

(8)

$$A={\displaystyle \frac{g\left({\alpha }_0\right)}{E{G}_f}},$$

(9)

$$x=D,$$

(10)

$$C={\displaystyle \frac{g^{\prime }\left({\alpha }_0\right)}{E{G}_f}}{c}_f.$$

(11)

Hence, having a graph of the ${\displaystyle \frac{1}{{\sigma }_N^2}}$ vs. D relationship (plotted for different values of the specimen depth D), one can compute the slope A and the intercept C of the corresponding regression line. These values allow the establishment of the fracture energy and the critical effective crack extension from the following formulae:

$$G_f={\displaystyle \frac{g\left({\alpha }_0\right)}{EA}},$$

(12)

$$c_f={\displaystyle \frac{Cg\left({\alpha }_0\right)}{{Ag}^{\prime }\left({\alpha }_0\right)}}.$$

(13)

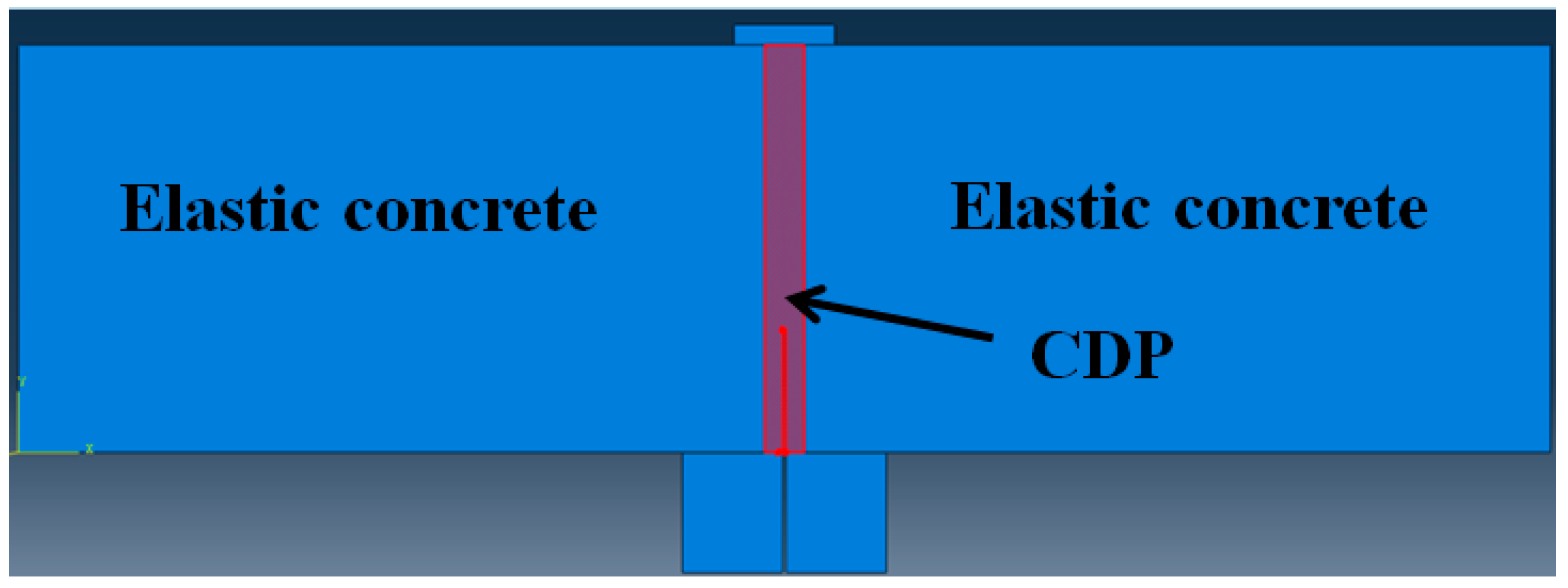
3.2. Concrete Damaged Plasticity (CDP) Model

The authors of this paper decided to recreate numerically the gap test using the finite element method (FEM) in ABAQUS/CAE software, version 2017 [19]. To describe the material behavior of concrete, they applied the concrete damaged plasticity (CDP) model. This model was proposed by Lubliner et al. [20] and developed by Lee & Fenves [21]. The yield function in the stress space is expressed in the following form:

$$F={\displaystyle \frac{1}{1-\alpha }}\left[q+3\alpha p+\beta \left({\tilde{\epsilon }}^p\right)〈{\widehat{\sigma }}_{max}〉-\gamma 〈{-\widehat{\sigma }}_{max}〉\right]-{\sigma }_c\left({\tilde{\epsilon }}_c^p\right)=0,$$

(14)

where p is the effective hydrostatic pressure, q is the Mises equivalent effective stress, α is a parameter depending on the relationship of the uniaxial and biaxial compressive strength, $\beta \left({\tilde{\epsilon }}^p\right)$ is a function of plastic strain, defined separately in tension and compression, γ is a parameter of shape of the yield surface, and σ_max is the maximal principal effective stress. The symbol 〈〉 represents Macaulay’s bracket. Introduction of the damage parameter d allows the effective stress to be defined according to the following equation:

$$\widehat{\sigma }={\displaystyle \frac{\sigma }{1-d}},$$

(15)

where σ represents stress in undamaged material. It is also introduced in the stress–strain relationship as follows:

$$\mathit{\sigma }=\left(1-d\right){\mathit{D}}_o^{el}:\left(\mathit{\epsilon }-{\mathit{\epsilon }}_{\mathit{p}\mathit{l}}\right),$$

(16)

where ${\mathit{D}}_o^{el}$ is the initial stiffness matrix in the elastic state. Taking into account different behaviors of concrete in tension and compression, the damage parameter is defined according to the formula:

$$1-d=\left(1-s_t{d}_c\right)\left(1-s_c{d}_t\right),$$

(17)

where d_c and d_t are damage parameters in compression and tension, respectively, and s_t and s_c denote stiffness recovery functions. The plastic flow is non-associated in the CDP model; so the separate plastic potential function is defined as follows:

$$G=\sqrt{{\left(ϵf_{t}tan\mathsf{\psi }\right)}^2+q^2}-ptan\mathsf{\psi },$$

(18)

where $ϵ$ is the eccentricity of the plastic potential flow and ψ is dilatancy angle. A viscoplastic regularization is also introduced in the CDP model according to the Duvaut–Lions formula [22]:

$${\dot{\mathit{\epsilon }}}_{\mathit{v}}^{\mathit{p}\mathit{l}}={\displaystyle \frac{1}{\mu }}\left({\mathit{\epsilon }}^{\mathit{p}\mathit{l}}-{\mathit{\epsilon }}_{\mathit{v}}^{\mathit{p}\mathit{l}}\right),$$

(19)

where μ is the relaxation time (an optional parameter in the CDP model) and the bottom index v means the viscous part of the plastic strains. The importance of activation of the viscous term in the investigation of the deterministic size effect was shown in the work of Winnicki et al. [23], but this paper did not discuss the gap test.

The other optional input in the CDP model is the damage conditions, specified separately in tension and compression. The authors of this paper demonstrated that the definition of the damage conditions in tension played a significant role in the numerical recreation of the gap test.

The authors of this paper decided to choose the CDP model not only because of their experience with this model, but also because it is still widely used and discussed by other scientists, who perform their FEM calculation in Abaqus software. The popularity of this model is demonstrated by its wide range of applications and also in recent research. Wang et al. [24] presented development and implementation of this model for concrete under freeze–thaw cycles. Bilal et al. [25] discussed selection of the CDP model parameters, which seems to be the most important issue when using this model. There are also scientists who have shown the usefulness of this model for other quasi-brittle material, for instance masonry structures [26].

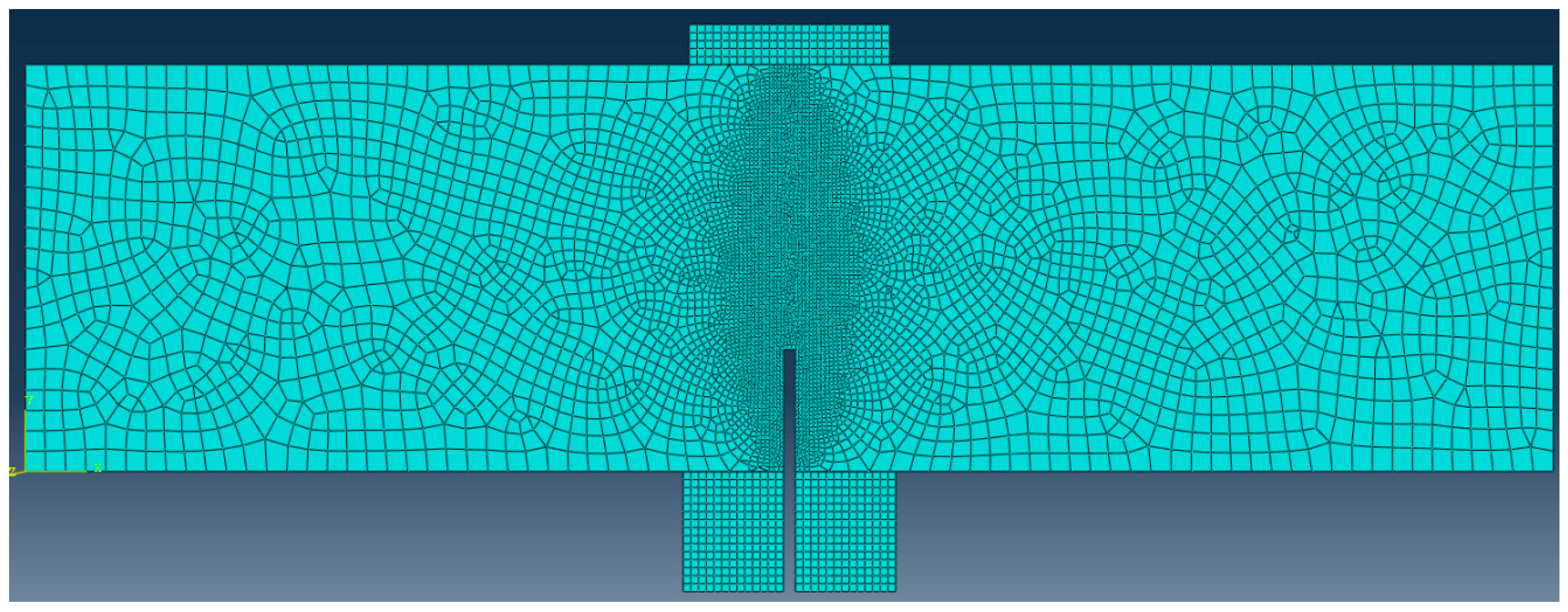
3.3. Setup of the Numerical Model

Properties of the specimen were taken from the work of Nguyen et al. [1]. It allowed the comparison of results of their laboratory tests with results of numerical simulations performed by the authors of this paper. Geometry of the basic (the smallest) specimen is presented in Figure 2. The other specimens were two and four times larger, but the thickness of all the specimens and pads remained the same and was equal to 101.6 mm. All the pads were scaled with the same aspect ratio as the specimen (2:1 and 4:1); in the case of the smallest specimen (1:1), the dimensions of the poly-propylene pads were 50 mm width and 60 mm height, and the steel pads were 50 mm width and 10 mm height.

Details of the numerical modeling of the specimen are presented in Figure 3, Figure 4 and Figure 5. Numerical analysis was divided into two steps. In the first step two end supports were inactive, and the whole specimen was supported by poly-propylene pads. In the second step, after full yielding of the pads, the end supports were activated. Displacement control was applied during the whole analysis, with a displacement imposed on a top plate made of steel. The specimen and the pads were meshed with four-node plane stress finite elements with reduced integration and enhanced hourglass control (the so-called CPS4R finite elements in the Abaqus software). A fine mesh was applied in the notched zone of the specimen with a finite element size of 1 mm. The rest of the specimen was meshed with 5 mm large elements (see Figure 4). All the parts (the specimen and the pads) were connected with the use of a constraint called “Tie” in Abaqus (with the specimen as “master” and the pads as “slave” surfaces). The constraint “Tie” means a full bond (compatibility of corresponding degrees of freedom) between connected elements and is a default option in the Abaqus code.

The mechanical properties of concrete, poly-propylene, and steel are listed in

Table 1. Mechanical properties of concrete.

Property	Value
Elastic modulus	35 GPa
Poisson’s ratio	0.167
Compressive strength of concrete	40.5 MPa
Dilatancy angle	15 degrees
Tensile strength	3.5 MPa
Fracture energy	142 Nm−1
Relaxation time	10−4 s
fb0/fc0	1.16

,

Table 2. Compressive behavior of concrete.

Yield Stress [MPa]	Inelastic Strain
16.2	0
40.5	0.001837
32.4	0.003037

,

Table 3. Concrete tension damage conditions.

Damage Parameter	Cracking Strain
0	0
0.99	0.0733

,

Table 4. Basic mechanical properties of poly-propylene and steel.

Property	Value
Elastic modulus of steel	210 GPa
Poisson’s ratio of steel	0.30
Elastic modulus of poly-propylene	1.8 GPa
Poisson’s ratio of poly-propylene	0.38

and

Table 5. Inelastic behavior of poly-propylene.

Yield Stress [MPa]	Inelastic Strain
20.0	0
30.0	0.0085
36.3	0.0159
40.0	0.0233
45.0	0.0392
47.0	0.0631
48.0	0.1392

. The f_b0/f_c0 means a ratio of compressive strength of concrete in biaxial compression to compressive strength in uniaxial compression (1.16 as a default value for concrete). Compressive behavior of concrete was defined by inputting points laying on the stress–inelastic strain curve while tensile behavior of concrete was defined with the use of the fracture energy. Mechanical parameters (Table 1) and non-linear compressive behavior of concrete (Table 2) were assumed according to the codes [27,28]. The fracture energy was calculated with the formula given by the fib Model Code [28]:

$$G_f=73f_t^{0.18},$$

(20)

where f_t denotes tensile strength of concrete, assumed as equal to 3.5 MPa. The fracture energy was used to define the post-failure stress–strain relationship for concrete in tension. The cracking displacement at which complete loss of strength takes place is calculated based on the assumed value of G_f and with the assumption of the linear stress–strain post-failure relationship. Thanks to this approach, the results of FEM calculations remain mesh-independent, which is known as the so-called “fracture energy trick” [29].

A choice of proper values of the dilatancy angle and the relaxation time was previously discussed by the authors [30,31,32]. Szczecina & Winnicki [30,32] showed that the value of the relaxation time higher than 10⁻⁴ s leads to unphysical behavior of concrete in tension. In these papers they also proved that the proper value of the dilatancy angle should be 15 degrees or lower. Wosatko et al. [31] demonstrated that relatively small values of the dilatancy angle allow the fulfillment of all conditions of the basic numerical test, the so-called Willam’s test [33].

As mentioned before, the CDP model offers an optional definition of damage parameter and damage conditions. The authors of this paper specified the damage parameter as presented in Table 3. The conditions were defined with a linear approach, starting with a default (in the Abaqus code) value of the damage parameter and the cracking strain equal to 0 and the final value of the damage parameter slightly lower than 1 (the Abaqus software does not allow the entry of this value as equal to 1). The final value of the cracking strain was calculated based on the laboratory results obtained by Nguyen et al. [1]. Separate computations were performed on the same specimen neglecting the damage. The gap test was performed with three different values of the normal stress (the T-stress) in poly-propylene pads, and namely 0, 0.4f_c, and 0.9f_c, where f_c is the compression strength of concrete. In the cases of 0.4f_c and 0.9f_c, the stress in pads was controlled by varying of the width of poly-propylene pads. For instance, in the case of the normal stress equal to 0.9f_c, the width of the poly-propylene pads was reduced 2.25 times to ensure the same (0.9/0.4 = 2.25) growth of the stress. The zero value of the normal stress means that there was no gap test, but a regular three-point bending of the specimen (in other words there were no poly-propylene pads and no gap between the end supports and the specimen).

To avoid the problem typical for non-linear finite element analysis (stress localization, unphysical results), the specimen was divided into subparts with different material definitions (see Figure 5). The CDP material model was applied in the notched zone, which is the most interesting and important (crack propagation zone). The width of the notched zone was equal to 10 mm and was scaled (2:1 and 4:1, respectively) in the cases of the larger specimens.

Finite element calculations were performed in two steps, as described earlier. Yielding of pads was controlled, and the static scheme of the specimen changed only when full yielding of pads occurred. For each step, the full-Newton solution technique was applied with initial and maximal increment size equal to 10⁻² and minimum increment size 10⁻⁹.

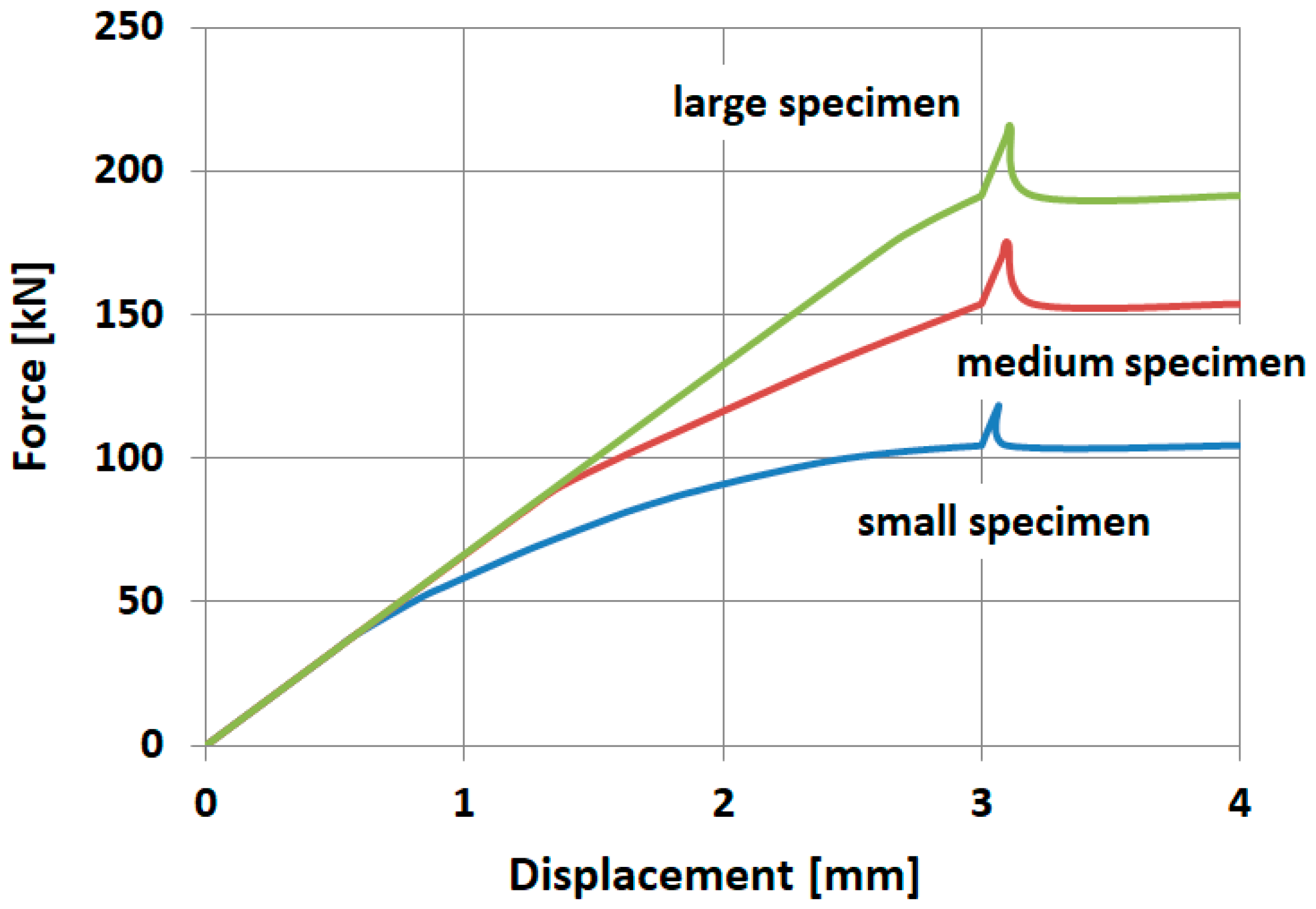
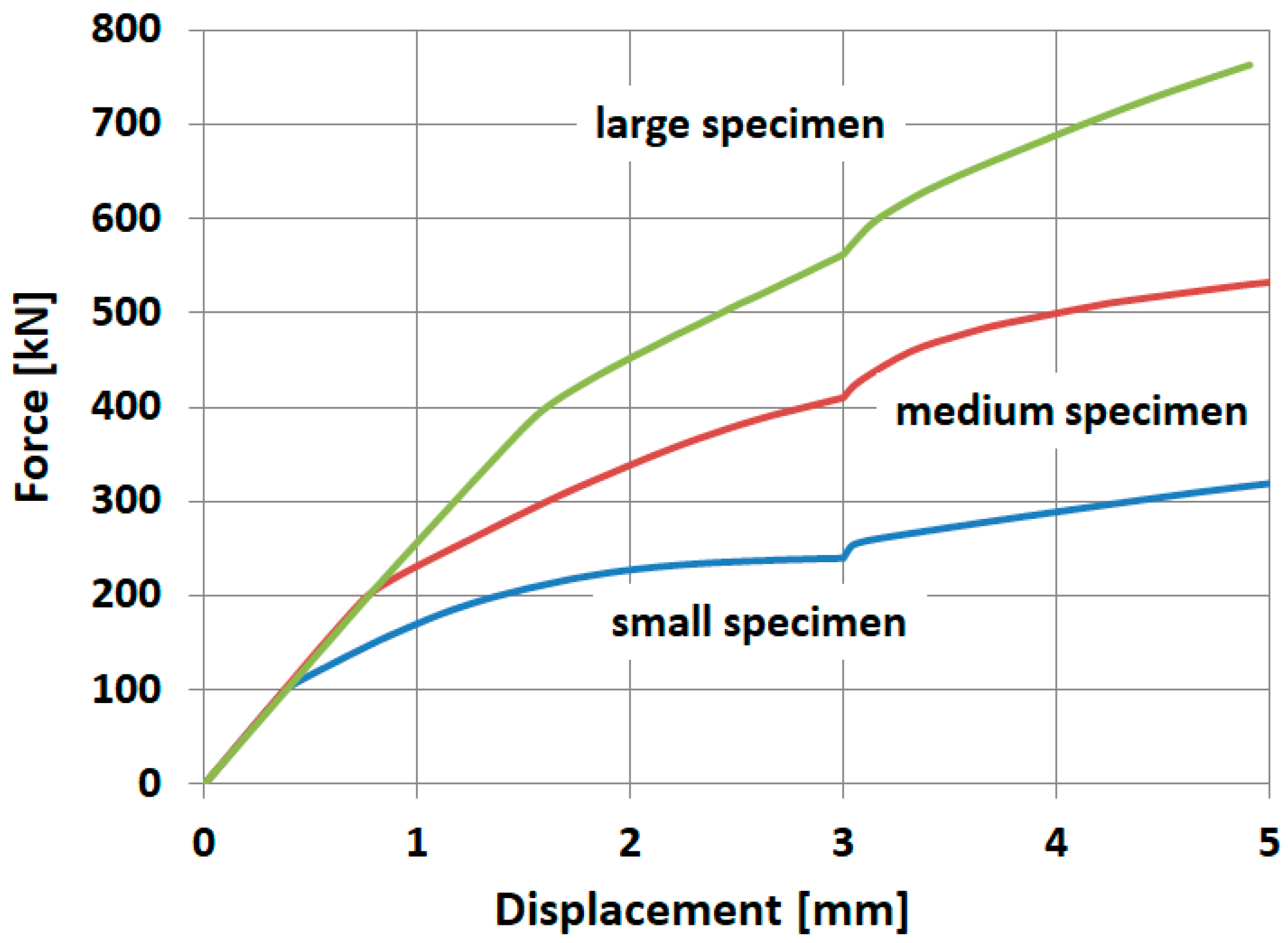
4. Results

The results presented in this section contain the following output:

• A force vs. displacement diagram and an extracted peak force; the force means vertical reaction in the steel pad, where the displacement was imposed;
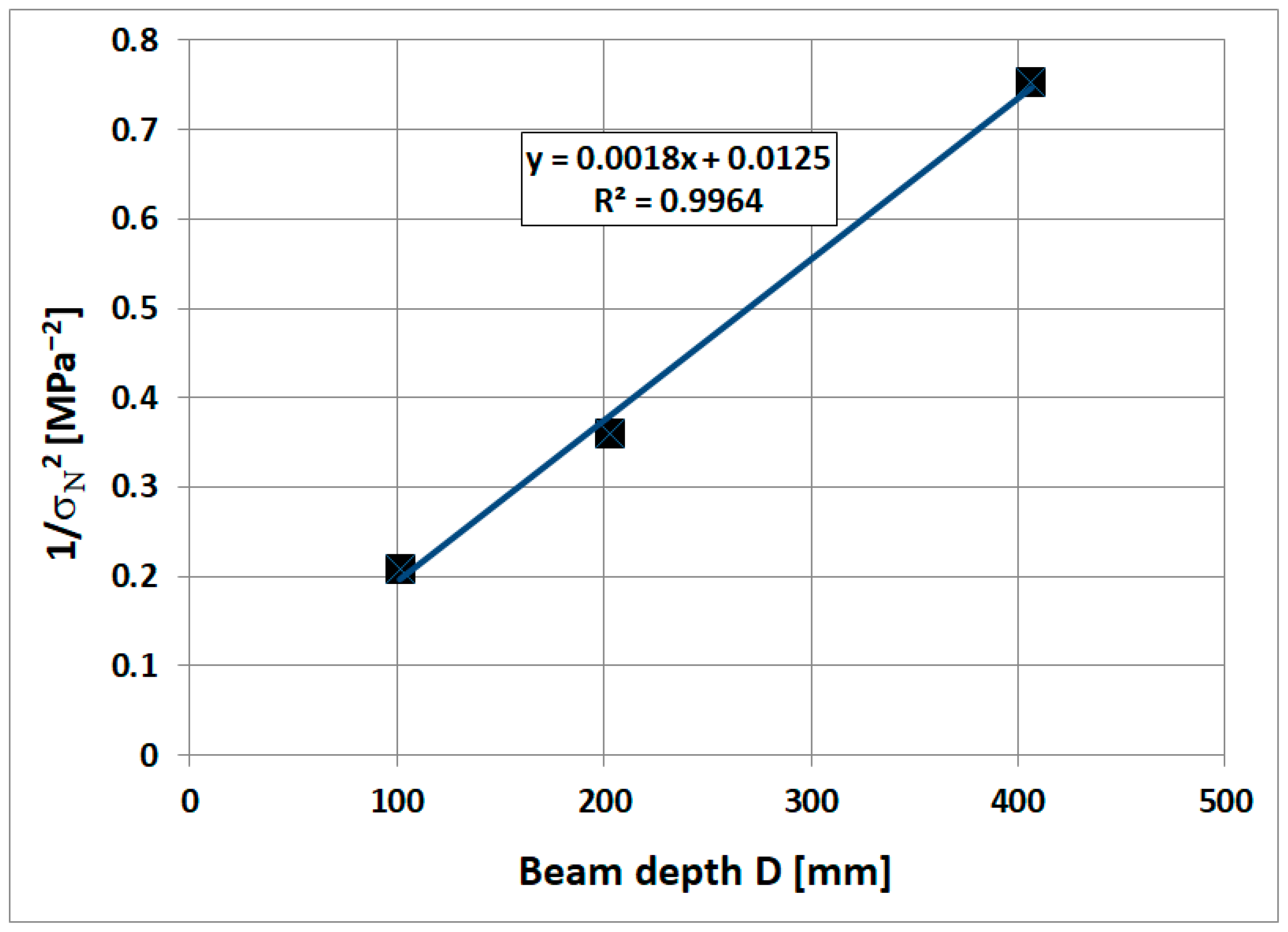
• A nominal stress σ_N vs. beam depth diagram with a linear regression line and calculations of the initial fracture energy G_f.

As mentioned before, the gap test was performed numerically on three different sizes of specimen (further in the text called “small”, “medium”, and “large” beams; dimensions of the small beam are presented in Figure 2) and three different values of the normal stress (the T-stress) in the pads (0, 0.4f_c and 0.9f_c). Calculations of the fracture energy were performed according to Formulas (1)–(13). The input data into these formulae was as follows: beam depth D = 101.6 mm (small), 202.3 mm (medium) and 406.4 mm (large beam), beam and pads thickness b = 101.6 mm (constant), beam half-span L = 381 mm, notch depth a = 0.3D, pads width 50 mm, notch width 3 mm.

The force–displacement relationships are presented in Figure 6, Figure 7 and Figure 8. The graphs were plotted simultaneously for all sizes of the beams, and separately for different normal stress in the pads. Please note that the results presented in the above-mentioned figures were obtained with specified damage conditions. In contrast to these results, the same relationship was plotted in the case when the damage was neglected—see Figure 9. In Figure 6 and Figure 7, one can see clear peaks of force (the peak loads were extracted from these peaks) and a clear plateau for the small specimen. The gap required for full yielding of poly-propylene pads was equal to 3 mm. On the other hand, when the damage conditions were neglected (Figure 9), there were no peaks and plateaus in the graphs; so it was impossible to extract the peak force. Neglecting the damage, the CDP model is not useful for numerical reproduction of the gap test.

The main goal of the gap test is calculation of the initial fracture energy G_f with the use of the size effect law. The results of the calculations and regression lines are presented in

Table 6. Basic results of calculations, normal stress (T-stress) in pads equal to 0.4f_c.

D [mm]	Peak Load [kN]	Nominal Stress σN [MPa]	1/σN2 [MPa−2]
101.6	22.6	2.19	0.21
203.2	34.4	1.67	0.36
406.4	47.6	1.15	0.75

,

Table 7. Basic results of calculations, normal stress (T-stress) in pads equal to 0.9f_c.

D [mm]	Peak Load [kN]	Nominal Stress σN [MPa]	1/σN2 [MPa−2]
101.6	12.0	1.16	0.74
203.2	19.0	0.92	1.18
406.4	26.0	0.63	2.52

and

Table 8. Basic results of calculations, normal stress (T-stress) in pads equal to 0.

D [mm]	Peak Load [kN]	Nominal Stress σN [MPa]	1/σN2 [MPa−2]
101.6	17.7	1.71	0.34
203.2	23.5	1.14	0.77
406.4	35.4	0.86	1.36

and Figure 10, Figure 11 and Figure 12. The peak load presented in Table 6 and Table 7 was calculated as a difference of a maximal force and its value on the plateau, as in Nguyen et al. [1]. Equations of the regression lines with the mean squared errors are displayed in the graphs. The initial fracture energy was calculated according to Formula (12), and the results are as follows:

• G_f = 255.5 Nm⁻¹ in the case of the T-stress equal to 0.4f_c;
• G_f = 76.6 Nm⁻¹ in the case of the T-stress equal to 0.9f_c;
• G_f = 139.3 Nm⁻¹ in the case of the T-stress equal to 0.

Assuming the initial value of the fracture energy G_f0 = 142.0 Nm⁻¹, the authors obtained the following ratios of G_f/G_f0: 1.80, 0.54, and 0.98, respectively. The correctness of the adopted research methodology is proven by the fact that the value of the assumed fracture energy (142 Nm⁻¹) is very close to the value obtained in the calculations (139.3 Nm⁻¹). This also means that the initial fracture energy varies with the T-stress, which is consistent with the finding reported earlier by prof. Bažant and his co-workers [1].

The critical effective crack extension c_f, also interpreted as a characteristic fracture processing zone (FPZ) size [1], was calculated according to Formula (13). The results are as follows:

• c_f = 2.01 cm if the normal stress is equal to 0;
• c_f = 1.01 cm if the normal stress is equal to 0.4f_c;
• c_f = 1.67 cm if the normal stress is equal to 0.9f_c.

The calculated FPZ size is relatively long (in comparison with the notch width equal to 3 mm), which is consistent with the non-linear fracture mechanics for quasi-brittle materials. In the linear elastic fracture mechanics (which is not the case for concrete), the FPZ is a single point at the notch tip. In the case of quasi-brittle materials, a large softening zone in the FPZ should occur, and that is why the FPZ should be of greater length.

Finally, the authors of this paper decided to compare their results with the results obtained by Nguyen et al. [1]. In Figure 13 we can see red dots which indicate the ratios G_f/G_f0 obtained with the use of the CDP model, and blue dots which are the results reported in [1]. Exact values of the obtained G_f/G_f0 ratios and relative errors (assuming the results by Nguyen et al. [1] as reference values) are as follows:

• in case of 0.4f_c: 1.80 (authors) and 1.74 [1], relative error: 3.45%;
• in case of 0.9f_c: 0.67 (authors) and 0.54 [1], relative error: 24.07%;
• in case of 0f_c: 0.98 (authors) and 1.00 [1], relative error: 2.00%.

According to Nguyen et al. [1], the compressive stress in the fracture processing zone σ_T is slightly smaller than the stress under the pads σ_pad, which explains the difference between the solid and the dashed line in Figure 13. The values of the ratio are very similar, and the overall tendency is the same, namely the initial fracture energy grows with the growth of the normal stress (the T-stress) and then (when the ratio of the normal stress (the T-stress) to the compressive strength is around 0.8) falls rapidly. This means that the use of the CDP model allows results to be obtained which are consistent with the experiment, but only if the damage conditions are specified.

5. Discussion

The authors of this paper demonstrated that the CDP model can effectively and accurately reproduce the gap test. The FEM calculation results are consistent with the laboratory results of Nguyen et al. [1]. The only issue requiring further refinement is the obtaining of a more pronounced plateau before the initiation of the cracking process in the force–displacement diagram for medium-sized and large beams. However, this did not prevent the calculation of the initial fracture energy, as the peak in the diagram following the plateau allowed for the reading of the peak force. The usefulness of the CDP model is therefore beyond doubt, despite the concerns raised earlier in the works [6,7] and discussed in the introduction to this article. An important finding of the authors of this article is the necessity of defining the damage conditions for concrete in tension, because without them, the force–displacement diagram has neither a plateau nor a force peak, and therefore the results are unsuitable for calculating the initial fracture energy using the size effect law. A no less important achievement of the authors of this paper is the demonstration that for the normal stress (the T-stress) equal to 0.9f_c, the initial fracture energy is reduced by almost half compared to its base value. This effect could not be demonstrated using the CDPM2 model, as noted in [6]. It turns out, therefore, that the CDP model can correctly reproduce the gap test despite its isotropic tensorial nature (or, more precisely, the definition of failure criteria using tensor invariants).

A physical mechanism that explains how the T-stress affects the fracture energy has already been described by Nguyen et al. [1]. The fracture energy in the specimen initially rises (an ascending part of the curve in Figure 13) because of a pressure on inclined microcracks and grain interlock. For higher values of the T-stress, the fracture energy value decreases because of the formation of axial splitting cracks, which lead to expansion of the fracture processing zone. The same authors [1] cast doubts on material models with plasticity-type failure criteria based on tensor invariants, stating that the Mohr envelope breaks down when expansive damage takes over. However, the authors of this paper showed that the CDP model (also of isotropic tensorial nature) reproduces the gap test well but only if the damage conditions in tension are defined.

Confirming previous gap test results using the CDP model also has practical implications. This model is available in the commercial Abaqus software, making it widely used by structural designers. Accounting for variations in the initial fracture energy can be useful, especially in complex stress states. Correct reproduction of the gap test using the size effect law is also crucial for researchers, as the sizes of structural elements tested in laboratories are usually much smaller than the actual structures. Recommendations derived from the gap test regarding the initial fracture energy should be incorporated into future structural design manuals and standards. It has been shown that the initial fracture energy can vary significantly under certain specific conditions.

6. Conclusions

Based on the results of the study, the following conclusions can be drawn:

• The CDP model can recreate the gap test correctly, but only when the damage conditions in tension are specified;
• The initial fracture energy changes with the changing normal stress (the T-stress) in the same way as in the research of Nguyen et al. [1], and the gap test revealed this fact;
• A clear plateau before the initiation of the cracking process in the force–displacement diagram has not previously been obtained in the case of the medium and the large specimen, but this fact did not disturb the extraction of the peak force.
• The authors of this paper intend to continue their work on the gap test, especially in terms of the following:
• Using different material models and different software;
• Calculating the total fracture energy from the force vs. CMOD (crack mouth opening displacement) diagram;
• Performing the gap test for other materials, for instance ceramics or fiber-reinforced concrete.

There has already been some effort put into the gap test for other materials. Brockmann & Salviato [9] performed the test on carbon fiber composites, demonstrating criticality of crack-parallel compression. Bažant et al. [7] presented preliminary results of the gap test, performed on an aluminum beam, but their work was still in progress. Nguyen et al. [1] also mentioned (when describing the significance of their work) that results obtained in the gap test are crucial for concrete, rock, fiber composites, ceramics, sea ice, and wood. As we can see, there is still a lot of scientific work to be done on this topic.