Energy Consumption Analysis of 2Z-X(B) Planetary Input-Coupled Hydro-Mechanical Tractor Transmission
Abstract
1. Introduction
2. Materials and Methods
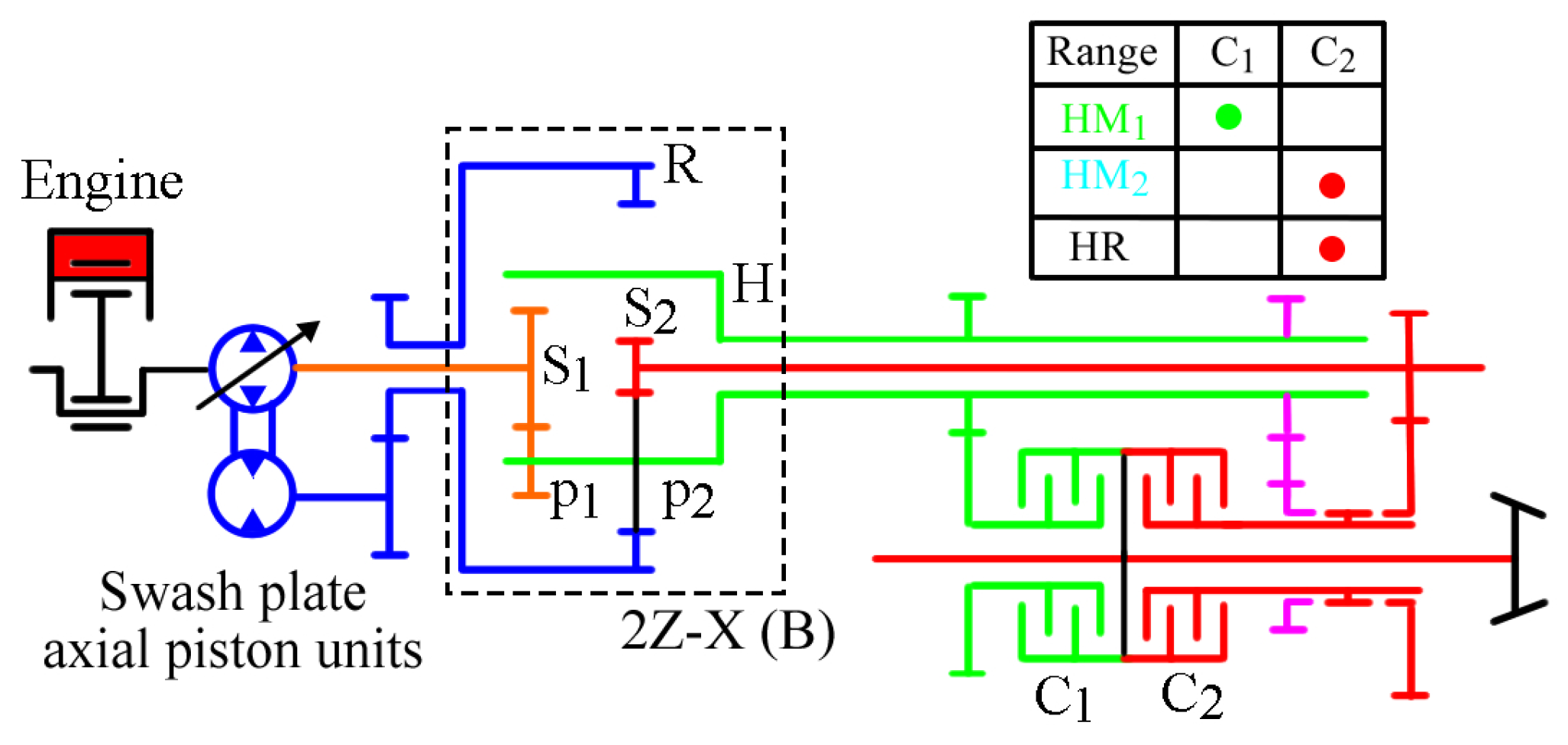
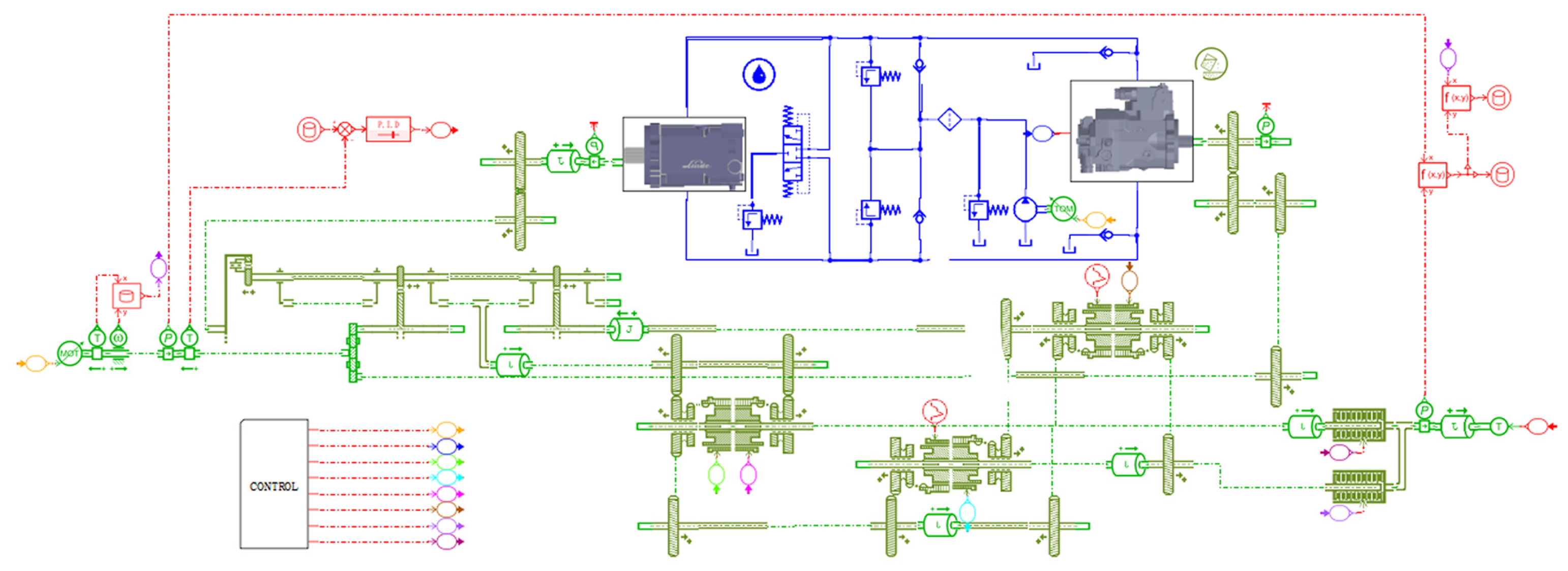
2.1. Powertrain
2.2. Modeling
2.2.1. Swash Plate Axial Piston Units
2.2.2. Gear Pairs and Planetary Gear Sets
2.2.3. Energy Consumption Calculation
2.2.4. Model Limitations
- (1)
- Case New Holland’s 4-range and 2-range HMTs are designed to address distinct market demands. To facilitate a fair comparison between two different power-level transmission systems and to elucidate the relationship between HMT configuration and energy consumption, we have reselected the engine (WP6T180E21, Weichai Power Co., Ltd., Weifang, China), pump (A4VG32, Bosch Rexroth, Shanghai, China), and motor (A6VM63, Bosch Rexroth, Shanghai, China) for the HMTs. This adjustment results in the two drivetrains under study being theoretical constructs; thus, the calculated outcomes cannot be directly equated to actual product performance.
- (2)
- The model presented in this study is an adaptation of an energy consumption calculation model for Simpson HMT, originally developed by our research group in an earlier phase and experimentally validated across multiple operating conditions [22]. Given that both Simpson and 2Z-X(B) planetary gear sets can be decomposed or equivalent to two standard 2Z-X(A) planetary gear sets, their technical routes are consistent. Unlike the original model, this study replaces the hydraulic system simulation sub model based on energy and flow conservation in the original model with the hydraulic system efficiency map obtained from manufacturer experiments, thereby limiting the source of calculation errors to the high-efficiency mechanical transmission part. This treatment is theoretically more reliable because mechanical transmission, mainly gear transmission, has high efficiency, and its calculation error within a certain range has a very limited impact on the overall calculation results.
- (3)
- A limitation of this model is that the meshing efficiency of the gear pair has not been calibrated and is treated as a constant (e.g., 0.98), a common practice in engineering calculations. This approach suffices for the theoretical analysis and comparative work conducted herein, as the primary objective is to identify patterns rather than obtain precise numerical values. However, if the model is to be used for precise evaluation of specific product performance, it will be necessary to calibrate the transmission parameters via bench testing, and where required, employ optimization algorithms to adjust these parameters.
3. Results
3.1. Speed Characteristics
- (1)
- This HMT is capable of starting from zero speed with maximum displacement () in HM1 range. Consequently, it eliminates the need for an additional dedicated hydrostatic range for starting, which simplifies the overall transmission system structure.
- (2)
- The transmission ratio of the HMT is continuously adjustable, with the ratios of adjacent ranges seamlessly interconnected. This allows the HMT to achieve speed synchronization prior to range shifting, thereby significantly enhancing the shifting smoothness of the tractor.
- (3)
- The absolute value of the displacement ratio of the pump to motor at the theoretical shift point is less than 1, enabling the HMT to achieve speed synchronization even when the swash plate axial piston units experience speed loss.
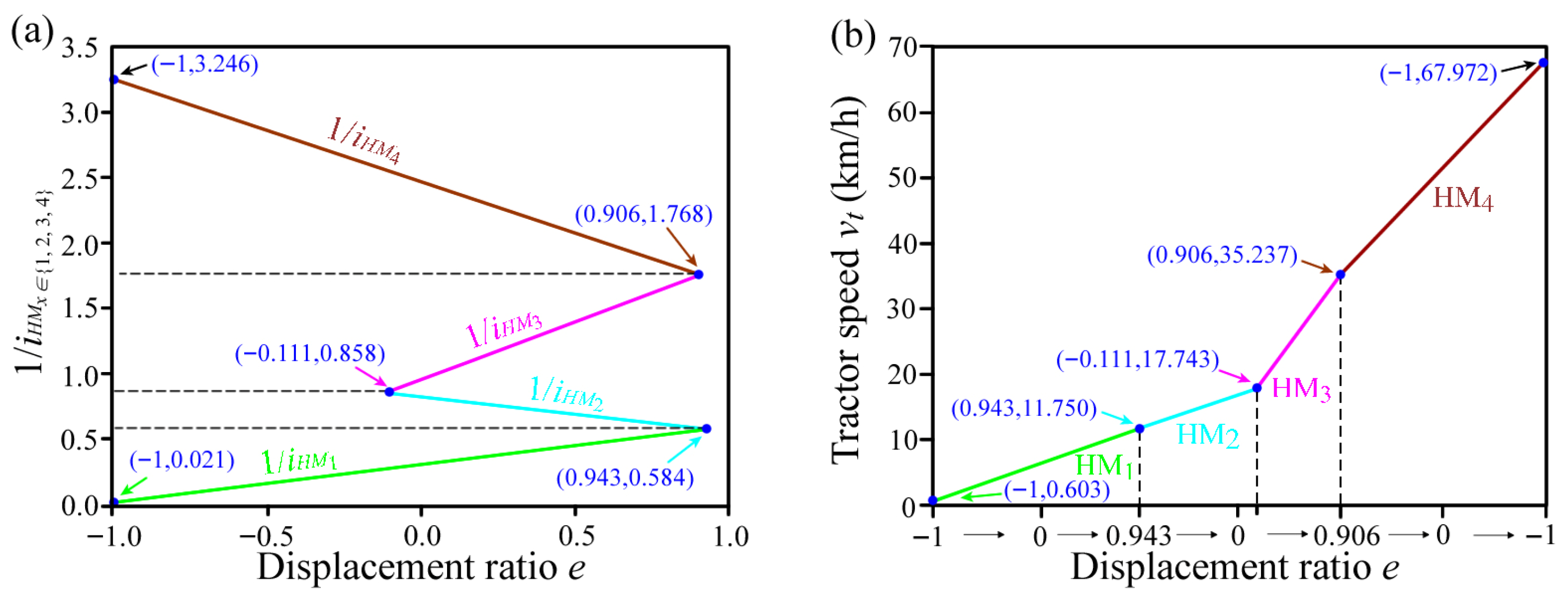
3.2. Power Characteristics
- (1)
- For ranges HM1/HM3: when the displacement ratio of the pump to motor is negative, the mechanical power input from the sun gear S1 flows partly along the planet carrier to the output shaft, and the other part flows back to the hydraulic motor along the ring gear to form parasitic power; when the displacement ratio of the pump to motor is positive, the mechanical power input from the sun gear S1 and the hydraulic power input from the ring gear flow to the output shaft through the planet carrier together after the confluence, and there is no parasitic power.
- (2)
- For ranges HM2/HM4: when the displacement ratio of the pump to motor is positive, part of the mechanical power input from the sun gear S1 flows along the sun gear S2 to the output shaft, and the other part flows back to the hydraulic motor along the ring gear to form parasitic power; when the displacement ratio of the pump to motor is negative, the mechanical power input from the sun gear S1 and the hydraulic power input from the ring gear flow together to the output shaft through the sun gear S2 after the confluence, and there is no parasitic power.
- (3)
- The direction of change in the displacement ratio depicted in the figure corresponds to the acceleration direction of the HMT. It is evident that parasitic power occurs on the side with lower output speed within each operating range. This parasitic power does not contribute to external work and results in internal energy loss, significantly impacting the transmission efficiency of the HMT.

- (1)
- The HMT features a near-100% hydrostatic power portion during startup. Post-startup, the HMT restricts the hydrostatic power portion to less than 34% via strategic range shifting. This approach prevents efficiency degradation by mitigating excessive energy consumption within the hydraulic system.
- (2)
- With the zero displacement point serving as the dividing line, the hydrostatic power portion on the high-speed side of each range is smaller than that on the low-speed side, a phenomenon clearly associated with parasitic power.
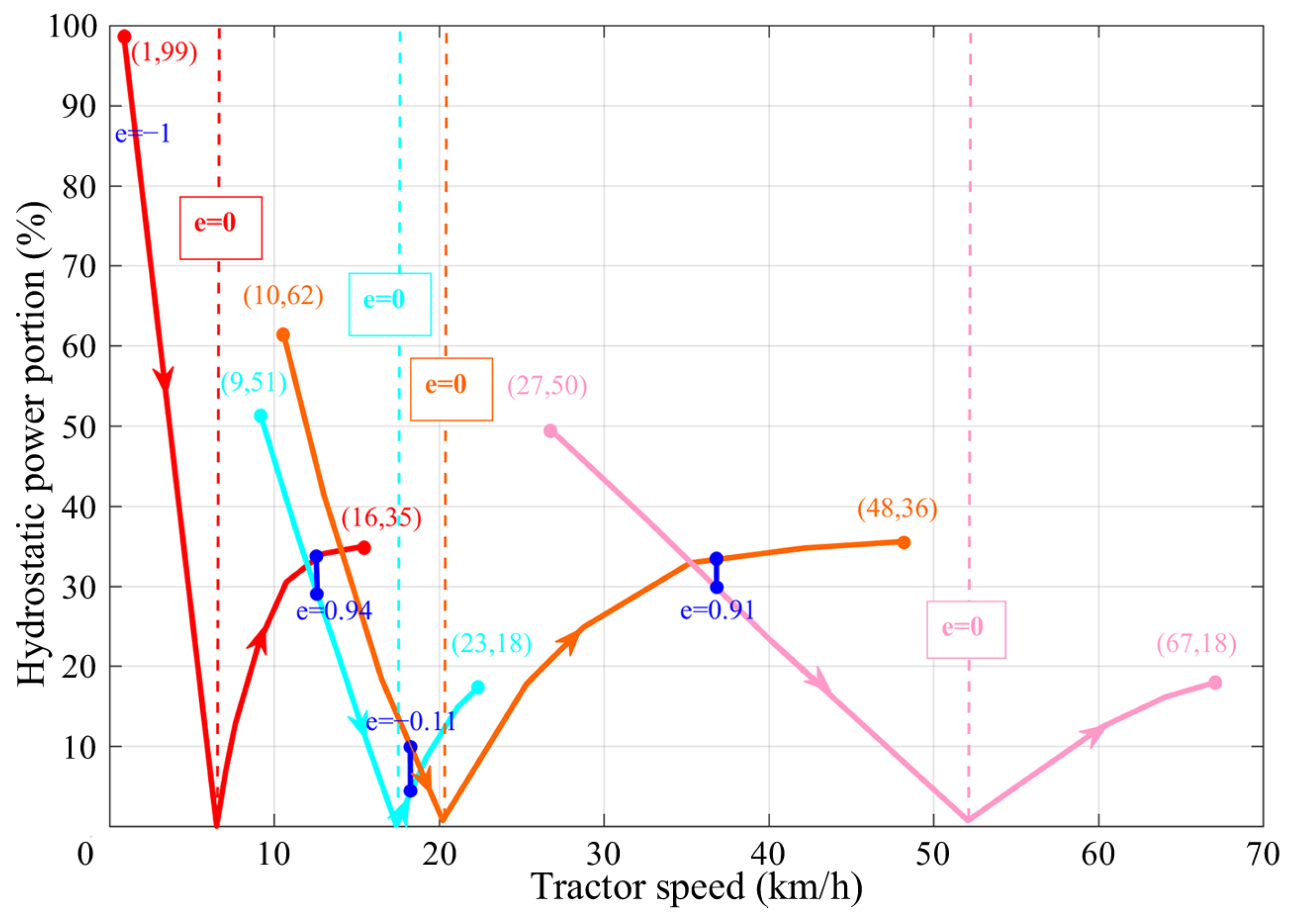
3.3. Efficiency Characteristics
3.3.1. Full Load Efficiency
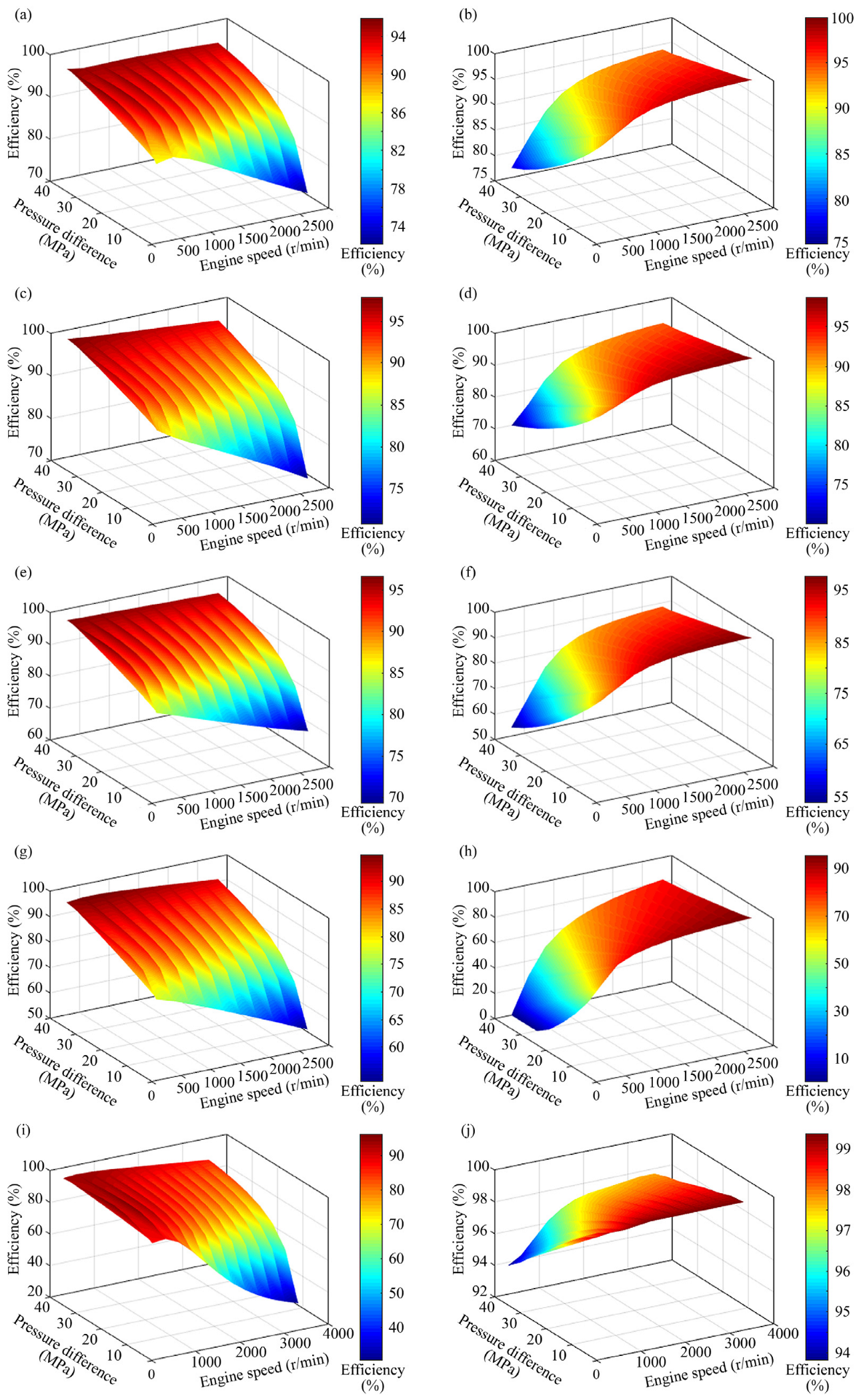
- (1)
- The maximum full-load efficiency of the HMT is around 95%, which is comparable to the efficiency of the HM8 transmission disclosed by Claas. For any range, the HMT only uses the speed range under its partial pump displacement.
- (2)
- Viscous damping influences cause the full-load efficiency of the HMT to decrease as engine speed increases. Specifically, when engine speed rises from 1000 r/min to 2200 r/min, the maximum transmission efficiency of the HMT drops from 95% to 93%.
- (3)
- At low engine speeds, the high-speed side of each range exhibits higher efficiency than the low-speed side, primarily due to parasitic power losses. As engine speed increases, however, the high-speed side of each range experiences greater viscous damping losses compared to the low-speed side, causing these efficiency differences to diminish or become insignificant.
- (4)
- Under the condition of meeting the load power requirements, the HMT achieves the necessary operating speed by adjusting different engine speeds, thereby ensuring the HMT consistently operates at high transmission efficiency.
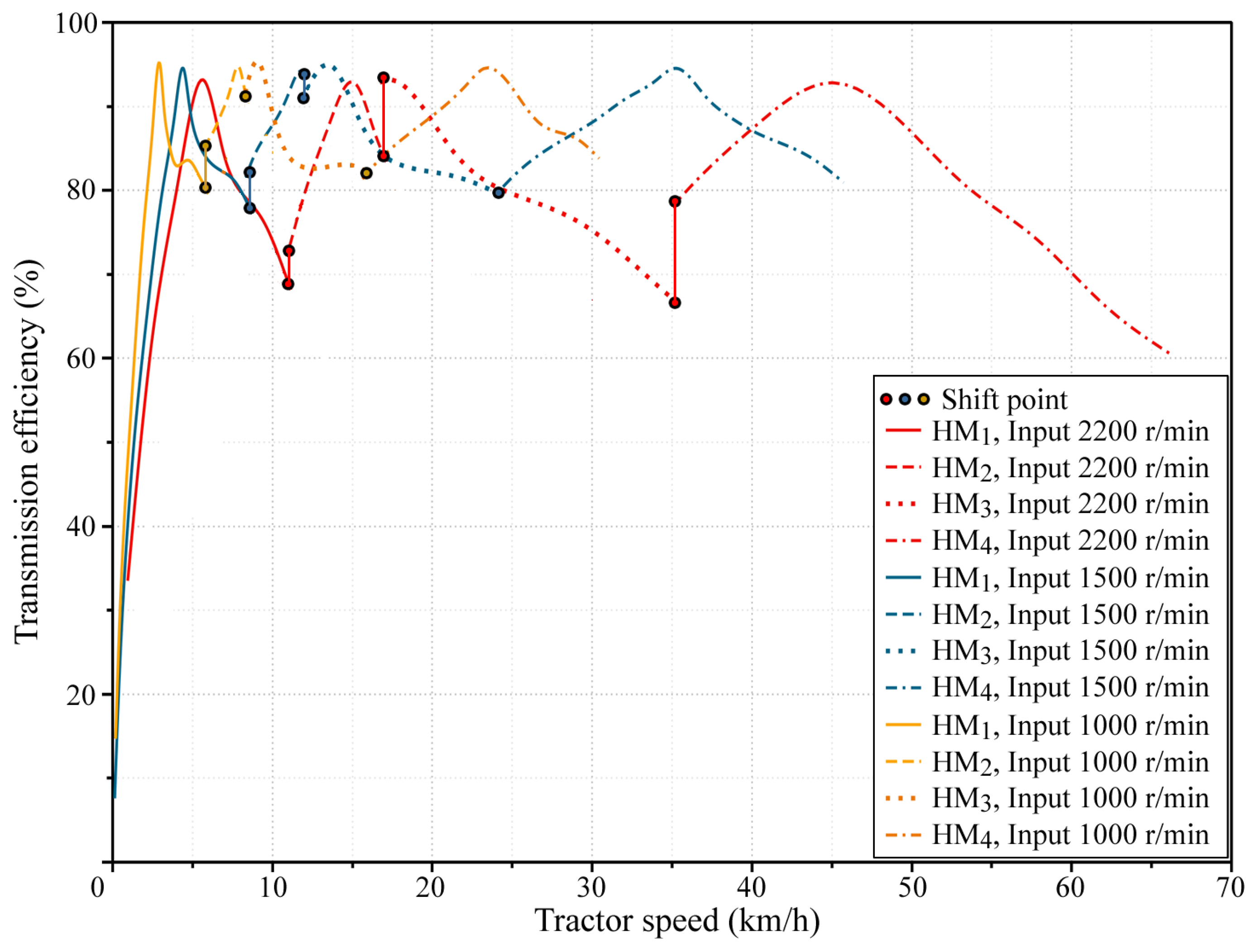
3.3.2. Partial Load Efficiency
- (1)
- Within each operating range, the absolute value of the pump-to-motor displacement ratio initially decreases and subsequently increases as engine speed rises. This behavior dictates a corresponding pattern for the hydrostatic power portion, resulting in a ‘U’-shaped distribution of the HMT’s efficiency contour. The mechanical point of the HMT (where e = 0) is situated at the midpoint of this ‘U’ shape, and the HMT exhibits high transmission efficiency within this region.
- (2)
- The efficiency contour exhibiting a ‘U’ shape is, in fact, a closed annular curve. This occurs because as load torque increases, the proportion of HMT’s basic energy consumption relative to total energy consumption decreases, thereby enhancing the transmission’s efficiency. However, when load torque becomes excessively high, the volumetric efficiency of both the pump and motor declines sharply, leading to speed loss and a reduction in overall transmission efficiency. Since the load torque necessary to close the ‘U’ curve exceeds the boundary of the engine’s external characteristic curve, this phenomenon is not observable in the diagram.
- (3)
- As tractor speed increases, the ‘U’ central area within the same range shifts toward higher engine speeds in response to changes in the displacement ratio. Theoretically, by maintaining the transmission at a consistently lower displacement ratio, an ‘engine-HMT’ control strategy optimized for maximum efficiency can be achieved.
- (4)
- As the HM2 and HM3 ranges shift at lower pump displacements, their high-efficiency regions converge, thereby expanding the engine’s speed range for high HMT efficiency and enhancing the flexibility of ‘engine-HMT’ power matching.
- (5)
- At a tractor speed of 6 km/h, the optimal efficiency region of the HMT is situated in the upper right corner of the engine map, overlapping with the engine’s high-power operating range. This indicates that the HMT can simultaneously satisfy both efficiency and power demands when engaged in heavy-duty operations such as ploughing at this speed.
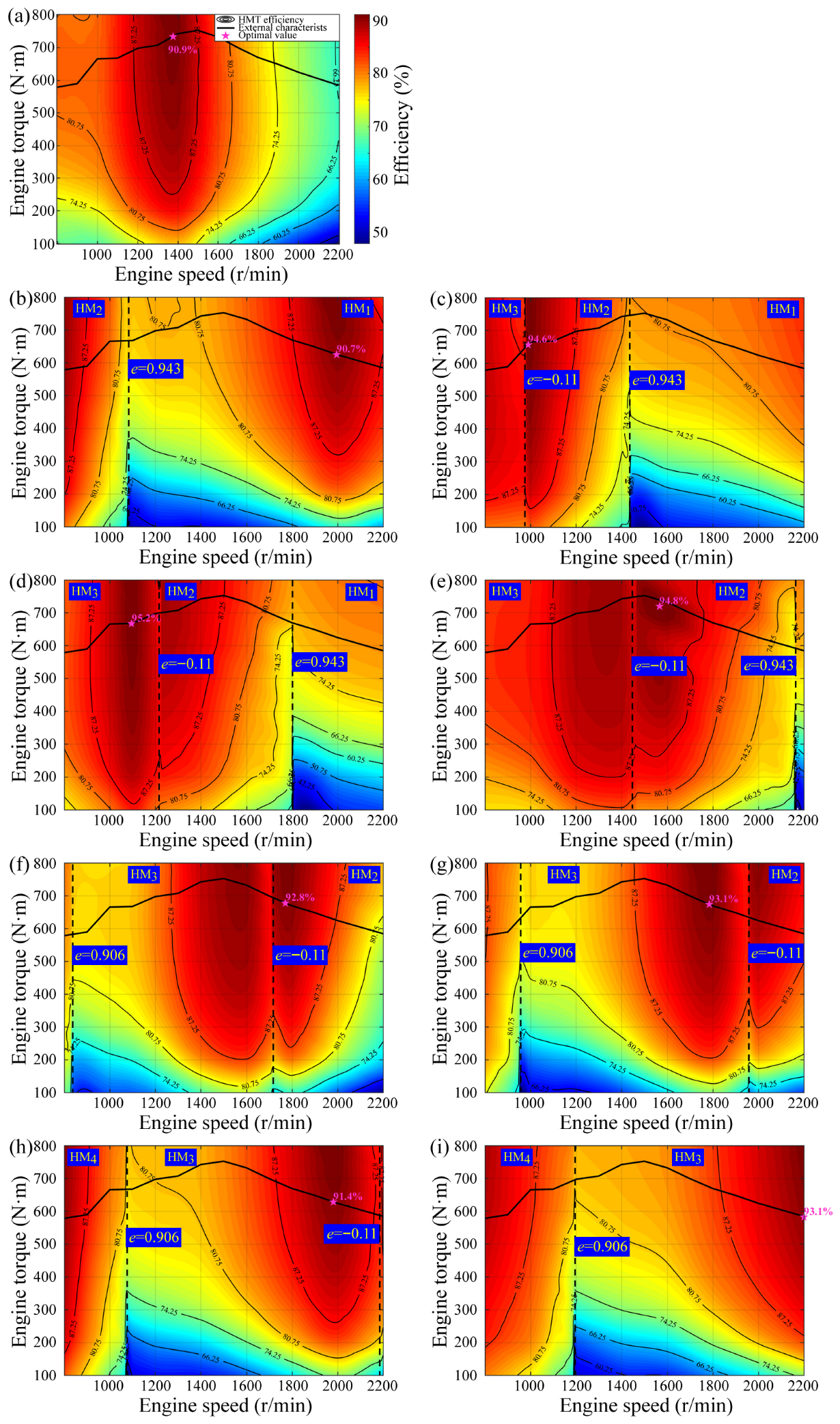
3.4. Fuel Consumption Characteristics
- (1)
- At varying operating speeds, the fuel consumption of the tractor exhibits a comparable distribution and behavior pattern to the efficiency of the HMT. This indicates that the transmission efficiency of the HMT exerts a more significant influence on the tractor’s fuel efficiency than the engine itself.
- (2)
- A tractor speed of 6 km/h remains appropriate for heavy-load operations like ploughing. At this speed, the tractor effectively balances its power output with fuel efficiency.
- (3)
- The fuel consumption of the HMT tractor is notably higher under light load conditions, particularly when the engine’s load torque falls below 300 N·m. To mitigate this, it is recommended to operate in higher HMT ranges during light loads and to enhance engine torque by adjusting the HMT ratio downward.

4. Discussion
4.1. Comparison with Case New Holland 2-Range HMT
- (1)
- The efficiency of the HMT on the high-speed side of each range is significantly better than that on the low-speed side. Different from the 4-range HMT, this trend does not weaken with the increase of engine speed, which is very beneficial to the road transportation conditions of tractors.
- (2)
- Reducing the speed regulation range enhances tractor reliability by lowering shift frequency. However, fewer ranges increase the hydrostatic power portion of HMTs, reducing their efficiency at the low-speed side of each range. This results in a pronounced efficiency fluctuation before and after shifts, a phenomenon particularly pronounced at low engine speeds, potentially causing torque shocks during shifting. These factors must be considered when developing HMT shift control and speed control strategies.
- (3)
- The efficiency of the two HMTs is further assessed at the rated engine speed. As per Renius’ statistical data [27], tractors operate within the speed range of 4–12 km/h for 68% of their lifecycle, a concentrated interval critical for heavy and medium load tasks such as plowing and harrowing. Using an efficiency threshold of 80%, the 2-range HMT exhibits high efficiency between 6–12 km/h, while the 4-range HMT performs optimally in the 4–8 km/h range. By comparison, the 2-range HMT offers greater advantages, as its operational speed range of 8–12 km/h encompasses a broader spectrum of heavy and medium load conditions, making it indispensable.
- (1)
- The optimal efficiency point of the 2-range HMT at 8 km/h shifts to the upper right corner of the efficiency map, corresponding to the high-power output region of the HMT. This adjustment balances the HMT’s energy consumption with the tractor’s power output. In contrast, the 4-range HMT exhibits an optimal operating speed of 6 km/h under heavy load conditions.
- (2)
- Unlike the 4-range HMT, the 2-range HMT features a broad speed regulation range within a single range, eliminating the distinct ‘U’-shaped profile typically observed in its efficiency and fuel consumption distribution.
- (3)
- The 2-range HMT exhibits significant efficiency variations in the transitional zone between its two ranges. This indicates that efficiency differences before and after shifting must be accounted for in the development of HMT control strategies, both under full load and partial load conditions. Failure to do so can result in abrupt fluctuations in engine torque during shifts.
4.2. Comparison with Other Tractor HMTs
- (1)
- The efficiency of HMT can surpass that of power-shift transmissions in energy consumption only if it exceeds the target efficiency established by Renius—a goal that presents significant challenges. To date, aside from Fendt’s Vario, few HMTs have fully achieved this standard. The Vario transmission employs a unique 2Z-X(A) planetary output coupled configuration, featuring 45 variable bent axis units co-developed by Fendt and Sauer Sundstrand. This design enables the HMT to maintain high efficiency across a broad speed ratio range. Due to the technical complexity involved, most existing HMTs instead utilize a multi-range planetary input-coupled configuration. Further research is needed to determine whether the 2Z-X(B) configuration can be integrated with the planetary output coupled setup.
- (2)
- Both Case New Holland and Hofer’s HMT employ planetary input-coupled configurations. In comparison to Vario, their efficiency curves display a distinct hump shape. while this configuration does not fully adhere to the standard proposed by Renius, it attains the target efficiency within the mid-range of each range and outperforms Vario.
- (3)
- Unlike Hofer’s VDC, Case New Holland and Fendt’s HMT systems lack a Hydrostatic starting range; instead, they employ a power-split range to facilitate tractor startup, thereby simplifying the HMT structure.
- (4)
- Despite differing tractor design speeds, Case New Holland’s 4-range HMT and Hofer’s VDC demonstrate consistent efficiency variation patterns, with the former achieving superior maximum efficiency. While the efficiency within the key operational speed range has been optimized for Case New Holland’s 2-range HMT, its overall performance remains relatively low. This is attributed to the smaller number of ranges and lower application power, resulting in a larger hydrostatic power portion and a higher basic energy consumption portion.
5. Conclusions
- (1)
- Using the pump-to-motor displacement ratio e = 0 as the boundary, parasitic power exists on the low-speed side of the HMT within the same range. This results in the HMT’s efficiency being higher on the high-speed side than on the low-speed side across all ranges, regardless of whether it is a 2-range or 4-range HMT. As engine speed increases, the friction energy loss due to viscous damping diminishes the aforementioned efficiency differences in the 4-range HMT; however, the 2-range HMT consistently retains this disparity.
- (2)
- As there is no hydrostatic range, the hydrostatic power portion of this type of HMT approaches 100% upon startup. During the transmission design phase, it must be ensured that the hydrostatic power portion of the HMT decreases to a lower level at the minimum field operating speed. Typically, this operating speed corresponds to 4 km/h at rated engine speed.
- (3)
- Regardless of whether it is a 2-range or 4-range HMT, tractor fuel consumption at the same speed and range varies with changes in pump displacement. This indicates that efficiency characteristics exert a more significant influence on tractor fuel economy than the engine’s inherent fuel consumption. Consequently, developing an efficiency-prioritized HMT control strategy is feasible.
- (4)
- The 2-range HMT has a simpler structure compared to the 4-range HMT; however, its efficiency exhibits significant variation before and after a range shift. Despite the transmission ratio remaining constant pre- and post-shift, the torque fluctuations resulting from efficiency changes can affect engine performance. This necessitates careful consideration when developing HMT shift control strategies and speed regulation approaches.
- (5)
- The optimal engine speed and HMT displacement ratio vary across different ranges as tractor speed changes. When tractor speed reaches 6 km/h, the optimal efficiency point of the 4-range HMT shifts to the high-power region, enabling the tractor to perform heavy-duty operations like ploughing with minimal fuel consumption. In contrast, the ideal heavy-load operating speed for the 2-range HMT is 8 km/h. During the transmission design phase, engineers should analyze local tractor operating conditions to optimize HMT efficiency at typical operating speeds.
- (6)
- When operating at the same tractor speed and HMT range, the 4-range HMT exhibits a pronounced ‘U’-shaped characteristic in its efficiency and fuel consumption distribution. This pattern arises from variations in the hydrostatic power portion as engine speed changes. In contrast, due to the broader speed range of each individual range, the 2-range HMT does not display a comparable efficiency and fuel consumption profile.
- (7)
- The HMT utilizing 2Z-X(B) planetary gear sets demonstrates superior transmission performance, achieving peak efficiency exceeding 90%. Its efficiency curve exhibits a hump-like shape, analogous to that of traditional HMT systems based on 2Z-X(A) planetary gear sets. Theoretically, 2Z-X(B) can be decomposed into two variants of 2Z-X(A), which likely explains the comparable performance between the two HMT types. Unlike Fendt’s Vario, the efficiency of HMT based on the 2Z-X(B) planetary gear set does not fully meet Renius’ proposed standards; however, it exhibits significantly higher local efficiency than Vario under specific operating conditions. Multi-range technology and planetary output coupled technology may represent viable approaches to further reduce energy consumption in 2Z-X(B)-based HMT systems.
- (8)
- A key finding of this study indicates that, when evaluated from a full lifecycle perspective, tractors equipped with 2Z-X(B) HMT demonstrate comparable fuel economy to those equipped with 2Z-X(A) HMT.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, Y.; Zhou, Z.; Yan, X. Unified modeling of a tractor performance prototype based on ontology. Trans. Can. Soc. Mech. Eng. 2022, 46, 477–489. [Google Scholar] [CrossRef]
- Li, B.; Pan, J.; Li, Y.; Ni, K.; Huang, W.; Jiang, H.; Liu, F. Optimization method of speed ratio for power-shift transmission of agricultural tractor. Machines 2023, 11, 438. [Google Scholar] [CrossRef]
- Li, J.; Zhai, Z.; Song, Z.; Fu, S.; Zhu, Z.; Mao, E. Optimization of the transmission characteristics of an HMCVT for a high-powered tractor based on an improved NSGA-II algorithm. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 2831–2849. [Google Scholar] [CrossRef]
- Wang, J.; Xia, C.; Fan, X.; Cai, J. Research on transmission characteristics of hydromechanical continuously variable transmission of tractor. Math. Probl. Eng. 2020, 2020, 6978329. [Google Scholar] [CrossRef]
- İnce, E.; Güler, M.A. On the advantages of the new power-split infinitely variable transmission over conventional mechanical transmissions based on fuel consumption analysis. J. Clean. Prod. 2020, 244, 118795. [Google Scholar] [CrossRef]
- Macor, A.; Rossetti, A. Fuel consumption reduction in urban buses by using power split transmissions. Energy Convers. Manag. 2013, 71, 159–171. [Google Scholar] [CrossRef]
- Wang, G.; Zhao, Y.; Song, Y.; Xue, L.; Chen, X. Optimizing the fuel economy of hydrostatic power-split system in continuously variable tractor transmission. Heliyon 2023, 9, e15915. [Google Scholar] [CrossRef]
- Seeger, J. Wirkungsgraduntersuchung des systems “Dieselmotor-Leistungsverzweigtes Getriebe”. Öl Hydraul. Pneum. 2001, 45, 672–677. [Google Scholar]
- Ahn, S.; Choi, J.; Kim, S.; Lee, J.; Choi, C.; Kim, H. Development of an integrated engine-hydro-mechanical transmission control algorithm for a tractor. Adv. Mech. Eng. 2015, 7, 1687814015593870. [Google Scholar] [CrossRef]
- Ramdan, M.I.; Stelson, K.A. Optimal design of a power-split hybrid hydraulic bus. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 1699–1718. [Google Scholar] [CrossRef]
- Bukashkin, A.Y.; Dobretsov, R.Y.; Galyshev, Y.V. Split transmission of tractor with automatic gearbox. Procedia Eng. 2017, 206, 1728–1734. [Google Scholar] [CrossRef]
- Rao, Z. Design of Planetary Gear Transmission, 2nd ed.; Chemical Industry Press Co., Ltd.: Beijing, China, 2019. [Google Scholar]
- Li, J.; Zhao, Y.; Zhai, Z.; Han, B.; Du, Y.; Wang, L.; Zhu, Z. Research on design and analysis method of the double planetary HMCVT based on high efficiency transmission. Agriculture 2020, 12, 1958. [Google Scholar] [CrossRef]
- Xia, Y.; Sun, D.; Qin, D.; Zhou, X. Optimisation of the power-cycle hydro-mechanical parameters in a continuously variable transmission designed for agricultural tractors. Biosyst. Eng. 2020, 193, 12–24. [Google Scholar] [CrossRef]
- Chen, Y.; Qian, Y.; Lu, Z.; Zhou, S.; Xiao, M.; Bartos, P.; Xiong, Y.; Jin, G.; Zhang, W. Dynamic characteristic analysis and clutch engagement test of HMCVT in the high-power tractor. Complexity 2021, 2021, 8891127. [Google Scholar] [CrossRef]
- Liu, M.; Li, W.; Xu, L.; Li, Y.; Zhao, T.; Hou, S. Coordinated dual-rolling control of shifting in HMCVT based on KF-MPC algorithm with anti-disturbance capabilities. Comput. Electron. Agric. 2024, 227, 109561. [Google Scholar] [CrossRef]
- Rossetti, A.; Macor, A. Multi-objective optimization of hydro-mechanical power split transmissions. Mech. Mach. Theory 2013, 62, 112–128. [Google Scholar] [CrossRef]
- Rossetti, A.; Macor, A.; Scamperle, M. Optimization of components and layouts of hydromechanical transmissions. Int. J. Fluid Power 2017, 18, 123–134. [Google Scholar] [CrossRef]
- Nguyen, V.T. Study on Dynamic Characteristics of Hydro Mechanical Continuously Variable Transmission of Tractor. Ph.D. Thesis, Nanjing Agricultural University, Nanjing, China, 2013. [Google Scholar]
- Zhang, Z.; Li, X.; Peng, Z.; Jing, C.; Yang, S.; Chen, Z. Full-condition efficiency model and power loss analysis of hydro-mechanical CVT. Trans. CSAE 2024, 40, 48–58. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, K.; Xiao, M.; Zhou, M. HMCVT steady state transmission efficiency based on HST-EGT torque ratio. Trans. CSAM 2021, 52, 533–541. [Google Scholar] [CrossRef]
- Wang, G. Study on Characteristics, Control and Fault Diagnosis of Tractor Hydro-Mechanical CVT. Ph.D. Thesis, Nanjing Agricultural University, Nanjing, China, 2014. [Google Scholar]
- Rossetti, A.; Macor, A. Control strategies for a powertrain with hydromechanical transmission. Energy Procedia 2018, 148, 978–985. [Google Scholar] [CrossRef]
- D’Andrea, D.; Risitano, G.; Alberti, F. Fuel consumption reduction and efficiency improvement in urban street sweeper using power split with lockup clutch transmission. Appl. Sci. 2022, 12, 10160. [Google Scholar] [CrossRef]
- Cammalleri, M.; Rotella, D. Functional design of power-split CVTs: An uncoupled hierarchical optimized model. Mech. Mach. Theory 2017, 116, 294–309. [Google Scholar] [CrossRef]
- Rotella, D.; Cammalleri, M. Direct analysis of power-split CVTs: A unified method. Mech. Mach. Theory 2018, 121, 116–127. [Google Scholar] [CrossRef]
- Renius, K.T. Fundamentals of Tractor Design, 1st ed.; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Meyer, H.J. Fahrzeuggetriebetechnik Getriebe in Traktoren; Technische Universität Berlin: Berlin, Germany, 2009. [Google Scholar]

| Tractor Speed (km/h) | Fuel Consumption of HMT Tractor [g/(kW·h)] | Weighting Coefficient (%) | ||||
|---|---|---|---|---|---|---|
| CNH 4-Range HMT | CNH 2-Range HMT | Hofer VDC HMT | Fendt Vario HMT | Ideal HMT by Renius | ||
| 4 | 19.22 | 20.66 | 22.14 | 16.40 | 16.49 | 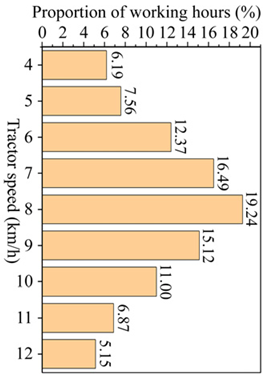 |
| 5 | 21.08 | 22.63 | 24.06 | 19.73 | 19.91 | |
| 6 | 31.82 | 33.97 | 35.87 | 32.13 | 32.19 | |
| 7 | 42.47 | 42.44 | 44.86 | 42.73 | 42.92 | |
| 8 | 52.24 | 50.80 | 50.25 | 49.78 | 50.07 | |
| 9 | 42.39 | 41.66 | 39.41 | 39.10 | 39.34 | |
| 10 | 31.35 | 30.85 | 28.33 | 28.46 | 28.61 | |
| 11 | 20.00 | 19.44 | 17.75 | 17.82 | 17.88 | |
| 12 | 15.59 | 14.96 | 13.43 | 13.38 | 13.41 | |
| Weighted fuel consumption [g/(kW·h)] | 276.17 | 277.42 | 276.09 | 259.53 | 260.81 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, F.; Kong, Y.; Liu, F.; Luo, N.; Jin, Z.; Zhao, Y.; Wang, G. Energy Consumption Analysis of 2Z-X(B) Planetary Input-Coupled Hydro-Mechanical Tractor Transmission. Appl. Sci. 2025, 15, 12576. https://doi.org/10.3390/app152312576
Ge F, Kong Y, Liu F, Luo N, Jin Z, Zhao Y, Wang G. Energy Consumption Analysis of 2Z-X(B) Planetary Input-Coupled Hydro-Mechanical Tractor Transmission. Applied Sciences. 2025; 15(23):12576. https://doi.org/10.3390/app152312576
Chicago/Turabian StyleGe, Fuxing, Ying Kong, Fengping Liu, Nana Luo, Zhuo Jin, Yehui Zhao, and Guangming Wang. 2025. "Energy Consumption Analysis of 2Z-X(B) Planetary Input-Coupled Hydro-Mechanical Tractor Transmission" Applied Sciences 15, no. 23: 12576. https://doi.org/10.3390/app152312576
APA StyleGe, F., Kong, Y., Liu, F., Luo, N., Jin, Z., Zhao, Y., & Wang, G. (2025). Energy Consumption Analysis of 2Z-X(B) Planetary Input-Coupled Hydro-Mechanical Tractor Transmission. Applied Sciences, 15(23), 12576. https://doi.org/10.3390/app152312576






