Modeling the Coupled Stress Relaxation and SEI Evolution in Preload-Constrained Lithium-Ion Cells
Abstract
1. Introduction
2. Method
2.1. Experiment
2.2. Calendar Aging Model Description
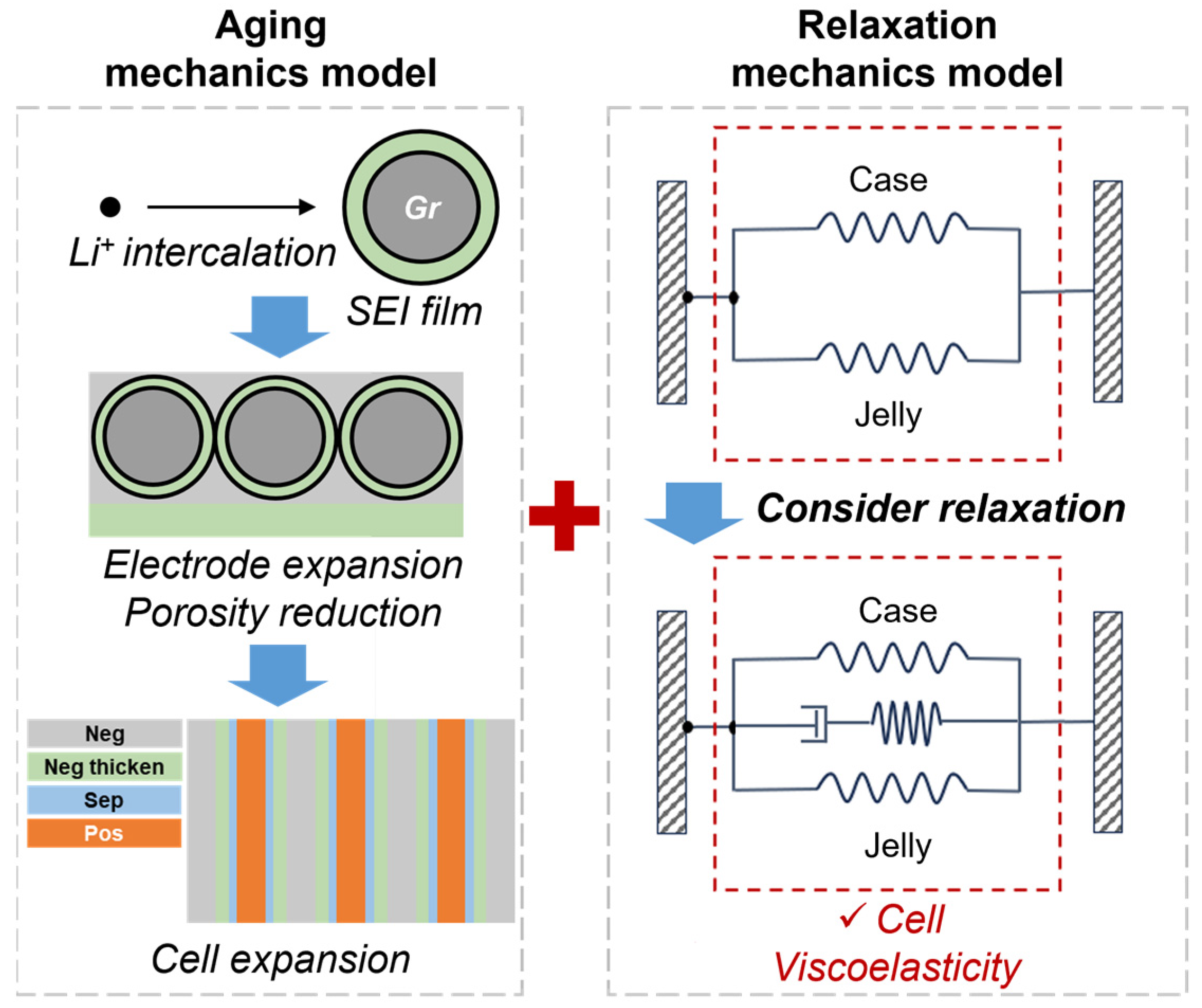
2.3. Mechanical Relaxation Model Description
3. Results and Discussion
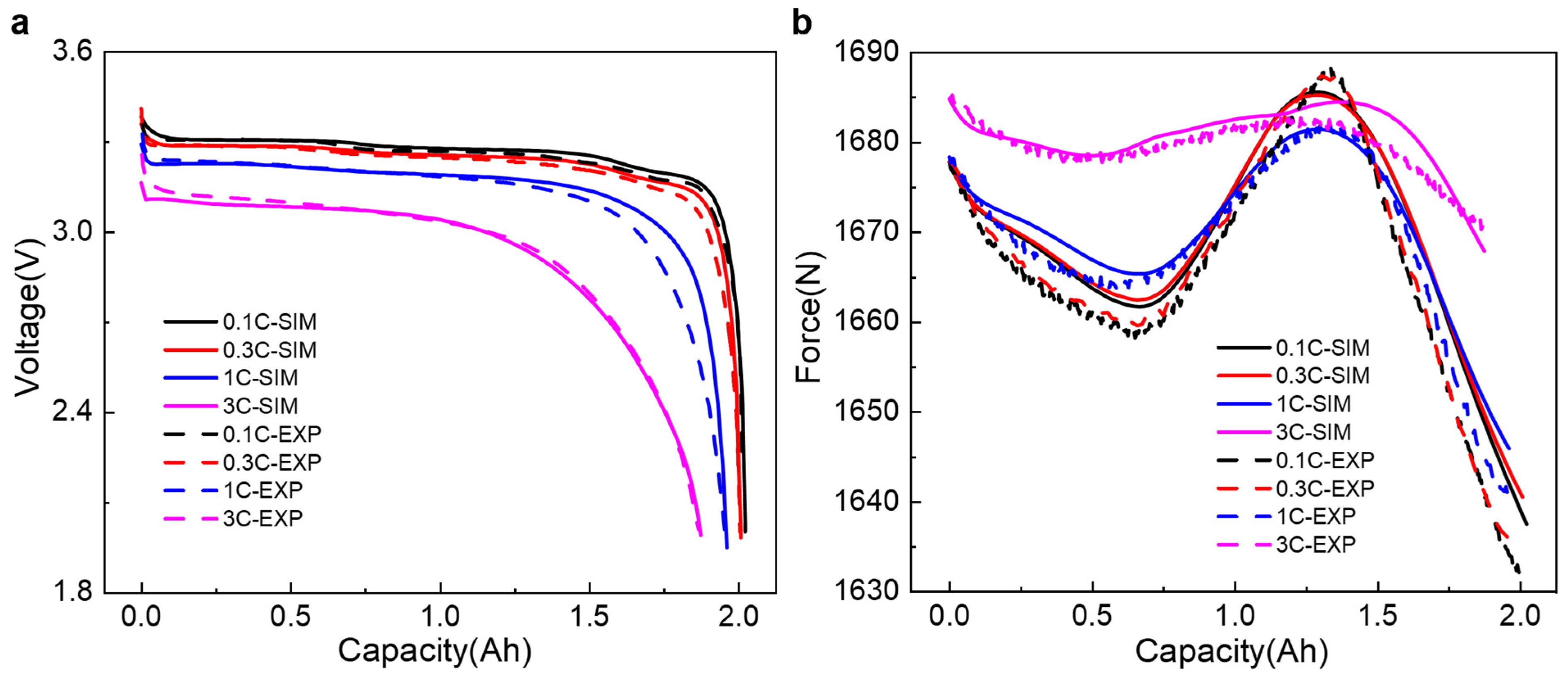
3.1. Model Validation
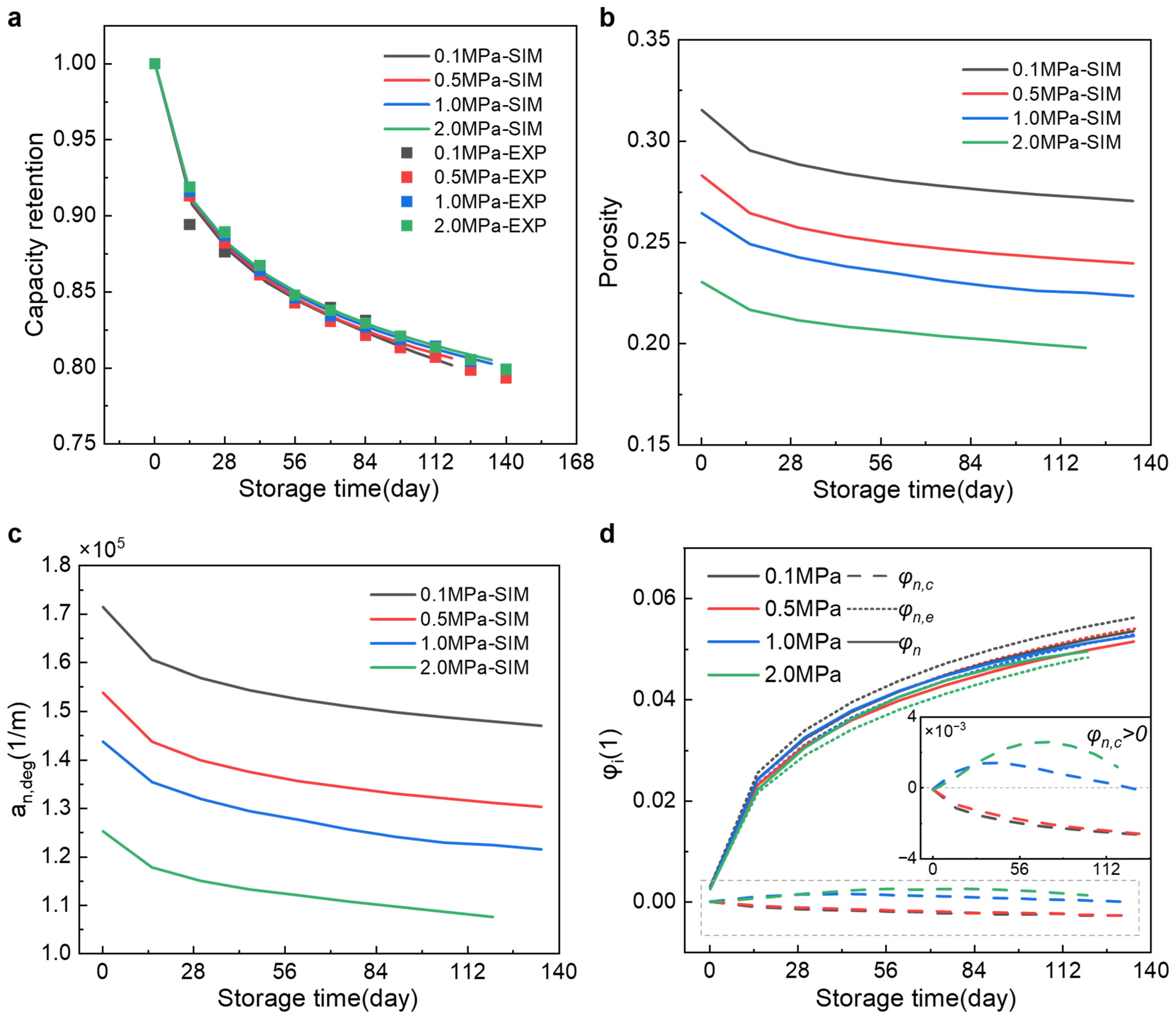
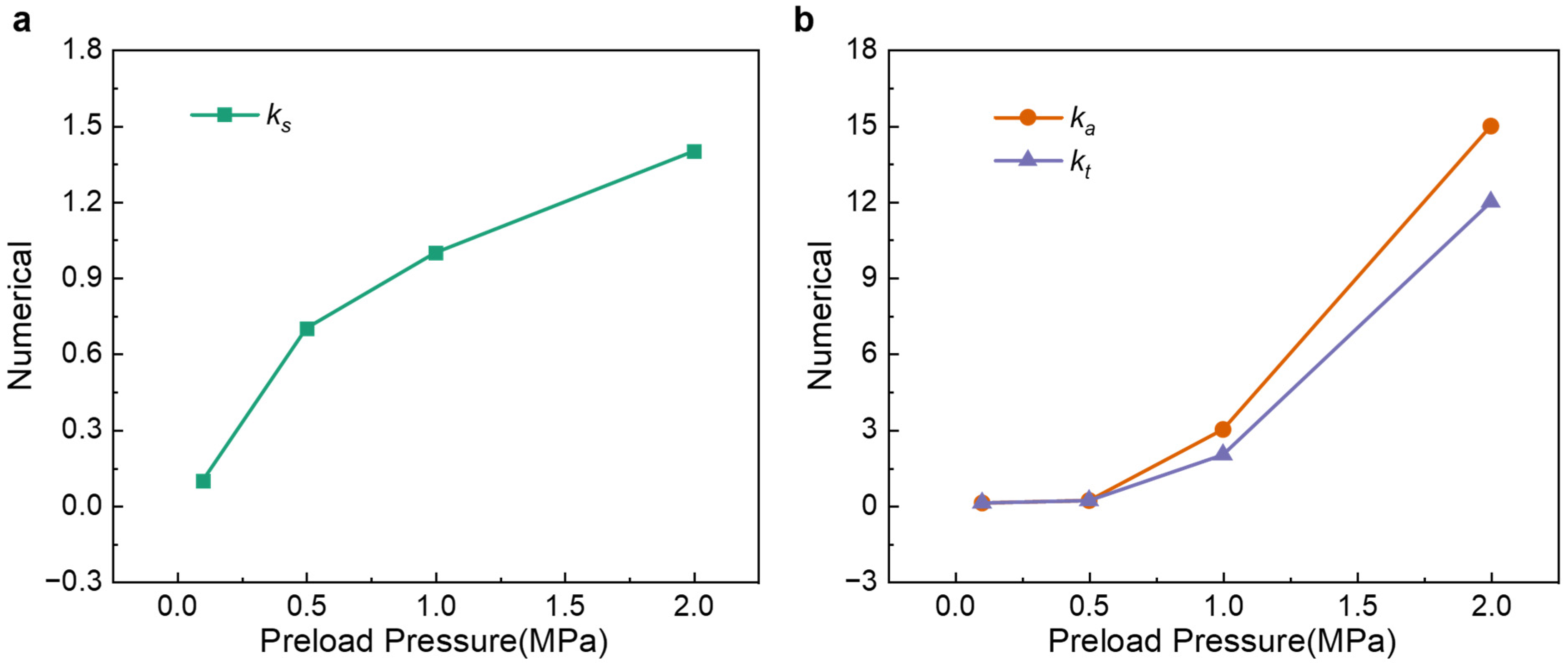
3.2. Capacity Retention and Aging Pressure Response
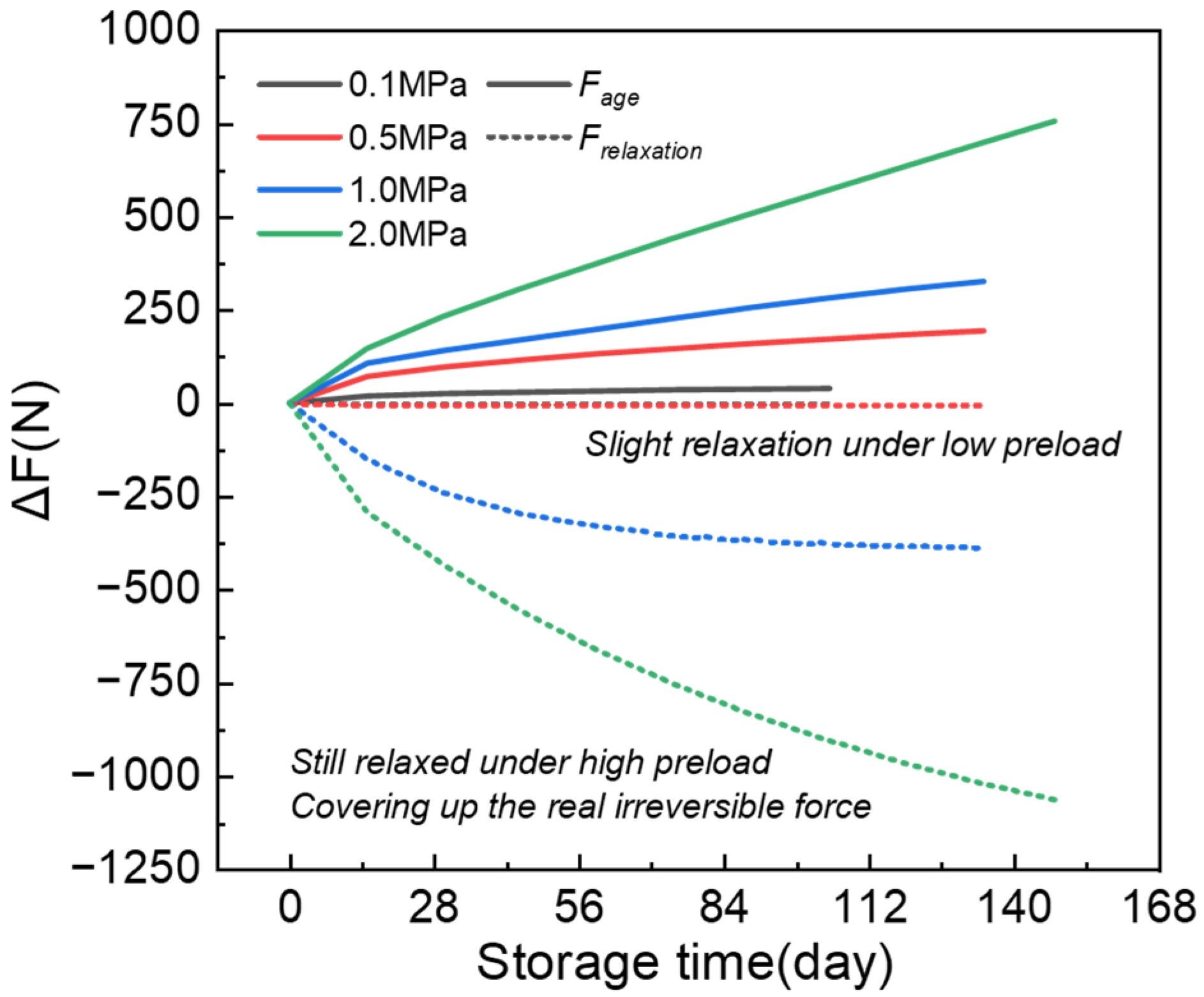
3.3. Influence of Preload on Relaxation Dynamics
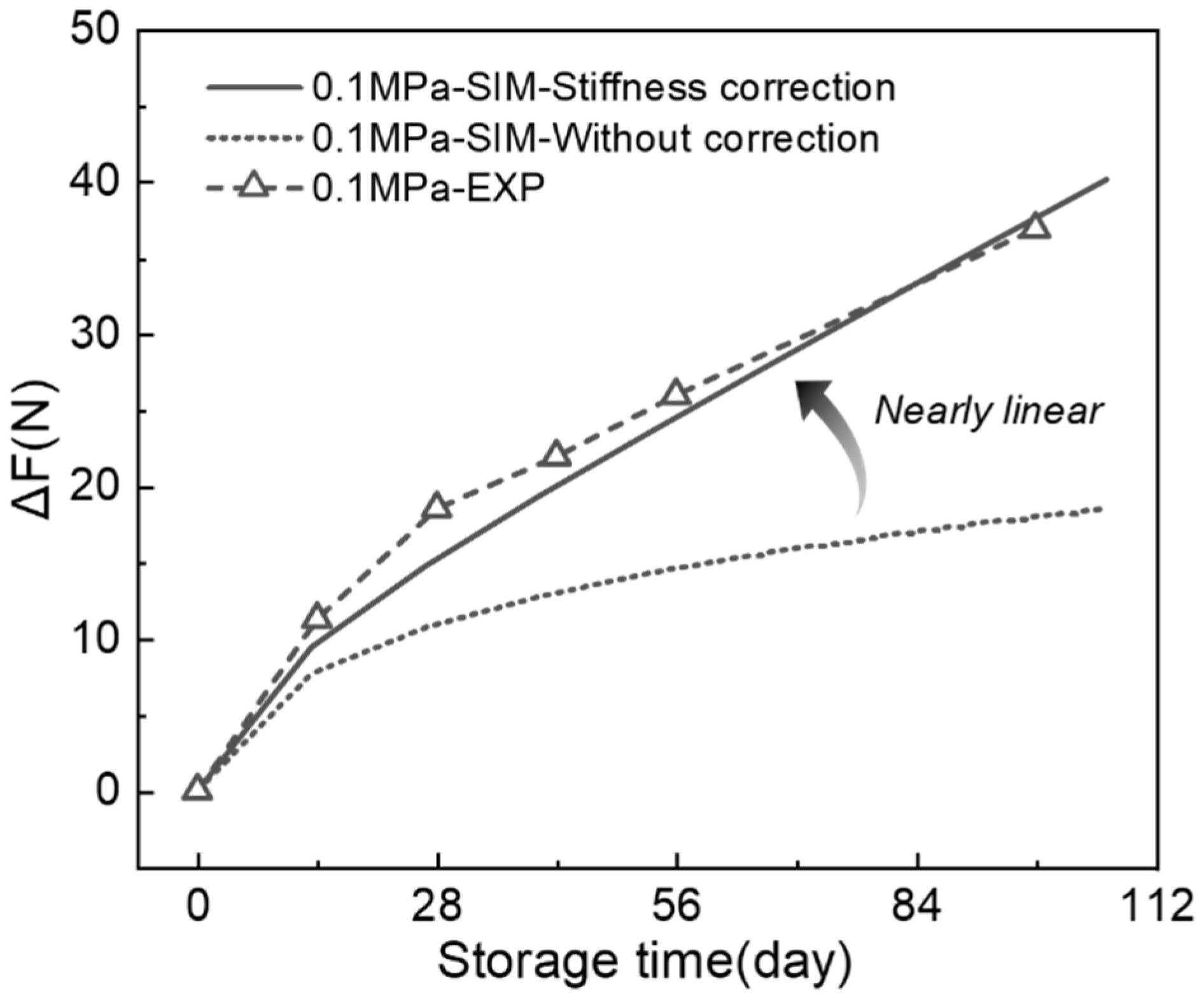
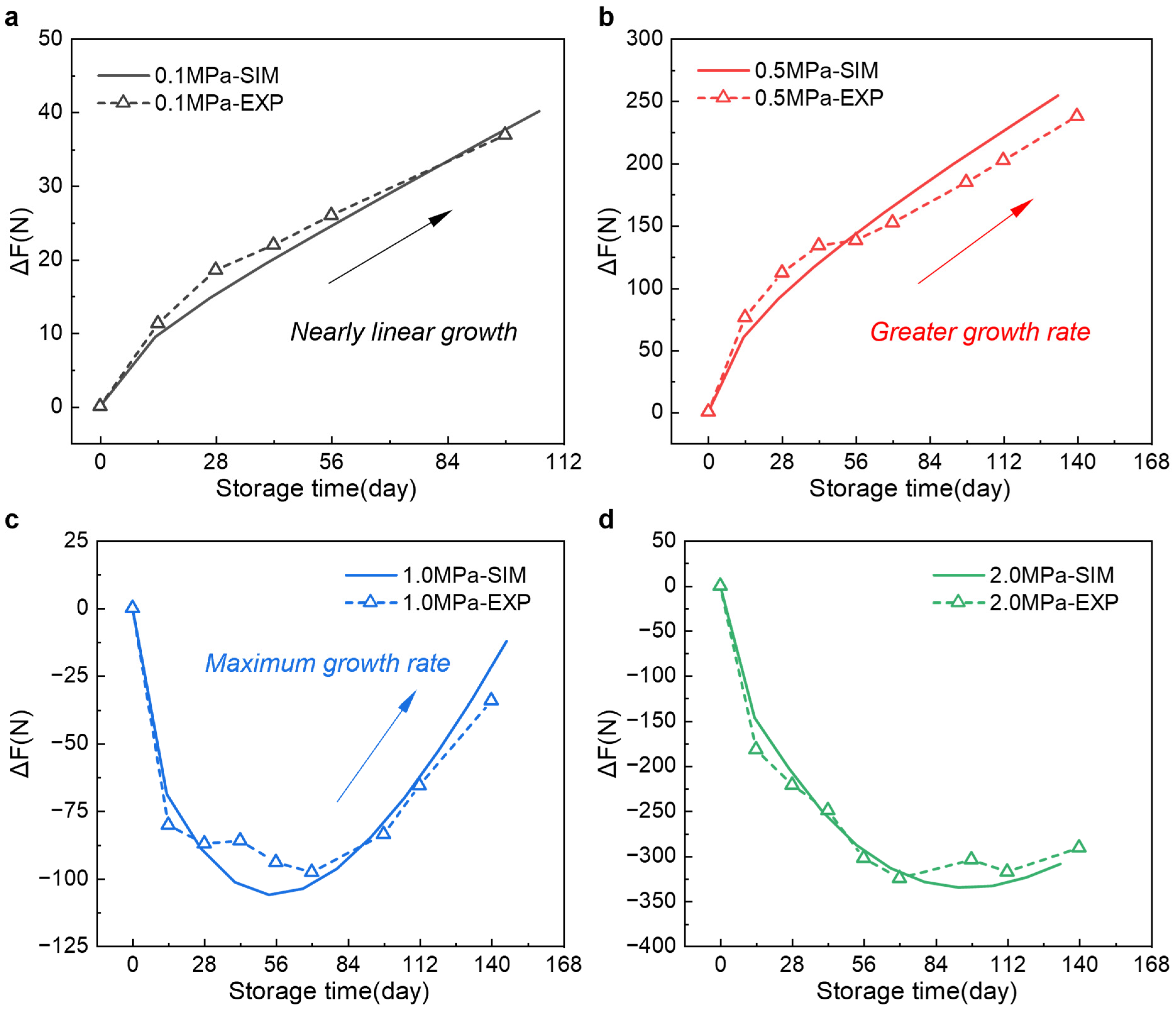
3.4. Decoupling Irreversible and Relaxation Forces
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| List of Symbols: | |
| F | Faraday constant (96,487 C·mol−1) |
| c | concentration (mol·m−3) |
| D | diffusion coefficient (m2·s−1) |
| t+ | transference number |
| i0 | exchange current density (A·m−2) |
| j | volumetric current density (A·m−3) |
| r | particle radius (m) |
| k | kinetic rate constant (m·s−1) |
| U | open-circuit potential (V) |
| M | molecular weight (kg·mol−1) |
| T | temperature (K) |
| R | film resistance (Ω) |
| L | length (m) |
| N | number of layers |
| K | stress–strain curve |
| V | electrode volume (m3) |
| Greek: | |
| ϕ | potential (V) |
| η | overpotential (V) |
| α | charge transfer coefficient |
| ε | volume fraction |
| δ | thickness (m) |
| σ | electronic conductivity (S·m−1) |
| ρ | density (kg·m−3) |
| θ | lithium content stoichiometric coefficient |
| Subscripts: | |
| n | negative |
| p | positive |
| spt | separator |
| e | electrolyte phase |
| s | solid phase |
| int | intercalation |
| tot | total |
| EC | ethylene carbonate |
| SEI | solid-electrolyte interphase |
| rev | reversible |
| irrev | irreversible |
| avg | average |
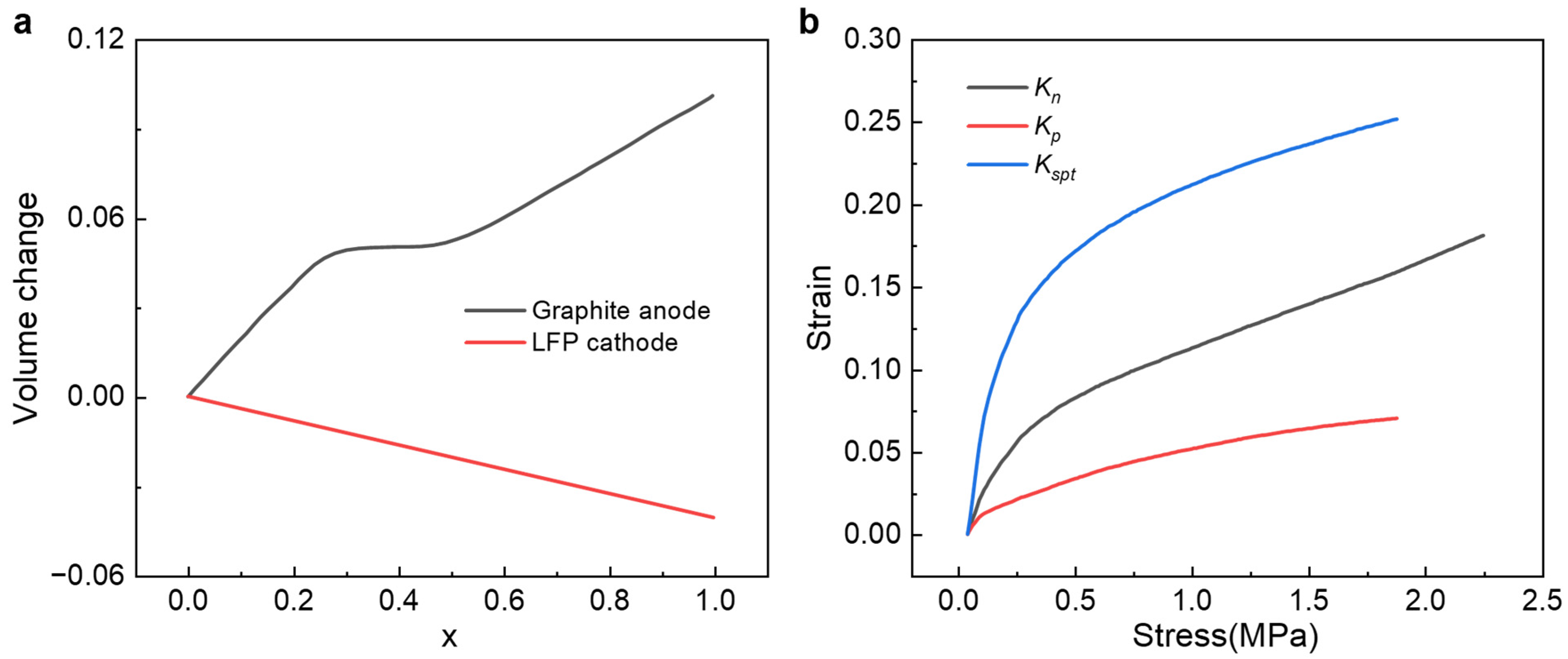
Appendix A
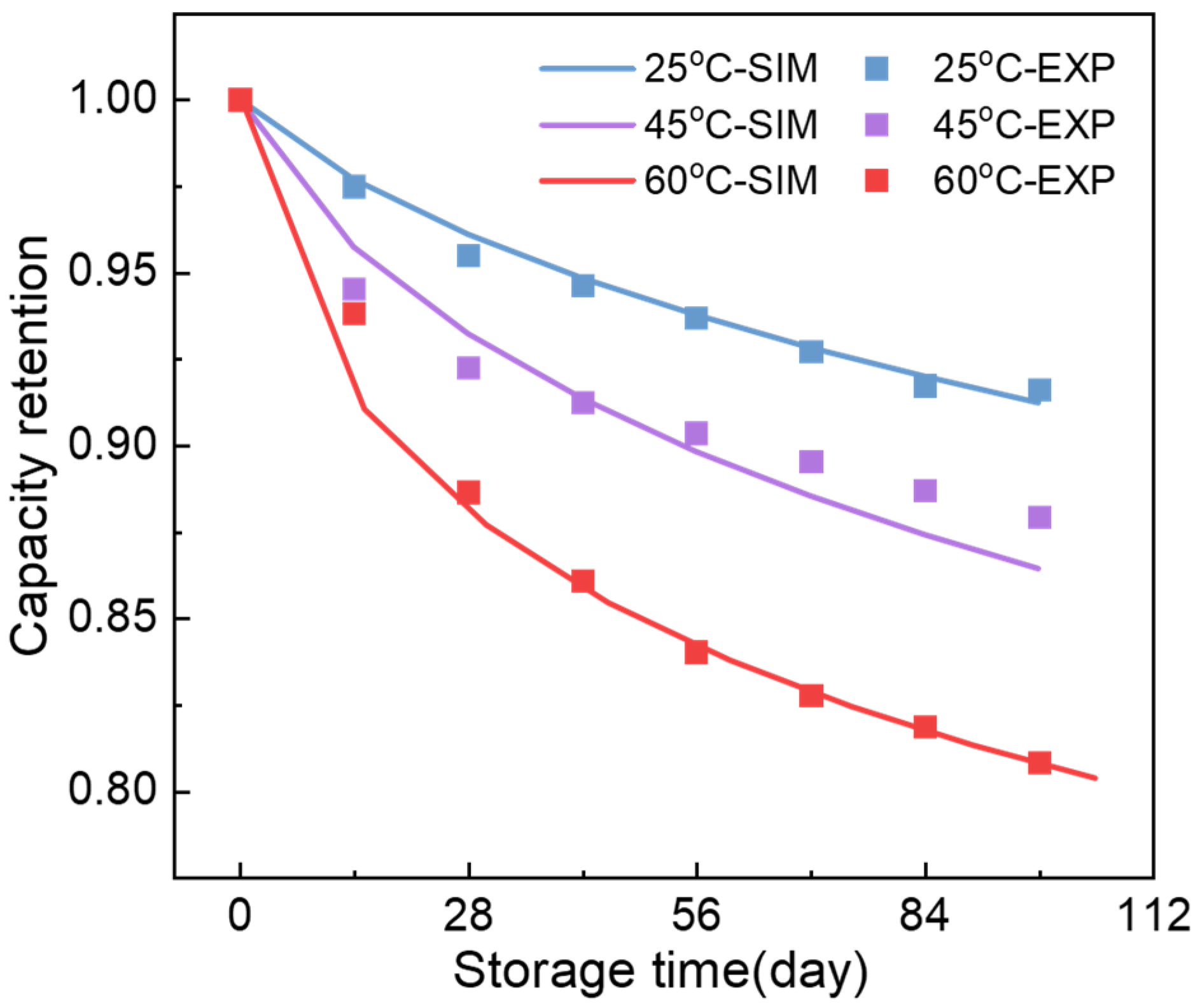
Appendix B
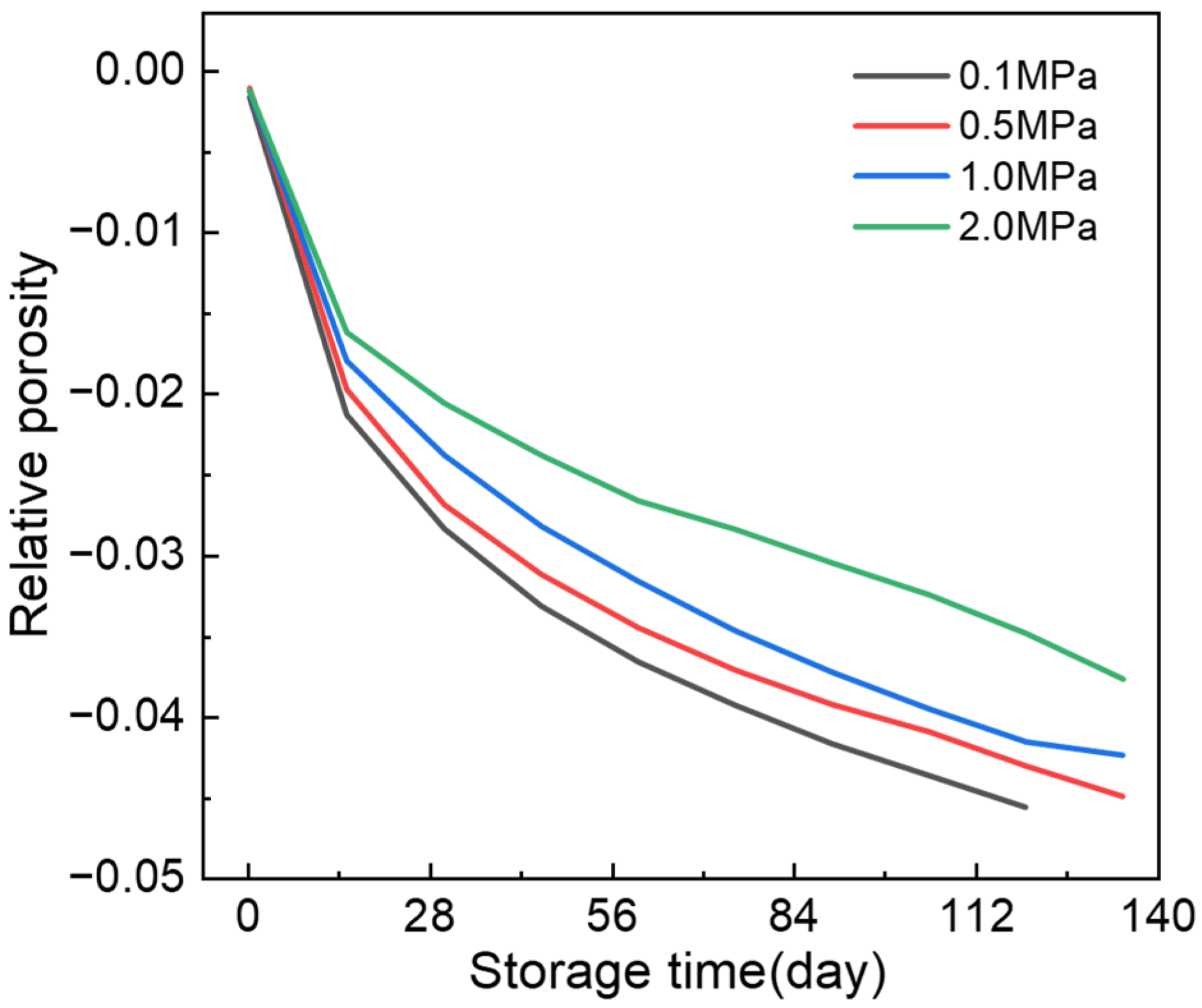
Appendix C
References
- Choi, J.W.; Aurbach, D. Promise and reality of post-lithium-ion batteries with high energy densities. Nat. Rev. Mater. 2016, 1, 16013. [Google Scholar] [CrossRef]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A review on the key issues of the lithium ion battery degradation among the whole life cycle. ETransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Duan, J.; Tang, X.; Dai, H.; Yang, Y.; Wu, W.; Wei, X.; Huang, Y. Building safe lithium-ion batteries for electric vehicles: A review. Electrochem. Energy Rev. 2020, 3, 1–42. [Google Scholar] [CrossRef]
- Thackeray, M.M.; Wolverton, C.; Isaacs, E.D. Electrical energy storage for transportation—Approaching the limits of, and going beyond, lithium-ion batteries. Energy Environ. Sci. 2012, 5, 7854–7863. [Google Scholar] [CrossRef]
- Keil, P.; Schuster, S.F.; Wilhelm, J.; Travi, J.; Hauser, A.; Karl, R.C.; Jossen, A. Calendar aging of lithium-ion batteries. J. Electrochem. Soc. 2016, 163, A1872. [Google Scholar] [CrossRef]
- Wu, H.; Jia, H.; Wang, C.; Zhang, J.G.; Xu, W. Recent progress in understanding solid electrolyte interphase on lithium metal anodes. Adv. Energy Mater. 2021, 11, 2003092. [Google Scholar] [CrossRef]
- Pinson, M.B.; Bazant, M.Z. Theory of SEI formation in rechargeable batteries: Capacity fade, accelerated aging and lifetime prediction. J. Electrochem. Soc. 2012, 160, A243. [Google Scholar] [CrossRef]
- Wang, A.; Kadam, S.; Li, H.; Shi, S.; Qi, Y. Review on modeling of the anode solid electrolyte interphase (SEI) for lithium-ion batteries. NPJ Comput. Mater. 2018, 4, 15. [Google Scholar] [CrossRef]
- Safari, M.; Delacourt, C. Modeling of a commercial graphite/LiFePO4 cell. J. Electrochem. Soc. 2011, 158, A562. [Google Scholar] [CrossRef]
- Yang, X.-G.; Leng, Y.; Zhang, G.; Ge, S.; Wang, C.-Y. Modeling of lithium plating induced aging of lithium-ion batteries: Transition from linear to nonlinear aging. J. Power Sources 2017, 360, 28–40. [Google Scholar] [CrossRef]
- Reddy, S.K.M.; Shang, W.; White, R.E. Mathematical model for SEI growth under open-circuit conditions. J. Electrochem. Soc. 2022, 169, 090505. [Google Scholar] [CrossRef]
- Deshpande, R.; Verbrugge, M.; Cheng, Y.-T.; Wang, J.; Liu, P. Battery cycle life prediction with coupled chemical degradation and fatigue mechanics. J. Electrochem. Soc. 2012, 159, A1730. [Google Scholar] [CrossRef]
- Weng, A.; Olide, E.; Kovalchuk, I.; Siegel, J.B.; Stefanopoulou, A. Modeling battery formation: Boosted sei growth, multi-species reactions, and irreversible expansion. J. Electrochem. Soc. 2023, 170, 090523. [Google Scholar] [CrossRef]
- Chung, H.; Kim, J.; Bae, Y.S.; Moon, J. Predictive modeling of lithium-ion battery degradation: Incorporating SEI layer growth and mechanical stress factors. J. Mech. Sci. Technol. 2024, 38, 6157–6167. [Google Scholar] [CrossRef]
- Li, J.L.; Wang, Y.N.; Sun, S.Y.; Zheng, Z.; Gao, Y.; Shi, P.; Zhao, Y.J.; Li, X.; Li, Q.; Zhang, X.Q. Understanding and regulating the mechanical stability of solid electrolyte interphase in batteries. Adv. Energy Mater. 2025, 15, 2403845. [Google Scholar] [CrossRef]
- Schommer, A.; Corzo, M.O.; Henshall, P.; Morrey, D.; Collier, G. Stack pressure on lithium-ion pouch cells: A comparative study of constant pressure and fixed displacement devices. J. Power Sources 2025, 629, 236019. [Google Scholar] [CrossRef]
- Müller, V.; Scurtu, R.-G.; Memm, M.; Danzer, M.A.; Wohlfahrt-Mehrens, M. Study of the influence of mechanical pressure on the performance and aging of Lithium-ion battery cells. J. Power Sources 2019, 440, 227148. [Google Scholar] [CrossRef]
- Deich, T.; Storch, M.; Steiner, K.; Bund, A. Effects of module stiffness and initial compression on lithium-ion cell aging. J. Power Sources 2021, 506, 230163. [Google Scholar] [CrossRef]
- Li, Q.; Liu, H.; Ye, Y.; Li, K.J.; Wu, F.; Li, L.; Chen, R. The critical importance of stack pressure in batteries. Nat. Energy 2025, 10, 1064–1073. [Google Scholar] [CrossRef]
- Gor, G.Y.; Cannarella, J.; Prévost, J.H.; Arnold, C.B. A model for the behavior of battery separators in compression at different strain/charge rates. J. Electrochem. Soc. 2014, 161, F3065. [Google Scholar] [CrossRef]
- Laresgoiti, I.; Käbitz, S.; Ecker, M.; Sauer, D.U. Modeling mechanical degradation in lithium ion batteries during cycling: Solid electrolyte interphase fracture. J. Power Sources 2015, 300, 112–122. [Google Scholar] [CrossRef]
- Rashid, M.; Gupta, A. Mathematical model for combined effect of SEI formation and gas evolution in Li-ion batteries. ECS Electrochem. Lett. 2014, 3, A95. [Google Scholar] [CrossRef]
- Bernhard, R.; Metzger, M.; Gasteiger, H.A. Gas evolution at graphite anodes depending on electrolyte water content and SEI quality studied by on-line electrochemical mass spectrometry. J. Electrochem. Soc. 2015, 162, A1984. [Google Scholar] [CrossRef]
- Deshpande, R.D.; Bernardi, D.M. Modeling solid-electrolyte interphase (SEI) fracture: Coupled mechanical/chemical degradation of the lithium ion battery. J. Electrochem. Soc. 2017, 164, A461. [Google Scholar] [CrossRef]
- Lundkvist, A.; Larsson, P.-L.; Iyer, A.H.; Olsson, E. Discrete element modelling of the elastic-plastic and viscoelastic properties of a lithium-ion battery electrode layer. Powder Technol. 2024, 443, 119873. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. Stress evolution and capacity fade in constrained lithium-ion pouch cells. J. Power Sources 2014, 245, 745–751. [Google Scholar] [CrossRef]
- De Sutter, L.; Berckmans, G.; Marinaro, M.; Wohlfahrt-Mehrens, M.; Berecibar, M.; Van Mierlo, J. Mechanical behavior of Silicon-Graphite pouch cells under external compressive load: Implications and opportunities for battery pack design. J. Power Sources 2020, 451, 227774. [Google Scholar] [CrossRef]
- von Kessel, O.; Deich, T.; Hahn, S.; Brauchle, F.; Vrankovic, D.; Soczka-Guth, T.; Birke, K.P. Mechanical impedance as a tool for electromechanical investigation and equivalent modeling of lithium-ion batteries. J. Power Sources 2021, 508, 230337. [Google Scholar] [CrossRef]
- Chen, S.; Wei, X.; Zhang, G.; Wang, X.; Feng, X.; Dai, H.; Ouyang, M. Mechanical strain signal based early warning for failure of different prismatic lithium-ion batteries. J. Power Sources 2023, 580, 233397. [Google Scholar] [CrossRef]
- Ding, S.; Wang, L.; Dai, H.; He, X. Prognosticating nonlinear degradation in lithium-ion batteries: Operando pressure as an early indicator preceding other signals of capacity fade and safety risks. Energy Storage Mater. 2025, 75, 103998. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, W.-K.; Yin, Y.; Nan, J.; Wang, W.; Jiang, J.; Yang, X.-G. A hierarchical electrochemical-thermal-mechanical coupled model capable of predicting non-uniform behaviors in large-format Li-ion cells. J. Power Sources 2025, 629, 236049. [Google Scholar] [CrossRef]
- Yang, X.-G.; Wang, C.-Y. Understanding the trilemma of fast charging, energy density and cycle life of lithium-ion batteries. J. Power Sources 2018, 402, 489–498. [Google Scholar] [CrossRef]
- Garrick, T.R.; Huang, X.; Srinivasan, V.; Weidner, J.W. Modeling volume change in dual insertion electrodes. J. Electrochem. Soc. 2017, 164, E3552. [Google Scholar] [CrossRef]
- Kim, J.-S.; Lee, D.-C.; Lee, J.-J.; Kim, C.-W. Optimization of lithium-ion battery pouch cell for maximization of energy density while preventing internal short circuit caused by separator failure under crush load. J. Electrochem. Soc. 2021, 168, 030536. [Google Scholar] [CrossRef]
- Jiang, H.; He, Y.; Li, X.; Jin, Z.; Yu, H.; Li, D. Effect of the charge rate on the mechanical response of composite graphite electrodes: In situ experiment and mathematical analysis. Phys. Chem. Chem. Phys. 2024, 26, 1245–1254. [Google Scholar] [CrossRef]
- Sethuraman, V.A.; Van Winkle, N.; Abraham, D.P.; Bower, A.F.; Guduru, P.R. Real-time stress measurements in lithium-ion battery negative-electrodes. J. Power Sources 2012, 206, 334–342. [Google Scholar] [CrossRef]

| Cell Design Information | ||||
|---|---|---|---|---|
| Parameter | Unit | Cathode | Separator | Anode |
| Thickness | um | 82.5 | 13 | 64.5 |
| Size | mm | 74 × 57 | / | 77 × 60 |
| Mass loading | mg/cm2 | 19.9 | / | 9.65 |
| Electrolyte concentration | mol/L | / | 1.0 | / |
| Model parameters | ||||
| Particle radius | um | 0.65 | / | 10.737 |
| Active material fraction | / | 0.66911 | / | 0.64044 |
| Porosity | / | 0.2976 | 0.32915 | |
| Bruggeman’s coefficient | / | 2.1112 | 2.3171 | |
| Maximum concentration | mol/m3 | 22,186 | / | 31,249 |
| Stoichiometric coefficients (0% SOC) | / | 0.85873 | / | 0.1288 |
| Stoichiometric coefficients (100% SOC) | / | 0.011369 | / | 0.7752 |
| Solid conductivity | S/m | 6.75 | / | 100 |
| Mechanical parameters | ||||
| Modulus | 1/GPa | 70 (Al) | / | 110 (Cu) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Li, X.; Yang, Z.; Li, H.; Liu, S.; Shi, J.; Fan, X.; Cong, Z.; Feng, X.; Yang, X.-G. Modeling the Coupled Stress Relaxation and SEI Evolution in Preload-Constrained Lithium-Ion Cells. Appl. Sci. 2025, 15, 12528. https://doi.org/10.3390/app152312528
Li J, Li X, Yang Z, Li H, Liu S, Shi J, Fan X, Cong Z, Feng X, Yang X-G. Modeling the Coupled Stress Relaxation and SEI Evolution in Preload-Constrained Lithium-Ion Cells. Applied Sciences. 2025; 15(23):12528. https://doi.org/10.3390/app152312528
Chicago/Turabian StyleLi, Jinhan, Xue Li, Zhihao Yang, Hao Li, Shuaibang Liu, Jintao Shi, Xingcun Fan, Zifeng Cong, Xiaolong Feng, and Xiao-Guang Yang. 2025. "Modeling the Coupled Stress Relaxation and SEI Evolution in Preload-Constrained Lithium-Ion Cells" Applied Sciences 15, no. 23: 12528. https://doi.org/10.3390/app152312528
APA StyleLi, J., Li, X., Yang, Z., Li, H., Liu, S., Shi, J., Fan, X., Cong, Z., Feng, X., & Yang, X.-G. (2025). Modeling the Coupled Stress Relaxation and SEI Evolution in Preload-Constrained Lithium-Ion Cells. Applied Sciences, 15(23), 12528. https://doi.org/10.3390/app152312528






