Visual Servo-Based Real-Time Eye Tracking by Delta Robot
Abstract
1. Introduction
2. Robot Architecture
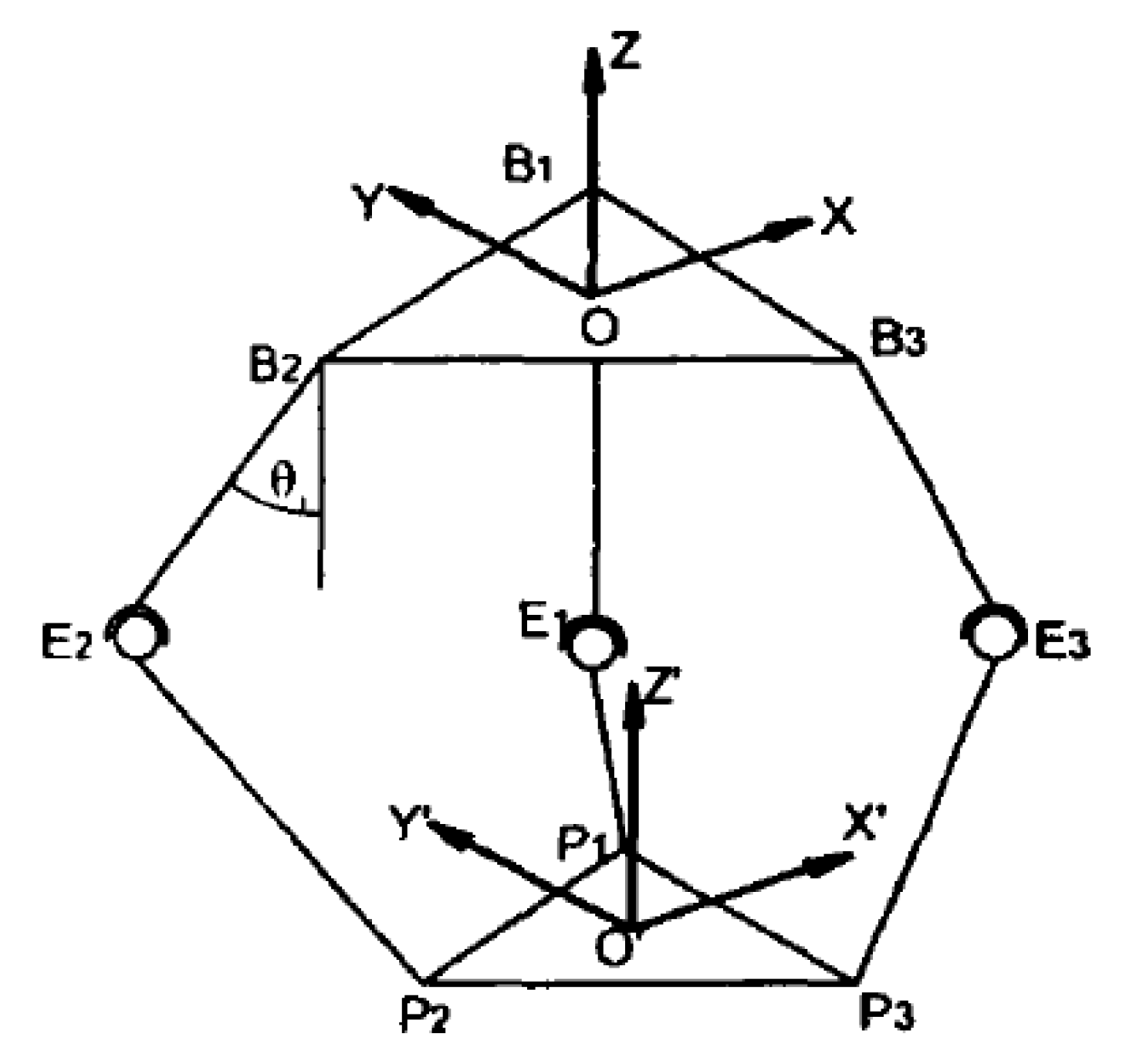
2.1. Design of the Delta Parallel Structure
2.2. Kinematics Analysis
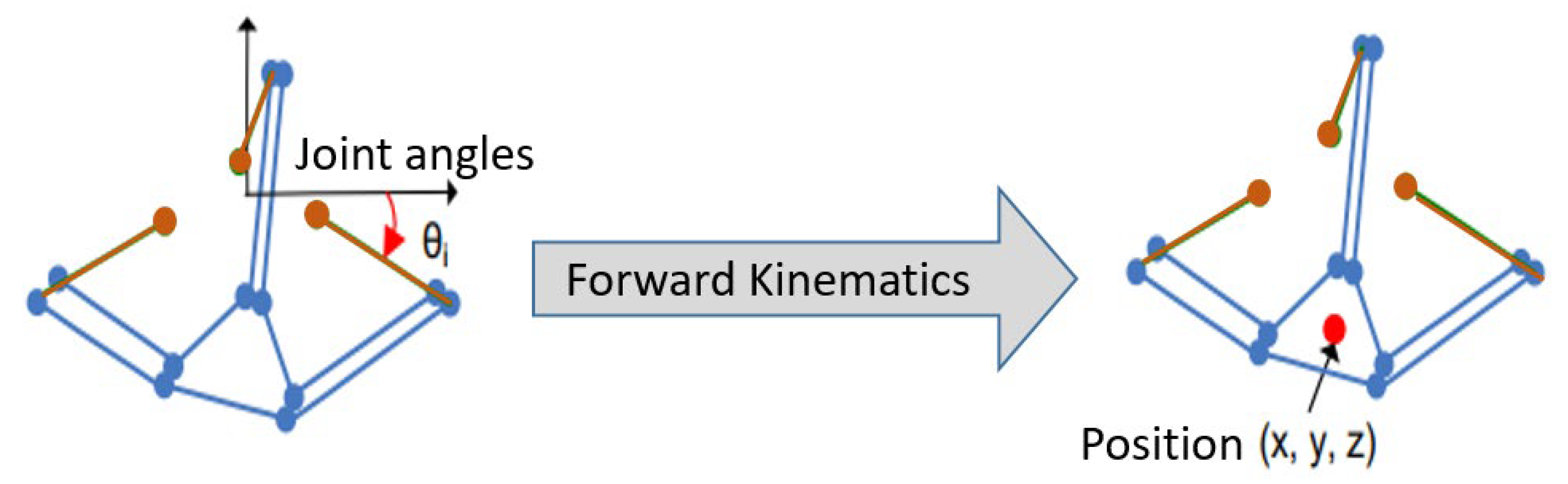
2.2.1. Forward Kinematics
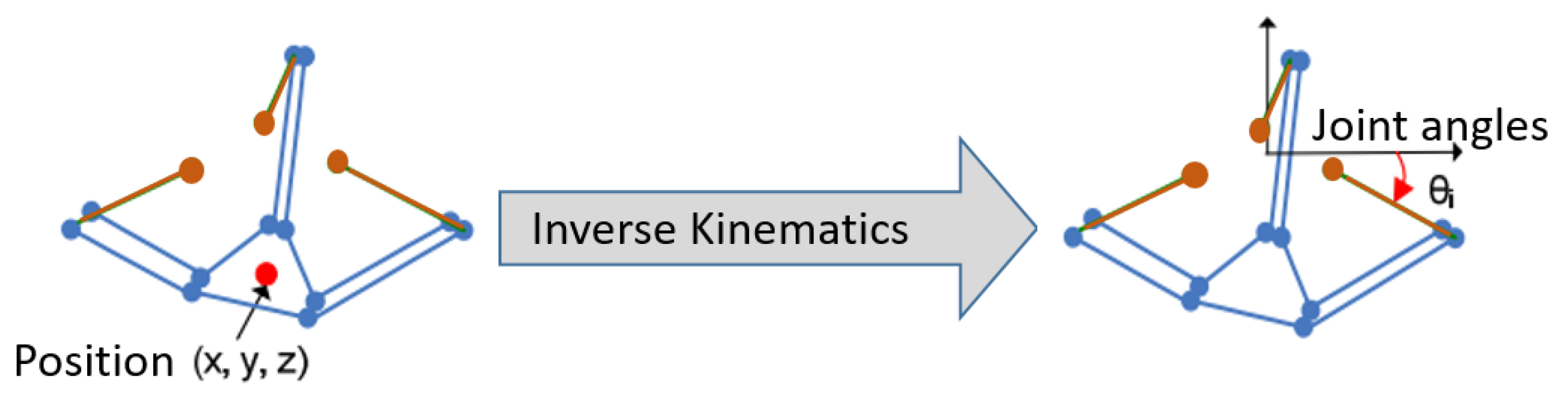
2.2.2. Inverse Kinematics
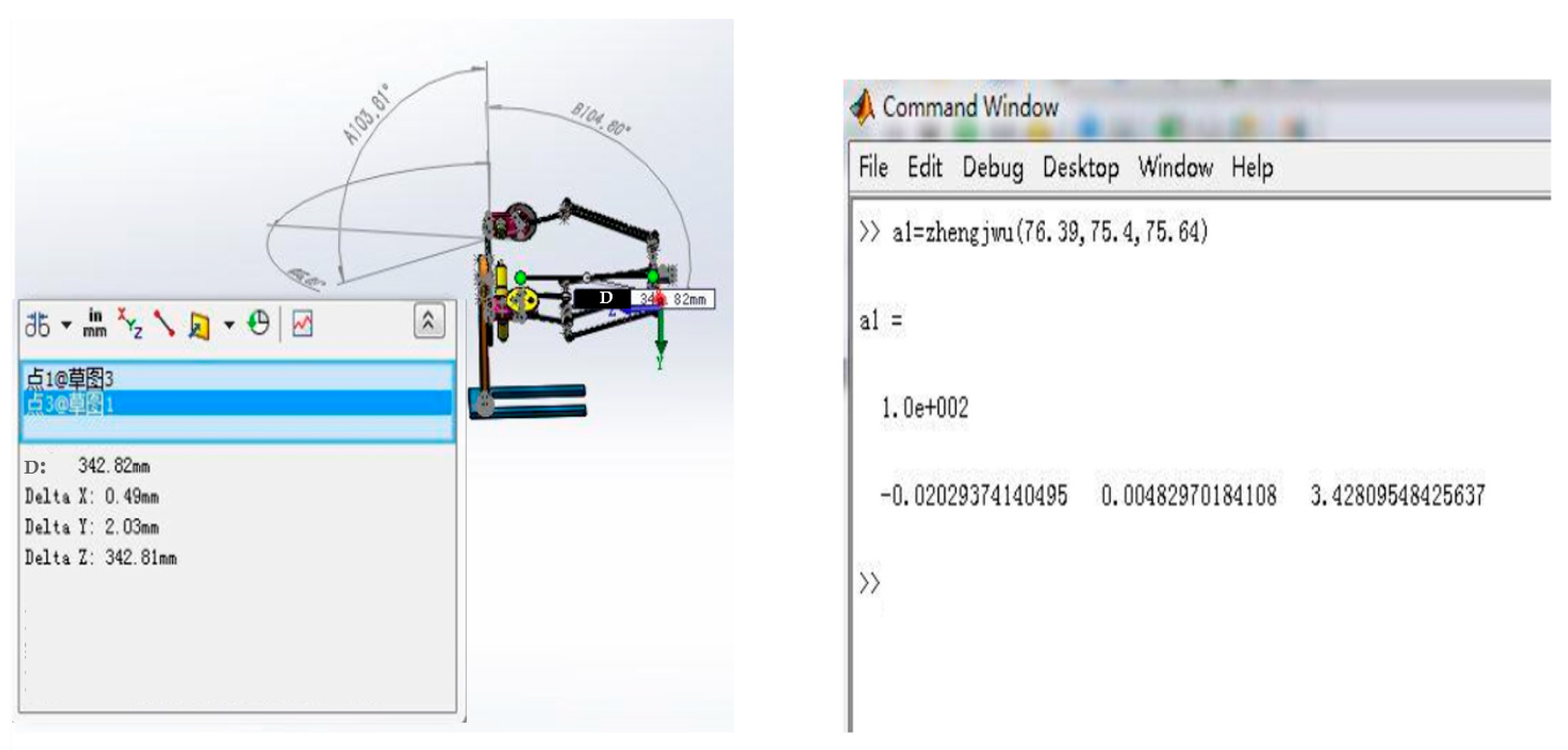
2.3. Verification of Kinematics Solution
3. System Implementation
4. Results and Discussion
4.1. Position Tracking of Delta Robot
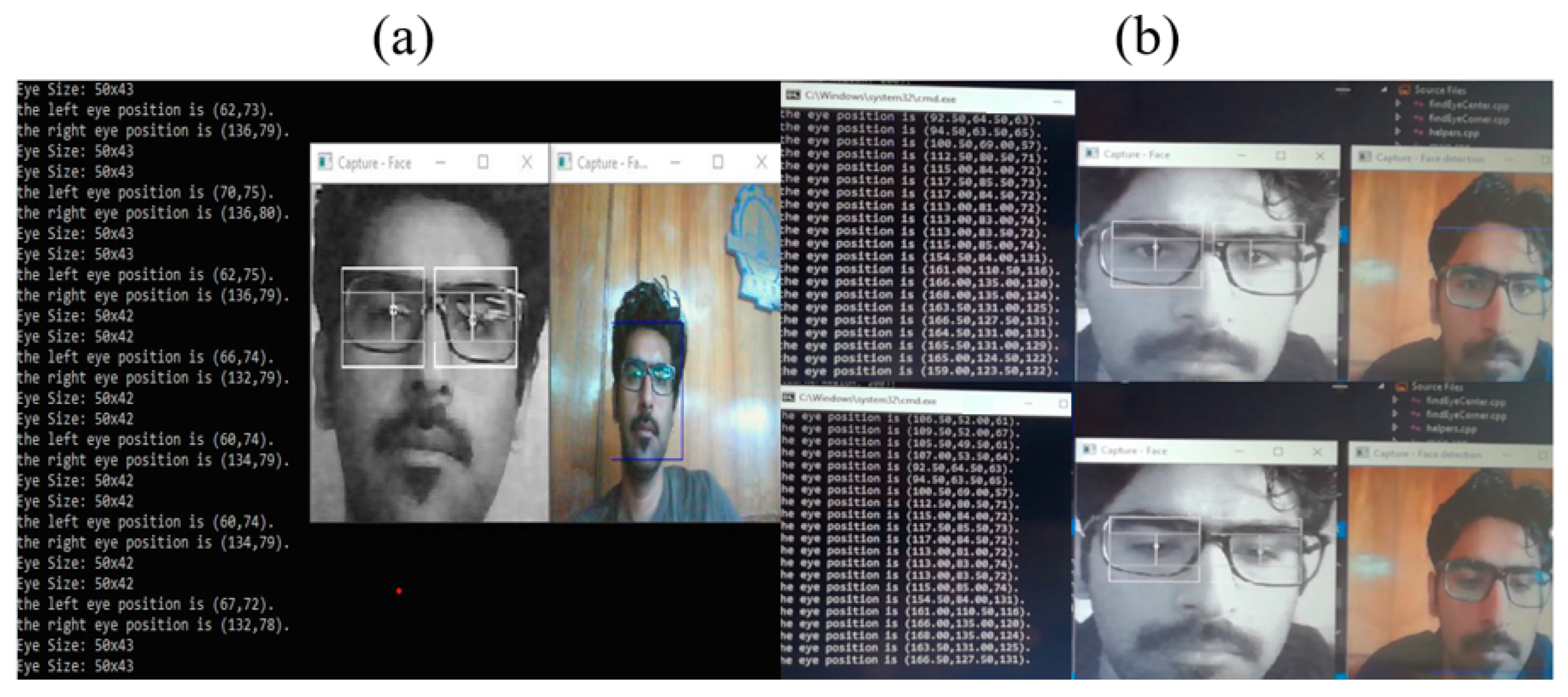
4.2. Eye Tracking
4.3. Experimental Validation
4.4. Dual Operating Characteristics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, H. Research on Control System of Delta Robot Based on Visual Tracking Technology. J. Phys. Conf. Ser. 2021, 1883, 012110. [Google Scholar] [CrossRef]
- Li, M.; Milojevic, A.; Handroos, H. Robotics in Manufacturing—The Past and the Present. In Technical, Economic and Societal Effects of Manufacturing 4.0; Palgrave Macmillan Cham: London, UK, 2020; pp. 85–95. ISBN 978-3-030-46102-7. [Google Scholar]
- Brinker, J.; Funk, N.; Ingenlath, P.; Takeda, Y.; Corves, B. Comparative Study of Serial-Parallel Delta Robots with Full Orientation Capabilities. IEEE Robot. Autom. Lett. 2017, 2, 920–926. [Google Scholar] [CrossRef]
- McClintock, H.; Temel, F.Z.; Doshi, N.; Koh, J.-S.; Wood, R.J. The MilliDelta: A High-Bandwidth, High-Precision, Millimeter-Scale Delta Robot. Sci. Robot. 2018, 3, eaar3018. [Google Scholar] [CrossRef] [PubMed]
- Bulej, V.; Stanček, J.; Kuric, I. Vision Guided Parallel Robot and Its Application for Automated Assembly Task. Adv. Sci. Technol. Res. J. 2018, 12, 150–157. [Google Scholar] [CrossRef] [PubMed]
- Correa, J.E.; Toombs, J.; Toombs, N.; Ferreira, P.M. Laminated Micro-Machine: Design and Fabrication of a Flexure-Based Delta Robot. J. Manuf. Process. 2016, 24, 370–375. [Google Scholar] [CrossRef]
- Rehman, S.U.; Raza, M.; Khan, A. Delta 3D Printer: Metal Printing. J. Electr. Eng. Electron. Control. Comput. Sci. 2019, 5, 19–24. [Google Scholar]
- Mitsantisuk, C.; Stapornchaisit, S.; Niramitvasu, N.; Ohishi, K. Force Sensorless Control with 3D Workspace Analysis for Haptic Devices Based on Delta Robot. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 1747–1752. [Google Scholar]
- Singh, B.; Sellappan, N.; Kumaradhas, P. Evolution of Industrial Robots and Their Applications. Int. J. Emerg. Technol. Adv. Eng. 2008, 3, 763–768. [Google Scholar]
- Hoai, P.L.; Cong, V.D.; Hiep, T.T. Design a Low-Cost Delta Robot Arm for Pick and Place Applications Based on Computer Vision. FME Trans. 2023, 51, 99–108. [Google Scholar] [CrossRef]
- Kratchman, L.B.; Blachon, G.S.; Withrow, T.J.; Balachandran, R.; Labadie, R.F.; Webster, R.J. Design of a Bone-Attached Parallel Robot for Percutaneous Cochlear Implantation. IEEE Trans. Biomed. Eng. 2011, 58, 2904–2910. [Google Scholar] [CrossRef] [PubMed]
- Dan, V.; Stan, S.-D.; Manic, M.; Balan, R. Mechatronic Design, Kinematics Analysis of a 3 DOF Medical Parallel Robot. In Proceedings of the 2010 3rd International Symposium on Resilient Control Systems, Idaho Falls, ID, USA, 10–12 August 2010; pp. 101–106. [Google Scholar]
- Bahaghighat, M.; Akbari, L.; Xin, Q. A Machine Learning-Based Approach for Counting Blister Cards Within Drug Packages. IEEE Access 2019, 7, 83785–83796. [Google Scholar] [CrossRef]
- Moradi Dalvand, M.; Shirinzadeh, B. Motion Control Analysis of a Parallel Robot Assisted Minimally Invasive Surgery/Microsurgery System (PRAMiSS). Robot. Comput.-Integr. Manuf. 2013, 29, 318–327. [Google Scholar] [CrossRef]
- Pisla, D.; Gherman, B.; Vaida, C.; Suciu, M.; Plitea, N. An Active Hybrid Parallel Robot for Minimally Invasive Surgery. Robot. Comput.-Integr. Manuf. 2013, 29, 203–221. [Google Scholar] [CrossRef]
- Kuo, C.-H.; Dai, J.S. Kinematics of a Fully-Decoupled Remote Center-of-Motion Parallel Manipulator for Minimally Invasive Surgery. J. Med. Devices 2012, 6, 021008. [Google Scholar] [CrossRef]
- Khalifa, A.; Fanni, M.; Mohamed, A.M.; Miyashita, T. Development of a New 3-DOF Parallel Manipulator for Minimally Invasive Surgery. Int. J. Med. Robot. Comput. Assist. Surg. 2018, 14, e1901. [Google Scholar] [CrossRef] [PubMed]
- Sahu, U.K.; Mishra, A.; Sahu, B.; Pradhan, P.P.; Patra, D.; Subudhi, B. Vision-Based Tip Position Control of a Single-Link Robot Manipulator. In Proceedings of the International Conference on Sustainable Computing in Science, Technology and Management (SUSCOM), Jaipur, India, 26–28 February 2019. [Google Scholar] [CrossRef]
- Fang, Y.; Liu, X.; Zhang, X. Adaptive Active Visual Servoing of Nonholonomic Mobile Robots. IEEE Trans. Ind. Electron. 2012, 59, 486–497. [Google Scholar] [CrossRef]
- Ficocelli, M.; Janabi-Sharifi, F. Adaptive Filtering for Pose Estimation in Visual Servoing. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the Next Millennium (Cat. No.01CH37180), Maui, HI, USA, 29 October–3 November 2001; Volume 1, pp. 19–24. [Google Scholar]
- Gridseth, M.; Ramirez, O.; Quintero, C.P.; Jagersand, M. ViTa: Visual Task Specification Interface for Manipulation with Uncalibrated Visual Servoing. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3434–3440. [Google Scholar]
- Rouhollahi, A.; Azmoun, M.; Masouleh, M.T. Experimental Study on the Visual Servoing of a 4-DOF Parallel Robot for Pick-and-Place Purpose. In Proceedings of the 2018 6th Iranian Joint Congress on Fuzzy and Intelligent Systems (CFIS), Kerman, Iran, 28 February–2 March 2018; pp. 27–30. [Google Scholar]
- Hu, C.-Y.; Chen, C.-R.; Tseng, C.-H.; Yudha, A.P.; Kuo, C.-H. Visual Servoing Spanner Picking and Placement with a SCARA Manipulator. In Proceedings of the 2016 IEEE International Conference on Industrial Technology (ICIT), Taipei, Taiwan, 14–17 March 2016; pp. 1632–1637. [Google Scholar]
- Asadi, K.; Jain, R.; Qin, Z.; Sun, M.; Noghabaei, M.; Cole, J.; Han, K.; Lobaton, E. Vision-Based Obstacle Removal System for Autonomous Ground Vehicles Using a Robotic Arm. arXiv 2019, arXiv:1901.08180. [Google Scholar] [CrossRef]
- Hafez, H.; Marey, M.; Tolbah, F.; Abdelhameed, M. Survey of Visual Servoing Control Schemes for Mobile Robot Navigation. Sci. J. Oct. 6 Univ. 2017, 3, 41–50. [Google Scholar] [CrossRef]
- Shi, H.; Chen, J.; Pan, W.; Hwang, K.-S.; Cho, Y.-Y. Collision Avoidance for Redundant Robots in Position-Based Visual Servoing. IEEE Syst. J. 2019, 13, 3479–3489. [Google Scholar] [CrossRef]
- López-Nicolás, G.; Özgür, E.; Mezouar, Y. Parking Objects by Pushing Using Uncalibrated Visual Servoing. Auton. Robot. 2019, 43, 1063–1078. [Google Scholar] [CrossRef]
- Olsson, A. Modeling and Control of a Delta-3 Robot. Master’s Thesis, Lund University, Lund, Sweden, 2009. [Google Scholar]
- Prempraneerach, P. Delta Parallel Robot Workspace and Dynamic Trajectory Tracking of Delta Parallel Robot. In Proceedings of the 2014 International Computer Science and Engineering Conference (ICSEC), Khon Kaen, Thailand, 30 July–1 August 2014; pp. 469–474. [Google Scholar]



| Translational Workspace | Rotation Range | Linear Motion Speed | Angular Motion Speed | Feedback Force | Torque |
|---|---|---|---|---|---|
| 120 × 100 mm | ±60 | 8 mm/s | 10 r/min | 20 N | 0.3 N·m |
| Serial Number (sr) | Example | SolidWorks 3D (mm) | Matlab (mm) | Error | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | Δ | ||||
| 1 | −30 | −30 | −30 | 0 | 0 | 124.14 | 0 | 0 | 124.14 | 0 |
| 2 | 7.99 | 0 | 8.44 | 2.43 | 3.31 | 151.41 | 2.44 | 3.31 | 151.41 | 0.01 |
| 3 | 59.98 | 74.16 | 23.6 | −19 | −103.8 | 277.6 | −18.97 | −103.8 | 277.63 | 0.121 |
| 4 | 19.1 | −14 | −12 | −43.57 | 2.56 | 160.74 | −43.58 | 2.57 | 160.74 | 0.014 |
| 5 | −6.2 | 23.86 | 6.6 | 33.54 | −24.6 | 183.42 | 33.54 | −24.59 | 183.42 | 0.01 |
| 6 | 67.03 | 61.91 | 18.8 | −62 | −82.25 | 270.4 | −62.09 | −82.24 | 270.42 | 0.017 |
| 7 | 3.33 | −0.63 | 41.1 | 30.92 | 64.38 | 191.82 | 30.93 | 64.39 | 191.82 | 0.014 |
| 8 | 24.84 | 46.44 | 43.2 | 44.71 | −6.89 | 261.39 | 44.71 | −6.9 | 261.39 | 0.01 |
| 9 | 76.39 | 75.4 | 75.6 | −2.3 | 0.49 | 342.81 | −2.03 | 0.48 | 342.81 | 0.01 |
| 10 | 24.17 | 44.86 | 47.3 | 49 | 5.23 | 262.1 | 49.02 | 5.24 | 262.14 | 0.014 |
| 11 | 22.61 | 63.6 | 18 | 43.4 | −90.2 | 235 | 43.38 | −90.2 | 235.03 | 0.01 |
| 12 | 37.03 | 73.61 | 25.6 | 36.1 | −102.5 | 259.5 | 36.1 | −102.5 | 259.53 | 0.01 |
| 13 | 53.82 | 26.47 | 49.8 | −37 | 45.79 | 271.8 | −36.95 | 45.8 | 271.8 | 0.014 |
| 14 | 27.53 | 61.65 | 68.3 | 87 | 16.46 | 284.6 | 87.03 | 16.45 | 284.63 | 0.017 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Memon, M.M.; Hussain, A.; Mohammed, A.; Manthar, A.; Li, S.; Lin, W. Visual Servo-Based Real-Time Eye Tracking by Delta Robot. Appl. Sci. 2025, 15, 12521. https://doi.org/10.3390/app152312521
Memon MM, Hussain A, Mohammed A, Manthar A, Li S, Lin W. Visual Servo-Based Real-Time Eye Tracking by Delta Robot. Applied Sciences. 2025; 15(23):12521. https://doi.org/10.3390/app152312521
Chicago/Turabian StyleMemon, Maria Muzamil, Aarif Hussain, Abdulrhman Mohammed, Ali Manthar, Songjing Li, and Weiyang Lin. 2025. "Visual Servo-Based Real-Time Eye Tracking by Delta Robot" Applied Sciences 15, no. 23: 12521. https://doi.org/10.3390/app152312521
APA StyleMemon, M. M., Hussain, A., Mohammed, A., Manthar, A., Li, S., & Lin, W. (2025). Visual Servo-Based Real-Time Eye Tracking by Delta Robot. Applied Sciences, 15(23), 12521. https://doi.org/10.3390/app152312521








