Research on Power Battery Recycling Decision Considering Deposit System Under Online Platform Recycling Mode
Featured Application
Abstract
1. Introduction
- (1)
- How does the ownership of recycling pricing right reshape the effect of deposit systems, and then affect the overall efficiency of the supply chain?
- (2)
- Which deposit collection mode can achieve the optimal recycling and technology investment effect with minimum social cost?
- (3)
- Given the policy and market environment, how should manufacturers and online platforms choose the combination model of “deposit + pricing power” to maximize their profits?
2. Literature Review
3. Problem Description and Assumptions
- (1)
- This paper assumes that the market demand for power batteries [34] is where represents the total potential market demand, p1 denotes the retail price, and signifies the deposit.
- (2)
- The quantity of retired power batteries recovered can be expressed as [35] . Without loss of generality, we normalize the price sensitivity coefficient in the collection function to 1. This not only facilitates selecting appropriate measurement units for recycling prices and quantities but also simplifies calculations. Therefore, without compromising the nature of our model, we assume [15]. Thus, Among these, represents the sensitivity coefficient of consumer investment in blockchain technology, indicating that blockchain technology exerts a positive influence on recycling volumes. By adopting blockchain traceability technology, enterprises enhance the credibility of product data through its tamper-proof nature, thereby gaining consumer trust and effectively stimulating market demand growth [36].
- (3)
- To ensure that all entities achieve positive returns, the following conditions must be met: ,
- (4)
- In reference to the research hypothesis on return on investment [37], we assume that the blockchain investment cost is a quadratic function of the investment level. Here, represents the difficulty coefficient of blockchain technology investment.
- (5)
- To ensure that all equilibrium solutions are greater than zero, it is necessary to satisfy .
- (6)
- For simplicity, assume that battery manufacturers recycle all waste batteries collected from the market.
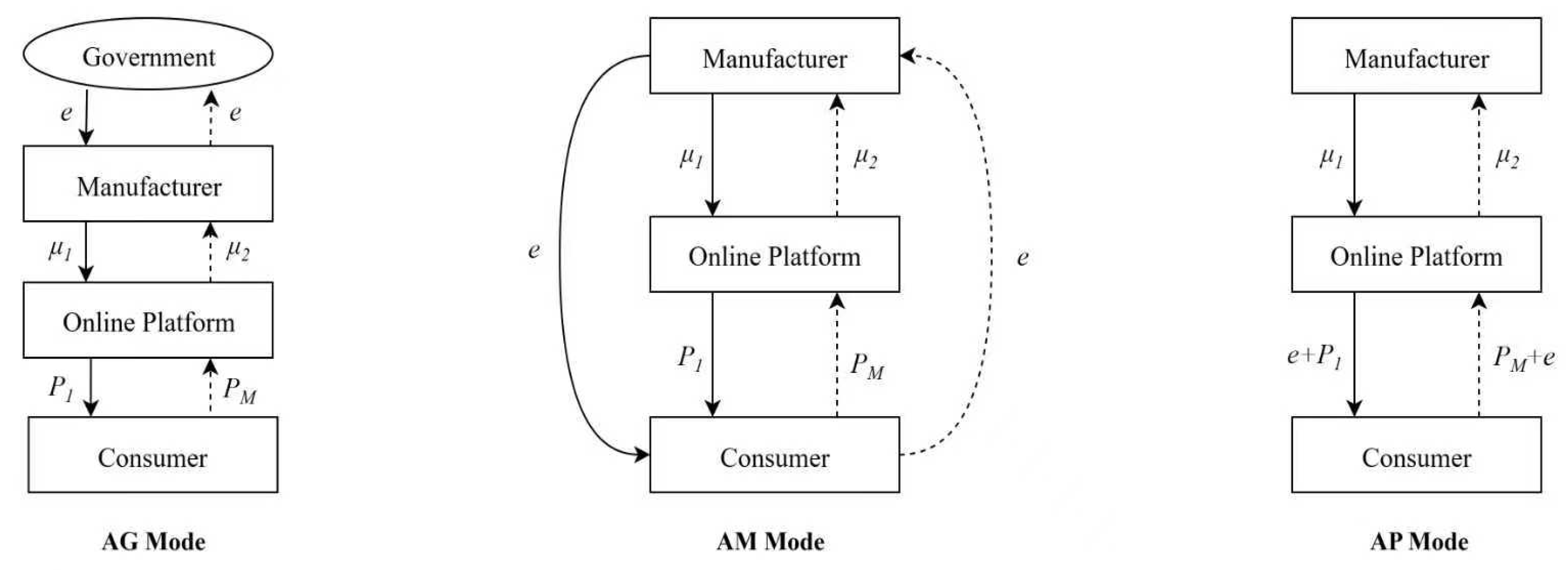
4. Decision-Making Research on Closed-Loop Supply Chains for Power Batteries in Online Platform Agency Recycling Models
4.1. Model Development and Analysis
4.1.1. Decision-Making Research Under the Government Deposit Scheme for Manufacturers (AG)
4.1.2. Decision-Making Research in Manufacturer-to-Consumer Deposit Models (AM)
4.1.3. Decision-Making Research on Online Platform Deposit Collection Models for Consumers (AP)
4.2. Comparative Analysis
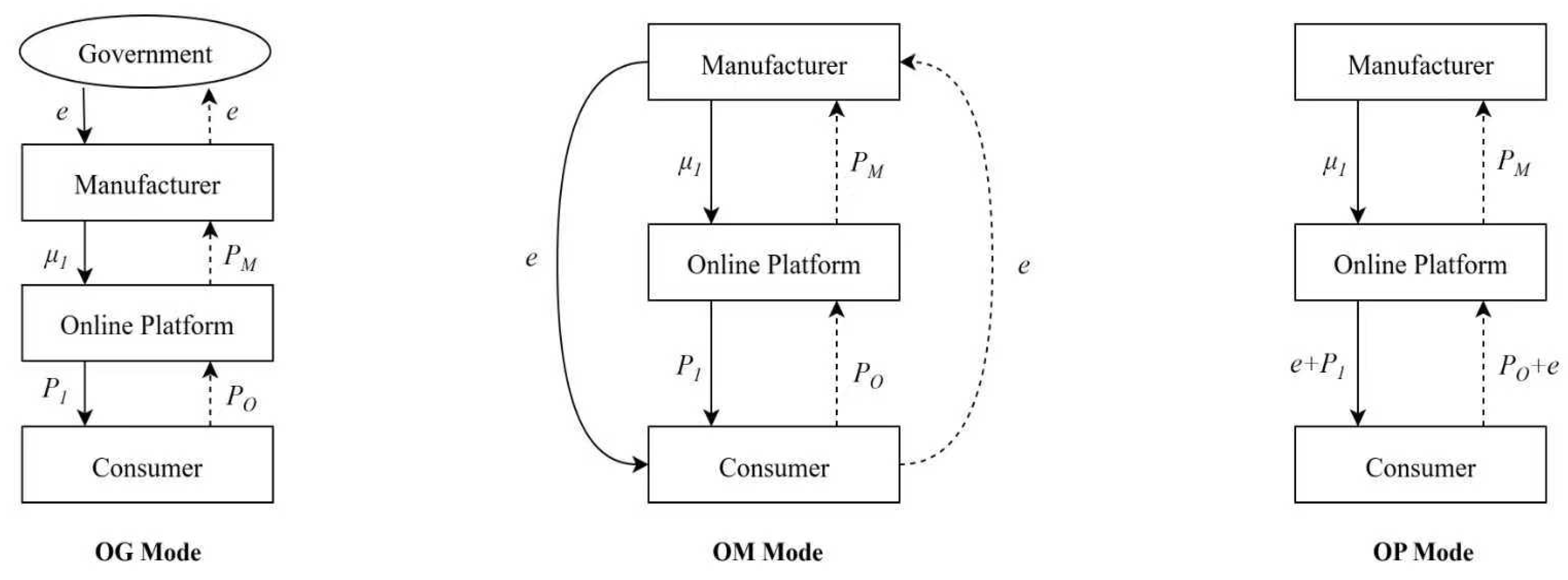
5. Decision-Making Research on Closed-Loop Supply Chains for Power Batteries in Online Platform-Commissioned Recycling Models
5.1. Model Development and Analysis
5.1.1. Decision-Making Research Under the Government Deposit Scheme for Manufacturers (OG)
- (1)
- As the deposit amount increases, the government collects higher deposits from manufacturers, directly raising their costs. Manufacturers have strong incentives to boost battery recycling rates to minimize deposit losses or secure refunds, prompting them to incentivize online platforms by increasing recycling commissions . Faced with higher commission incentives, online platforms will increase blockchain investment to boost recycling volumes. An increase in indicates greater consumer sensitivity to the impact of blockchain technology investment. Higher blockchain investment levels by online platforms can more effectively attract consumer participation in battery recycling activities, as blockchain investment enhances information transparency and trust. Online platforms have greater motivation to increase blockchain investment levels to earn more recycling commission income, so this investment monotonically increases with . When increases, it means the cost per unit of additional blockchain investment rises significantly. When considering the investment–output ratio, online platforms reduce blockchain investment levels due to excessively high costs, so this investment decreases with . As increases, manufacturers transform higher costs for dismantling and recycling non-gradable batteries, resulting in reduced net profits from recycling. Manufacturers may consequently lower the recycling commission , thereby reducing incentives for online platforms to invest in blockchain technology. Thus, decreases with increasing . When increases, online platforms gain higher profits from each successful battery recycling procedure. However, under the OG model, higher may cause platforms to rely more on commission income rather than blockchain investment to boost recycling volume. Therefore, decreases with increasing . For parameter , when < + , the profit V1 from secondary utilization (battery reuse) plus dismantling cost exceeds the profit from non-reusable batteries. This indicates that secondary utilization is relatively more profitable. As increases, the proportion of recycled batteries suitable for direct secondary utilization rises, giving manufacturers greater incentive to boost recycling rates. This, in turn, motivates online platforms to increase blockchain investments to acquire more high-quality batteries, resulting in an increasing . Conversely, when ≥ + , non-recycling becomes more cost-effective. An increase in may reduce manufacturers’ incentives for recycling, prompting online platforms to decrease investments. Thus, decreases.
- (2)
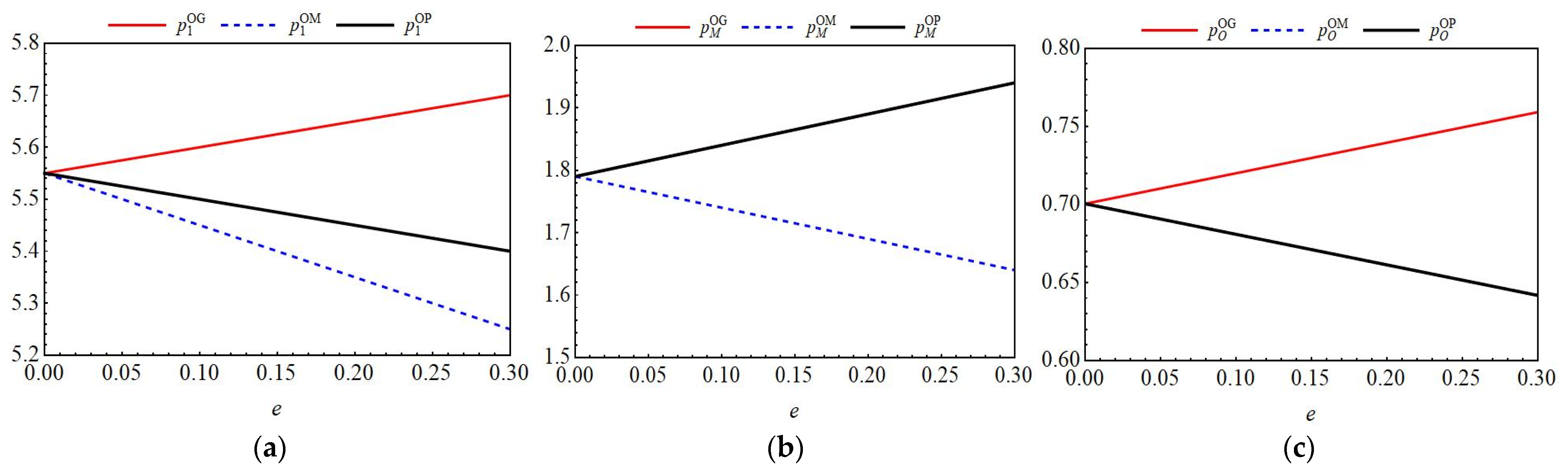
- When the deposit increases, the government collects higher deposits from manufacturers, raising their costs. To maintain profits, manufacturers pass this cost onto online platforms by raising wholesale prices. As sales agents, online platforms reflect these higher procurement costs when setting retail prices, causing them to increase with . When the unit production cost rises, manufacturers’ total production costs increase. To maintain profit levels, manufacturers raise the wholesale prices of power batteries, which forces online platforms to increase retail prices to sustain their profit margins. Thus, the retail price increases with . An increase in potential total market demand indicates robust market demand for power batteries. Online platforms possess greater pricing power in this market environment. To capture higher profits, they raise retail prices for power batteries, which thus increase with . When manufacturers increase sales commissions paid to online platforms, their sales costs rise and may be passed on through higher wholesale prices. Online platforms factor in this elevated cost base when setting retail prices, consequently raising them, and hence retail prices increase with .
- (3)
- As the deposit increases, the government collects higher deposits from manufacturers. To ensure sufficient recycling rates and avoid deposit losses or secure refunds, manufacturers raise recycling prices to directly incentivize consumer participation, resulting in an enhanced relationship with . When dismantling costs rise, manufacturers face higher disposal expenses for non-recyclable batteries, reducing their net profits from recycling. To maintain profitability in recycling activities, manufacturers lower recycling prices to control costs, causing recycling prices to decrease with . When recycling commission increases, online platforms gain higher returns from recycling, boosting their recycling incentives. Manufacturers need not set excessively high recycling prices to guarantee sufficient collection volumes under these conditions, so recycling prices decrease with . For parameter , when < + , secondary utilization yields relatively higher returns. As increases, manufacturers raise recycling prices to attract consumers and acquire more high-value batteries suitable for secondary utilization, so recycling prices increase with . Conversely, when ≥ + , non-recycling becomes more cost-effective. Increasing may prompt manufacturers to avoid excessive investment in low-return channels, thereby lowering recycling prices. Thus, recycling prices decrease with .
- (4)
- As increases, the cost of blockchain investment for online platforms rises, reducing their willingness to invest. To compensate for the potential decline in recycling volumes, platforms must raise recycling prices to directly incentivize consumer participation, causing to increase with . When the deposit e increases, manufacturers’ costs rise, potentially prompting them to incentivize platforms by raising commission . To meet higher recycling targets, online platforms raise recycling prices to attract more consumers, causing them to increase with . As increases, consumers become more sensitive to the recycling advantages offered by blockchain investments. Even with lower recycling prices set by online platforms, consumers are more willing to participate in recycling due to blockchain technology investments. In this scenario, online platforms can reduce recycling prices to save costs, so it decreases with . As dismantling costs increase, manufacturers’ net profits decrease, potentially lowering commission . Online platforms then reduce recycling prices to maintain profits, so it decreases with . For parameter , when < + , secondary utilization becomes more profitable. As increases, online platforms, incentivized by manufacturers, raise recycling prices to acquire more batteries suitable for secondary use, so recycling prices increase with . Conversely, when ≥ + , online platforms lower recycling prices to control costs, so recycling prices decrease with .
5.1.2. Decision Research (OM) in the Manufacturer-to-Consumer Deposit Model
5.1.3. Decision Research (OP) on the Manufacturer-to-Consumer Deposit Model
5.2. Comparative Analysis
6. Numerical Analysis of Closed-Loop Supply Chains for Power Batteries Under Two Recycling Models
6.1. Numerical Analysis of a Closed-Loop Supply Chain for Power Batteries Under an Online Platform Agency Recycling Model
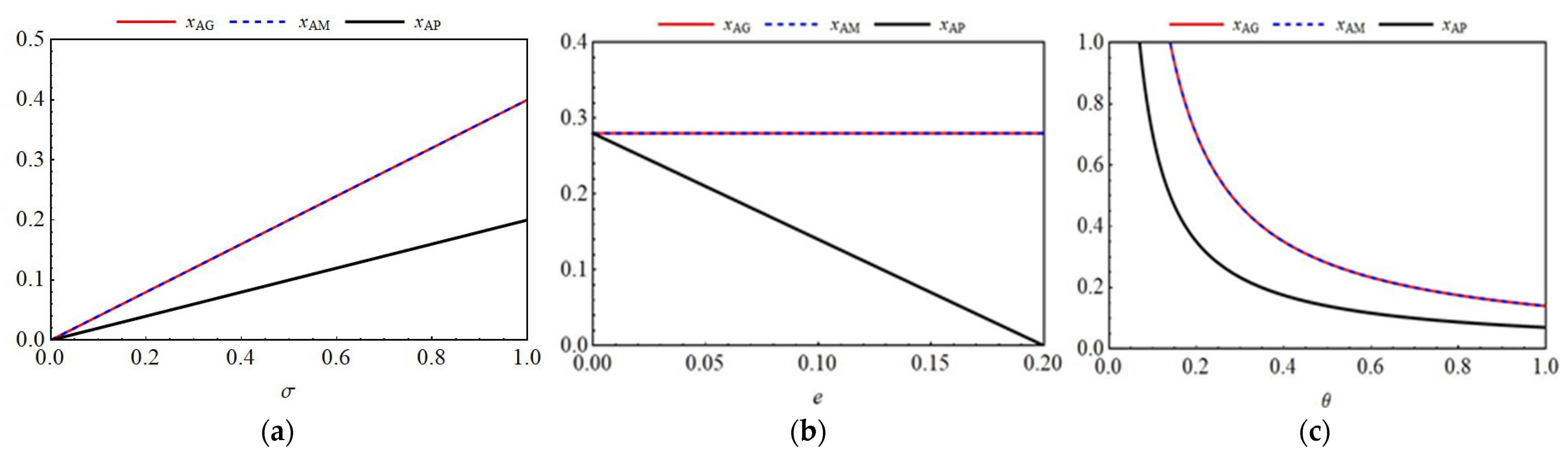
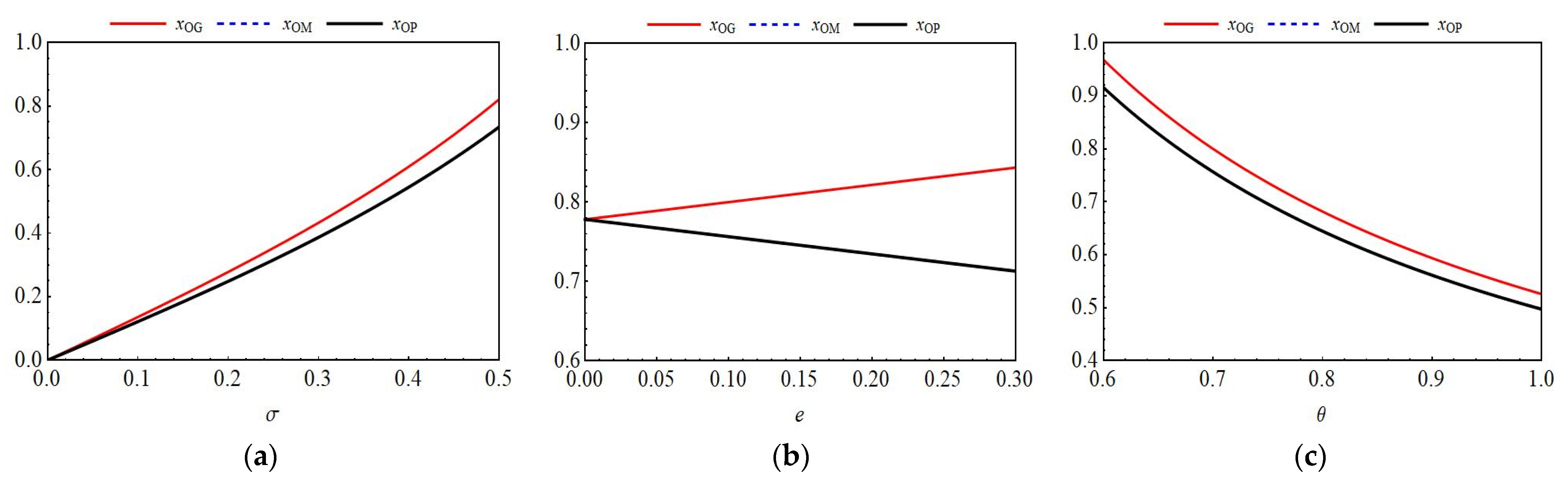
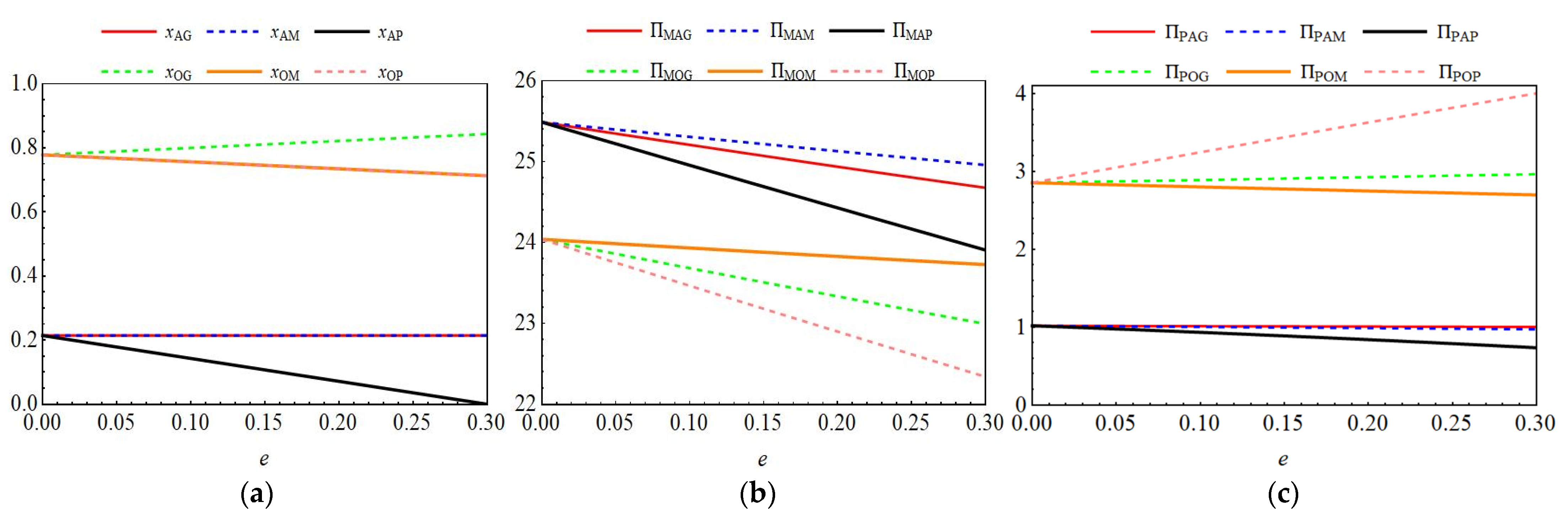
6.1.1. Impact of Key Parameters on Blockchain Investment Levels
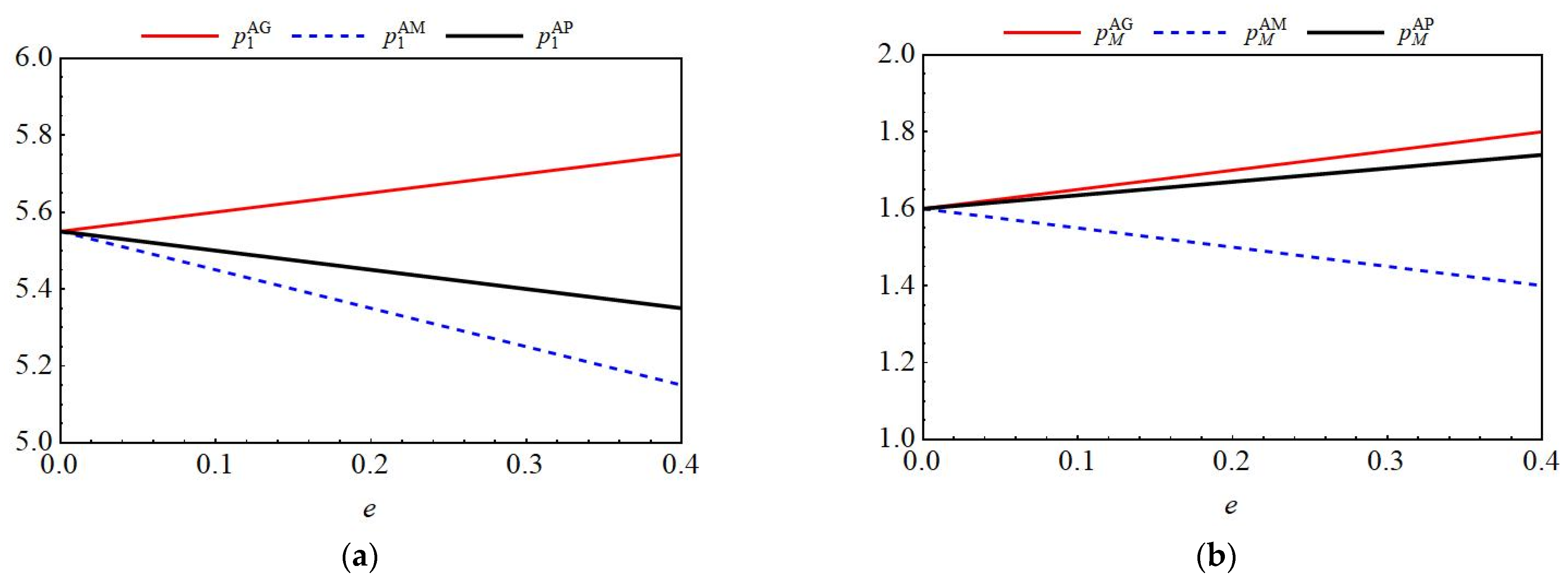
6.1.2. The Impact of Key Parameters on Price Decision-Making Among Different Entities
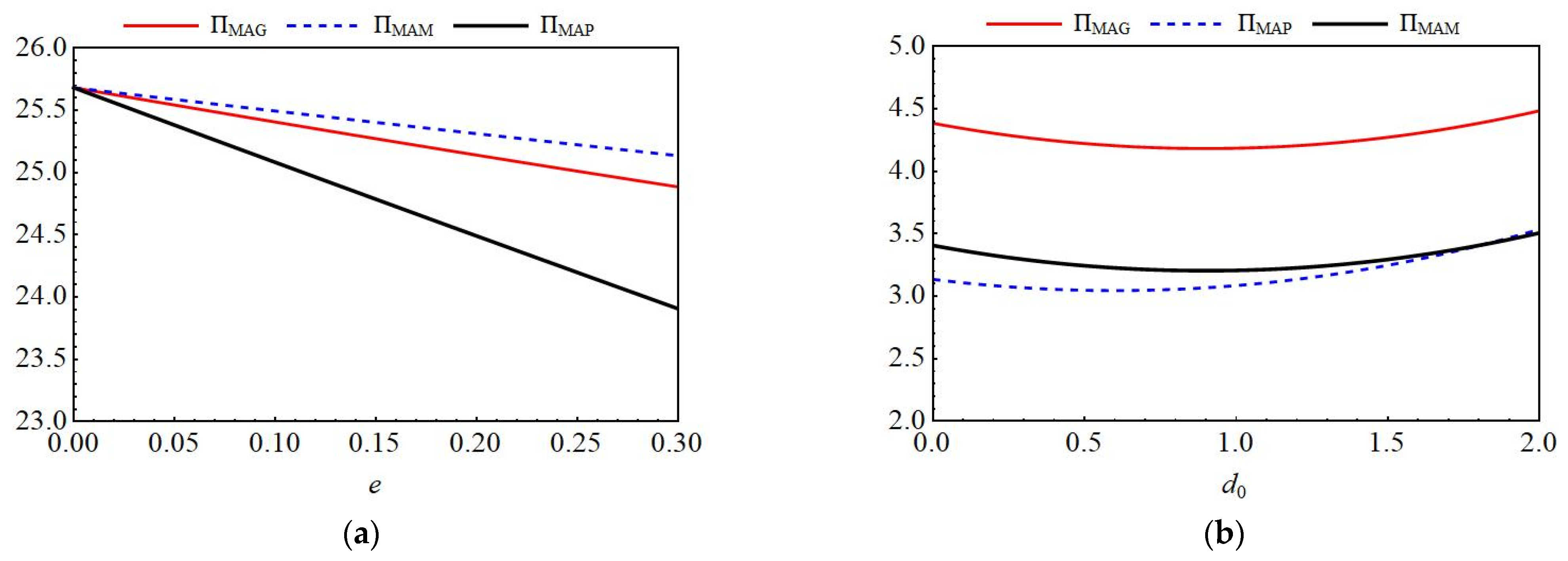
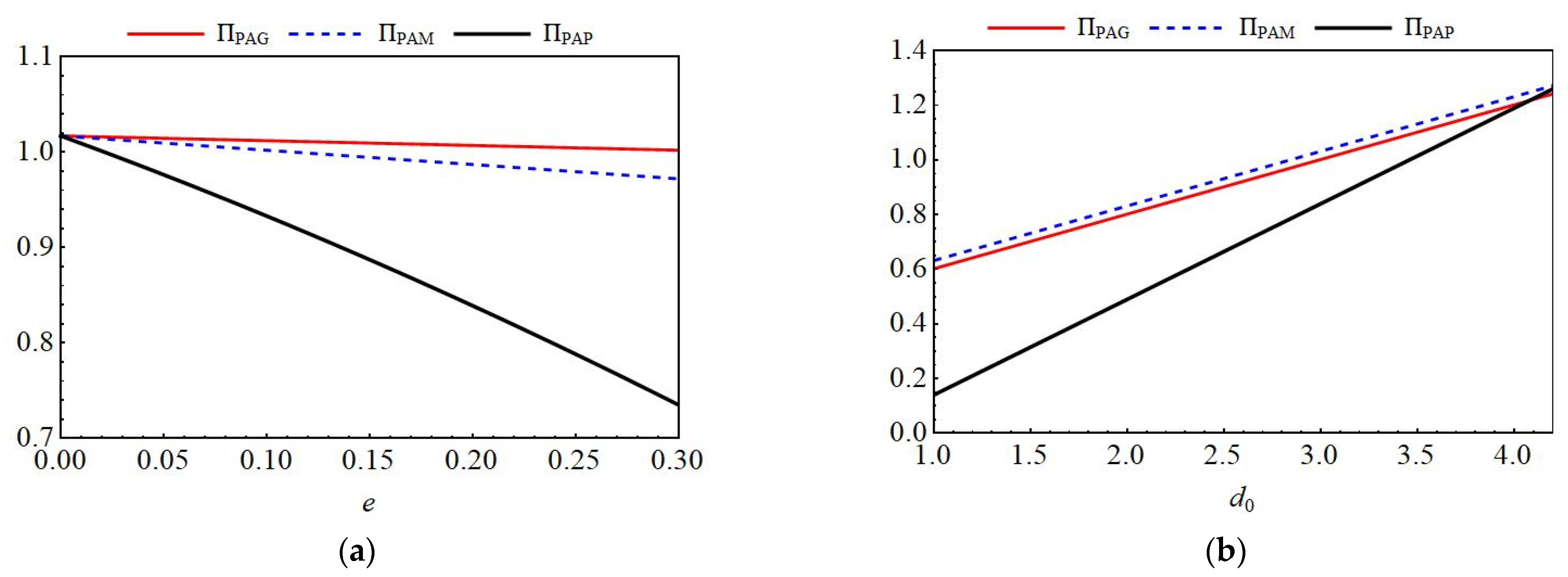
6.1.3. The Impact of Key Parameters on Optimal Profit for Different Entities
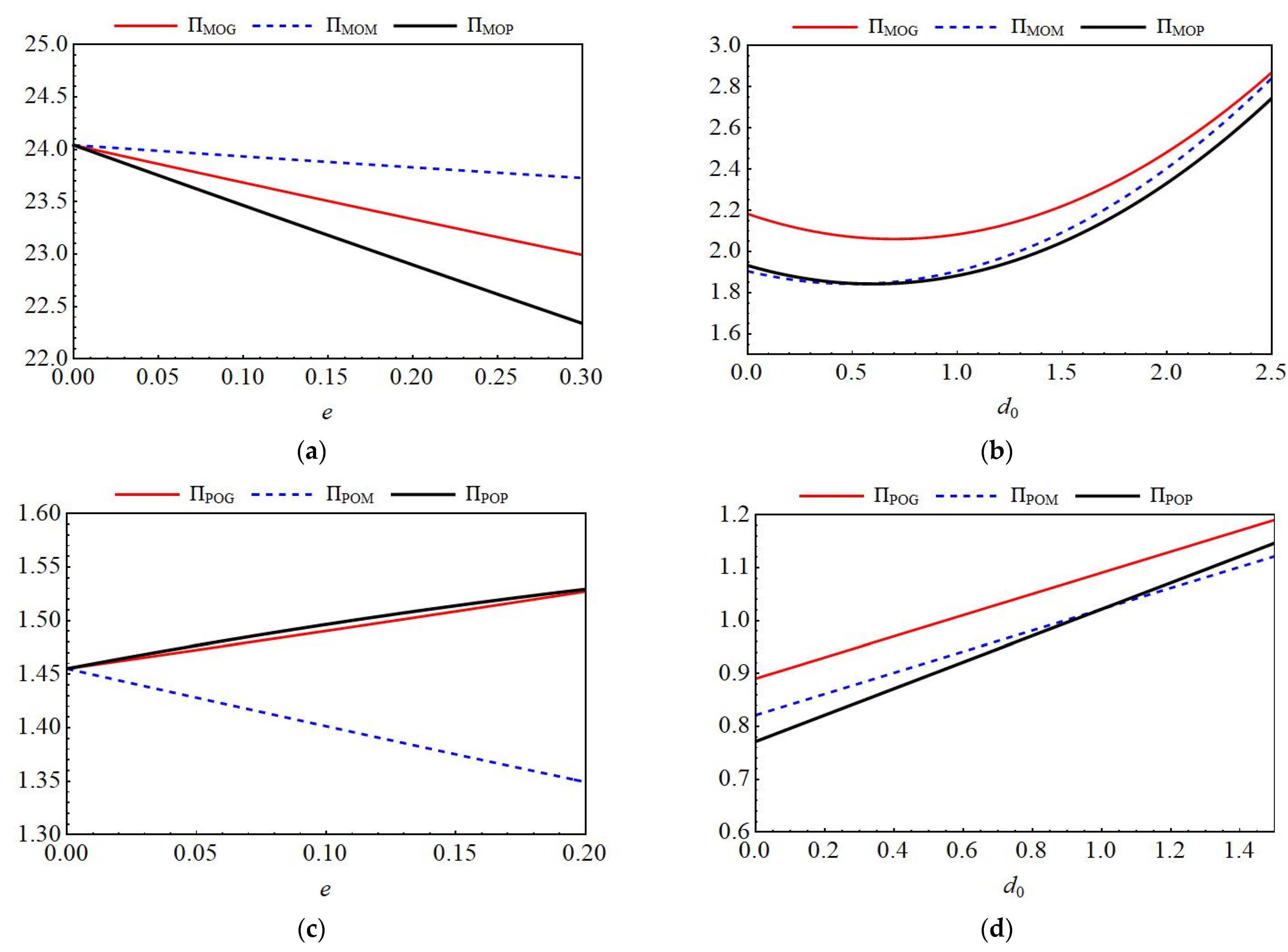
6.2. Numerical Analysis of a Closed-Loop Supply Chain for Power Batteries Under Online Platform-Commissioned Recycling Model
6.2.1. Impact of Key Parameters on Blockchain Investment Levels
6.2.2. The Impact of Key Parameters on Price Decision-Making Among Different Entities
6.2.3. The Impact of Key Parameters on Optimal Profit for Different Entities
6.3. Comparative Analysis of Decision-Making in Closed-Loop Supply Chains for Power Batteries Under Two Recycling Models
7. Discussions
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Xiao, M.; Xu, C.; Xie, F. Research on the impact of information sharing and government subsidy on competitive power battery recycling. J. Clean. Prod. 2024, 467, 142989. [Google Scholar] [CrossRef]
- Du, J.; Li, Q.; Qiao, F. Estimation of vehicle emission on mainline freeway under isolated and integrated ramp metering strategies. Environ. Eng. Manag. J. 2018, 17, 1237–1248. [Google Scholar] [CrossRef]
- Richa, K.; Babbitt, C.W.; Gaustad, G. Eco-efficiency analysis of a lithium-ion battery waste hierarchy inspired by circular economy. J. Ind. Ecol. 2017, 21, 715–730. [Google Scholar] [CrossRef]
- Lai, X.; Cao, Q. In-depth investigation of battery recycling: Strengthening the safety line of electric vehicles. Qinzhou Daily 2024, 1, 8–15. [Google Scholar]
- Gu, X.; Leromonachou, P. Developing pricing strategy to optimise total profits in an electric vehicle battery closed loop supply chain. J. Clean. Prod. 2018, 203, 376–385. [Google Scholar] [CrossRef]
- Zhang, Q.; Jin, W. Optimal decisions of power battery production and repurposing rate under different repurposed battery markets and repurposing parties. Int. J. Prod. Res. 2025, 1–16. [Google Scholar] [CrossRef]
- Gu, X.; Huang, M.; Zhou, L. Reimagining government subsidy policies: Facilitating echelon utilization and sustainable practices for retired battery systems. Comput. Ind. Eng. 2025, 208, 111437. [Google Scholar] [CrossRef]
- Riexinger, G.; Doppler, J.; Haar, C.; Trierweiler, M.; Buss, A.; Schöbel, K.; Ensling, D.; Bauernhansl, T. Integration of traceability systems in battery production. Procedia CIRP 2020, 93, 125–130. [Google Scholar] [CrossRef]
- Yao, F.; Zhu, J.; Yan, Y. Subsidy strategies for green design power battery closed-loop supply chain under equity concerns. Syst. Sci. Math. 2024, 44, 2730–2750. [Google Scholar]
- Nan, J.; Li, H. Two-type game analysis on the coexistence of price competition and technical cooperation of retired power battery recycling. Syst. Sci. Math. 2025, 1–24. [Google Scholar]
- Centobelli, P.; Cerchione, R.; Del Vecchio, P.; Oropallo, E.; Secundo, G. Blockchain technology for bridging trust, traceability and transparency in circular supply chain. Inf. Manag. 2022, 59, 7. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, C. A dynamic analysis of a green closed-loop supply chain with different on-line platform smart recycling and selling models. Comput. Ind. Eng. 2025, 200, 110748. [Google Scholar] [CrossRef]
- Wu, W.; Zhang, M.; Jin, D. Decision-making analysis of electric vehicle battery recycling under different recycling models and deposit-refund scheme. Comput. Ind. Eng. 2024, 191, 110109. [Google Scholar] [CrossRef]
- Li, J.; Liu, F.; Zhang, J.Z.; Li, L.; Ferreira, J. Forward–reverse blockchain traceability: Promoting electric vehicles with battery recycling in the presence of subsidy. Ann. Oper. Res. 2024, 1–28. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, Y.; Cheng, T.C.E.; Sun, Y. Optimal decisions and coordination of a supply chain in the hybrid recycling mode with traceability and fairness concern. Int. J. Prod. Res. 2024, 63, 5292–5316. [Google Scholar] [CrossRef]
- Gong, B.; Gao, Y.; Liu, Z. Selection of recycling channels for power battery closed-loop supply chain under government fund system. Comput. Integr. Manuf. Syst. 2023, 305, 3123–3137. [Google Scholar]
- Zhang, C.; Tian, Y.; Han, M. Recycling mode selection and carbon emission reduction decisions for a multi-channel closed-loop supply chain of electric vehicle power battery under cap-and-trade policy. J. Clean. Prod. 2022, 375, 134060. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, Q.; Guan, X. Recycling channel design and coordination in a reverse supply chain with customer green preference. Transp. Res. Part E Logist. Transp. Rev. 2023, 179, 103329. [Google Scholar] [CrossRef]
- Li, X. Collection mode choice of spent electric vehicle batteries: Considering collection competition and third-party economies of scale. Sci. Rep. 2022, 12, 6691. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Z.; Yang, S. Study on deposit return system of closed-loop supply chain under manufacturer competition. Chin. J. Manag. Sci. 2021, 29, 179–188. [Google Scholar]
- Liu, Z.; Li, K.W.; Tang, J. Optimal operations of a closed-loop supply chain under a dual regulation. Int. J. Prod. Econ. 2021, 233, 107991. [Google Scholar] [CrossRef]
- Huang, C.; Li, D. Research on pricing and profit distribution in closed-loop supply chains based on non-cooperative-cooperative dual-type games with deposit-returned recyclers. Chin. J. Manag. Sci. 2022, 32, 166–177. [Google Scholar]
- Huang, Y.; Liu, Y.; Zheng, B. Research on deposit refund systems based on government-driven and market-driven approaches: Analysis of recycling decisions considering closed-loop supply chain competition. Oper. Res. Manag. Sci. 2024, 33, 51–56. [Google Scholar]
- Bravo, M.; Molina, N.; Cerro, M. Exploring blockchain applications in the transition to a circular economy: A comprehensive sector-focused review. Procedia Comput. Sci. 2024, 241, 564–569. [Google Scholar] [CrossRef]
- Li, F. Packaging anti-counterfeiting information traceability method based on blockchain traceability. Comput. Meas. Control. 2024. [Google Scholar]
- Wei, P.; Ma, S.; Yan, X.B. Consumer service level-oriented resilience optimization for e-commerce supply chain considering hybrid strategies with blockchain adoption. Int. J. Prod. Res. 2024, 62, 7226–7260. [Google Scholar]
- Wang, Y.; Gao, J.; Cheng, T. Does blockchain technology need to be introduced in the closed-loop supply chain based on product lifecycle management? Comput. Ind. Eng. 2024, 188, 109881. [Google Scholar] [CrossRef]
- Zhang, T.; Dong, P.; Chen, X. The impacts of blockchain adoption on a dual-channel supply chain with risk-averse members. Omega 2023, 114, 102747. [Google Scholar] [CrossRef]
- Li, J.; Wang, L.; Quan, P. Impact of blockchain technology on remanufacturing supply chains with CSR investments. China Circ. Econ. 2024, 38, 34–45. [Google Scholar]
- Wu, X.; Fan, Z.; Li, G. Strategic analysis for adopting blockchain technology under supply chain competition. Int. J. Logist. Res. Appl. 2023, 26, 1384–1400. [Google Scholar] [CrossRef]
- Suvadarshini, P.; Biswas, I.; Srivastava, S. Impact of reverse channel competition, individual rationality, and information asymmetry on multi-channel closed-loop supply chain design. Int. J. Prod. Econ. 2023, 259, 108818. [Google Scholar] [CrossRef]
- Wan, N.; Fan, J.; Wu, X. The cost-sharing mechanism for blockchain technology adoption in the platform-led e-commerce supply chain. J. Syst. Sci. Syst. Eng. 2025, 34, 156–179. [Google Scholar] [CrossRef]
- Chang, F.; Chi, M.; Fan, S.; Choi, T. Who should invest in blockchain technology under different pricing models in supply chains? Europ. J. Oper. Res. 2024, 319, 777–792. [Google Scholar]
- Wang, W.; Fan, L.; Yang, S. The impact of manufacturers sharing recycling investment costs on closed-loop supply chain decisions. Stat. Decis. Mak. 2018, 34, 57–61. [Google Scholar]
- Feng, Z.; Xiao, T.; Chai, C. Recycling and pricing strategies in a third-party recycler-led two-tier closed-loop supply chain. Chin. J. Manag. Sci. 2018, 26, 118–127. [Google Scholar]
- Lin, Q.; Liu, M.; Wang, X. Green supply chain decision-making incorporating blockchain information transmission functions. Comput. Integr. Manuf. Syst. 2024, 30, 355–368. [Google Scholar]
- Wang, M.; Li, Y.; Shi, W. Dynamic decision-making on corporate end-of-life product recycling under different environmental regulations. Syst. Eng. Theory Pract. 2020, 40, 103–118. [Google Scholar]
- Yan, Y.; Cao, J.; Zhou, Y.; Zhou, G.; Chen, J. Decisions for power battery closed-loop supply chain: Cascade utilization and extended producer responsibility. Ann. Oper. Res. 2024, 1–14. [Google Scholar] [CrossRef]
- Dan, P.; Wang, Z.; Wang, M.; Andrea, A.; Xiao, T. Online collection channel and government subsidy strategy of retired power batteries considering cascade utilization. Comput. Ind. Eng. 2025, 209, 111417. [Google Scholar] [CrossRef]
| Paper | Deposit Collection Method | Blockchain Investment | Online Platform Recycling Model | CLSC | |||
|---|---|---|---|---|---|---|---|
| Policy-Driven | Market-Driven | Invested by Manufacturers | Invested by Retailers | Invested by Online Platforms | |||
| Suvadarshini et al. (2023) [31] | ✓ | ✓ | |||||
| Wu et al. (2024) [13] | ✓ | ✓ | |||||
| Huang et al. (2024) [23] | ✓ | ✓ | ✓ | ||||
| Wu et al. (2024) [15] | ✓ | ✓ | |||||
| Chen and Zhang (2024) [12] | ✓ | ✓ | |||||
| Wan et al. (2025) [32] | ✓ | ||||||
| Li et al. (2024) [14] | ✓ | ✓ | |||||
| Gong et al. (2021) [16] | ✓ | ✓ | ✓ | ||||
| Chang et al. (2024) [33] | ✓ | ✓ | |||||
| This paper | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| Notations | Definitions |
|---|---|
| Parameter | |
| Total potential market demand. | |
| Consumer sensitivity coefficient of blockchain technology investment. | |
| Manufacturer revenue from tiered utilization market. | |
| Manufacturer revenue from remanufacturing new batteries. | |
| Product unit deposit. | |
| Proportion of recycled batteries suitable for tiered utilization. | |
| Manufacturer disassembly technology cost. | |
| Sales commission rate. | |
| Recycling commission rate. | |
| Difficulty coefficient of blockchain technology investment. | |
| Supplier’s new battery wholesale price. | |
| Decision variable | |
| Retail price of power batteries. | |
| Manufacturer’s recycling price for power batteries. | |
| Online platform recycling price for power batteries. | |
| Blockchain investment level. | |
| Function | |
| DA | Number of requests under no-deposit policy. |
| DB | Number of requests under deposit policy. |
| Total number of power batteries recycled. | |
| Supply chain member profit. | |
| Recycling mode (AG, AM, AP, OG, OM, OP). | |
| M: Manufacturer, P: Online platform. |
| Symbol | Value | Unit | Reference |
|---|---|---|---|
| 3/10 | unit | Chen and Zhang (2024) [12] Wan et al. (2025) [32] | |
| 0.5/0.7 | — | ||
| 0.1/0.2/0.3 | RMB/unit | ||
| — | |||
| 0.2/0.3 | — | ||
| 0.5/0.7 | — | ||
| 0.2/0.7 | RMB/unit | Yan et al. (2024) [38] Dan et al. (2025) [39] | |
| 4 | RMB/unit | ||
| 3 | RMB/unit | ||
| — | |||
| 0.2 | RMB/unit |
| Conditions | Best Model (Manufacturer Perspective) | Best Model (Platform Perspective) | Optimal Model (Government Perspective) |
|---|---|---|---|
| High market demand | OG/AM | OG/OP | OG |
| Low market demand | AM/OG | AM/OG | AM/OG |
| High-Level Blockchain Investment Incentive Objectives | OG | OG | OG |
| Low Retail Price (Consumer Cost) Target | AM | AM | AM |
| High Recycling Rate Target | OG | OG | OG |
| Manufacturer Profit Maximization | AM/OG | - | - |
| Platform Profit Maximization | - | OG/OP | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, C.; Cui, Y.; Wan, Z. Research on Power Battery Recycling Decision Considering Deposit System Under Online Platform Recycling Mode. Appl. Sci. 2025, 15, 12514. https://doi.org/10.3390/app152312514
Ji C, Cui Y, Wan Z. Research on Power Battery Recycling Decision Considering Deposit System Under Online Platform Recycling Mode. Applied Sciences. 2025; 15(23):12514. https://doi.org/10.3390/app152312514
Chicago/Turabian StyleJi, Chunyi, Yuxi Cui, and Ziyin Wan. 2025. "Research on Power Battery Recycling Decision Considering Deposit System Under Online Platform Recycling Mode" Applied Sciences 15, no. 23: 12514. https://doi.org/10.3390/app152312514
APA StyleJi, C., Cui, Y., & Wan, Z. (2025). Research on Power Battery Recycling Decision Considering Deposit System Under Online Platform Recycling Mode. Applied Sciences, 15(23), 12514. https://doi.org/10.3390/app152312514





