Fault Prediction Method Towards Rolling Element Bearing Based on Digital Twin and Deep Transfer Learning
Abstract
1. Introduction
2. Related Works
2.1. Deep Transfer Learning-Based Fault Prediction
2.2. DT-Based Fault Prediction
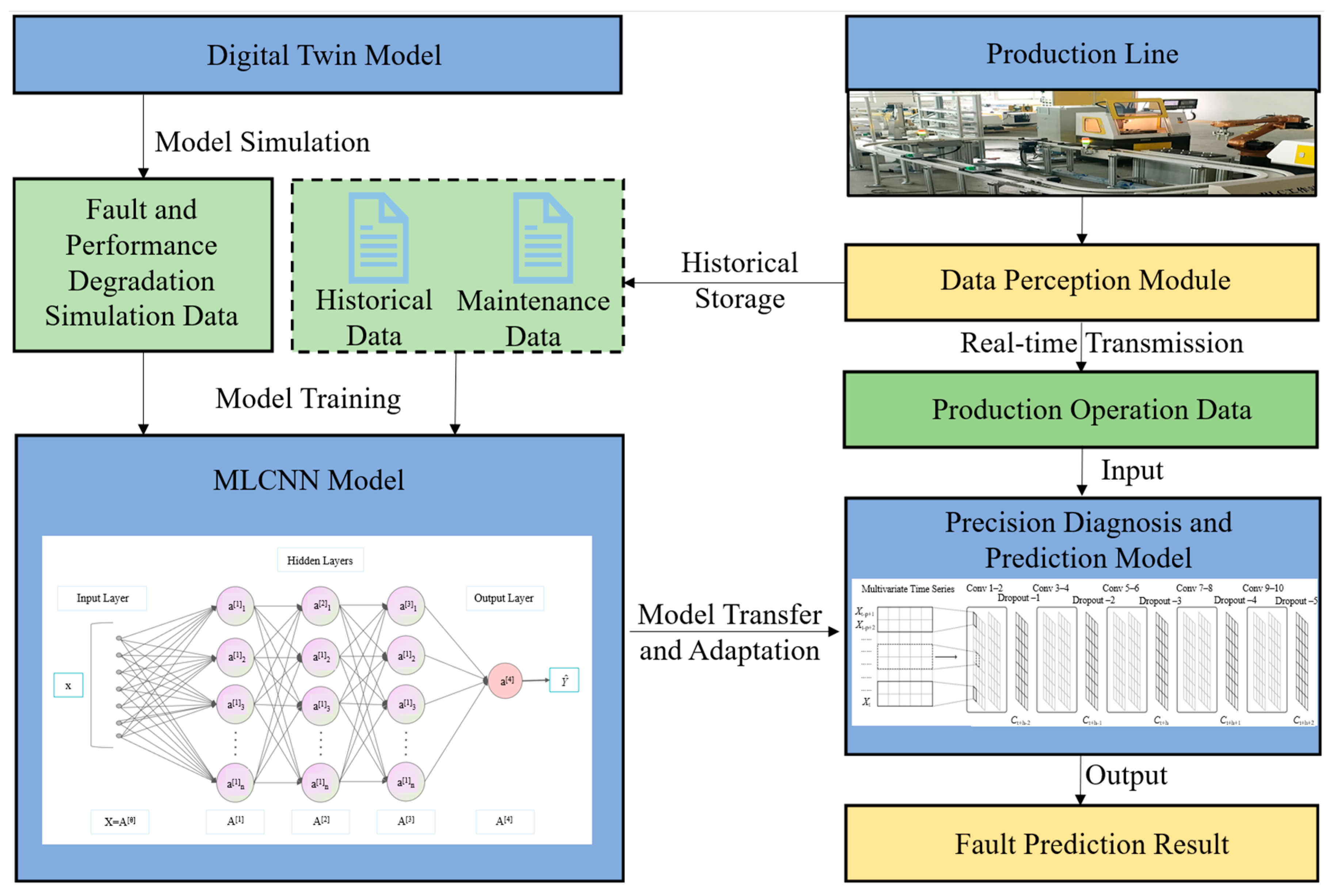
3. The Proposed Method
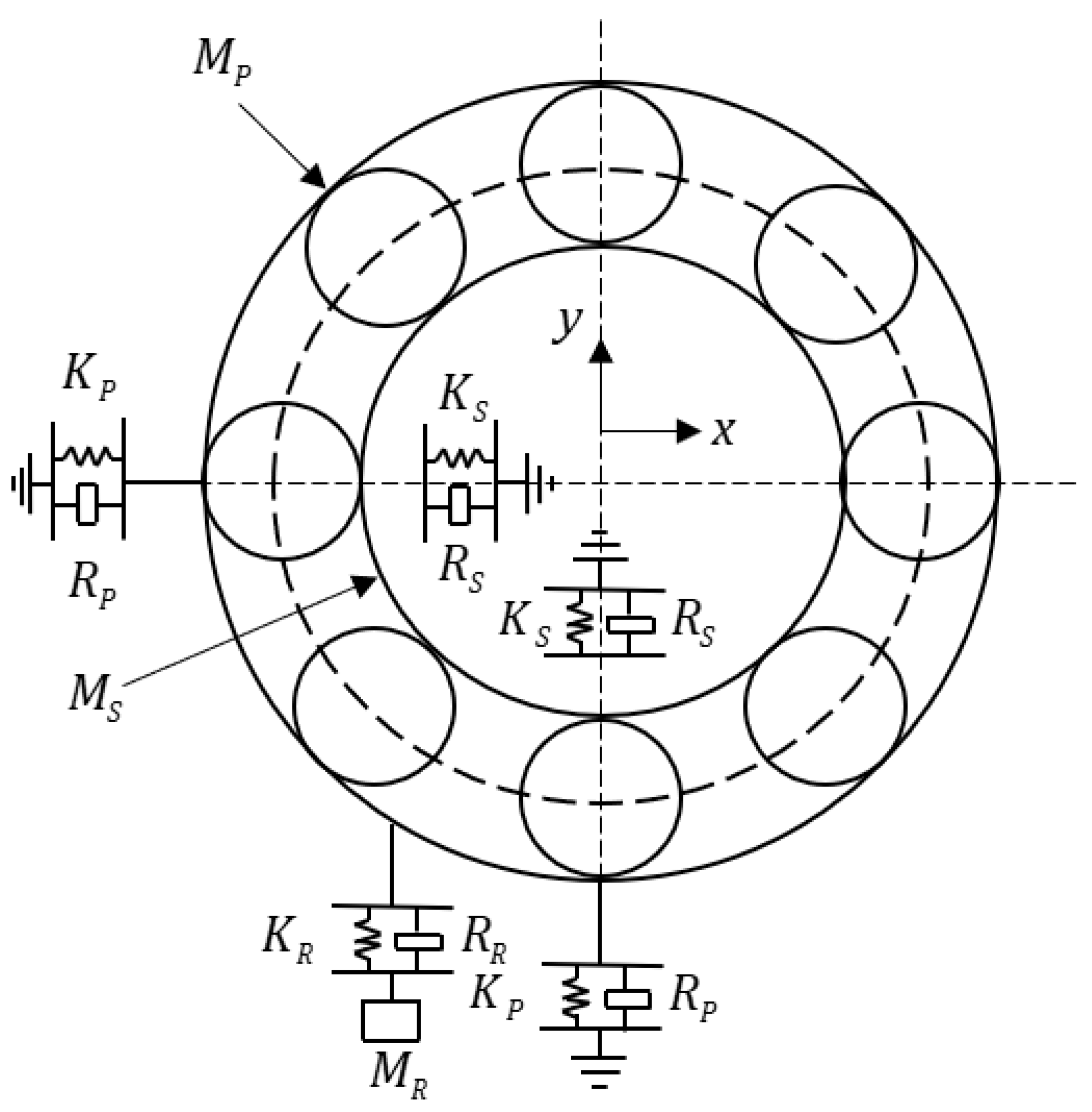
3.1. DT Model
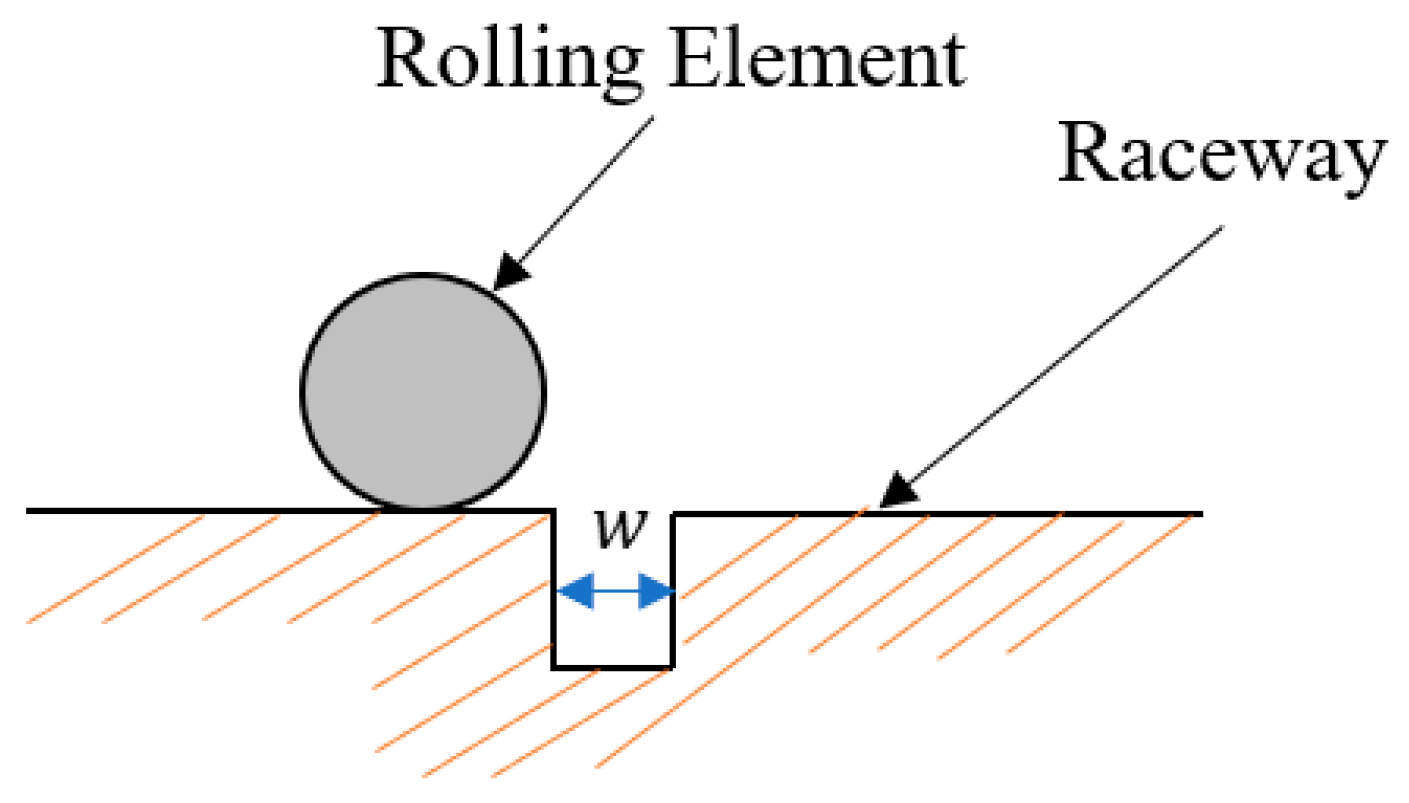
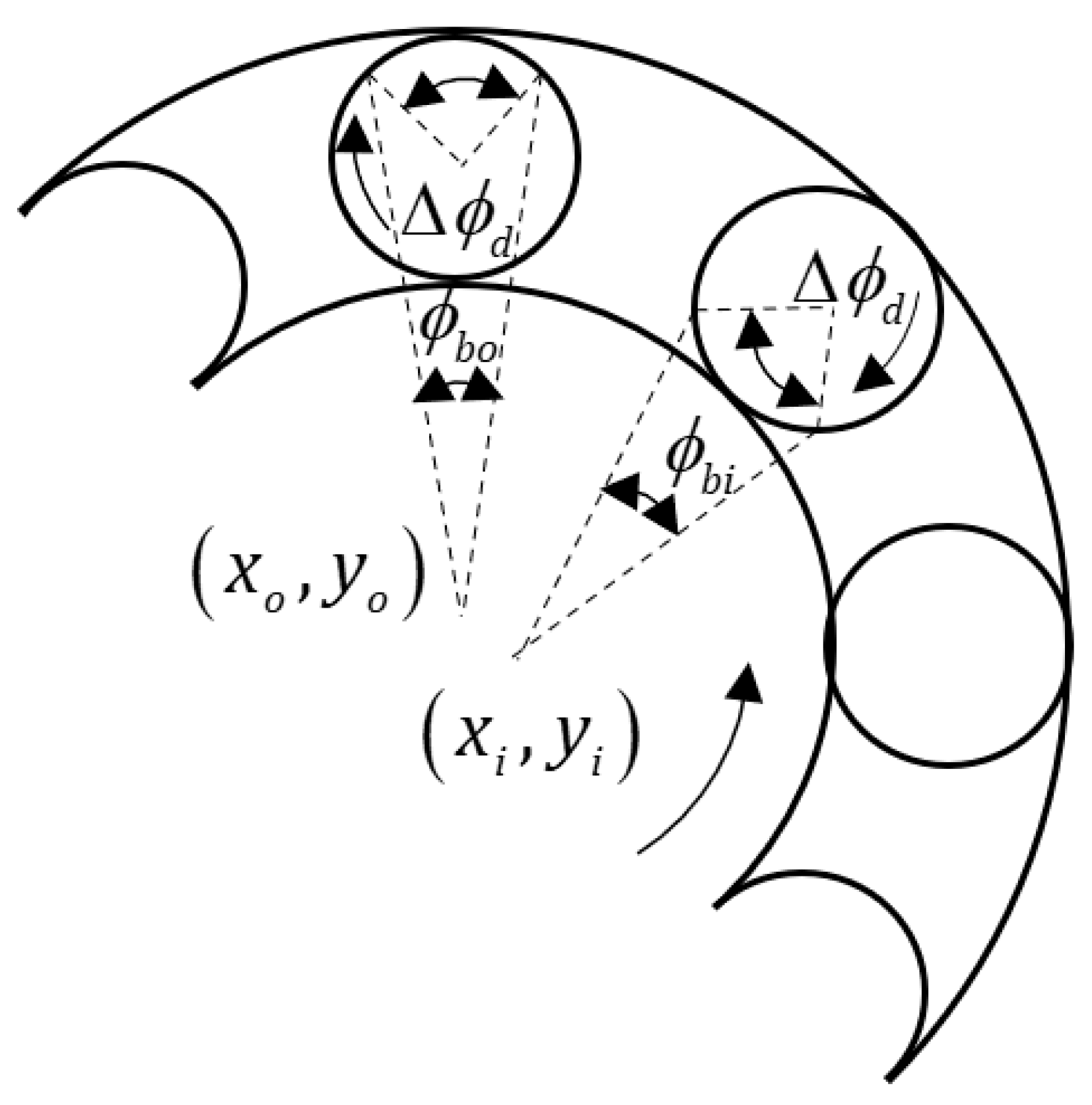
Local Fault Modeling
- (1)
- Outer Ring Fault
- (2)
- Inner Ring Fault
- (3)
- Rolling Element Fault
3.2. MLCNN
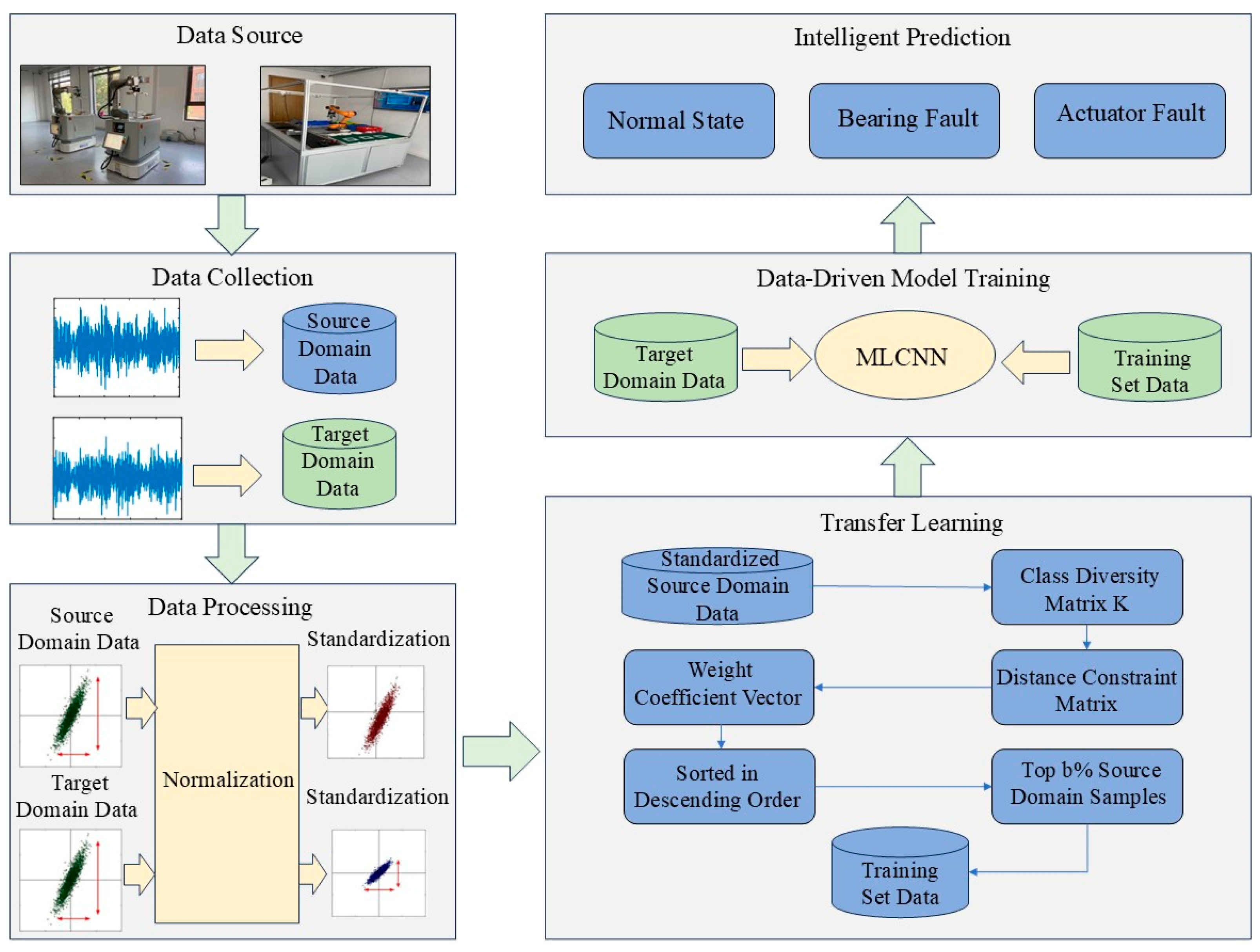
3.3. DT-Assisted Deep Transfer Learning Method
3.3.1. Problem Description
3.3.2. Model Structure
3.3.3. Optimization Objective
| Algorithm 1. Pseudocode for DT-assisted deep transfer learning algorithm |
| 1. Initialize Source domain data , Target domain data , Matrix weights , Maximum iteration count and set values ,, , , , , , 2. Calculate the class diversity matrix using Equation (27) 3. Calculate the distance diversity matrix using Equation (28) 4. While 5. Normalize the source domain samples and input them, using the Adam algorithm to solve for the weight parameters 6. 7. 8. 9. 10. Sort the source domain data in descending order based on the weight coefficient vector 11. Select the top b% of the data to form the training set 12. Input the training set data 13. Use grid search to optimize the hyperparameters 14. Diagnose the target domain data and obtain the final fault status 15. Compare with the original labels and calculate the diagnosis accuracy 16. End |
3.3.4. Intelligent Prediction Process
- (1)
- State Space Model Transformation: Based on the performance degradation laws of the DT model, the state transformation is performed, calculating the internal state of the DT system and generating fault simulation data.
- (2)
- Construction of MLCNN-Based Data-Driven Model: The source domain data is used to train the MLCNN model, enabling data feature learning and fault prediction.
- (3)
- Deep Transfer Learning Algorithm: Knowledge from the source domain DT model is transferred to the target domain MLCNN data-driven model. During the transfer learning process, the model parameters are adjusted to adapt to the characteristics of the target domain data, thereby improving the model’s generalization ability.
- (4)
- Intelligent Prediction Analysis: Based on the intelligent prediction results from DT-assisted deep transfer learning, the predicted value is analyzed to determine if it exceeds the threshold. If the threshold is exceeded, maintenance operations are performed; otherwise, the process returns to step 2 for iteration.
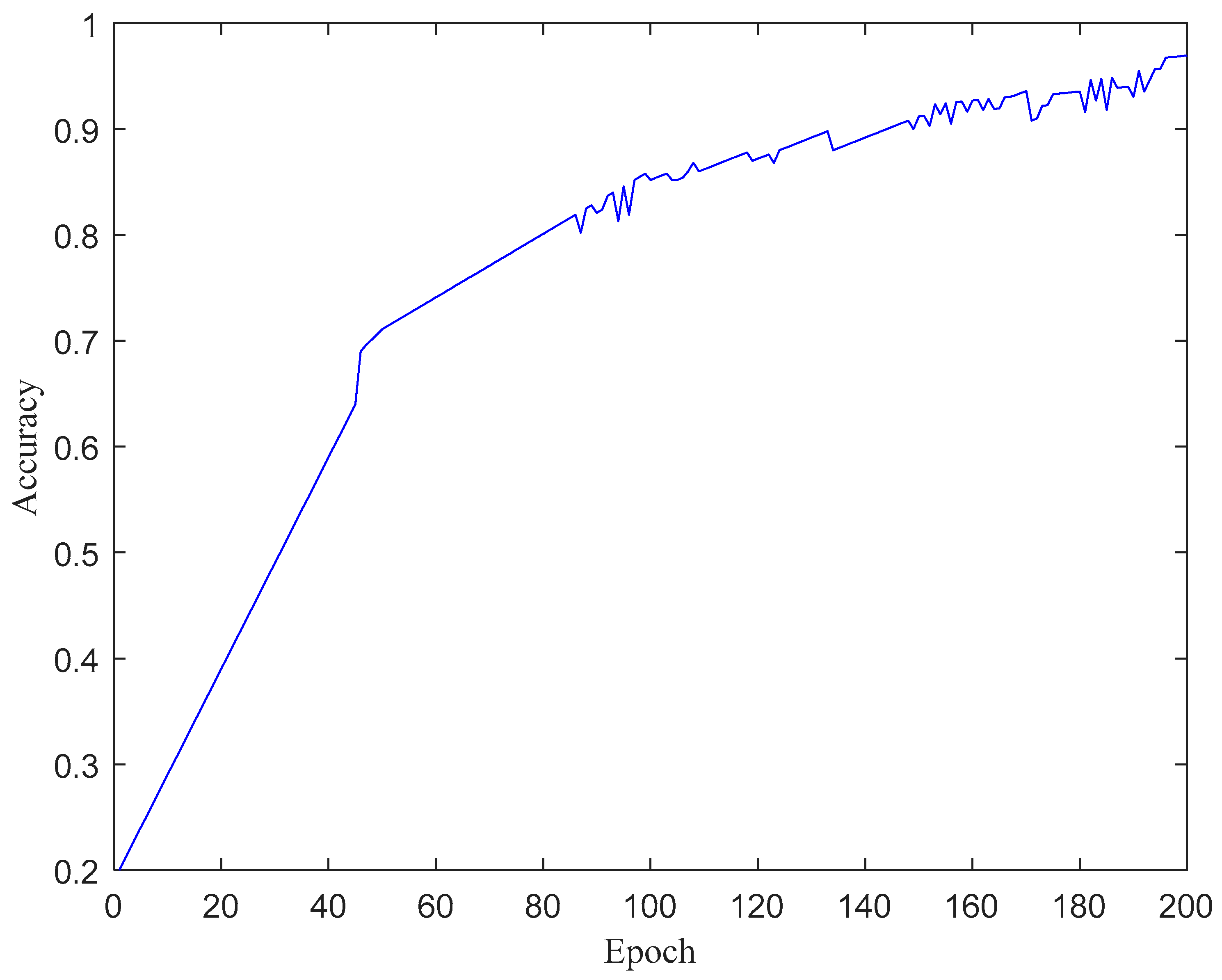
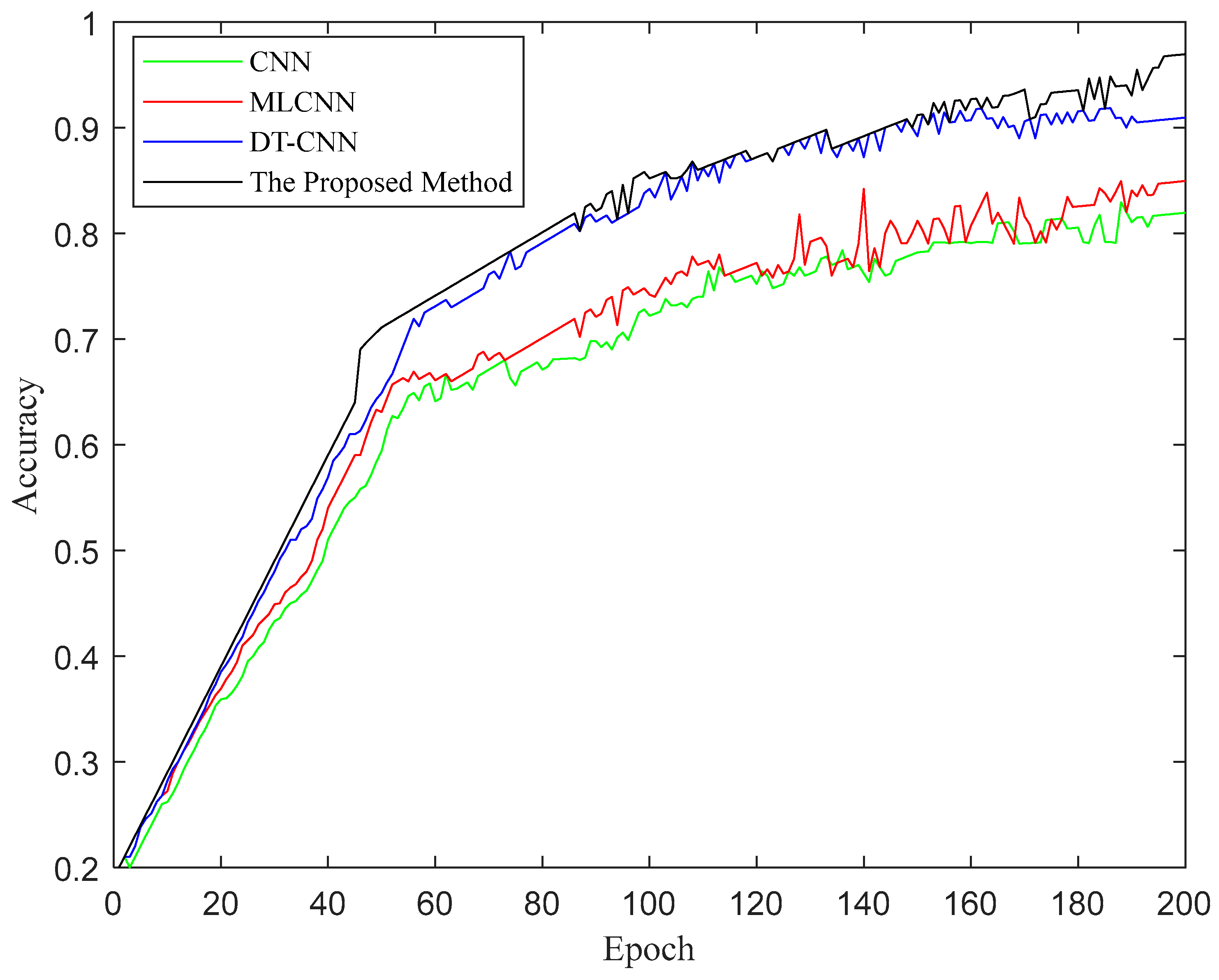
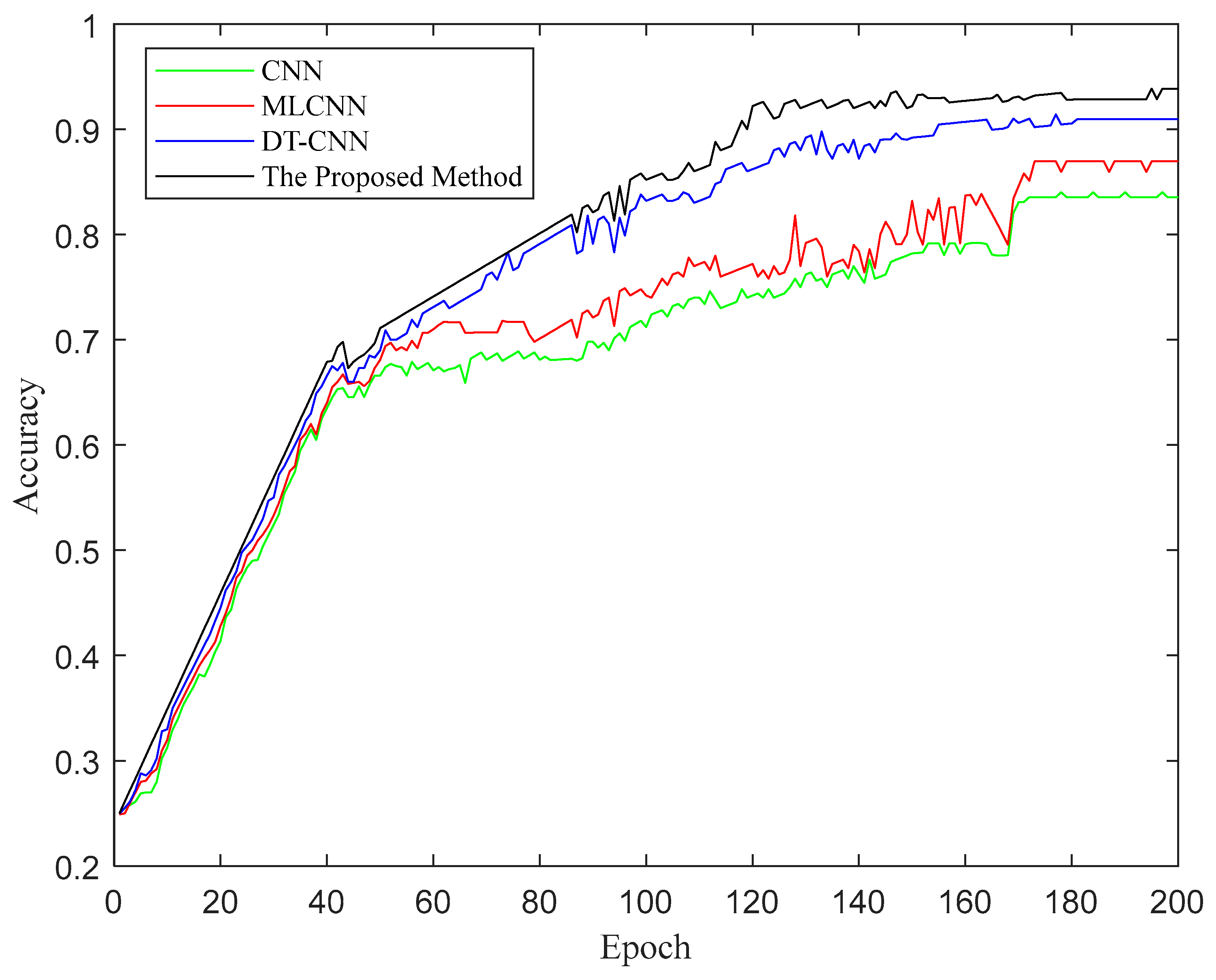
4. Case Study
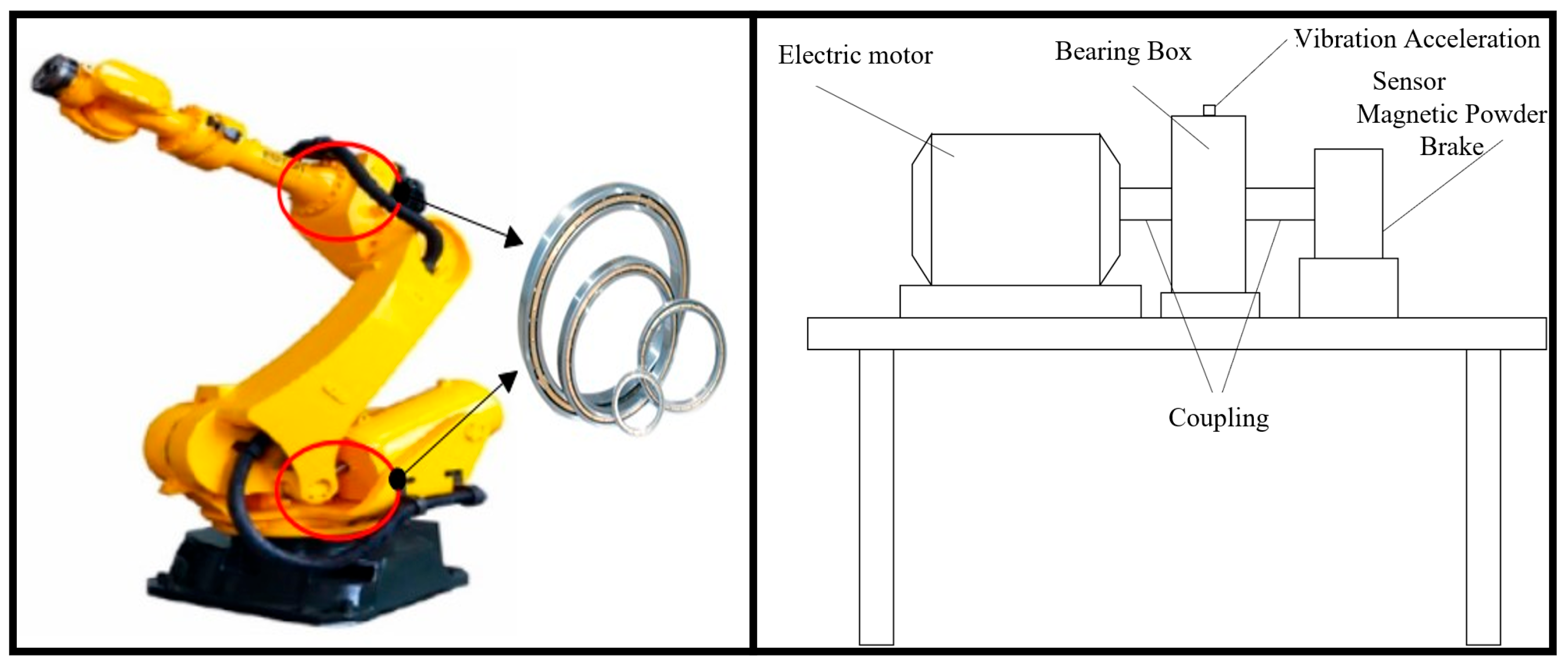
4.1. Experimental Platform Setup
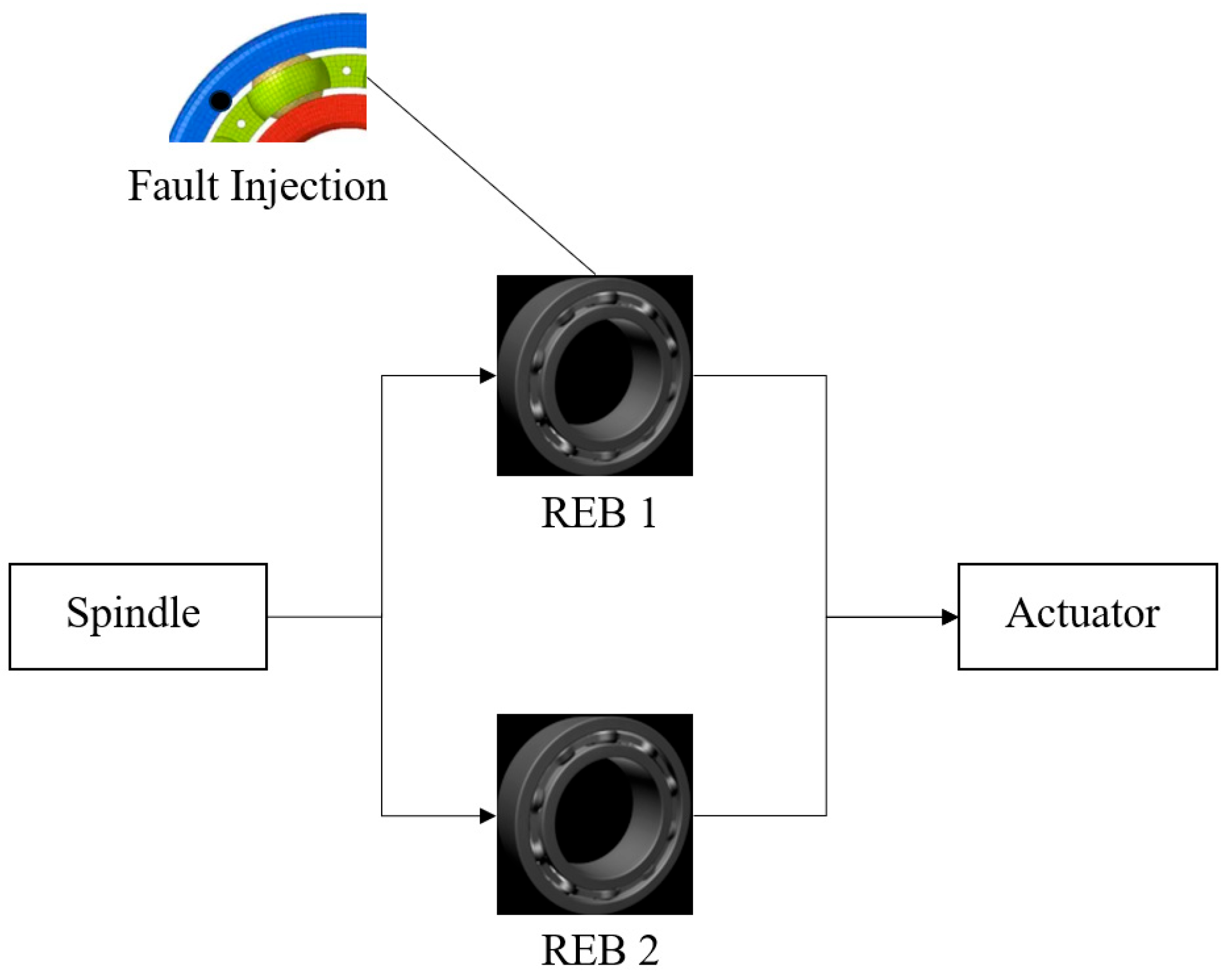
4.2. Construction of the REB DT Model and Fault Injection
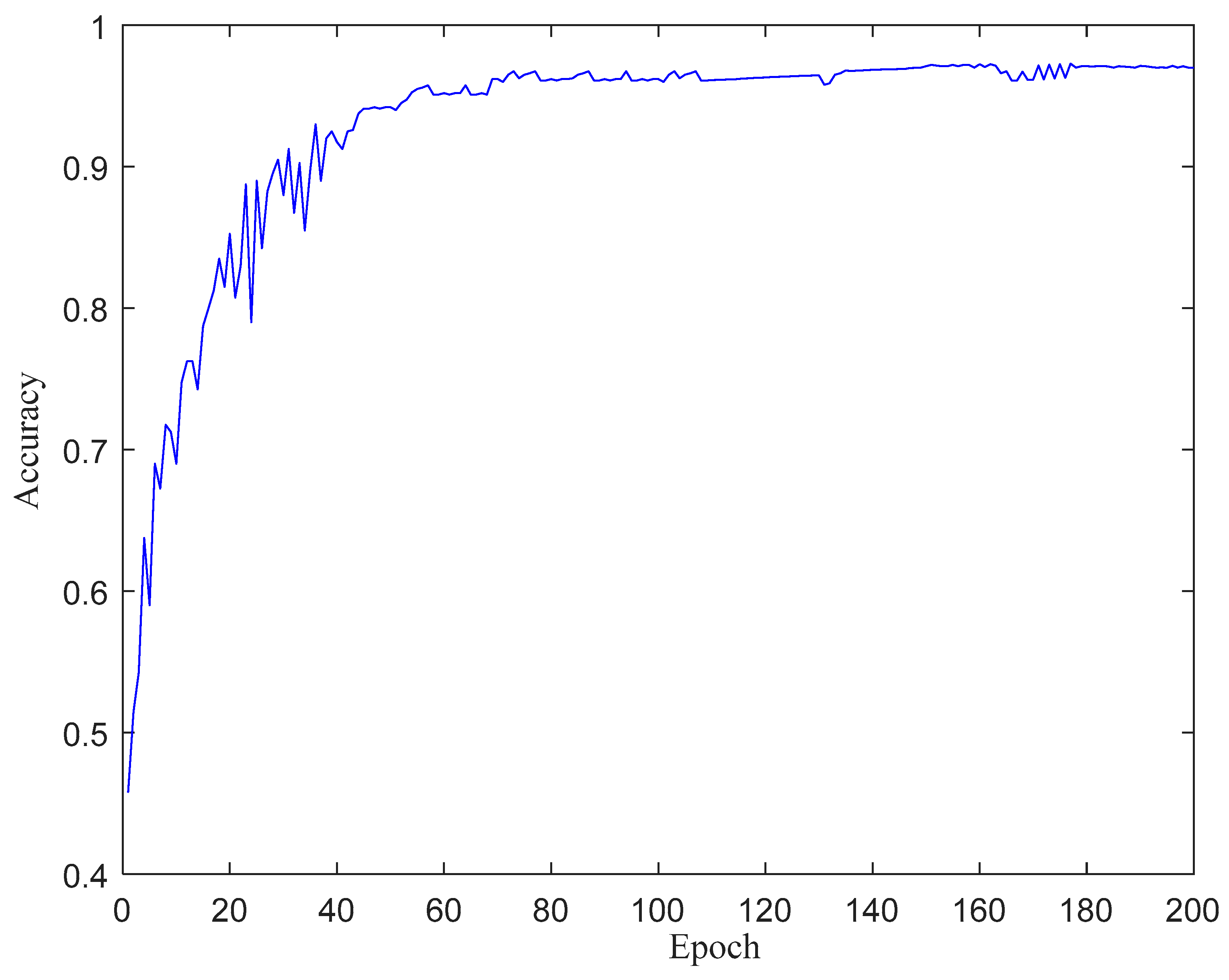
4.3. Construction of MLCNN Data-Driven Model and Actual Fault Transfer
5. Discussions
6. Conclusions
- (1)
- A REB fault diagnosis DT framework based on the combination of dynamic models and deep transfer learning is proposed. This transforms the traditional passive maintenance cycle into an active, preventive maintenance strategy for the entire lifecycle. Virtual entities can not only train models in virtual space to detect potential issues and fault evolution, but also interact and collaborate with physical entities for synchronous state monitoring and predictive analysis, until the end of life.
- (2)
- A five-degree-of-freedom dynamic twin model of the REB is constructed using MATLAB/Simulink. This model simulates and generates a large balanced dataset containing four fault states under varying operating conditions. The proposed dynamic twin model comprehensively and accurately maps the physical entity’s state behavior.
- (3)
- Breaking the limitations of traditional machine learning, which relies on large amounts of historical data, requires data preprocessing, and suffers from cold-start issues, a fault diagnosis algorithm based on MLCNN and transfer learning is proposed. This algorithm enables end-to-end real-time fault diagnosis of REBs from raw one-dimensional vibration signals, solving the problem of small samples in practical production and the need to retrain the model from scratch when operating conditions change.
- (4)
- Using the large balanced dataset simulated by DT technology, the model is pre-trained. The trained model is then transferred to actual REB operation, where it is fine-tuned and trained using real, imbalanced data to create a reliable REB fault model. This approach reduces diagnostic costs and processing time, significantly improving fault diagnosis accuracy.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sahu, D.; Dewangan, R.K.; Matharu, S.P.S. Hybrid CNN-LSTM model for fault diagnosis of rolling element bearings with operational defects. Int. J. Interact. Des. Manuf. 2025, 19, 5737–5748. [Google Scholar] [CrossRef]
- Li, Z.; Kristoffersen, E.; Li, J. Deep transfer learning for failure prediction across failure types. Comput. Ind. Eng. 2022, 172, 108521. [Google Scholar] [CrossRef]
- Keshun, Y.; Puzhou, W.; Peng, H.; Yingkui, G. A sound-vibration physical-information fusion constraint-guided deep learning method for rolling bearing fault diagnosis. Reliab. Eng. Syst. Safe. 2025, 253, 110556. [Google Scholar] [CrossRef]
- Lu, Q.; Li, M. Digital twin-driven remaining useful life prediction for rolling element bearing. Machines 2023, 11, 678. [Google Scholar] [CrossRef]
- Pandiyan, M.; Babu, T.N. Systematic review on fault diagnosis on rolling-element bearing. J. Vib. Eng. Technol. 2024, 12, 8249–8283. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, C.; Wu, J.; Xie, Y.; Shen, W.; Wu, J. Deep learning-based bearing fault diagnosis using a trusted multiscale quadratic attention-embedded convolutional neural network. IEEE Trans. Instrum. Meas. 2024, 73, 3513215. [Google Scholar] [CrossRef]
- Habbouche, H.; Amirat, Y.; Benkedjouh, T.; Benbouzid, M. Digital twin-based gearbox fault diagnosis using variational mode decomposition and dynamic vibration modeling. Measurement 2025, 246, 116669. [Google Scholar] [CrossRef]
- Misbah, I.; Lee, C.K.; Keung, K.L. Fault diagnosis in rotating machines based on transfer learning: Literature review. Knowl.-Based Syst. 2024, 283, 111158. [Google Scholar] [CrossRef]
- Yang, B.; Lei, Y.; Li, X.; Li, N. Targeted transfer learning through distribution barycenter medium for intelligent fault diagnosis of machines with data decentralization. Expert Syst. Appl. 2024, 244, 122997. [Google Scholar] [CrossRef]
- Zhao, L.; Xie, T.; Wei, Y.; Liu, Y.; Qin, Y. Overview of digital twin-driven rotating machinery fault diagnosis: Status and trends. Meas. Sci. Technol. 2025, 36, 052001. [Google Scholar] [CrossRef]
- Wang, D.; Chen, C. Multilevel feature encoder for transfer learning-based fault detection on acoustic signal. Inform. Fusion 2025, 121, 103128. [Google Scholar] [CrossRef]
- Chen, X.; Yang, R.; Xue, Y.; Huang, M.; Ferrero, R.; Wang, Z. Deep transfer learning for bearing fault diagnosis: Asystematic review since 2016. IEEE Trans. Instrum. Meas. 2023, 72, 3508221. [Google Scholar] [CrossRef]
- Yan, P.; Abdulkadir, A.; Luley, P.P.; Rosenthal, M.; Schatte, G.A.; Grewe, B.F.; Stadelmann, T. A comprehensive survey of deep transfer learning for anomaly detection in industrial time series: Methods, applications, and directions. IEEE Access 2024, 12, 3768–3789. [Google Scholar] [CrossRef]
- Xiang, S.; Li, P.; Luo, J.; Qin, Y. Micro transfer learning mechanism for cross-domain equipment RULprediction. IEEE Trans. Autom. Sci. Eng. 2025, 22, 1460–1470. [Google Scholar] [CrossRef]
- Zheng, L.; Zhu, Y.; Zhou, Y. Meta-transfer learning-based method for multi-fault analysis and assessment in power system. Appl. Intell. 2024, 54, 12112–12127. [Google Scholar] [CrossRef]
- Zheng, B.; Huang, J.; Ma, X.; Zhang, X.; Zhang, Q. An unsupervised transfer learning method based on SOCNN and FBNN and its application on bearing fault diagnosis. Mech. Syst. Signal Process. 2024, 208, 111047. [Google Scholar] [CrossRef]
- Pathak, K.A.; Kafle, P.; Vikram, A. Deep learning-based defect detection in film-coated tablets using a convolutional neural network. Int. J. Pharm. 2025, 671, 125220. [Google Scholar] [CrossRef]
- Azad, M.M.; Shah, A.U.R.; Prabhakar, M.N.; Kim, H.S. Deep learning-based autonomous morphological fracture analysis of fiber-reinforced composites. Eng. Fail. Anal. 2025, 170, 109292. [Google Scholar] [CrossRef]
- He, D.; Zhao, J.; Jin, Z.; Huang, C.; Zhang, F.; Wu, J. Prediction of bearing remaining useful life based on a two-stage updated digital twin. Adv. Eng. Inform. 2025, 65, 103123. [Google Scholar] [CrossRef]
- Sohel, R. AI-driven fault detection and predictive maintenance in electrical power systems: A systematic review of data-driven approaches, digital twins, and self-healing grids. Am. J. Adv. Technol. Eng. Solut. 2025, 1, 258–289. [Google Scholar]
- Mikołajewska, E.; Mikołajewski, D.; Mikołajczyk, T.; Paczkowski, T. Generative AI in AI-based digital twins for fault diagnosis for predictive maintenance in Industry 4.0/5.0. Appl. Sci. 2025, 15, 3166. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, Y.; Chen, Z. Fault diagnosis method for proton exchange membrane fuel cell system based on digital twin and unsupervised domain adaptive learning. Int. J. Hydrogen Energy 2024, 50, 1207–1219. [Google Scholar] [CrossRef]
- Gong, S.; Li, S.; Zhang, Y.; Zhou, L.; Xia, M. Digital twin-assisted intelligent fault diagnosis for bearings. Meas. Sci. Technol. 2024, 35, 106128. [Google Scholar] [CrossRef]
- Ye, W.; Liu, X.; Zhao, X.; Fu, H.; Cai, Y.; Li, H. A data-driven digital twin architecture for failure prediction of customized automatic transverse robot. IEEE Access 2024, 12, 59222–59235. [Google Scholar] [CrossRef]
- Yin, Y.; Chen, H.; Meng, X.; Xie, H. Digital twin-driven identification of fault situation in distribution networks connected to distributed wind power. Int. J. Elec. Power Energ. Syst. 2024, 155, 109415. [Google Scholar] [CrossRef]
- Xue, R.; Zhang, P.; Huang, Z.; Wang, J. Digital twin-driven fault diagnosis for CNCmachine tool. Int. J. Adv. Manuf. Technol. 2024, 131, 5457–5470. [Google Scholar] [CrossRef]
- Grieves, M. Intelligent digital twins and the development and management of complex systems. Digit. Twin 2024, 1, 8. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R.B. Simulating gear and bearing interactions in the presence of faults: Part I. The combined gear bearing dynamic model and the simulation of localised bearing faults. Mech. Syst. Signal Pract. 2008, 22, 1924–1951. [Google Scholar] [CrossRef]
- Dong, Y.; Li, Y.; Zheng, H.; Wang, R.; Xu, M. A new dynamic model and transfer learning based intelligent fault diagnosis framework for rolling element bearings race faults: Solving the small sample problem. ISA Trans. 2022, 121, 327–348. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Huang, K.; Zheng, Z. Towards better forecasting by fusing near and distant future visions. Proc. AAAI Conf. Artif. Intell. 2020, 34, 3593–3600. [Google Scholar] [CrossRef]
- Zhang, C.; Qin, F.; Zhao, W.; Li, J.; Liu, T. Research on rolling bearing fault diagnosis based on digital twin data and improved ConvNext. Sensors 2023, 23, 5334. [Google Scholar] [CrossRef] [PubMed]
- Qin, Y.; Liu, H.; Mao, Y. Faulty rolling bearing digital twin model and its application in fault diagnosis with imbalanced samples. Adv. Eng. Inform. 2024, 61, 102513. [Google Scholar] [CrossRef]
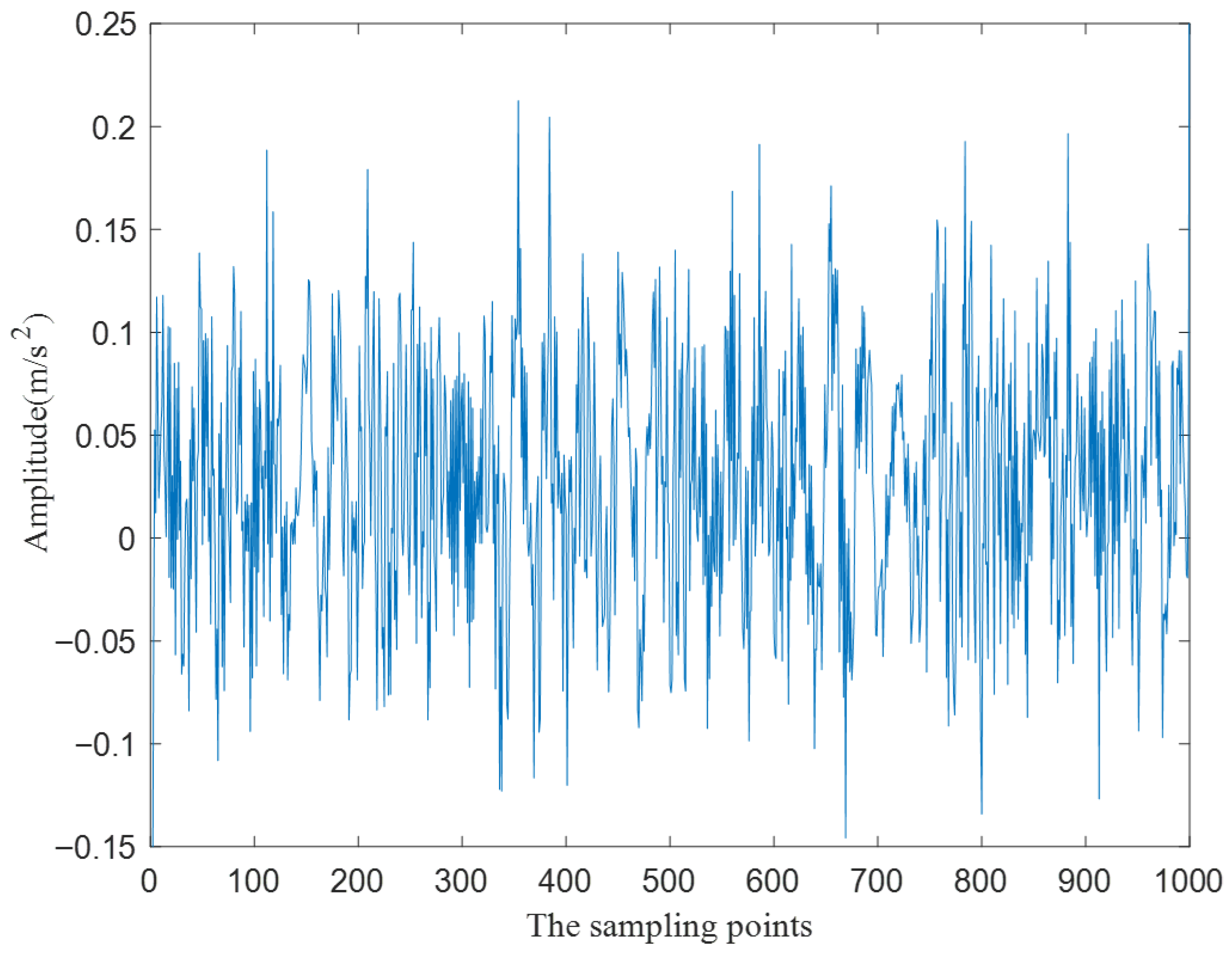
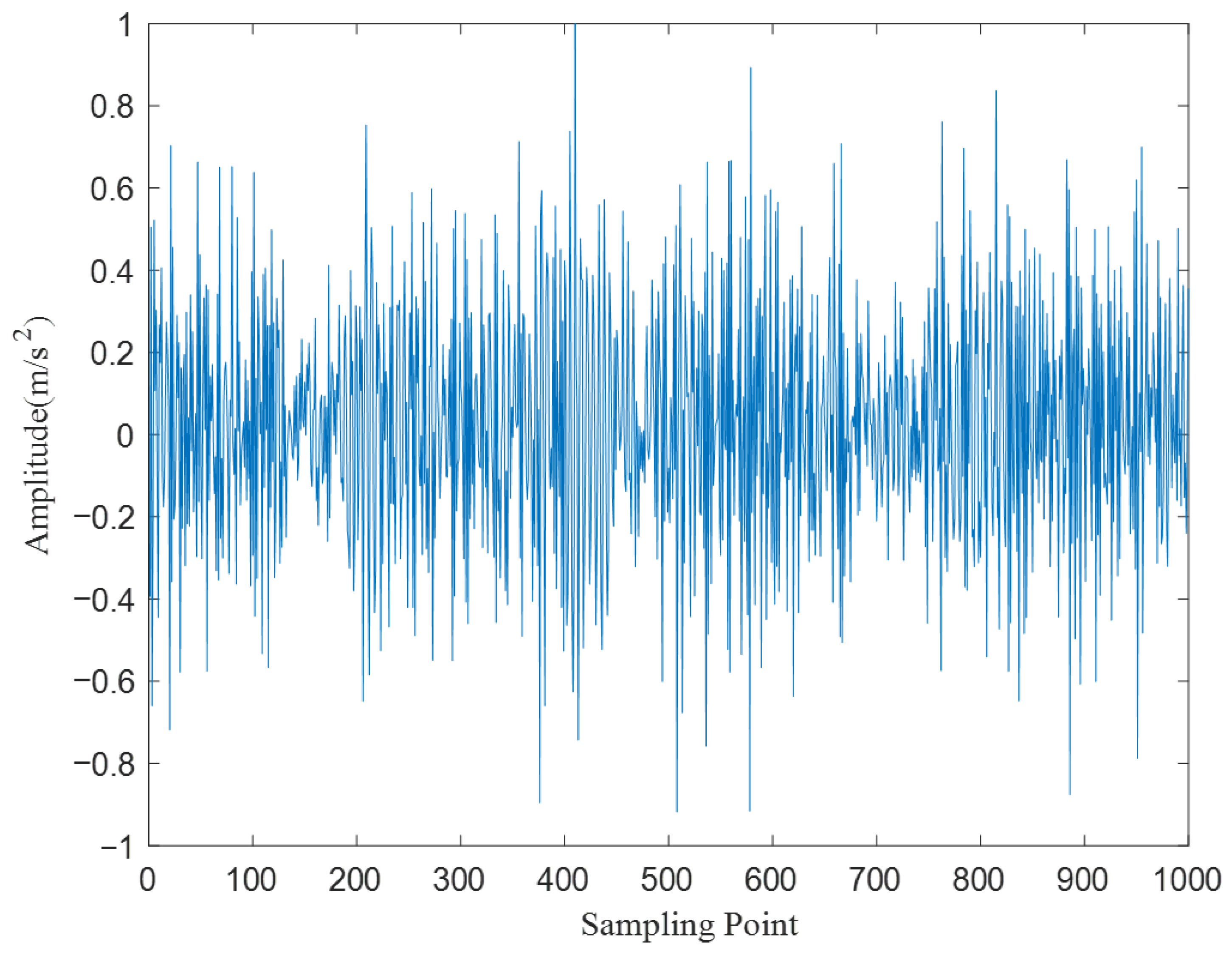
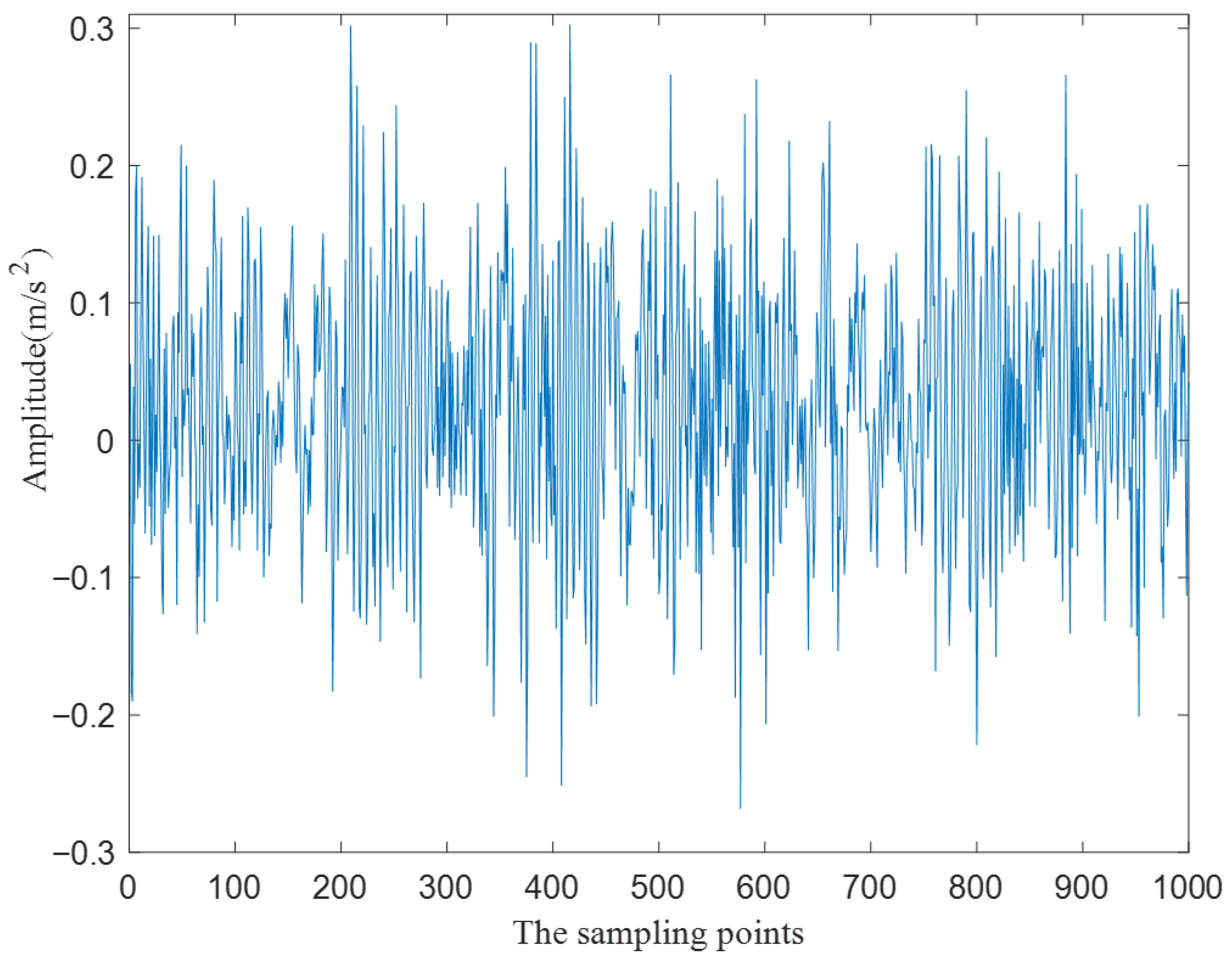
| Fault Type | Speed (rpm/min) | |||
|---|---|---|---|---|
| Normal REB | 400 | 500 | 600 | 700 |
| Inner Ring Fault of REB | 400 | 500 | 600 | 700 |
| Outer Ring Fault of REB | 400 | 500 | 600 | 700 |
| Rolling Element Fault of REB | 400 | 500 | 600 | 700 |
| Data | Peak Value | RMS Value | Skewness | Frequency Domain Feature |
|---|---|---|---|---|
| Actual Data | 6 g | 10.3 g | 542 | 120 Hz |
| DT Data | 6.3 g | 10.4 g | 562 | 122 Hz |
| Error | 5% | 0.97% | 7.54% | 1.67% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Q.; Li, M. Fault Prediction Method Towards Rolling Element Bearing Based on Digital Twin and Deep Transfer Learning. Appl. Sci. 2025, 15, 12509. https://doi.org/10.3390/app152312509
Lu Q, Li M. Fault Prediction Method Towards Rolling Element Bearing Based on Digital Twin and Deep Transfer Learning. Applied Sciences. 2025; 15(23):12509. https://doi.org/10.3390/app152312509
Chicago/Turabian StyleLu, Quanbo, and Mei Li. 2025. "Fault Prediction Method Towards Rolling Element Bearing Based on Digital Twin and Deep Transfer Learning" Applied Sciences 15, no. 23: 12509. https://doi.org/10.3390/app152312509
APA StyleLu, Q., & Li, M. (2025). Fault Prediction Method Towards Rolling Element Bearing Based on Digital Twin and Deep Transfer Learning. Applied Sciences, 15(23), 12509. https://doi.org/10.3390/app152312509







