Recalibrated Relationship of P-Wave Velocity in a Coal Seam with Depth in the South-Western Upper Silesian Coal Basin
Abstract
1. Introduction
2. Theoretical Background
- The rock mass is homogeneous and isotropic, and a circular excavation with a radius r has been made within it. The surrounding rock mass is initially under hydrostatic stress p0, and the radial support pressure exerted by the lining is constant and equal to pi.
- The problem is axially symmetric along the axis of the excavation; therefore, σθ and σr denote the tangential and radial stresses, respectively. The principal stresses σ1 and σ3 correspond to the maximum and minimum principal stresses, assuming that the stresses along the excavation axis take intermediate values. Plane strain conditions are considered, independent of the stress state along the axis of the excavation.
- It is assumed that the equilibrium equation of the Lamé problem is satisfied, which, in cylindrical coordinates, takes the following form:
- The rock mass initially behaves as a linearly elastic material, and its strength is described by the Mohr–Coulomb failure criterion expressed as:
- In the plastic zone, at the boundary with the residual plastic zone, the behavior of the rock mass is described by the Mohr–Coulomb failure criterion in the form:
- Outside the plastic zone, the rock mass behaves elastically, and Hooke’s law applies in this zone:
- υ—Poisson ratio,
- —radial and tangential strains, respectively.
3. Geological Setting
4. Methods and Data
4.1. Preparation of the Dataset
4.2. Modeling of the Velocity–Depth Relationship
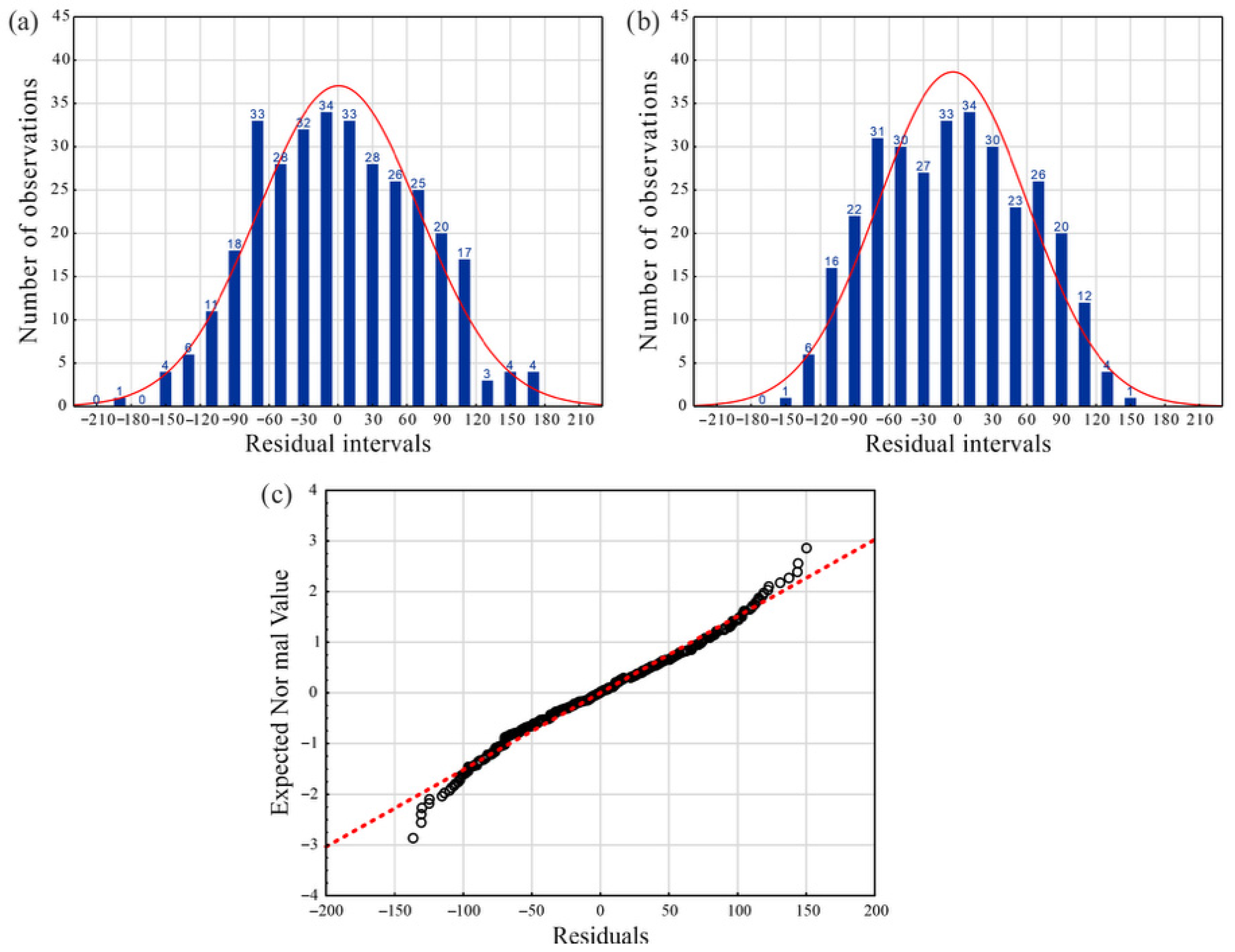
4.3. Verification of Statistical Models
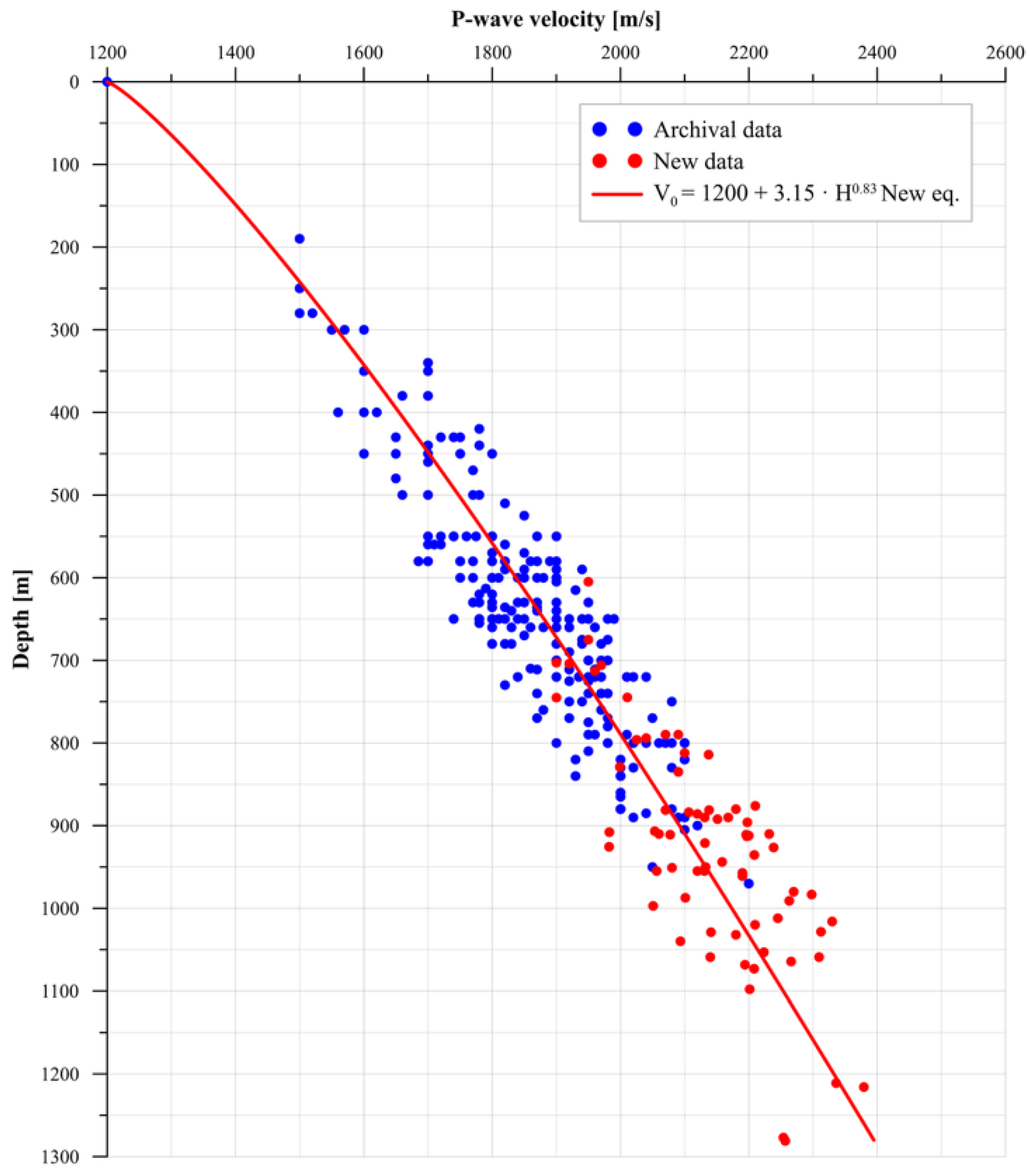
5. Results and Discussion
6. Conclusions
- Compared to the archival Dubiński relationship, the updated model predicts velocities at depths reaching 1281 m, thereby improving the accuracy of seismic anomaly calculations used for assessing relative stress changes. In terms of assumptions, the new model more accurately reflects the character of the velocity–depth relationship.
- Regression analysis confirmed that the power-law model best described the velocity–depth relationship, yielding R2 = 0.86 and RMSE = 65.3 m/s. The heterogeneity factor calculated for the analyzed depth intervals ranged from 2.72% to 3.64%, with an average value of 3.27%. This indicates low variability between the measured and modeled P-wave velocities throughout the studied coal seam dataset. Outlier detection and residual analysis were systematically applied to enhance the model’s robustness.
- The new regional relationship is consistent with earlier local models for Zofiówka and Jastrzębie mines but provides greater robustness due to its broader empirical basis.
- The calculation procedure can be utilized to develop velocity models for various geological and mining conditions in underground mines at continuously increasing depths. The results highlight the need for further data acquisition from depths exceeding 1300 m and from additional geological settings of the Upper Silesian Coal Basin to refine and validate the empirical model.
- The practical contribution results from the updated relationship, which enables more reliable identification of anomalous stress zones and supports the optimization of rockburst prevention strategies during deep mining.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dubiński, J. Seismic Method of Anticipating Assessment of Rockburst Hazard in Hard Coal Mines; Research Works of Central Mining Institute: Katowice, Poland, 1989. (In Polish) [Google Scholar]
- Jiráňková, E.; Petroš, V.; Šancer, J. The Assessment of Stress in an Exploited Rock Mass Based on the Disturbance of the Rigid Overlying Strata. Int. J. Rock Mech. Min. Sci. 2012, 50, 77–82. [Google Scholar] [CrossRef]
- Burtan, Z.; Chlebowski, D. The Effect of Mining Remnants on Elastic Strain Energy Arising in the Tremor-Inducing Layer. Energies 2022, 15, 6031. [Google Scholar] [CrossRef]
- Brown, E.T.; Hoek, E. Underground Excavations in Rock; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Brady, B.H.G.; Brown, E.T. Rock Mechanics for Underground Mining; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Qi, Q.; Pan, Y.; Shu, L.; Li, H.; Jiang, D.; Zhao, S.; Zou, Y.; Pan, J.; Wang, K.; Li, H. Theory and Technical Framework of Prevention and Control with Different Sources in Multi-Scales for Coal and Rock Dynamic Disasters in Deep Mining of Coal Mines. J. China Coal Soc. 2018, 43, 1801–1810. [Google Scholar] [CrossRef]
- Konicek, P.; Waclawik, P. Stress Changes and Seismicity Monitoring of Hard Coal Longwall Mining in High Rockburst Risk Areas. Tunn. Undergr. Space Technol. 2018, 81, 237–251. [Google Scholar] [CrossRef]
- Pilecki, Z. Dynamic Analysis of Mining Tremor Impact on Excavation in Coal Mine. In FLAC and Numerical Modeling in Geomechanics; CRC Press: Boca Raton, FL, USA, 1999; pp. 397–400. [Google Scholar]
- Zhang, C.; Ye, J.; Liu, N.; Xie, Q.; Hu, M.; Li, L. True triaxial modeling test of high-sidewall underground caverns subjected to dynamic disturbances. J. Rock Mech. Geotech. Eng. 2025, 17, 2109–2132. [Google Scholar] [CrossRef]
- Assefa, E.; Tilahun, K.; Assefa, S.M.; Jilo, N.Z.; Pantelidis, L.; Sachpazis, C. Stability evaluation of tunnels in steeply dipping layered rock mass using numerical models: A case study. Sci. Rep. 2025, 15, 2046. [Google Scholar] [CrossRef]
- Zou, Q.; Chen, Z.; Zhan, J.; Chen, C.; Gao, S.; Kong, F.; Xia, X. Morphological evolution and flow conduction characteristics of fracture channels in fractured sandstone under cyclic loading and unloading. Int. J. Min. Sci. Technol. 2023, 33, 1527–1540. [Google Scholar] [CrossRef]
- Chlebowski, D.; Burtan, Z. Mining-Induced Seismicity during Development Works in Coalbeds in the Context of Forecasts of Geomechanical Conditions. Energies 2021, 14, 6675. [Google Scholar] [CrossRef]
- Chlebowski, D.; Burtan, Z. Geomechanical Analysis of the Main Roof Deformation in Room-and-Pillar Ore Mining Systems in Relation to Real Induced Seismicity. Appl. Sci. 2024, 14, 5710. [Google Scholar] [CrossRef]
- Szreder, Z.; Pilecki, Z.; Klosinski, J. Effectiveness of recognition of exploitation edge influence with the help of profiling of attenuation and velocity of seismic wave. Gospod. Surowcami Miner.–Miner. Resour. Manag. 2008, 24, 215–226. [Google Scholar]
- Szreder, Z.; Barnaś, M. Assessment of the Impact of an Overlying Coal Seam Edge Using Seismic Profiling of Refracted P-Wave Velocity. E3S Web Conf. 2017, 24, 01007. [Google Scholar] [CrossRef]
- Tajduś, A.; Cała, M.; Tajduś, K. The Influence of a Normal Fault on the Initial State of Stress in a Rock Mass. Stud. Geotech. Mech. 2016, 38, 109–121. [Google Scholar] [CrossRef]
- Pilecka, E.; Stec, K.; Chodacki, J.; Pilecki, Z.; Szermer-Zaucha, R.; Krawiec, K. The Impact of a High-Energy Mining-Induced Tremor in a Fault Zone on Damage to Buildings. Energies 2021, 14, 4112. [Google Scholar] [CrossRef]
- Dubiński, J.; Konopko, W. Rock Bursts—Assessment, Prognosis, Defeating; Central Mining Institute (GIG): Katowice, Poland, 2000. (In Polish) [Google Scholar]
- Chlebowski, D.; Burtan, Z. Geophysical and Analytical Determination of Overstressed Zones in an Exploited Coal Seam: A Case Study. Acta Geophys. 2021, 69, 701–710. [Google Scholar] [CrossRef]
- Łapczyński, M.; Pilecki, Z.; Krawiec, K.; Słomian, A.; Pilecka, E.; Łątka, T. Modelling of P-Wave Velocity Changes in Coal Seams with Increased Depth: A Case Study. Sci. Rep. 2025, 15, 3413. [Google Scholar] [CrossRef] [PubMed]
- Evison, F.F. A Coal Seam as a Guide for Seismic Energy. Nature 1955, 176, 1224–1225. [Google Scholar] [CrossRef]
- Krey, T. Channel Waves as a Tool of Applied Geophysics in Coal Mining. Geophysics 1963, 28, 701–714. [Google Scholar] [CrossRef]
- Krey, T. In-seam Seismic Exploration Techniques. Coal Explor. 1976, 1, 227–255. [Google Scholar]
- Körmendi, A.T.; Bodoky, T.; Hermann, L.; Dianiska, L.; Kálmán, T. Seismic Measurements for Safety in Mines. Geophys. Prospect. 1986, 34, 1022–1037. [Google Scholar] [CrossRef]
- Hatherly, P. Coal Seam Mapping by Underground In-Seam Seismic Surveys. Geoexploration 1987, 24, 285–294. [Google Scholar] [CrossRef]
- Dresen, L.; Rüter, H. Seismic Coal Exploration. Part B: In-Seam Seismics; Graham & Trotman: London, UK, 1994. [Google Scholar]
- Hosseini, N.; Oraee, K.; Shahriar, K.; Goshtasbi, K. Passive Seismic Velocity Tomography on a Longwall Mining Panel Based on the Simultaneous Iterative Reconstructive Technique (SIRT). J. Cent. South Univ. 2012, 19, 2297–2306. [Google Scholar] [CrossRef]
- Schott, W.; Waclawik, P. On the Quantitative Determination of Coal Seam Thickness by Means of In-Seam Seismic Surveys. Can. Geotech. J. 2015, 52, 1496–1504. [Google Scholar] [CrossRef]
- Teng, J.; Li, S.; Jia, M.; Lian, J.; Liu, H.; Li, G.; Wang, W.; Volker, S.; Feng, L.; Yao, X.; et al. Research and Application of In-Seam Seismic Survey Technology for Disaster-Causing Potential Geology Anomalous Body in Coal Seam. Acta Geol. Sin. (Engl. Ed.) 2020, 94, 10–26. [Google Scholar] [CrossRef]
- Kokowski, J.; Szreder, Z.; Pilecka, E. Reference P-wave Velocity in Coal Seams at Great Depths in the Jastrzębie Coal Mine. E3S Web Conf. 2019, 133, 01011. [Google Scholar] [CrossRef]
- Ladanyi, B. Use of the Long-Term Strength Concept in the Determination of Ground Pressure on Tunnel Linings. In Proceedings of the 3rd Congress of the International Society for Rock Mechanics, Denver, CO, USA, 1–7 September 1974; Volume II, Part B. pp. 1150–1156. [Google Scholar]
- Nieć, M.; Sermet, E.; Salamon, E. Variation of Coal Quantity Accumulated in the Mississippian to Pennsylvanian Coal Seams (Upper Silesia and Lublin Coal Basins, Poland): A Reflection of Changes in Climate and CO2 Availability. Geol. Q. 2023, 67, 8. [Google Scholar] [CrossRef]
- Sermet, E.; Nieć, M.; Chećko, J.; Górecki, J. Hard Coal Resource Base in Poland for Underground Gasification; Central Mining Institute: Katowice, Poland, 2018. (In Polish) [Google Scholar]
- Mehdipour, V.; Rabbani, A.R.; Kadkhodaie, A. A practical approach to derive heterogeneity index using an integrated petrophysical data analysis. Sci. Rep. 2025, 15, 7526. [Google Scholar] [CrossRef] [PubMed]
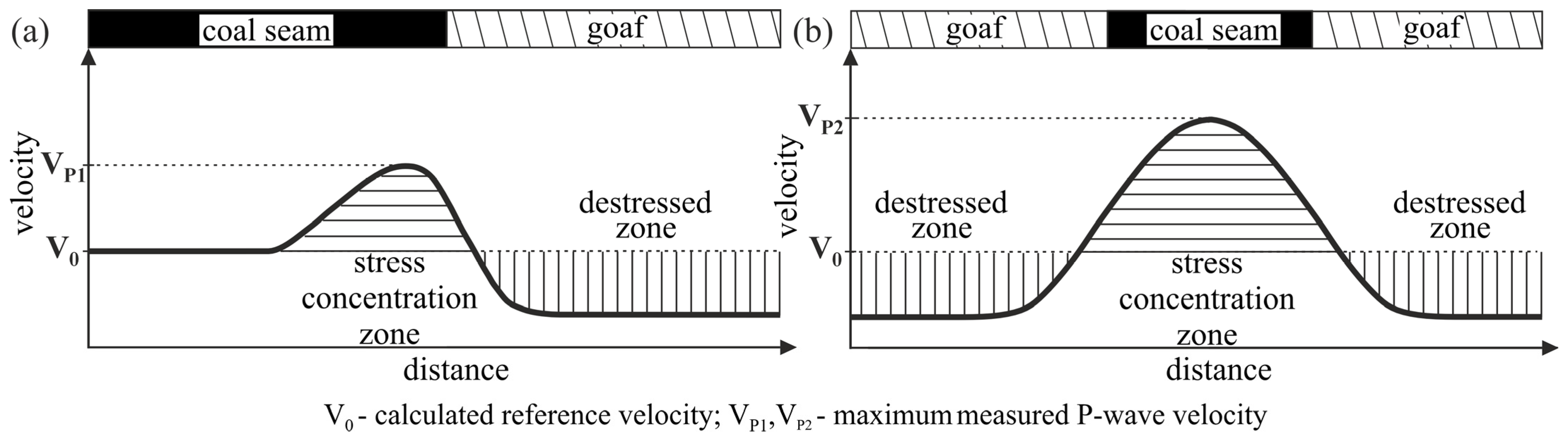
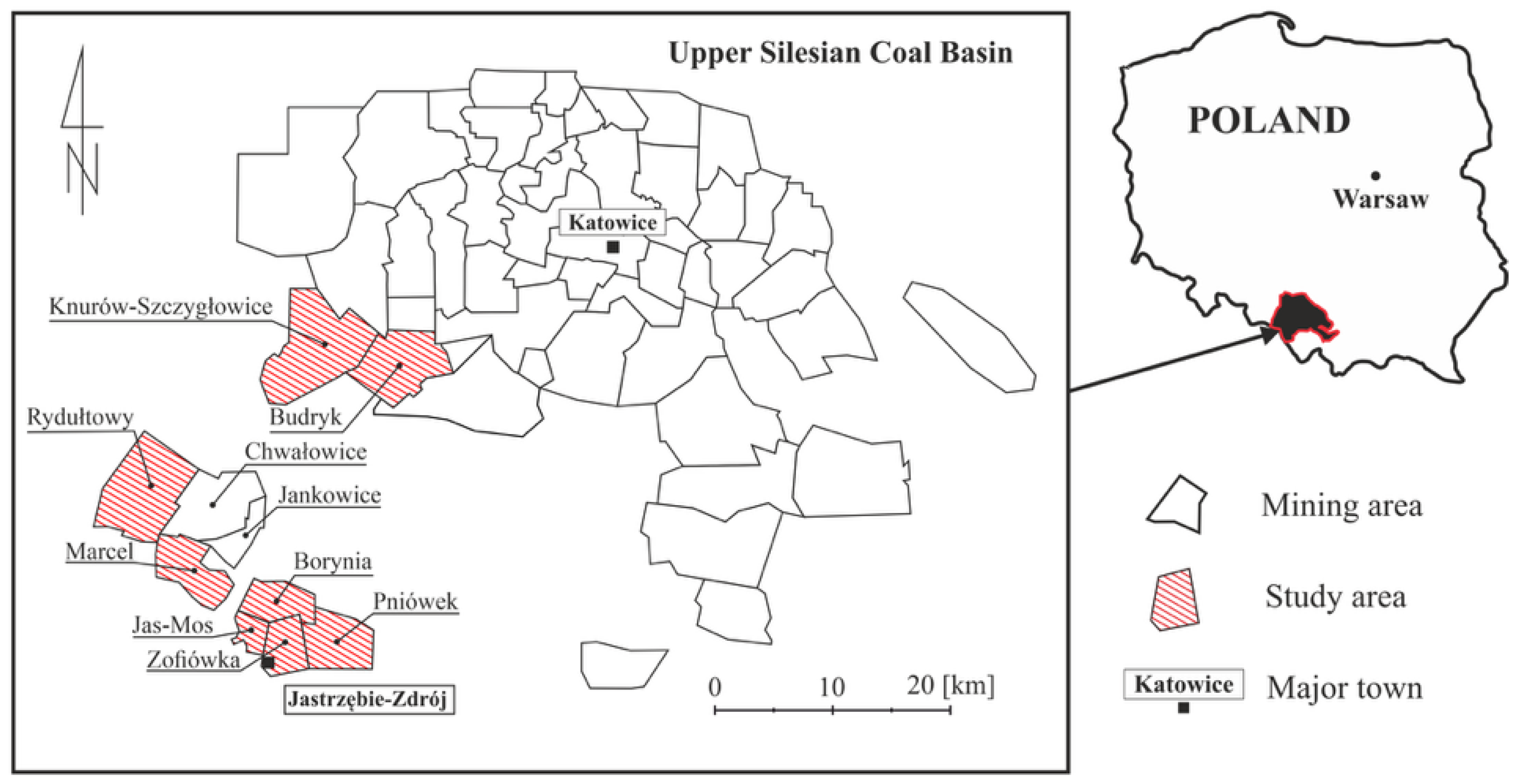


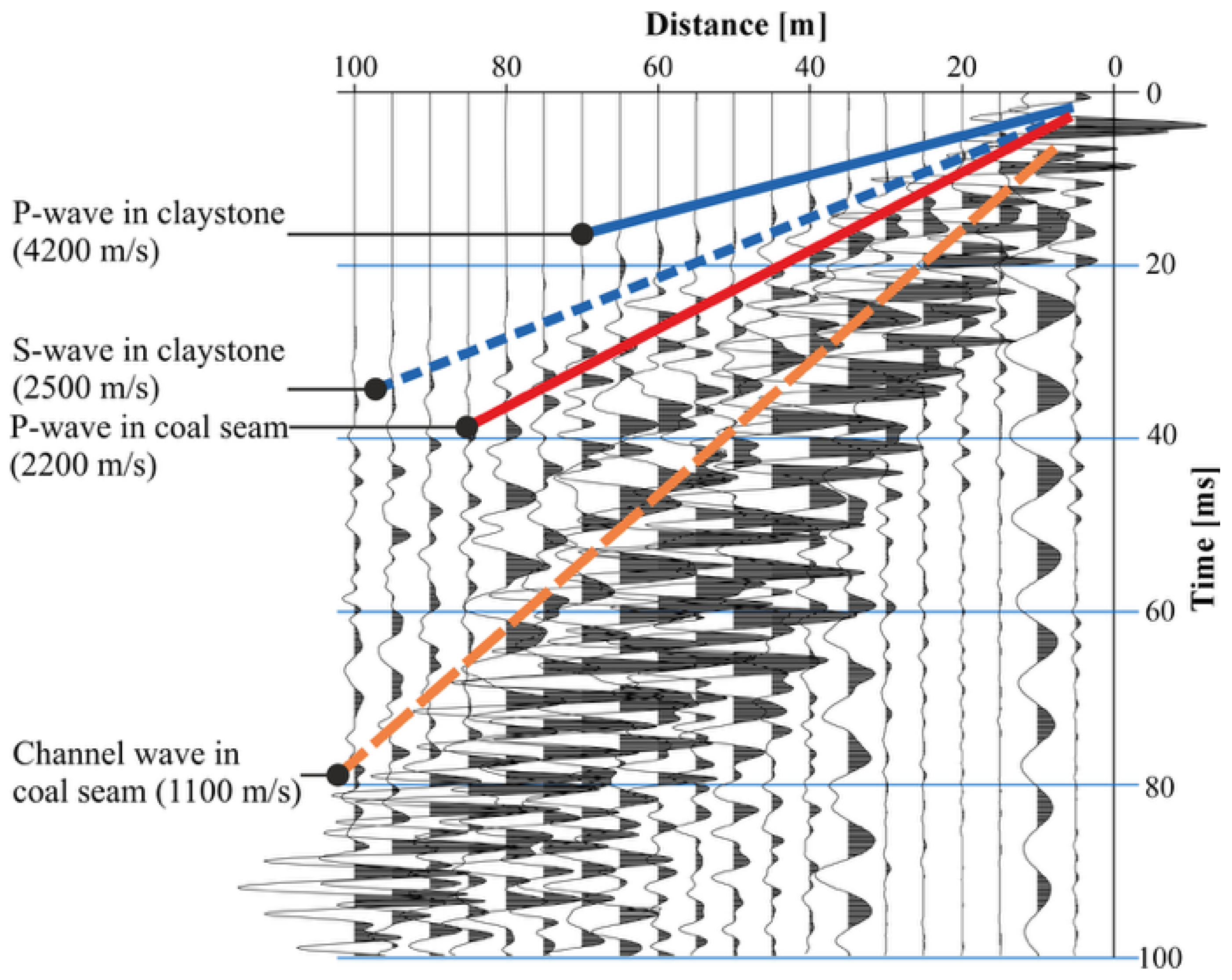
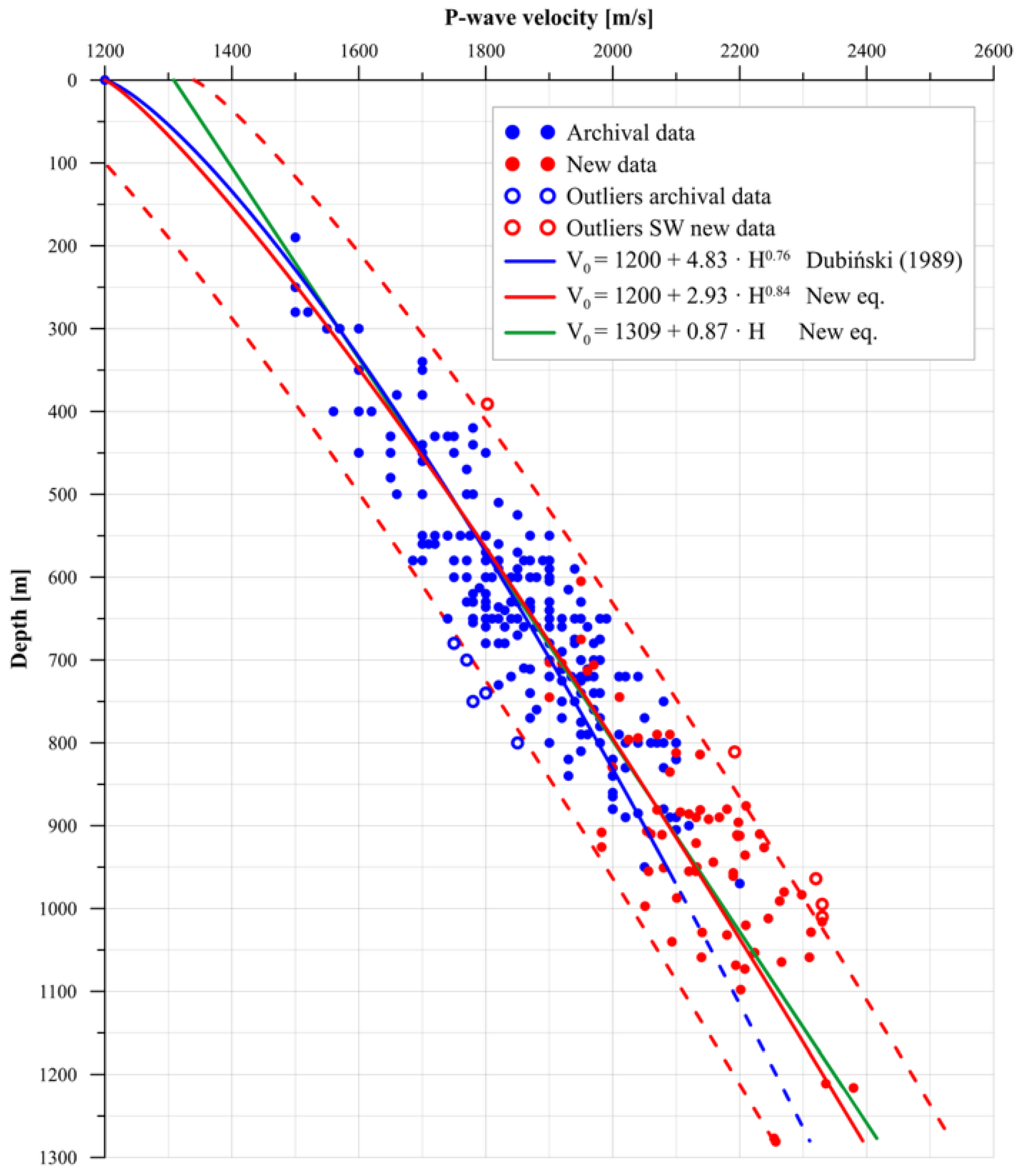


| Degree of Relative Stress Change | Scale of Relative Stress Increase | Positive Seismic Anomaly [%] | Increase in Relative Stress [%] | Negative Seismic Anomaly [%] | Decrease in Relative Stress [%] |
|---|---|---|---|---|---|
| 0 | very low | below 5 | below 20 | above −7.5 | below 25 |
| 1 | low | 5 to15 | 20 to 60 | −7.5 to −15 | 25 to 55 |
| 2 | medium | 15 to 25 | 60 to 140 | −15 to −25 | 55 to 80 |
| 3 | high | above 25 | above 140 | below −25 | above 80 |
| Stratigraphy | Lithological Series | Local Stratigraphy | Maximum Thickness of Coal-Bearing Formations [m] | Total Number of Coal Seams and Partings | Maximum Total Coal Thickness [m] | Coal Seam Numbers | |
|---|---|---|---|---|---|---|---|
| Pennsylvanian | Krakow Sandstone | Libiąż | 560 | 38 | 48 | 111–119 | |
| Łaziska | 1080 | 201–216 | |||||
| Mudstone | Orzesze * | Orzesze | 2000 | 158 | 112 | 301–327 | |
| Załęże | 328–364 | ||||||
| Ruda * | 401–406 | ||||||
| Upper Silesian Sandstone | Ruda | 810 | 61 | 80 | 407–420 | ||
| Zabrze (Saddle, Anticlinal) | 140 | 501–510 | |||||
| Mississippian | Paralic | Poruba | 1100 | 263 | 99 | 601–630 | |
| Jaklovec | 350 | 701–723 | |||||
| Hrušov | 1300 | 801–848 | |||||
| Petřkovice | 760 | 901–920 | |||||
| No. | Coal Mine | Depth [m] | Measured Velocity of the P-wave [m/s] | No. | Coal Mine | Depth [m] | Measured Velocity of the P-wave [m/s] |
|---|---|---|---|---|---|---|---|
| 1 | Zofiówka | 704 | 1920 | 38 | Jastrzębie | 745 | 1900 |
| 2 | Zofiówka | 745 | 2011 | 39 | Jastrzębie | 886 | 2120 |
| 3 | Zofiówka | 884 | 2106 | 40 | Jastrzębie | 812 | 2100 |
| 4 | Zofiówka | 890 | 2168 | 41 | Jastrzębie | 957 | 2190 |
| 5 | Zofiówka | 907 | 2054 | 42 | Jastrzębie | 713 | 1960 |
| 6 | Zofiówka | 911 | 2196 | 43 | Jastrzębie | 706 | 1970 |
| 7 | Zofiówka | 926 | 1982 | 44 | Jastrzębie | 675 | 1950 |
| 8 | Zofiówka | 927 | 2239 | 45 | Jastrzębie | 955 | 2131 |
| 9 | Zofiówka | 936 | 2209 | 46 | Jastrzębie | 955 | 2120 |
| 10 | Zofiówka | 944 | 2159 | 47 | Jastrzębie | 881 | 2070 |
| 11 | Zofiówka | 950 | 2133 | 48 | Jastrzębie | 794 | 2040 |
| 12 | Zofiówka | 951 | 2080 | 49 | Jastrzębie | 835 | 2090 |
| 13 | Zofiówka | 983 | 2298 | 50 | Jastrzębie | 880 | 2180 |
| 14 | Zofiówka | 987 | 2101 | 51 | Jastrzębie | 876 | 2210 |
| 15 | Zofiówka | 1016 | 2330 | 52 | Jastrzębie | 912 | 2200 |
| 16 | Zofiówka | 1029 | 2313 | 53 | Jastrzębie | 980 | 2270 |
| 17 | Zofiówka | 1029 | 2141 | 54 | Jastrzębie | 829 | 1999 |
| 18 | Zofiówka | 1032 | 2180 | 55 | Jastrzębie | 995 | 2330 |
| 19 | Zofiówka | 1053 | 2223 | 56 | Jastrzębie | 1010 | 2330 |
| 20 | Zofiówka | 1059 | 2140 | 57 | Rydułtowy | 1216 | 2379 |
| 21 | Zofiówka | 1059 | 2310 | 58 | Rydułtowy | 1211 | 2336 |
| 22 | Zofiówka | 1065 | 2266 | 59 | Marcel | 605 | 1950 |
| 23 | Zofiówka | 1068 | 2194 | 60 | Marcel | 1012 | 2245 |
| 24 | Zofiówka | 1073 | 2208 | 61 | Marcel | 1020 | 2210 |
| 25 | Zofiówka | 790 | 2090 | 62 | Marcel | 911 | 2078 |
| 26 | Zofiówka | 790 | 2070 | 63 | Marcel | 991 | 2263 |
| 27 | Pniówek | 814 | 2137 | 64 | Marcel | 921 | 2131 |
| 28 | Pniówek | 811 | 2191 | 65 | Marcel | 896 | 2198 |
| 29 | Borynia | 913 | 2197 | 66 | Marcel | 391 | 1752 |
| 30 | Borynia | 955 | 2056 | 67 | Knurów-Szczygłowice | 997 | 2051 |
| 31 | Borynia | 910 | 2232 | 68 | Knurów-Szczygłowice | 908 | 1983 |
| 32 | Borynia | 796 | 2025 | 69 | Knurów-Szczygłowice | 910 | 2060 |
| 33 | Borynia | 890 | 2131 | 70 | Budryk | 1281 | 2257 |
| 34 | Borynia | 881 | 2138 | 71 | Budryk | 1277 | 2254 |
| 35 | Borynia | 892 | 2151 | 72 | Budryk | 1098 | 2201 |
| 36 | Jastrzębie | 964 | 2320 | 73 | Budryk | 1040 | 2093 |
| 37 | Jastrzębie | 703 | 1900 | 74 | Budryk | 961 | 2190 |
| Parameter | New Data | Archival Data |
|---|---|---|
| Number of measured velocity values | 74 | 252 |
| Min. measurement depth [m] | 391 | 190 |
| Max. measurement depth [m] | 1281 | 970 |
| Min. P-wave velocity [m/s] | 1802 | 1500 |
| Max. P-wave velocity [m/s] | 2379 | 2200 |
| Average P-wave velocity [m/s] | 2141 | 1859 |
| Name of Model | Reference Velocity V0 Relationship | Coefficient of Determination R2 | Standard Deviation σ |
|---|---|---|---|
| Dubiński (1989) [1] | 0.77 | 64 | |
| Jastrzębie Coal Mine | 0.82 | 63 | |
| Zofiówka Coal Mine | 0.85 | 61 | |
| South-western USBC | 0.86 | 70 |
| Estimated Parameter | Value of Estimated Parameter | Standard Error | Lower Confidence Limit | Upper Confidence Limit |
|---|---|---|---|---|
| a b | 3.15 0.83 | 0.44 0.02 | 2.29 0.79 | 4.01 0.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łapczyński, M.; Pilecki, Z.; Burtan, Z.; Pilecka, E.; Kozioł, P.; Łątka, T. Recalibrated Relationship of P-Wave Velocity in a Coal Seam with Depth in the South-Western Upper Silesian Coal Basin. Appl. Sci. 2025, 15, 12505. https://doi.org/10.3390/app152312505
Łapczyński M, Pilecki Z, Burtan Z, Pilecka E, Kozioł P, Łątka T. Recalibrated Relationship of P-Wave Velocity in a Coal Seam with Depth in the South-Western Upper Silesian Coal Basin. Applied Sciences. 2025; 15(23):12505. https://doi.org/10.3390/app152312505
Chicago/Turabian StyleŁapczyński, Maciej, Zenon Pilecki, Zbigniew Burtan, Elżbieta Pilecka, Piotr Kozioł, and Tomasz Łątka. 2025. "Recalibrated Relationship of P-Wave Velocity in a Coal Seam with Depth in the South-Western Upper Silesian Coal Basin" Applied Sciences 15, no. 23: 12505. https://doi.org/10.3390/app152312505
APA StyleŁapczyński, M., Pilecki, Z., Burtan, Z., Pilecka, E., Kozioł, P., & Łątka, T. (2025). Recalibrated Relationship of P-Wave Velocity in a Coal Seam with Depth in the South-Western Upper Silesian Coal Basin. Applied Sciences, 15(23), 12505. https://doi.org/10.3390/app152312505






